当移动机械臂在室内环境中执行抓取任务时,主要挑战之一是如何高效地避开障碍并且成功抓取目标物。在室内环境较为复杂、障碍物较多的情况下,移动机械臂的抓取规划成功率会受到障碍物的影响,并且抓取规划成功率低也会导致RRT的规划时间增加。因此,移动机械臂首先要预处理环境信息,然后生成并到达优化后的停靠位置,再进行抓取。
随着机器人技术的不断发展,固定位置操作的机械臂不能满足多方面需求,而且机械臂需要安全高效地在动态环境中工作。移动机械臂所面临的环境更加复杂,若移动机械臂搜寻路径效率不高,则会严重影响其工作质量。因此如何快速地规划出一条有效的安全路径极具研究意义与实际应用价值[1-3]。在较狭窄或较拥挤场所中,移动机械臂需要根据环境中的信息快速获取目标的位置,然后结合机械臂抓取空间的评价标准,得到优化后的底盘停靠位置,最后结合RRT算法避开障碍物,完成目标点抓取任务。
对于移动机械臂避障抓取问题,早期大多数研究都是对移动机械臂进行分散控制,即先控制移动底盘到达目标位置,然后再进行机械臂的运动规划避障抓取。例如,先进行移动底盘导航定位及地图创建[4-5],然后进行机械臂运动规划及轨迹生成[6];现在有部分研究涉及移动底盘与机械臂的全身控制,通过协调控制移动机械臂缩短控制时间,并且能够实现在狭小空间调整位姿抓取[7-8]。其中都未提及到该如何结合环境信息、机械臂位置信息和各约束条件,生成物体抓取的最优停靠位置等相关问题。
对于机械臂抓取过程中的避障问题,文献[9]首次提出应用于机器人路径规划的虚拟力场方法——人工势场法,文献[10-11]提出一种基于A*算法的移动机械臂无碰抓取方法,文献[12]在传统蚁群算法的基础上,引入带方向信息的全局启发因子来提高最优路径的搜索效率,能够在较短时间内规划出满足条件的最优路径。文献[13]提出一种改进的快速扩展随机树算法(Rapidly-exploring Random trees, RRT)。文献[14]提出低振荡人工势场−自适应快速扩展随机树(Adaptive Rapidly-exploring Random Trees, ARRT)混合算法进行路径规划。文献[15]设计基于双向RRT算法的运动规划方法,有效地解决仿人机器人的抓取操作问题。上述算法都未考虑将机械臂连杆与障碍物碰撞条件加入避障。
本文对环境中目标物及障碍物的识别、定位[16-17]采用的是aruco码[18]标记以及在动作捕捉系统下粘贴感应点的方法。在不同的约束条件下,如何找到移动机械臂优化后的停靠位置,提高移动机械臂抓取物体的规划成功率是主要挑战。本文重点研究如何在更短时间内提高移动机械臂在多障碍物环境下的避障抓取规划成功率,主要贡献如下:(1) 分析了机械臂结合夹爪碰撞约束条件且无障碍物的抓取空间;(2) 分析了移动底盘、机械臂末端以及机械臂连杆与障碍物之间碰撞的多约束条件;(3) 提出了移动机器人在有障碍物的环境下优化停靠位置的计算方法,有效地提高了移动机器人进行抓取任务规划的效率。
1 硬件规格图1为研究中使用的移动机械臂,包括加拿大Clearpath公司生产的ridgeback移动底盘、优傲机器人公司生产的UR5协作式机械臂和Robotiq公司生产的三指夹爪。其中ridgeback移动底盘装有4个麦克纳姆轮,为全方位移动小车;UR5为六关节机械臂,末端负载为5 kg;Robotiq夹爪为自适应三指夹爪,可抓取多种不同形状物体。Realsense相机安装在机械臂末端,其还使用了动作捕捉系统,目的是建立环境中各物体的位置信息。电脑通过网络端口连接控制移动机械臂,通过局域网连接动作捕捉系统传输数据。

|
图 1 移动机械臂硬件 Figure 1 Mobile manipulator hardware |
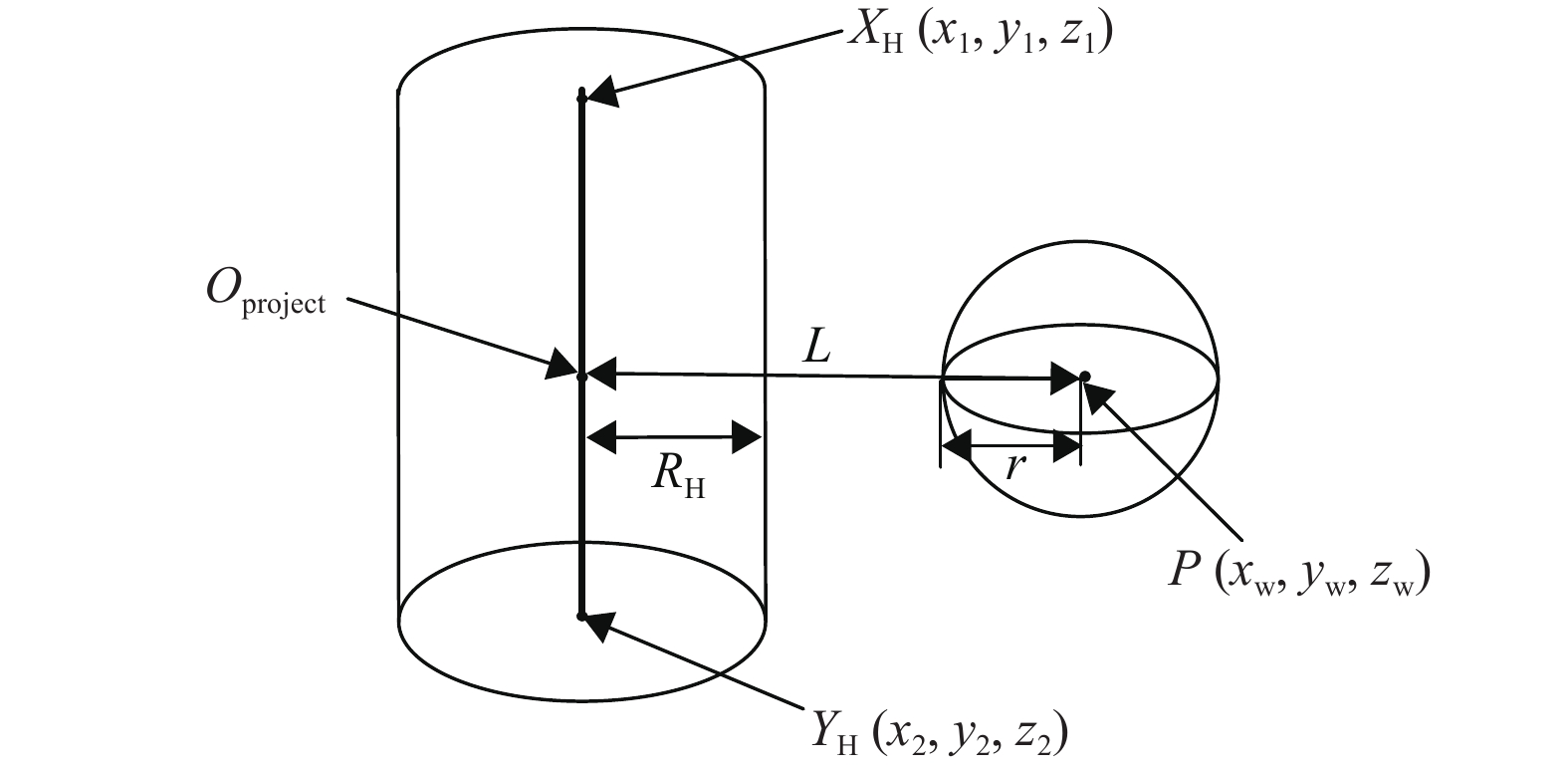
根据任务要求,碰撞约束条件主要包括在对工作空间进行分析时的夹爪与机械臂自身连杆的碰撞和在进行RRT避障规划时的机械臂末端、连杆与障碍物的碰撞。此处将夹爪和障碍物简化为球体,则碰撞约束问题简化为求空间中一点到一条线段的最短距离是否满足条件。
如图2所示,问题描述为
|
图 2 碰撞约束条件分析 Figure 2 Analysis of collision constraints |
| $ {O}_{\text{project}}={X}_{\mathrm{H}}+t \left({Y}_{\mathrm{H}}-{X}_{\mathrm{H}}\right) $ | (1) |
| $ t=\frac{\begin{array}{c}\left({x}_{1}-{x}_{\mathrm{w}}\right)\left({x}_{1}-{x}_{2}\right)+\left({y}_{1}-{y}_{\mathrm{w}}\right)\left({y}_{1}-{y}_{2}\right)+\\ \left({z}_{1}-{z}_{\mathrm{w}}\right)\left({z}_{1}-{z}_{2}\right)\end{array}}{({x}_{1}-{x}_{2}{)}^{2}+({y}_{1}-{y}_{2}{)}^{2}+({z}_{1}-{z}_{2}{)}^{2}}\quad\qquad $ | (2) |
| $ L=\left\{\begin{array}{l}\sqrt{\begin{array}{l}{\left[\left({x}_{1}-{x}_{\mathrm{w}}\right)+t \left({x}_{2}-{x}_{1}\right)\right]}^{2}+\\ {\left[\left({y}_{1}-{y}_{\mathrm{w}}\right)+t \left({y}_{2}-{y}_{1}\right)\right]}^{2}+\\ {\left[\left({z}_{1}-{z}_{\mathrm{w}}\right)+t \left({z}_{2}-{z}_{1}\right)\right]}^{2}\end{array}}\;\;\begin{array}{l}\;\\,\;\;1>t>0\end{array}\\ \sqrt{\begin{array}{l}({x}_{1}-{x}_{\mathrm{w}}{)}^{2}+({y}_{1}-{y}_{\mathrm{w}}{)}^{2}+\\ ({z}_{1}-{z}_{\mathrm{w}}{)}^{2}\end{array}}\;\;\;\;\;\;\;\;\;\;\begin{array}{l}\;\\,\;\;t \leqslant 0\end{array}\\ \sqrt{\begin{array}{l}({x}_{2}-{x}_{\mathrm{w}}{)}^{2}+({y}_{2}-{y}_{\mathrm{w}}{)}^{2}+\\ ({z}_{2}-{z}_{\mathrm{w}}{)}^{2}\end{array}}\;\;\;\;\;\;\;\;\;\;\begin{array}{l}\;\\,\;\;t \geqslant 1\end{array}\end{array}\right. $ | (3) |
根据式(2)计算
| $ L>(r+{R}_{\mathrm{H}}) $ | (4) |
为移动底盘提供停靠策略之前,需要在无障碍物环境下,先对结合夹爪碰撞约束的机械臂进行工作空间的分析。
根据上述碰撞约束的判断和机械臂抓取情况,物体在机械臂基座上方和前方,机械臂工作空间区域为(x:0~900 mm,y:−900~900 mm,z:0~900 mm),依次按比例划分为
| 表 1 2种抓取方式划分规则 Table 1 Division Rules of two grab modes |
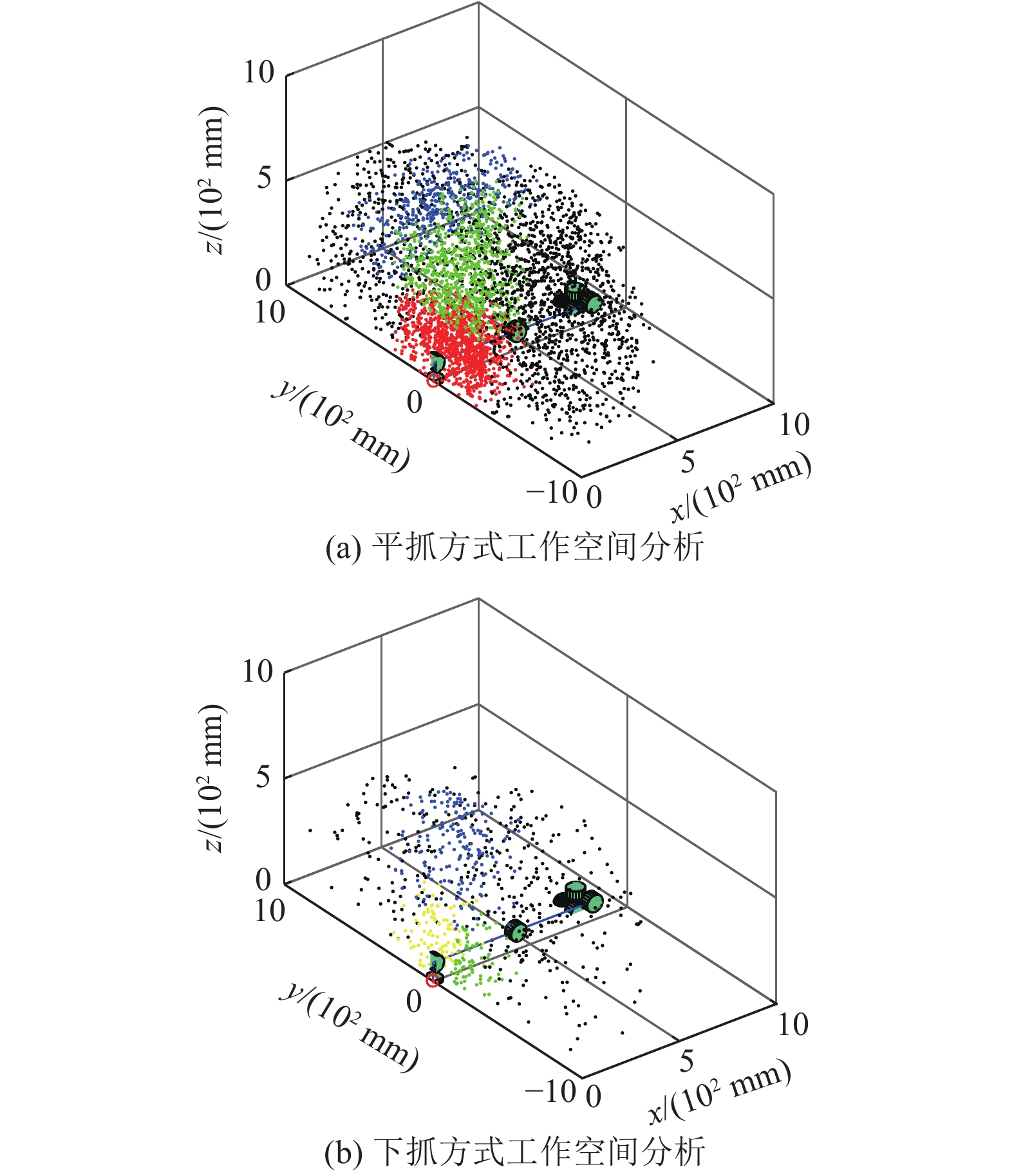
实验得到了平抓、下抓抓取方式满足碰撞约束条件的工作空间网格分布,见图3。
|
图 3 机械臂抓取空间分析 Figure 3 Analysis of grasping space of manipulator |
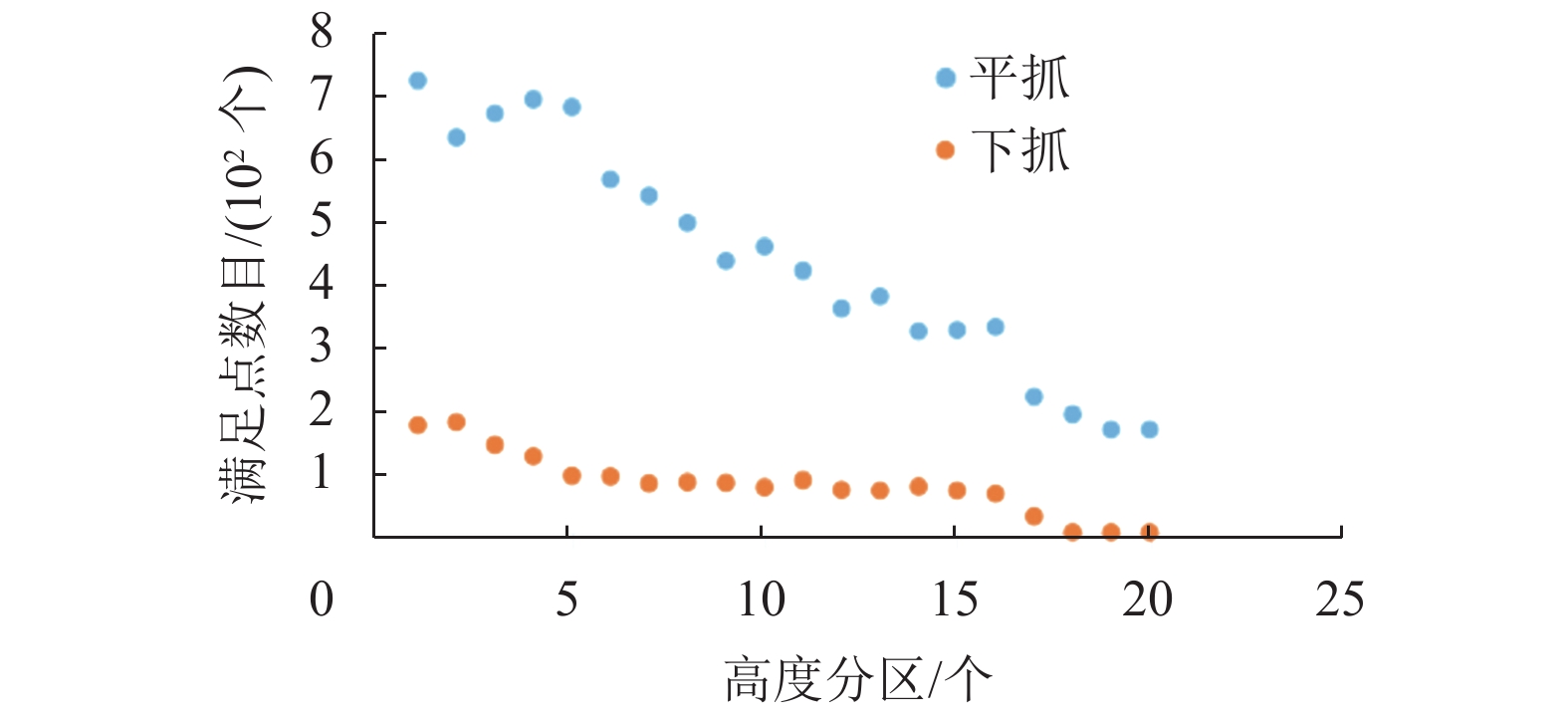
将机械臂工作空间可达到的高度0~1000 mm依次划分为0~20个区域,平抓与下抓抓取方式在机械臂空间高度上满足点数目的对比见图4。
根据图3~4可知在机械臂的工作区域(x:0~300 mm,y:−300~300 mm,z:0~300 mm)中,选取合适抓取姿态会有较高的抓取规划成功率。
|
图 4 平抓与下抓对比 Figure 4 Comparison of flat grip and down grip |
根据上面对机械臂工作空间的分析,可知机械臂的可抓取性会随物体在抓取空间内的位置变化而变化,为综合评价机械臂抓取质量,下文使用上述实验数据来综合评价抓取质量
定义
| $ \begin{aligned} & {Q}_{1}=\left\{\begin{array}{l}1,\;\;\;\; a <b\\ 0, \;\;\;\; a\geqslant b\end{array}\right. \\& {Q}_{2}=\left\{\begin{array}{l}3,\;\;\;\; 0\leqslant \left|d\right|<320\;\mathrm{mm}\\ 2, \;\;\;\;320\leqslant \left|d\right|<640\;\mathrm{mm} \\1, \;\;\;\;640\leqslant \left|d\right|<960\;\mathrm{mm}\\ 0,\;\;\;\; {\text{其他}}\end{array}\right. \\& {Q}_{3}=\left\{\begin{array}{l}3,\;\;\;\; 0\leqslant \left|h\right|<320\;\mathrm{mm}\\ 2{, }\;\;\;\;{320 \leqslant }\left|h\right|<640\;\mathrm{mm}\\ 1, \;\;\;\;640\leqslant \left|h\right|<960\;\mathrm{mm}\\ 0, \;\;\;\;{\text{其他}}\end{array}\right.\\& {Q}_{4}=\left\{\begin{array}{l}3,\;\;\;\; {\text{平抓}}\\ 1,\;\;\;\; {\text{下抓}}\end{array}\right. \end{aligned} $ | (5) |
最终抓取质量评分为
针对移动机械臂工作环境中存在障碍物等情况,结合2.2和2.3节,本文提出了移动底盘停靠位置优化算法,并且加入碰撞约束的RRT算法,使机械臂末端在空间中进行避障抓取。
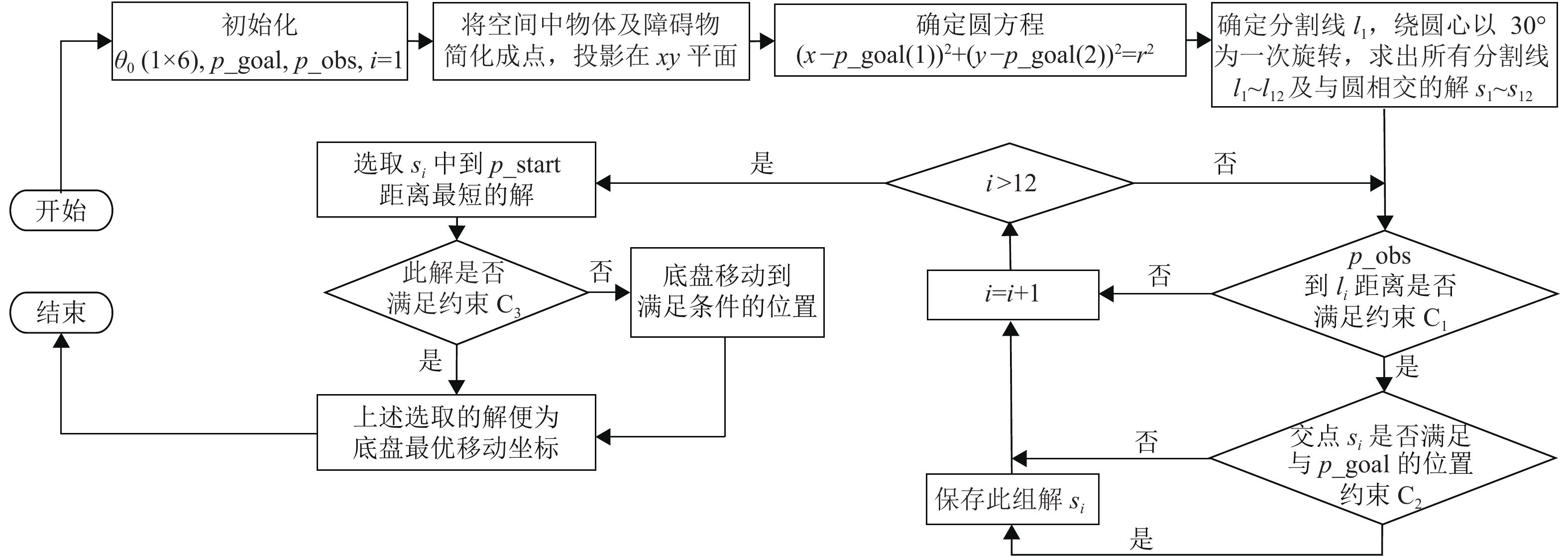
成功抓取目标物体的关键是移动底盘的优化位置搜索,针对在桌面上抓取物体,移动底盘停靠位置优化算法流程图如图5所示。
|
图 5 移动底盘停靠位置优化算法 Figure 5 Parking position optimization algorithm of mobile chassis |
其中机械臂初始六关节角为
为了评估移动底盘停靠位置优化方法的有效性,结合上述对机械臂抓取工作空间的分析,限定物体的高度及抓取方式之后,抓取过程只涉及到物体与移动机械臂底盘的距离,使用提出的算法进行仿真,并在实体机器人上进行实验。该算法在Intel Core i5-8300HQ的PC上运行(2.3 GHz) MATLAB版本2016b实验。对比移动底盘不移动与加入移动底盘停靠位置优化算法在抓取物体上的区别,结果表明加入移动底盘停靠位置优化方法后,计算时间更短,抓取成功率更高。
3.1 仿真未加入移动底盘停靠位置优化算法的移动机械臂保持位置不变,直接运行RRT避障规划算法,生成机械臂末端轨迹点。加入移动底盘停靠位置优化算法,移动机械臂会移动到优化位置,然后机械臂旋转朝向目标物体,再采用RRT避障规划算法规划末端点轨迹。
下文在几组不同条件下验证加入移动底盘停靠位置优化算法的可行性。考虑机械臂平抓方式比下抓方式抓取成功率更高,并且实际环境中物体摆放位置有一定高度,验证中采用平抓方式。其中障碍物及夹爪简化为球体,半径r设置为40 mm;连杆近似为圆柱体,半径RH设置为40 mm,移动机械臂底盘起点均为坐标系中的(0, 0, 0)位置。选取可执行率均值、路径点完全执行次数、总规划路径点数和RRT规划时间均值作为评价指标,可执行率为一组测试中机械臂可执行路径点数目与总规划路径点数目的比值。
3.1.1 空间单障碍物靠近目标物体避障仿真实验此实验中,障碍物位置为(400 mm, 400 mm, 400 mm),目标点位置为(500 mm, 500 mm, 400 mm),机械臂起始六关节角为(30°, −75°, −104°, −29°, 91°, 231°)。加入移动底盘位置控制前后的对比见图6。
图7为20次测试下移动底盘是否移动在可执行率均值及规划时间均值上的对比。表2为移动底盘是否移动的评价指标数据对比。
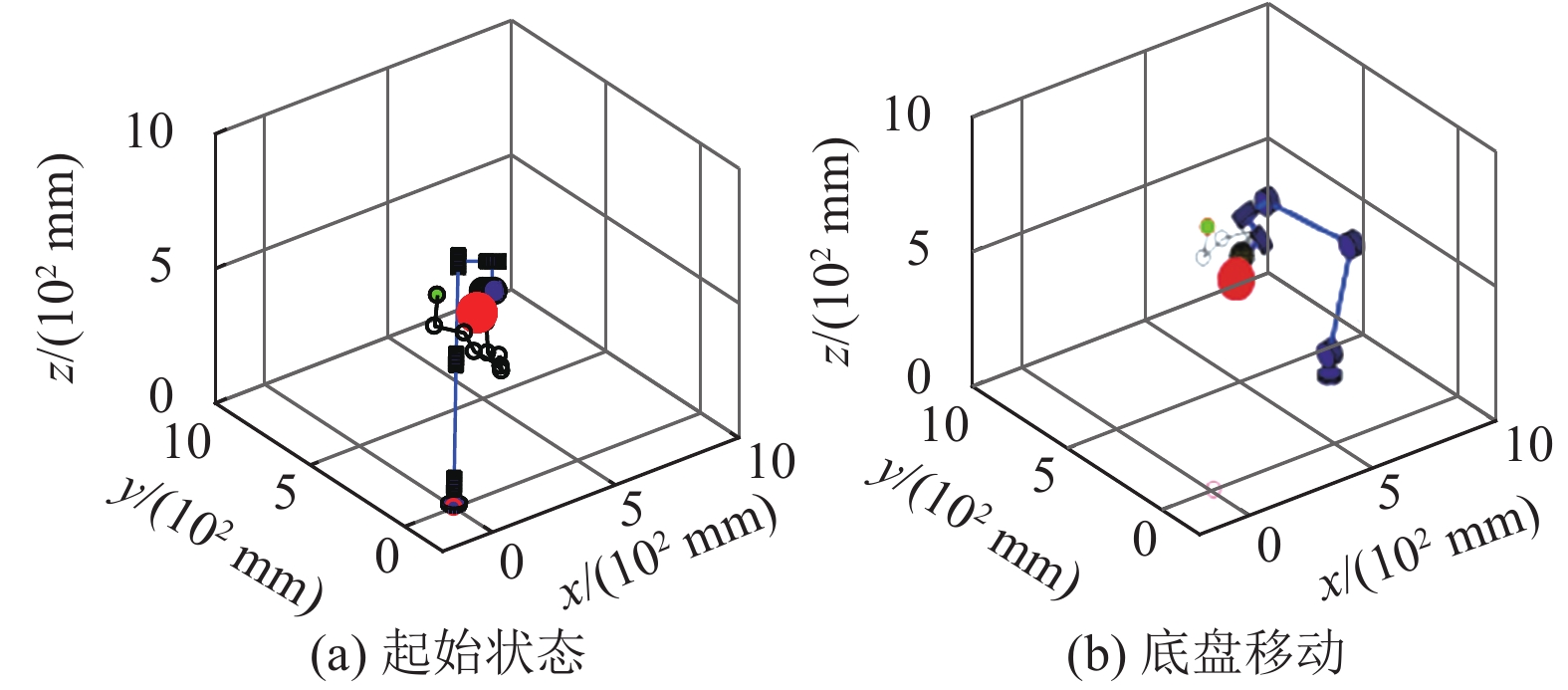
|
图 6 单障碍物靠近目标物体避障实验加入移动底盘位置控制前后对比 Figure 6 Comparison before and after adding mobile chassis position control in obstacle avoidance experiment when single obstacle approaching target object |
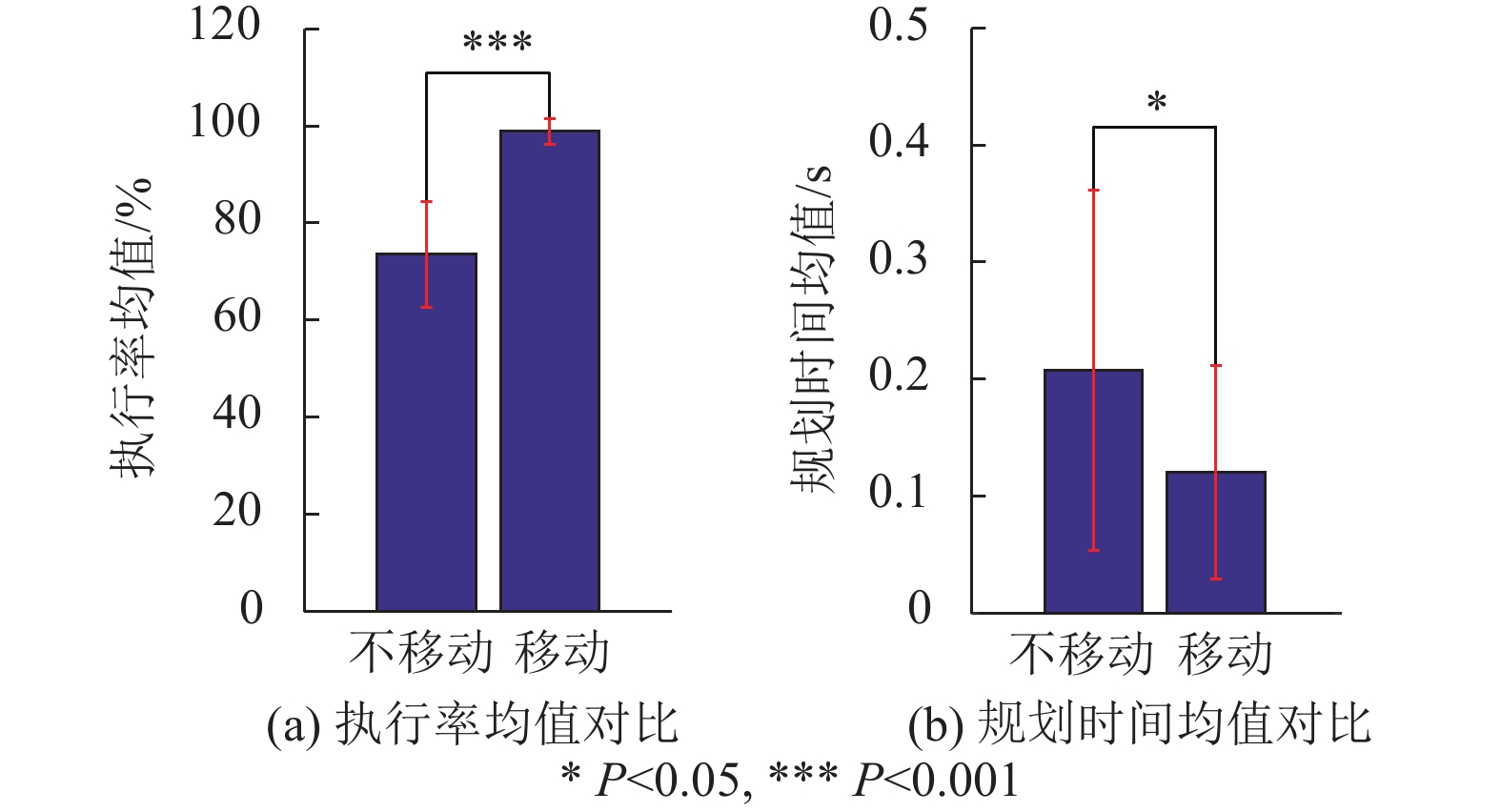
|
图 7 单障碍物靠近目标物体避障20次实验数据对比 Figure 7 Comparison of 20 experimental data in obstacle avoidance experiment when single obstacle approaching target object |
| 表 2 单障碍物靠近目标物体避障实验底盘是否移动的数据对比 Table 2 Data comparison of whether the chassis moves in obstacle avoidance experiment when single obstacle approaching target object |
此实验中,障碍物位置分别为(200 mm, 200 mm, 200 mm),(300 mm, 0 mm, 500 mm),(200 mm, 400 mm, 300 mm),目标点位置为(550 mm, 500 mm, 500 mm),机械臂起始六关节角为(−179°, −52°, 152°, −290°, 98°, −180°)。
加入移动底盘停靠位置优化算法仿真步骤如图8所示,移动机械臂的底盘先移动到计算得到的优化停靠位置,然后调整机械臂初始朝向,最后进行RRT算法避障。
图9为20次测试下移动底盘是否移动在可执行率均值和规划时间均值上的对比。表3为移动底盘是否移动的评价指标数据对比。
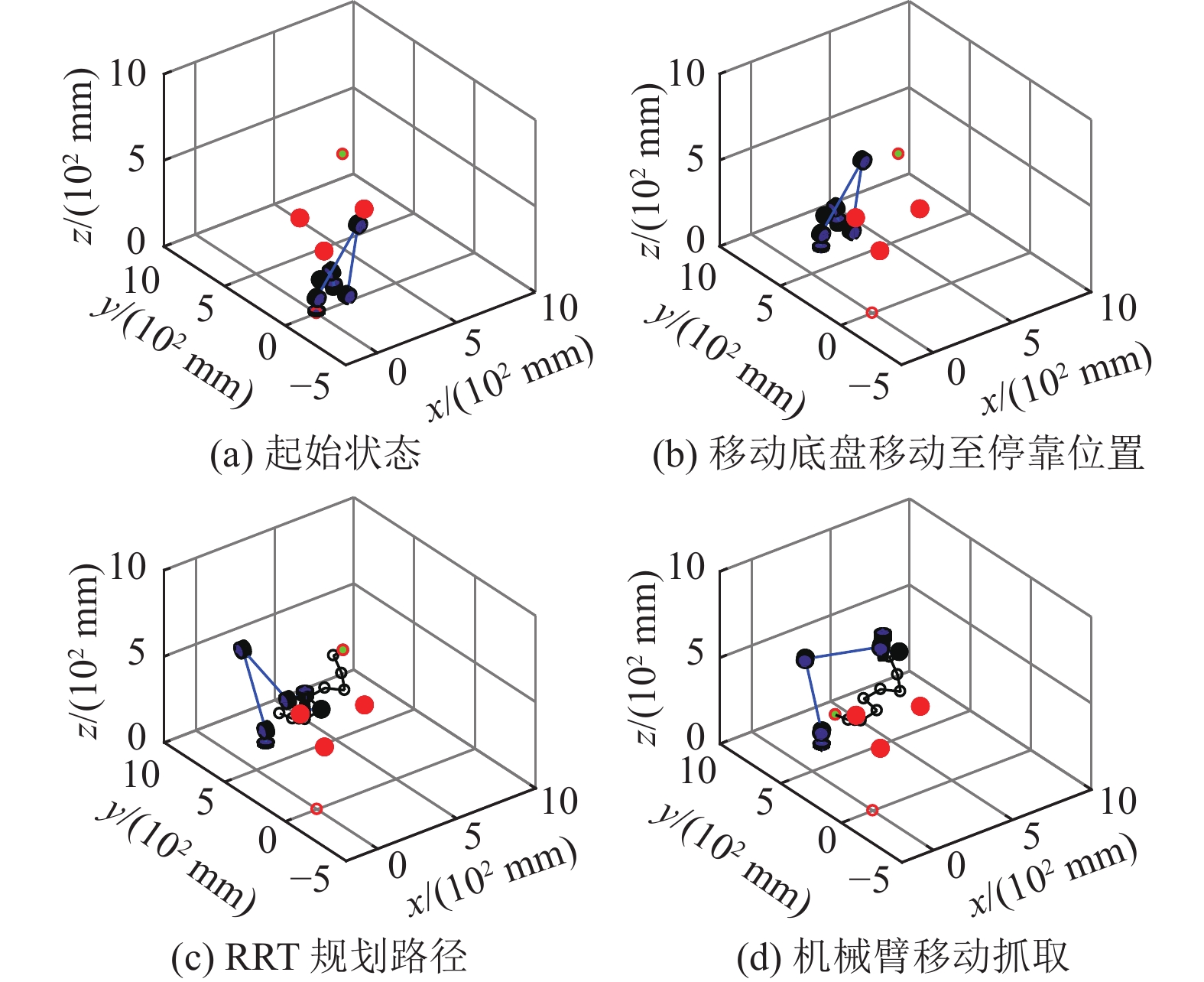
|
图 8 三障碍物避障实验移动机械臂仿真抓取 Figure 8 Simulation and grasping of mobile manipulator in three obstacles avoidance experiment |
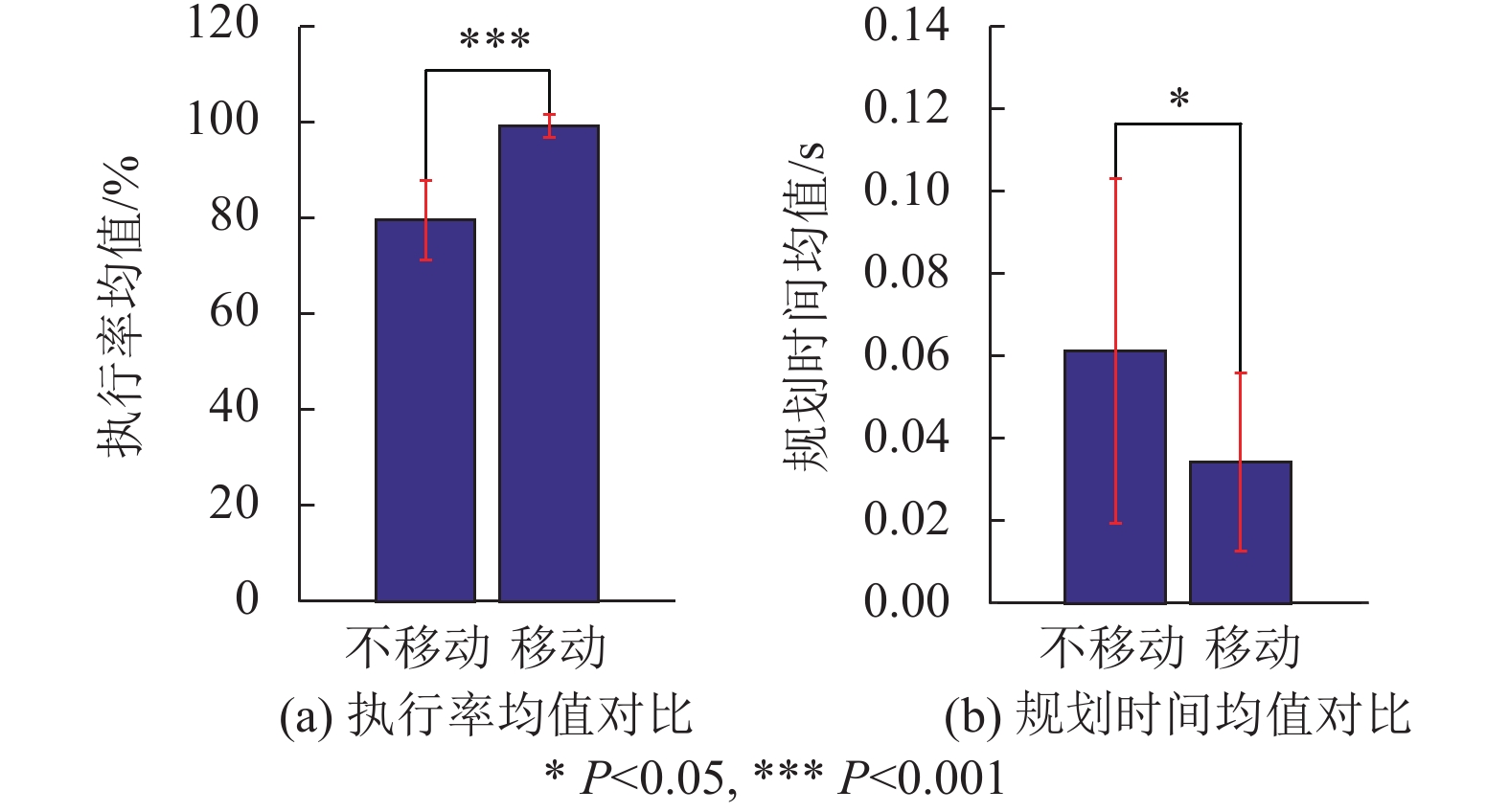
|
图 9 三障碍物避障20次实验数据对比 Figure 9 Comparison of 20 experimental data in three obstacles avoidance experiment |
| 表 3 三障碍物避障实验底盘是否移动的数据对比 Table 3 Data comparison of whether the chassis moves in three obstacles avoidance experiment |
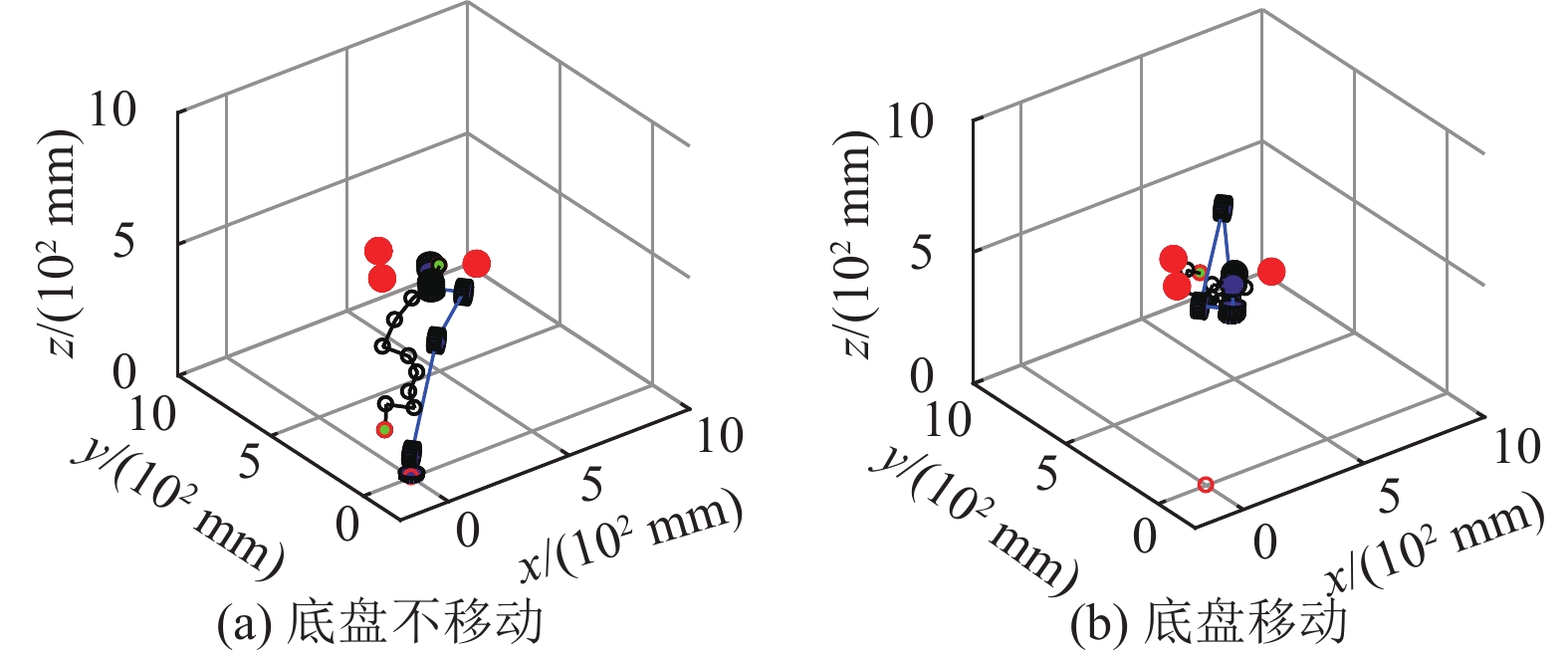
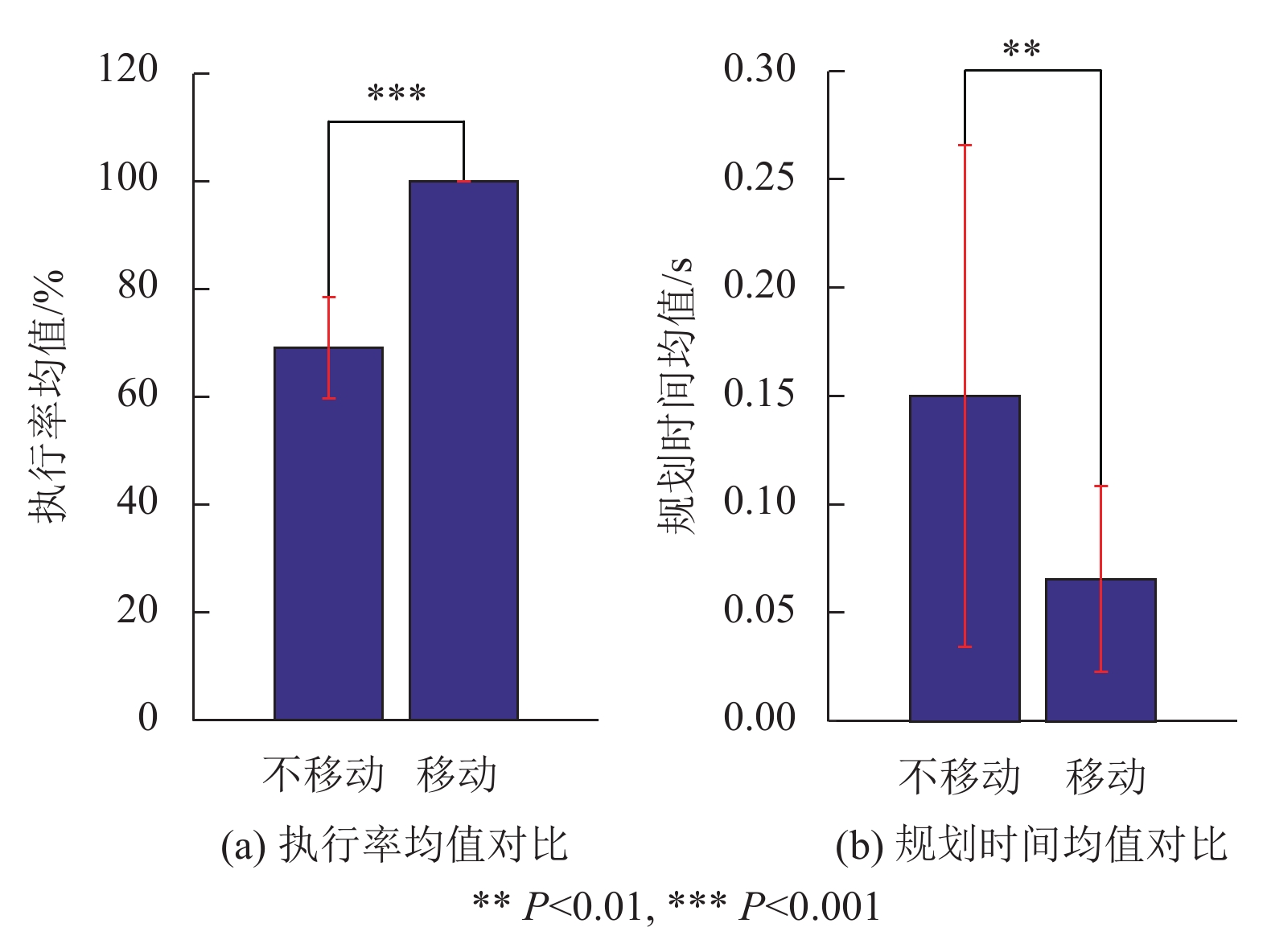
此实验中,障碍物位置分别为(400 mm, 700 mm, 400 mm),(500 mm, 300 mm, 500 mm),(300 mm, 550 mm, 400 mm),目标点位置为(500 mm, 500 mm, 400 mm),机械臂起始六关节角(−179°, −52°, 152°, −290°, 98°, −180°)。图10为加入移动底盘位置控制前后的对比。图11为20次测试下移动底盘是否移动在可执行率均值和规划时间均值上的对比。表4为移动底盘是否移动的评价指标数据对比。
|
图 10 三障碍物靠近目标物体避障实验加入移动底盘位置控制前后对比 Figure 10 Comparison before and after adding mobile chassis position control in obstacle avoidance experiment when three obstacles approaching target object |
|
图 11 三障碍物靠近目标物体避障20次实验数据对比 Figure 11 Comparison of 20 experimental data in obstacle avoidance experiment when three obstacles approaching target object |
| 表 4 三障碍物靠近目标物体避障实验底盘是否移动的数据对比 Table 4 Data comparison of whether the chassis moves in obstacle avoidance experiment when three obstacles approaching target object |
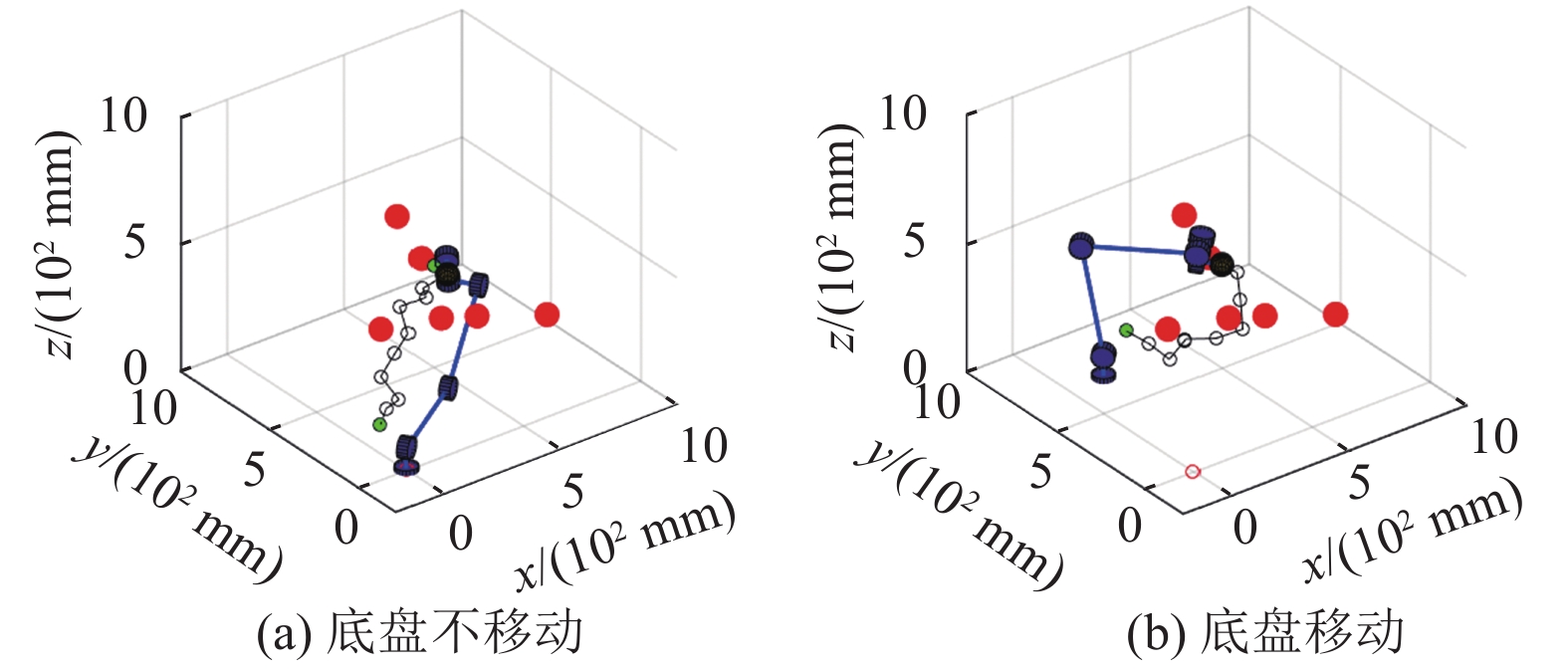
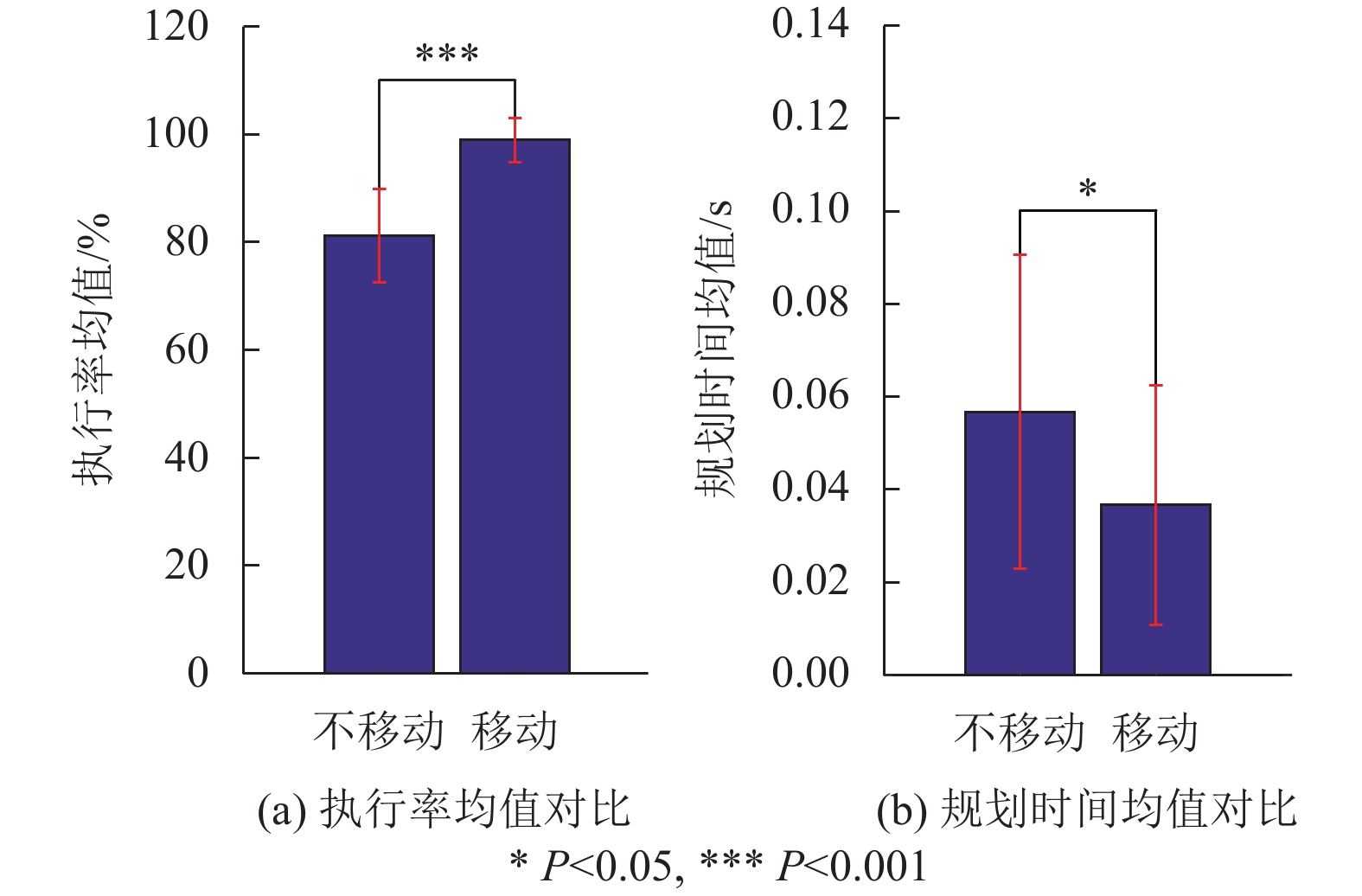
此仿真实验中,障碍物位置分别为(300 mm, 200 mm, 400 mm),(300 mm, 0 mm, 500 mm),(200 mm, 400 mm, 300 mm),(600 mm, 0 mm, 400 mm),(500 mm, 700 mm, 500 mm),(600 mm, 700 mm, 300 mm),目标点位置为(500 mm, 500 mm, 400 mm),机械臂起始六关节角设置为(−179°, −52°, 152°, −290°, 98°, −180°);图12为加入移动底盘位置控制前后的对比。图13为20次测试下移动底盘是否移动在可执行率均值和规划时间均值上的对比。表5为移动底盘是否移动的评价指标数据对比。
|
图 12 六障碍物避障实验加入移动底盘位置控制前后对比图 Figure 12 Comparison before and after adding mobile chassis position control in six obstacles avoidance experiment |
|
图 13 六障碍物避障20次实验数据对比 Figure 13 Comparison of 20 experimental data in six obstacles avoidance experiment |
| 表 5 六障碍物避障实验底盘是否移动的数据对比 Table 5 Data comparison of whether the chassis moves in six obstacles avoidance experiment |
在仿真环境中添加桌面条件,使其更符合实际机械臂抓取环境。3个障碍物的位置采用随机生成的方式,障碍物在桌面上方。目标位置为(500 mm, 500 mm, 400 mm),桌面以(850 mm, 800 mm, 210 mm)为角点,长、宽、高分别为600 mm、400 mm、80 mm,机械臂起始六关节角为(44, −42°, −104°, −29°, 91°, 231°)。图14为根据随机障碍物的位置生成移动底盘停靠优化位置后抓取的效果图。
图15为20次测试下移动底盘是否移动在可执行率均值和规划时间均值上的对比。表6为在有桌面和障碍物的情况下,考虑机械臂连杆与其之间的碰撞约束条件后,移动底盘是否移动的评价指标对比。
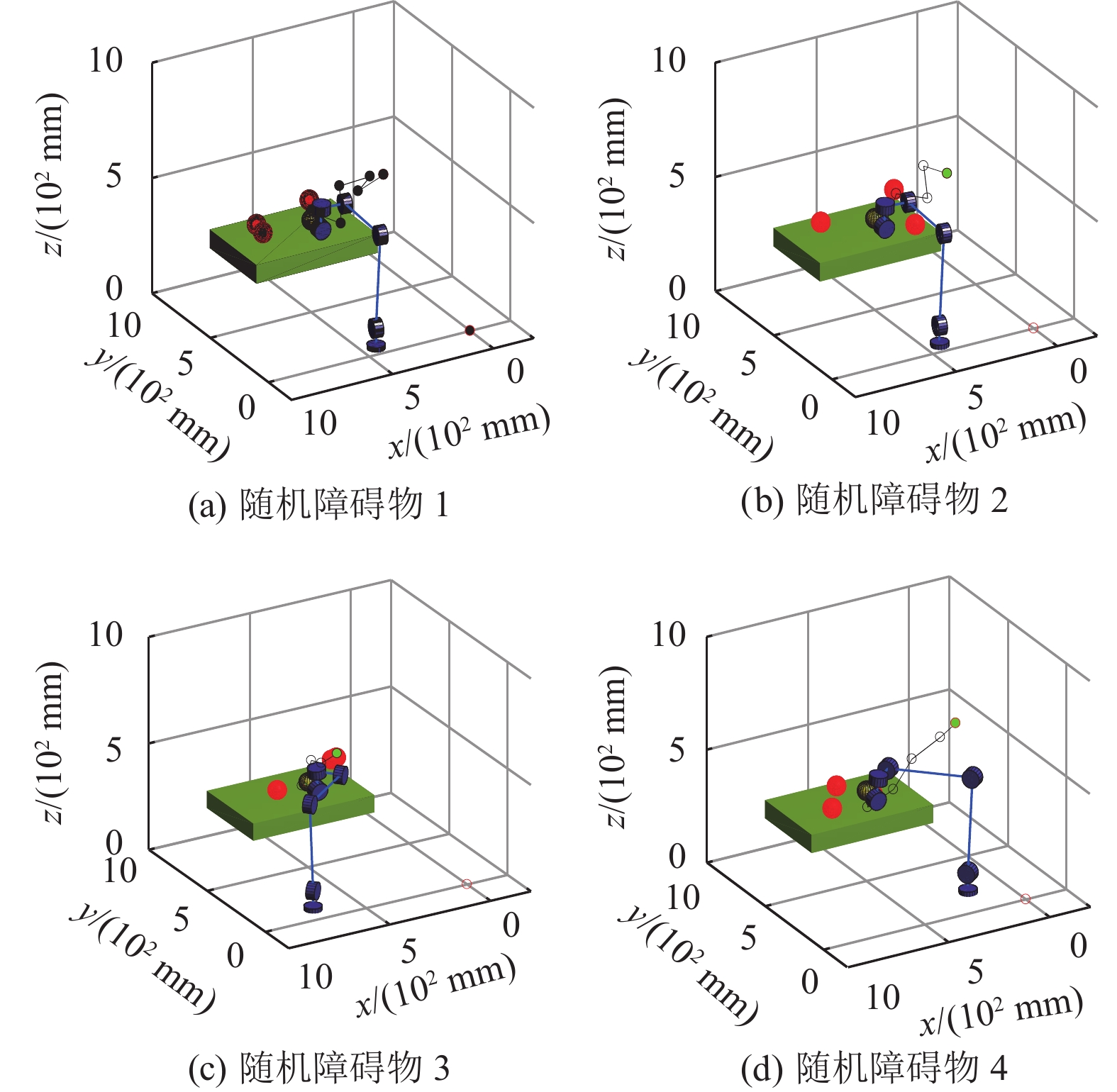
|
图 14 根据随机障碍物位置生成底盘停靠优化位置后抓取的效果图 Figure 14 Sketch of grabbing after the chassis stops at the optimized position is generated by the random obstacle position |
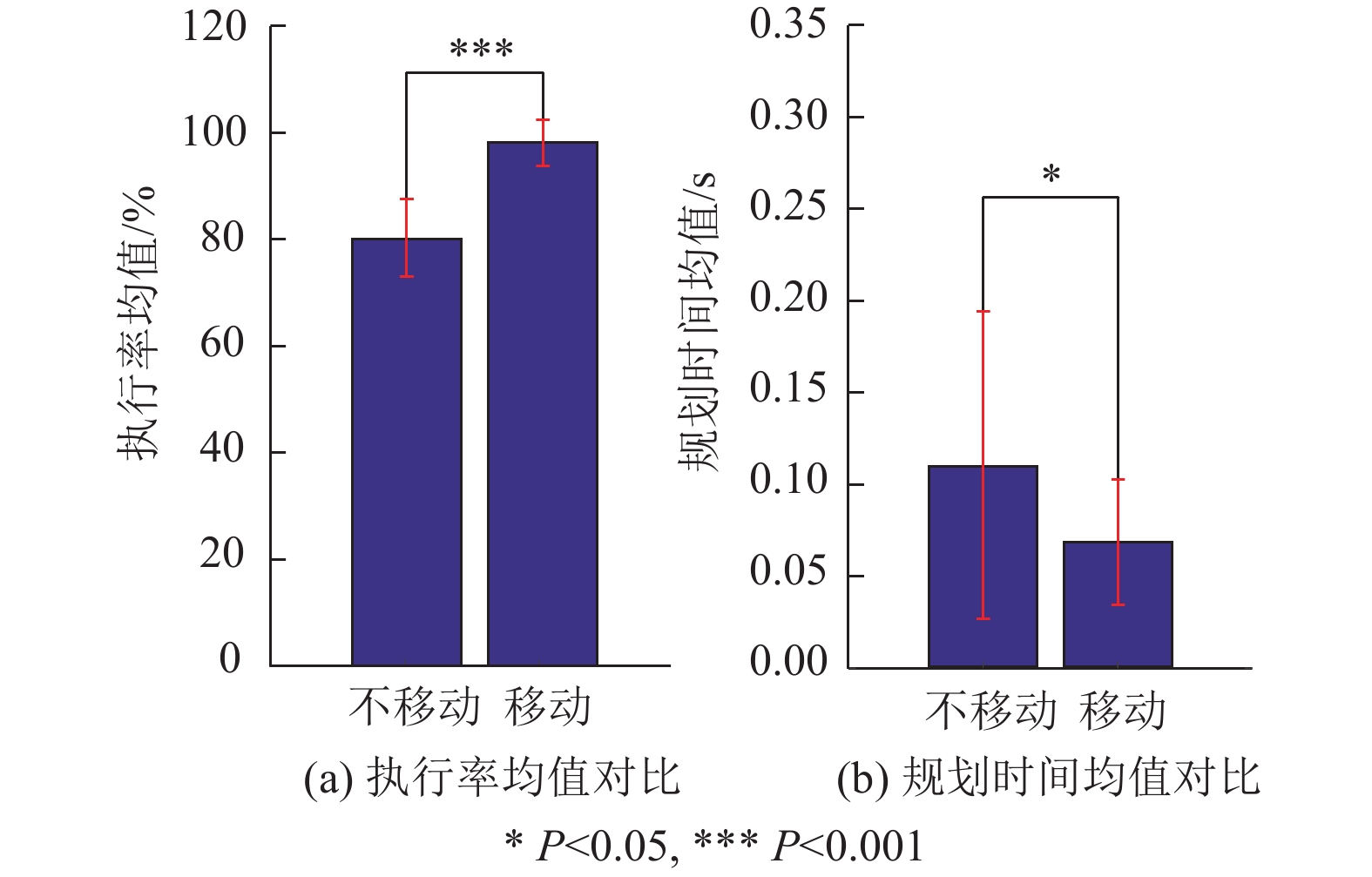
|
图 15 桌面避障20次实验数据对比 Figure 15 Comparison of 20 experimental data in desktop obstacle avoidance experiment |
| 表 6 桌面避障实验底盘是否移动的数据对比 Table 6 Data comparison of whether the chassis moves in desktop obstacle avoidance experiment |
在仿真环境中添加桌面条件,使其更加符合实际环境,分别针对正方体、长方体桌面进行了仿真。
正方体桌面仿真实验条件:长宽为
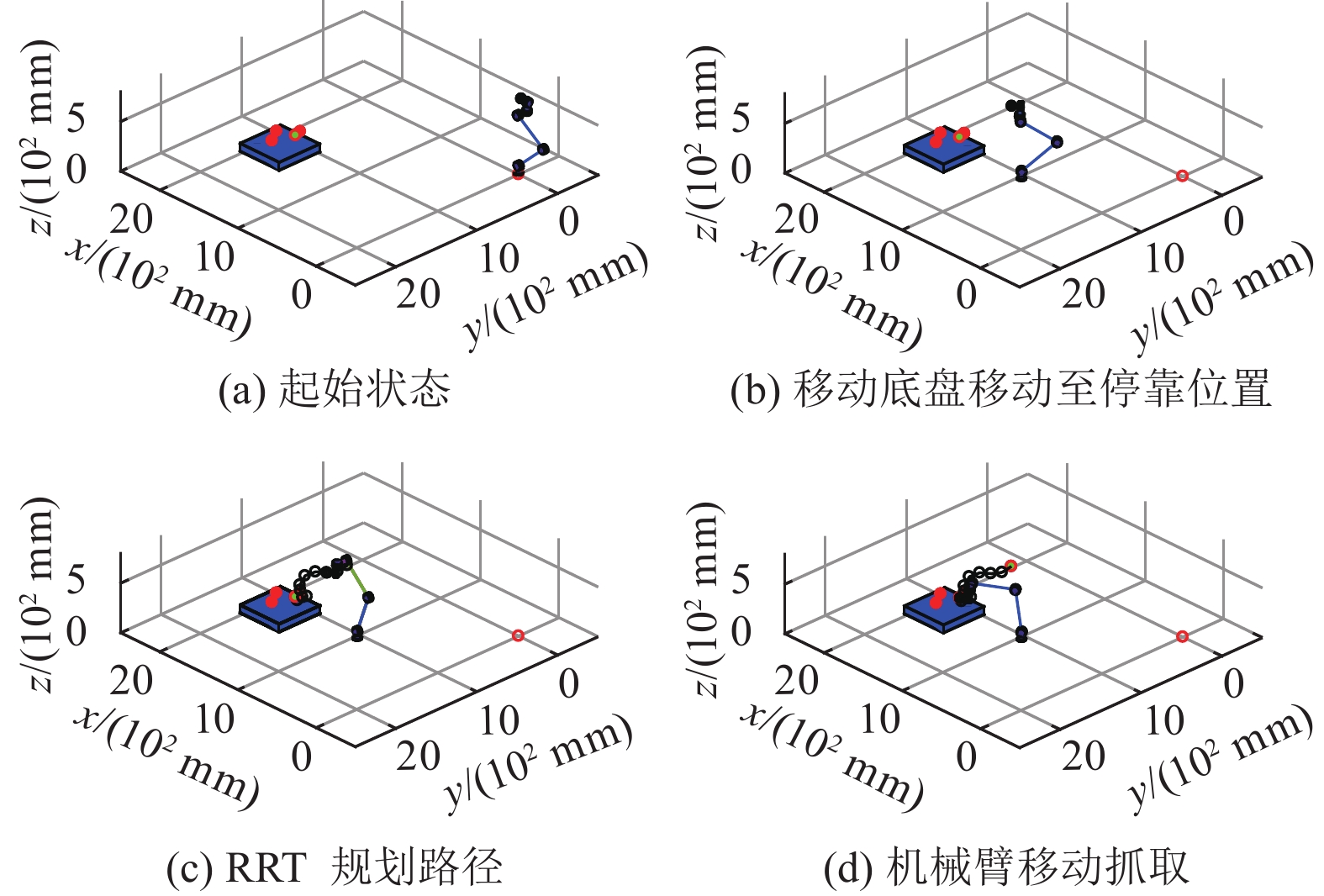
|
图 16 正方体桌面下移动机械臂抓取过程 Figure 16 Grasping process of mobile manipulator under cube table |
长方体桌面实验条件:长宽为
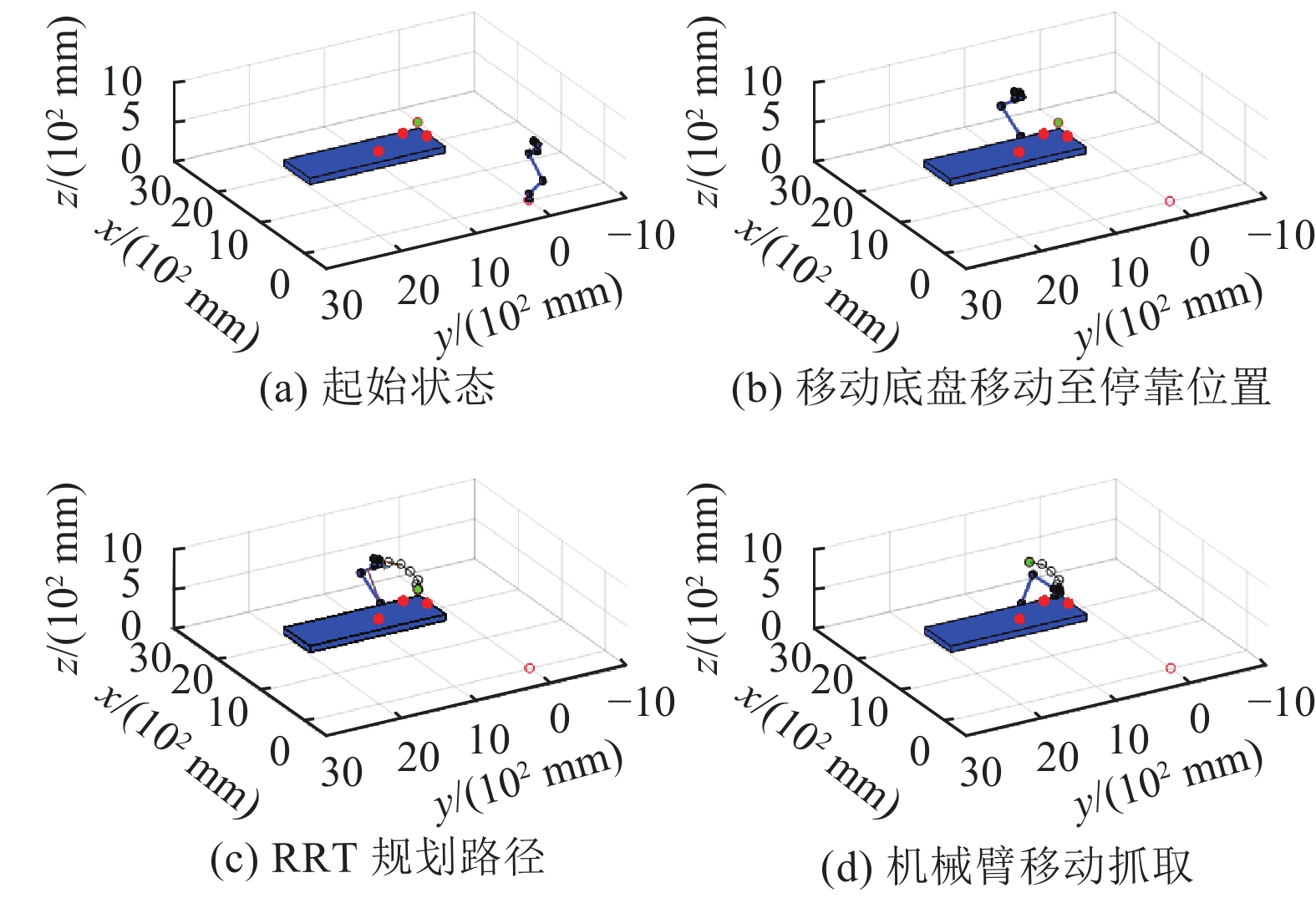
|
图 17 长方体桌面下移动机械臂抓取过程 Figure 17 Grasping process of mobile manipulator under cuboid table |
在正方体和长方体桌面上对目标物体及障碍物分别进行了实验,实际环境均在动作捕捉系统下搭建,桌面长宽根据仿真距离搭建,障碍物用方盒代替,目标物体用水瓶代替。
图18显示的是移动机械臂抓取正方体桌面上的目标物体,正方体桌面长宽为

|
图 18 移动机械臂抓取正方体桌面上的目标物 Figure 18 The mobile manipulator grabs the object on the cube table top |
图19显示的是移动机械臂抓取长方体桌面上的目标物体。长方体桌面长宽为

|
图 19 移动机械臂抓取长方体桌面上的目标物 Figure 19 The mobile manipulator grabs the object on the cuboid table top |
图18和图19中,(a)和(b)为移动机械臂底盘移动至优化后的停靠位置;(c)和(d)为机械臂末端移动至目标物体;(e)和(f)为夹爪闭合夹取目标物体并举起。
4 讨论上述仿真实验数据显示,不同条件下加入移动底盘停靠位置优化算法后可提高可执行率及增加路径点完全执行次数。
仿真实验3.1.1显示当单个障碍物较大且靠近目标物体时,移动机械臂不移动的情况下不存在能完全执行路径点到达目标点的情况;而底盘的移动能有效地提高目标物体的抓取规划成功率,并缩短规划时间。
样机实验实现了目标物体的成功抓取,证明了仿真计算的移动底盘停靠位置优化算法及RRT避障算法在实际应用中的可行性。
与之前的方法相比,本文所提出的加入连杆碰撞约束的RRT避障方法增强了机械臂的可操作性与避障能力;移动底盘停靠位置优化算法不仅提高了规划速度,而且提高了物体的抓取规划成功率。未来的研究将集中在动态方面,根据实时环境监测提出移动底盘实时搜寻移动位置的控制策略。
| [1] |
孟偲, 王田苗. 一种移动机器人全局最优路径规划算法[J].
机器人, 2008, 37(3): 217-222.
MENG C, WANG T M. A global optimal path planning algorithm for mobile robot[J]. Robot, 2008, 37(3): 217-222. DOI: 10.3321/j.issn:1002-0446.2008.03.005. |
| [2] |
张宏钊, 刘顺桂, 姜勇, 等. 基于可操作度的移动机械臂路径规划研究[J].
自动化与仪表, 2018, 33(10): 45-49.
ZHANG H Z, LIU S G, JIANG Y, et al. Research on mobile manipulator path planning based on operability[J]. Automation & Instrumentation, 2018, 33(10): 45-49. |
| [3] |
GROVES P D. Principles of GNSS, inertial, and multisensor integrated navigation systems, 2nd edition [Book review][J].
IEEE Aerospace and Electronic Systems Magazine, 2015, 30(2): 26-27.
DOI: 10.1109/MAES.2014.14110. |
| [4] |
LAU B, SPRUNK C, BURGARD W. Efficient grid-based spatial representations for robot navigation in dynamic environments[J].
Robotics and Autonomous Systems, 2013, 61(10): 1116-1130.
DOI: 10.1016/j.robot.2012.08.010. |
| [5] |
汪盛民, 林伟, 曾碧. 未知环境下基于虚拟子目标的对立Q学习机器人路径规划[J].
广东工业大学学报, 2019, 36(1): 51-56.
WANG S M, LIN W, ZENG B. Path planning of opposite Q learning robot based on virtual sub-target in unknown environment[J]. Journal of Guangdong University of Technology, 2019, 36(1): 51-56. DOI: 10.12052/gdutxb.180044. |
| [6] |
肖林, 周文辉. 移动机械臂的协调运动方案设计及验证[J].
中山大学学报(自然科学版), 2016, 55(2): 52-57.
XIAO L, ZHOU W H. Design and verification of coordinated motion scheme for mobile manipulators[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(2): 52-57. |
| [7] |
BROCK O, PARK J, TOUSSAINT M. Mobility and manipulation[M]. Berlin:Springer International Publishing, 2016, : 1007-1036.
|
| [8] |
ISKANDAR M, QUERE G, HAGENGRUBER A, et al. Employing whole-body control in assistive robotics[C]// IEEE International Conference on Intelligent Robots and Systems. Macau: IEEE, 2019: 5643-5650.
|
| [9] |
KIM S, JANG K, PARK S, et al. Whole-body control of non-holonomic mobile manipulator based on hierarchical quadratic programming and continuous task transition[C]//2019 IEEE 4th International Conference on Advanced Robotics and Mechatronics (ICARM). Toyonaka: IEEE, 2019: 414-419.
|
| [10] |
王洪斌, 尹鹏衡, 郑维, 等. 基于改进的A*算法与动态窗口法的移动机器人路径规划[J].
机器人, 2020, 42(3): 346-353.
WANG H B, YIN P H, ZHENG W, et al. Mobile robot path planning based on improved A* algorithm and dynamic window method[J]. Robot, 2020, 42(3): 346-353. |
| [11] |
杜峰, 苏丽颖, 焦继乐, 等. 移动机械臂无碰抓取方法的研究[J].
机械科学与技术, 2016, 35(4): 535-538.
DU F, SU L Y, JIAO J L, et al. A method for collision-free grasp of mobile manipulator[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(4): 535-538. |
| [12] |
王宪, 杨国梁. 基于改进蚁群算法的机器人轨迹规划[J].
计算机系统应用, 2010, 19(11): 79-82.
WANG X, YANG G L. Robot trajectory planning based on improved ant colony algorithm[J]. Computer Systems & Applications, 2010, 19(11): 79-82. DOI: 10.3969/j.issn.1003-3254.2010.11.018. |
| [13] |
代彦辉, 梁艳阳, 谢钢. 基于RRT搜索算法的六自由度机械臂避障路径规划[J].
自动化技术与应用, 2010, 19(11): 79-82.
DAI Y H, LIANG Y Y, XIE G. The mechanical arm of six-dof obstacle avoidance path planning based on rapid-exploring random trees[J]. Techniques of Automation and Applications, 2010, 19(11): 79-82. |
| [14] |
陈满意, 张桥, 张弓, 等. 多障碍环境下机械臂避障路径规划[J].
计算机集成制造系统, 2021, 27(4): 990-998.
CHEN M Y, ZHANG Q, ZHANG G, et al. Research on obstacle avoidance path planning of manipulator in multiple obstacles environment[J]. Computer Integrated Manufacturing Systems, 2021, 27(4): 990-998. |
| [15] |
杜爽, 尚伟伟, 刘坤, 等. 基于双向RRT算法的仿人机器人抓取操作[J].
中国科学技术大学学报, 2016, 46(1): 12-20.
DU S, SHANG W W, LIU K, et al. Bidirectional RRT algorithm based grasping manipulation of humanoid robots[J]. Journal of University of Science and Technology of China, 2016, 46(1): 12-20. |
| [16] |
GUO Y, BENNAMOUN M, SOHEL F, et al. 3D object recognition in cluttered scenes with local surface features: a survey[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(11): 2270-2287.
DOI: 10.1109/TPAMI.2014.2316828. |
| [17] |
GOKBERK C R, VERBEEK J, SCHMID C. Multi-fold mil training for weakly supervised object localization[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 2409-2416.
|
| [18] |
HUANG Z, LI J, HUANG J, et al. Motion planning for bandaging task with abnormal posture detection and avoidance[J].
IEEE/ASME Transactions on Mechatronics, 2020, 25(5): 2364-2375.
DOI: 10.1109/TMECH.2020.2973674. |
 2021, Vol. 38
2021, Vol. 38

