为了应对未来海量数据、新兴的服务和动态应用场景的通信需求，学术界、工业界以及政府已启动第6代(6G)移动通信研究计划，通过采用太赫兹和可见光新频谱技术、全新信道编码、超大规模天线、全自由度双工、空天地海一体化通信等，提供每秒太比特速率、支撑平均每人1000+无线节点连接，并提供随时随地即时全息连接。随着立体覆盖、极致性能、深度连接、泛在连接、全息连接等6G愿景达成共识，智能终端和网元节点激增、个性化服务定制、多场景多业务动态叠加等问题给网络优化和管理带来严峻挑战。传统以规则式算法为核心的运行机理已无法应对规模和复杂性空前的6G网络。在此背景下，引入人工智能，借鉴其解决复杂非线性系统问题的能力，以及强大的预测和决策能力，能够促进网络智能化升级，突破无线网络发展瓶颈^[1-3]。

近年，人工智能和大数据挖掘技术的快速发展，为应对6G复杂挑战提供了有效助力。通过在网络终端、网元节点与网络架构、网络承载业务等多个层次嵌入智能，同时将人工智能的逻辑嵌入到网络结构中，使网络组件能够自主连接和控制，并能自动进行网络配置、自主分析和决策、主动优化网络故障,最终实现网络的自主发展，构建智慧内生的6G网络。有关无线网络智能化的研究和标准化工作已成为业界的研究热点。2020年11月中兴通讯发布首份无线网络智能化白皮书，通过在无线网络的规划、建设、维护、优化以及运营等各阶段全面引入人工智能，并基于网络分析、控制和管理三大能力，保障网络连接和性能承诺，实现无线网络的单域自治闭环。然而，人工智能在提高无线网络的效能、灵活性和自治能力的同时，也存在新的安全挑战。在大多数情况下，人工智能任务是在数据中心进行计算和部署的，其中的学习机制需要大量的网络数据训练模型。而这些网络数据除了机密文件、隐私信息，还包含人的生物特征识别信息、家庭电器控制信息、车辆的自动驾驶控制信息等敏感信息。一旦恶意用户攻击数据中心，将会导致这些信息的泄露，进而对用户的财产甚至生命造成威胁^[4]。

联邦学习是一种新兴的分布式机器学习架构^[5]。在联邦学习中，大规模移动设备使用本地存储的数据执行训练任务，并将训练的本地模型参数上传到数据中心聚合。与传统基于数据中心的集中式训练方式相比，联邦学习只需要上传训练好的模型参数，能有效减少数据传输开销，提升对用户隐私数据的保护。目前，谷歌已在谷歌输入法Gboard上测试联邦学习^[6]。当联邦学习应用到未来无线网络中，仍面临着一些严峻的挑战。移动设备有限的资源以及复杂多变的无线传输环境将导致信号严重失真以及模型聚合误差，进而使联邦学习的收敛速率和预测准确率下降。Chen等^[7]研究了无线网络中的联邦学习训练过程，提出联合移动设备选择和无线资源分配的优化方案，以实现最小化联邦学习损失函数的目标。Ni等^[8]提出使用智能反射面辅助本地模型参数传输，通过优化移动设备的发送功率和智能反射面的相移，以实现最小化联邦学习聚合模型平均均方误差的目标。Lu等^[9]将联邦学习应用到车联网中，通过选择训练精度高和训练速度快的移动车辆完成模型聚合，提高全局模型的预测准确率。但上述研究均忽略了移动设备参与模型聚合的意愿问题。在联邦的模型训练过程中，移动设备会产生大量计算和通信开销。自私的移动设备不愿意无偿参与模型训练，这将使模型聚合样本减少，进而导致全局模型聚合性能下降。针对联邦学习资源协作激励机制的研究相对较少。Le等^[10]提出使用组合拍卖博弈，基站作为买方向移动设备发布训练任务，移动设备作为卖方根据训练任务需要的资源、本地训练准确率以及相应能量开销，向基站提交出价。基站确定竞拍成功者并支付相应报酬。Sun等^[11]研究了联邦学习在无人机网络中的应用，提出使用斯塔克伯格博弈激励地面移动设备参与模型训练。但在实际无线网络中，买卖双方存在信息非对称性，即考虑隐私信息的保护，移动设备作为卖方不愿意向买方揭露自身真实信息，例如可用资源、本地模型训练准确率、模型训练能量开销等。因此，买方难以制定相应报酬。

为了解决以上问题，本文主要研究工作如下。

(1) 在6G无线网络中，构建基于联邦学习的终端到终端(Device to Device，D2D)数据共享框架。本地接入点采集移动终端的任务请求，并将采集的任务请求发布给模型训练终端。模型训练终端根据自身存储的数据训练本地模型，并把训练好的本地模型上传给本地接入点聚合。本地接入点和模型训练终端迭代地训练全局模型，然后将训练好的全局模型反馈给任务请求终端。最后，任务请求终端向模型训练终端支付相应报酬，以补偿模型训练过程中的资源消耗。

(2) 考虑任务请求终端和模型聚合终端之间的信息非对称性，提出基于迭代双边拍卖的资源协作激励机制。模型训练方作为卖方，任务请求方作为买方。本地接入点充当拍卖师，引导买卖双方根据各自联邦学习性能需求以及可用资源出价，并根据买卖双方的出价进行最优模型训练资源分配和定价，以实现最大化联邦学习市场的总效用。

(3) 根据真实数据集，对提出的资源协作激励机制进行仿真实验验证。结果表明，本文提出的基于双边拍卖的联邦学习资源协作激励机制可以提高联邦学习模型的准确率，并且减少模型训练损失。同时，在买卖双方信息非对称性情况下，最大化联邦学习市场效用。

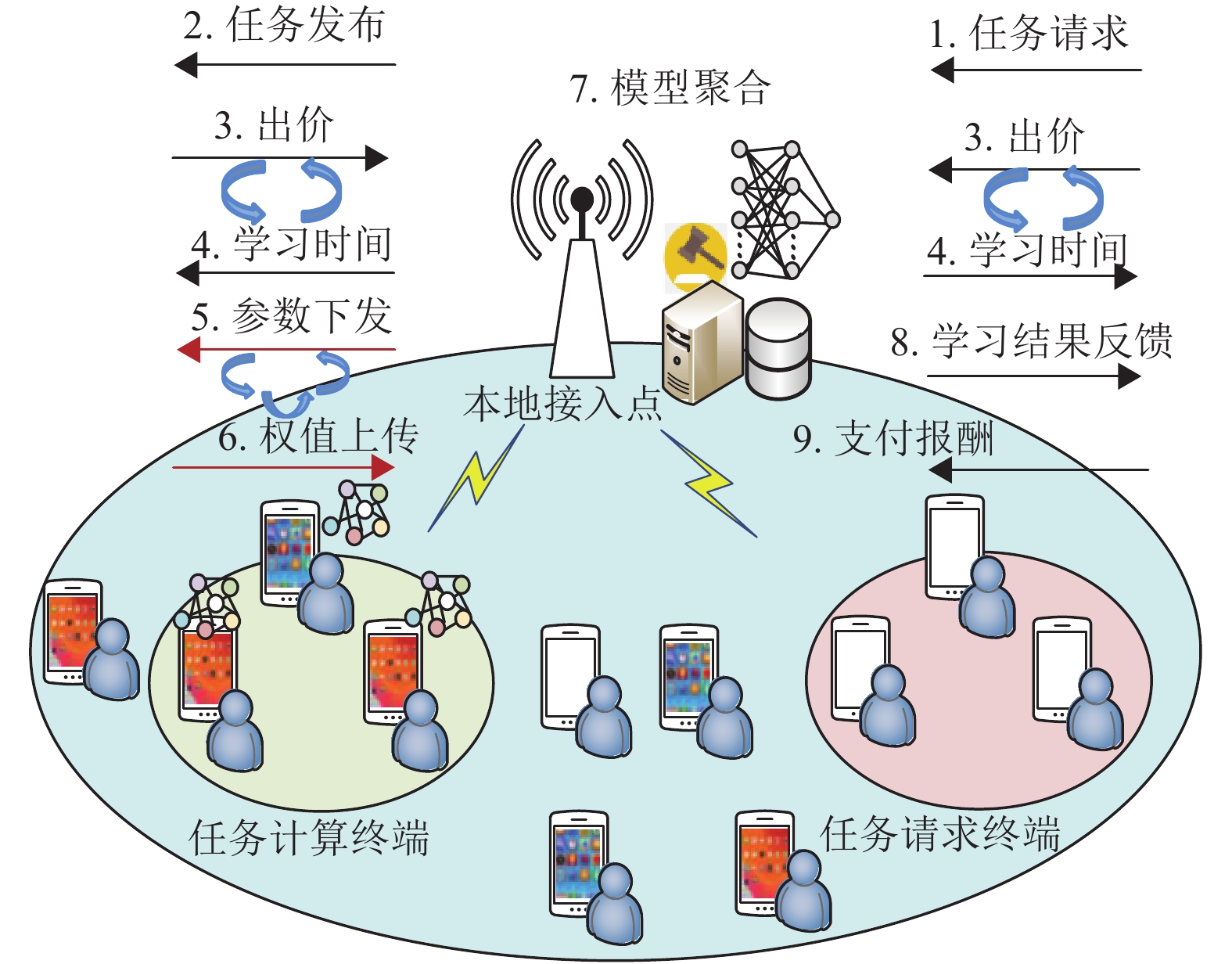
1 系统模型

本文构建的系统模型如图1所示。考虑6G网络中的D2D通信场景，其中，本地接入点配有边缘计算服务器，具有较强的计算和存储功能。同时，本地接入点部署有人工智能模块，可通过感知、预测、挖掘、推理对多维网络信息进行认知和分析，并做出相应决策。在本地接入点的覆盖范围内，分布有多个智能终端，智能终端之间以D2D通信的方式共享数据。此处的数据共享是指根据本地存储的数据进行联邦的任务计算，并将计算结果反馈给请求方，例如，流行音乐、电影、游戏等多媒体内容的推荐。本地接入点协助建立智能终端用户之间的D2D通信链路。考虑当前有Q个任务请求终端，表示为 $ {\cal{Q}}\triangleq $ {1,2,···, Q},任务请求终端 $ {q},\;{q}\in {\cal{Q}} $ , 发送共享数据请求Req_q。本地接入点采集共享数据请求，并将采集的共享数据请求发布给R个任务计算终端，表示为 $ {\cal{R}}\triangleq \{{1,2,}{ \cdots },{}{R}{}\}{} $ 。每个任务计算终端存储有任务请求终端需要的数据，存储关于共享数据请求Req_q的数据表示为 $ {\cal{D}}_{q}= \{{\cal{D}}_{{1q}}, $ $ {{}{\cal{D}}}_{{2q}}, \cdots ,{{}{\cal{D}}}_{{rq}}\} $ ， ${q}\in {\cal{Q}}$ ， ${\cal{D}}_{rq}=\{({{x}}_{{rq},{1}},{y}_{{rq},{1}}),({{x}}_{{rq}{,2}},{y}_{{rq}{,2}}), \cdots, $ $ ({{x}}_{{rq},{D}_{r{q}}},{y}_{{rq},{D}_{r{q}}})\}$ 。任务计算终端采用联邦学习完成计算任务。在联邦学习中，任务计算终端根据本地存储的数据 $ {\cal{D}}_{q} $ ，执行本地模型训练，并将训练好的本地模型参数上传到本地接入点聚合。任务计算终端和本地接入点迭代地交互训练模型，直到获得训练模型 $ {\cal{M}}_{q} $ 和模型参数w_q，以实现最小化损失函数f (w_q)的目标。具体优化问题构造如下：

$ \mathop {{\rm{min}}}\limits_{{w_q}} \frac{{1}}{{{R}}}\sum _{r=1}^{R}\frac{1}{{\cal{D}}_{rq}}\sum _{i=1}^{{\cal{D}}_{rq}}{f}_{i}\left({w}_{q},{x}_{rq,i},{y}_{rq,i}\right) $

(1)

其中： $ {f}_{i}\left({w}_{q},{x}_{rq,i},{y}_{rq,i}\right) $ 是关于数据样本 $ \left({x}_{rq,i},{y}_{rq,i}\right) $ 和参数w_q的损失函数。

在本地训练过程中，任务计算终端 $ {r},{}{r}\in {\cal{R}} $ 根据本地存储的数据 $ {\cal{D}}_{rq} $ 使用梯度下降法寻找模型参数w_rq，以最小化本地训练模型的损失函数。在第t次本地训练迭代中，任务计算终端r根据模型参数w_rq $ \left({t}-1\right) $ 和本地梯度下降 $\nabla $ F_rq $ \left({w}_{rq}\left(t-1\right)\right) $ ，训练本地模型参数w_rq $ \left({t}\right) $ 。

$ \begin{split} {w}_{rq}\left({t}\right)= &{w}_{rq}\left({t}-1\right)-\varUpsilon \cdot \nabla {F}_{rq}\left({w}_{rq}\left(t-1\right)\right) , \\& \forall {r}\in {\cal{R}},{q}\in {\cal{Q}} \end{split}$

(2)

其中： $ \varUpsilon $ 表示梯度下降的学习速率。任务计算终端 $ {r} $ 发送本地模型参数到本地接入点聚合，以更新全局模型。本地接入点的聚合模型表示为

$ {\cal{M}}_{q}=\frac{1}{R}\sum _{r=1}^{R}{\cal{D}}_{rq}{w}_{rq} ,\;\; \forall {r}\in {\cal{R}},\;\;{q}\in {\cal{Q}} $

(3)

1.1 联邦学习的计算模型

任务计算终端r根据本地存储的数据 $ {\cal{D}}_{rq} $ 训练本地模型参数时，贡献的计算资源表示为 $ {f}_{rq}^{C} $ ，即CPU周期频率。训练一个数据样本需要的CPU周期表示为 $ {c}_{r} $ 。因此，在本地训练过程中，任务计算终端r一次本地迭代的计算时延表示为

$ {T}_{rq}^{\mathrm{c}\mathrm{m}\mathrm{p}}=\frac{{b}_{r}{\cal{D}}_{rq}{c}_{r}}{{f}_{rq}^{C}} , \forall {r}\in {\cal{R}},{q}\in {\cal{Q}} $

(4)

其中： $ {b}_{r} $ 表示训练数据 $ {\cal{D}}_{rq} $ 的批量大小。用 $ {\vartheta }_{r} $ 表示任务终端r本地训练的准确率，任务终端r本地训练的迭代次数表示为 $ \mathrm{lg}\left(\dfrac{1}{{\vartheta }_{r}}\right) $ ^[12]。因此，任务终端r本地训练的总时延表示为

$ {T}_{rq}^{C}=\mathrm{lg}\left(\frac{1}{{\vartheta }_{r}}\right){T}_{rq}^{\mathrm{c}\mathrm{m}\mathrm{p}} $

(5)

1.2 联邦学习的通信模型

每个任务计算终端使用正交频分多址接入技术(Orthogonal Frequency Division Multiple Access, OFDMA)将训练的本地模型参数发送到本地接入点聚合。任务终端r分配到的子信道表示为 $ {W}_{rq} $ ，每个子信道的带宽均为 $ {W}_{0} $ 。从任务计算终端r到本地接入点的数据速率表示为

$ {R}_{rq}=\sum _{s=1}^{{W}_{rq}}{W}_{0}{\mathrm{l}\mathrm{o}\mathrm{g}}_{2}\Bigg(1+\frac{{P}_{rq}^{s}{|{h}_{rq}^{s}|}^{2}}{{\displaystyle\sum }_{r'\in {\cal{R}}\backslash \left\{r\right\}}{P}_{r'q}^{s}{|{h}_{r'q}^{s}|}^{2}+{N}_{0}}\Bigg) $

(6)

其中， $ {P}_{rq}^{s} $ 表示任务计算终端r在子信道s上的发送功率， $ {{s}\in W}_{rq} $ ； ${|{h}_{rq}^{s}|}^{2}$ 表示任务计算终端r到本地接入点子信道s的信道增益； ${\sum }_{{r}'\in {\cal{R}}\backslash \left\{r\right\}}{P}_{{r}'q}^{s}{|{h}_{{r}^{{'}}q}^{s}|}^{2}$ 表示任务终端r′共用子信道s产生的干扰； $ {N}_{0} $ 表示噪声功率。任务终端r发送本地训练模型参数的时延表示为

$ {T}_{rq}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}}=\frac{\left|{{w}}_{rq}\right|}{{R}_{rq}} $

(7)

其中： $ \left|{{w}}_{rq}\right| $ 表示本地训练模型参数的大小。根据式(5)和式(7)，任务计算终端r参与联邦学习一次全局迭代的时延表示为

$ {T}_{rq}^{gt}={T}_{rq}^{C}+{T}_{rq}^{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{s}} $

(8)

基于以上分析，如果任务计算终端在本地训练过程中贡献更多计算资源，同时在本地模型参数传输过程中分配更多通信资源，例如分配更多发送功率和子信道等，式(2)中本地模型训练和式(3)中全局模型训练的收敛速率会加快。然而，任务计算终端资源有限，而且其处理自身数据业务也需要消耗资源。因此，为了激励任务终端贡献资源参与联邦学习，有必要设计合适的资源协作激励机制，以补偿任务终端的资源消耗。

2 基于迭代双边拍卖的联邦学习资源协作激励机制

本文提出基于迭代双边拍卖的联邦学习资源协作激励机制，以激励任务计算终端贡献自身资源参与联邦学习的模型训练。迭代双边拍卖广泛用于经济学中，解决信息非对称性情况下的买卖双方交易问题。拍卖师设计合适的价格机制引导买卖双方真实地出价，以揭露买卖双方隐藏的信息，最终实现交易均衡的目标。已有研究^[13]证明迭代双边拍卖具有个体理性、弱预算均衡和高经济效率等特征，适用于具有多个买卖双方的交易场景。

在设计的基于迭代双边拍卖的联邦学习资源协作激励机制中，本地接入点充当拍卖师，任务发布终端和任务计算终端分别充当买方和卖方。考虑任务发布终端q, $ {q}\in {\cal{Q}} $ , 需要任务计算终端r, r $ \in {\cal{Q}} $ 在一次全局迭代计算时延为 $ {{{T}}}_{qr}^{gt(-1)} $ 。定义任务请求终端q, $ {q}\in {\cal{Q}} $ 的请求时延向量为 ${\boldsymbol{T}}_{qr}^{gt(-1)}\triangleq ({T}_{qr}^{gt(-1)}{:}\forall {r}\in {\cal{R}})$ ，任务请求终端q的效用函数表示为 ${F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)})$ , $ {q}\in {\cal{Q}} $ ，此处的效用函数是指任务请求终端在请求时延范围内收到联邦学习结果获的效用。Q个任务请求终端的总效用函数表示为 $\displaystyle\sum _{q=1}^{Q}{F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)})$ ，其中，效用函数 $ {F}_{q}( \cdot ) $ 是关于请求时延向量 $ {\boldsymbol{T}}_{qr}^{gt(-1)} $ 的递增且严格凹的函数。每个任务计算终端根据每个任务请求终端的请求Req_q做出相应响应Req_r，而且给出在一次全局迭代的接受时延 $ {\varGamma }_{rq}^{gt(-1)} $ 。定义任务计算终端r( $ {r}\in {\cal{R}} $ )的接受时延向量为 $ {\boldsymbol{\varGamma }}_{rq}^{gt(-1)}\triangleq ({\varGamma }_{rq}^{gt(-1)}{:}\forall r\in {\cal{R}}) $ ，任务计算终端r的成本函数表示为 $ {C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)}) $ , $ r\in {\cal{R}} $ ，此处的成本函数是指任务计算终端在接受时延范围内参与联邦学习模型训练产生等资源开销。R个任务计算终端的总效用函数表示为 $\displaystyle\sum _{r=1}^{R}{C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)})$ ，其中，效用函数 $ {C}_{r}( \cdot ) $ 是关于接受时延向量 $ {\boldsymbol{\varGamma }}_{rq}^{gt(-1)} $ 的递增且严格凹的函数。

2.1 问题构造

可以看出，任务计算终端和任务请求终端的效用函数是相互矛盾的，如果独立地对请求时延和接受时延做决策，难以使双方达成共识。为了解决此困难，本地接入点充当拍卖师，通过构建最大化联邦学习市场总效用的优化问题，求解最优时延向量 $ ({{\boldsymbol{T}}_{qr}^{gt(-1)},{\boldsymbol{\varGamma }}}_{rq}^{gt(-1)}) $ 。具体优化问题构造如下

$ \left\{\begin{aligned} & \mathop {{\rm{max}}}_{{\boldsymbol{T}}_{qr}^{gt( { - 1} )},{\boldsymbol{\varGamma}} _{rq}^{gt( { - 1} )}} \sum _{q=1}^{Q}{F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)})+\sum _{r=1}^{R}{C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)}) \\& {\rm{s.t}}.\;\;\; {\rm{C}}1: {T}_{qr}^{gt(-1)}\geqslant {T}_{q}^{gt,\mathrm{m}\mathrm{a}\mathrm{x}(-1)} , {}\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\;\;\;{\rm{C}}2: {\varGamma }_{rq}^{gt(-1)}\leqslant {\varGamma }_{r}^{gt,\mathrm{m}\mathrm{i}\mathrm{n}(-1)} , {}\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\;\;\; {\rm{C}}3: {T}_{qr}^{gt(-1)}={\varGamma }_{rq}^{gt(-1)}{},\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\; \;\;{\rm{C}}4: {T}_{qr}^{gt(-1)}\geqslant 0,{\varGamma }_{rq}^{gt(-1)}\geqslant 0,\forall {q}\in {\cal{Q}},r\in {\cal{R}} \end{aligned}\right. $

(9)

其中：C1表示每个任务请求终端的请求时延应满足其能容忍的最大时延 $ {T}_{q}^{gt,\mathrm{m}\mathrm{a}\mathrm{x}\left(-1\right)} $ 。C2表示每个任务计算终端的接受时延不能超过其最小学习时延 $ {\varGamma }_{r}^{gt,\mathrm{m}\mathrm{i}\mathrm{n}\left(-1\right)} $ 。C3表示每个任务请求终端的请求时延应和每个任务计算终端的接受时延相等。C4表示每个任务请求终端的请求时延和每个任务计算终端的接受时延均应大于或等于零。

2.2 问题求解

优化问题式(9)的目标函数是严格凹的函数，限制条件C1~C4在可行域范围内是严格凸的^[14]。因此，优化问题有唯一的最优解 $ ({{\boldsymbol{T}}_{qr}^{gt(-1)\circ },{\boldsymbol{\varGamma }}}_{rq}^{gt(-1)\circ }) $ 。优化问题式(9)的Karush-Kuhn-Tucker (KKT)条件推导如下。

$ \tag{10a}\frac{\partial {F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)\circ })}{\partial {T}_{qr}^{gt(-1)}}={\lambda }_{qr}+{\tau }_{qr} $

$ \tag{10b}\frac{\partial {C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)\circ })}{\partial {\varGamma }_{rq}^{gt(-1)}}={\tau }_{qr}-{\sigma }_{rq} $

式中： $ {\lambda }_{qr} $ ， $ {\tau }_{qr} $ 和 $ {\sigma }_{rq} $ 表示拉格朗日乘子。由于任务请求终端和任务计算终端不会向本地接入点揭露各自的效用函数 $ {F}_{q}\left( \cdot \right) $ 和 $ {C}_{r}\left( \cdot \right) $ ，本地接入点无法通过KKT条件求解最优解。因此，本地接入点需要设计合理的价格策略以引导任务请求终端和任务计算终端出价，以揭露各自的隐藏信息。

定义任务请求终端q, $ {q}\in {\cal{Q}} $ 的出价向量为 $ {\boldsymbol{X}}_{qr}^{gt}\triangleq ({x}_{qr}^{gt}{:}\forall {r}\in {\cal{R}}) $ ，每个任务计算终端r, $ {r}\in {\cal{R}} $ 的出价向量为Y $ \triangleq ({y}_{rq}^{gt}{:}\forall r\in {\cal{R}}) $ 。这些出价表征了任务请求终端的需求，以及任务计算终端的服务成本。本地接入点根据双方的出价，构造如下新的优化问题，确定最优联邦学习时延。具体优化问题构造如下

$ \left\{\begin{aligned} & \mathop {{\rm{max}}}_{{\boldsymbol{T}}_{qr}^{gt\left( { - 1} \right)},{\boldsymbol{\varGamma}} _{rq}^{gt\left( { - 1} \right)}} \sum _{q=1}^{Q}\sum _{r=1}^{R}\left(x_{qr}^{gt}{\rm{lo}}{{\rm{g}}_2}T_{qr}^{gt\left( { - 1} \right)} - \frac{{y_{rq}^{gt}}}{2}{(\varGamma _{rq}^{gt\left( { - 1} \right)})^2}\right) \\& {\rm{s.t.}}\; {\rm{C}}1: {T}_{qr}^{gt\left(-1\right)}\geqslant {T}_{q}^{gt,\mathrm{m}\mathrm{a}\mathrm{x}\left(-1\right)} , {}\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\; {\rm{C}}2: {\varGamma }_{rq}^{gt\left(-1\right)}\leqslant {\varGamma }_{r}^{gt,\mathrm{m}\mathrm{i}\mathrm{n}\left(-1\right)} , {}\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\; {\rm{C}}3: {T}_{qr}^{gt\left(-1\right)}={\varGamma }_{rq}^{gt\left(-1\right)}{},\forall {q}\in {\cal{Q}},r\in {\cal{R}} , \\& \;\;\;\;\;\; {\rm{C}}4: {T}_{qr}^{gt\left(-1\right)}\geqslant 0,{\varGamma }_{rq}^{gt\left(-1\right)}\geqslant 0,\forall {q}\in {\cal{Q}},r\in {\cal{R}} \end{aligned}\right. $

(11)

可以看出，优化问题式(11)和(9)有相同的限制条件，但是优化目标各不相同。根据KKT条件，可推导出以下等式。

$\tag{12a} {T}_{qr}^{gt\left(-1\right)*}=\frac{{x}_{qr}^{gt}}{{\lambda }_{qr}+{\tau }_{qr}} $

$ \tag{12b}{\varGamma }_{rq}^{gt\left(-1\right)*}=\frac{{\tau }_{qr}-{\sigma }_{rq}}{{y}_{rq}^{gt}} $

可以看出，式(12a)~(12b)和式(10a)~(10b)不相同，如果任务请求终端和任务计算终端按照式(13)出价。

$\tag{13a} {x}_{qr}^{gt}={T}_{qr}^{gt(-1)*}\frac{\partial {F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)\circ })}{\partial {T}_{qr}^{gt(-1)}} $

$\tag{13b} {y}_{rq}^{gt}=\frac{1}{{\varGamma }_{rq}^{gt(-1)*}}\frac{\partial {C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)\circ })}{\partial {\varGamma }_{rq}^{gt(-1)}} $

优化问题式(11)的最优解和优化问题式(9)的最优解相等，即 $ {\boldsymbol{T}}_{qr}^{gt\left(-1\right)*}\triangleq {\boldsymbol{T}}_{qr}^{gt\left(-1\right)\circ } $ ， $ {\boldsymbol{\varGamma }}_{rq}^{gt\left(-1\right)*}\triangleq {\boldsymbol{\varGamma }}_{rq}^{gt\left(-1\right)\circ } $ 。因此，需要设计合适的价格策略，引导任务请求终端和任务计算终端按照式(13)出价。

定义任务请求终端q, $ {q}\in {\cal{Q}} $ 的支付函数为 $ {Z}_{q}({\boldsymbol{T}}_{qr}^{gt\left(-1\right)}) $ ，任务请求终端通过求解如下效益函数最大化问题，获得最优出价 $ {x}_{qr}^{gt*} $ 。

$ \left\{ \begin{aligned} & \underset{{x}_{{qr}}^{{gt}}}{\mathrm{max}}{F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)})-{Z}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)})\\& {\rm{s.t}}. \;\; {x}_{qr}^{gt}\geqslant 0 , \;{}\forall \;{q}\in {\cal{Q}},r\in {\cal{R}} \end{aligned} \right.$

(14)

优化问题式(14)的解应满足式(15)条件

$ \frac{\partial {F}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)\circ })}{\partial {T}_{qr}^{gt(-1)}}=\frac{\partial {Z}_{q}({\boldsymbol{T}}_{qr}^{gt(-1)\circ })}{\partial {x}_{qr}^{gt}}={\lambda }_{qr}+{\tau }_{qr} $

(15)

类似地，定义任务计算终端r, r $ \in {\cal{R}} $ 的补偿函数为 $ {H}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)}) $ ，任务计算终端通过求解式(16)的效益函数最大化问题，获得最优出价 $ {y}_{rq}^{gt*} $ 。

$ \left\{\begin{aligned} & \underset{{y}_{{rq}}^{{gt}}}{\mathrm{max}}{H}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)})-{C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)}) \\& {\rm{s.t}}. \;\;\; {y}_{rq}^{gt}\geqslant 0 ,\; {}\forall {q}\in {\cal{Q}},\;r\in {\cal{R}} \end{aligned} \right. $

(16)

优化问题式(16)的解应满足式(17)条件。

$ \frac{\partial {C}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)})}{\partial {\varGamma }_{rq}^{gt(-1)}}=\frac{\partial {H}_{r}({\boldsymbol{\varGamma }}_{rq}^{gt(-1)})}{\partial {y}_{rq}^{gt}}=\frac{{({y}_{rq}^{gt})}^{2}}{{\tau }_{qr}-{\sigma }_{rq}} $

(17)

为了引导任务请求终端和任务计算终端按照式(13)出价，相应的价格规则定义为

$ {Z}_{q}\left({x}_{qr}^{gt}\right)=\sum _{q=1}^{Q}\sum _{r=1}^{R}{x}_{qr}^{gt} $

(18)

$ {H}_{r}\left({y}_{rq}^{gt}\right)=\sum _{q=1}^{Q}\sum _{r=1}^{R}\frac{{\left({\tau }_{qr}-{\sigma }_{rq}\right)}^{2}}{{y}_{rq}^{gt}} $

(19)

优化问题式(11)和价格规则式(18)~(19)求出的最优请求时延和最优接受时延，可保证优化问题式(9)实现最大化联邦学习市场效用的目标。可以看出，最优请求时延 $ {T}_{qr}^{gt\left(-1\right)*} $ 和最优接受时延 $ {\varGamma }_{rq}^{gt\left(-1\right)*} $ 与优化问题式(14)和式(16)的出价有关。因此，优化问题式(11)、(14)和(16)需要迭代地求解。本地接入点初始化请求时延 $ {T}_{qr}^{gt\left(-1\right)} $ 、接受时延 $ {\varGamma }_{rq}^{gt\left(-1\right)} $ 以及拉格朗日乘子，并广播初始化值。每个任务请求终端和任务计算终端根据初始值求解问题式(14)和(16)，计算最优出价，并将最优出价发送给本地接入点。然后，本地接入点根据接收的出价更新请求时延 $ {T}_{qr}^{gt\left(-1\right)} $ 、接受时延 $ {\varGamma }_{rq}^{gt\left(-1\right)} $ 以及拉格朗日乘子。本地接入点、任务请求终端和任务计算终端迭代地求解问题式(11)、(14)和(16)，直到请求时延和接受时延收敛。

3 仿真结果

本节通过实验验证提出的基于迭代双边拍卖的联邦学习资源协作激励机制的性能。考虑任务请求终端个数Q为5，任务计算终端个数R为10。所有终端随机地分布在本地接入点覆盖范围内。采用真实数据集CIFAR10^[15]进行联邦学习实验仿真。任务请求终端最大容忍学习时延 $ {T}_{q}^{gt,\mathrm{m}\mathrm{a}\mathrm{x}\left(-1\right)} $ 的取值范围为[200，300] s, 任务计算终端最小接受学习时延 $ {\varGamma }_{r}^{gt,\mathrm{m}\mathrm{i}\mathrm{n}\left(-1\right)} $ 的取值范围为[60，200] s。为了与提出方案对比，设计基于固定价格的资源协作激励机制，即任务请求终端根据固定单位价格向任务计算终端支付报酬。

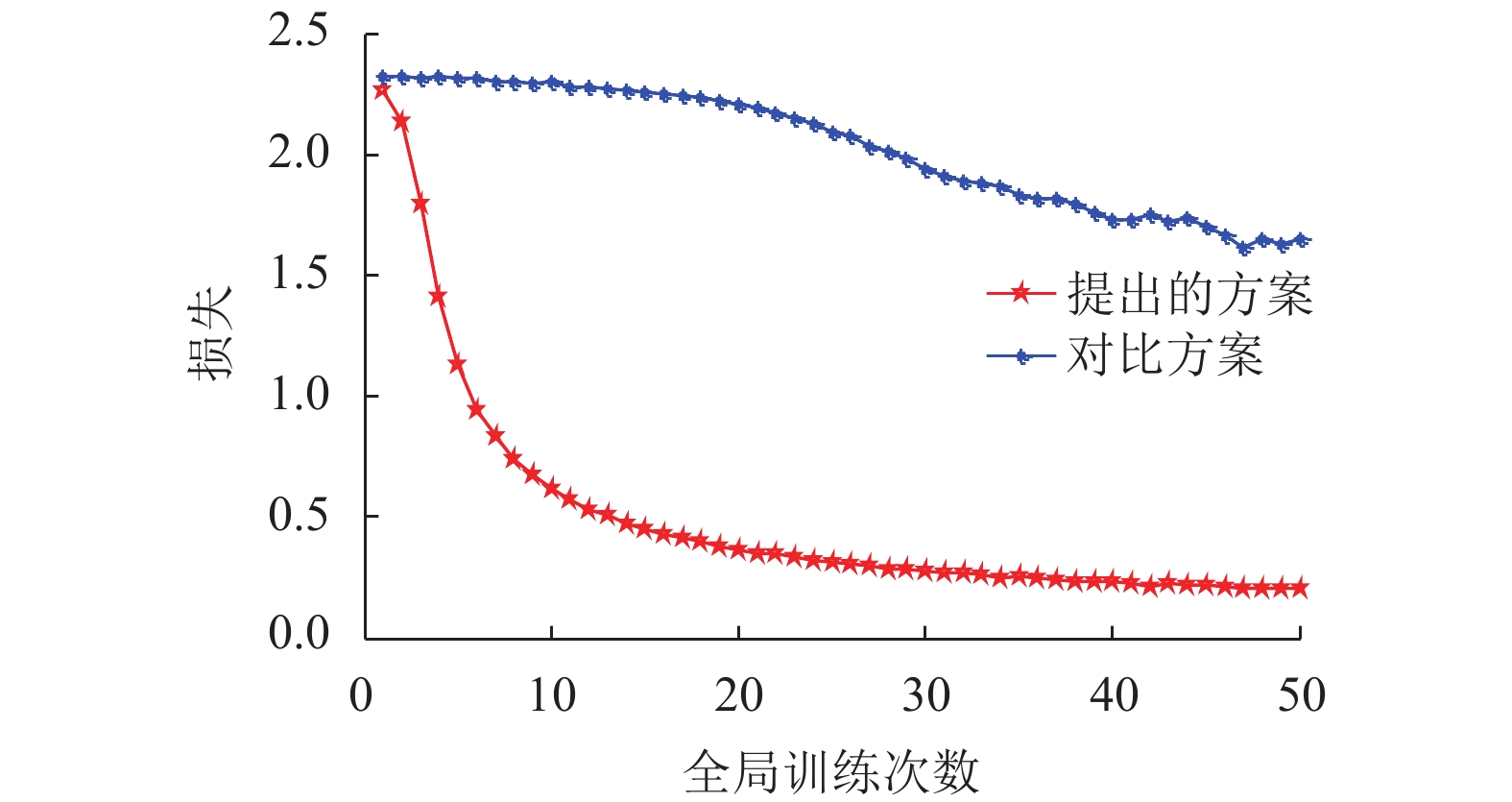
图2对比了两种方案的模型训练损失。从图中可以看出，随着全局训练次数增加，两种方案的损失先降低，然后收敛到固定值。提出方案的损失比对比方案的损失低，因为提出方案可激励所有任务计算终端贡献资源参与联邦学习。对比方案中，任务计算终端不能获得最大效益，因此，部分任务计算终端不愿意参与联邦学习，上传的本地模型参数减少，导致聚合模型损失增加。

图3对比了两种方案的模型准确率。从图中可以看出，随着全局训练次数增加，两种方案的模型准确率先增加，然后收敛到固定值。提出方案的准确率比对比方案的准确率高，因为，提出方案可保证任务计算终端的效益函数最大化，从而激励任务计算终端提供高质量的本地模型参数。对比方案中，任务计算终端不能获得最大的效益，因此，任务计算终端可能提供低质量的本地模型参数，导致聚合模型准确率降低。

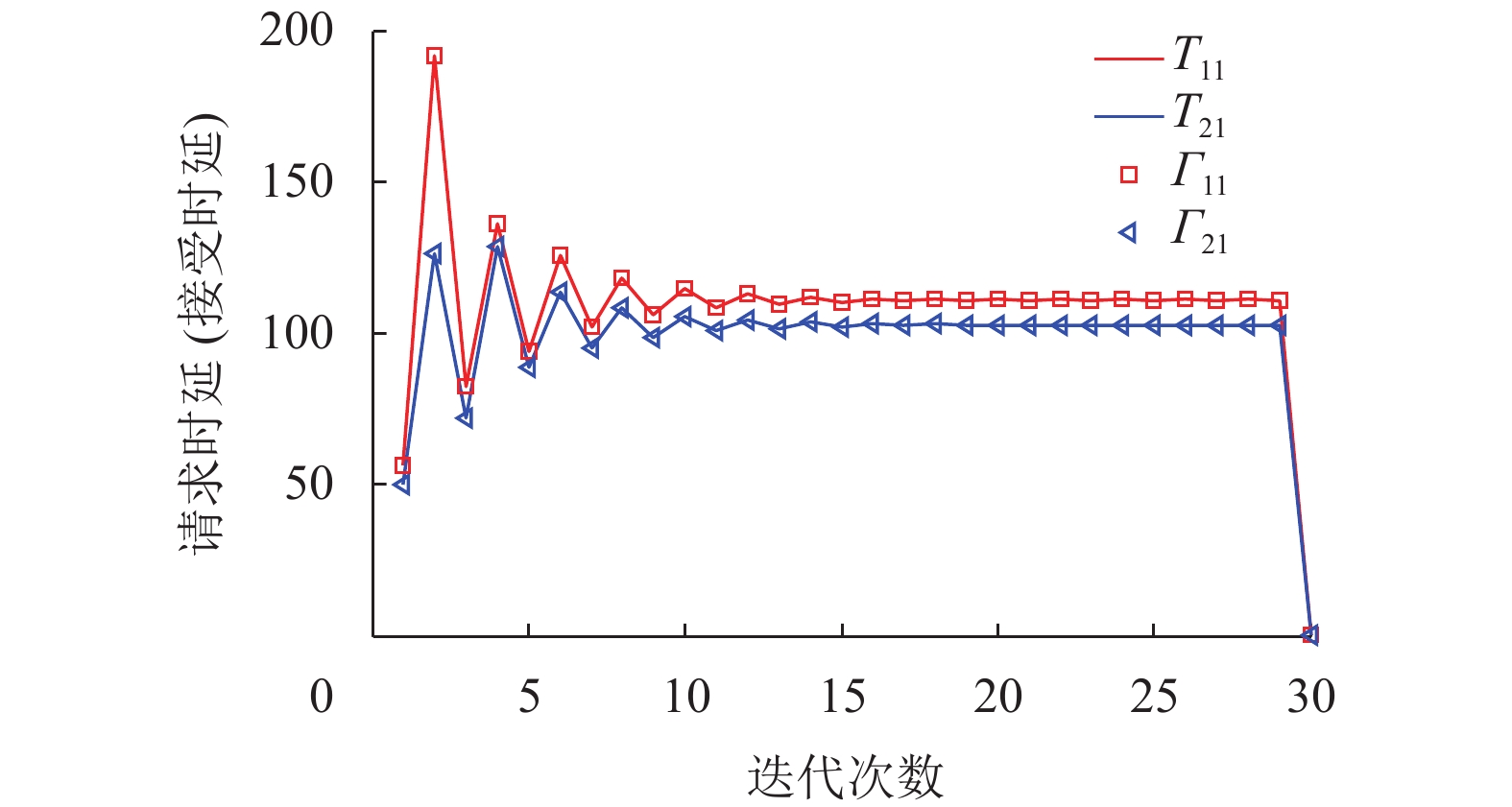
图4展示了任务请求终端q的请求时延 $ {T}_{qr}^{gt} $ 以及任务计算终端r的接受时延 $ {\varGamma }_{rq}^{gt} $ 。以q=1，q=2和r=1，r=2为例。从图中可以看出，请求时延与接受时延相等，证明了提出方案的有效性，即 $ {T}_{qr}^{gt}={\varGamma }_{rq}^{gt} $ 。此外，在迭代13次之后，请求时延和接受时延均收敛到最优解。因此，提出方案可以有效引导任务计算终端和任务请求终端真实地出价，以揭露双方的隐藏信息(即双方的效用函数)，最终获得最大化联邦学习市场总效用的最优请求时延和接受时延。

4 结论

本文提出了6G网络D2D通信的联邦学习框架。移动终端通过联邦学习实现数据共享。针对自私的移动设备不愿意参与模型训练问题，提出基于迭代双边拍卖的资源协作机制。其中，任务计算终端作为卖方，任务请求终端作为买方，本地接入点根据买卖双方的出价对模型训练时延和定价做出决策，在买卖双方信息非对称情况下最大化联邦学习市场总效用。仿真实验表明，提出的机制可以显著提高联邦学习的准确率，降低训练损失，而且具有良好的收敛性。