2. 澳门科技大学 资讯科技学院,澳门 999078
2. Faculty of Information Technology, Macau University of Science and Technology, Macau 999078, China
从“德国工业4.0”到“中国制造2025”,智能制造领域已逐渐成为未来工业发展的制高点,而自动化检测作为贯穿设计、生产与管理等制造领域各重要环节的关键技术,已被世界多国列为优先发展领域,与通信和计算机技术具有同等重要地位。近年来,随着航空航天、材料研发、生物医学等领域的快速发展,现代自动化检测技术对测试手段及相关仪器也提出了更多更高的要求,如高灵敏度、高精度、多功能、内部透视测量等。因此,研发基于新原理的高性能测量方法具有极其重要的意义。
层析成像技术,如计算机断层扫描(Computed Tomography, CT)、超声层析成像(Ultrasound Tomography, UT)、激光共聚焦显微成像(Laser Scanning Confocal Microscope, LSCM)、光学相干层析成像(Optical Coherence Tomography, OCT)等,作为探测物体内部结构信息的最直接手段,一直是国际无损检测领域的研究热点。根据成像原理的不同,这些层析成像技术分别适用于不同被测对象和成像尺度。其中,OCT作为一种基于低相干干涉原理的层析成像技术,它具有微米级层析分辨率和毫米级深度量程,可广泛适用于聚合物、陶瓷、复合材料等透明/半透明物体。该技术自1991年被HUANG D等[1]发表之后,在近30年中得到了快速的发展和广泛的应用[2-5]。尤其是与定量相位、散斑追踪以及相衬等方法进一步结合后,最近还衍生了一系列功能型层析成像方法。他们通过对光程差变化量的高灵敏度检测,揭示物体内部物理量的微弱变化[6-16]。其中,相衬OCT是一种可在测量物体内部形貌同时重构其在力学载荷下位移与应变场的层析成像新方法,能实现材料内部各向异性力学特性的表征与测试,是目前材料检测领域的前沿方向[17-18]。
相衬OCT最早由TORRE-IBARRA M等于2006年提出,它在利用干涉信号幅频特性重构材料内部截面轮廓形貌的基础上,还采用干涉相位对位移的高灵敏特性,实现物体内部纳米级离面位移场的测量[17]。进一步结合矢量梯度等应变场计算方法后,该技术还能实现材料内部应变场的重构,其应变测量灵敏度和动态范围可分别达到10−6和103。得益于相衬OCT的高灵敏特性,该方法最近被广泛应用于材料内部全场力学行为的测试,以实现各向异性力学行为的表征[18-23]。此外,在结合了相衬OCT的快速测量能力和深度分辨能力后,相关学者还将其拓展应用于多种材料内部的检测与监测当中,如多层结构热变形场层析测量、聚合物固化过程的可视化监测、材料内部微缺陷检测等。本文旨在介绍相衬OCT成像原理及其在检测领域典型应用的基础上,对该技术的未来发展进行探讨与展望。
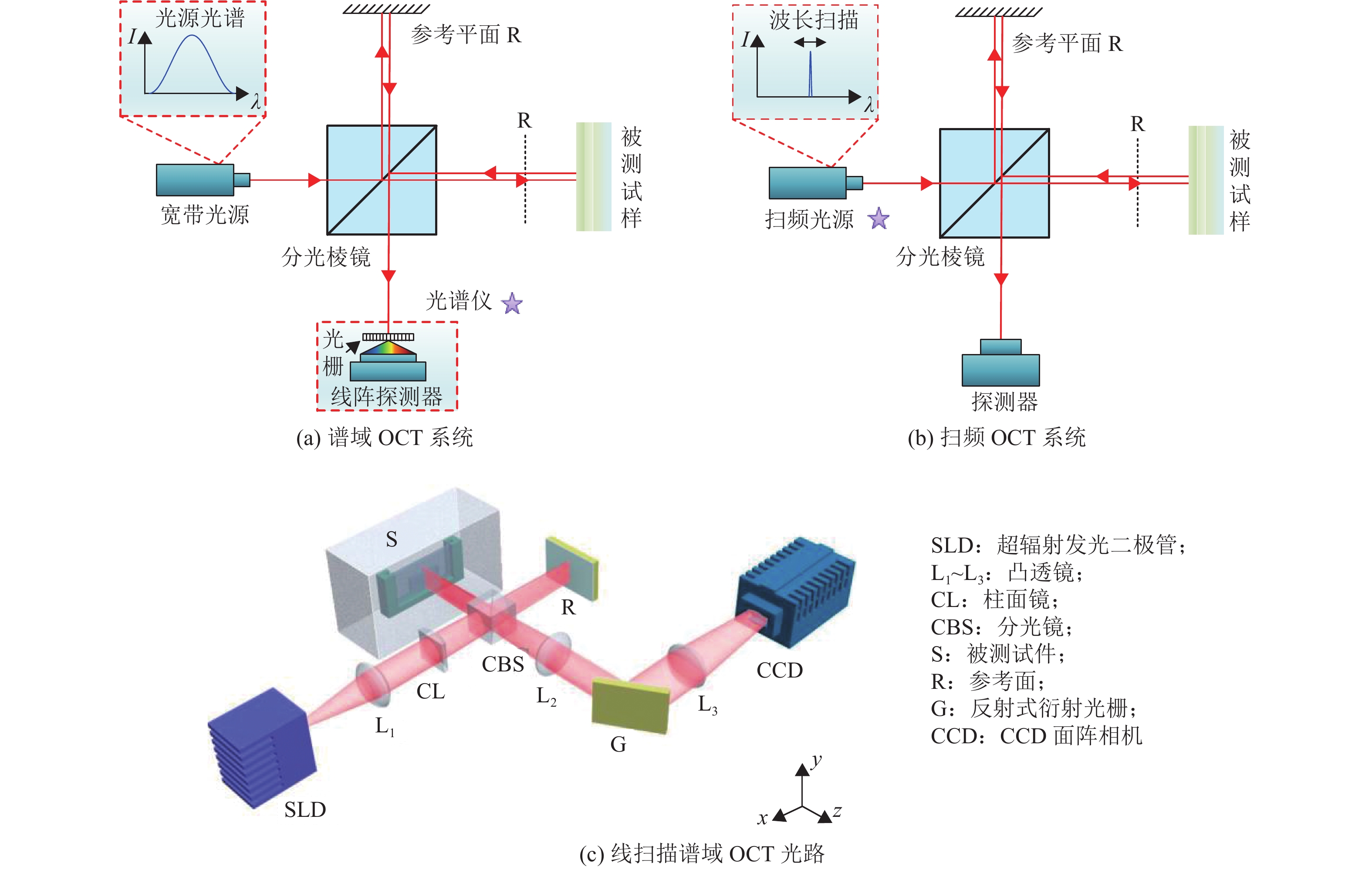
1 相衬光学相干层析原理OCT通常采用宽带光源空间调制或窄带光源时间调制的方式获得参考面与被测试样之间的干涉光谱,因此其光学系统可被分为谱域OCT和扫频OCT两种,如图1(a)和(b)所示。再结合透镜成像原理后,上述系统可分别用于材料二维截面和三维体结构信息的层析成像。图1(c)展示的即为一种可用于材料二维截面成像的线扫描谱域OCT的光学系统结构。利用上述OCT系统采集到的干涉信号可表示为
|
图 1 成像系统示意图 Figure 1 Schematic of the imaging systems |
| $ \begin{split} & I(k,{t_n}) = {I_0} + 2\sum\limits_{j = 1}^M {\sqrt {{I_R}{I_j}} \cos [{\phi _j}(k,{t_n})]} \hfill + \\&\qquad 2\sum\limits_{i = 1}^M {\sum\limits_{j = i + 1}^M {\sqrt {{I_i}{I_j}} \cos [{\phi _i}(k,{t_n}) - {\phi _j}(k,{t_n})]} } \hfill \end{split} $ | (1) |
其中:k=2π/λ为波数,λ为波长,tn为采样时间,I0为干涉信号的直流分量,M为试样内参与干涉的表面个数,IR为参考光强,Ii和Ij为试样内第i和第j个表面的反射光强,ϕ表示相位。式中等号右侧第2项为参考面与试样内各表面干涉形成的互相干分量,第3项为试样内各表面相互干涉形成的自相干分量。由于互相干分量沿k轴的变化频率为fk=Λj/π,因此该信号的频率fk对应于试样内部光学深度Λj;而该分量的幅值又与试样内散射光强Ij正相关,因此其幅频特性即试样内部三维体层析形貌。基于上述原理,OCT在空气介质中的层析分辨率可定义为
| $ \delta _z = \frac{{{\lambda _c^2}}}{{\lambda _w}} $ | (2) |
深度量程为
| $ \varDelta _z = \frac{{N{\lambda _c^2}}}{{4\lambda _w }} $ | (3) |
其中:δz受限于光源带宽λw和光源中心波长λc,它通常是5~15 μm;Δz则受限于干涉测量系统沿光谱轴的采样率N,它通常是1~3 mm。在实际应用中,可采用增加光源带宽或开发超分辨算法的方式满足更高分辨的检测需要。为此,相关学者在结合波长合成、压缩感知等方法和算法的基础上,还相继开发了多种高分辨OCT成像方法[24-27]。
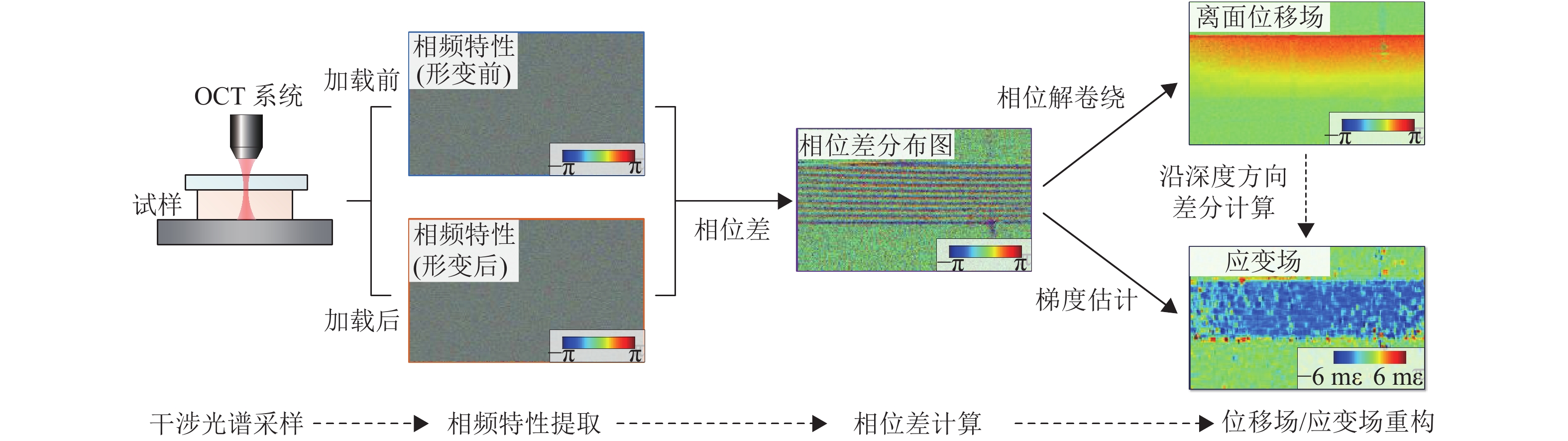
除了采用幅频特性获得被测材料内部截面形貌信息外,结合了相衬技术的OCT还能用于材料内部微变形场重构,其测量原理如下。首先,采用OCT系统获得式(1)所述随时间变化的干涉光谱,并对形变前后采集到的干涉光谱的相频特性进行差分相位ϕdiff,得到光程差的变化量Λdiff
| $ \varLambda_{\rm{diff}} (x,y,z,{t_n}) = \frac{{{\lambda _c}}}{{4{\text{π}} }}\phi_{\rm{diff}} (x,y,z,{t_n}) $ | (4) |
忽略形变过程材料的折射率变化,可根据光程差与距离之间的物理关系进一步得到各层材料离面位移wj与光程差变化量Λdiff之间的关系
| $ \varLambda _{\rm{diff}} = ({n_0} - n){w_1} + n{w_j} $ | (5) |
其中:n0和n分别是空气和被测材料的折射率。从式(4)可以看出,相位差每变化2π代表光程差变化了光源中心波长λc的一半,也即约420 nm。因此,基于相衬方法的OCT技术能实现优于1 nm灵敏度的全场光程差变化测量。但需要注意的是,在从相位差计算光程差变化量的过程中还需进行相位解卷绕计算,以消除2π相位模糊效应。
对相位差ϕdiff沿深度z方向进行梯度估计后,还可以得到
| $ \varPhi _{\rm{diff}}(x,y,z,t) = \frac{{4{\text{π}} \delta _z}}{{{\lambda _c}}}{\varepsilon _z}(x,y,z,{t_n}){n_0} $ | (6) |
其中:εz为试样深度方向的正应变。上述梯度估计过程可以在相位解卷绕后获得的离面位移场中采用最小二乘等方法进行,也可直接在卷绕相位场采用矢量平均等方法进行,如图2所示[28-30]。值得一提的是,尽管结合了相衬方法的OCT技术能够实现离面位移的高灵敏测量,但当位移量超过层析分辨率时(也即约10 μm时)会产生散斑退相关现象,从而限制了该方法的动态测量范围。为解决该问题,近年来相关学者还相继开发了基于位移估计和噪声定位的一系列跨像素差分相位算法[31-32]。
|
图 2 相衬OCT测量方法示意图 Figure 2 Schematic of the phase-contrast OCT system |
相衬OCT是一种适用于材料内部微变形场层析测量的有效方法,因此它可拓展应用于温度变化过程中材料内部热变形场的测量。但由于材料热变形过程中折射率也会同时发生改变,而且相关研究显示材料热变形过程的应变量和折射率变化量为同一量级。因此,在利用相衬OCT测量热变形场的过程中,还需在式(6)基础上考虑折射率的变化量。2015年,ZHANG Y等[33]在考虑多层材料折射率温度系数不同的前提下,提出了一种多层结构热变形的位移场计算新模型
| $ \begin{split} & w(x,y,z) = \frac{{\phi_{\rm{diff}} (x,y,z)}}{{2{k_c} {n_l}}} + \frac{1}{{{n_l}}}\sum\limits_{i = 1}^l \{ [w(x,y,{z_{i - 1}}) -\\&\qquad w(x,y,{z_i})] {n_{i - 1}} + ({z_{i - 1}} - {z_i}) \Delta {n_{i - 1}} \} + \\&\qquad ({z_l} - z) \frac{{\Delta {n_l}}}{{{n_l}}} + w(x,y,{z_l}) \end{split}$ | (7) |
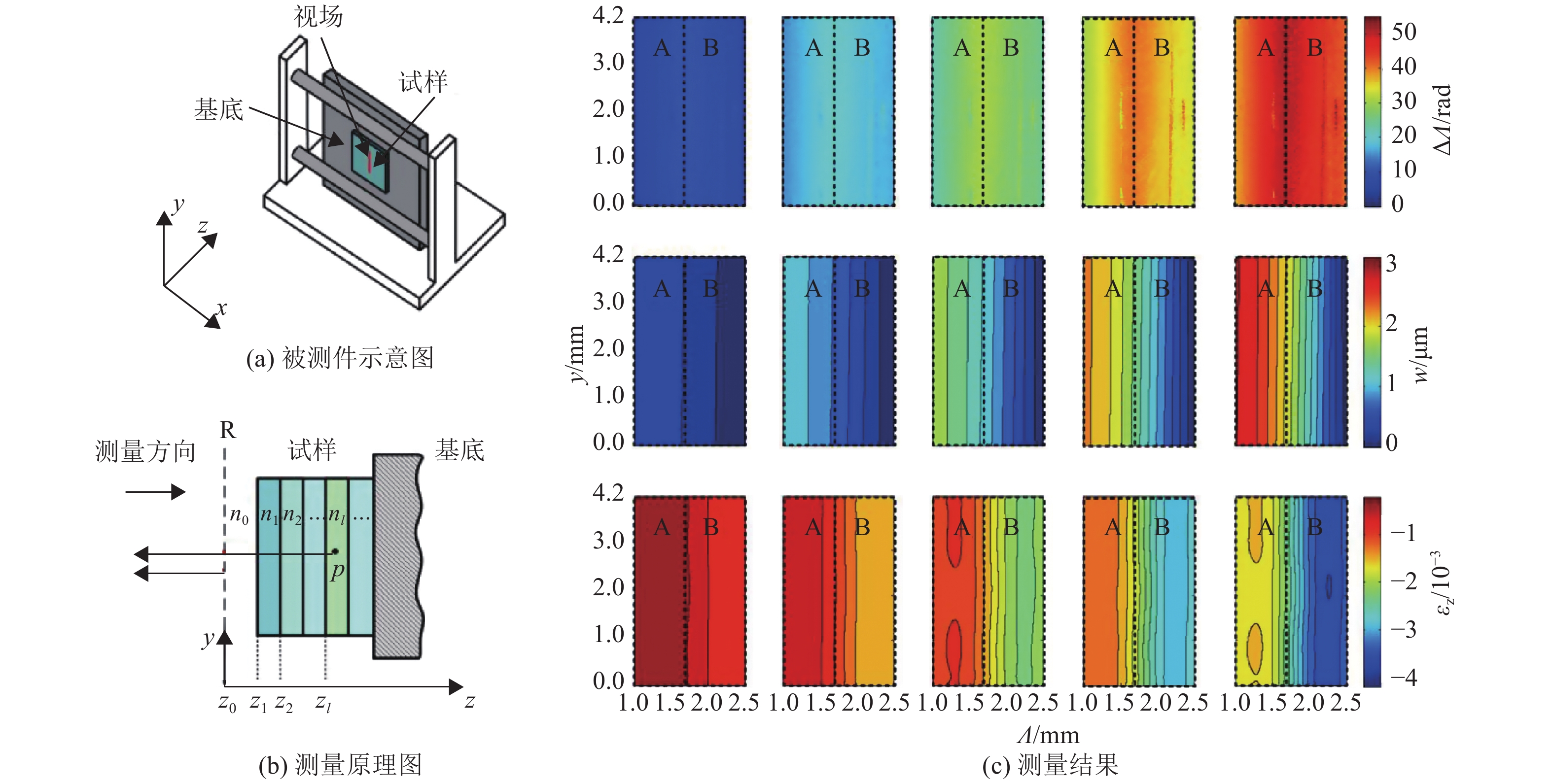
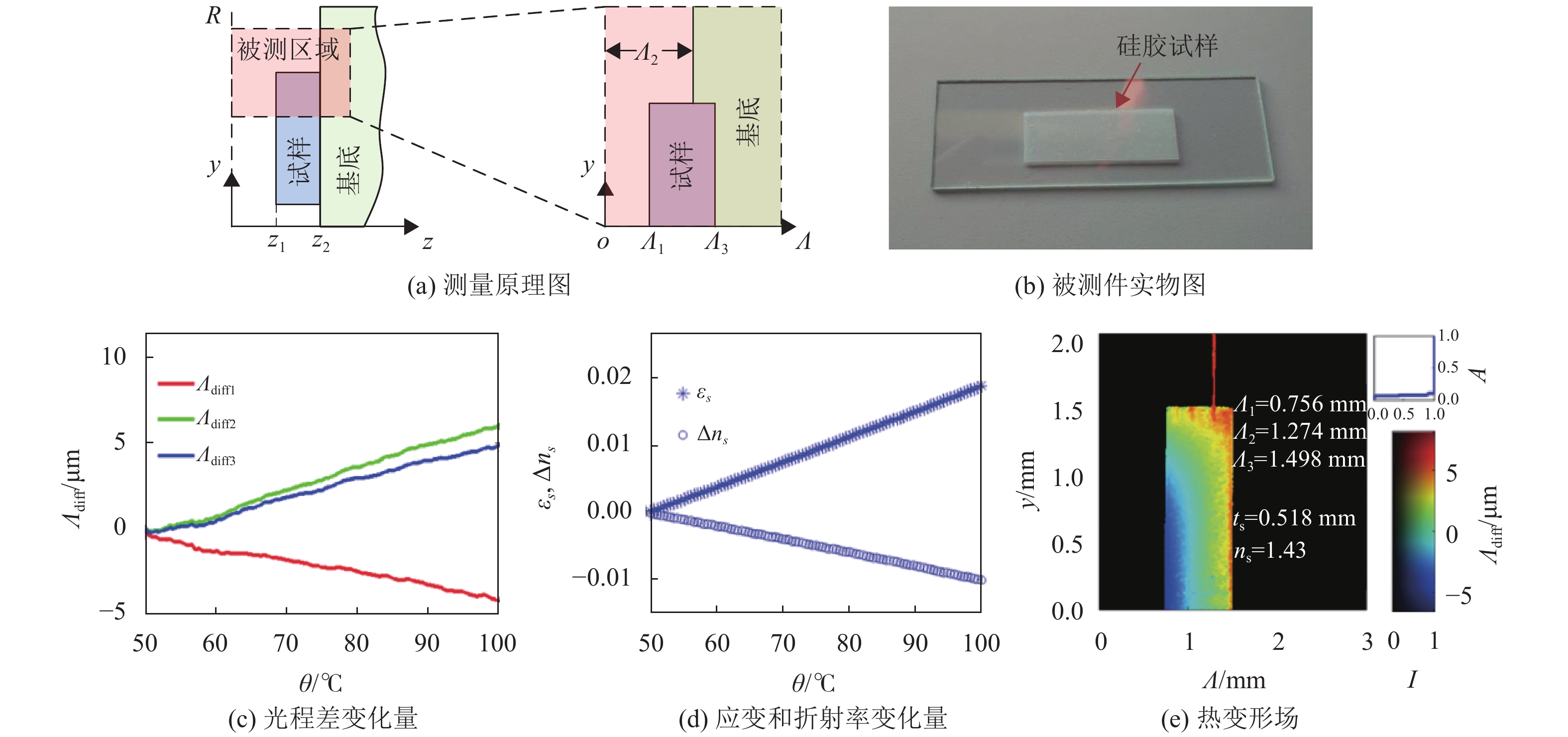
其中:zl表示第l层材料前表面的深度,nl和Δnl分别表示第l层材料的折射率和折射率变化量。基于该模型,他们利用相衬OCT实现了多层结构内部热变形场的准确测量,如图3所示。从结果可以看出,在测量具有不同热膨胀系数的双层薄膜时,差分相位沿深度变化的梯度呈现先增后减的趋势。此时若不考虑折射率变化,将会导致计算出前后两层材料分别处于收缩和膨胀过程的错误结果。而在采用改进后模型计算的位移与应变场中能够看到,两层材料均处于收缩过程,只是收缩程度不同,这与实际情况一致。此外,基于应变计算的双层材料热膨胀系数与参考值一致,验证了上述新模型的可靠性。尽管结合了位移场计算新模型的相衬OCT可实现材料内部热变形场的准确测量,但其在实际应用中仍需要在测量之前对材料的折射率和温度系数进行预先测定,具体实现较为繁琐。为此,相关学者又设计了一种实验方法,利用相衬OCT同时测量了折射率、温度系数和材料内部热变形场[34]。如图4所示,该方法在测量材料内部热变形场过程中,同时监测了试样基底表面的光程差及其变化量。图4(e)中的I和A分别为归一化后的强度和幅值。首先,该方法可获得被测对象的厚度d=Λ2−Λ1,以及被测对象的折射率n=(Λ3−Λ1)/(Λ2−Λ1)。然后,再根据光程差变化量与形变、折射率变化量之间的关系,可进一步得到材料的折射率变化量
| $ \Delta n = \frac{{ {\varLambda _{{\rm{diff}}3}} - {\varLambda _{{\rm{diff}}1}}}}{d} - \frac{{ {\varLambda _{{\rm{diff}}2}} - {\varLambda _{{\rm{diff}}1}}}}{d} \cdot \frac{n}{{{n_0}}} $ | (8) |
其中:Λdiff1、Λdiff2和Λdiff3分别为试样前、后表面以及基底前表面的光程差变化量。从图4所示实验结果可以看出,基底前表面光程差变化量Λdiff3与其他两个光程差变化量均为微米级,表明其影响在折射率变化量测量中不可忽略,须同步监测;而应变和折射率变化量在热变形过程处于同一量级,印证了前文所述折射率变化量在热变形场重构过程的不可忽略性。
|
图 3 双层薄膜A和B的热变形场层析测量[33] Figure 3 Thermal deformation measurement of a dual-layered film A and B[33] |
|
图 4 基于相衬OCT的材料折射率温度系数和热变形场同时测量[34] Figure 4 Simultaneous measurement of refractive index variation and thermal deformation field by using the phase-contrast OCT[34] |
除了可用于材料内部全场力学性能表征与测试之外,相关学者近期还发现结合了相衬方法的OCT技术可拓展用于聚合物固化过程的可视化监测。聚合物是一类由简单结构单元重复连接而成的高分子化合物材料,具有易改性、易加工、低导电、低导热、高耐腐和高比强等特点,在国防建设、工业制造、生物医学等多领域发挥重要作用。而聚合物在制备成型期间需经历由低分子到高分子的转变过程,期间连续变化的力学和流变学特性对聚合物材料的最终性能有着至关重要的影响。然而,现有方法都只能用于聚合物固化过程的整体固化度监测,无法用于了解和研究聚合物固化过程存在的空间分布特征。针对该问题,DONG B和PAN B[35]在2020年开发了基于相衬OCT的聚合物固化过程监测方法,它利用OCT的层析测量能力和相衬技术的高灵敏特性,成功观测了具有深度分布特征的聚合物凝胶过程以及双层聚合物固化过程,首次实现了聚合物内部空间分辨的固化过程可视化监测,其测量原理如下。
由于聚合物固化会同时产生形变和折射率变化,而且由于材料内部固化过程具有各向异性分布的特征,因此可将式(6)改写为
| $ \Delta \varPhi_{\rm{diff}} (x,y,z,t) = \frac{{4{\text{π}} }}{{{\lambda _c}}}[{\varepsilon _z}(x,y,z,{t_n}){n_0} + \Delta n(x,y,z,{t_n})]\delta z $ | (9) |
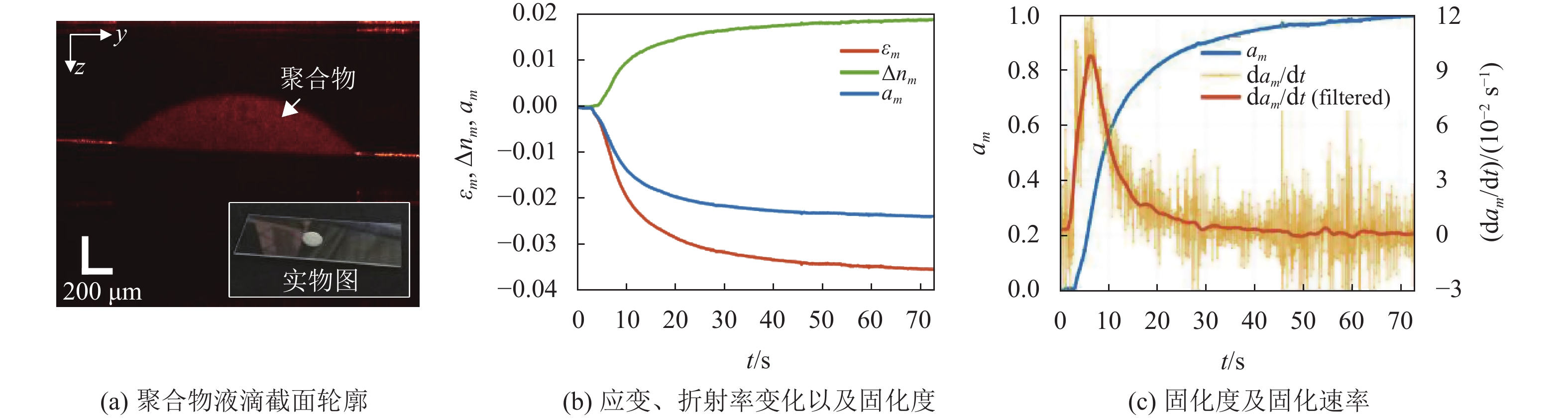
能够发现,相衬OCT在固化过程测量到的相位深度梯度是由应变和折射率变化量组成的一个复合量。在传统固化监测方法中,收缩应变和折射率变化量是用于监测聚合物固化程度的两个常用指标,因此其两者组成的复合量也可用于监测聚合物固化程度。为此,相关学者首先进行了验证实验,同时监测了聚合物试样固化过程的收缩应变、折射率变化量以及相位深度梯度。从图5所示结果可以看出,上述3个物理量随时间的变化趋势相同,表明相位深度梯度可作为一个固化监测的有效指标。
基于上述结论,他们分别对单层聚合物试样和双层聚合物试样进行了实验测量,如图6所示[35]。从双层聚合物试样测量结果中能够发现,尽管层析截面轮廓(左图)中难以分辨上下两层聚合物液滴,但是从相位差分布图(右上图)以及应变速率分布图(右下图)能够看出两层材料固化速率的明显不同,验证了方法的深度分辨能力;从单层聚合物试样测量结果中能够看出,在聚合物由液态转变为凝胶态的过程中,存在明显的由表及里的深度分布特征。并且由于固化光源分布于聚合物液滴左上侧,因此还能清晰地观测到凝胶点从左至右的变化过程。由于该方法首次实现了聚合物内部固化过程空间分布的可视化监测,该成果近期还得到了美国物理联合会《科学之光》的专题报道。

|
图 6 基于相衬OCT的聚合物内部固化过程可视化监测结果[35] Figure 6 Visualizing the polymer curing process by using the phase-sensitive OCT [35] |
结合相衬OCT的高灵敏特性和缺陷材料受力变形过程普遍表现出的应力集中现象,相关学者还开发了一种基于相衬OCT的微缺陷可靠辨识方法[36]。从式(2)可以看出,OCT的层析分辨率通常为微米级,因此采用直接成像方式观测反射率奇异点可实现10 μm以上缺陷的辨识。但这种基于层析形貌测量的缺陷检测方式存在两个主要问题:(1) 无法检测尺度小于10 μm的缺陷,而且难以准确辨识尺度接近10 μm的缺陷。基于OCT测量的半透明被测试样内部通常呈散斑状分布,因此即使缺陷尺度略大于层析分辨率,仍难以准确区分散斑点与缺陷点。(2) 难以对复杂结构内部缺陷进行可靠辨识。对于复合材料等内部结构复杂的材料,即使从形貌测量结果中能观测到反射率奇异点,但仍难以准确区分增强材料与缺陷点。相衬OCT作为一种微形变全场测量方法,在结合应力集中现象后,可通过形变奇异点实现材料内部层析分辨率以下的微小缺陷的准确辨识。而且考虑到相位差分布与形变正相关,因此直接观察卷绕相位分布中的奇异点就能实现缺陷辨识。基于此,相关学者利用相衬OCT分别对4类试样在降温过程进行了测试,如图7所示[36]。图7(a)所示为一各向同性材料的测量结果,从其形貌测量结果和相位差分布结果中均不存在奇异点可知,该材料不存在内部缺陷;图7(b)所示为另一各向同性材料的测量结果,从其形貌测量结果和相位差分布结果中均存在奇异点可知,该材料存在内部缺陷。而且从形貌测量结果中能够清晰观测到该缺陷大小为百微米级;图7(c)所示为第三种各向同性材料的测量结果,其形貌测量结果不存在奇异点,但相位差分布结果中存在奇异点,表明该材料内存在层析测量结果无法辨识的微米/亚微米级缺陷;图7(d)所示为一各向异性材料的测量结果,其形貌测量结果存在奇异点,而相位差分布结果中不存在奇异点,表明材料内部的高反射率点是材料内部增强材料而非内部缺陷。上述4类实验结果验证了基于相位分布的缺陷辨识方法一方面提高了缺陷辨识的灵敏度,可识别微米/亚微米级缺陷;另一方面还提高了缺陷识别的可靠性,可准确判断材料自身结构及缺陷点,具有比形貌测量更高的识别率和灵敏度。

|
图 7 基于相衬OCT的材料内部缺陷检测结果[36] Figure 7 Detecting the internal defect by using the phase-contrast OCT[36] |
OCT作为近年来发展迅速的一种层析成像技术,在结合了相衬方法后它可拓展应用于透明/半透明物体内部位移与应变的全场高灵敏测量,被广泛用于材料内部各向异性力学特性表征、聚合物内部固化过程可视化监测、物体内部微小缺陷高灵敏辨识等多个方面,目前已成为无损检测领域研究热点。该技术特点可总结如下:
(1) 微米级层析分辨率:OCT以低相干干涉方式从干涉光谱的幅频和相频特性分别提取被测对象内部的形貌和形变信息,其层析分辨率受限于系统对干涉光谱信号的采样带宽,通常为5~15 μm。因此该方法非常适用于内部复杂结构材料的表征与测试,如各类纤维增强复合材料等[37-38]。
(2) 纳米级位移测量灵敏度:相衬OCT利用干涉信号相位灵敏的特性,实现材料内部位移与应变场的测量。由于相位差每变化2π代表光程差变化了光源中心波长的一半,因此其测量灵敏度可达纳米级。再结合OCT毫米级的深度量程,该方法的应变测量灵敏度也可达到10−6,也即微应变级。所以,该方法特别适用于材料内部微形变的测试,如温度变化以及聚合物固化收缩导致的材料形变。
(3) 适用于透明/半透明材料:相衬OCT通常采用近红外波段宽带光源/扫频光源对物体内部进行层析测量,因此其普遍适用于透明和半透明物体,包括聚合物、复合材料、陶瓷等。近年来,大量学者也在探索基于中红外、太赫兹波的OCT成像方法,因此该技术在未来还有望拓展应用于非透明材料的表征与测试当中[39-40]。
综上所述,相衬OCT是一种极具前景的非接触式全场检测技术,未来可服务于各类高性能材料的研发与测试,为工业制造、生物医学、航空航天等领域的发展提供有力的技术支撑。
| [1] |
HUANG D, SWANSON E A, LIN C P, et al. Optical coherence tomography[J].
Science, 1991, 254(5035): 1178-1181.
DOI: 10.1126/science.1957169. |
| [2] |
FUJIMOTO J G, PITRIS C, BOPPART S A, et al. Optical coherence tomography: an emerging technology for biomedical imaging and optical biopsy[J].
Neoplasia, 2000, 2(1-2): 9-25.
DOI: 10.1038/sj.neo.7900071. |
| [3] |
SU R, KIRILLIN M, CHANG E W, et al. Perspectives of mid-infrared optical coherence tomography for inspection and micrometrology of industrial ceramics[J].
Optics Express, 2014, 22(13): 15804-15819.
DOI: 10.1364/OE.22.015804. |
| [4] |
BOER J F D, LEITGEB R, WOJTKOWSKI M. Twenty-five years of optical coherence tomography: the paradigm shift in sensitivity and speed provided by Fourier domain OCT[J].
Biomedical Optics Express, 2017, 8(7): 3248-3280.
DOI: 10.1364/BOE.8.003248. |
| [5] |
董博, 潘兵. 光学相干层析及其在实验力学中的应用[J].
科学通报, 2020, 65(20): 2094-2105.
DONG B, PAN B. Optical coherence tomography and its applications in experimental mechanics: a review[J]. Chinese Science Bulletin, 2020, 65(20): 2094-2105. DOI: 10.1360/TB-2020-0121. |
| [6] |
SUN C, STANDISH B, VUONG B, et al. Digital image correlation-based optical coherence elastography[J].
Journal of Biomedical Optics, 2013, 18(12): 121515.
DOI: 10.1117/1.JBO.18.12.121515. |
| [7] |
FU J, PIERRON F, RUIZ P D. Elastic stiffness characterization using three-dimensional full-field deformation obtained with optical coherence tomography and digital volume correlation[J].
Journal of Biomedical Optics, 2013, 18(12): 121512.
DOI: 10.1117/1.JBO.18.12.121512. |
| [8] |
LIU P, GROVES R M, BENEDICTUS R. Optical coherence elastography for measuring the deformation within glass fiber composite[J].
Applied Optics, 2014, 53(22): 5070-5077.
DOI: 10.1364/AO.53.005070. |
| [9] |
ZAITSEV V Y, MATVEYEV A L, MATVEEV L A, et al. Optical coherence elastography for strain dynamics measurements in laser correction of cornea shape[J].
Journal of Biophotonics, 2017, 10(9): 1450-1463.
|
| [10] |
BOER J, MILNER T E, GEMERT M, et al. Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography[J].
Optics Letters, 1997, 22(12): 934-936.
DOI: 10.1364/OL.22.000934. |
| [11] |
YASUNO, MAKITA, SUTOH, et al. Birefringence imaging of human skin by polarization-sensitive spectral interferometric optical coherence tomography[J].
Optics Letters, 2002, 27(20): 1803-1805.
DOI: 10.1364/OL.27.001803. |
| [12] |
LEITGEB R A, WERKMEISTER R M, BLATTER C, et al. Doppler optical coherence tomography[J].
Progress in Retinal & Eye Research, 2014, 41(10): 26-43.
|
| [13] |
WESTPHAL V, YAZDANFAR S, ROLLINS A M, et al. Real-time, high velocity-resolution color Doppler optical coherence tomography[J].
Optics Letters, 2002, 27(1): 34-36.
DOI: 10.1364/OL.27.000034. |
| [14] |
KENNEDY B F, WIJESINGHE P, SAMPSON D D. The emergence of optical elastography in biomedicine[J].
Nature Photonics, 2017, 11(4): 215-221.
DOI: 10.1038/nphoton.2017.6. |
| [15] |
LARIN K V, SAMPSON D D. Optical coherence elastography-OCT at work in tissue biomechanics[J].
Biomedical Optics Express, 2017, 8(2): 1172-1202.
DOI: 10.1364/BOE.8.001172. |
| [16] |
NICHALUK L, IYER R R, UNTRACHT G R, et al. Photonic force optical coherence elastography for three-dimensional mechanical microscopy[J].
Nature Communications, 2017, 9(1): 2079.
|
| [17] |
TORRE-IBARRA M, RUIZ P D, HUNTLEY J M. Double-shot depth-resolved displacement field measurement using phase-contrast spectral optical coherence tomography[J].
Optics Express, 2006, 14(21): 9643-9656.
DOI: 10.1364/OE.14.009643. |
| [18] |
TORRE-IBARRA M, RUIZ P D, HUNTLEY J M. Simultaneous measurement of in-plane and out-of-plane displacement fields in scattering media using phase-contrast spectral optical coherence tomography[J].
Optics Letters, 2009, 34: 806-808.
DOI: 10.1364/OL.34.000806. |
| [19] |
LIU H, DONG B, BAI Y, et al. Perspective measurement of the out-of-plane displacement and normal strain field distributions inside glass fibre-reinforced resin matrix composite[J].
Strain, 2015, 51(3): 198-205.
DOI: 10.1111/str.12133. |
| [20] |
董博, 徐金雄, 白玉磊, 等. 快速和高精度透视测量玻璃纤维/树脂复合材料构件内部的离面位移[J].
复合材料学报, 2014, 31(2): 331-337.
DONG B, XU J X, BAI Y L, et al. Rapid and high-precision measurement of out-of-plane displacement inside the glass fiber/polymer composite[J]. Acta Materiae Compositae Sinica, 2014, 31(2): 331-337. |
| [21] |
ZHANG W, DONG B, ZHANG W, et al. Depth-resolved measurement of the compression displacement fields on the front and rear surfaces of an epoxy sample[J].
Optica Applicata, 2018, 48(2): 311-323.
|
| [22] |
DONG B, ZHANG Y, YE S, et al. Dual-channel phase-contrast spectral optical coherence tomography for simultaneously measuring axial and normal to B-scan off-axial displacements[J].
Optics and Lasers in Engineering, 2017, 96: 35-38.
DOI: 10.1016/j.optlaseng.2017.04.007. |
| [23] |
周延周, 朱文卓, 董博, 等. 树脂基复合材料内部离面位移场和应变场分布的动态测量[J].
光学精密工程, 2014, 12: 3217-3223.
ZHOU Y Z, ZHU W Z, DONG B, et al. Dynamical measurement of out-of-plane displacement field and strain field inside resin composite[J]. Optics and Precision Engineering, 2014, 12: 3217-3223. |
| [24] |
LV Z, BAI Y, HE Z, et al. Super-resolution reconstruction of speckle phase in depth-resolved wavelength scanning interference using the total least-squares analysis[J].
Journal of the Optical Society of America. A, Optics, image science, and vision, 2019, 36(5): 869-876.
DOI: 10.1364/JOSAA.36.000869. |
| [25] |
XU J, LIU Y, DONG B, et al. Improvement of the depth resolution in depth-resolved wavenumber-scanning interferometry using multiple uncorrelated wavenumber bands[J].
Appl Opt, 2013, 52(20): 4890-4897.
DOI: 10.1364/AO.52.004890. |
| [26] |
BAI Y, ZHOU Y, HE Z, et al. Compressed-sensing wavenumber-scanning interferometry[J].
Optics & Laser Technology, 2018, 98: 229-233.
|
| [27] |
BAI Y, ZHOU Y, HE Z, et al. Wavenumber synthesis approach to high-resolution wavenumber scanning interference using a mode-hoped laser[J].
Optics Express, 2018, 26(5): 5441-5451.
DOI: 10.1364/OE.26.005441. |
| [28] |
KENNEDY B F, KOH S H, MCLAUGHLIN R A, et al. Strain estimation in phase-sensitive optical coherence elastography[J].
Biomedical Optics Express, 2012, 3(8): 1865-1879.
DOI: 10.1364/BOE.3.001865. |
| [29] |
MATVEYEV A L, MATVEEV L A, SOVETSKY A A, et al. Vector method for strain estimation in phase-sensitive optical coherence elastography[J].
Laser Physics Letters, 2018, 15(6): 065603.
DOI: 10.1088/1612-202X/aab5e9. |
| [30] |
ZAITSEV V Y, MATVEYEV A L, MATVEEV L A, et al. Optimized phase gradient measurements and phase-amplitude interplay in optical coherence elastography[J].
Journal of Biomedical Optics, 2016, 15(6): 065603.
|
| [31] |
ZAITSEV V Y, MATVEYEV A L, MATVEEV L A, et al. Hybrid method of strain estimation in optical coherence elastography using combined sub-wavelength phase measurements and supra-pixel displacement tracking[J].
Journal of Biophotonics, 2016, 9(5): 499-509.
DOI: 10.1002/jbio.201500203. |
| [32] |
DONG B, ZHANG Y, PAN B. Enhancing the dynamic range of phase-sensitive optical coherence elastography by overcoming speckle decorrelation[J].
Optics Letters, 2018, 43(23): 5805-5808.
DOI: 10.1364/OL.43.005805. |
| [33] |
ZHANG Y, DONG B, BAI Y, et al. Measurement of depth-resolved thermal deformation distribution using phase-contrast spectral optical coherence tomography[J].
Optics Express, 2015, 23(21): 28067-28075.
DOI: 10.1364/OE.23.028067. |
| [34] |
DONG B, XIE S, HE Z, et al. Simultaneous measurement of temperature-dependent refractive index and depth-resolved thermal deformation fields inside polymers[J].
Polymer Testing, 2017, 65: 297-300.
|
| [35] |
DONG B, PAN B. Visualizing curing process inside polymers[J].
Applied Physics Letters, 2020, 116(5): 054103.
DOI: 10.1063/1.5141827. |
| [36] |
DONG B, PAN B, ZHANG Y, et al. Microdefect identification in polymers by mapping depth-resolved phase-difference distributions using optical coherence tomography[J].
Polymer Testing, 2018, 68: 233-237.
DOI: 10.1016/j.polymertesting.2018.04.023. |
| [37] |
DUNKERS J P, PHELAN F R, SANDERS D P, et al. The application of optical coherence tomography to problems in polymer matrix composites[J].
Optics & Lasers in Engineering, 2001, 35(3): 135-147.
|
| [38] |
LIU P, GROVES R M, BENEDICTUS R. Optical coherence tomography for the study of polymer and polymer matrix composites[J].
Strain, 2014, 50(5): 436-443.
DOI: 10.1111/str.12095. |
| [39] |
NISHII H, NAGATSUMA T, IKEO T. Terahertz imaging based on optical coherence tomography[J].
Photonics Research, 2014, 2(4): 1-5.
|
| [40] |
ISRAELSEN N M, PETERSEN C R, BARH A, et al. Real-time high-resolution mid-infrared optical coherence tomography[J].
Light: Science & Applications, 2019, 8(1): 11.
|
 2021, Vol. 38
2021, Vol. 38