为了在软弱地基上修建路、堤(坝)等设施,传统方法是预先对软土进行处理(如采用砂井−堆载或/和真空预压等),以减小其沉降和提高其承载能力。但该类方法施工周期较长,工后(不均匀)沉降可能依然较大。桩撑式技术是近十多年来兴起的一种在软弱地基上修建路堤的新方法。它通过在软土中设置桩和桩帽,并在其上铺设加筋体(土工布、土工格栅等),最后再在加筋体上填土修筑路堤。实践结果表明,该方法施工速度快,工后沉降小且均匀,具有广阔的应用前景。
研究结果表明[1-6],源自于路堤的荷载(自重以及其上其他荷载),一部分通过填土中形成的土拱直接传给了相邻的桩,其余的则通过加筋体间接传给了桩和其下的地基土(如果有并考虑其支撑作用的话)。前者称之为“荷载A”,后者称为“荷载B+荷载C”。“荷载B”和“荷载C”分别指间接传给桩和地基土的那部分荷载。
基于上述荷载传递机理,桩撑式路堤的设计自然也分为两步:第一步即为确定“荷载A”。该方面的研究比较深入、广泛,也取得了丰富的成果[7-12];第二步就是确定“荷载B”和“荷载C”。该步的关键是依据加筋体的荷载−变形特性确定加筋体受荷后的变形以及加筋体内的拉力及其变化。这是因为,“荷载B”就是加筋体在桩帽内边缘处拉力的竖直分量,而一旦确定出加筋体的变形,则可利用地基变形模型(如Winkler模型等)计算出“荷载C”。
但应指出的是,虽然加筋体的拉力与应变之间可用简单的线性关系表示(见下文的式(13)),但因应变与位移之间是高度非线性的,因此,利用加筋体受力平衡条件最终形成的荷载−变形关系仍然是一组高度的非线性微分方程组,不易求解[13]。有鉴于此,目前常用的方法是:以加筋体的受力平衡方程为基础,再附加一些其他假定条件,以期求得加筋体的变形和拉力。其中假定加筋体中拉力是均匀变化以及加筋体变形后为圆弧或二次抛物线是最为常见的[14-16]。但现有的研究结果表明,作用在加筋体内的拉力一般不是均匀的,通常在中间最小、在桩帽内边缘处最大[3-5,9];而变形后的加筋体最接近三次抛物线[5]。
综上可见,如何确定加筋体的变形和拉力仍是桩撑路堤设计中有待解决的问题。本文针对平面应变条件下的加筋体,首先推导出了相应的平衡方程,并据此分析仅仅利用平衡方程不可能求得加筋体变形和拉力的原因,最后提出了一种利用加筋体平衡条件和变形相容条件确定加筋体变形和拉力的简单数值解法。
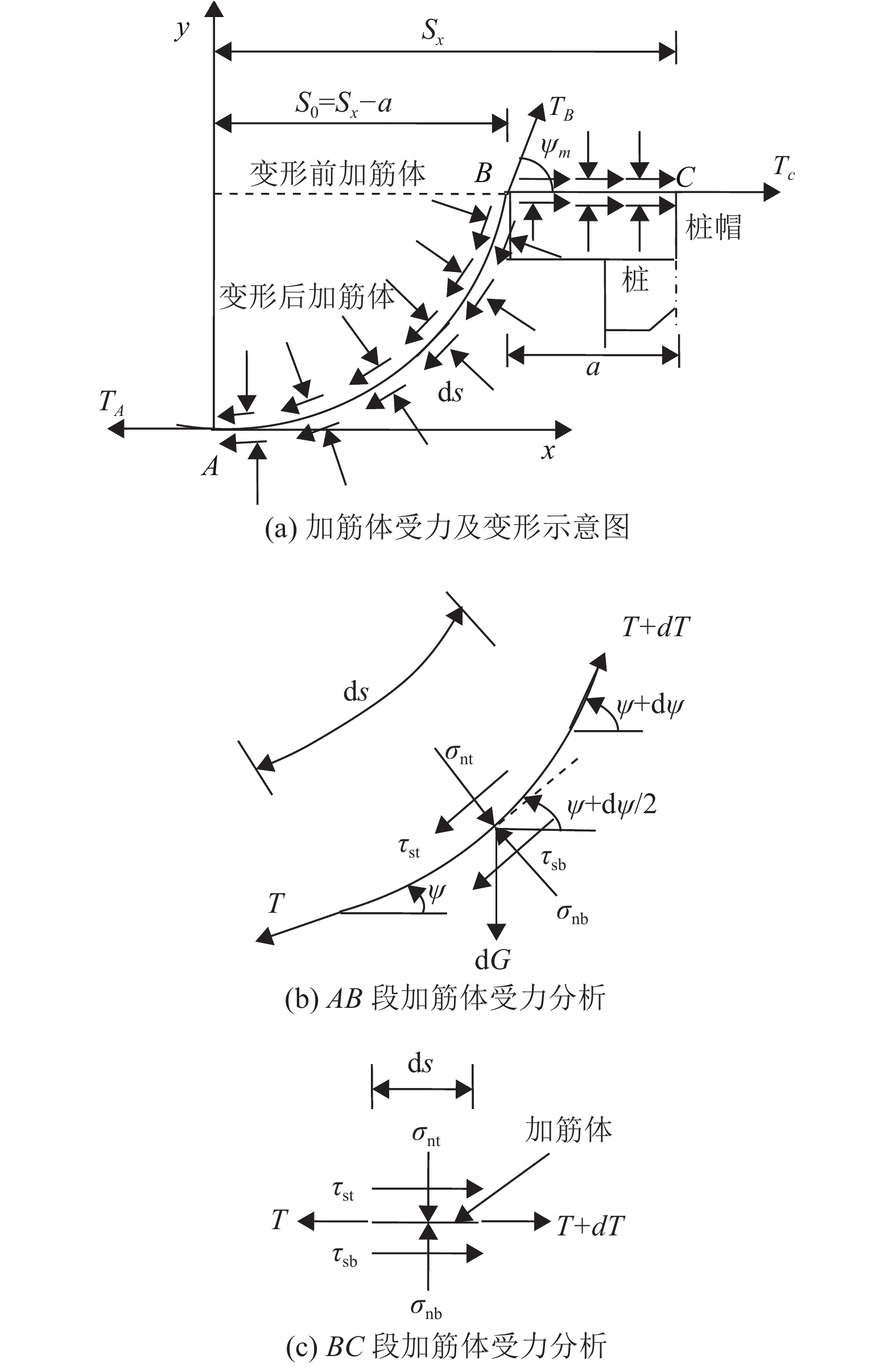
1 加筋体的受力平衡方程设相邻两根桩的中心距为2Sx,桩帽宽度为2a,净间距为2S0=2(Sx−a)。由于加筋体和作用在其上的荷载通常是对称的,因此可取相邻两桩中心线与桩帽中心线之间的加筋体为对象,如图1(a)示。该加筋体可以分为AB和BC两段。其中AB段和BC段的下表面分别与地基土及桩帽上表面接触。设加筋体单位长度的重量为γG。
|
图 1 加筋体的变形及受力分析 Figure 1 Deformation and loading of the GR |
在该段加筋体中取一长度为ds的微元体,设该微元两端受到的拉力分别为T和T+dT,与水平面的倾角分别为ψ和ψ+dψ,其受力如图1(b)示。其中σnt和τst是加筋体以上填土作用在加筋体上表面的法向应力和剪应力;而σnb和τsb是加筋体以下土体作用在加筋体下表面的法向应力和剪应力,自重为dG=γGds。令
| $ {{{\sigma }}_{\rm{n}}} = {{{\sigma }}_{\rm{nt}}} - {{{\sigma }}_{\rm{nb}}},{{{\tau }}_{\rm{s}}} = {\tau _{\rm{st}}} - {\tau _{\rm{sb}}}$ | (1) |
σn和τs分别称为净法向应力和合剪应力,这样,该微元体在水平和垂直方向的受力平衡条件分别为
| $ \begin{split} & ({{T}} + {\rm{d}}{{T}})\cos (\psi + {\rm{d}}\psi ) - {{T}}\cos \psi + \\&{{{\sigma }}_{\rm{n}}}{\rm{d}}s\sin \left(\psi + \frac{{{\rm{d}}\psi }}{2}\right) - {{{\tau }}_{\rm{s}}}{\rm{d}}s\cos \left(\psi + \frac{{{\rm{d}}\psi }}{2}\right) = 0 \end{split} $ | (2) |
| $ \begin{split} & ({{T}} + {\rm{d}}{{T}})\sin (\psi + {\rm{d}}\psi ) - {{T}}\sin \psi - {{{\sigma }}_{\rm{n}}}{\rm{d}}s\cos \left(\psi + \frac{{{\rm{d}}\psi }}{2}\right) -\\& {{{\tau }}_{\rm{s}}}{\rm{d}}s\sin \left(\psi + \frac{{{\rm{d}}\psi }}{2}\right) - {\rm{d}}{{G}} = 0 \end{split} $ | (3) |
将式(2)和(3)中的三角函数求和项展开,注意到dψ→0并略去与二阶无穷小量dψds有关的项,则有
| $ - {{T}}\sin \psi \frac{{{\rm{d}}\psi }}{{{\rm{d}}s}} + \cos \psi \frac{{{\rm{d}}{{T}}}}{{{\rm{d}}s}} + {{{\sigma }}_{\rm{n}}}\sin \psi - {{{\tau }}_{\rm{s}}}\cos \psi = 0 $ | (4) |
| $ {{T}}\cos \psi \frac{{{\rm{d}}\psi }}{{{\rm{d}}s}} + \sin \psi \frac{{{\rm{d}}{{T}}}}{{{\rm{d}}s}} - {{{\sigma }}_{\rm{n}}}\cos \psi - {{{\tau }}_{\rm{s}}}\sin \psi - {\gamma _G} = 0 $ | (5) |
将式(4)两边乘以cosψ与式(5)两边乘以sinψ后相加、将式(4)两边乘以sinψ与式(5)两边乘以cosψ后相减,则式(4)、(5)的平衡方程可改写为
| $ \frac{{{\rm{d}}{{T}}}}{{{\rm{d}}s}} - {{{\tau }}_{\rm{s}}} - {\gamma _G}\sin \psi = 0 $ | (6) |
| $ {{T}}\frac{{{\rm{d}}\psi }}{{{\rm{d}}s}} - {{{\sigma }}_{\rm{n}}} - {\gamma _G}\cos \psi = 0 $ | (7) |
式(6)和(7)中
| $ \frac{{{\rm{d}}x}}{{{\rm{d}}s}} = \cos \psi ,\;\frac{{{\rm{d}}y}}{{{\rm{d}}s}} = \sin \psi $ | (8) |
对于水平的BC段加筋体,由于其在AB段荷载作用下有伸长的趋势,因此其表面剪应力的方向与AB段相反,如图1(c)示。该段水平和竖直方向的受力平衡方程分别为
| $ \frac{{{\rm{d}}{{T}}}}{{{\rm{d}}s}} + {{{\tau }}_{\rm{s}}} = 0, $ | (9) |
| $ {{{\sigma }}_{\rm{n}}} + {\gamma _G} = 0 $ | (10) |
值得注意的是,由于剪应力在B点反向,因此整个加筋体ABC在桩帽内边缘处的拉力最大,这与实验和数值分析结果是一致的[5]。有鉴于此,从设计的角度看(即控制最大值)就没有必要对BC段进行分析了。此时B点可以看做是加筋体的固定端。这就是目前普遍采用的加筋体分析模型[1-5,14-16]。此外,由于加筋体的自重通常远小于所受到的外荷,因此可不予考虑。
式(6)、(7)、(9)是关于T和ψ的一阶微分方程(式(10)是个自平衡方程),只有利用其已知边界条件才能完全确定。但目前仅能利用加筋体对称于y轴的特点得到关于ψ的边界条件(即当x=0时ψ=0),而关于T的边界条件(即TA、TB和TC中任意一个)却是未知的。由此可见,由于边界条件的不完备,仅仅利用加筋体的受力平衡方程是不可能确定出变形后加筋体的形状(可以用ψ表示)和拉力T的。正因如此,才在目前的加筋体变形和拉力分析中附加了其他假定或简化。
2 均布法向荷载作用下加筋体的变形和拉力文献[14-15]的作者认为,由于桩撑路堤通常都是修建在软土地基上的,因此,软土对加筋体下表面的摩擦力τsb通常很小可以不计。另一方面,虽然作用于加筋体上、下表面的法向应力σnt和σnb沿加筋体不是均匀分布的,但其差值(即净法向应力σn)可以假定为均匀的,或者可以等效为均匀的。
从式(6)、(9)可以看出,只有不考虑作用在加筋体表面的剪应力,加筋体中的拉力T才是均匀的。此外,利用式(7)、(8)不难得到以下方程
| $ \int {\frac{{{{{\sigma }}_{\rm{n}}}}}{{{T}}}} {\rm{d}}x = \sin \psi + {C_1},\int {\frac{{{{{\sigma }}_{\rm{n}}}}}{{{T}}}} {\rm{d}}y = - \cos \psi + {C_2} $ | (11) |
式(11)中,C1和C2是两个积分常数,可利用边界条件x=0和y=0时ψ=0确定。如果进一步假定σn是常值,则上式可改写为
| $ {x^2} + {\left(y - \frac{{{T}}}{{{{{\sigma }}_{\rm{n}}}}}\right)^2} = {\left(\frac{{{T}}}{{{{{\sigma }}_{\rm{n}}}}}\right)^2} $ | (12) |
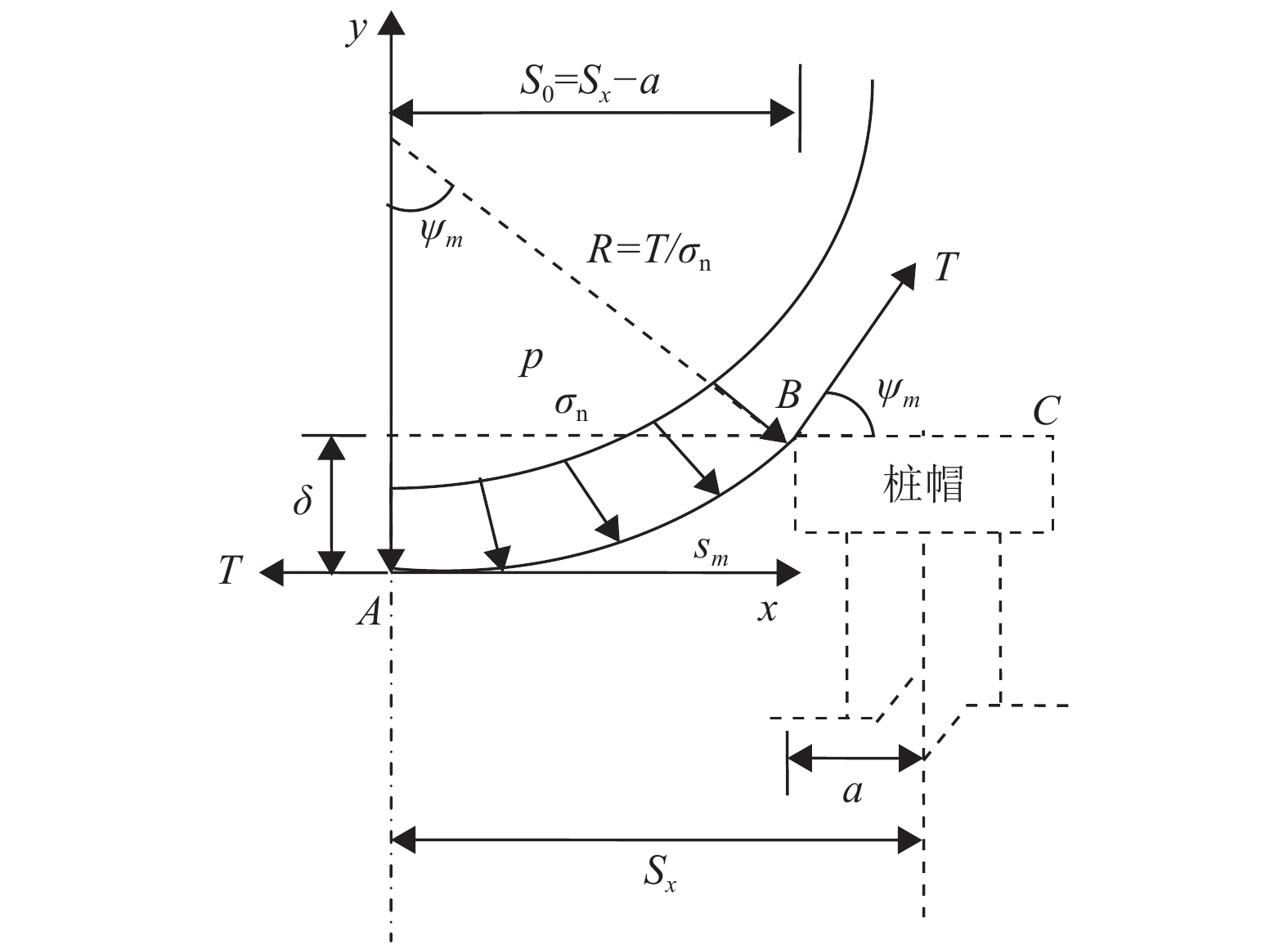
此时加筋体变形后的曲线是圆心位于y轴、半径R=T/σn的圆弧,如图2示。由此可见,只有在不考虑加筋体表面摩擦力并且作用在加筋体表面的法向应力为均匀分布的条件下,加筋体的拉力才是均匀的,变形后的加筋体也才是圆弧。
|
图 2 均布法向应力作用下加筋体的变形 Figure 2 Deformation of GR under normal uniform distribution load |
设加筋体的拉伸刚度为KG,拉力T与应变ε之间的关系为
| $ {{T}} = {{{K}}_{{G}}}{\rm{\varepsilon }} $ | (13) |
式(13)中注意到加筋体拉力均匀时其应变也是均匀的,故整个加筋体ABC范围内的应变为
| $ \varepsilon =\frac{{s}_{m}+a}{{S}_{0}+a}-1=\frac{R{\psi }_{m}-{S}_{0}}{{S}_{0}+a}=\frac{1}{1+{n}_{a}}\left(\frac{T{\psi }_{m}}{{\sigma }_{{\rm{n}}}{S}_{0}}-1\right) $ | (14) |
式(14)中,na=a/S0,而sm和ψm分别为AB段加筋体变形后的弧长和最大倾角(见图2)。将式(14)代入(13)有
| $ {{T}}=\frac{\xi {K}_{G}}{{\psi }_{m}-(1+{n}_{a})\xi }$ | (15) |
式(15)中
| $ \xi = {{{N}}_{\rm{n}}}/{K_G},\;{{{N}}_{\rm{n}}} = {S_0}{{{\sigma }}_{\rm{n}}} $ | (16) |
显然,Nn就是作用在AB段加筋体上的总法向荷载。
此外,从图2可见
| $ \sin {\psi _m} = \frac{{{S_0}}}{R} = \frac{{{{{N}}_{\rm{n}}}}}{{{T}}} $ | (17) |
联立式(15)、(16)、(17)消去T有
| $ {\psi }_{m}-\sin{\psi }_{m}=(1+{n}_{a})\xi $ | (18) |
这样,对于给定的参数ξ,由式(18)确定出ψm后,将ψm代入式(17)即可求出加筋体内的拉力T。即
| $ {{T}} = {K_T}{{{N}}_{\rm{n}}} $ | (19) |
式(19)中
| $ {K}_{T}=\frac{1}{\sin{\psi }_{m}} $ | (20) |
称为加筋体的拉力放大倍数。由此可见,加筋体的拉力T等于总法向荷载的KT倍。由于Ψm≤π/2,故KT≥1,即加筋体的拉力不会小于所受的总荷载。
此外,利用式(8)和图2不难得到加筋体的最大竖向位移δ为(见图2)
| $ \frac{\delta }{{S}_{0}}=\tan\frac{{\psi }_{m}}{2}={K}_{T}-\sqrt{{K}_{T}^{2}-1} $ | (21) |
若不考虑桩帽范围内加筋体的变形,可令na=0,此时参数ξ与ψm、KT和δ/S0之间的关系见表1。
| 表 1 参数ξ与Ψm、KT和δ/S0之间的关系(na=0) Table 1 Relations among parameters ξ, Ψm, KT and δ/S0 (na=0) |
从加筋体的受力平衡方程(6)~(7)和(9)~(10)可以看出,当作用在加筋体表面的荷载比较复杂时,要想推导出变形和拉力的解析解是比较困难的。另一方面,如前所述,目前利用方程(6)~(7)和(9)~(10)确定加筋体的变形和拉力时所做的附加假定都是没有理论依据的。为解决上述问题,本文提出以下数值解法。该方法仅将加筋体的变形关系(即式(13))与平衡方程联系起来,并无其他任何假设。
数值解法就是将求解微分方程(6)~(7)和(9)~(10)转化为求解其差分方程。但应注意的是,由于加筋体受荷后会变形,在平面中的位置以及变形后的长度都是未知的,但无论加筋体如何变形,它都限制在两桩之间,因此,差分最好沿水平向进行。
对图1(a)所示的加筋体AC,首先对AB段由最低点A开始水平向右分成n个子段,即水平向的差分长度Δxk=S0/n。设第k个子段(1≤k≤n)的弧长度为Δsk,段起点和终点与水平面的夹角分别为ψk和ψk+1=ψk+Δψk,受到的拉力分别为Tk和Tk+1=Tk+ΔTk,作用在加筋体表面的净法向应力和合剪应力分别为σnk和τsk,则式(6)和(7)可变换为
| $\left\{ {\begin{array}{*{20}{c}} {\Delta {{{T}}_k}}\\ {\Delta {\psi _k}} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} {{{{\tau }}_{{\rm{s}}k}} + {\gamma _G}\sin {\psi _k}}\\ {\dfrac{{{{{\sigma }}_{{\rm{n}}k}} + {\gamma _G}\cos {\psi _k}}}{{{{{T}}_k}}}} \end{array}} \right\}\Delta {s_k} $ | (22) |
式(22)中
| $ \Delta {s}_{k}=\frac{\Delta {x}_{k}}{\cos{\psi }_{k}}=\frac{{S}_{0}}{n}\frac{1}{\cos{\psi }_{k}} $ | (23) |
对BC范围内的加筋体,只需要方程(9)。同理,从B点起将其划分为m个子段,即水平向差分长度Δxk=a/m(1≤k≤m)。这样式(9)可变换为
| $ \Delta {{{T}}_k} = - {{{\tau }}_{{\rm{s}}k}}\Delta {s_k} = - {{{\tau }}_{{\rm{s}}k}}\frac{a}{m} $ | (24) |
对式(22)和(23)逐段求解,即可得到各子段的拉力Tk以及AB范围内各子段的倾角ψk和弧长Δsk。
应注意的是,逐段求解式(22)和(23)的前提是已知加筋体在最低点A处的拉力TA以及第1个子段的倾角ψ1。鉴于第1个子段的加筋体接近水平,故可取ψ1≤2°;至于TA,起始计算时可赋一大于零的小数或大数(如TA=0.1或104 kN/m),以后通过迭代自动调整。
显然,根据几何条件,整个AC范围内加筋体变形后的长度S应当为
| $ S=a+\sum _{k=1}^{n}\Delta {s}_{k}=a+\frac{{S}_{0}}{n}\sum _{k=1}^{n}\frac{1}{\cos{\psi }_{k}} $ | (25) |
式(25)中的倾角ψk和弧长Δsk由方程(22)和(23)求得。另一方面,利用式(23)和(24)求出各子段段首及段尾的拉力Tk和Tk+1=Tk+ΔTk后,也可利用加筋体的拉力与变形之间的关系式(13),依据拉力求出变形后整个加筋体的长度S′(等于原始长度(s0+a)与拉力产生的长度之和)。即
| $ \begin{split} & S' = \left( {{s_0} + a} \right) + \frac{{{S_0}}}{{n{K_G}}}\sum_{k = 1}^n\frac{{{{{T}}_k} + {{{T}}_{k + 1}}}}{2} + \\& \frac{a}{{m{K_G}}}\sum_{k = 1}^m\frac{{{{{T}}_k} + {{{T}}_{k + 1}}}}{2} \end{split}$ | (26) |
显然,如果起始假定的TA是正确的,则根据加筋体的变形相容条件,S与S′应当是相等的。即
| $ f = 1 - S/S' = 0 $ | (27) |
如果不等,则重新调整TA进行迭代,直至 f 满足允许误差为止。由此可见,上述算法实际上就是非线性方程(27)关于TA的求解。这样,利用一般非线性方程的求解方法(如迭代法、对分区间法等),即可确定出TA,进而求出整个加筋体的变形和拉力。
4 算例假设相邻两桩的中心距2Sx =2.5 m,桩帽宽度2a=1 m (即Sx=1.25 m,a=0.5 m,S0=0.75 m),加筋体张拉刚度KG=1 500 kN/m。
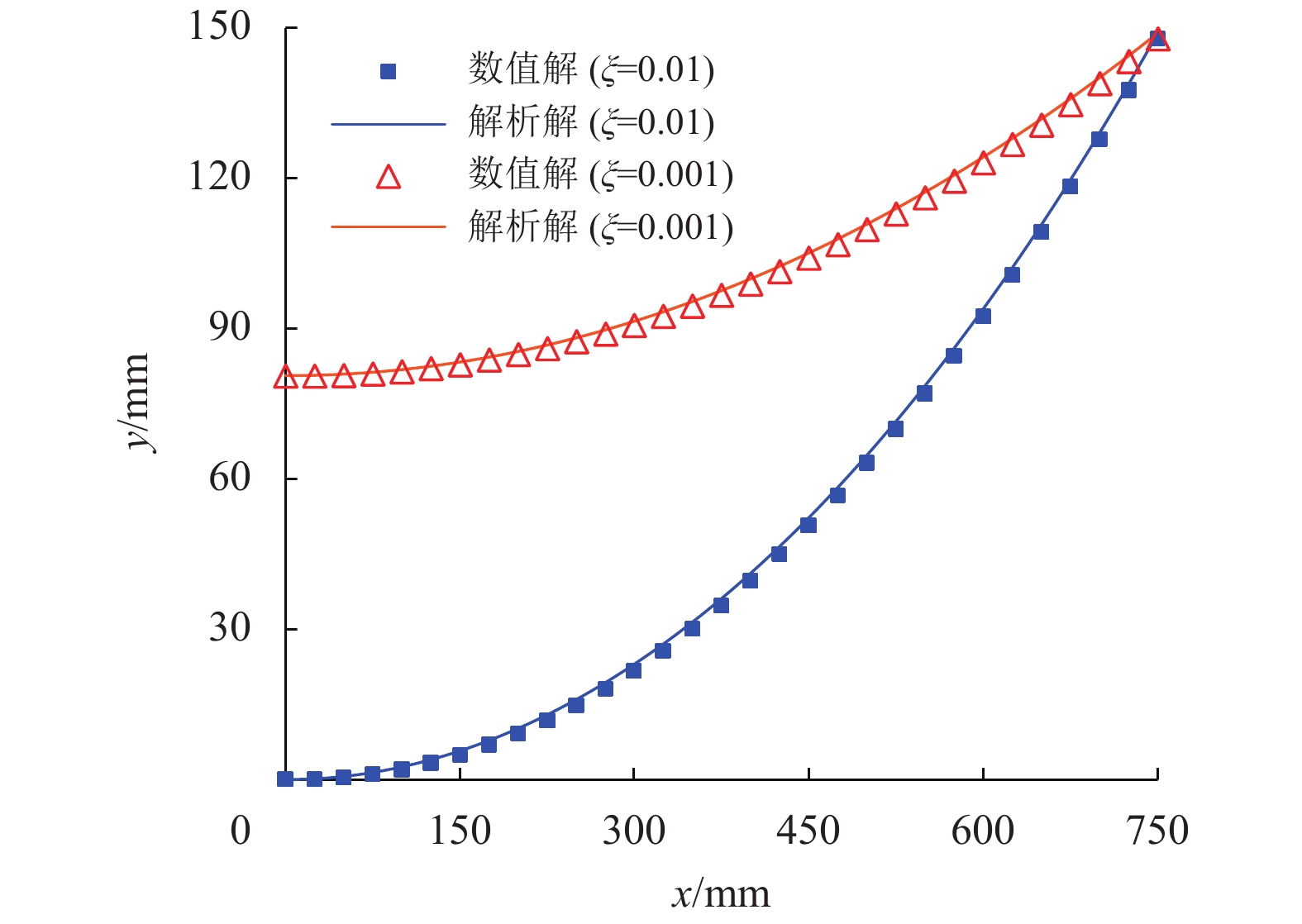
4.1 算例1设加筋体上仅作用有净法向应力σn,其值分别为2 kN/m和20 kN/m (即ξ分别为0.001和0.01),不考虑桩帽范围内加筋体的变形(即na=0)。取TA的起始值为0.1 kN/m,n=20。数值解与式(12)解析解得到的加筋体变形后曲线比较如图3,其他物理量比较见表2。显然,两者的计算结果是比较吻合的。
|
图 3 均布法向荷载作用下加筋体的变形曲线 Figure 3 Deformated shape of the GR under the normal uniform distibution load |
| 表 2 解析解与数值解的比较(na=0) Table 2 Comparison of analytical with numerical results (na=0) |
如果进一步计入桩帽以上加筋体的变形(此时na=a/S0=0.5/0.75=2/3,取m=10),则当ξ=0.01时加筋体的拉力为32.64 kN/m,最大倾角Ψm=27.36°,最大竖向位移δ=176.56 mm,其长度由起始的1 250 mm变为1 277.8 mm。这些结果与前述解析解基本一致。此外,如果与不考虑桩帽范围内加筋体的结果(见表2)比较则不难发现,考虑时加筋体的拉力有一定程度的减小,而变形则明显增大。
4.2 算例2假定不计地基土的抗力(即σnb=τsb=0),并且填土作用在加筋体上表面的法向应力σnt和剪应力τst达到极限平衡(即τst=σnttanφ),则由式(4)可得
| $ {{T}} = {{{T}}_A}{\rm{exp}}\left( {{\rm{\psi}} {\rm{tan}}{\rm{\varphi}} } \right).$ | (28) |
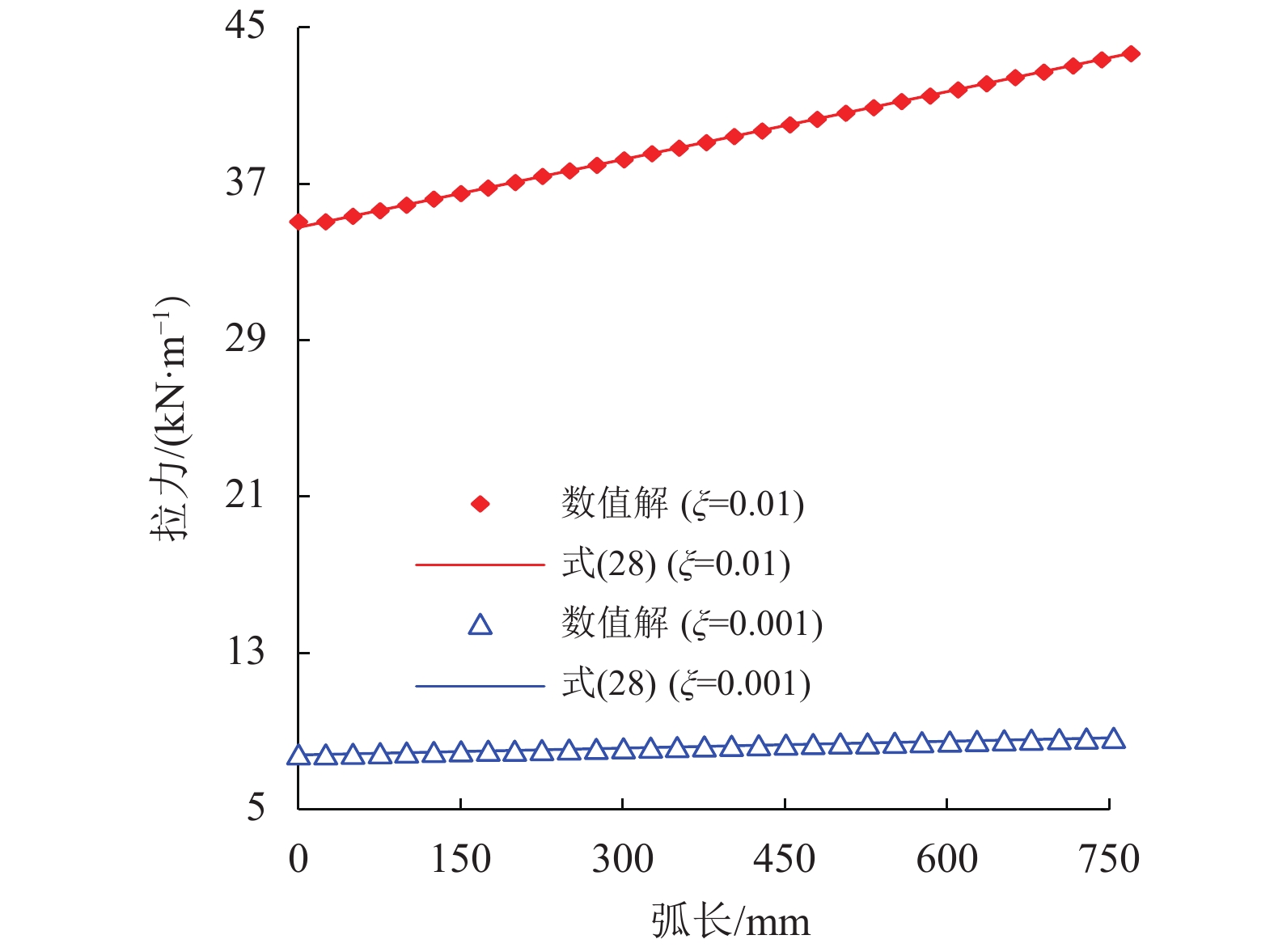
这就是著名的皮带传动拉力公式(其中的tanφ相当于皮带与皮带轮之间的摩擦系数)。其他计算条件同算例1。部分数值计算结果见表3,其中加筋体的变形曲线与图3大致相同,而拉力与式(28)的比较如图4,显然两者几乎是一致的。
| 表 3 算例2计算结果 Table 3 Calculating results for the example 2 |
|
图 4 加筋体中拉力随弧长的变化 Figure 4 Variation of tension of the GR with the arc length |
此外,当ξ分别为0.001和0.01时,由数值方法得到的作用在加筋体上的水平和竖直向荷载分别为−0.73 kN/m与1.579 kN/m以及−5.635 kN/m与16.75 kN/m,这样,作用在加筋体水平及竖向的合力分别为:
当ξ=0.001时
| $ \begin{split} & \sum {{{F}}_{{x}}} = {{{T}}_{{A}}} - {{{T}}_{{B}}}{\rm{cos}}{\varPsi _{{m}}} + 0.73 = 7.84 - \\&\qquad 8.7{\rm{1cos}}{{10.53}^{\circ }} + 0.73 \approx 0\\& {\sum {{{F}}_{{y}}} = {{{T}}_{{B}}}{\rm{sin}}{\varPsi _{{m}}} - 1.579 = 8.71{\rm{sin}}{{10.53}^{\circ }} - 1.579 \approx 0} \end{split} $ |
当ξ=0.01时
| $ \begin{split} & \sum {{{F}}_{{x}}} = {{{T}}_{{A}}} - {{{T}}_{{B}}}\cos {\varPsi _{{m}}} + 5.635 = \\&\qquad 34.84 - 43.74\cos {{22.7}^{\circ }} + 5.635 \approx 0\\& {\sum {{{F}}_{{y}}} = {{{T}}_{{B}}}\sin {\varPsi _{{m}}} - 16.75 = {\rm{ }}43.74\sin {{22.7}^{\circ }} - 16.75 \approx 0} \end{split} $ |
由此可见,作用在加筋体上的荷载是平衡的。
4.3 算例3VanEekelen等[5]提出了一种“同心拱(concentric arches)”模型。该模型能够较好地反映路堤填料、加筋体以及地基土之间的相互作用,其计算结果也能较好地符合现场及模型试验结果。该模型分二维和三维两种,详情可参见文献[5]。
在二维条件下,设无黏性填土的高度为H,重度为γ,有效内摩擦角为φ,被动土压力系数为Kp=tan2(π/4+φ/2),填土表面超载为p,这样,根据同心拱模型,作用在加筋体上的荷载为竖直向下的切向应力σθ:
| $ {{{\sigma}} }_{\theta }={P}_{X2D}{r}^{{K}_{P}-1}+{Q}_{2D}r $ | (29) |
式(29)中,0≤r≤Sx为从加筋体对称轴(即图1(a)中y轴)算起的矢径(水平距离),其余为
| $ {P}_{X2D}={K}_{P}{H}_{xg2D}^{1-{K}_{P}}\left[\gamma H+p-\gamma {H}_{xg2D}^{1-{K}_{P}}\frac{{K}_{P}-1}{{K}_{P}-2}\right] $ | (30) |
| $ {Q}_{2D}={K}_{P}\frac{\gamma }{{K}_{P}-2} $ | (31) |
参数Hxg2D取值如下:
对H≥Sx的完全拱:Hxg2D=Sx
对H<Sx的不完全拱:Hxg2D=0.5H
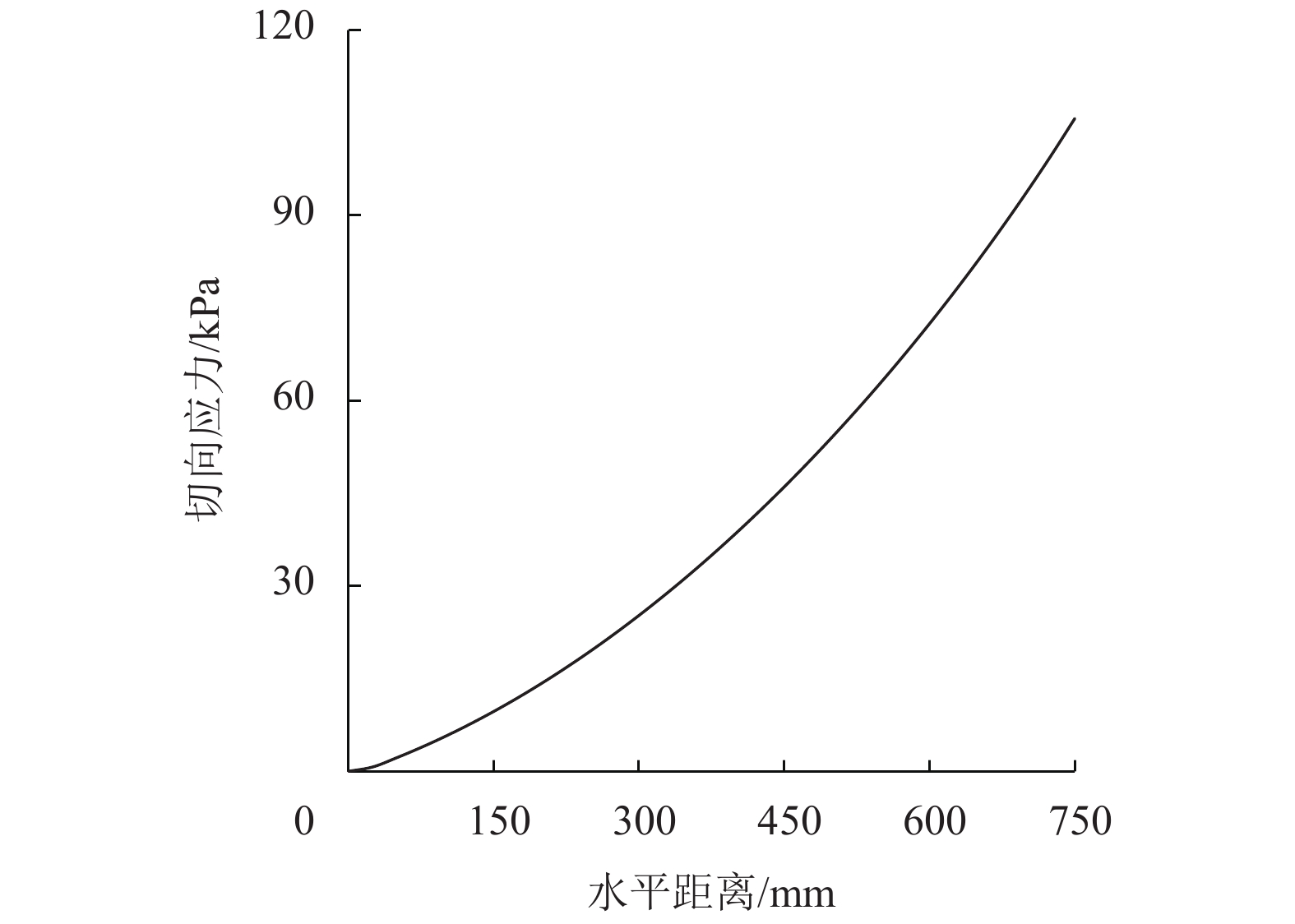
从式(29)可以看出,作用在加筋体上的荷载是曲线变化的,难以利用式(6)~(7)和(9)~(10)得出变形曲线及拉力的解析解。现利用本文数值方法求解该问题(不考虑桩帽范围内加筋体的变形)。其计算参数为:填土高度H=5.8 m,重度γ=18.2 kN/m3,超载p=0,内摩擦角φ=300,n=30。其余参数同算例1。利用式(29)绘出的作用在加筋体上的竖向荷载σθ如图5所示。
|
图 5 作用在加筋体上的竖向荷载 Figure 5 Vertical load acting on the GR |
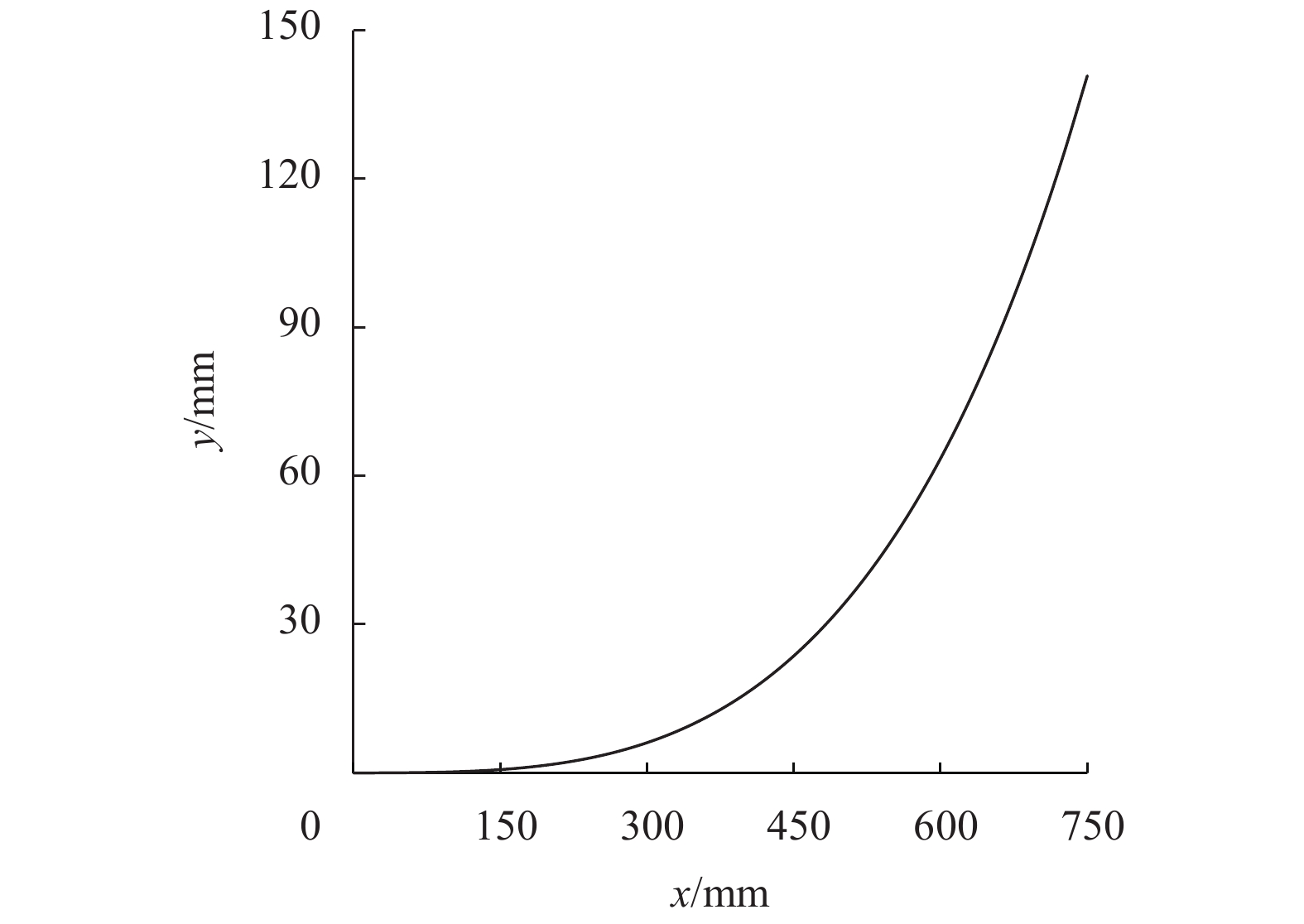
由数值方法得到的变形后加筋体曲线(形状)如图6所示。其中变形后长度为775.77 mm,最大倾角Ψm=35.89°,最大竖向位移δ=140.75 mm。
|
图 6 加筋体变形后的曲线 Figure 6 Deformated curve of the GR |
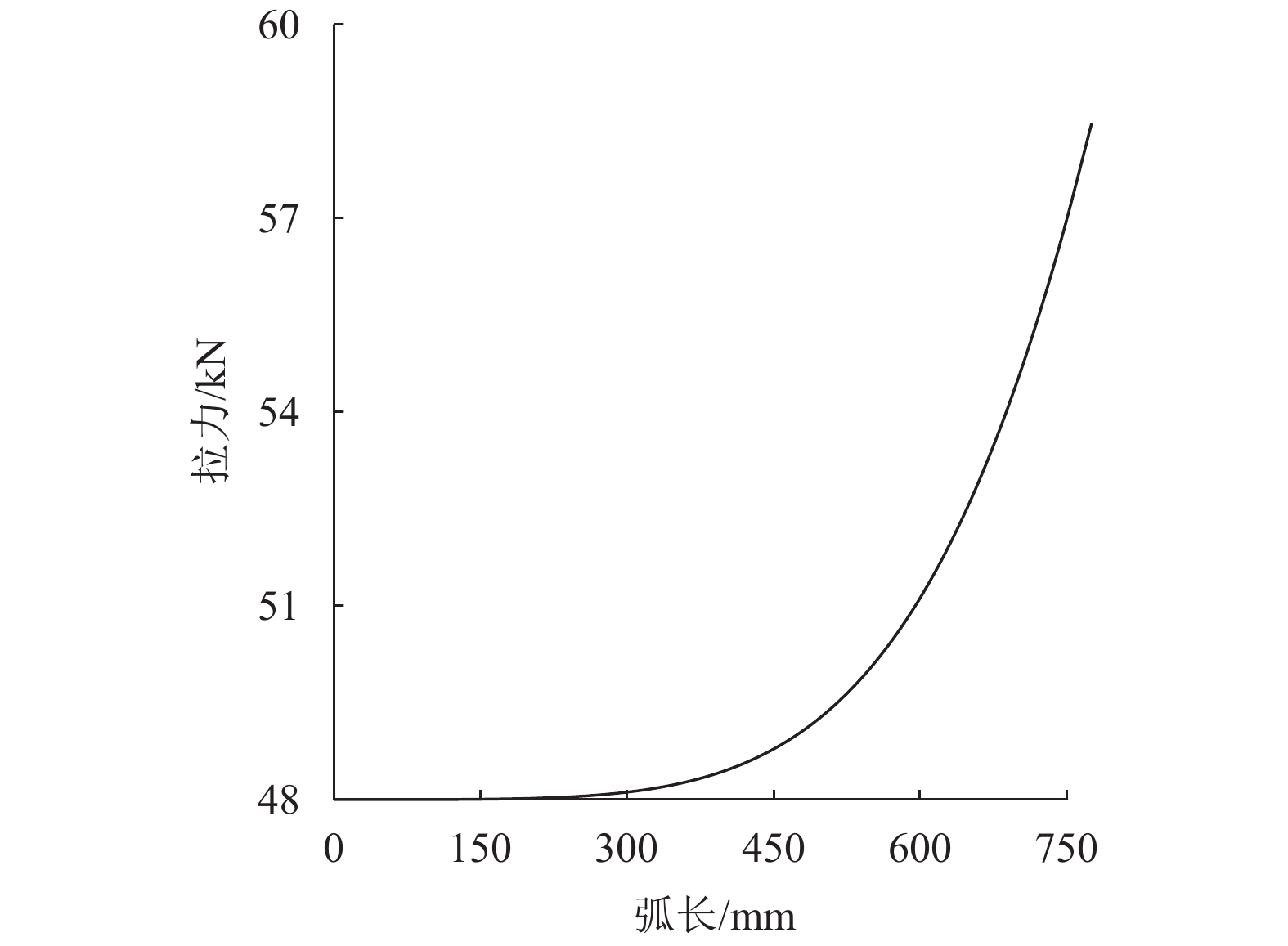
加筋体内拉力随变形后弧长的变化如图7所示,其中最小拉力TA=48 kN/m,最大拉力TB=58.46 kN/m。此外,对式(29)在0≤r≤S0=0.75 m范围内积分,可以得到作用在加筋体上的总竖向荷载Fy≈36.5 kN/m。利用这些数据,易于验证作用在加筋体上的水平及竖向力也是满足平衡条件的。
|
图 7 加筋体的拉力随弧长的变化 Figure 7 Variation of tension with the arc |
Low等[13]基于Eekelen土拱模型[5]及Winkler地基模型,在无超载且仅考虑均匀分布的净法向应力σn的条件下(如本文第3节所述,此时变形后的加筋体为圆弧),提出了如下确定加筋体变形和拉力的计算方法(已转化为本文符号):
| $ {{{\sigma}} }_{\rm{nt}}=\frac{\gamma ({K}_{p}-1)({S}_{x}-a)}{{K}_{p}-2}+\gamma \left(1-\frac{a}{{S}_{x}}\right)^{{K}_{p}-1}\left[H-\frac{{S}_{x}\left({K}_{p}-1\right)}{{K}_{p}-2}\right] $ | (32) |
| $ {{{\sigma}}}_{\rm{nb}}=k\delta $ | (33) |
式(33)中k为加筋体以下土体的基床系数。而变形后加筋体的最大倾角ψm和最大竖向位移δ可联立以下两式通过迭代法确定:
| $ \beta =\frac{\delta }{2{S}_{0}}=\frac{1}{2k{S}_{0}}\left[{{{\sigma}} }_{\rm{nt}}-\frac{{K}_{G}}{{S}_{0}}\left({\psi }_{m}-\sin{\psi }_{m}\right)\right] $ | (34) |
| $ {\psi }_{m}={\sin}^{-1}\left(\frac{4\beta }{1+4{\beta }^{2}}\right) $ | (35) |
求出δ后,再代入式(33)即可得到σnb,进而利用式(1)可确定出作用在加筋体上的净法向应力σn。加筋体的应变ε按下式确定:
| $ \varepsilon =\frac{{\psi }_{m}}{\sin{\psi }_{m}}-1 $ | (36) |
其拉力T仍依据式(19)确定。
假定填土高度H=5.8 m,重度γ=18.2 kN/m3,内摩擦角φ=30°,基床系数k=2 000 kN/m3。在这些条件下,由式(32)可得σnt=48.922 kPa,由式(26)可得ψm=3.73°,δ=24.42 mm,由式(33)可得σnb=48.83 kPa,由式(1)、(36)和(13)可得σn=0.092 kPa及T=1.06 kN/m。
现与本文方法进行比较。将KG=1 500 kN/m、σn=0.092 kPa及S0=0.75 m 代人式(16)及(18)可得ξ=4.594×10−5和ψm=3.73°。此外,由式(21)和(19)可得δ=24.42 mm及T=1.06 kN/m。显然,两种方法的计算结果几乎是相同的。
5 结语(1) 只有在不考虑加筋体表面摩擦力并且作用在加筋体表面的法向应力为均匀分布的条件下,加筋体内的拉力才是均匀的,变形后的加筋体也才是圆弧。
(2) 由于边界条件的不完备,仅仅利用加筋体的受力平衡方程是不可能确定出变形后加筋体的变形和拉力的。
(3) 将加筋体的平衡条件与变形相容条件(即利用加筋体的平衡方程求出的加筋体长度应当与加筋体原始长度及拉力产生的长度之和相同)相结合,可以弥补平衡方程边界条件的不完备,并且能够较为准确地确定出加筋体的变形和拉力。该方法简单易行,适用于各种荷载条件及大、小变形的加筋体。
| [1] |
FILZ G M, SLOAN J A. Load distribution on geosynthetic reinforcement in column-supported embankments[C]//Stability and Performance of Slopes and Embankments. Reston: ASCE, 2013: 1822-1830.
|
| [2] |
HELLO B L, VILLARD P. Embankments reinforced by piled and geosynthetics-numerical and experimental studies dealing with the transfer of load on the soil embankment[J].
Engineering Geology, 2009, 106: 78-91.
DOI: 10.1016/j.enggeo.2009.03.001. |
| [3] |
NAUGHTON P J, KEMPTON G T. Comparison of analytical and numerical analysis design methods for piled embankments[C]//ASCE Geo-Institute and IFAI Geosynthetic Institute. Austin: ASCE, 2005: 1-10.
|
| [4] |
VAN EEKELEN S J M, BEUIJEN A. Dutch research on basal reinforced piled embankments[C]//Geo-Congress2013. California: ASCE, 2013: 1838-1847.
|
| [5] |
VAN EEKELEN S J M, BEZUIJEN A, VON TOL A F. An analytical model for arching in Piled embankments[J].
Geotextiles and Geomembranes, 2013, 39: 78-102.
DOI: 10.1016/j.geotexmem.2013.07.005. |
| [6] |
郑俊杰, 张军, 马强, 等. 路桥过渡段桩承式加筋路堤现场试验研究[J].
岩土工程学报, 2012, 34(2): 355-362.
ZHENG J J, ZHANG J, MA Q, et al. Experimental investigation of geogrid-reinforced and pile-supported embankment at bridge approach[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 355-362. |
| [7] |
CHEN Y M, CAO W P, CHEN R P. An experimental investigation of soil arching within basal reinforced and unreinforced piled embankments[J].
Geotextiles and Geomembranes, 2008, 26: 164-174.
DOI: 10.1016/j.geotexmem.2007.05.004. |
| [8] |
陈福全, 李阿池. 桩承式加筋路堤的改进设计方法研究[J].
岩土工程学报, 2007, 29(12): 1804-1808.
CHEN F Q, LI A C. Improved design method of geosynthetic reinforced pile supported embankments on soft soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(12): 1804-1808. DOI: 10.3321/j.issn:1000-4548.2007.12.010. |
| [9] |
曹卫平, 陈仁朋, 陈云敏. 桩承式加筋路堤土拱效应试验研究[J].
岩土工程学报, 2007, 29(3): 436-441.
CAO W P, CHEN R P, CHEN Y M. Experimental investigation on soil arching in piled reinforced embankments[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(3): 436-441. DOI: 10.3321/j.issn:1000-4548.2007.03.021. |
| [10] |
费康, 刘汉龙. 桩承式加筋路堤的现场试验及数值分析[J].
岩土力学, 2009, 30(4): 1004-1012.
FEI K, LIU H L. Field test study and numerical analysis of a geogrid-reinforced and pile-supported embankment[J]. Rock and Soil Mechanics, 2009, 30(4): 1004-1012. DOI: 10.3969/j.issn.1000-7598.2009.04.025. |
| [11] |
TSIATAS G C, KATSIKADELIS J T. Nonlinear analysis of elastic space cable-supported membranes[J].
Engineering Analysis with Boundary Elements, 2011, 35: 1149-1158.
DOI: 10.1016/j.enganabound.2011.05.005. |
| [12] |
ABUSHARAR S W, ZHENG J J, CHEN B G, et al. A simplified method for analysis of a piled embankment reinforced with geosynthetics[J].
Geotextiles and Geomembranes, 2009, 27: 39-52.
DOI: 10.1016/j.geotexmem.2008.05.002. |
| [13] |
LOW B K, TANG S K, CHOA V. Arching in Piled embankments[J].
Journal of Geotechnical Engineering, 1994, 120(11): 1917-1938.
DOI: 10.1061/(ASCE)0733-9410(1994)120:11(1917). |
| [14] |
JONES C, LAWSON C R. Geotextile reinforced piled embankments[C]//Proc. 4th Int. Conf. on Geotextiles. Geomembranes and Related Products. Rotterdam: Balkema, 1990, 155-160.
|
| [15] |
强小俊, 赵有明, 胡荣华. 桩网结构支承路堤土拱效应改进算法[J].
中国铁道科学, 2009, 30(4): 7-11.
QIANG X J, ZHANG Y M, HU R H. Improved algorithm for the soil arching effect of pile-net supported embankments[J]. China Railway Science, 2009, 30(4): 7-11. DOI: 10.3321/j.issn:1001-4632.2009.04.002. |
| [16] |
庄妍, 王康宇, 刘汉龙. 桩承式路堤中加筋体工作机理研究[J].
岩土工程学报, 2013, 35(S1): 294-299.
ZHUANG Y, WANG K Y, LIU H L. Reinforcement performance of piled embankments[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(S1): 294-299. |
 2021, Vol. 38
2021, Vol. 38

