电动汽车电能补给方式主要分为插充模式和换电模式两种。插充模式虽为当前电动汽车的主要充电模式,但换电模式因电能补给快、节能减排和经济效益较高等优势,故目前仍有发展[1]。本文设定在“集中充电、统一配送”的换电模式下,对充换电基础设施的选址定容规划问题进行进一步研究与完善。
“集中充电、统一配送”模式主要由集中充电站和电池换电站两个部分组成。其中集中充电站的作用是对待换电池进行集中存储、集中充电,再统一配送至各个电池换电站;而电池换电站的作用是对电动汽车进行电池更换服务,并对更换后的待换电池进行收集并运送至集中充电站进行充电[2]。“集中充电、统一配送”模式的研究较为新颖,对于该模式下集中充电站和电池换电站选址定容的研究更是少之又少,目前尚处于起步探索阶段。文献[3]提出一种初选、精选二阶段优化方法,结合改进型免疫遗传算法对某区域的电池换电站进行规划;文献[4]提出一种以运营商投资成本和用户换电便利性为目标的优化模型,通过混沌猫群算法作出最优规划;文献[5]提出以偏离最短路径行驶的偏差路径和电动汽车进站后的等待时间为目标的双目标混合整数规划模型;文献[6]以建设成本和用户广义充电成本为目标,引入便捷系数,从而得到选址与定容的模型;文献[7]建立以充电网络服务能力与配电系统网络损耗为目标的电动汽车充电网络规划模型,并采用遗传算法对该模型求解;文献[8]以电池换电站物流运输成本和建设成本为目标,提出了一种基于路径优化的选址定容规划模型;文献[9]在用户一周出行活动及充电过程的基础上,提出基于用户出行需求的电动汽车充电站优化规划模型。上述研究对于站点选址定容问题的考虑不够全面,不仅对于集中充电站和电池换电站的联合考虑因素较少,还忽略站点选址所造成的交通流量变化及用户充换电成本变化的影响。
电动汽车电池换电站的选址定容在“集中充电、统一配送”模式中起到至关重要的作用,不仅会因集中充电站与电池换电站的配送距离影响电池配送成本,还会对交通流量、用户换电便利程度和换电成本等因素造成影响。本文考虑集中充电站的影响,以年建设投资成本、电池换电站的选址满意度和年电池换电成本为目标,建立电池换电站选址定容规划的多目标决策模型。引入模糊熵权法将多目标决策模型转化成单目标权重模型,避免单一主观决策或客观决策所带来的弊端。采用Voronoi图与改进蝙蝠算法相结合,对电池换电站的换电服务区域作出均匀划分,并自动生成选址及规模大小,从而在多目标决策加权总值最小化的条件下,生成电池换电站选址定容规划的最优解,解决电池换电站分布和配置不合理以及选址定容决策困难的问题。以广东省某市某区域规划为例,验证所提模型和算法的合理性及可行性。
1 电池换电站选址定容数学模型在电池换电站选址定容规划过程中,不仅应考虑各站的建设、运营和电池配送方面的总成本,还要考虑建站对于交通流量和用户换电便利程度的影响,以及站点选址对于电池换电站内电池更换机的台数和待换电用户排队等待耗时的影响。
1.1 目标函数 1.1.1 年建设投资成本年建设投资成本主要由集中充电站的年建设投资成本、电池换电站的年建设投资成本和年电池配送成本3个部分组成。
其中,集中充电站的年建设投资成本主要包括土地、电池配送车辆、充电机及其相关设施的购置及维护检修、站内工作人员工资等[10]。集中充电站j的年建设投资成本如式(1)所示。
| ${f_{{\rm{CT}},j}} = ({w_j} + {e_j}c)\frac{{{r_0}{{(1 + {r_0})}^{{m_j}}}}}{{{{(1 + {r_0})}^{{m_j}}} - 1}}(1 + \delta )$ | (1) |
式中,wj为集中充电站j的基建投资成本;ej为集中充电站j内购置的充电机及其相关设施的套数;c为每套充电机相关设施的单价;r0为贴现率;mj为集中充电站j的运营年限;δ为相关运维成本及人员工资等运营管理成本的等效系数。
电池换电站的年建设投资成本包括设施投资成本和运营管理成本[11]。设施投资成本主要包括土地、电池更换机相关设施等费用。运营管理成本主要为换电站中工作人员的工资、设备维护和配送车辆往返耗油等成本。电池换电站i的年建设投资成本如式(2)所示。
| ${f_{{\rm{BS}},i}} = ({w_i} + q{N_i} + g{N_i}^2)\frac{{{r_0}{{(1 + {r_0})}^{{m_i}}}}}{{{{(1 + {r_0})}^{{m_i}}} - 1}}(1 + \delta )$ | (2) |
其中,wi为电池换电站i的固定投资成本;q为电池更换机单价;Ni为电池换电站i中的电池更换机数量;g为电池更换机相关投资成本折算系数;r0为贴现率;mi为换电站i的运营年限;δ为运营管理成本的等效系数。
年电池配送成本主要由电池配送数量和集中充电站到电池换电站之间的配送距离决定。集中充电站j到各电池换电站的年电池配送成本表示为
| ${f_{{\rm{BD}}}} = d\gamma \sum\limits_{i \in {I_{{\rm{BS}}}}} {\varepsilon m{s_i}{r_{ij}}} $ | (3) |
式中,d为年运营天数,取为365 d;γ为电池配送成本的等效系数;ε为城市公路的非直线系数;m为电池的备用系数;si为电池换电站i的日配送车辆数;rij为电池换电站i到集中充电站j的欧氏距离;IBS为电池换电站集合。
综上,年建设投资总成本表示为
| ${f_1} = \sum\limits_{i \in {I_{{\rm{BS}}}}} {{f_{{\rm{BS}},i}} + \sum\limits_{j \in {J_{{\rm{CT}}}}} {({f_{{\rm{CT}},j}} + {f_{{\rm{BD}}}})} } $ | (4) |
式中,fBS,i为各电池换电站的年建设投资成本;fCT, j为各集中充电站的年建设投资成本;fBD为年电池配送成本;IBS为电池换电站集合;JCT为集中充电站集合。
1.1.2 电池换电站的选址满意度电池换电站的选址会影响换电路径上的交通流量与用户车辆电池换电的便利程度。选址满意度包括换电需求权重距离和换电需求满意度[12],主要由各换电需求点的交通流量权重及各需求点间是否存在有电池换电站决定,换电需求点取为各社区的几何中心点。选址满意度的数学模型表示为
| ${f_2} = \omega {D_{{\rm{DT}}}} - (1 - \omega ){F_{{\rm{SA}}}}$ | (5) |
| ${D_{{\rm{DT}}}} = \sum\limits_{{k_1}} {\sum\limits_{{k_2}} {{P_{{k_1}}}{d_{{k_1}{k_2}}}{X_{{k_1}{k_2}}},{k_1},{k_2} \in {K_{{\rm{US}}}}} } $ | (6) |
| ${F_{{\rm{SA}}}} = \sum\limits_{q = 1}^{{n_q}} {{f_q}{Y_q}} $ | (7) |
式中,
年电池换电成本包括电池换电站的换电服务运行成本和待换电用户的排队等待耗时成本两部分[13]。电池换电站的选址规划,决定着各站内电池更换机的台数,从而决定了各站的换电服务运行成本;而站内电池更换机的台数,又决定了待换电用户的排队等待耗时。
假设用户的换电行为可用排队论中M/M/c/∞/∞模型进行表示,则电池换电站i中有n辆电动汽车进行换电服务时的概率Pn,i为
| $ {P}_{n,i}=\left\{ {\begin{array}{*{20}{c}}\dfrac{{P}_{0,i}}{n!}({\rho }_{i}{N}_{i}{)}^{n},1\leqslant n\leqslant {N}_{i}\\ \dfrac{{P}_{0,i}}{{N}_{i}!{N}_{i}{}^{n-{N}_{i}}}{({\rho }_{i}{N}_{i})}^{n},n>{N}_{i}\end{array}} \right.$ | (8) |
| ${P_{0,i}} = {\left[ {\sum\limits_{m = 1}^{{N_i} - 1} {\frac{{{{({\rho _i}{N_i})}^m}}}{{m!}}} + \frac{{{{({\rho _i}{N_i})}^{{N_i} - 1}}}}{{({N_i} - 1)!}}\left( {\frac{1}{{1 - {\rho _i}}}} \right)} \right]^{{\rm{ - }}1}}$ | (9) |
| ${\rho _i} = \frac{\lambda }{{{N_i}\mu }}$ | (10) |
式中,ρi为电池换电站i的换电服务强度;λ=nk /tb为服从泊松分布的单位时间内到达电池换电站的电动汽车数量,其中nk为电动汽车日换电需求量,tb为日换电高峰期时段;μ=1 /ts为电池更换机的平均服务速率,其中ts为每台电动汽车的平均换电时间。
根据里特公式(Ritter formula),可得待换电用户在电池换电站i的排队队伍长度平均值Li为
| ${L_i} = \frac{{{\lambda ^{{N_i}}}{P_{0,i}}{\rho _i}}}{{{\mu ^{{N_i}}}{N_i}!{{(1 - {\rho _i})}^2}}} + \frac{\lambda }{\mu }$ | (11) |
综上,年电池换电成本表示为
| ${f_3} = d\sum\limits_{i \in {I_{{\rm{BS}}}}} {({N_i}{C_{{\rm{RC}}}}h + {L_i}{C_{{\rm{WC}}}}{t_{\rm{b}}})} $ | (12) |
式中,h为换电站日运营时长;CRC为每台电池更换机单位时间内的换电服务运行成本;CWC为待换电用户在电池换电站单位时间内的排队等待耗时成本。
1.2 约束条件各站点的选址定容还应考虑建站经济性、站点分布和配置合理性及用户换电便利性等因素,从而对多目标决策作出约束。
(1) 电池换电站个数约束为
| $\sum\limits_{j = 1}^n {{X_{ij}} \leqslant {W_{{\rm{ch}}}}} $ | (13) |
式中,Wch为电动汽车电池换电站的总个数,此约束代表在网络中最多建设Wch个电池换电站。
(2) 电池更换机配置数量的不等式约束为
| ${N_{{\rm{s,}}\min }} \leqslant {N_i} \leqslant {N_{{\rm{s,}}\max }},i \in {I_{{\rm{BS}}}}$ | (14) |
式中,Ns,min和Ns,max分别为电池更换机配置数量的最小和最大值;IBS为电池换电站集合。
(3) 为避免电池换电站的布局过于密集,各换电站之间的距离约束表示为
| $\varepsilon {D_{{i_1}{i_2}}} \geqslant {D_{\min }};{i_1},{i_2} \in {I_{{\rm{BS}}}},{i_1} \ne {i_2}$ | (15) |
式中,
(4) 充电机及其相关设施配置约束为
| ${e_j} \geqslant {e_{j,\min }} = \frac{{b{P_{j,\Sigma }}}}{\alpha },j \in {J_{{\rm{CT}}}}$ | (16) |
式中,ej,min为集中充电站j内充电机及其相关设施的最小套数限制;b为充电效率;Pj,Σ为集中充电站j的电池配送区域内的日换电需求负荷预测总量;α为集中充电站中每台充电机的最大输出功率。
(5) 为使各电池换电站内待换电用户的排队队伍长度不趋于无穷大,其换电服务强度应小于1,即各电池换电站的换电服务强度约束为
| ${\rho _i} = \frac{\lambda }{{{N_i}\mu }} < 1$ | (17) |
对于多目标决策问题来说,直接给定变量权重或专家评价打分给出权重,属于主观赋权法,但该法主观性较强,并不能客观综合考虑各种因素。而熵权法虽然是一种客观赋权法,但却也无法考虑决策者的主观意见。因此本文引入一种模糊熵权法[14],使得该多目标决策问题既能避免过度依赖客观权重而导致决策偏差,又能将主观决策因素考虑在内。
对于具有x个目标的多目标决策问题,假设其采用熵权法计算得到的x个目标权重集合为ν={ν1, ν2,···,νx},采用模糊权重法计算得到的x个目标权重集合为σ ={σ1,σ2,···,σx},则基于模糊熵权法得到的第i个目标函数的权重为
| ${\eta _i} = \frac{{{\nu _i}{\sigma _i}}}{{\displaystyle\sum\limits_{i = 1}^x {{v_i}{\sigma _i}} }}$ | (18) |
从而将电动汽车电池换电站选址定容的多目标决策问题结合模糊熵权法转化成单目标优化问题,新目标函数(即加权总值)如式(19)所示。
| ${f_{{\rm{new}}}} = {\eta _1}{f_1} + {\eta _2}{f_2} + {\eta _3}{f_3}$ | (19) |
蝙蝠算法(Bats Algorithm,BA) 由Yang Xin She教授于2010年提出,是一种基于群体智能的启发式搜索算法[15]。其在优化过程中通过调整蝙蝠个体的响度与脉冲率,改变个体自身的位置,根据适应度函数值权衡个体所处位置的优与劣,使用较好的可行解替换较劣的解,从而追随最优的蝙蝠个体,进而找到全局最优解。在一个D维空间中,第i只蝙蝠个体在探测过程中的位置和速度在t时刻的更新公式为
| $\left\{ {\begin{array}{*{20}{l}} {{f_i} = {f_{\min }} + ({f_{\max }} - {f_{\min }})\beta } \\ {v_i^{t + 1} = v_i^t + (x_i^t - x^*){f_i}} \\ {x_i^{t + 1} = x_i^t + v_i^t} \end{array}} \right.$ | (20) |
式中,fi为第i只蝙蝠个体当前的频率;fmin和fmax分别为蝙蝠个体频率的最小值和最大值;β为[0,1]之间的随机数;xit为t时刻第i只蝙蝠个体所在的位置;vit为t时刻第i只蝙蝠个体所对应的速度;
传统BA算法中速度的变化策略由于没有采用惯性权重,从而在求解该多维复杂问题时全局寻优能力较差,无法得到理想的收敛结果。但惯性权重的选取既不能过大也不能太小,更不宜随机选取[16],因此本文采用惯性权重随进化代数的增加而线性减小的方法,增强全局搜索能力,减小收敛的随机性,提高收敛性能。惯性权重λ表示为
| $\lambda = {\lambda _{\min }} + \frac{{({\lambda _{{\rm{max}}}} - {\lambda _{\min }})({T_{\max }} - T)}}{{{T_{\max }}}}$ | (21) |
式中,λmax、λmin分别为惯性权重的最大值和最小值;T为当前进化代数;Tmax为最大进化代数。
2.2.2 引入加速因子、学习因子和个体极值策略传统BA算法在蝙蝠个体移动阶段仅考虑当前最佳个体的位置信息,却忽略了自身可能找到的最优解,从而导致种群多样性的减少,使得寻优效率及效果大大降低,容易在求解复杂多维优化问题时陷入局部极值[17]。受粒子群算法(Particle Swarm Optimization,PSO)的启发,在蝙蝠个体的移动阶段引入个体极值x′进行协同搜索,并采用加速因子p、学习因子c进行非线性反余弦加速,从而进行速度的更新。令式(20)中的β=p,结合式(21),可得速度更新公式为
| $\left\{ {\begin{array}{*{20}{l}} {{f_i} = {f_{\min }} + ({f_{\max }} - {f_{\min }})p} \\ v_i^{t + 1} = \lambda v_i^t + {{f}_{i}}\cdot {{r}_{1}}\cdot ({x}'-x_{i}^{t})+{{c}_{i}}{{r}_{2}}({{x}^{*}}-x_{i}^{t}) \end{array}} \right.$ | (22) |
式中,λ同式(21);x′为个体极值;r1、r2分别为[0, 1]之间的随机数;p为加速因子,ci为学习因子,其表达式分别为
| $\left\{ {\begin{array}{*{20}{l}} {p = 1 - \arccos \left( {\dfrac{{ - 2T/{T_{\max }} + 1}}{{\rm{{\text{π}} }}}} \right)} \\ {c_i = {f_{\max }} + ({f_{\min }} - {f_{\max }})p} \end{array}} \right.$ | (23) |
式中,T为当前进化代数;Tmax为最大进化代数。
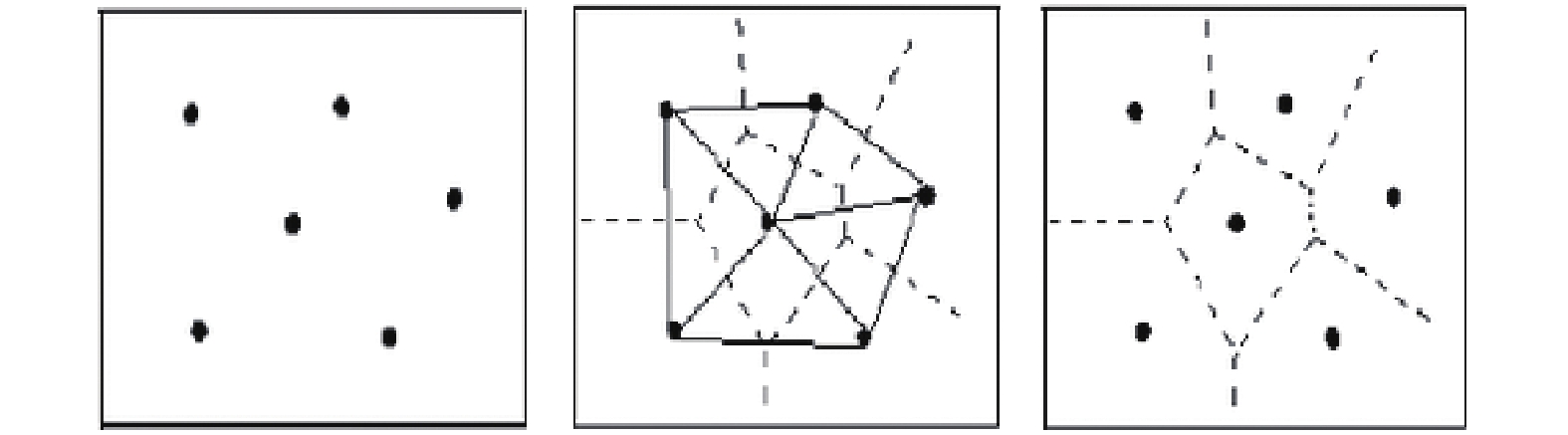
2.3 Voronoi图与改进蝙蝠算法的联合优化求解流程 2.3.1 Voronoi图与电池换电站换电服务区域的划分Voronoi图,又称为泰森多边形(Thiessen polygon)或Dirichlet图,它是由连接最邻近的两邻点间的直线作出的垂直平分线所构成的连续多边形,其生成方法如图1所示。设pk为点集p={p1, p2, ···, pn}里的一个种子点,其Voronoi区域rk的数学定义为
|
图 1 Voronoi图的生成方法 Figure 1 The generation method of Voronoi diagram |
| ${r_k} = \{ x \in X|d(x,{p_k}) < d(x,{p_j})\} $ | (24) |
式中,j=1,2,3,···,n,且j≠k;d(x,pk)为x与pk两点间的欧氏距离。
本文利用其按距离划分邻近区域的特性,结合改进蝙蝠算法,对各配送区域内的电池换电站进行换电服务区域的划分。通过求出电池换电站建站数与多目标决策加权总值的关系,确定电池换电站的最佳建站数。将种群中生成的电池换电站选址方案集合对应Voronoi图中的点集p,并将其中所有最邻近的两邻点用垂直平分线进行划分,从而划分出各电池换电站的换电服务区域。并根据各服务区域内包含的换电需求点,确定各服务区域内的换电服务需求量,进而对各电池换电站进行定容。
2.3.2 求解步骤步骤1:输入各换电需求点、集中充电站的位置坐标,以及日换电需求负荷预测、电动汽车预测总数和交通流量权重等参数信息,并根据式(25)计算用户换电需求点k的电动汽车日换电需求量nk。
| ${n_k} = {f_{{\rm{ceil}}}}\left( {S\beta \frac{{{P_k}}}{{{P_{i,\Sigma }}}}} \right),i \in {I_{{\rm{BS}}}}$ | (25) |
式中,fceil为向上取整函数;S为各电池换电站换电服务区域内的电动汽车总数;β为日换电概率,取为0.1;Pk为换电需求点k的日换电需求负荷预测;Pi,Σ为电池换电站i的换电服务区域内的日换电需求负荷预测总量。
步骤2:根据各集中充电站的坐标作出Voronoi图,从而划分出各集中充电站的电池配送区域。通过各配送区域的日换电需求负荷预测总量、充电机的最大输出功率和充电效率,根据式(16)可得各集中充电站内应购置的充电机及其相关设施的套数。
步骤3:在配送区域j内随机生成n个电池换电站,其坐标集表示为z={(x1,y1),(x2,y2),···,(xn,yn)},编码时将其表示为
| $Z = [{x_1},{x_2}, \cdots ,{x_n},{y_1},{y_2}, \cdots ,{y_n}]$ | (26) |
当蝙蝠种群数为m时,其初始坐标编码时则表示为
| $Z = \left[ {\begin{array}{*{20}{c}} {x_1^1}&{x_2^1}& \cdots &{x_n^1}&{y_1^1}&{y_2^1}& \cdots &{y_n^1} \\ {x_1^2}&{x_2^2}& \cdots &{x_n^2}&{y_1^2}&{y_2^2}& \cdots &{y_n^2} \\ \vdots & \vdots &{}& \vdots & \vdots & \vdots &{}& \vdots \\ {x_1^i}&{x_2^i}& \cdots &{x_n^i}&{y_1^i}&{y_2^i}& \cdots &{y_n^i} \\ \vdots & \vdots &{}& \vdots & \vdots & \vdots &{}& \vdots \\ {x_1^m}&{x_2^m}& \cdots &{x_n^m}&{y_1^m}&{y_2^m}& \cdots &{y_n^m} \end{array}} \right]$ | (27) |
步骤4:在配送区域j内以初始随机生成的电池换电站站址坐标作出Voronoi图,根据划分出的换电服务区域确定各电池换电站的规模(即电池更换机数量),再由式(1)~(4)得到年建设投资成本f1。各电池换电站内电池更换机数量Ni的数学表述为
| ${N_i} = {f_{{\rm{ceil}}}}\left( {\frac{1}{{{n_{\rm{q}}}}}}{\displaystyle\sum\limits_{k \in {K_{{\rm{US}}}}} {{r_{\rm{c}}}{n_k}} } \right)$ | (28) |
式中,fceil和nk同式(25);rc为各换电服务区域内用户同时到达电池换电站的概率,取为0.4;nq为每台电池更换机的最大排队车辆数,取为4辆。
步骤5:输入所有换电需求点的交通流量权重,计算各换电需求点间的欧氏距离,判断所有换电需求点间是否存在有电池换电站,判断各电池换电站的选址是否满足交通流量条件,进而由式(5)~(7)计算出电池换电站的选址满意度f2。
步骤6:通过输入用户换电需求点、随机生成的电池换电站站址坐标以及各站的换电服务强度、站内电池更换机台数和平均换电服务速率,由式(8)~(12)可得年电池换电成本f3。
步骤7:将以上所有种群中计算得出的年建设投资成本f1、选址满意度f2和年电池换电成本f3作为模糊熵权法的评价指标数据,计算各目标的熵权重和模糊权重,再根据式(18)得出基于模糊熵权法的各目标权重η1、η2、η3,并根据式(19)将多目标优化决策模型转化成单目标权重模型,得到新目标函数(即加权总值)fnew。
步骤8:将新目标函数利用改进后的蝙蝠算法循环执行步骤4~7,从而更新蝙蝠个体的速度和位置并生成新的电池换电站站址坐标,计算适应值,记录个体极值x′和全局极值x*,直至达到最大迭代次数或寻优至预定收敛精度为止。
步骤9:选择下一电池配送区域j+1,循环执行步骤3~8,直至所有配送区域均寻优完毕,输出所有配送区域的全局最优解。
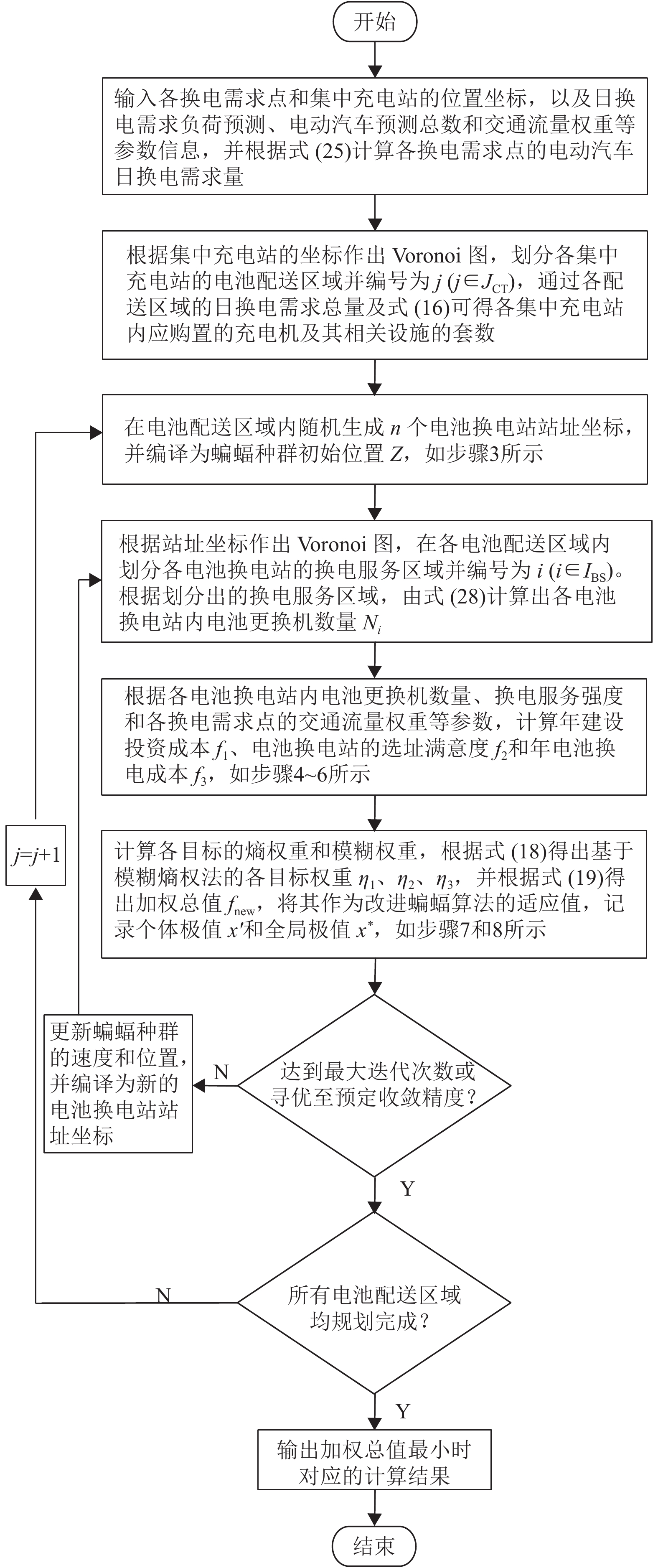
Voronoi图与改进蝙蝠算法联合优化求解的整体流程框图如图2所示。
|
图 2 Voronoi图与改进蝙蝠算法联合优化求解的整体流程 Figure 2 The process of joint optimization of Voronoi diagram and improved bats algorithm |
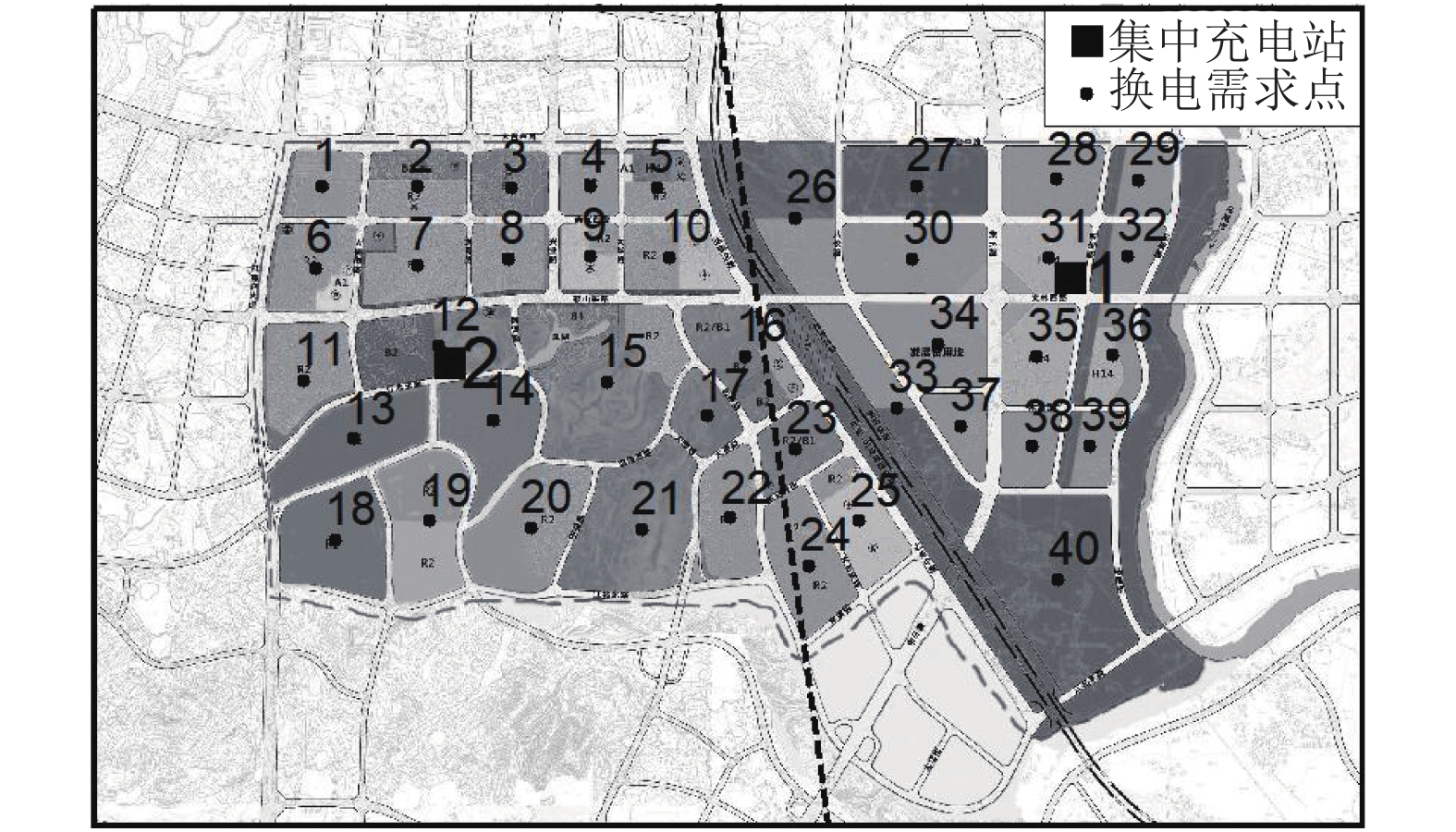
以广东省某市区电池换电站规划选址为例,该区域面积为24.6 km2,共分为40个社区,取每个社区的几何中心点作为电动汽车换电需求点,其中集中充电站的选址已事先通过专家评价打分选定。根据集中充电站1和2的坐标作Voronoi图,划分成两个电池配送区域,如图3所示。图中方形黑点为集中充电站的位置,其旁边的数值为集中充电站编号;黑色分界虚线为两座集中充电站的电池配送区域边界,以集中充电站编号划分成配送区域1和2;圆形黑点为换电需求点,其上方的数值为换电需求点的序号。各配送区域中换电需求点的序号、日换电需求负荷预测和交通流量权重如表1所示。
|
图 3 各换电需求点和集中充电站的分布 Figure 3 Distribution of battery swapping demand points and centralized charging stations |
| 表 1 换电需求点的序号、日换电需求负荷预测和交通流量权重 Table 1 Order number of battery swapping demand points, load forecasting and traffic flow weight |
假设集中充电站中每台充电机的最大输出功率α为10 kW,充电效率b为90%。每座集中充电站固定投资成本wj为300万元,每座电池换电站固定投资成本wi为100万元,运营管理成本δ取基建或固定投资成本的10%;电池换电站中电池更换机单价q为70万元/台,更换机相关投资成本折算系数g为1.6万元/台2。贴现率r0为0.08,集中充电站和电池换电站的运营年限mj和mi均取20年;城市道路的弯曲系数ε为1.4;城市中车辆行驶的平均速度v为40 km/h;折衷权重ω为0.6;日换电高峰期时段tb主要为上班(7:00~9:00)和下班(17:00~19:00)时段,即为4 h;每台车辆的平均换电时间ts为0.1 h;电池换电站日运营时长t为24 h;换电服务运行成本CRC为50元/h;排队等待耗时成本CWC为25元/h。IBA算法中设置蝙蝠种群数m为20,最大迭代次数Tmax为300代,惯性权重的最小值λmin和最大值λmax分别为0.4和0.9,蝙蝠个体频率的最小值fmin和最大值fmax分别为0.5和2.5。
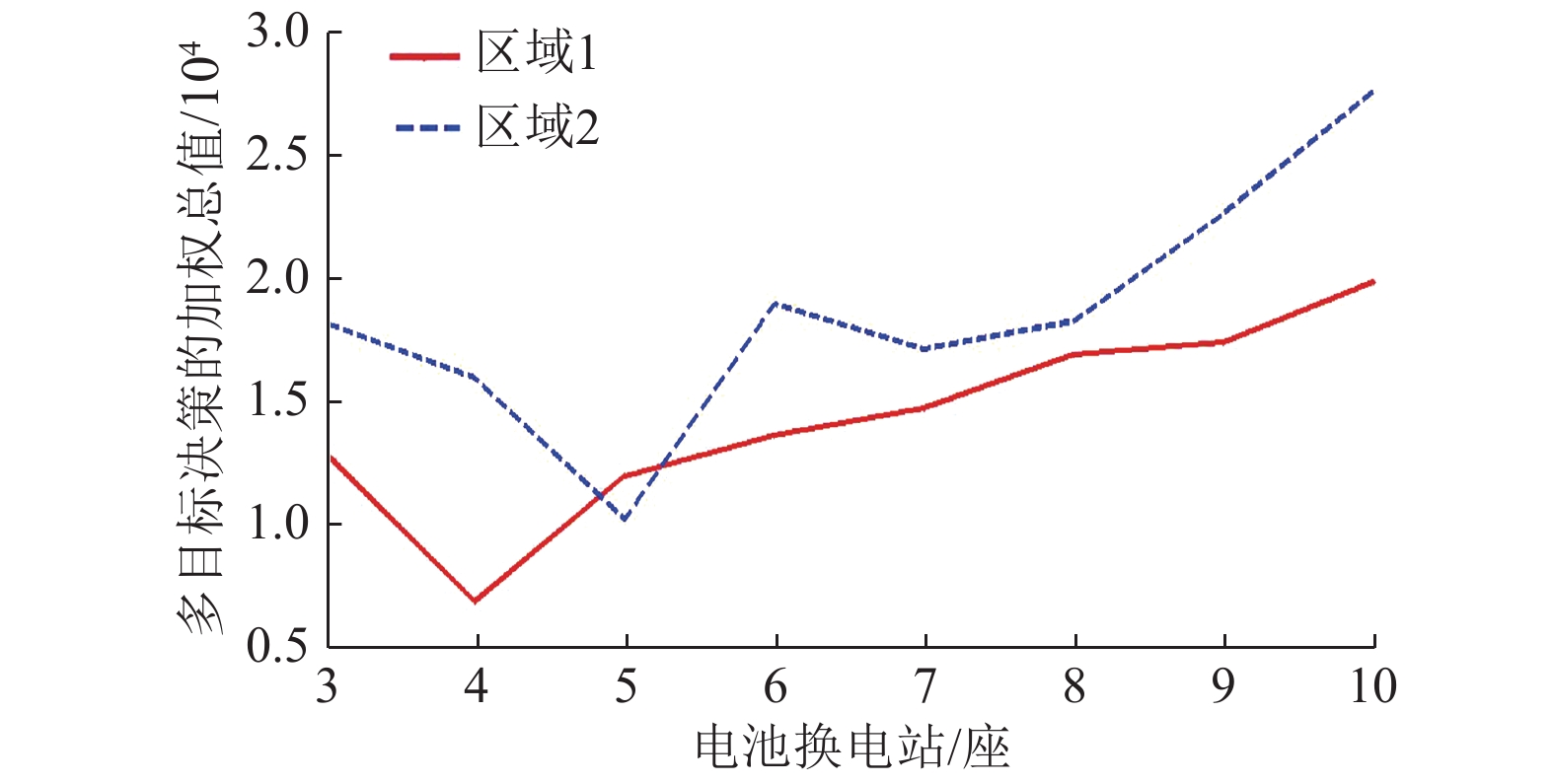
根据2.3.2节的求解步骤,两座集中充电站的配送区域中电池换电站个数与加权总值关系的运算结果如图4所示。若电池换电站数量过少,则会由于用户与换电站距离过远且站内电池更换机数量太多,导致年电池换电成本和换电站年建设投资成本的增加,进而导致加权总值过高;而电池换电站数量过多又会由于所有换电站的年建设投资成本过高同样导致加权总值过高。由图4可知,当集中充电站1的配送区域(即区域1)中电池换电站建站数为4座时,加权总值最低,为0.8369×104;同理当集中充电站2的配送区域(即区域2)中电池换电站建站数为5座时,加权总值最低,为1.1254×104。
|
图 4 电池换电站建站数与加权总值的关系 Figure 4 Relationship between the number of battery swapping stations and weighted gross |
电池换电站的站址位置分布及其换电服务区域的划分如图5所示,图中方形黑点与黑色分界虚线的含义与图3相同;三角形点代表区域1和区域2分别求解到的电池换电站最优选址布局,其旁边的数值为电池换电站编号;网格状直线为Voronoi图划分出的各电池换电站换电服务区域范围;圆形点为换电需求点,其旁边的数值为电池换电服务隶属的电池换电站编号。由图5可知,右边的区域1由1座集中充电站和4座电池换电站组成,其中电池换电站1的换电需求服务社区为5个,换电站2的换电需求服务社区为4个,换电站3的换电需求服务社区为5个,换电站4的换电需求服务社区为4个;区域1共服务社区有18个。左边的区域2由1座集中充电站和5座电池换电站组成,其中电池换电站1的换电需求服务社区为4个,换电站2的换电需求服务社区为3个,换电站3的换电需求服务社区为5个,换电站4的换电需求服务社区为6个,换电站5的换电需求服务社区为4个;区域2共服务的社区有22个。

|
图 5 最优布局方案及换电服务区域划分 Figure 5 Optimal planning and the division of battery swapping service area |
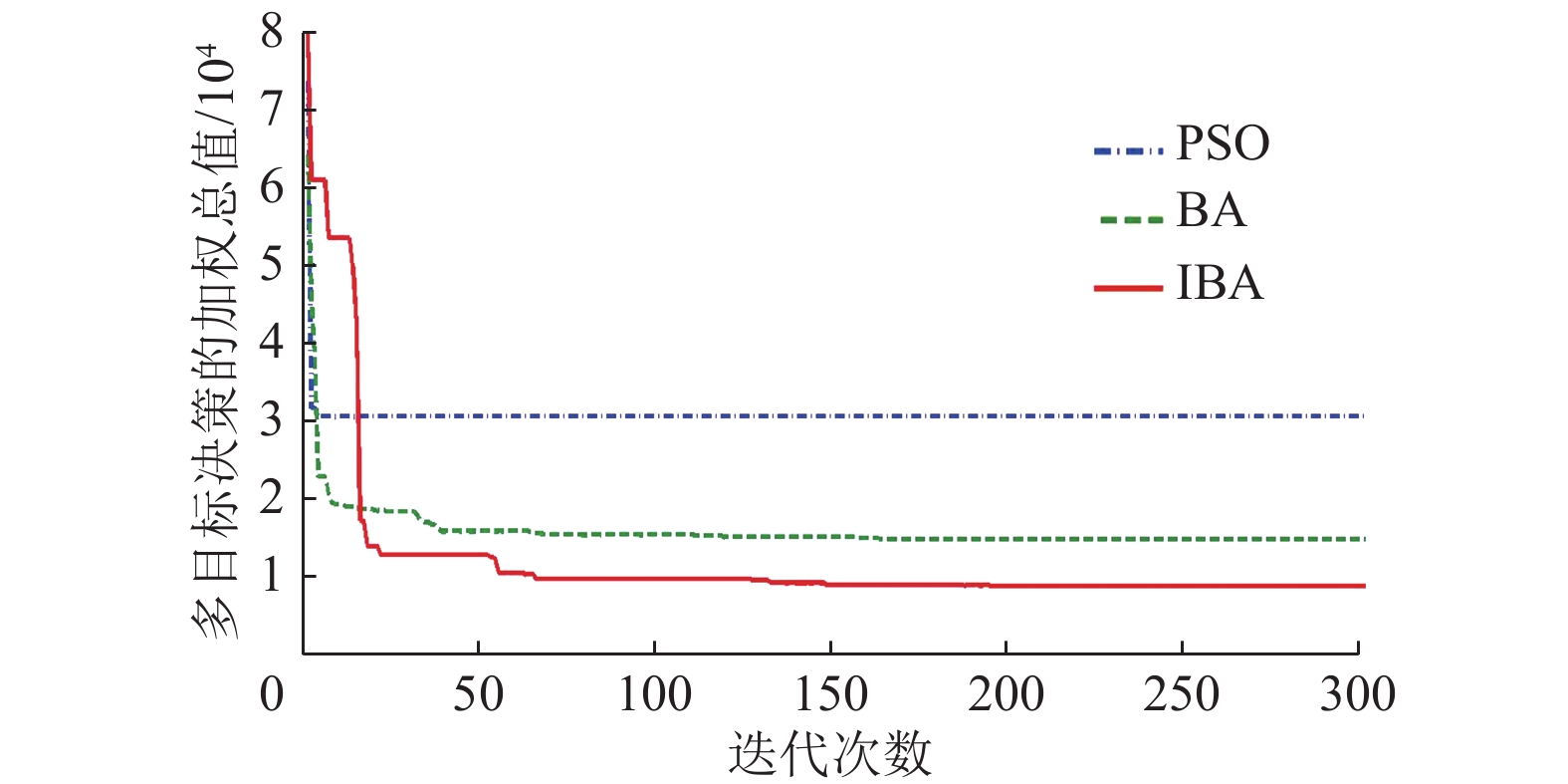
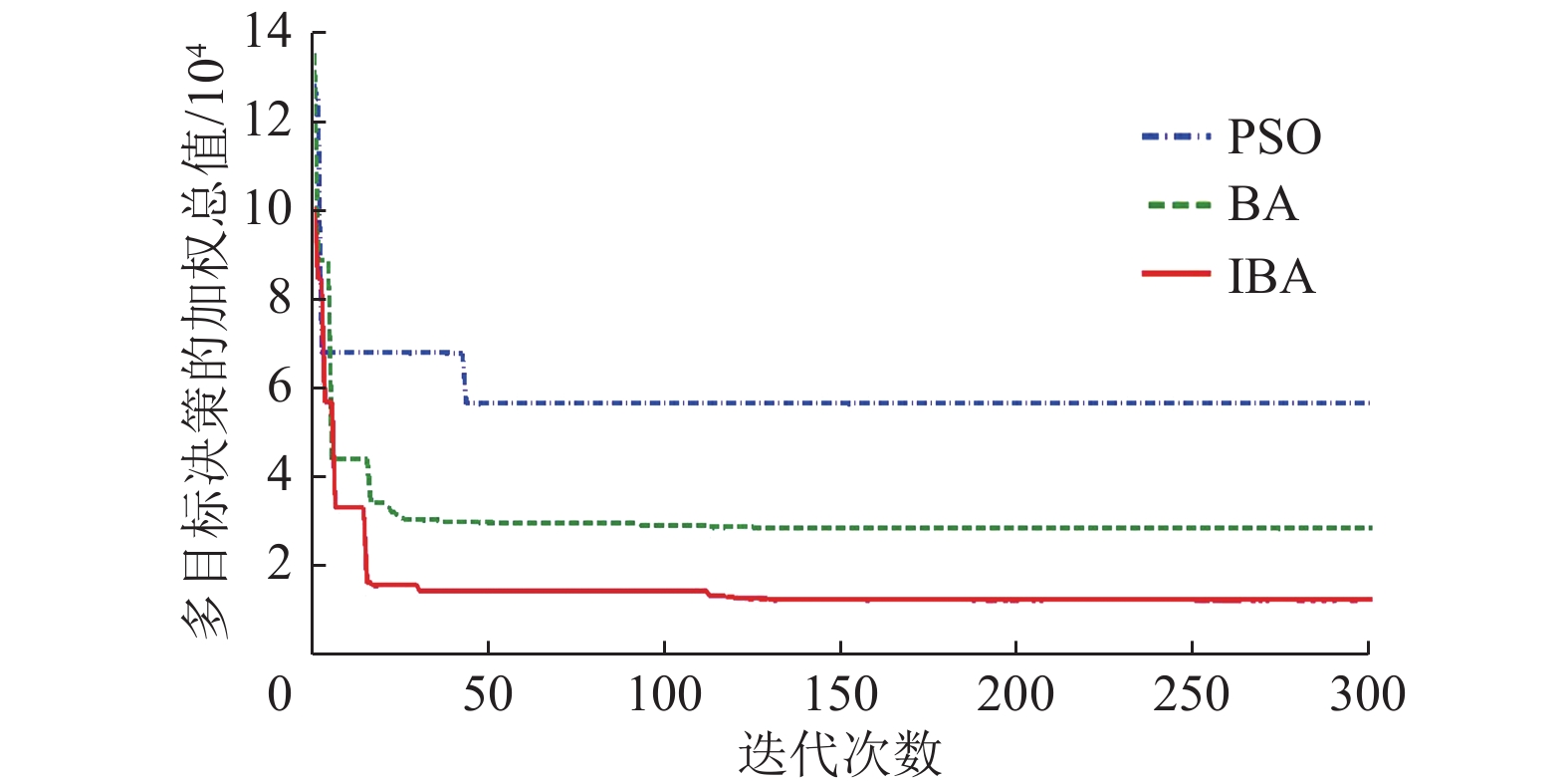
分别采用PSO、BA和IBA 3种算法的仿真结果对比如图6和图7所示。由图可知,PSO收敛速度虽快,但很快就陷入了局部最优,且寻优能力最差;BA收敛速度较PSO慢,但寻优能力强于PSO;IBA收敛速度虽最慢,但寻优能力与BA相比有较大提升,全局寻优能力最强。3种算法的优化计算结果如表2所示,由于PSO的寻优能力最差,电池换电站的选址布局最不合理,从而使每个换电站内配置的电池更换机台数增多,导致年建设投资成本和换电服务运行成本的增加。同时由于选址布局规划的不合理,导致每条换电路径上的交通流量增多,且待换电用户每次排队换电的队伍过长,既降低了电池换电站的选址满意度,又增加了待换电用户的排队等待耗时成本,最终导致加权总值的增加。由此可知,本文所提IBA算法的选址定容布局规划结果最为理想。
|
图 6 区域1三种算法仿真结果对比 Figure 6 Comparison of simulation results of three algorithms for the first region |
|
图 7 区域2三种算法仿真结果对比 Figure 7 Comparison of simulation results of three algorithms for the second region |
| 表 2 3种算法优化结果对比 Table 2 Comparison of optimization results of three algorithms |
正如传统燃油车需要汽油作为驱动力,电动汽车的普及同样离不开充换电设施的大规模投入。本文针对电动汽车电池换电模式下的“集中充电,统一配送”模式,考虑并结合多方面因素,提出了以年建设投资成本、电池换电站选址满意度和年电池换电成本为目标的多目标决策模型。通过广东省某市区集中充电站和电池换电站选址定容规划及3种优化算法对比的结果,得出以下结论:
(1) IBA算法在传统BA算法的基础上引入惯性权重和考虑个体极值引导速度更新的策略,与PSO和传统BA算法相比,提高了全局寻优能力及搜索速度,在电池换电站选址定容的问题上具有更好的求解效率和性能。
(2) 将IBA算法与Voronoi图结合,对该选址定容模型进行联合求解,提出求解电池换电站选址定容问题的新思路,并通过算例验证了方法的有效性。
(3) 电池换电站选址定容规划属于复杂的多目标决策问题,规划时应考虑集中充电站的影响,对各站的建设投资成本和电池配送成本作出决策;同时还应考虑选址建站对于交通流量和用户换电便利程度、换电服务运行成本和用户排队等待耗时成本的影响。
本文未充分考虑电动汽车的车辆类型和动力类型、用户的插充和换电习惯及集中充电站的配网损耗和规划等,待日后继续研究和完善。
| [1] |
陈良亮, 张浩, 倪峰, 等. 电动汽车能源供给设施建设现状和发展探讨[J].
电力系统自动化, 2011, 35(14): 11-17.
CHEN L L, ZHANG H, NI F, et al. Present situation and development trend for construction of electric vehicle energy supply infrastructure[J]. Automation of Electric Power Systems, 2011, 35(14): 11-17. |
| [2] |
田莉. 新能源汽车充换电站商业化运营模式研究[J].
北方经贸, 2019, 9(2): 49-50, 63.
TIAN L. Research on commercial operation mode of charging and swapping power station of new energy vehicles[J]. Northern Economy and Trade, 2019, 9(2): 49-50, 63. |
| [3] |
王善立, 成天乐. 基于两阶段智能优化算法的电动汽车换电站选址[J].
电工技术, 2019, 20(51): 119-122.
WANG S L, CHENG T L. Location selection of electric vehicle power station based on two-stage intelligent optimization algorithms[J]. Electrical Engineering and Technology, 2019, 20(51): 119-122. |
| [4] |
张昊杰, 薛太林, 杨擎宇. 基于混沌猫群算法的电动汽车充电站最优规划[J].
自动化与仪表, 2020, 35(8): 6-10, 25.
ZHANG H J, XUE T L, YANG Q Y. Optimal planning of charging station for electric vehicle based on chaos cat swarm optimization[J]. Automation and Instrumentation, 2020, 35(8): 6-10, 25. |
| [5] |
朱书研, 杨斌, 朱小林. 考虑偏差路径的电动汽车充电站选址和定容[J].
上海海事大学学报, 2019, 40(1): 44-50.
ZHU S Y, YANG B, ZHU X L. Location and capacity of electric vehicle charging station considering deviation path[J]. Journal of Shanghai Maritime University, 2019, 40(1): 44-50. |
| [6] |
罗清玉, 田万利, 贾洪飞. 考虑通勤需求的电动汽车充电站选址与定容模型[J].
吉林大学学报(工学版), 2019, 49(5): 1471-1477.
LUO Q Y, TIAN W L, JIA H F. Electric vehicle charging station location and fixed capacity model considering commuting needs[J]. Journal of Jilin University (Engineering Edition), 2019, 49(5): 1471-1477. |
| [7] |
丁丹军, 戴康, 张新松, 等. 基于模糊多目标优化的电动汽车充电网络规划[J].
电力系统保护与控制, 2018, 46(3): 43-50.
DING D J, DAI K, ZHANG X S, et al. Electric vehicle charging network planning based on fuzzy multi-objective optimization[J]. Power System Protection and Control, 2018, 46(3): 43-50. DOI: 10.7667/PSPC170006. |
| [8] |
代希雷, 张彭兴, 赖明勇, 等. 基于路径优化的电池配送站选址定容规划[J].
陕西电力, 2016, 44(12): 18-22.
DAI X L, ZHANG P X, LAI M Y, et al. Locating and sizing planning of battery distribution station based on path optimization[J]. Shaanxi Electric Power, 2016, 44(12): 18-22. |
| [9] |
陈静鹏, 艾芊, 肖斐. 基于用户出行需求的电动汽车充电站规划[J].
电力自动化设备, 2016, 36(6): 34-39.
CHEN J P, AI Q, XIAO F. Electric vehicle charging station planning based on user travel needs[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39. |
| [10] |
高赐威, 张亮, 薛飞, 等. 考虑集中型充电站定址分容的电网规划研究[J].
中国电机工程学报, 2012, 32(7): 40-46.
GAO C W, ZHANG L, XUE F, et al. Grid planning considering capacity and site of large-scale centralized charging stations[J]. Proceedings of the CSEE, 2012, 32(7): 40-46. |
| [11] |
熊虎, 向铁元, 祝勇刚, 等. 电动汽车电池更换站布局的最优规划[J].
电力自动化设备, 2012, 32(9): 1-5.
XIONG H, XIANG T Y, ZHU Y G, et al. Optimal planning of battery swapping stations of electrical vehicles[J]. Electric Power Automation Equipment, 2012, 32(9): 1-5. |
| [12] |
刘柏良, 黄学良, 程骏, 等. 含分布式电源及电动汽车充电站的配电网多目标规划研究[J].
电网技术, 2015, 39(2): 450-456.
LIU B L, HUANG X L, CHENG J, et al. Multi-objective planning of distribution network containing distributed generation and electric vehicle charging stations[J]. Power System Technology, 2015, 39(2): 450-456. |
| [13] |
张鹏兴, 郭嘉, 徐江平, 等. 集中充电站和电池更换点的联合规划选址[J].
电网技术, 2016, 40(11): 3489-3496.
ZHANG P X, GUO J, XU J P, et al. Joint planning and site selection of centralized charging station and battery swapping point[J]. Power System Technology, 2016, 40(11): 3489-3496. |
| [14] |
陈璟华, 邱明晋, 唐俊杰, 等. 模糊熵权法和CCPSO算法的含风电场电力系统多目标无功优化[J].
广东工业大学学报, 2018, 35(1): 35-40.
CHEN J H, QIU M J, TANG J J, et al. Multi-objective reactive power optimization in electric power system with wind farm based on fuzzy entropy weight method and CCPSO algorithm[J]. Journal of Guangdong University of Technology, 2018, 35(1): 35-40. DOI: 10.12052/gdutxb.170123. |
| [15] |
YANG X S. A new metaheuristic bat-inspired algorithm[J].
Computer Knowledge & Technology, 2010, 284: 65-74.
|
| [16] |
郭经韬. 含风电场的电力系统多目标最优潮流研究[D]. 广州: 广东工业大学, 2013.
|
| [17] |
周贤泉, 宋威, 张士昱, 等. 一种改进的蝙蝠算法[J].
传感器与微系统, 2019, 38(11): 139-143.
ZHOU X Q, SONG W, ZHANG S L, et al. An improved bats algorithm[J]. Transducer and Microsystem Technologies, 2019, 38(11): 139-143. |
 2021, Vol. 38
2021, Vol. 38