2. 澳门大学 科技学院,中国 澳门 999078
2. Faculty of Science and Technology, University of Macau, Macau 999078, China
基于柔性铰链的夹钳具有精度高、响应快等优点,在微机电系统、生物工程、光纤对接和航空航天等领域得到了广泛的应用[1-4]。柔性夹钳凭借其微操作能力,可精密夹持微小尺寸的物体,实现夹起−抓住−释放的全过程。然而,夹持过程中很难避免抓爪因输出力过大致使抓取物损坏的现象。基于此,研究者多采用常力机构设计柔性夹钳,常力机构可以在一定输入位移范围内提供几乎恒定的输出力[5]。
通常有2种方法能实现常力输出特性:(1) 使用力传感器和位移传感器,直接控制夹钳的输出力[6],Zhang等[7]设计了一种带有MEMS力传感器的自动机器人微操作系统,用于果蝇幼虫的生物学研究;(2) 采用弹簧储能结构,实现常力输出[8]。前者需建立精密控制系统,成本较高且结构复杂,后者为较主流的方法。但考虑到传统运动副存在间隙、易磨损且运动精度低等问题,学者采用柔顺机构来设计常力机构[9-11]。
柔顺机构利用柔性铰链的弹性变形实现力和运动的传递,具有无需装配、无运动副间隙和高运动精度等优点,被广泛用于高精度夹钳设计[12-13]。张赢斌[14]运用拓扑优化法设计了一种柔顺恒力微夹钳,优化后的结构能在一定输入位移范围内恒力夹取操作对象;时培成等[15]运用正负刚度组合原理,设计了具有准零刚度的座椅悬架系统,可实现低频和超低频隔振;Wang等[16]通过改变梁的形状,设计了一种柔性恒力夹持器,其可抓取不同尺寸的物体;Hao等[17]设计了一种常力柔顺平行夹钳,可恒力夹取脆性物体使其不受损坏;Liu等[18]设计了一种具有被动常力机构的夹持器,可输出530 mN恒力,抓爪的位移行程达220 μm。
为进一步降低抓取物损坏的概率,增大夹钳的常力输出范围,在放大模块与常力模块串联的基础上,设计一种具有限力输出保护特性的柔性夹钳。该夹钳结构不仅可保证抓爪末端在一定输出位移范围内恒力夹取物体,同时也可放大压电陶瓷的输入位移,实现大范围恒力输出,以适应不同尺寸大小的物体;其采用压电陶瓷驱动,一体化柔性机构实现常力输出,在能减少力触觉等多种传感器使用的同时也能保证高夹钳的输出精度。首先,利用伪刚体法,对桥式机构和杠杆机构进行建模,分别得到刚度与放大倍数关系式;然后,对屈曲梁的力学特性进行分析,推导出具有特定角度的导向梁的力−位移表达式;最后,通过MATLAB计算得出不同梁的结构参数均可影响常力模块的力学特性。
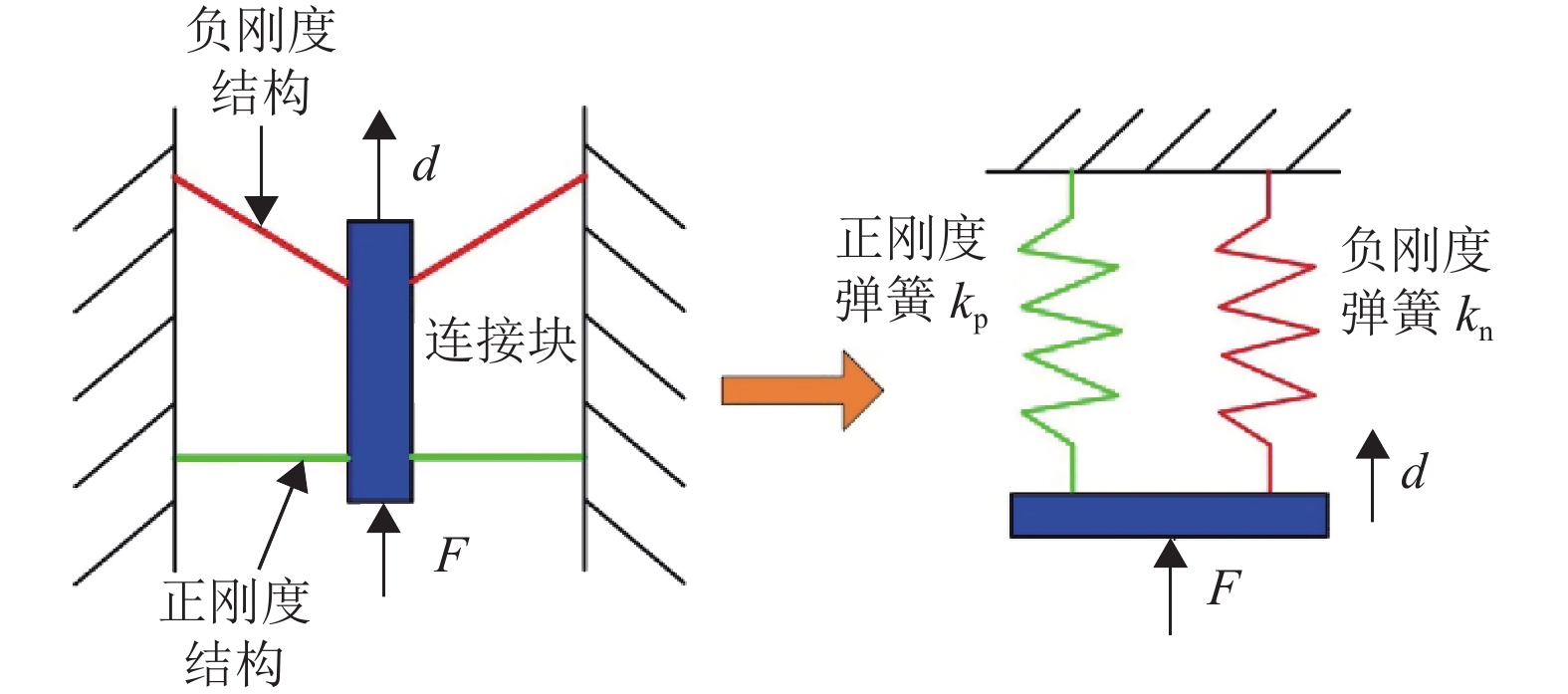
1 柔性夹钳的设计 1.1 常力原理柔性夹钳包含放大模块和常力模块,放大模块由桥式机构与杠杆机构组成;常力模块一般采用刚度组合机构、曲梁机构和形状优化机构等常力机构[19]。其中刚度组合机构较为常用,原理如图1所示,相较于其他常力机构,具有无摩擦、高输出精度和结构简单等优点;但具有对尺寸参数敏感和数学模型较复杂等缺点。
|
图 1 刚度组合常力机构原理 Figure 1 Stiffness combined principle for constant force mechanism |
依据刚度k的定义可知
| $ k = \frac{F}{d} $ | (1) |
其中F为机构所受的载荷,d为载荷作用下发生的变形。当F 随d的增大而增大时,刚度k为正;当F 随d的增大而减小时,刚度k为负;当F 随d的增大却不发生变化时,刚度k为零。综上,正负刚度组合的零刚度机构可实现常力输出。
由图1可知,刚度组合机构由正刚度结构与负刚度结构并联组成。在并联弹簧系统中,常力模块的刚度kc可表示为
| $ {k_{\rm{c}}} = \frac{{{k_{\rm{p}}}d + {k_{\rm{n}}}d}}{d} = {k_{\rm{p}}} + {k_{\rm{n}}} $ | (2) |
式(2)中kp、kn分别为正、负刚度弹簧的刚度。
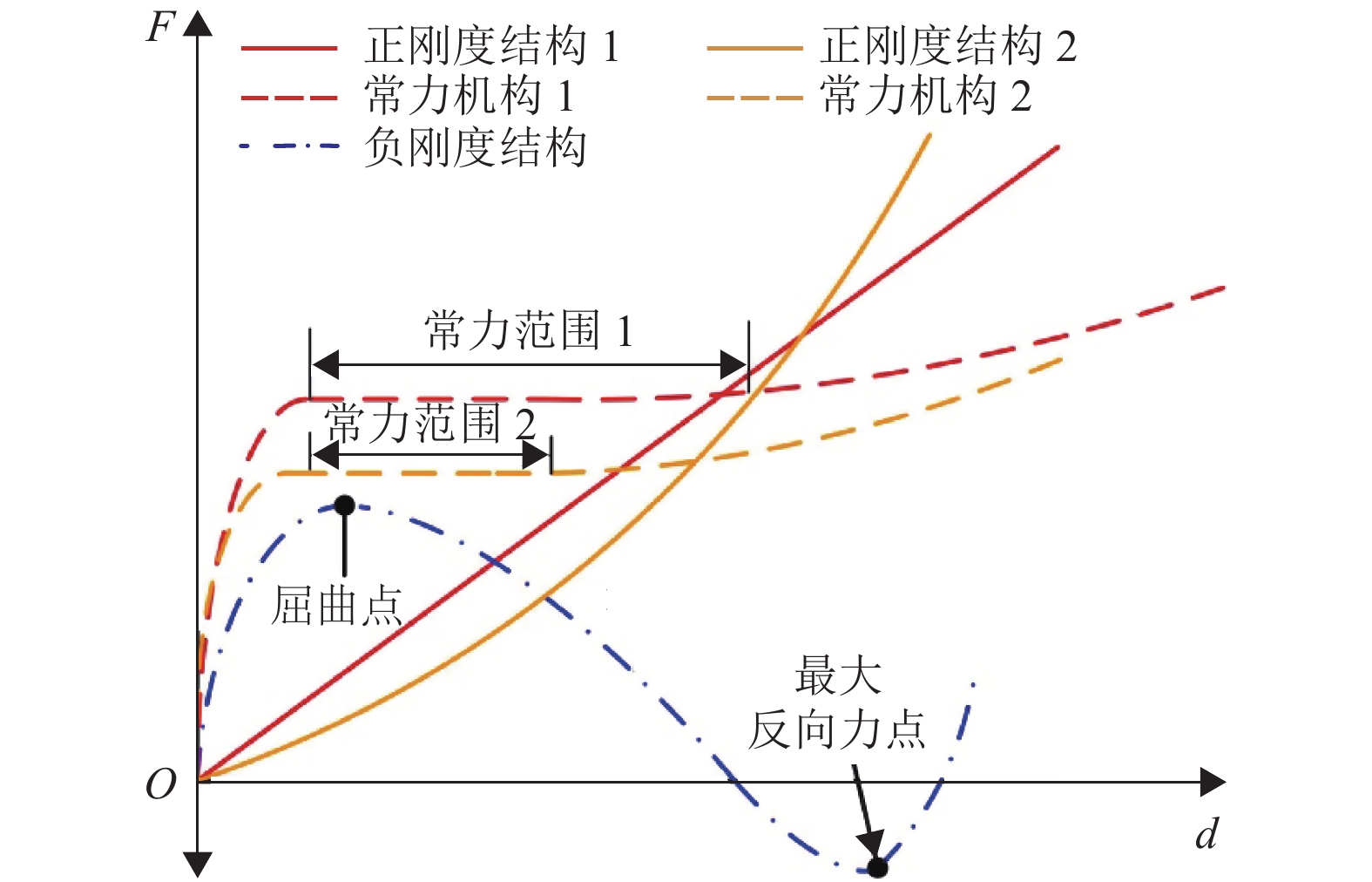
由式(2)可知,正负刚度相抵消可实现零刚度结构,其力−位移特性曲线如图2所示。常力机构在一定范围内表现出的常力特性,主要取决于正、负刚度结构的刚度性能。负刚度结构具有屈曲特性[20],其力−位移曲线存在屈曲点和最大反向力点。在屈曲点前和最大反向力点后,为正刚度特性;在两点之间,为负刚度特性。正刚度结构可分为线性正刚度结构1和非线性正刚度结构2。非线性正刚度结构未能充分利用负刚度结构的负刚度区域,使得常力范围较小。因此,正刚度结构趋近于线性,可更多地与负刚度区域形成常力区域。
|
图 2 常力机构力−位移特性曲线 Figure 2 Force-displacement characteristic of constant force mechanism |
其次,为使夹钳仍可提供恒力输出,放大模块与常力模块组合的刚度也必须为零。两模块以串联方式连接。在串联弹簧系统中,可得
| $ \Delta {{{x}}_{\rm{g}}} = \Delta {{{x}}_{\rm{a}}} + \Delta {{{x}}_{\rm{c}}} $ | (3) |
| $ {F_{\rm{g}}} = {k_{\rm{a}}}\Delta {{{x}}_{\rm{a}}} = {k_{\rm{c}}}\Delta {{{x}}_{\rm{c}}} $ | (4) |
其中Δxg、Δxa和Δxc分别为抓爪、放大模块和常力模块的输出位移,ka为放大模块的刚度,kc为常力模块的刚度,Fg为抓爪的输出力。
进一步可得
| $ {k_{\rm{g}}} = \frac{{{k_{\rm{a}}}{k_{\rm{c}}}}}{{{k_{\rm{a}}} + {k_{\rm{c}}}}} $ | (5) |
其中kg为夹钳的刚度。
由式(5)可知,当kc趋近于零时,kg趋近于零,抓爪的输出力趋近于恒定。综上,在放大模块与常力模块串联的基础上设计柔性夹钳的整体结构。
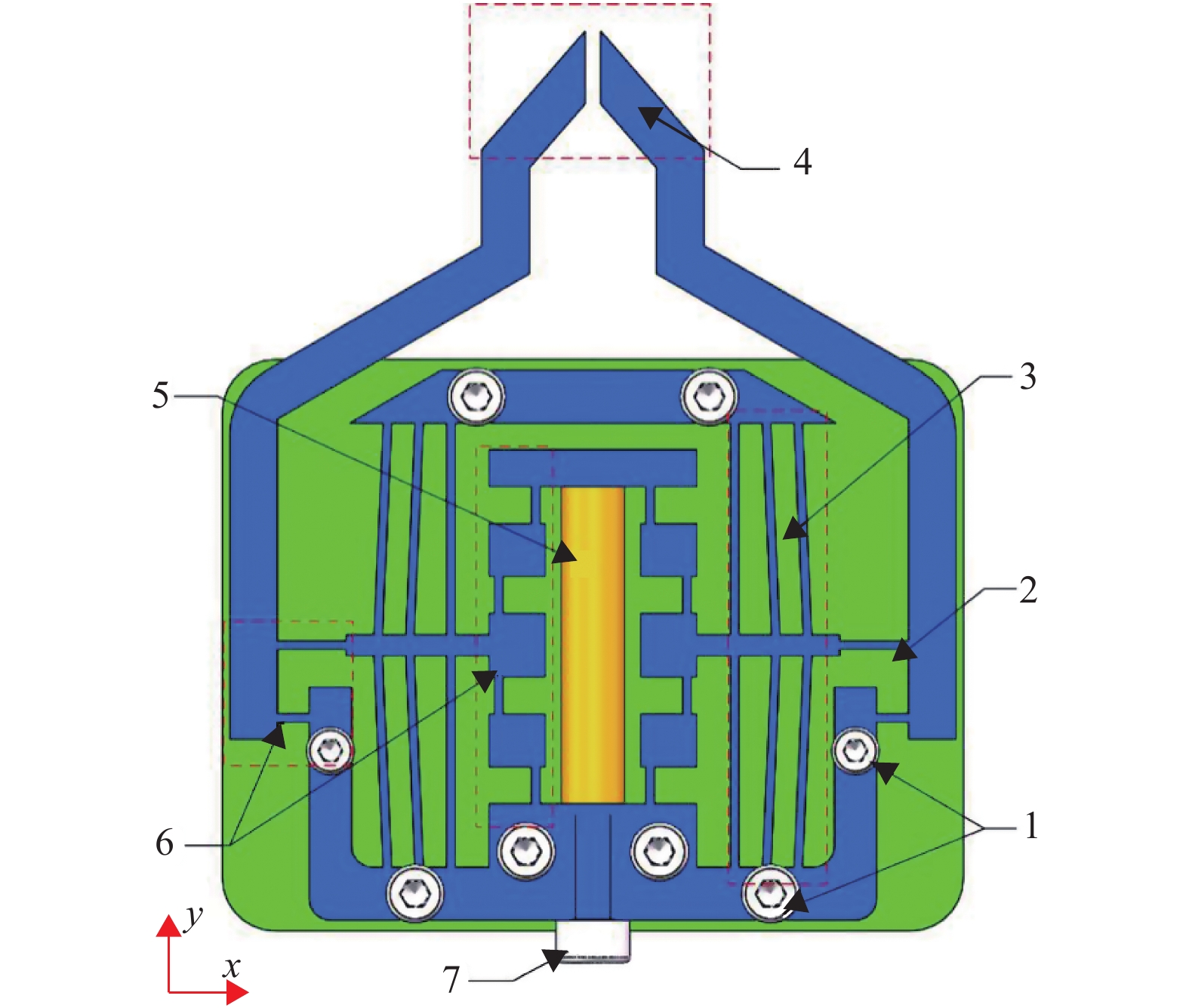
1.2 整体结构设计具有限力输出保护特性的柔性夹钳装配图如图3所示,夹钳采用平行式夹持的方式。该方式可提供一对相向夹紧力,物体不易滑落,且操作对象不受限制,可夹取多种尺寸、形状不一的物体。结构采用放大模块和常力模块串联的方式。放大模块由桥式机构和杠杆机构组成,可放大压电陶瓷驱动器的输出位移;常力模块由2根直梁和4根具有屈曲特性的双稳态梁组成,实现恒力输出。压电陶瓷在y方向输入位移,经由两模块作用传导,最终驱动抓爪在x方向运动,实现抓取操作。
|
图 3 具有限力输出保护特性的柔性夹钳装配图 Figure 3 Assembly diagram of the proposed flexible gripper 1. 固定螺栓;2. 底座;3. 常力模块;4. 抓爪末端;5. 压电陶瓷驱动器;6. 放大模块;7. 预紧螺栓 |
放大模块的作用是放大压电陶瓷的输出位移,使得抓爪有足够的输出空间夹持多种尺寸的物体。为确定放大模块的放大倍数与刚度的数学表达式,首先需要采用伪刚体模型法对其建模分析。
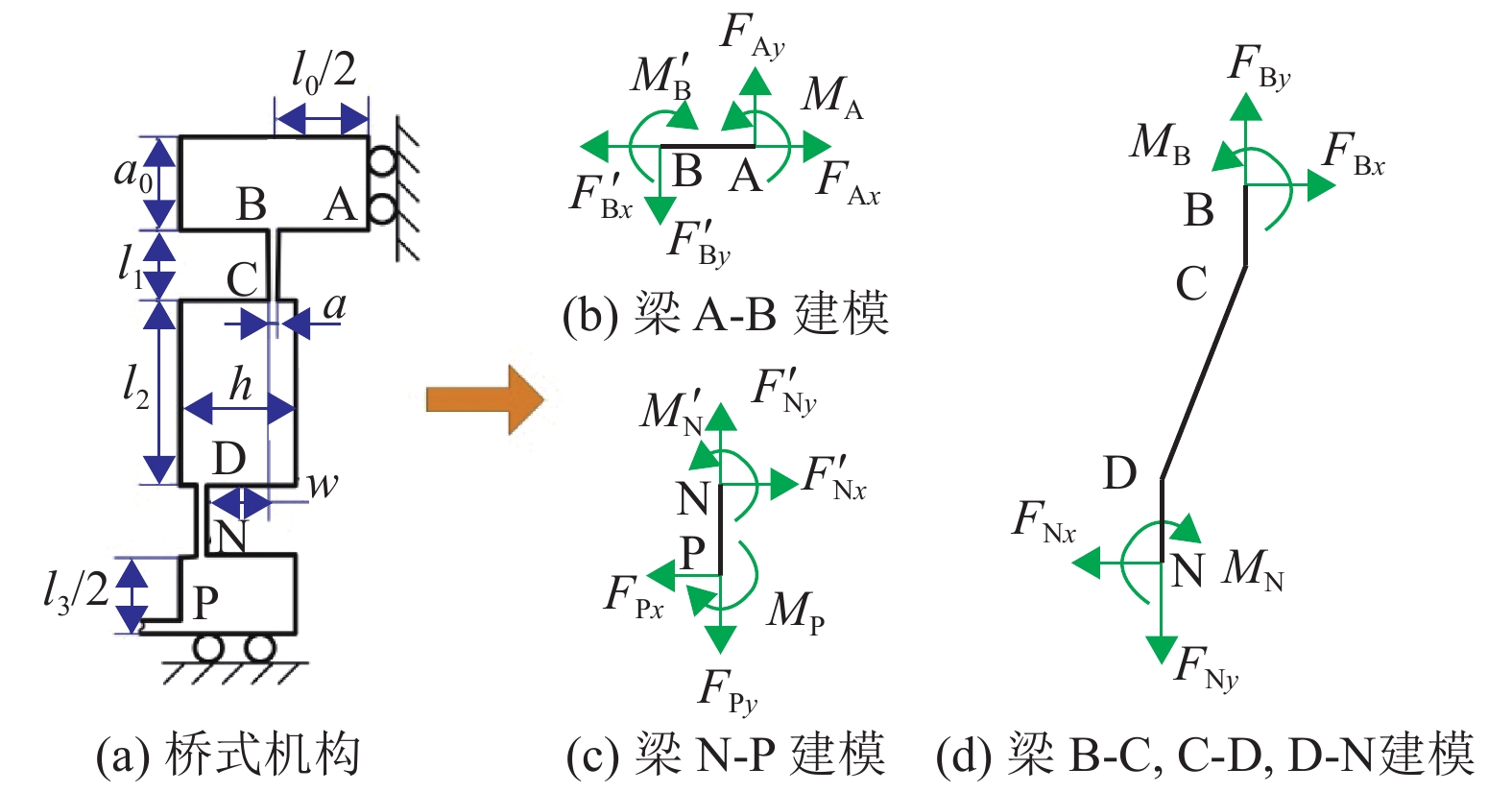
2.1 桥式机构分析正刚度结构由桥式机构和杠杆机构组成,对两种机构分别进行分析,桥式机构的1/4结构及建模如图4所示。
图4中,梁A-B、C-D和N-P分别为桥式机构的输入梁、连接梁和输出梁,B-C和D-N均表示直梁型铰链。l0、a0分别为输入梁的总长度、宽度,l2、h分别为连接梁的长度和宽度,l3为输出梁的总长度,l1、a分别为直梁型铰链的缺口长度和最小宽度,w为两直梁型铰链的水平距离。依据受力平衡原理,可得
| $ \left\{ \begin{split} & {{F_{{\rm{A}}y}}{\rm{ = }}{F_{{\rm{B}}y}} = {F_{{\rm{N}}y}} = {F_{{\rm{P}}y}} = \frac{{{F_{{\rm{in}}}}}}{2}} \\[-2pt] & {{F_{{\rm{A}}x}} {\rm{ = }} {F_{{\rm{B}}x}} = {F_{{\rm{N}}x}} = {F_{{\rm{P}}x}} = \frac{{{F_{{\rm{out}}}}}}{2}} \end{split} \right. $ | (6) |
式(6)中Fin、Fout分别为桥式机构的输入力和输出力。各梁中,由力矩平衡可得
| $ \quad\qquad\left\{ \begin{split} & {{M_{\rm{A}}} + \frac{{{F_{{\rm{A}}y}}{l_0}}}{2} = {{M}_{\rm{B}}'}} \\[-2pt] & {{{M}_{\rm{N}}'} = {M_{\rm{P}}} + \frac{{{{F}_{{\rm{P}}x}'}{l_3}}}{2}} \\[-2pt] & {{M_{\rm{B}}} + {F_{{\rm{B}}y}}w = {M_{\rm{N}}} + {F_{{\rm{B}}x}}\left( {2{l_1} + {l_2}} \right)} \end{split}\right. $ | (7) |
其中M为力矩
|
图 4 桥式机构及其建模 Figure 4 Schematic of bridge type mechanism |
进一步得到桥式机构力与位移的关系式为
| $ \left[ {\begin{array}{*{20}{c}} {{{{x}}_{{\rm{in}}}}} \\ {{{{x}}_{{\rm{out}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}} \\ {{C_{21}}}&{{C_{22}}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {{F_{{\rm{in}}}}} \\ {{F_{{\rm{out}}}}} \end{array}} \right] $ | (8) |
式(8)中xin、xout为桥式机构的输入位移和输出位移。
| $ \left\{ \begin{aligned} {C_{11}} = &\frac{2}{{{k_{{l_1}}}}} + \frac{1}{{{k_{{l_2}}}}} + \frac{1}{{{k_{{l_3}}}}} + \frac{1}{{4{k_{{\theta _0}}}}}\left( {{w^2} + w{l_0} + \frac{1}{3}l_0^2} \right) + \\[-3pt] &\frac{{{w^2}}}{{2{k_{{\theta _1}}}}} + \frac{{{w^2}}}{{12{k_{{\theta _2}}}}} + \frac{{{w^2}}}{{4{k_{{\theta _3}}}}} \\[-3pt] {C_{12}} = &\frac{1}{{4{k_{{\theta _0}}}}}\left( {w + \frac{1}{2}{l_0}} \right)\left( {2{l_1} + {l_2} + {a_0}} \right) + \frac{{w\left( {{l_1} + {l_2}} \right)}}{{2{k_{{\theta _1}}}}} +\\[-3pt] & \frac{{w{l_2}}}{{12{k_{{\theta _2}}}}} + \frac{w}{{4{k_{{\theta _3}}}}}\left( {2{l_1} + {l_2} + \frac{1}{2}{l_3}} \right) \\[-3pt] {C_{21}} = &\frac{1}{{4{k_{{\theta _0}}}}}\left( {w + \frac{1}{2}{l_0}} \right)\left( {2{l_1} + {l_2} + {a_0}} \right) + \frac{{w\left( {{l_1} + {l_2}} \right)}}{{2{k_{{\theta _1}}}}} +\\[-3pt] & \frac{{w{l_2}}}{{12{k_{{\theta _2}}}}} + \frac{w}{{4{k_{{\theta _3}}}}}\left( {2{l_1} + {l_2} + \frac{1}{2}{l_3}} \right) \\[-3pt] {C_{22}} = & \frac{1}{{{k_{{l_0}}}}} + \frac{{{{\left( {2{l_1} + {l_2} + {a_0}} \right)}^2}}}{{4{k_{{\theta _0}}}}} + \frac{1}{{2{k_{{\theta _1}}}}}\left( {\frac{4}{3}l_1^2 + 2{l_1}{l_2} + l_2^2} \right) +\\[-3pt] & \frac{{l_2^2}}{{12{k_{{\theta _2}}}}} + \frac{1}{{4{k_{{\theta _3}}}}}\left[ {{{\left( {2{l_1} + {l_2}} \right)}^2} + {l_3}\left( {2{l_1} + {l_2}} \right) + \frac{1}{3}l_3^2} \right] \end{aligned} \right.\!\!\!\!\!\!\! $ | (9) |
式(9)中
该计算只考虑桥式机构的平面刚度[22],可得
| $ \left\{ \begin{split} & {{k_{{l_0}}} = \frac{{2Eb{a_0}}}{{{l_0}}},{k_{{l_1}}} = \frac{{Eba}}{{{l_1}}},{k_{{l_2}}} = \frac{{Ebh}}{{{l_2}}},{k_{{l_3}}} = \frac{{2Ebh}}{{{l_3}}}} \\ & {{k_{{\theta _0}}} = \frac{{Eba_0^3}}{{6{l_0}}},{k_{{\theta _1}}} = \frac{{Eb{a^3}}}{{12{l_1}}},{k_{{\theta _2}}} = \frac{{Eb{h^3}}}{{12{l_2}}},{k_{{\theta _3}}} = \frac{{Eb{h^3}}}{{6{l_3}}}} \end{split}\right. $ | (10) |
式(10)中E为材料的杨氏模量,b为机构的厚度。
进一步,桥式机构的放大率λ1、输入刚度kin1和输出刚度kout1可分别表示为[21]
| $ {\lambda _1} = \frac{{{{{x}}_{{\rm{out}}}}}}{{{{{x}}_{{\rm{in}}}}}} = \frac{{{C_{21}}}}{{{C_{11}}}} $ | (11) |
| $ {k_{{\rm{in}}1}} = \frac{1}{{{C_{11}}}} $ | (12) |
| $ {k_{{\rm{out}}1}} = \frac{{{C_{11}}}}{{{C_{11}}{C_{22}} - {C_{12}}{C_{21}}}} $ | (13) |
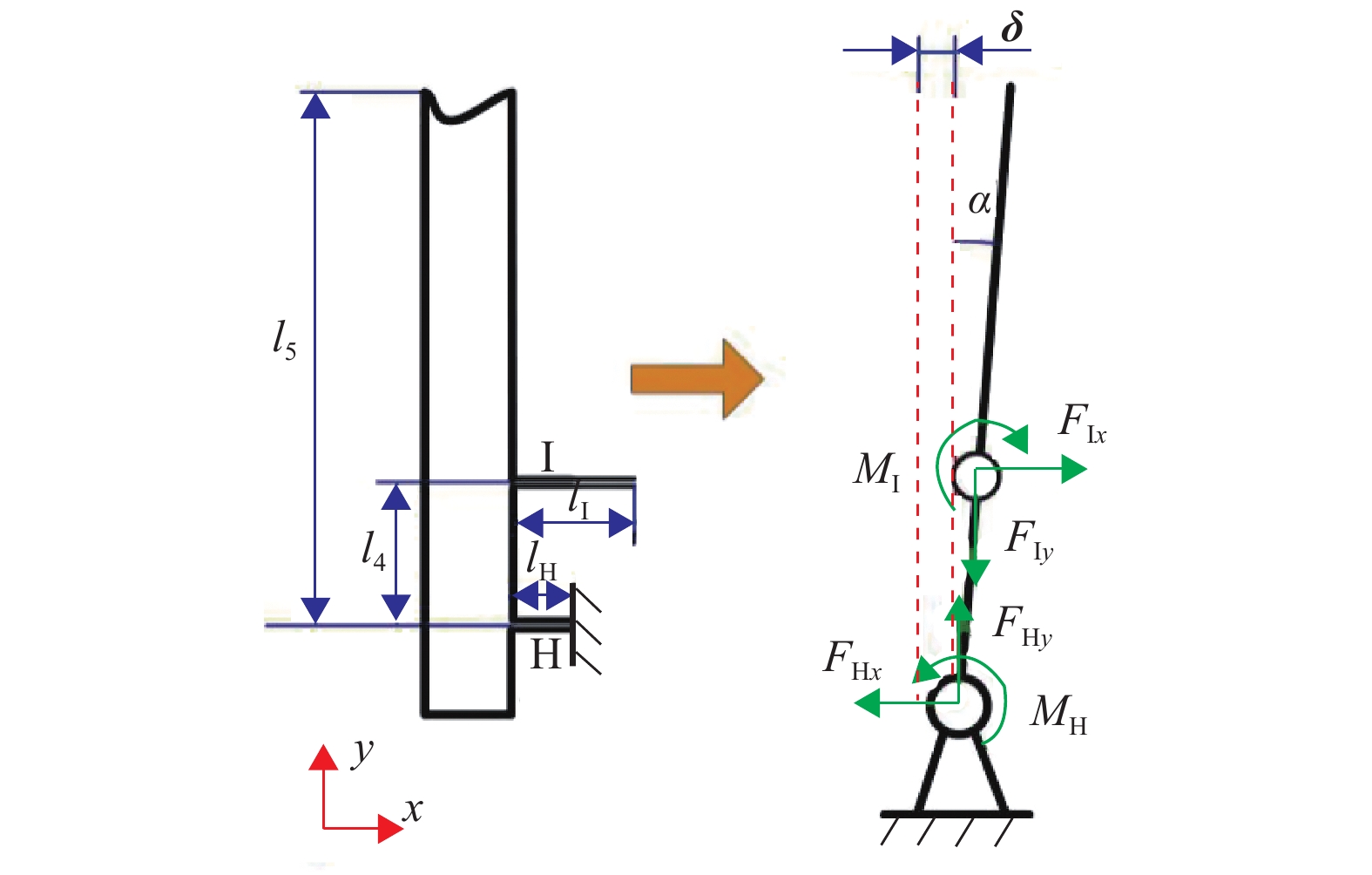
杠杆机构及其建模如图5所示。图5中,l4为直梁型铰链H、I之间的竖直距离,l5为铰链H到夹钳末端的竖直距离,lI、lH分别是直梁型铰链I、H的缺口长度。杠杆机构受到桥式机构传递的力作用,主要使铰链I受到牵引而转动,产生转角α。考虑到铰链H轴漂的影响,机构会产生一定的位移δ。
|
图 5 杠杆机构及其建模 Figure 5 Schematic of lever mechanism |
只考虑机构的平面刚度,杠杆机构可视为自由端无力作用,因此主要计算输入刚度。杠杆机构的放大率λ2和输入刚度Kin2为
| $ {\lambda _2}{\rm{ = }}\frac{{{l_5}\alpha + {{\delta}} }}{{{l_4}\alpha + {{\delta }}}} $ | (14) |
| $ {k_{{\rm{in}}2}} = \frac{{{F_{{\rm{I}}x}}}}{{{l_4}\alpha + {{\delta}} }} $ | (15) |
由静力平衡,可得
| $ \left\{ \begin{split} & {{F_{{\rm{I}}x}} = {F_{{\rm{H}}x}}} \\ & {{F_{{\rm{I}}x}}{l_4} + {M_{\rm{I}}} = {M_{\rm{H}}}} \end{split}\right. $ | (16) |
同时
| $ \left\{ \begin{split} & {{F_{{\rm{H}}x}} = {k_{{\rm{H}}x}}{{\delta}} } \\ & {{M_{\rm{H}}} = {k_{{\rm{H}}r}}\alpha ,{M_{\rm{I}}} = {k_{{\rm{I}}r}}\alpha } \end{split}\right. $ | (17) |
式(17)中kHx、kHr分别是铰链H沿x方向的轴向拉伸刚度和转角刚度,kIr是铰链I的转角刚度。结合图5,可得
| $ \left\{ \begin{aligned} & {{k_{{\rm{H}}x}} = \frac{{Eba}}{{{l_{\rm{H}}}}}} \\ & {{k_{{\rm{H}}r}} = \frac{{Eb{a^3}}}{{12{l_{\rm{H}}}}},{k_{{\rm{I}}r}} = \frac{{Eb{a^3}}}{{12{l_{\rm{I}}}}}} \end{aligned}\right. $ | (18) |
式(18)中a为铰链的最小宽度。
联立式(14)、(15)、(16)和(17),杠杆机构的放大率λ2和输入刚度kin2分别为
| $ {\lambda _2} = \frac{{{l_4}{l_5}{k_{{\rm{H}}x}} + {k_{{\rm{H}}r}} - {k_{{\rm{I}}r}}}}{{l_4^2{k_{{\rm{H}}x}} + {k_{{\rm{H}}r}} - {k_{{\rm{I}}r}}}} $ | (19) |
| $ {k_{{\rm{in}}2}} = \frac{{{k_{{\rm{H}}x}}\left( {{k_{{\rm{H}}r}} - {k_{{\rm{I}}r}}} \right)}}{{l_4^2{k_{{\rm{H}}x}} + {k_{{\rm{H}}r}} - {k_{{\rm{I}}r}}}} $ | (20) |
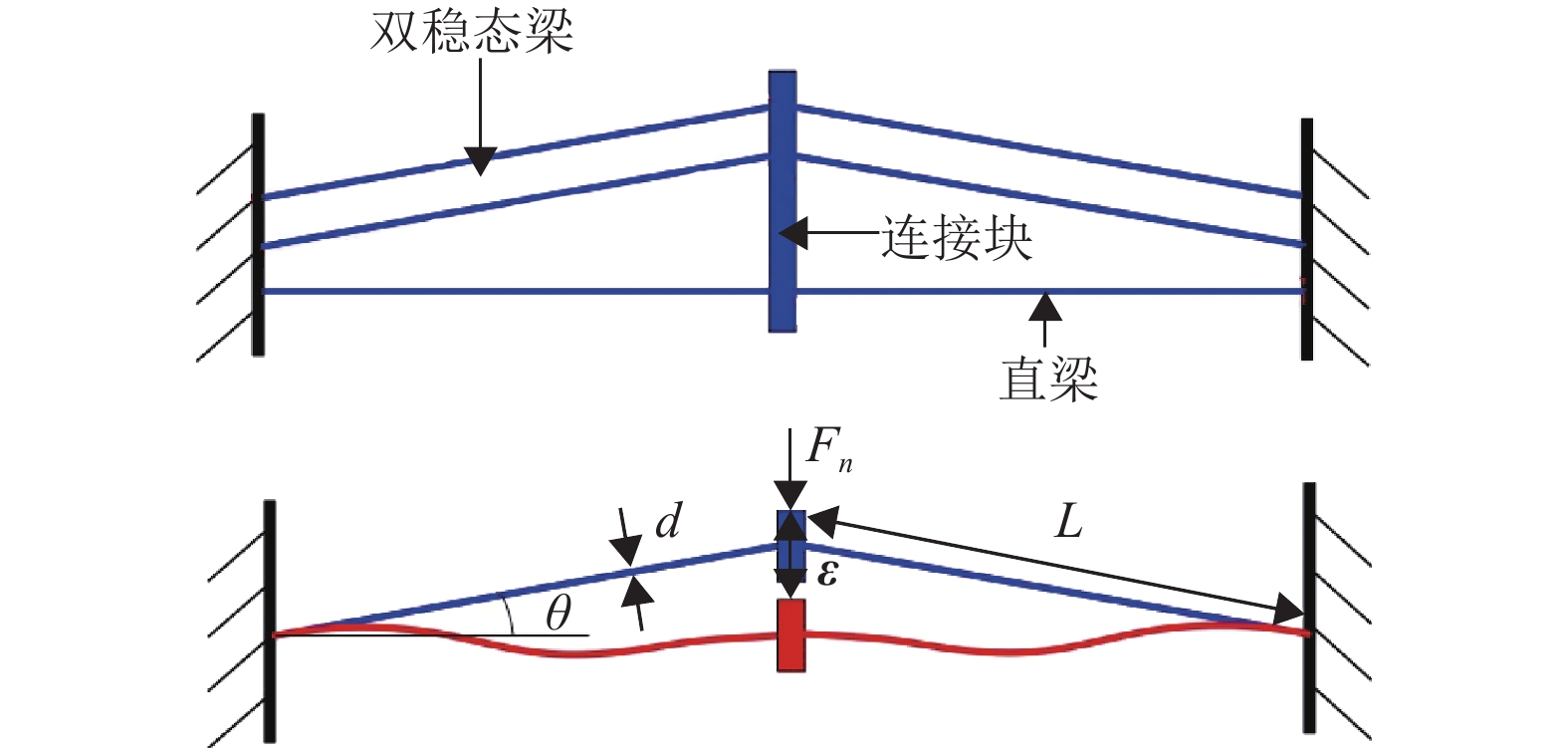
常力模块由2根直梁、4根倾斜导向梁(双稳态梁)和连接块组成。直梁与双稳态梁的主要区别为倾斜角度的不同,在此以倾斜导向梁作分析。常力模块的结构和双稳态梁建模如图6所示。当双稳态梁受到力Fn作用时,会出现屈曲行为发生变形。图6中,L为倾斜导向梁的实际长度,d为直梁与双稳态梁具有的相同宽度,θ为导向梁相对于垂直固定面平面的倾斜角度,ε为倾斜导向梁受到Fn作用而输出的位移。
|
图 6 常力模块的结构及双稳态梁的建模 Figure 6 The structure of the constant force module and the modeling of the bi-stable beam |
依据文献[23],倾斜导向梁第i个临界点的屈曲力可写为
| $ {F_i} = \frac{{4E{I_d}\varphi _i^2}}{{L_0^2}} $ | (21) |
式(21)中E为材料的弹性模量,Id =bd 3/12为倾斜导向梁的截面惯性矩,L0为倾斜导向梁第i个临界点处的小段长度,
计算双稳态梁的负刚度公式可用式(22)表示
| $ {k_{\rm{n}}} \approx \frac{{33E{I_d}}}{{{L^3}}} $ | (22) |
依据式(21)和式(22),该倾斜导向梁的力−位移关系式为
| $ {F_{\rm{n}}} = ES\frac{{{\varepsilon}} }{L}\left( {\frac{{{\varepsilon }}}{L} - \sin \theta } \right)\left( {\frac{{{\varepsilon}} }{L} - 2\sin \theta } \right) $ | (23) |
式(23)中S=bd为梁的横截面积。当θ为零,利用式(23)可求出直梁的力−位移关系式。
常力模块的主要参数如表1所示,其中Lu和Ls分别为双稳态梁和直梁的长度,θ为双稳态梁的倾斜角度,b为双稳态梁和直梁具有的相同厚度。
| 表 1 常力模块的主要参数 Table 1 Architecture parameters of constant force module |
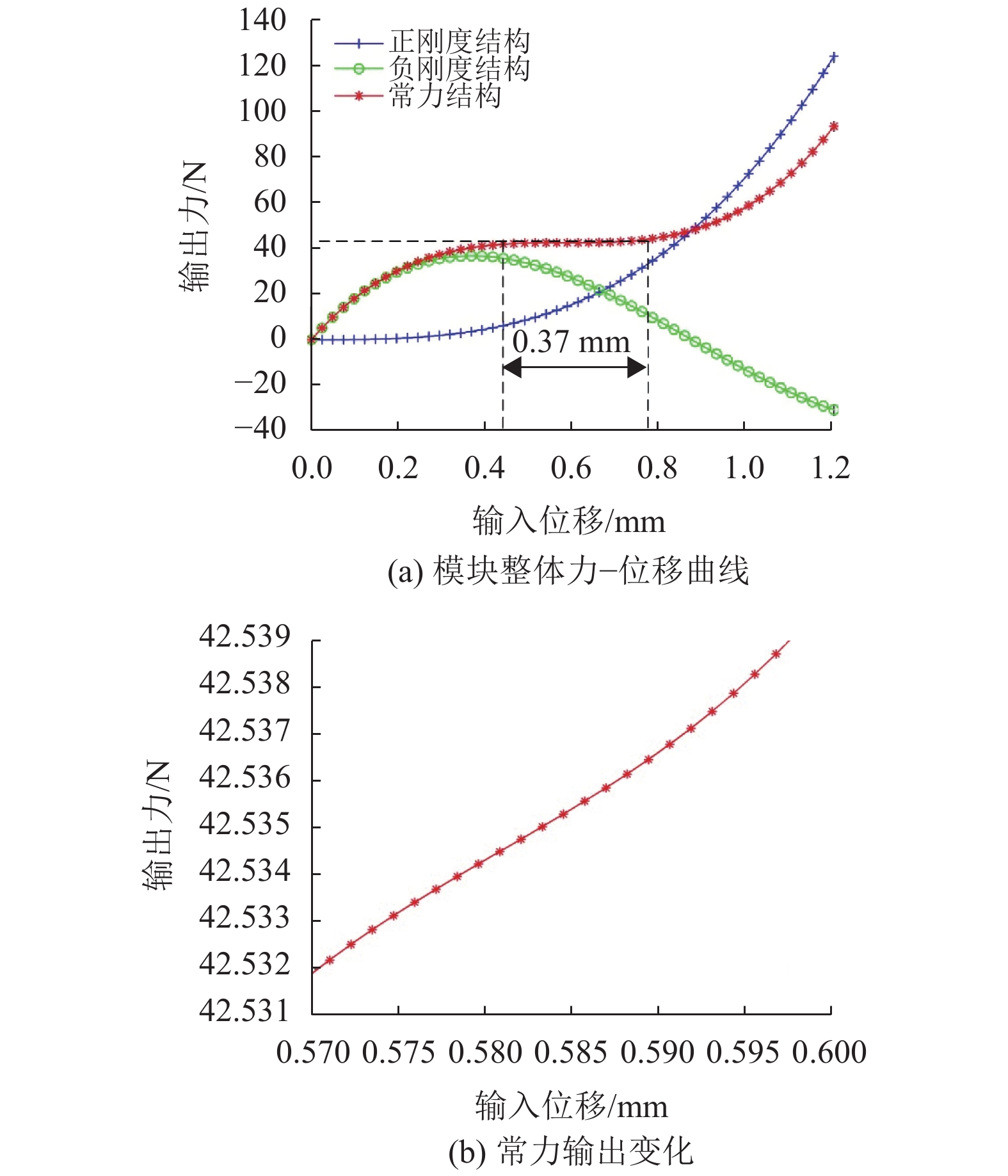
结合式(23),可得出该常力模块的力−位移曲线及常力部分的放大,如图7所示。由图7(a)可知,在输入位移0.41 mm左右常力结构曲线开始变得平整,用于驱动抓爪的恒定输出力大约为42.5 N,保持常力特性输出对应的输入位移区间大约是410~780 μm,表示在此位移区间内常力结构的正负刚度开始相互抵消,模块整体趋向于零刚度。结合图7(b),常力部分的输出力表现为曲折上升变化,其变化微小,恒力的变化范围大致为41.90~43.34 N。
|
图 7 常力模块力−位移变化曲线 Figure 7 Force-displacement characteristic of constant force module |
常力模块输出恒力的稳定性及其输出位移范围,是避免被抓取物损坏的关键因素。所得常力模块的力−位移曲线中,常力部分越平整,其零刚度特性就越好。因此,需进一步探究常力模块中各结构参数对力−位移输出特性的影响。
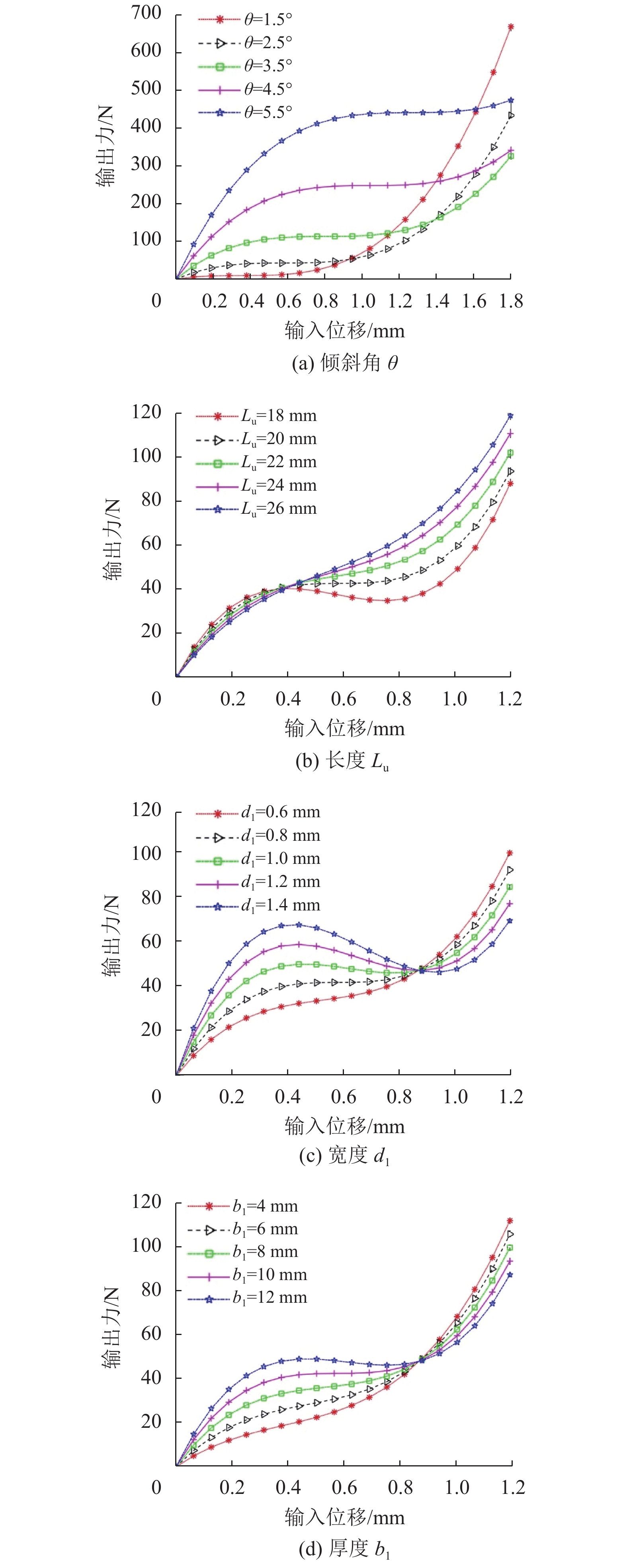
由式(23)和表1可知,模块的常力特性受到直梁和双稳态梁各结构参数的影响。分析某一参数对常力特性的影响时,其他参数应保持不变。为区别两种梁的参数变化,令d1、b1分别表示双稳态梁的宽度、厚度,d2、b2分别表示直梁的宽度、厚度。双稳态梁参数θ、Lu、d1和b1分别变化时,双稳态梁和模块的力−位移变化曲线如图8所示。相对应直梁参数Ls、d2和b2分别变化时,力−位移曲线如图9所示。
|
图 8 双稳态梁结构参数对常力模块性能的影响 Figure 8 The influence of structure parameters of bi-stable beam on the constant-force properties |
|
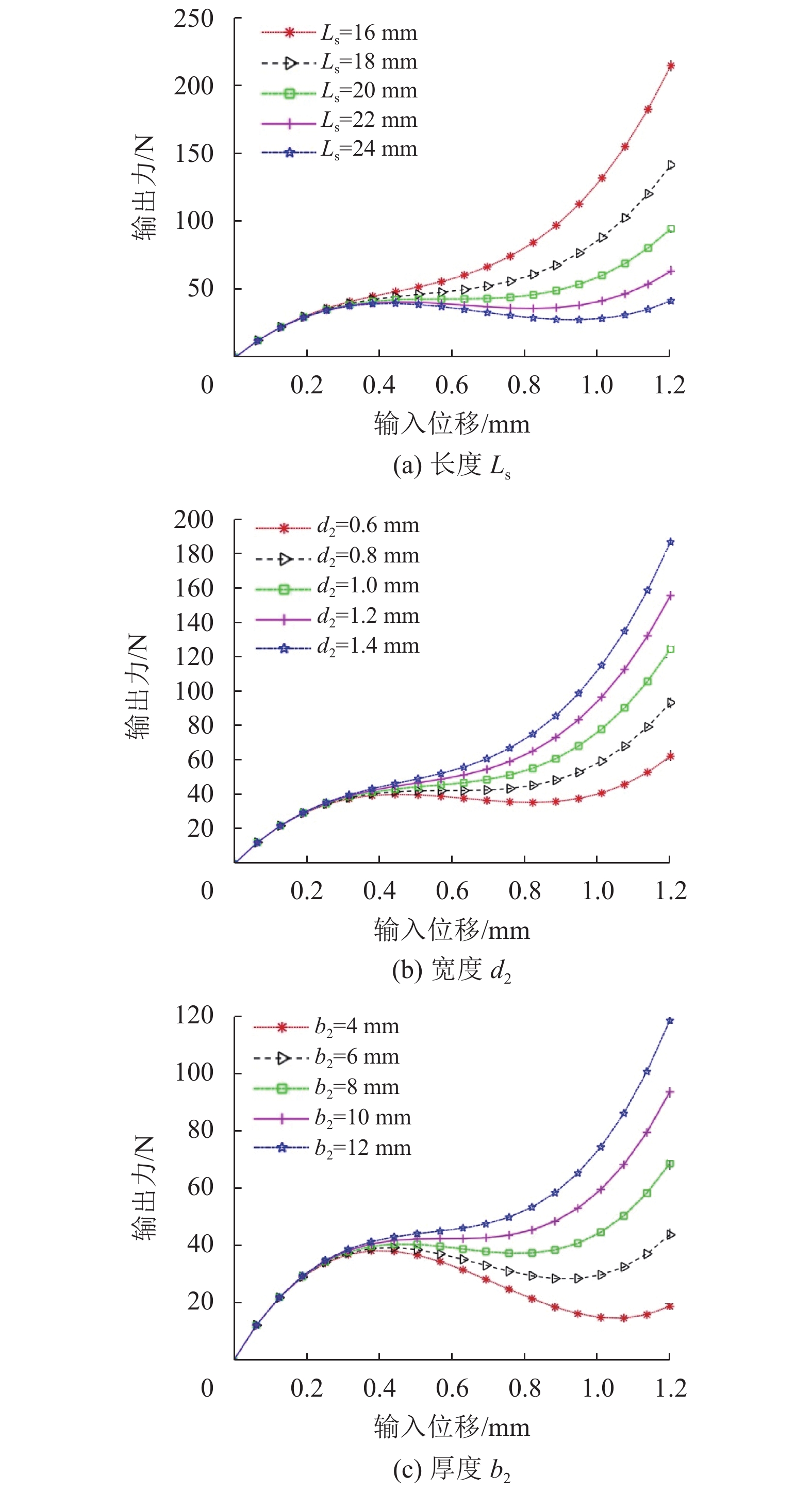
图 9 直梁结构参数对常力模块性能的影响 Figure 9 The influence of structure parameters of straight beam on the constant-force properties |
(1) 由图8(a)可知,倾斜角θ增大,双稳态梁的屈曲点会向位移更大的位置移动,且相应的输出力会增大。双稳态梁的负刚度变大,负刚度区域随之增大。常力范围增大,整体向位移更大的方向移动。
(2) 由图8(b)可知,长度Lu增大,双稳态梁的屈曲点会向位移更大的位置移动,相对应输出力几乎不变。在屈曲点之后,Lu越大,负刚度和常力范围越小,常力曲线趋向于正刚度曲线。这表明反映负刚度的力位移曲线越陡,负刚度值越大。
(3) 由图8(c)可知,宽度d1增大,屈曲点位置几乎不变,但输出力会增大,负刚度越大,常力范围越小,常力曲线趋向于负刚度曲线。
(4) 由图8(d)可知,厚度b1越大,负刚度曲线的变化与宽度d1引起的变化相似,但常力曲线的变化相较之下不显著。
(5) 由图9可知,当直梁宽度d2、厚度b2增大,正刚度值增大,常力范围减小,常力曲线趋向于正刚度曲线;当直梁长度Ls增大,正刚度值会减小,常力范围增大,但不明显。
因此,常力模块中,各导向梁的结构参数对其力学特性均有一定的影响。为获得稳定的常力值和较大的常力范围,需对不同梁的结构参数进一步调整和优化。
5 结论基于常力模块和放大模块串联的设计思路,提出了一种新型的具有限力输出保护特性的柔性夹钳构型。放大模块采用桥式机构与杠杆机构串联的形式,基于伪刚体法得到两机构的放大倍数和刚度的数学表达式。常力模块采用直梁和双稳态梁并联的形式,通过对柔顺梁的分析阐明了模块的力学特性。结合不同梁的结构参数进行分析,表明各参数对常力输出特性有不同的影响。其中,参数θ较大程度地影响了倾斜导向梁的力−位移输出特性。仿真求解得出用于驱动抓爪的恒定输出力为42.5 N,其恒力变化范围为41.90~43.34 N,对应的输入位移区间为410~780 μm。本文重点从机理上对具有限力输出保护特性的柔性夹钳构型机构进行前瞻性的构型设计和参数评估,揭示了关键尺度参数对常力输出特性的变化规律,为后续整体物理系统的搭建和测试提供了指导性的理论依据,同时,也为相似类型柔性夹钳在构型设计、尺度优化和拓展应用等方面的研究起到积极深入的推动作用。
| [1] |
丁严, 赖磊捷. 大行程无寄生位移柔性压电微夹钳结构设计[J].
压电与声光, 2019, 41(4): 562-565.
DING Y, LAI L J. Structural design of flexible piezoelectric micro-gripper without parasitic displacement in large stroke[J]. Piezoeletrics & Acoustooptics, 2019, 41(4): 562-565. |
| [2] |
张成, 褚金奎, 张然, 等. 柔性微夹钳的拓扑优化设计及制作工艺[J].
机械设计与研究, 2010, 26(5): 44-46.
ZHANG C, CHU J K, ZHANG R, et al. Topology optimized design and microfabrication of compliant microgripper[J]. Machine Design and Research, 2010, 26(5): 44-46. |
| [3] |
MATTEO V, ALDEN D, NICOLA P B. A comprehensive survey on microgrippers design: mechanical structure[J].
Journal of Mechanical Design, 2017, 139(060801): 1-26.
|
| [4] |
YANG Y L, WEI Y D, LOU J Q, et al. Design and control of a multi-DOF micromanipulator dedicated to multiscale micromanipulation[J].
Smart Materials and Structures, 2017, 26(11): 1-34.
DOI: 10.1088/1361-665X/aa8f73. |
| [5] |
余跃庆, 张志丹. 近似柔顺常力机构的研制及其实验研究[J].
北京工业大学学报, 2018, 38(3): 321-324.
YU Y Q, ZHANG Z D. Experimental study on approximate compliant constant-force mechanisms[J]. Journal of Beijing University of Technology, 2018, 38(3): 321-324. |
| [6] |
XIE Y, SUN D, TSE H Y G, et al. Force and manipulation strategy in robot-assisted microinjection on zebrafish embryos[J].
IEEE/ASME Transactions on Mechatronics, 2011, 16(6): 1002-1010.
DOI: 10.1109/TMECH.2010.2068055. |
| [7] |
ZHANG W, SOBOLEVSKL A, LI B, et al. An automated force-controlled robotic micromanipulation system for mechanotransduction studies of drosophila larvae[J].
IEEE Transactions on Automation Science and Engineering, 2016, 13(2): 789-797.
DOI: 10.1109/TASE.2015.2403393. |
| [8] |
张凯, 韩迎鸽, 李保坤, 等. 基于附加弹簧双滑块四杆机构的柔顺恒力机构设计[J].
机械传动, 2020, 44(4): 85-89.
ZHANG K, HAN Y G, LI B K, et al. Design of compliant constant-force mechanism based on additional spring double-slider four-bar mechanism[J]. Journal of Mechanical Transmission, 2020, 44(4): 85-89. |
| [9] |
CHEN Y H, LAN C C. An adjustable constant-force mechanism adaptive end-effector operations[J].
Journal of Mechanical Design, 2012, 134(031005): 1-9.
|
| [10] |
杨晓钧, 舒淦, 李兵. 含柔顺关节的空间RSSP常力机构建模与分析[J].
浙江大学学报(工学版), 2018, 52(2): 261-261.
YANG X J, SHU G, LI B. Modeling and analysis of spatial RSSP constant-force mechanism with compliant joints[J]. Journal of Zhejiang University (Engineering Science), 2018, 52(2): 261-261. DOI: 10.3785/j.issn.1008-973X.2018.02.008. |
| [11] |
陈晓东, 邓子龙, 高兴军, 等. 基于细胞变换的柔性恒力机械手设计[J].
机械传动, 2019, 43(12): 89-92.
CHEN X D, DENG Z L, GAO X J, et al. Design of flexible constant force manipulator based on metamorphic mechanism transform[J]. Journal of Mechanical Transmission, 2019, 43(12): 89-92. |
| [12] |
李玄, 周双武, 路松, 等. 基于二级杠杆机构的二自由度微定位平台设计与分析[J].
工程设计学报, 2020, 27(4): 533-540.
LI X, ZHOU S W, LU S, et al. Design and analysis of two-DOF micro-positioning platform based on two-level lever mechanism[J]. Chinese Journal of Engineering Design, 2020, 27(4): 533-540. DOI: 10.3785/j.issn.1006-754X.2020.00.063. |
| [13] |
伍威, 赵纪宇, 丁冰晓, 等. 新型空间大行程微夹持器的设计与分析[J/OL]. 机械科学与技术,2020:1-8(2020-11-06)[2021-01-12]. https://doi.org/10.13433/j.cnki.1003-8728.20200181.
WU W, ZHAO J Y, DING B X, et al. Design and analysis of a novel type of spatial micro-gripper with large displacement[[J/OL]. Mechanical Science and Technology for Aerospace Engineering, (2020-11-06)[2021-01-12]. https://doi.org/10.13433/j.cnki.1003-8728.20200181. |
| [14] |
张赢斌. 拓扑优化法设计恒力柔顺机构[D]. 西安: 西安电子科技大学, 2012.23-30.
|
| [15] |
时培成, 李云龙, 肖平, 等. 负刚度结构的座椅悬架优化及隔振分析[J/OL]. 机械科学与技术, 2020, 1-12(2020-05-07)[2021-01-12]. https://doi.org/10.13433/j.cnki.1003-8728.20200054.
SHI P C, LI Y L, XIAO P, et al. Optimization and vibration isolation analysis of seat suspension with negative stiffness structure[J/OL]. Mechanical Science and Technology for Aerospace Engineering, 2020, 1-12(2020-05-07)[2021-01-12]. https://doi.org/10.13433/j.cnki.1003-8728.20200054. |
| [16] |
WANG J Y, LAN C C. A constant-force compliant gripper for handling objects of various sizes[J].
Journal of Mechanical Design, 2014, 136(071008): 1-10.
|
| [17] |
HAO G B, JOHN M, KWVIN C. Simplified modeling and development of a bi-directionally adjustable constant-force compliant gripper[J].
Journal of Mechanical Engineering Science, 2017, 231(11): 2110-2123.
DOI: 10.1177/0954406216628557. |
| [18] |
LIU Y L, ZHANG Y L, XU Q S. Design and control of a novel compliant constant-force gripper based on buckled fixed-guided beams[J].
IEEE/ASME Transaction on Mechatronics, 2017, 22(1): 476-486.
DOI: 10.1109/TMECH.2016.2614966. |
| [19] |
WANG P Y, XU Q S. Design and modeling of constant-force mechanisms: a survey[J].
Mechanism and Machine Theory, 2018, 119: 1-21.
DOI: 10.1016/j.mechmachtheory.2017.08.017. |
| [20] |
ZHOU Z F, GAO Y Z, SUN L N, et al. A bistable mechanism with linear negative stiffness and large in-plane lateral stiffness: design, modeling and case studies[J].
Mechanical Sciences, 2020, 11(1): 75-89.
DOI: 10.5194/ms-11-75-2020. |
| [21] |
WANG F J, ZHAO X L, HUO Z C, et al. A 2-DOF nano-positioning scanner with novel compound decoupling-guiding mechanism[J].
Mechanism and Machine Theory, 2020, 155(104066): 1-14.
|
| [22] |
LINK M X, CAO J Y, JIANG Z, et al. Modular kinematics and statics modeling for precision positioning stage[J].
Mechanism and Machine Theory, 2017, 107: 274-282.
DOI: 10.1016/j.mechmachtheory.2016.10.009. |
| [23] |
HOLST G L, TEICHERTT G H, JENSEN B D. Modeling and experiments of buckling modes and deflection of fixed-guided beams in compliant mechanisms[J].
Journal of Mechanical Design, 2011, 133(051002): 1-10.
|
 2021, Vol. 38
2021, Vol. 38
