混流制造(Hybrid Flow Shop,HFS)是一种常用且主流的大批量定制生产(Mass Customization Production,MCP)组织模式,可以通过定制阶段并行机上的工艺参数满足客户多样化的产品需求。HFS本质上是一个NP-Hard难题[1],而其系统规模大、资源约束多的特性,导致了解空间过大难以求解的问题。
国内外很多研究团队对混流制造的调度问题进行了深入的研究。何军红等[2]针对在MES系统(Manufacturing Execution System,MES)生产调度模块的柔性作业车间问题,提出了3个阶段的优化调度算法,对具有10个库所、6个工件的HFS问题进行求解。王秀萍[3]针对柔性车间提出一种具有优先级的启发式算法,能够对10个库所、10个工件的问题求解。而何涛[4]针对智能制造柔性车间采用了改进过的遗传算法,将机器的选择与工件的顺序进行分段,对6个库所、4个工件的加工问题进行求解。在求解调度问题中,研究人员尝试了各类智能算法。如黄亚平[5]在基于汽轮机的智能调度系统上采用改进的蚁群算法解决生产调度问题,在调度任务发生变化时快速地根据上次调度结果进行重调度。又如田松龄[6]针对柔性车间,采用异步仿真时钟的蚁群并行搜索算法,减低资源共享型系统的运算成本。白俊峰[7]针对车间调度问题采用包含了精英保留策略与逆转变异机制的遗传算法,其在求解7个工件、5台机器的案例中能够有较好的效果。余璇[8]针对柔性调度问题提出一种混合遗传禁忌搜索算法,对问题模型进行优化并能够在
本文针对HFS大规模HFS系统的调度难题,使用MPN(Manufacturing Petri Net)[11]建模方式进行模型压缩,采用2段编码方式重塑染色体限定搜索范围,用包含粒子群机制(Particle Swarm Optimization,PSO)交叉子、模拟退火机制(Simulated Annealing Algorithm,SAA)变异子与邻域搜索机制的改进遗传算法来改进解搜索方向以优化大规模HFS问题的求解。
1 问题描述混合流水车间问题可以描述为:一共有n个待加工工件,它们需要经过s道工序进行加工,每道工序会存在
以图1为例,图1描述了一个包括了2个阶段工序的HFS系统。工序1有M型并行机2台和N型并行机2台,共4台,工序2有H型并行机2台和G型并行机2台一个共4台。对图1中的HFS系统采用MPN模型进行同类并行机压缩建模后,可以将一个4×2的HFS模型压缩成一个

|
图 1 混合流水车间案例 Figure 1 Case of hybrid flow workshop |
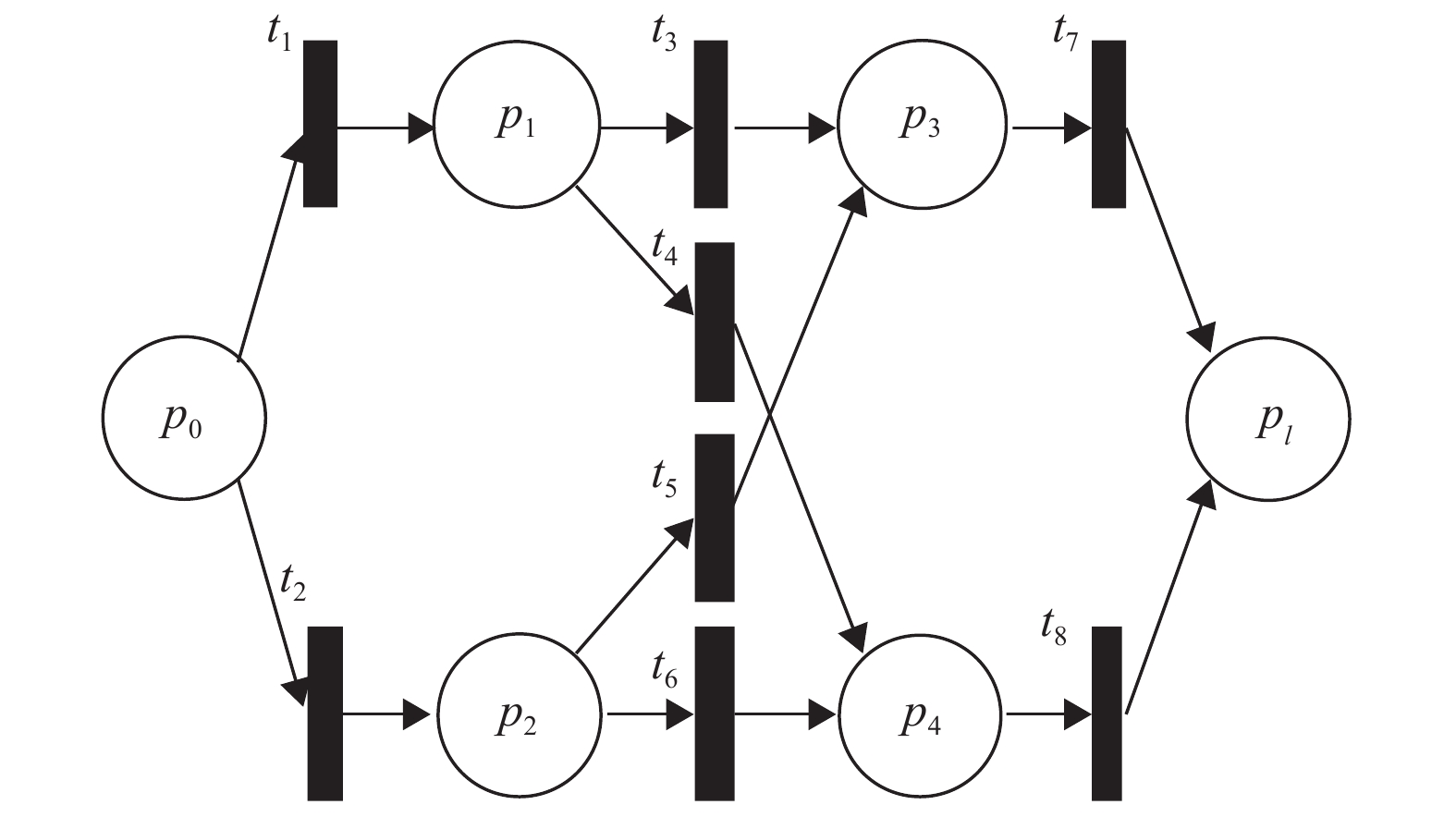
本文针对以上基于MPN的HFS调度,为了适应改进GA算法压缩解搜索空间的需求,在MPN的Petri模型基础上,加入用于描述工件加工可选路径的约束和生成作业集约束,避免算法运行时的盲目搜索。模型案例如图2所示。
|
图 2 基于案例的MPN模型 Figure 2 Case-based MPN model |
本文的MPN模型定义如下[11]:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11) Order是进入MPN的一个加工订单,包含了一定数量不同类型工件token集合。
2.2 优化目标| $\min C = \min (F({S_0} \to {S_l}))$ | (1) |
| $ {\rm{s.t.}}\;\left\{\begin{aligned} & \sum\limits_{r = 1}^R {{m_{\theta ,r}} = 1} \;(\theta {\text{选择}}r{\text{路径}}x=1{\text{否则}}x=0)\qquad\;\;\;\;\;\,(2)\\& {Q_{(\theta ,r)}} = {m_{\theta ,r}}\times\theta \times {{W}}{(M)_r}\qquad\qquad\qquad\qquad\quad\quad\;(3)\\& {{\rm{S}}_\tau }({p_i}) \leqslant {\rm{K}}({p_i})\,\qquad\quad\qquad\qquad\qquad\qquad\quad\quad\quad(4) \end{aligned} \right. $ |
其中,
式(1)表示优化目标为时间最短,
目前处理柔性加工问题的染色体结构有两种,将作业的选择与安排混合考虑[12]或分开考虑[13]。本文采用后者,将一个完整的染色体分为:路径选择段,作业安排段。选择段为染色体的第一段
染色体的编码算法1:
Step1 编码定义优先约束:编码染色体的选择段。
Step2 根据优先约束编码定义每一个阶段的资源约束:
(1) 从第一个安排段
(2) 把
(3) 编排
(4)
End
以图2的Petri网为例。假定place容量设置为

|
图 3 染色体编码结果 Figure 3 Chromosome coding results |
由染色体的编码算法1,可看出染色体将具体的调度方案分成了选择段与安排段。选择段确定了工件要以经过哪条加工路线的库所完成加工,即每个库所
很多使用染色体对车间问题进行求解时都会采用调整算法去掉部分的无用解[14-15],但由于调整方法简单且无法压缩解空间,所以对本文的大规模HFS问题不适用。在此本文设计了染色体安排段优化算法对染色体(解空间)的编码过程进行补充。
染色体安排段优化算法是在算法1编码的基础上,对
染色体安排段优化算法2:
Input:
Output:
<
Step1 染色体
Step2 通过
Step3 取出记录中最优的二元关系<
(1) 从
(2) 从排序结果中取出倒数第var个完成的作业
(3) 根据作业
(4) 查找作业
(5) 判断作业
(6)
Step4
Step5 判断是否到迭代次数
End
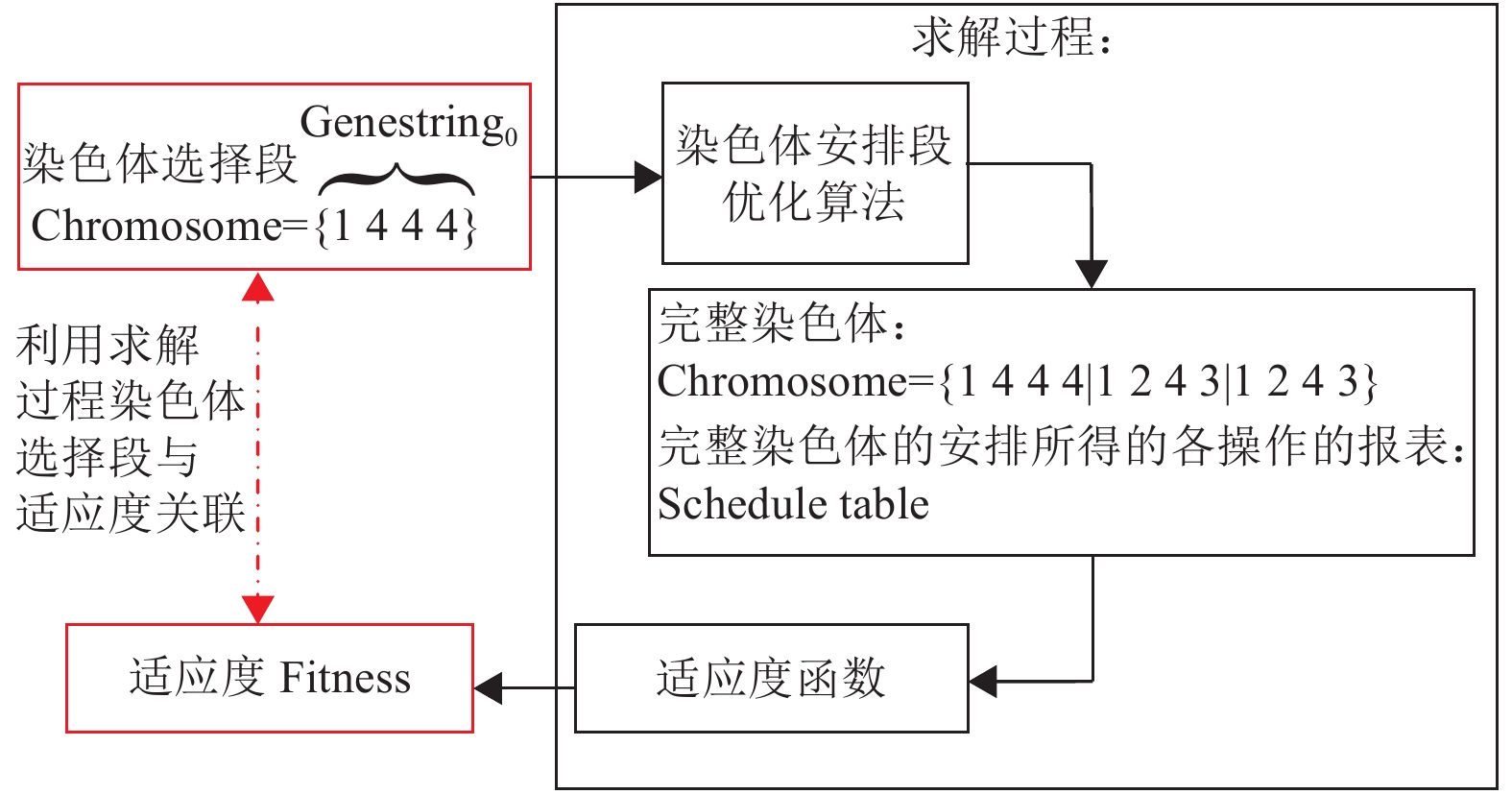
4 算法设计为了探索本文所研究的MPN模型下的HFS问题的优解,提出了一种改进的遗传算法(Improved Genetic Algorithm,IGA)。目前很多的遗传算法都会为其交叉变异添加新的机制[16],但是无法处理大规模问题。本算法结合了3种方法从3个方面解决了遗传算法在求解问题中所遇到的难题。(1) 本文会使用如图4的方式将染色体选择段与适应度进行关联,让遗传算法(IGA)把搜索的精力集中在搜寻最优的染色体选择段上,压缩可行解空间。(2) 本文的算法所使用的交叉子将采用粒子群优化(PSO)机制,而变异子将采用模拟退火算法(SAA)机制,这样的组合有利于改善遗传算法过早收敛的问题。(3) 算法还会对每次迭代的最优个体(Optimal Individual,OI)进行邻域搜索挖掘该个体的“潜力”。
|
图 4 以染色体选择段代替完整染色体与适应度进行关联 Figure 4 Using chromosome selection segments to connect with fitness |
交叉、变异、邻域搜索的运算只需要使用选择段即可,当需要进行染色体间比较时,染色体能够通过<Chromosome, schedule table>,获取详细信息并使用式(5)得出染色体的适应度来进行比较。这样便可在无需考虑无用解(不合理的染色体)的同时让遗传算法只去筛选选择段,压缩了解空间。之后出现的遗传算法的各种操作都是对染色体选择段进行操作,而且认为选择段就是一个完整的个体适应度函数。
| $ {\rm{Fitness}} = - {C_{\max }} $ | (5) |
为了提高算法收敛性,本文引入PSO机制(其中
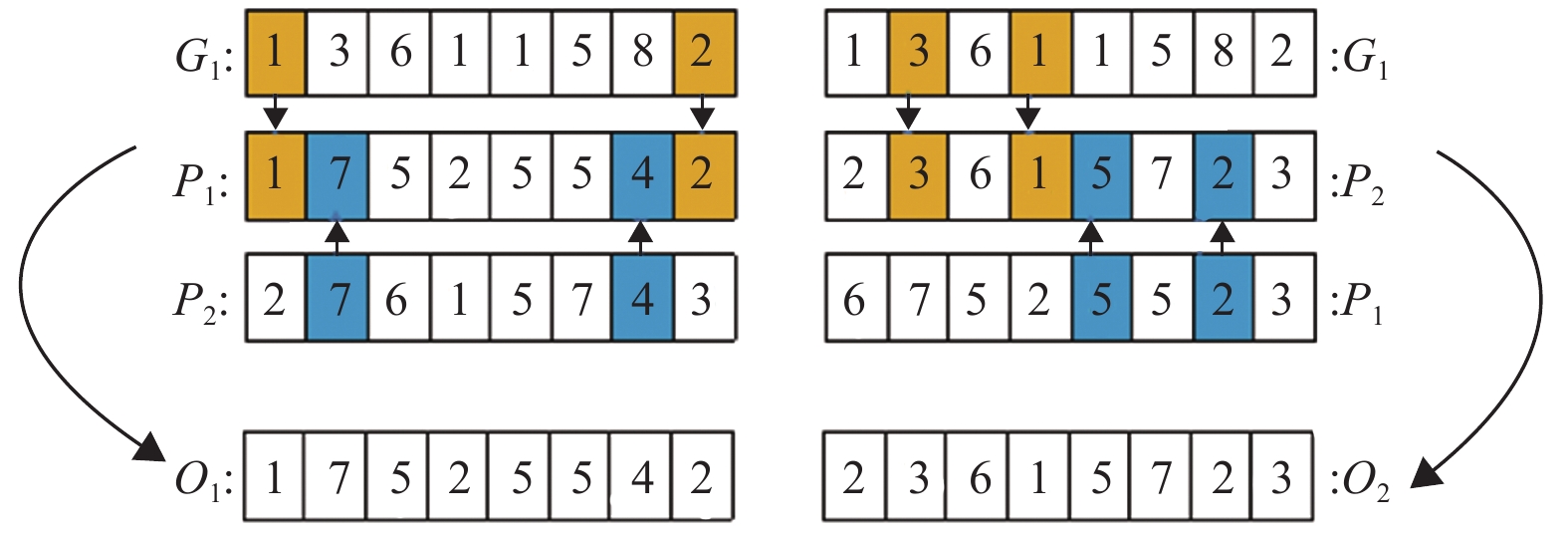
然后为交叉引入
|
图 5 交叉算子 Figure 5 Crossover operator |
由于PSO机制的添加,引导个体(本群内最优染色体)参与群内交叉能够引导染色体的生产方向,提高收敛性。
4.2.2 变异算子为了避免遗传算法过早收敛的弊端,本文改进了变异算子,引入新的模拟退火(SAA)机制,使用接收概率实现变异结果的条件接受,使用变异倾向函数实现变异的方向性指导,从而提高未出现基因序列的出现概率。两者组合可以帮助算法跳出局部最优解。
在本节中,变异算子设计如下:
Step1: 在个体中随机选择一个位置。
Step2: 在选择的位置上,通过突变趋势函数(式(6))和(式(7))所得出的可选基因元素(路径)的概率分布,从中按概率选取一个基因值(路径)替换原基因。
Step3:通过模拟退火法的接受概率判断是否接受该变异所得的染色体。
Step4:当代总群中的所有个体都执行过变异后,按照模拟退火中
其中,突变趋势函数将对每次迭代后出现在个体上每个位置的值进行计数,并获得在每个位置突变为不同值的相应概率,从而影响个体变异的倾向。
| $ \begin{split} {f_{{\rm{mt}}}}(\theta ,G) = &\Biggr(\frac{{{1 / {{\rm{sum}}({r_1},\theta ,G)}}}}{{\displaystyle \sum\limits_{n = 1}^N {{1 / {{\rm{sum}}({r_n},\theta ,G)}}} }},\cdots\frac{{{1 / {{\rm{sum}}({r_n},\theta ,G)}}}}{{\displaystyle \sum\limits_{n = 1}^N {{1 / {{\rm{sum}}({r_n},\theta ,G)}}} }},\cdots \Biggr.\\&\Biggr.\frac{{{1 / {{\rm{sum}}({r_N},\theta ,G)}}}}{{\displaystyle \sum\limits_{n = 1}^N {{1 / {{\rm{sum}}({r_n},\theta ,G)}}} }}\Biggr)\\[-30pt] \end{split} $ | (6) |
| ${\rm{sum}}(r{}_n,\theta ,G) = \sum\limits_{g = {G_0}}^G {{f_{\rm{s}}}({r_n},\theta ,g)} $ | (7) |
其中
由于Petri网模型的拓扑结构的原因,Chromosome个体的细微差别,会导致适应度存在巨大差异。为了能够激发当前系统发现的最优个体(OI),在遗传算法执行过交叉与变异后都会进行最优个体邻域搜索。
邻域搜索算法:
Input:
Step1: 如果
(1) 将
(2)按照突变趋势函数(6)、(7)将
Step2: 比较个体
Output:
其中基本邻域搜索函数是一个输入为最优个体选择段,输出为其邻域(只有一个位置的值与
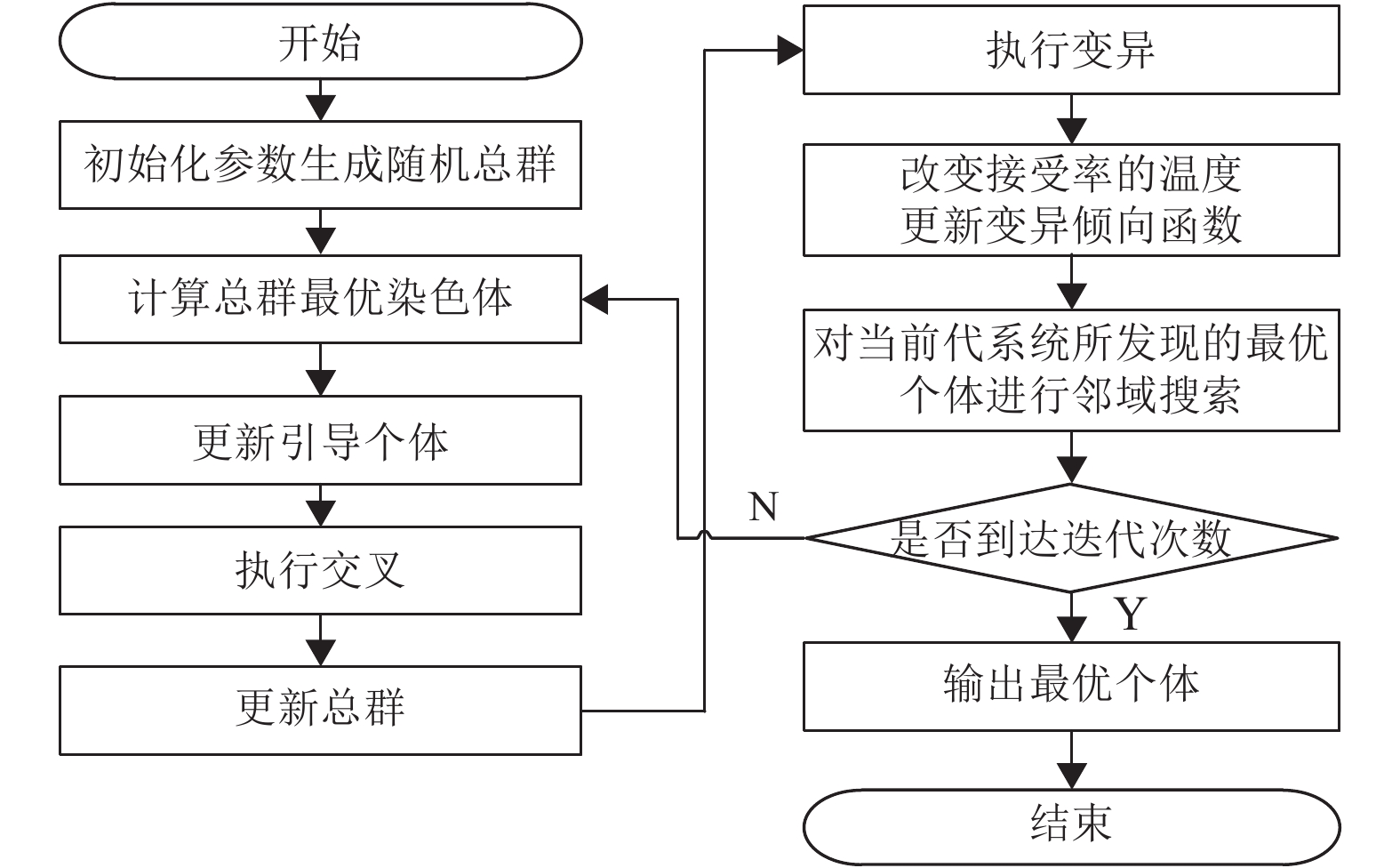
综合上述的算法模块,改进遗传算法的算法流程如图6所示。
|
图 6 算法流程图 Figure 6 Algorithm flowchart |
采用本团队所研究的基于覆铜板层压厂混流加工环境所构建的Petri 网模型为基础[11],并用同样的订单对本文的算法与所采用的模型的论文所提出的算法进行比较。该案例为某覆铜板生产车间案例。
Petri网模型中每个库所的容量参数:
| $ \begin{split} \{{{K}}{({p_i})\}^{\rm{T}}} =& \{ (1,1,2,2,2,2,2,2,2,2,2,2,2,2)|(i \in [1,14])\} \end{split} $ |
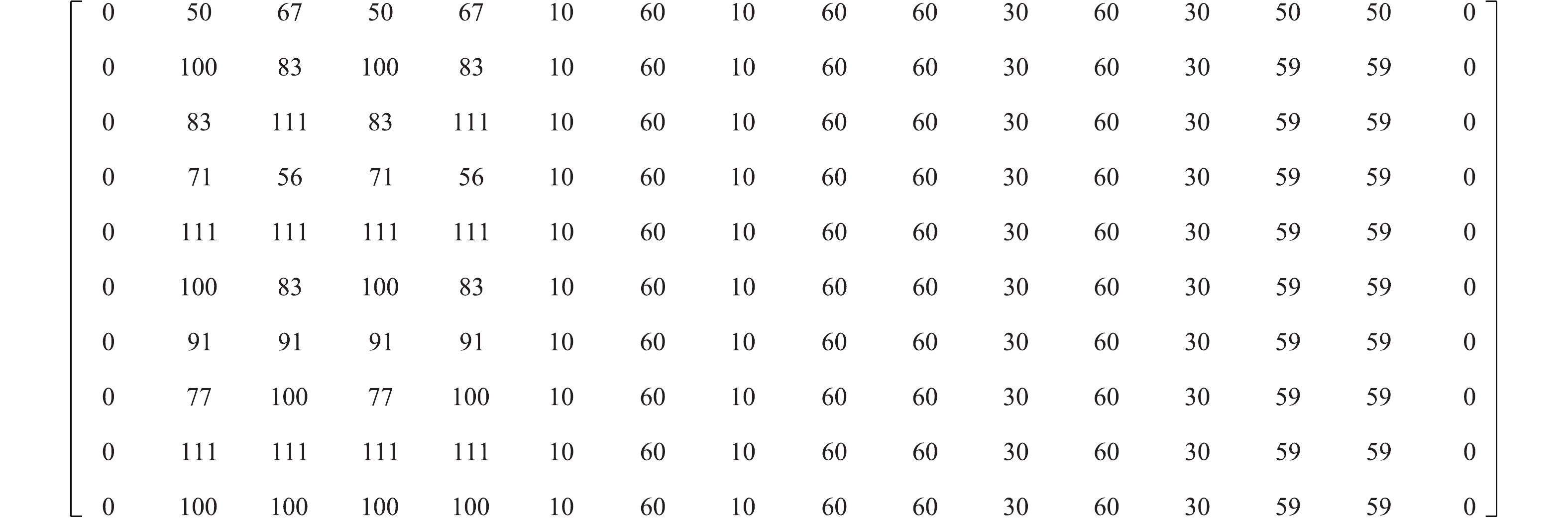
每个种类在库所中的加工时间矩阵D见图7,订单加工内容见表1,其中矩阵行为工件专利,列为库所
可设置的参数一共有7个:交叉率
|
图 7 加工时间矩阵D Figure 7 Processing time matrix D |
| 表 1 加工订单案例 Table 1 Case of processing orders |
前6个参数的实验范围如表2所示,分别为:
从表3得知
| 表 3 田口实验 Table 3 Taguchi experiment |
从图8可以获得最终的参数
| 表 2 前6个参数的实验范围 Table 2 The experimental range of the first 6 parameters |
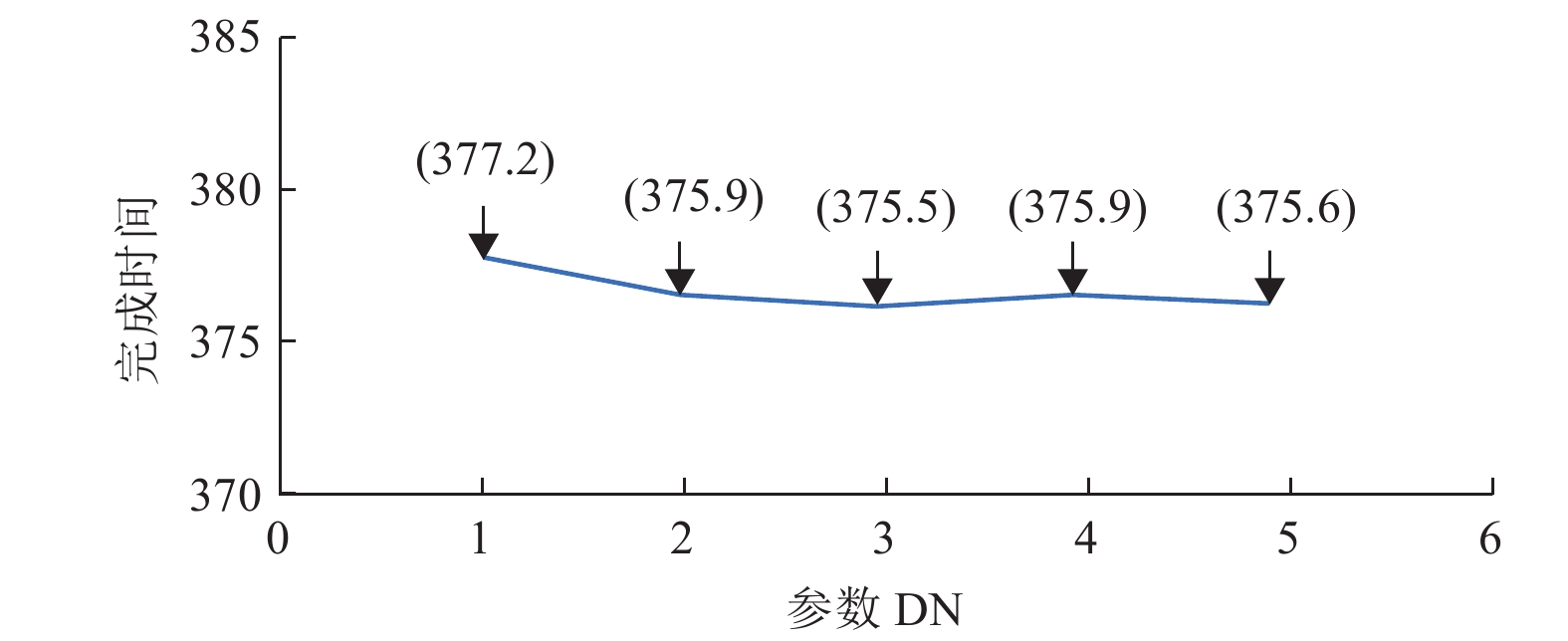
|
图 8 参数DN在之前所获得的最优的参数的基础上对其进行讨论 Figure 8 Parameters discussion on the basis of the optimal parameters obtained before |
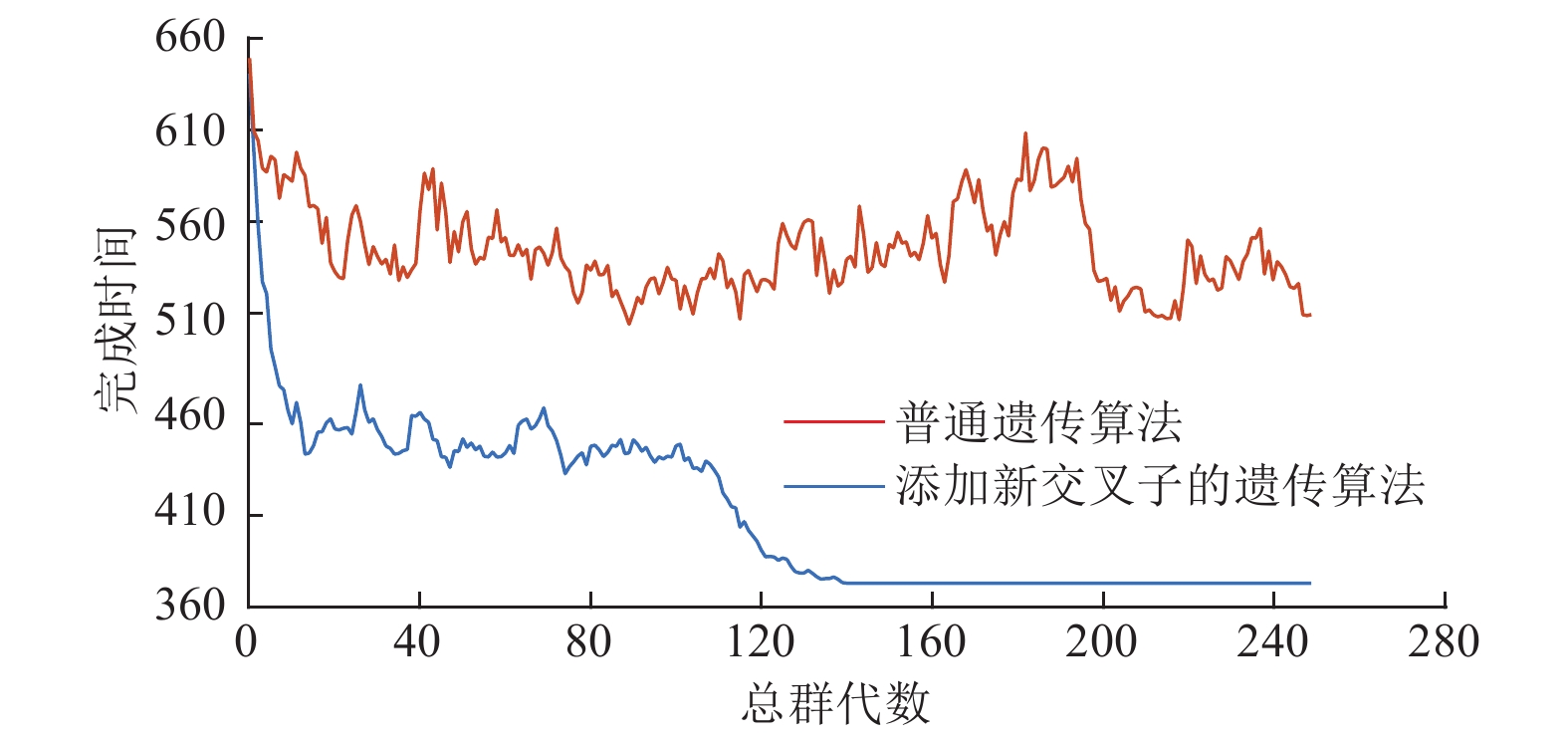
图9中,蓝色曲线所代表的遗传算法使用了具备粒子群优化(PSO)机制的交叉子,而棕色曲线则代表使用了普通交叉子的遗传算法。从图9可知,改进后的交叉子对遗传算法的收敛性有所改善。其曲线所代表的种群内各个体的
|
图 9 在250次迭代过程中,种群内个体的均值变化曲线对比 Figure 9 Comparison of mean change curves of individuals in the population during 250 iterations |
图10代表当前迭代次数出现过的最优个体的
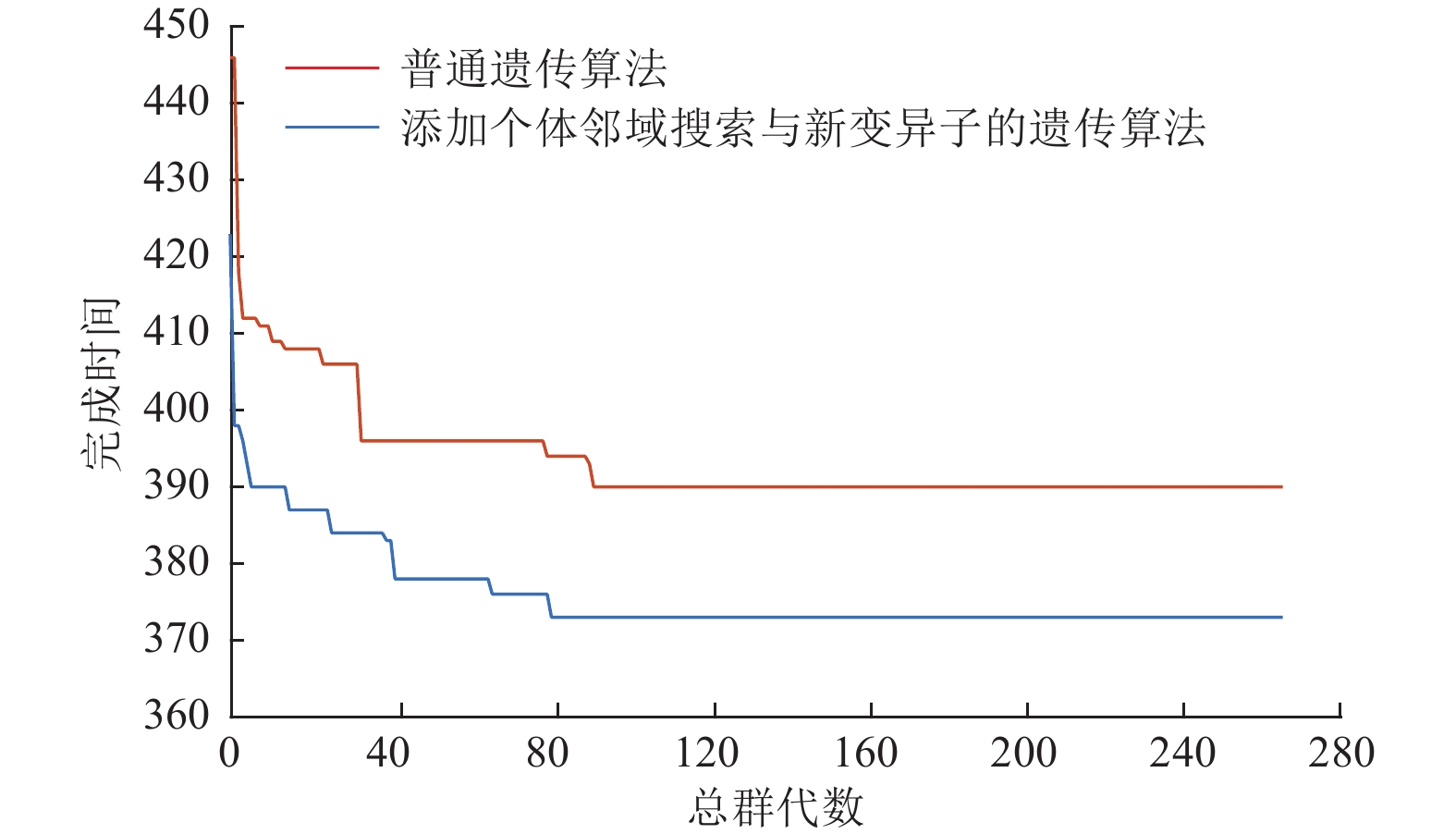
|
图 10 在250次迭代过程中,最优解的变化过程对比。 Figure 10 Comparison of the change process of the optimal solution during 250 iterations. |
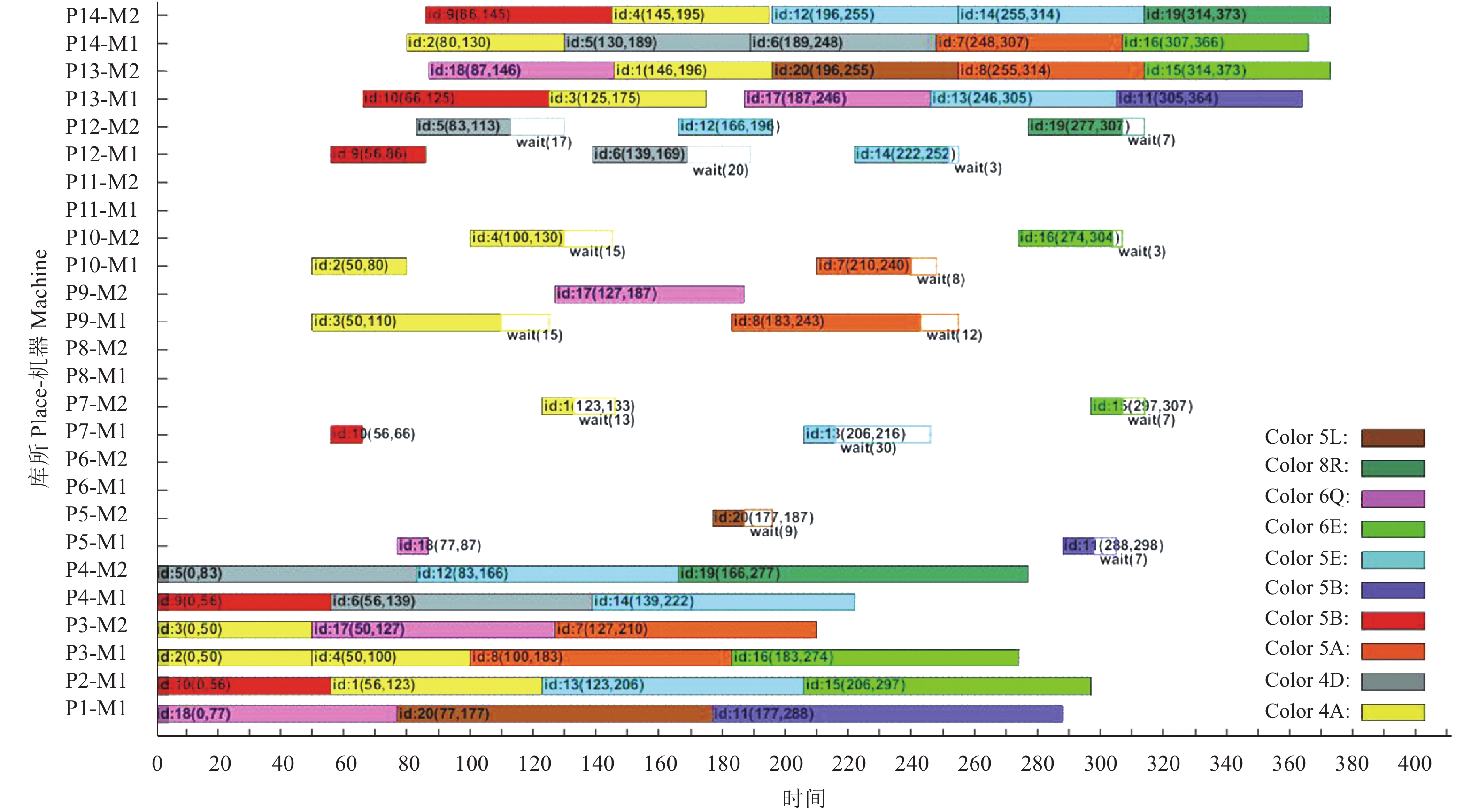
表4为相同MPN模型下相同案例中,采用文献[11]中的蚁群优化算法、标准遗传算法和采用本文的改进遗传算法进行对比所得的结果。采用改进遗传算法所得出的最优解373明显优于文献[11]蚁群算法中所得出的最优解393与标准遗传算法的523,而且达到最优的次数在100次中出现了83次,优化结果稳定。而文献[11]中的蚁群优化达到最优的次数有79次,虽然较为稳定但最优解却只有393。标准遗传算法因为无法适应大规模的混流车间问题,在最优解上只得到了523,到达的次数也只有25次。从中可以看出改进遗传算法相比于蚁群优化算法与标准遗传算法能够获得相对更优的优化结果且达到最优解更为稳定。如图11为案例最优结果甘特图。
| 表 4 效果对比 Table 4 Effect comparison |
|
图 11 实验结果甘特图 Figure 11 Gantt chart of experimental results |
为了解决基于MPN模型下的混流车间问题,本文采用了一种改进的遗传算法对优化的目标进行求解,并通过实验证明其有效性。最后获得的结论如下。
(1) 在每个染色体进行编码时,利用染色体安排段优化算法对染色体进行补全,并采用固定的求解过程让染色体的选择段与适应度进行绑定,可以有效压缩遗传算法的搜索空间,为HFS大规模问题的求解提供一个缩减后的解空间。
(2) 改进式遗传算法通过染色体进行交叉与变异时,分别使用粒子群与模拟退火的机制,可以提高遗传算法的搜索效率,为求解大规模HFS问题提供优质个体。
(3) 改进式遗传算法通邻域搜索让当前代所得的最优染色体(优质染色体)主动对自己进行优化,实现求解大规模HFS问题的精确搜索。
| [1] | |
| [2] |
何军红, 马国伟, 刘赛, 等. MES柔性作业车间调度优化算法的研究[J].
工业仪表与自动化装置, 2020(1): 26-32.
HE J H, MA G W, LIU S, et al. Research on MES flexible job shop scheduling optimization algorithm[J]. Industrial Instrumentation & Automation, 2020(1): 26-32. |
| [3] |
王秀萍. 一种面向柔性作业车间调度的启发式算法[J].
电脑知识与技术, 2017, 13(23): 216-218.
|
| [4] |
何涛.. 面向智能制造的柔性车间调度算法研究[J].
生产力研究, 2019(8): 132-135, 154.
HE T. Research on flexible shop scheduling algorithm for intelligent manufacturing[J]. Productivity Research, 2019(8): 132-135, 154. DOI: 10.3969/j.issn.1004-2768.2019.08.025. |
| [5] |
黄亚平, 王万良, 熊婧. 基于改进蚁群算法的智能调度系统设计与开发[J].
浙江工业大学学报, 2010, 38(3): 251-256.
HUANG Y P, WANG W L, XIONG J. Design and implementation of intelligent scheduling system based on improved ant colony algorithm[J]. Journal of Zhejiang University of Technology, 2010, 38(3): 251-256. DOI: 10.3969/j.issn.1006-4303.2010.03.004. |
| [6] |
田松龄, 陈东祥, 王太勇, 等. 一种异步蚁群算法求解柔性作业车间调度问题[J].
天津大学学报, 2016, 49(9): 920-928.
TIAN S L, CHEN D X, WANG T Y, et al. An asynchronous parallel ant colony optimization for flexible job-shop scheduling problem[J]. Journal of Tianjin University, 2016, 49(9): 920-928. |
| [7] |
白俊峰, 贾志浩, 白一辰. 基于改进遗传算法的车间调度问题研究[J].
现代制造技术与装备, 2019(12): 198-200.
BAI J F, JIA Z H, BAI Y C. Research on job shop scheduling problem based on improved genetic algorithm[J]. Modern Manufacturing Technology and Equipment, 2019(12): 198-200. DOI: 10.3969/j.issn.1673-5587.2019.12.092. |
| [8] |
余璇, 梁工谦, 董仲慧. 基于混合遗传禁忌搜索算法的多目标柔性作业车间调度[J].
机械制造, 2016, 54(8): 90-93.
YU X, LIANG G Q, DONG Z H. Multi-objective & flexible job-shop scheduling based on hybrid genetic tabu search algorithm[J]. Machinery, 2016, 54(8): 90-93. DOI: 10.3969/j.issn.1000-4998.2016.08.030. |
| [9] |
吴大立, 郑中祥, 尹项根, 等. 基于Petri网和多种群遗传算法的海洋核动力平台电力系统网络重构[J].
电力自动化设备, 2020, 40(8): 160-166.
WU D L, ZHENG Z X, YIN X G, et al. Network reconstruction of offshore nuclear power platform power system based on Petri net and multi-population genetic algorithm[J]. Electric Power Automation Equipment, 2020, 40(8): 160-166. |
| [10] |
田海霖, 洪良, 王艺翔, 等. 基于量子遗传算法优化粗糙-Petri网的电网故障诊断[J].
西安工程大学学报, 2018, 32(6): 678-684.
TIAN H L, HONG L, WANG Y X, et al. Optimization of power grid fault diagnosis of rough-Petri network based on quantum genetic algorithm[J]. Journal of Xi'an Polytechnic University, 2018, 32(6): 678-684. |
| [11] |
WANG M L, ZHONG R Y, DAI Q Y, et al. A MPN-based scheduling model for IoT-enabled hybrid flow shop manufacturing[J].
Advanced Engineering Informatics, 2016, 30(4): 728-736.
DOI: 10.1016/j.aei.2016.09.006. |
| [12] |
GHOLAMI O, SOTSKOV Y N, WERNER F, et al. A genetic algorithm for hybrid job-shop scheduling problems with minimizing the makespan or mean flow time[J].
Journal of Advanced Manufacturing Systems, 2018, 17(4): 461-486.
DOI: 10.1142/S0219686718500269. |
| [13] |
LIN C S, LEE I L, WU M C, et al. Merits of using chromosome representations and shadow chromosomes in genetic algorithms for solving scheduling problems[J].
Robotics and Computer-integrated Manufacturing, 2019, 58: 196-207.
DOI: 10.1016/j.rcim.2019.01.005. |
| [14] |
张国辉, 胡一凡, 孙靖贺. 改进遗传算法求解多时间约束的柔性作业车间调度问题[J].
工业工程, 2020, 23(2): 19-25.
ZHANG G H, HU Y F, SUN J H. An improved genetic algorithm for flexible job shop scheduling problem with multiple time constraints[J]. Industrial Engineering Journal, 2020, 23(2): 19-25. DOI: 10.3969/j.issn.1007-7375.2020.02.003. |
| [15] |
谢志强, 张伟涛, 杨静. 前移存在调整时间综合调度工序的算法[J].
机械工程学报, 2012, 48(12): 169-177.
XIE Z Q, ZHANG W T, YANG J. Algorithm of moving integrated scheduling procedures with set-up time forward[J]. Journal of Mechanical Engineering, 2012, 48(12): 169-177. DOI: 10.3901/JME.2012.12.169. |
| [16] |
DAI M, TANG D, GIRET A, et al. Multi-objective optimization for energy-efficient flexible job shop scheduling problem with transportation constraints[J].
Robotics & Computer Integrated Manufacturing, 2019, 59: 143-157.
|
 2021, Vol. 38
2021, Vol. 38

