伴随着信息科技的飞快发展,在许多热点研究领域, 如图像、声音、文本、视频和基因工程等,人们通常需要面对体量庞大的高维度数据[1-2]。为此,降维方法中的特征选择(Feature Selection)是处理此类数据的常规方法。根据某些指标,在不改变数据原始表示的前提下,特征选择从高维数据中挑选信息量最为丰富的维度构成特征子集,该过程各特征原始物理意义将得到维持[3],因此降维结果具备很好的解释性。在大部分情形下对全部特征进行采集将会是极其耗时耗力高开销的或者是不可能的[4-5],特征选择只针对选择的特征进行采集,故特征选择能减少待处理的数据量,有助于进一步分析处理数据。
依据标签信息是否可用,特征选择方法可分类为:无监督(Unsupervised)、半监督(Semi-supervised)和有监督(Supervised)方法[6]。因为现实大部分数据缺乏标签,对数据添加标签费力费时[7]。标签信息的缺乏使无监督学习难于其他两者。无监督特征选择可进一步分为3类:过滤式(Filter)、包裹式(Wrapper)和嵌入式(Embedding)[8]。此处主要介绍嵌入式。嵌入式方法将数据分布先验等数据属性纳入考虑,因此大多数情况下可以获得较优的特征信息。由于无监督特征选择具备捕获数据隐藏结构如局部流形结构和全局结构等的能力[9-10],因此捕捉学习前者结构的嵌入式无监督特征选择通常能得到良好的效果[11]。
目前特征选择方法大多数采用嵌入式无监督的方式构建模型,但其中有些方法使得降维后的低维子空间特征判别性不强且存在冗余,导致选择的特征不具有较强的代表性,影响模型的性能。本文通过将自适应图嵌入学习获得的聚类指示矩阵在回归中进行拟合,并对低维的投影子空间施加正交约束,以此选择出判别性强且非冗余的特征,并通过一个表征特征重要程度的特征权重对角矩阵,进行特征选择并形成特征子集,进行后续任务处理。
1 国内外研究现状国内外学者对于无监督特征选择方法进行了各种各样的探索。Cai等[12]提出多簇特征选择(Multi-Cluster Feature Selection, MCFS),使用
相较于以往方法,上述方法效果得到提升,但在降维过程中没有考虑对学习的投影子空间施加正交约束,以减少冗余特征的影响,提高选择特征的判别性。因此本文通过图嵌入局部结构学习,对数据间的相似图进行自适应调节,并将学习到的聚类指示矩阵作正交回归拟合,最后通过权重矩阵选择出判别性特征,该过程统一局部结构学习和特征选择在一个无监督框架中同时进行。
2 相关技术此处介绍本文使用的符号及运算,
根据局部距离,图嵌入局部结构学习为各个数据点自适应分配最优近邻,以此来学习相似度矩阵,并挖掘潜在几何结构。
本文采用欧氏距离作为距离度量,默认向量为列向量。已知数据集
通过添加关于
| $ \left\{\begin{split} & {\underset{{{S}}}{\rm{min}}\sum \limits_{i,j=1}^{n}{||{{x}}_{i}-{{x}}_{j}||}_{2}^{2}{s}_{ij}+\alpha {s}_{ij}^{2}}\\& { {\rm{s.t.}}\;{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1,{\rm{rank}}\left({{L}}_{{{S}}}\right)=n-c } \end{split}\right. $ | (1) |
由于
| $ {\sum }_{v=1}^{c}{\sigma }_{v}\left({{L}}_{{{S}}}\right)=\underset{{{F}}\in {{\bf{R}}}^{n\times c},{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}}{\rm{min}}{\rm{Tr}}({{{F}}}^{\rm{T}}{{L}}_{{{S}}}{{F}}) $ | (2) |
其中,
| $ \left\{\begin{split} & {\underset{{{S}},{{F}}}{\rm{min}}\sum \limits_{i,j=1}^{n}({||{{x}}_{i}-{{x}}_{j}||}_{2}^{2}{s}_{ij}+\alpha {s}_{ij}^{2})+2\,\beta\, {\rm{Tr}}({{{F}}}^{\rm{T}}{{L}}_{{{S}}}{{F}}) }\\& { {\rm{s.t.}}\;{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1,{{F}}\in {{\bf{R}}}^{n\times c},{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}} \end{split}\right. $ | (3) |
为了在投影子空间中保留关于数据样本更多的判别信息[16]并避免平凡解[17],对最小二乘回归(Least Square Regression, LSR)模型中的投影矩阵施加正交约束,得到正交回归模型(Orthogonal Regression)。对于该模型,
| $ \left\{\begin{split} & { \underset{{{W}}}{\rm{min}}{||{\left({{X}}{{W}}\right)}^{\rm{T}}+{{b}}{\bf{1}}_{n}^{\rm{T}}-{{Y}}||}_{{\rm{F}}}^{2}}\\& { {\rm{s.t.}}\;{{{W}}}^{\rm{T}}{{W}}={{I}}_{c} } \end{split}\right. $ | (4) |
Wu等[18]在式(3)基础上添加表示特征权重矩阵
| $ \left\{\begin{split} & {\underset{{{\omega }},{{W}}}{\rm{min}}{||{{{W}}}^{\rm{T}}{{\varOmega }}{{{X}}}^{\rm{T}}+{{b}}{\bf{1}}_{n}^{\rm{T}}-{{Y}}||}_{{\rm{F}}}^{2} }\\& { {\rm{s.t.}}\;{{{\omega }}}^{\rm{T}}{\bf{1}}_{d}=1,{{\omega }}\geqslant 0,{{{W}}}^{\rm{T}}{{W}}={{I}}_{c} } \end{split}\right. $ | (5) |
由于正交回归可视为约束在施蒂费尔流形(Stiefel Manifold)
将式(3)与式(5)联立,得到本文的目标函数,参见式(6)。式(6)将图嵌入局部结构学习与特征加权正交回归结合起来,获得一个统一的目标函数。其中:第一、二部分为图嵌入局部结构学习,自适应学习局部流形结构,即数据样本间的相似度矩阵;第三部分约束学习到的数据之结构图的连通分量个数与自然聚类的簇个数完全相等,以学习到更好的数据样本图结构;第四部分将局部流形结构学习得到的聚类指示矩阵在正交回归中拟合并获得权重矩阵。
进行联合学习是为了保留更多的判别信息并得到表征各个特征重要性的权重矩阵。整体框架模型参见式(6)。
| $ \left\{\begin{split} & { \underset{{{S}},{{F}},{{W}},{{b}},{{\omega }}}{\rm{min}}\sum\limits _{i,j=1}^{n}{||{{x}}_{i}-{{x}}_{j}||}_{2}^{2}{s}_{ij}+\alpha {s}_{ij}^{2} }+\\& {2\beta {\rm{Tr}}({{{F}}}^{\rm{T}}{{L}}_{{{S}}}{{F}})+\gamma {||{{{W}}}^{\rm{T}}{{\varOmega }}{{{X}}}^{\rm{T}}+{{b}}{\bf{1}}_{n}^{\rm{T}}-{{{F}}}^{\rm{T}}||}_{{\rm{F}}}^{2} }\\& { {\rm{s.t.}}\;\;{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1,{{{\omega }}}^{\rm{T}}{\bf{1}}_{d}=1,{{\omega }}\geqslant 0, }\\&\qquad { {{{W}}}^{\rm{T}}{{W}}={{I}}_{c},{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}} \end{split}\right. $ | (6) |
根据变量
| $ \left\{\begin{split} & { \underset{{{S}},{{F}},{{W}},{{\omega }}}{\rm{min}}\sum\limits _{i,j=1}^{n}{||{{x}}_{i}-{{x}}_{j}||}_{2}^{2}{s}_{ij}+\alpha {s}_{ij}^{2}}+\\& { 2\beta {\rm{Tr}}({{{F}}}^{\rm{T}}{{L}}_{{{S}}}{{F}})+\gamma {||{{H}}{{X}}{{\varOmega }}{{W}}-{{H}}{{F}}||}_{{\rm{F}}}^{2} }\\& {{\rm{s.t.}}\;\;{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1,{{{\omega }}}^{\rm{T}}{\bf{1}}_{d}=1,{{\omega }}\geqslant 0, }\\&\qquad { {{{W}}}^{\rm{T}}{{W}}={{I}}_{c},{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}} \end{split}\right. $ | (7) |
(1) 更新
| $ \underset{{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}}{\rm{min}}{\rm{Tr}}({{{F}}}^{\rm{T}}\left(2\beta {{L}}_{{{S}}}+\gamma {{H}}\right){{F}}-2{{{F}}}^{\rm{T}}(\gamma {{H}}{{X}}{{\varOmega }}{{W}})) $ |
等价于求解
| $ \left\{\begin{aligned} & \underset{{{{F}}}^{\rm{T}}{{F}}={{I}}_{c}}{\rm{min}}{\rm{Tr}}({{{F}}}^{\rm{T}}{{A}}_{1}{{F}}-2{{{F}}}^{\rm{T}}{{B}}_{1})\\ & {{A}}_{1}=2\beta {{L}}_{{{S}}}+\gamma {{H}},{{B}}_{1}=\gamma {{H}}{{X}}{{\varOmega }}{{W}} \end{aligned}\right. $ | (8) |
此归属UOPP问题,可由广义幂迭代算法[19]求解
(2) 更新
| $ \underset{{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1}{\rm{min}}\sum \limits_{j=1}^{n}{||{{x}}_{i}-{{x}}_{j}||}_{2}^{2}{s}_{ij}+\alpha {s}_{ij}^{2}+2\beta {\rm{Tr}}({{{F}}}^{\rm{T}}{{L}}_{{{S}}}{{F}}) $ |
等价于求解
| $ \underset{{{s}}_{i}^{\rm{T}}{\bf{1}}_{n}={1,0}\leqslant {{s}}_{i}\leqslant 1}{\rm{min}}{||{{s}}_{i}+\left(1/2\alpha \right){{u}}_{i}||}_{2}^{2} $ | (9) |
其中,
(3) 更新
| $ \underset{{{{W}}}^{\rm{T}}{{W}}={{I}}_{c}}{\rm{min}}{\rm{Tr}}({{{W}}}^{\rm{T}}{{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{X}}{{\varOmega }}{{W}}-2{{{W}}}^{\rm{T}}{{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{F}}) $ |
等价于求解
| $ \left\{\begin{aligned} & \underset{{{{W}}}^{\rm{T}}\;{{W}}={{I}}_{c}}{\rm{min}}{\rm{Tr}}({{{W}}}^{\rm{T}}{{A}}_{2}{{W}}-2{{{W}}}^{\rm{T}}{{B}}_{2})\\ & {{A}}_{2}={{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{X}}{{\varOmega }},{{B}}_{2}={{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{F}} \end{aligned}\right. $ | (10) |
同理,求解式(11)属于UOPP问题,可由广义幂迭代算法求得
(4) 更新
| $ \begin{split} & { \underset{{{{\omega }}}^{\rm{T}}{\bf{1}}_{d}=1,{{\omega }}\geqslant 0}{\rm{min}}{||{{H}}{{X}}{{\varOmega }}{{W}}-{{H}}{{F}}||}_{{\rm{F}}}^{2} } =\\ & { {\rm{Tr}}({{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{X}}{{\varOmega }}{{W}}{{{W}}}^{\rm{T}})-{\rm{Tr}}(2{{\varOmega }}{{{X}}}^{\rm{T}}{{H}}{{F}}{{{W}}}^{\rm{T}}) } =\\ & {{{{\omega }}}^{\rm{T}}({({{{X}}}^{\rm{T}}{{H}}{{X}})}^{\rm{T}}\circ ({{W}}{{{W}}}^{\rm{T}})){{\omega }}-{{{\omega }}}^{\rm{T}}{\rm{diag}}(2{{{X}}}^{\rm{T}}{{H}}{{F}}{{{W}}}^{\rm{T}}) } \end{split} $ |
原问题转换为
| $ \left\{\begin{aligned} & \underset{{{{\omega }}}^{\rm{T}}{\bf{1}}_{d}=1,{{\omega }}\geqslant 0}{\rm{min}}{{{\omega }}}^{\rm{T}}{{Z}}{{\omega }}-{{{\omega }}}^{\rm{T}}{{z}}\\ & {{Z}}=({{{X}}}^{\rm{T}}{{H}}{{X}})\circ ({{W}}{{{W}}}^{\rm{T}})\\ & {{z}}={\rm{diag}}(2{{{X}}}^{\rm{T}}{{H}}{{F}}{{{W}}}^{\rm{T}}) \end{aligned}\right. $ | (11) |
其中,
此处介绍更新
初始化:随机矩阵
参数
过程:
① 更新
② 对
③ 更新
重复步骤①~③直到收敛。
基于上述算法,交替更新
为验证本文提出的JGEFW的有效性,根据文献[21]将JGEFW与几种常见的无监督特征选择算法,包括拉普拉斯分数(Laplacian Score, LS)、多簇特征选择(MCFS)、无监督判别特征选择(Unsupervised Discriminative Feature Selection, UDFS)、双自表示和流形正则化的鲁棒无监督特征选择(Dual Self-representation and Manifold Regularization, DSRMR)以及包含所有特征的基线模型(Baseline)进行对比。
根据文献[21]选择在4个公开数据集YALE、TOX、ISOLET和COIL上进行比较,且设定选择特征数范围均为
实验评估指标包括聚类准确率(Accuracy, ACC)和标准化互信息(Normalized Mutual Information, NMI)。这两者取值范围均为
| $ {\rm{ACC}}=\frac{1}{n}{\sum }_{i}\delta ({r}_{i},{\rm{map}}({g}_{i}\left)\right) $ | (12) |
其中,
| $ {\rm{MI}}={\sum }_{{\lambda }_{{\mu }_{1}}\in {{\varLambda }},{{\lambda }}_{{\mu }_{2}}^{'}\in {{{\varLambda }}}^{'}}p({\lambda }_{{\mu }_{1}},{\lambda }_{{\mu }_{2}}')\log \frac{p({\lambda }_{{\mu }_{1}},{\lambda }_{{\mu }_{2}}')}{p({\lambda }_{{\mu }_{1}})p({\lambda }_{{\mu }_{2}}')} $ | (13) |
其中,
| $ {\rm{NMI}}({{\varLambda }},{{{\varLambda }}}')=\frac{{\rm{MI}}}{\sqrt{E\left({{\varLambda }}\right)E\left({{{\varLambda }}}'\right)}} $ | (14) |
其中,
实验采用的4个公开数据集简介,如表1所示。
| 表 1 数据集简要信息 Table 1 Brief information of datasets |
YALE数据集属于人脸图像数据集,其包含15个人共165张的灰度图像,每个人包含11张不同面部表情和环境的图像,包括中心光、左光、右光、快乐、正常、悲伤、困倦、惊讶、戴眼镜和眨眼[23]。
TOX数据集属于生物数据集,共包含4个类别的171个样本,每个样本维度为5 748维。
ISOLET数据集是从30个测试者每人读出两次全部英文字母收集而来,样本共1 560个,维度为617。
COIL数据集包含1 440张图像,共20类物品,每个物品有72张图像,其来源于相机以固定间隔5°的角度拍摄得到每类物品的图像,裁剪大小为32×32像素,故维度为1 024维。
4.3 各算法参数设置根据文献[21],设置所有对比算法相似度矩阵近邻关系由
表2~3分别展示几种无监督特征选择算法在各数据集上,经参数搜索后选取最优参数且选取各特征选择数情况下的最佳聚类结果及相应的标准差,同时表2~3最后一行为各个算法在全部数据集上的平均聚类效果。表中加粗项表示在该数据集效果最优,下划线项表示在该数据集上效果次优,对比算法结果均由文献[21]给出。
|
表 2 几种无监督特征选择算法在各数据集聚类准确率(%)
|
|
表 3 几种无监督特征选择算法在各数据集标准化互信息(%)
|
由表2可知,本方法在各数据集和平均聚类准确率上效果均为最优,同时在YALE、ISOLET、COIL和平均聚类准确率与次优效果相比均有较大的提升。由表3可知,本方法在YALE上效果为最优,且与次优效果相比有较大的提升,而在TOX、ISOLET和平均标准化互信息为次优,由于Baseline模型对全部特征进行利用而不加以选择,因此对于某些包含噪声和冗余特征较少的数据集而言,该做法有时也能获得较好的效果,但并无包含降维操作。
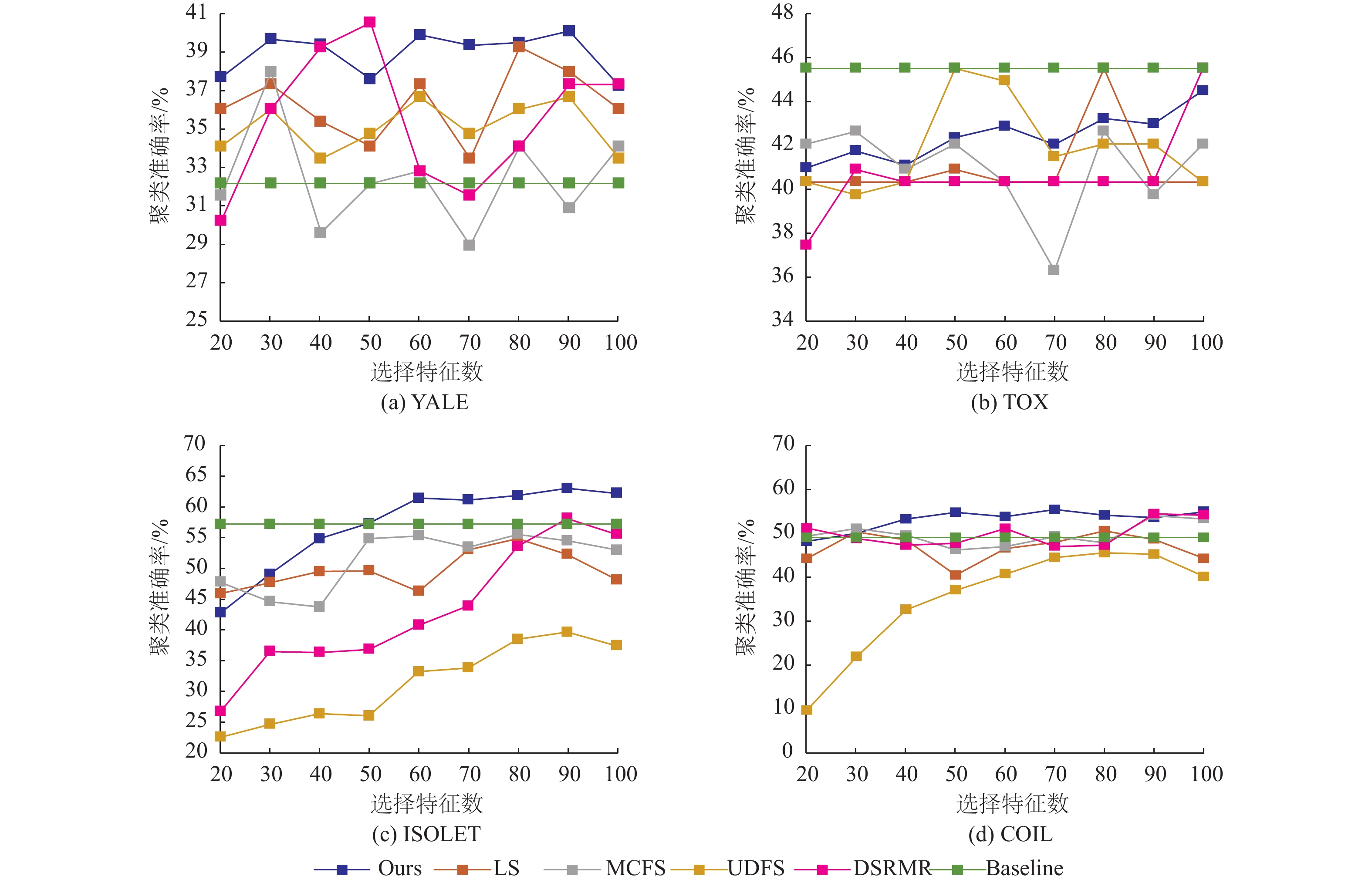
4.4.2 评估指标随各特征选择数的变化图1~2分别表示在不同聚类指标下几种不同的特征选择算法在各数据集上选择不同特征数时的聚类效果。图中横坐标表示不同的选择选择数,纵坐标分别表示以聚类准确率(ACC,%)和标准化互信息(NMI,%)作为聚类指标时的值。由于文献[21]并无给出对比算法在各选择特征数的实际数值,故该部分数据是根据该论文设置,实际运行代码获得的,得到的各对比算法实际最优效果允许与表2~3存在差距。
|
图 1 各数据集几种算法不同特征选择数的聚类准确率(%)比较 Figure 1 Results on clustering evaluation metric of ACC (%) of different numbers of selected features of all compared unsupervised feature selection methods on all datasets |
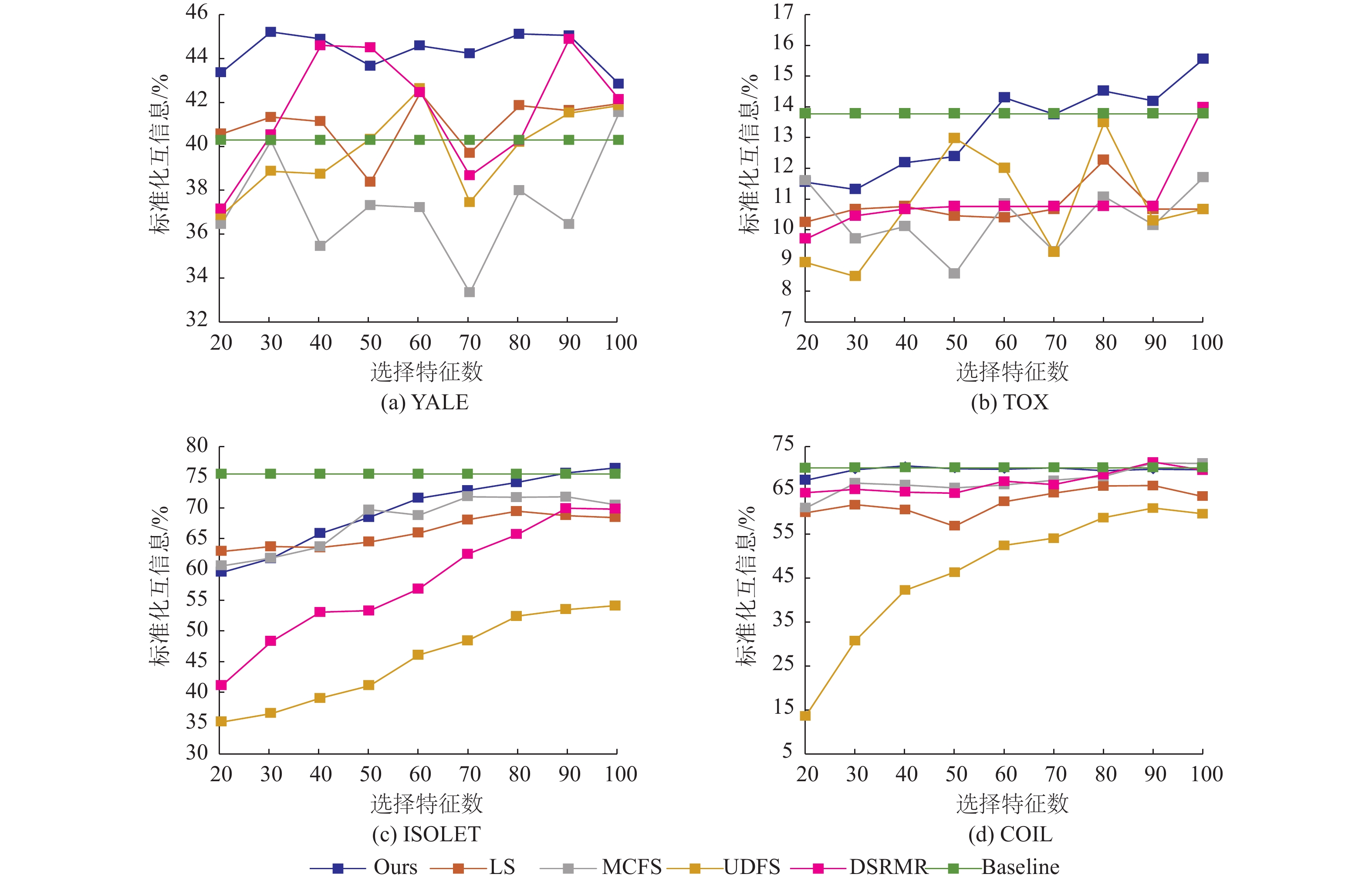
|
图 2 各数据集几种算法不同特征选择数的标准化互信息(%)比较 Figure 2 Results on clustering evaluation metric of NMI (%) of different numbers of selected features of all compared unsupervised feature selection methods on all datasets |
由图1可知,本方法在YALE上聚类准确率变动较为波动,与其他对比算法情况相似,且在大多数选择特征数范围优于其他对比算法;在TOX上聚类准确率大致呈整体上升趋势,且在大多数选择特征数范围效果均优于LS、MCFS和DSRMR;在ISOLET上随着选择特征数增加,效果大致呈上升趋势,与大多数对比算法变化趋势一致,且在选择特征数为
由图2可知,本方法在YALE上标准化互信息变动较为波动,与其他对比算法情况相似,但在选择特征数为30时标准化互信息为所有对比算法下的最优,表明JGEFW在选择特征数较小时便能选择出判别性强的信息;在TOX上标准化互信息大致呈上升趋势,与其他对比算法趋势完全不同,且当选择特征数在大于70的范围内,标准化互信息均为所有对比算法下的最优;在ISOLET上随着选择特征数增加,标准化互信息大致呈提升趋势,与其他绝大多数对比算法变化趋势相同,且在选择特征数为100时标准化互信息优于Baseline的效果;在COIL上随着选择特征数增加,标准化互信息在Baseline算法上下波动,表明本算法能有效学习到数据间的潜在几何结构,并对判别力强的特征加以选择。
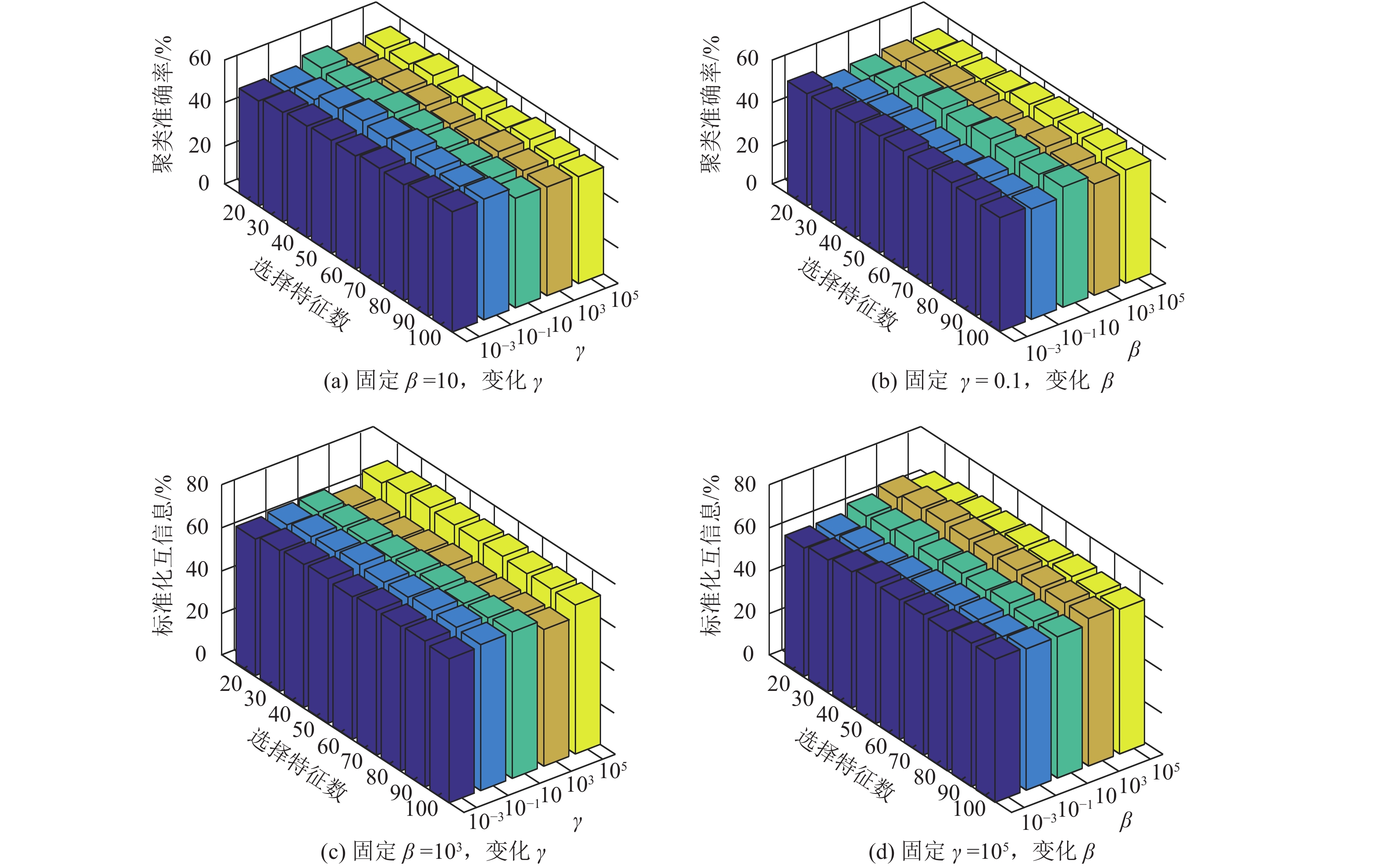
4.4.3 参数敏感性分析为探究算法的性能,进行参数敏感性分析实验(Parameter Sensitivity),以考虑各参数变动对模型的影响。此处以COIL数据集为例,在最优聚类准确率效果中先固定
由图3可知,JGEFW的聚类准确率随着选择特征数、
|
图 3 本方法在COIL的参数敏感性分析实验结果 Figure 3 Parameters sensitivity analysis about clustering evaluation metric of the proposed method on COIL dataset |
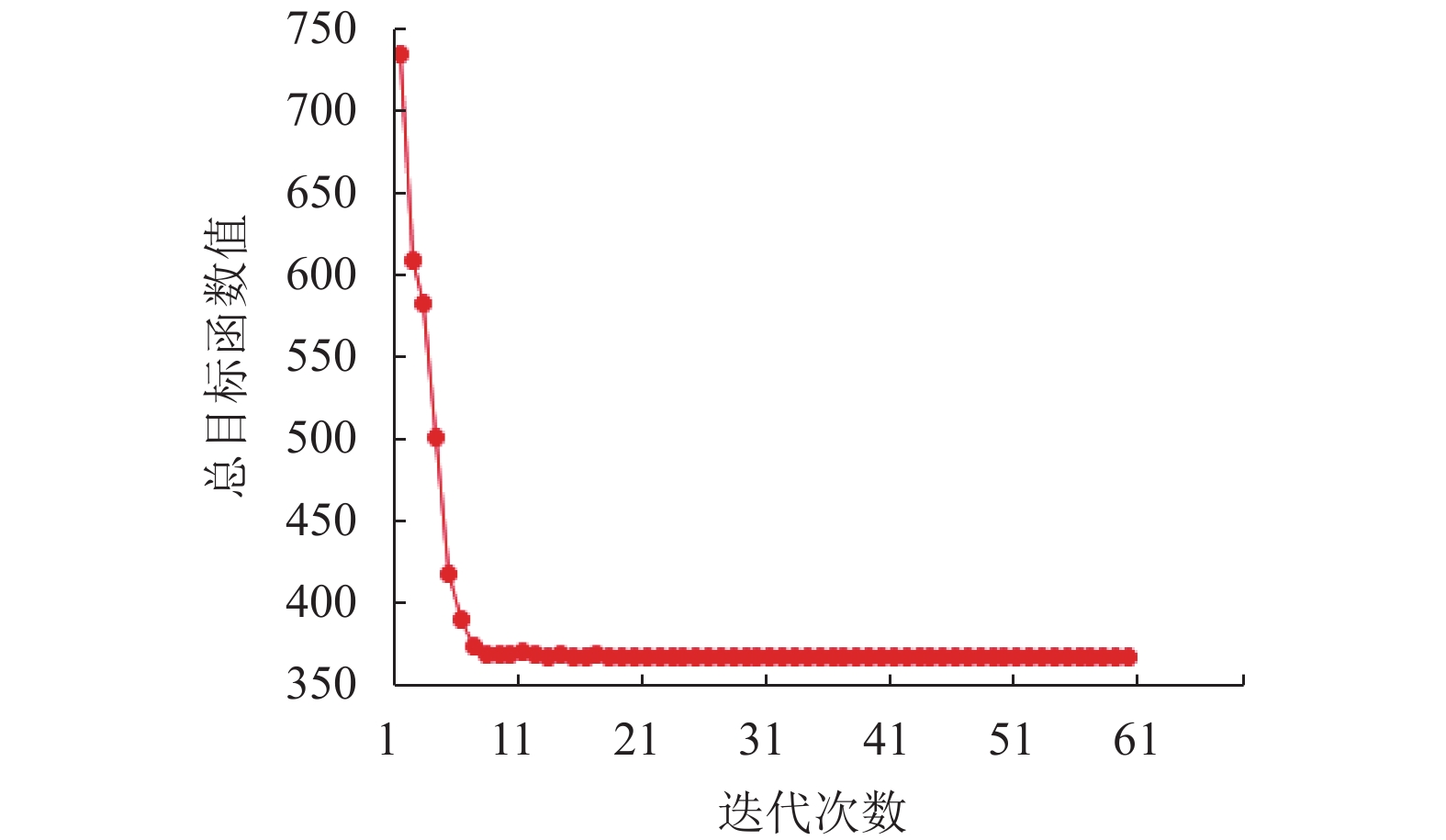
此处以COIL数据集为例,其他数据集上的收敛情况与此相似,目标函数值的收敛曲线如图4所示。由图4可知,随着迭代次数逐渐增加,目标函数值不断减少,最后趋于一个稳定值,表明该算法是收敛的。
|
图 4 本方法在COIL数据集上的收敛结果示意 Figure 4 Result of convergence experiments of the proposed method on COIL dataset |
本文给出了一种改进的无监督特征选择算法,称为JGEFW。通过局部结构学习自适应地调节数据的相似图,使其满足自然聚类的簇的要求,提高图构造的准确度。并通过加权特征回归的方法,使图构造的聚类指示矩阵在正交回归中拟合以学习权重矩阵,并挑选出权重值大的判别特征和非冗余特征形成特征子集。实验结果表明,JGEFW的性能在平均情况下优于其他对比的特征选择方法。未来工作将尝试提高模型的聚类性能和迭代速度。
| [1] |
HU J, LI Y, GAO W, et al. Robust multi-label feature selection with dual-graph regularization[J].
Knowledge-Based Systems, 2020, 203: 106126.
DOI: 10.1016/j.knosys.2020.106126. |
| [2] |
费伦科, 秦建阳, 滕少华, 等. 近似最近邻大数据检索哈希散列方法综述[J].
广东工业大学学报, 2020, 37(3): 23-35.
FEI L K, QIN J Y, TENG S H, et al. Hashing for approximate nearest neighbor search on big data: A survey[J]. Journal of Guangdong University of Technology, 2020, 37(3): 23-35. DOI: 10.12052/gdutxb.190123. |
| [3] |
HOU C, NIE F, YI D, et al. Feature selection via joint embedding learning and sparse regression[C]//IJCAI International Joint Conference on Artificial Intelligence. Spain: Morgan Kaufmann, 2011: 1324-1329.
|
| [4] |
WANG S, WANG H. Unsupervised feature selection via low-rank approximation and structure learning[J].
Knowledge-Based Systems, 2017, 124: 70-79.
DOI: 10.1016/j.knosys.2017.03.002. |
| [5] |
刘艳芳, 李文斌, 高阳. 基于自适应邻域嵌入的无监督特征选择算法[J].
计算机研究与发展, 2020, 57(8): 1639-1649.
LIU Y F, LI W B, GAO Y. Adaptive neighborhood embedding based unsupervised feature selection[J]. Journal of Computer Research and Development, 2020, 57(8): 1639-1649. DOI: 10.7544/issn1000-1239.2020.20200219. |
| [6] |
滕少华, 冯镇业, 滕璐瑶, 等. 联合低秩表示与图嵌入的无监督特征选择[J].
广东工业大学学报, 2019, 36(5): 7-13.
TENG S H, FENG Z Y, TENG L Y, et al. Joint low-rank representation and graph embedding for unsupervised feature selection[J]. Journal of Guangdong University of Technology, 2019, 36(5): 7-13. DOI: 10.12052/gdutxb.190048. |
| [7] |
ZHENG W, YAN H, YANG J. Robust unsupervised feature selection by nonnegative sparse subspace learning[J].
Neurocomputing, 2019, 334: 156-171.
DOI: 10.1016/j.neucom.2019.01.015. |
| [8] |
DING D, YANG X, XIA F, et al. Unsupervised feature selection via adaptive hypergraph regularized latent representation learning[J].
Neurocomputing, 2020, 378: 79-97.
DOI: 10.1016/j.neucom.2019.10.018. |
| [9] |
TENG L, FENG Z, FANG X, et al. Unsupervised feature selection with adaptive residual preserving[J].
Neurocomputing, 2019, 367: 259-272.
DOI: 10.1016/j.neucom.2019.05.097. |
| [10] |
LIU X, WANG L, ZHANG J, et al. Global and local structure preservation for feature selection[J].
IEEE Transactions on Neural Networks and Learning Systems, IEEE, 2014, 25(6): 1083-1095.
DOI: 10.1109/TNNLS.2013.2287275. |
| [11] |
DU L, SHEN Y D. Unsupervised feature selection with adaptive structure learning[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Sydney: ACM, 2015-August: 209-218.
|
| [12] |
CAI D, ZHANG C, HE X. Unsupervised feature selection for multi-cluster data[C]//Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2010: 333-342.
|
| [13] |
QIAN M, ZHAI C. Robust unsupervised feature selection[C]//IJCAI International Joint Conference on Artificial Intelligence. Beijing: Morgan Kaufmann, 2013: 1621-1627.
|
| [14] |
LI Z, YANG Y, LIU J, et al. Unsupervised feature selection using nonnegative spectral analysis[C]//Proceedings of the AAAI Conference on Artificial Intelligence. Toronto: AAAI, 2012: 1026-1032.
|
| [15] |
NIE F, WANG X, HUANG H. Clustering and projected clustering with adaptive neighbors[C]//Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014: 977-986.
|
| [16] |
XU X, WU X, WEI F, et al. A general framework for feature selection under orthogonal regression with global redundancy minimization[J].
IEEE Transactions on Knowledge and Data Engineering, 2021, 99: 1-1.
DOI: 10.1109/TKDE.2021.3059523. |
| [17] |
ZHAO H, WANG Z, NIE F. Orthogonal least squares regression for feature extraction[J].
Neurocomputing, 2016, 216: 200-207.
DOI: 10.1016/j.neucom.2016.07.037. |
| [18] |
WU X, XU X, LIU J, et al. Supervised feature selection with orthogonal regression and feature weighting[J].
IEEE Transactions on Neural Networks and Learning Systems, 2020, 32(5): 1831-1838.
|
| [19] |
NIE F, ZHANG R, LI X. A generalized power iteration method for solving quadratic problem on the Stiefel manifold[J].
Science China(Information Sciences), 2017, 60(11): 5-11.
|
| [20] |
HUANG J, NIE F, HUANG H. A new simplex sparse learning model to measure data similarity for clustering[C]//IJCAI International Joint Conference on Artificial Intelligence. Buenos Aires: Morgan Kaufmann, 2015: 3569-3575.
|
| [21] |
LIU Y, YE D, LI W, et al. Robust neighborhood embedding for unsupervised feature selection[J].
Knowledge-Based Systems, 2020, 193: 105462.
DOI: 10.1016/j.knosys.2019.105462. |
| [22] |
LI X, ZHANG H, ZHANG R, et al. Generalized uncorrelated regression with adaptive graph for unsupervised feature selection[J].
IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(5): 1587-1595.
DOI: 10.1109/TNNLS.2018.2868847. |
| [23] |
THARWAT A, GABER T, IBRAHIM A, et al. Linear discriminant analysis: a detailed tutorial[J].
AI Communications, 2017, 30(2): 169-190.
DOI: 10.3233/AIC-170729. |
| [24] |
SHANG R, WANG W, STOLKIN R, et al. Non-negative spectral learning and sparse regression-based dual-graph regularized feature selection[J].
IEEE Transactions on Cybernetics, IEEE, 2018, 48(2): 793-806.
DOI: 10.1109/TCYB.2017.2657007. |
 2021, Vol. 38
2021, Vol. 38