车辆换道是基本驾驶行为之一，不合理的换道行为可能会导致道路交通拥堵^[1]。车辆换道的早期研究^[2-5]都是根据现实车辆获取信息方式和人工驾驶的前向特征进行模型构建，如MITSIM模型^[2]、最小安全换道距离模型^[3]、STCA模型^[4]及其改进的STCA-I模型^[5]等。但是人工驾驶会因视觉的障碍使上述模型对提高交通效率具有局限性。随着车路协同技术的发展，有学者探讨在未来车路信息交互的方式下新的车辆协同换道机制^[6]。李珣等^[6]提出车路协同技术下基于行车指引的改进STCA双车道模型STCA-M，利用了网联车辆(Connected vehicles, CV)信息共享的特性，提高了换道频率。但这类模型局限于元胞自动机理论状态离散化的特点，无法精确地模拟车辆在真实场景下的换道轨迹，主要用作微观交通流的研究。

智能网联汽车(Connected and Automated vehicle, CAV)是拥有完善的车辆控制系统并且能实时与周围车辆分享路况信息的智能车辆，能够有效弥补人为因素的缺陷^[7-8]。近些年，针对CAV环境下的协同换道研究取得不少进展^[9-14]。杨刚等^[10]建立新的安全距离模型，根据车辆轨迹规划实现车辆并行场景下的协同换道。Li等^[11]提出一个两阶段的路径规划框架允许多辆CAV同时换道并且不用考虑碰撞约束。但由于上述方法较为复杂并且会随着换道过程中增加的协作车辆数量进一步增加控制问题的维度和计算复杂性^[13]，不具有普适性。而多智能体系统属于分布式人工智能，具有自治性、鲁棒性、高效和低成本等优势^[15-17]。如果从多智能体系统(Multi-agents System, MAS)一致性控制的角度出发，将车联网下的CAVs抽象成二维的动态系统，则可以有效利用多智能体系统理论设计分布式控制器进行协同控制^[18]。

最近研究表明，分散的CAVs通过形成速度和间距一致的队形，可以提高燃油经济性和行驶安全^[19-21]。目前，大部分车辆集群研究^[22-24]主要集中在单个集群稳定控制方面，对多集群、集群间换道研究^[25-26]相对较少。面向未来CAVs集群驾驶的交通环境，本文参考多智能体系统理论，提出基于多集群系统的车辆协同控制框架，实现换道场景下的车辆集群控制。车辆分组可以有效降低多车协同控制问题的计算复杂性并且提高换道效率^[27-28]，为此，本文提出了分布式集群划分算法。在该基础上，本文提出适用于集群空间分配的间距控制算法和相应的控制协议，将整个换道过程划分为稀疏纵向间距阶段和车道变更阶段，通过提前增大车辆间的安全间距解决避碰的高纬度约束导致控制问题求解复杂的难点^[11]。同时，所提控制协议保证车辆纵向速度的一致性，从而保证了换道过程的安全。

1 预备知识和问题描述 1.1 预备知识

假设道路上存在 $k$ 个集群，单个集群内车辆由单个领导者车辆(编号为0)和若干个跟随者车辆(编号为 $1,2, \cdots ,n$ )组成。本文使用加权有向图 ${{G}} = \left\{ {{{V}},{{E}},{{A}}} \right\}$ 描述单个集群内 $n + 1$ 辆车之间的通信拓扑结构。其中 ${{V}} = \left\{ {0,1,2, \cdots, n} \right\}$ 表示顶点集， ${{E}} \subseteq {{V}} \times {{V}}$ 表示边集， ${{A}} = \left[ {{a_{ij}}} \right]$ 是与 ${{G}}$ 对应的非负加权邻接矩阵。如果 $\left( {i,j} \right) \in {{E}}$ ，那么 ${a_{ij}} = 1$ ，否则 ${a_{ij}} = 0$ 。本文假设 ${{G}}$ 中没有自环，即 ${a_{ii}} = 0,i \in n$ 。节点的领域集定义为： ${N_i} = \left\{ {j|{a_{ij}} = 1} \right\}$ 。对应于 ${{G}}$ 的拉普拉斯矩阵 ${{L}} = \left[ {{l_{ij}}} \right]$ ，其中 ${l_{ii}} = \sum\nolimits_{j \ne i} {a{}_{ij}} $ ， ${l_{ij}} = - {a_{ij}}$ 。定义 ${{G}}$ 的连接矩阵 ${{K}} = {\rm{diag}}({k_1},{k_2}, \cdots ,{k_n})$ ，用于描述跟随者车辆获取领导者车辆信息的情况。其中，若跟随者能获取领导者的信息，则 ${k_i} > 0$ ,否则 ${k_i} = 0$ 。本文采用BDL(Bidirectional Leader)通信拓扑结构^[18]，若无特殊说明， ${k_i} = 1$ 。与连接矩阵对应的期望间距矩阵 ${{Q}} = [{r_i}]$ ，定义 ${r_i} = - i \times d$ ，用于描述跟随者与领导者的期望间距，其中 $d$ 是安全间距。对应有车辆之间的期望间距矩阵 ${{P}} = \left[ {{r_{ij}}} \right]$ 。

对于第 $k$ 个集群内的跟随者车辆 $i$ 的控制器为

$ \left\{ \begin{aligned} & {\dot x_i^k\left( t \right) = v_i^k\left( t \right)} \\ & {\dot v_i^k\left( t \right) = u_i^k\left( t \right)} \end{aligned} \right. $

(1)

$x_i^k,v_i^k,u_i^k$ 分别是跟随车 $i$ 的位置、速度和控制输入。

对于第 $k$ 个集群的领导者车辆L的控制器为

$ \left\{ \begin{aligned} & {\dot x_{\rm{L}}^k\left( t \right) = v_{\rm{L}}^k\left( t \right)} \\ & {\dot v_{\rm{L}}^k\left( t \right) = u_{\rm{L}}^k\left( t \right)} \end{aligned}\right. $

(2)

$x_{\rm{L}}^k,v_{\rm{L}}^k,u_{\rm{L}}^k$ 分别是领导者L的位置、速度和控制输入。

1.2 问题描述

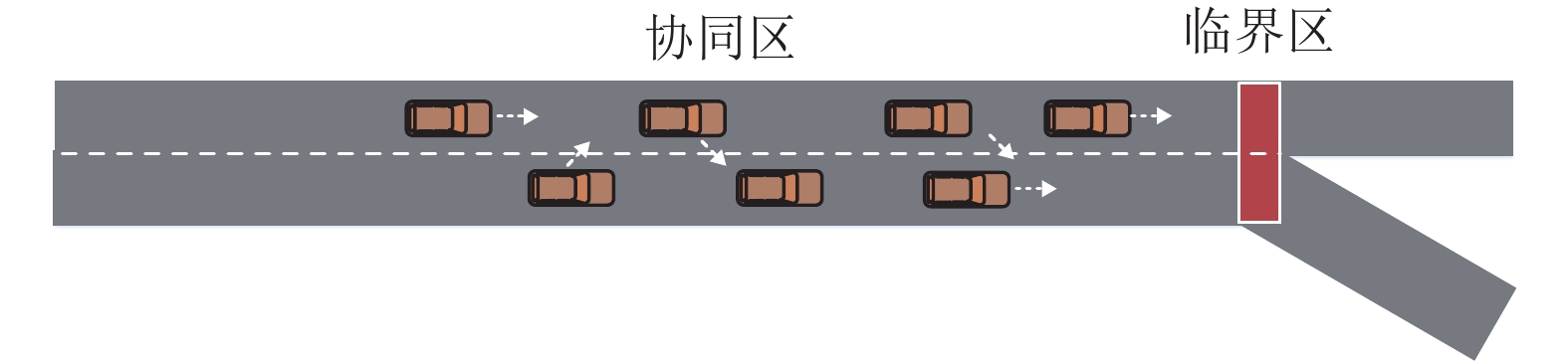
车辆协同换道的目标是车辆在行驶的过程中，利用传感器、通信设备等设备，同时兼顾安全性与高效性，实现多车之间的配合，为换道车辆制造换道所需安全间距^[13]。本文以高速公路的出口匝道区域的强制换道^[29-30]为研究背景，智能网联车辆为研究对象，聚焦于车辆协同换道策略的研究。如图1所示，考虑双车道平行的高速公路上有 $ m $ 辆车，其中有 $ n $ 辆智能车辆根据不同的目的地而需要在出口匝道前实施强制换道操作。文献[31]说明，早期的车道变更操作，能够延迟或消除瓶颈处的自组织拥堵现象。基于以上思想，本文只关注在出口匝道瓶颈处前的协同换道区域路段，进行车辆的协同控制研究。

2 车辆协同控制框架

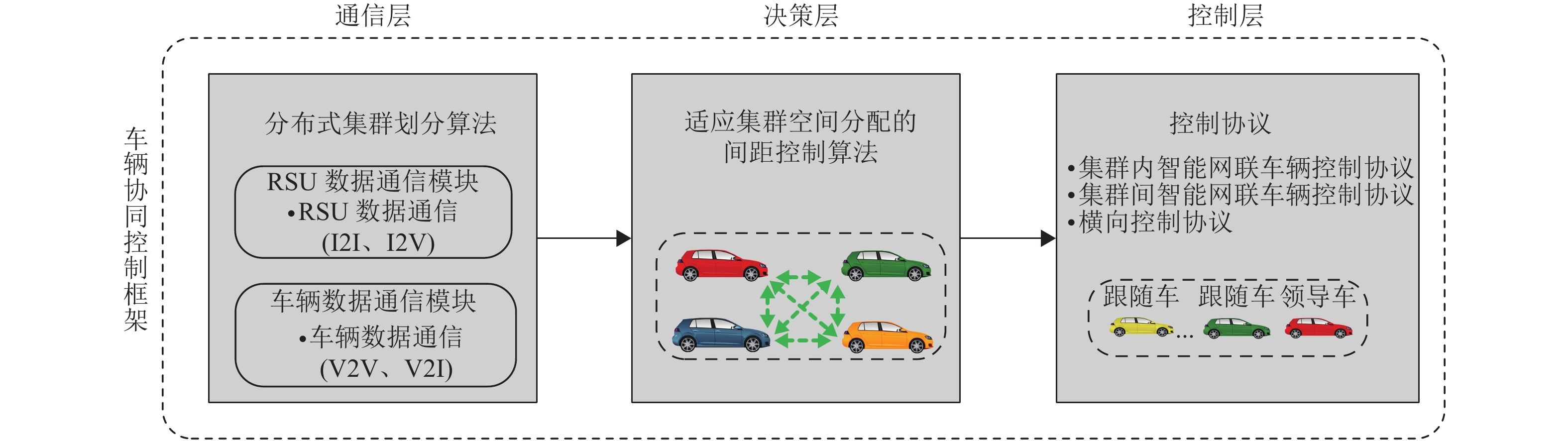
从单车智能控制，过渡到多车协同驾驶，车辆之间的交互与决策尤为关键。目前CAV环境下的协同换道研究^{[9, 11-14]}，大多采用路径规划和轨迹跟踪算法模拟车辆协同换道的轨迹，但其优化控制函数往往复杂且难以求解。为此，本文基于CAVs实时通信的特点，构建出分层的车辆协同控制框架，如图2所示。

通信层采用分布式集群划分算法，将多车协同控制简化为多集群系统的合作交互问题；决策层解决车辆之间的冲突问题，考虑车辆的驾驶意图、换道顺序，提出了适应集群空间分配的间距控制算法，使分散的车辆形成稀疏纵向间距的多集群系统，让换道车辆拉大与前后车辆的间距从而达到换道所需间距；控制层采用提出的集群内和集群间控制协议，使集群内、集群间车辆达到决策层的期望速度与间距；当满足换道条件，目标车辆依据所提横向控制器完成车道变更。

为了方便策略的研究，本文提出以下假设：

(1) CAVs都配置先进的传感器以测量位置、速度等动态变化的状态信息。

(2) CAVs可以感知并与周围车辆交换实时状态信息，并且不存在通信时延和丢包。

2.1 分布式集群划分算法

如果车道上的多辆CAV彼此相距很远，此时同时进行换道操作，相互之间几乎没有影响。集群间换道亦是同理，通过协调集群间的间距，便可实现多个集群内多车辆同时进行换道。如果考虑集中式的方式对车道上所有车辆进行协调控制，所花费的计算开销极大，并且不易实现。本文通过划分集群的方法，只需控制单个集群内、集群间的车辆，实现对车辆的分布式控制，近似实现全局控制的效果。分布式集群划分算法如下所示。

输入：车辆 $ {{i}} $ 及通信范围的邻居车辆集合 $ {{{S}}}_{{{i}}} $ 的状态信息

输出：车辆 $ {{i}} $ 及邻居车辆集合 $ {{{S}}}_{{{i}}} $ 的所属集群 $ {\rm{Grou}}{{\rm{p}}_{{k}}} $

初始化:

　(1) $ {S}_{i}\ne {\varnothing },j={1,2},\cdots ,m{;} $

　(2) 定义集群内最大的车辆数目为 $ N $ 辆；

　(3) 车辆集合 $ U={S}_{i}\cup i $ 的位置信息按纵向方向递减排序，纵向位置最大的车辆编号设为 $ {V}_{1} $ ，以此类推；

　(4) 若编号为 $ {V}_{1} $ 的车辆尚未分组，则 $ {V_1} \in {\rm{Grou}}{{\rm{p}}_1} $ ；否则记录编号 $ {V}_{1} $ 的车辆所属集群 $ {\rm{Grou}}{{\rm{p}}_k} $ ；

过程：

(1) 计算相邻车辆的纵向距离 $ {d}_{j(j-1)}=\left|{x}_{j}-{x}_{j-1}\right| $ ；

(2) 若 $ {d_{j(j - 1)}} < {d_{j,{\rm{desired}}}} $ 并且当前集群 $ {\rm{Grou}}{{\rm{p}}_k} $ 内的车辆数目小于N辆， ${V_j} \in {\rm{Grou}}{{\rm{p}}_k}$ ;否则 ${V_j} \in {\rm{Grou}}{{\rm{p}}_{k + 1}}$ ；

对编号为 ${V}_{2},{V}_{3},\cdots ,{V}_{m}$ 的车辆重复执行以上过程。

${d_{i,{\rm{desired}}}}$ 由IDM模型^[28]确定，确保可能发生换道冲突的车辆被划分到同一集群中：

$ {d_{i,{\rm{desired}}}}(t) = {d_{\min }} + \max \left\{ {{T_{{\rm{safe}}}}{v_i}(t) + \frac{{{v_i}(t)\Delta {v_i}(t)}}{{2\sqrt {{a_{\max }}{b_{\max }}} }}} \right\} $

(3)

其中 ${d_{\min }}$ 是静止时车辆间距离最小值， ${T_{{\rm{safe}}}}$ 是安全换道时间， ${a_{\max }},{b_{\max }}$ 分别是车辆 $i$ 最大舒适加速度和最大舒适减速度。 ${v_i}(t)$ 是车辆 $i$ 的速度， $\Delta {v_i}$ 是车辆 $i$ 与前方车辆 $i{\rm{ - }}1$ 的速度差值。分布式划分集群算法完成后，集群内的车辆选定BDL通讯拓扑^[18]结构建立连接。

2.2 控制协议及一致性分析

为了能够模拟变道，控制层需要设计车辆横向和纵向运动的控制协议。本文的纵向控制协议的设计采用速度与距离线性叠加的方式，克服了单一速度或距离跟踪效果不一致的缺陷，即考虑车辆与邻居车辆和领导者车辆之间的车头间距差和速度差。横向控制是为了使车辆在进行变道机动时实现平滑的横向轨迹。本文的纵向控制器包括集群内和集群间两部分。

集群内的纵向控制器采用Li等^[23]提出的一致性协议：

$ \left\{ \begin{aligned} & \dot x_i^k\left( t \right) = v_i^k\left( t \right) \\ & \dot v_i^k\left( t \right) = \dot v_{\rm{L}}^k(t) - \sum\limits_{j \in {N_i}(t)} a_{ij}^k\left[ {\gamma _1}\left( {x_i^k\left( t \right) - x_j^k\left( t \right) - r_{ij}^k} \right) +\right. \\ & \;\;\;\;\;\;\left. {\gamma _2}\left( {v_i^k\left( t \right) - v_j^k\left( t \right)} \right) \right] - \beta \left[ {\gamma _1}\left( {x_i^k\left( t \right) - x_{\rm{L}}^k(t) - r_{i{\rm{L}}}^k} \right) +\right. \\ & \;\;\;\;\;\;\left. {\gamma _2}\left( {v_i^k\left( t \right) - v_{\rm{L}}^k\left( t \right)} \right) \right] \end{aligned}\right. $

(4)

控制协议(4)用于集群内跟随者更新自己的控制输入。 $\dot v_{\rm{L}}^k(t)$ 是第 $k$ 组领导者车辆的加速度， ${N_i}(t)$ 是车辆 $i$ 在 $t$ 时刻第 $k$ 组通信范围内的邻居车辆， ${r_{ij}}$ 代表车辆 $i$ 及集群内其邻居车辆 $j$ 之间期望的纵向间距， ${r_{ij}} = - {r_{ji}}$ 。 ${r_{i{\rm{L}}}}$ 代表车辆与集群领导者之间的期望纵向间距。 ${\gamma _1},{\gamma _2}$ 是控制增益，均大于0。 $\;\beta $ 是权重，表示受领导者影响的大小， $\;\beta > 0$ 。

集群间的纵向控制器如式(5)所示。

$ \left\{ \begin{aligned} & \dot x_{\rm{L}}^k( t ) = v_{\rm{L}}^k( t ) \\ & \dot v_{\rm{L}}^k( t ) = \dot v_{\rm{VL}}^k(t) -\sigma [ {{\gamma _3}} ( {x_{\rm{L}}^k( t ) - x_{\rm{VL}}^k( t ) - r_{\rm{LVL}}^k} ) +\\&\qquad {\gamma _4} {( {v_{\rm{L}}^k( t ) - v_{\rm{VL}}^k( t )} )} ] \end{aligned}\right. $

(5)

如果两个集群间隔较小，需要考虑集群间车辆的换道冲突，依据控制协议(5)调整至合适状态。前置集群 $k{\rm{ - }}1$ 的末尾车辆作为当前集群 $k$ 的虚拟领导者(Virtual Leader, VL)约束真实领导者L的控制输入。 $x_{\rm{VL}}^k$ 是虚拟领导者的位置状态， $v_{\rm{L}}^k,v_{{\rm{VL}}}^k$ 分别是集群 $k$ 真实领导者、虚拟领导者的速度状态， ${r_{\rm{LVL}}}$ 是两者的期望纵向间距。 ${\gamma _3},{\gamma _4}$ 是非负控制增益， $\sigma $ 是权重系数且 $\sigma > 0$ 。

定理1 　假设集群间的通信拓扑结构是连通的，当采用控制协议(7)，可实现集群间车辆的群一致性。

$ \left\{ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } \left\| {x_{\rm{L}}^k\left( t \right) - x_{\rm{VL}}^k\left( t \right) - r_{\rm{LVL}}^k} \right\| = 0 \\& \mathop {\lim }\limits_{t \to \infty } \left\| {v_{\rm{L}}^k(t) - v_{\rm{VL}}^k(t)} \right\| = 0 \end{aligned}\right. $

(6)

即当前集群的真实领导者 ${\rm{L}}$ 与近邻的上一集群的末尾车辆(当前集群的虚拟领导者 ${\rm{VL}}$ )的车间距离形成期望间距 ${r_{\rm{LVL}}}$ ，并且速度保持一致。

证明 　通过求解控制协议(5)所示的微分方程得到车辆的运动轨迹，进而分析控制协议的稳定性和一致性。

控制协议(5)可视为非齐次微分方程，如式(7)所示。

$ \begin{split} & \ddot x_{\rm{L}}^k\left( t \right) + {d_2}\dot x_{\rm{L}}^k\left( t \right) + {d_1}x_{\rm{L}}^k\left( t \right) = \ddot x_{\rm{VL}}^k\left( t \right) +\\&\qquad {d_2}\dot x_{\rm{VL}}^k\left( t \right) + {d_1}\left( {x_{\rm{VL}}^k\left( t \right) + r_{\rm{LVL}}^k} \right) \end{split} $

(7)

求得式(7)的通解为

$ x_{\rm{L}}^k(t) = {(x_{\rm{L}}^k)^ * }(t) + c_{\rm{L}}^kX_{\rm{L}}^k(t) $

(8)

其中， ${(x_{\rm{L}}^k)^ * }(t)$ 为非齐次微分方程的特解，

$ {(x_{\rm{L}}^k)^ * }(t){\rm{ = x}}_{\rm{VL}}^k(t) + r_{\rm{LVL}}^k $

(9)

则通解可表示为

$ x_{\rm{L}}^k(t) = x_{\rm{VL}}^k + r_{\rm{LVL}}^k + c_{\rm{L}}^kX_{\rm{L}}^k(t) $

(10)

其中， $c_{\rm{L}}^k$ 为常系数， $X_{\rm{L}}^k\left( t \right)$ 为方程(11)的通解。

$ \ddot x_{\rm{L}}^k\left( t \right) + {d_2}\dot x_{\rm{L}}^k\left( t \right) + {d_1}x_{\rm{L}}^k\left( t \right) = 0 $

(11)

根据式(7)可得

$ \mathop {\lim }\limits_{t \to \infty } \left\| {X_{\rm{L}}^k} \right\| = 0 $

(12)

根据公式(8)可得

$ c_{{L}}^kX_{\rm{L}}^k\left( t \right) = x_{\rm{L}}^k\left( t \right) - x_{\rm{VL}}^k\left( t \right) - r_{\rm{LVL}}^k $

(13)

因为 $c_{{L}}^k$ 是常系数，根据式(12)~(13)，可推导出

$ \mathop {\lim }\limits_{t \to \infty } \left\| {x_{\rm{L}}^k(t) - x_{\rm{VL}}^k(t) - r_{\rm{LVL}}^k} \right\| = \mathop {\lim }\limits_{t \to \infty } \left\| {c_{\rm{L}}^kX_{\rm{L}}^k(t)} \right\| = 0 $

(14)

进一步可以推导出

$ \mathop {\lim }\limits_{t \to \infty } \left\| {v_{\rm{L}}^k(t) - v_{\rm{VL}}^k(t)} \right\| = \mathop {\lim }\limits_{t \to \infty } \left\| {c_{\rm{L}}^kX_{\rm{L}}^k(t)} \right\| = 0 $

(15)

定理1证毕。

横向控制器如式(16)所示。

$ \left\{ \begin{aligned} & \dot p_i^k\left( t \right) = \omega _i^k\left( t \right) \\& \dot \omega _i^k\left( t \right) = - \sum\limits_{j \in {G_i}(t)} {a_{ij}^k\left[ {{\gamma _5}(p_i^k(t) - p_j^k(t)) + {\gamma _6}(\omega _i^k(t) - \omega _j^k(t))} \right]} - \\ & \;\;\;\;\;\;\;\;\alpha [{\gamma _5}(p_i^k(t) - {\rm{tar}}_i^k) + {\gamma _6}(\omega _i^k(t) - 0)] \end{aligned} \right. $

(16)

其中 $p_i^k,\omega _i^k$ 为集群 $k$ 中车辆 $i$ 的横向位置和横向速度， ${\rm{tar}}_i^k$ 是集群 $k$ 的换道车辆 $i$ 的目标车道横向位置坐标。注意， $G_i(t)$ 与 $N_i(t)$ 是不同的， $G_i(t)$ 是车辆 $i$ 在集群 $k$ 内目标车道上保持直行的邻居车辆集合。 $p_i^k,\omega _i^k$ 是集群 $k$ 的横向位置和横向速度， ${\gamma _5},{\gamma _6}$ 是控制增益，均为非负参数。 $\alpha $ 是权重系数， $\alpha > 0$ 。如果对于车辆 $i$ 在集群 $k$ 内 $G_i^k(t){\rm{ = }}\emptyset $ ，则横向控制器可写为

$ \dot \omega (t) = - \alpha \left[ {{\gamma _5}(p_i^k(t) - p_0^k(t)) + {\gamma _6}(\omega _i^k(t) - \omega _0^k(t))} \right] $

(17)

控制协议(16)的证明过程与控制协议(4)类似，具体可参照文献[23]。

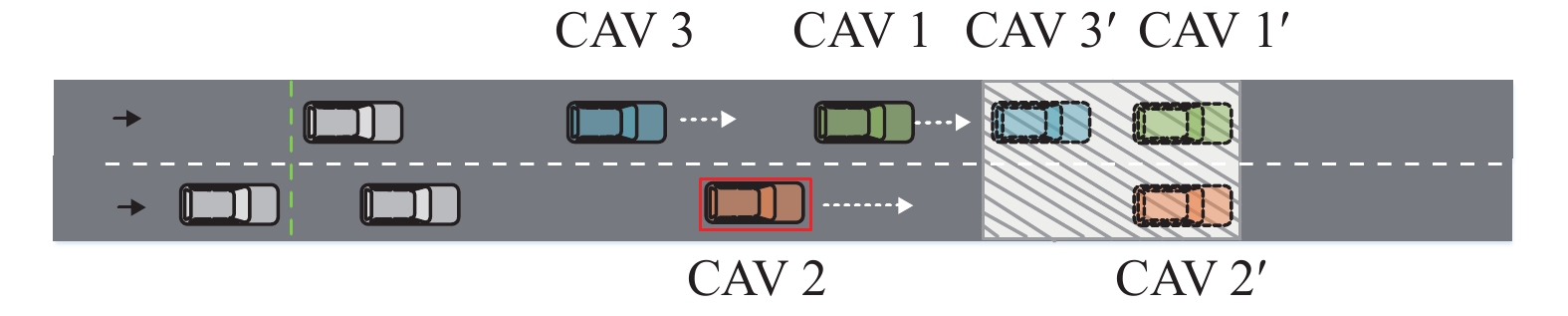
2.3 适应集群空间分配的间距控制算法

本节主要说明决策层处理集群内和集群间车辆换道冲突问题，包括换道车辆与没有换道需求的车辆以及相邻换道车辆之间的冲突。为了解决上述问题，本文将协同换道过程分为两个阶段：稀疏纵向间距阶段和换道阶段。稀疏纵向间距阶段依据本文所提的适应集群空间分配的间距控制算法，车辆按照预定的期望间距进行重新排列，形成稀疏纵向间距的多集群系统，使换道车辆能扩大与前后车辆的间距至合适的换道安全间距。在换道阶段，CAVs从稀疏队形开始，有效地避免了轨迹规划等方法^{[9, 11-14]}由于避碰的高纬度约束导致优化控制函数难以求解的问题。在换道过程中，系统应用纵向的一致性控制协议(4)和控制协议(5)维持CAVs纵向速度不变，将换道控制解耦成单一的横向控制，简化了横向控制器的设计。依据横向控制协议(16)实现安全准确的换道。

智能联网车辆 $i$ 在纵向方向上的期望换道安全定义为 ${R_i}$ ，车辆 $i$ 在纵向方向上的期望跟随安全间距定义为 ${r_i}$ 。车辆间距调整如图3所示。

在每个更新时刻,有换道需求的车辆都会检测当前时刻是否满足换道条件，即当前集群内其他车辆速度收敛一致，且车辆 $i$ 与前后车辆达到安全间距并稳定。如果满足换道条件，进入换道阶段。换道车辆 $i$ 依据控制协议(16)调整横向状态；纵向期望间距维持不变，若此时车辆 $i$ 为集群领导者并且当前集群需要集群间协同，依据控制协议(5)继续运动，否则当前领导者车辆控制输入 $u_{{L}}^k = 0$ ;若此时车辆 $i$ 为跟随者，依据控制协议(4)继续运动。适应集群空间分配的间距控制算法如下所示。

输入：集群 $ {\rm{Group}}_{{k}} $ 内所有车辆状态信息

输出：多车完成协同换道

初始化：

　(1) 定义集群内最大的车辆数目为 $ N $ 辆。

　(2) 对集群 $ {\rm{Grou}}{{\rm{p}}_k} $ 的所有车辆按纵向位置递减排序，纵向位置最大的车辆标记为领导者(true leader)，其他车辆为跟随者(follower)，依次为 $1, \cdots ,N - 1$ 。

过程：

若当前车辆 $ i $ 为集群 $ {\rm{Grou}}{{\rm{p}}_k} $ 的领导者：

(1) 计算车辆 $ i $ 与上一集群 $ {\rm{Group}}_{k-1} $ 纵向距离最小的车辆 $ j $ 的距离 $ {d}_{ij}\left(t\right)=\left|{x}_{i}\left(t\right)-{x}_{j}\left(t\right)\right| $ ，与式(3)中的 $ {d_{i,{\rm{desired}}}} $ 比较；若 $ {d_{ij}}\left( t \right) > {d_{i,{\rm{desired}}}}$ ，则不需要进行集群间协同；否则需要进行集群间协同；

(2) 若考虑集群间协同，与上一个集群 $ {\rm{Group}}_{k-1} $ 的末尾车辆 $ j $ 建立通信，并作为当前集群 $ k $ 的虚拟领导者(virtual leader)；若领导者 $ i $ 或虚拟领导者 $ j $ 有换道需求，则期望间距 $ {r_{{\rm{LVL}}}} = $ $ {R_i} $ ；若领导者 $ i $ 或虚拟领导者 $ j $ 均无换道需求，且行驶在同一车道上，则期望间距 $ {r_{{\rm{LVL}}}} = {r_i} $ ；若领导者 $ i $ 或虚拟领导者 $ j $ 均无换道需求，且行驶在不同车道上，则期望间距 $ {r_{{\rm{LVL}}}} = 0 $ ；

(3) 领导者 $ i $ 依据控制协议(5)调整纵向状态。

若当前车辆 $ i $ 为集群 $ {\rm{Group}}_{k} $ 的跟随者， $ i\in {\rm{Group}}_{k},i= $ $ {1,2},\cdots ,N-1 $ ：

(1) 计算与集群内真实领导者的期望间距：

将车辆 $ i $ 所在原始车道前方车辆标记为 $ {\rm{PO}} $ 。

若当前车辆 $ i $ 有换道需求，则期望间距为 $ {r_{i{\rm{L}}}} = {r_{(i - 1){\rm{L}}}} + {R_i} $ ；

若当前车辆 $ i $ 无换道需求，且当前集群内存在原始车道前方车辆 $ {\rm{PO}} $ ，则期望间距 ${r_{i{\rm{L}}}} = {r_{\left( {{\rm{PO}}} \right){\rm{L}}}} + {r_i}$ ；

若当前车辆 $ i $ 无换道需求，且当前集群内不存在原始车道前方车辆 $ {\rm{PO}} $ ，若领导者无换道需求，则期望间距 ${r}_{i{\rm{L}}}=0$ ；若领导者有换道需求， $ {r}_{i{\rm{L}}}={R}_{i} $ ；

(2)计算与同一集群内邻居车辆 $ j $ 的期望间距 $ {r}_{ij}= $ $ {r}_{i{\rm{L}}}-{r}_{j{\rm{L}}} $ ；

(3)跟随者依据控制协议(4)调整纵向状态；

对集群内的车辆重复执行以上过程。

通过适应集群空间分配的间距控制算法和控制协议(4)，可以实现在集群内车辆纵向速度收敛到一致，达到与真实领导者的期望间距并保持稳定。

$ \left\{ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } \left\| {x_i^k\left( t \right) - x_{\rm{L}}^k\left( t \right) - r_{i{\rm{L}}}^k} \right\| = 0 \\& \mathop {\lim }\limits_{t \to \infty } \left\| {v_i^k(t) - v_{\rm{L}}^k(t)} \right\| = 0 \end{aligned}\right. $

(18)

而对于需要考虑集群间协同的情形，需要考虑虚拟领导者的选取。通过适应集群空间分配的间距控制算法和控制协议(5)可实现集群间主从领导者速度收敛一致，达到期望间距并稳定：

$ \left\{ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } \left\| {x_{\rm{L}}^k\left( t \right) - x_{\rm{VL}}^k\left( t \right) - r_{\rm{LVL}}^k} \right\| = 0 \\& \mathop {\lim }\limits_{t \to \infty } \left\| {v_{\rm{L}}^k(t) - v_{\rm{VL}}^k(t)} \right\| = 0 \end{aligned}\right. $

(19)

在换道阶段，纵向方向上期望间距和速度保持不变，横向期望间距设为目标车道的横向坐标，依据控制协议(16)，横向速度最终收敛为0，横向位置达到目标车道坐标：

$ \left\{ \begin{aligned} & \mathop {\lim }\limits_{t \to \infty } \left\| {p_i^k\left( t \right) - {\rm{tar}}_i^k} \right\| = 0 \\& \mathop {\lim }\limits_{t \to \infty } \left\| {\omega _i^k(t) - 0} \right\| = 0 \end{aligned}\right. $

(20)

3 实验结果与分析

本文以高速公路的出口匝道区域的强制换道为研究背景，聚焦于车辆协同换道策略的研究。车辆的初始纵向和横向位置分别为 $ {\left({76,2}\right)}^{\rm{T}},{\left({68,1}\right)}^{\rm{T}},{\left({64,2}\right)}^{\rm{T}} $ ， $ {\left({62,1}\right)}^{\rm{T}},{\left({56,2}\right)}^{\rm{T}},{\left({49,2}\right)}^{\rm{T}},{\left({36,1}\right)}^{\rm{T}},{\left({25,2}\right)}^{\rm{T}},{\left({16,2}\right)}^{\rm{T}} $ 。所有车辆的初始纵向、横向速度都为 $ {\left({10,0}\right)}^{\rm{T}} $ 。模拟了5辆智能联网车辆的换道情形，分别是CAV3-5,CAV8-9，其中，当目标车道是车道1、车道2时， ${\rm{tar}}_i^k$ 分别为1 m和2 m。

仿真的一些初始条件如下：对于纵向控制器而言，位置差增益参数 $ {\gamma }_{1},{\gamma }_{3} $ 都设为1，速度差增益参数 $ {\gamma }_{2},{\gamma }_{4} $ 都设为2。对于横向控制器而言，位置差增益参数 $ {\gamma }_{5} $ 设为1，速度差增益参数 $ {\gamma }_{6} $ 设为1，目的是让换道过程更加舒适。权重系数 $ \alpha $ 设为3， $\,\beta ,\;\sigma $ 都设为1。换道安全间距 $ {R}_{i} $ 为10 m，跟随安全间距 $ {r}_{i} $ 为10 m。

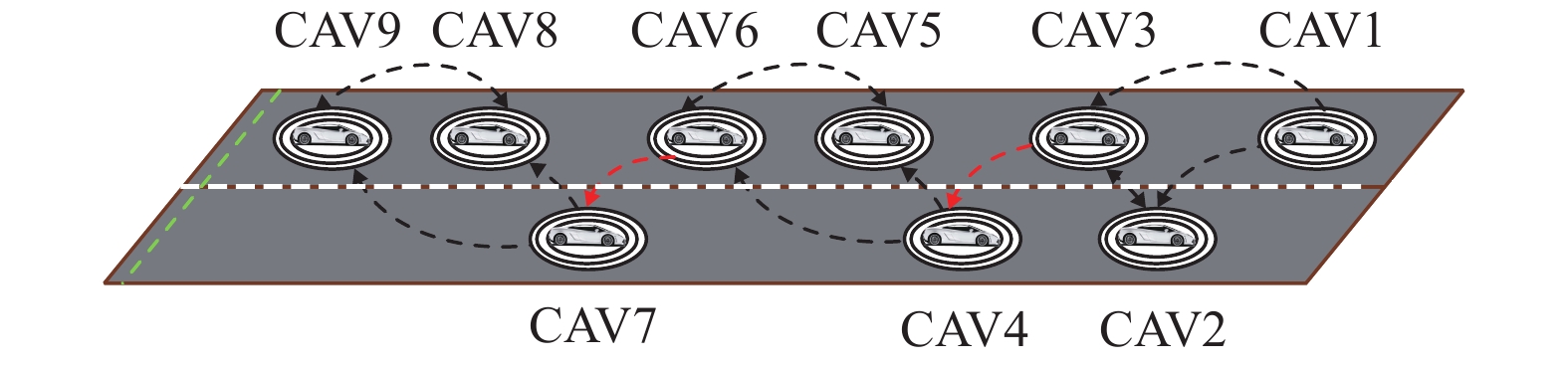
首先，通信层执行分布式集群划分算法，获取车辆所属集群，并依据BDL通信拓扑结构^[18]与集群内其他车辆建立通信。当集群内最大车辆数设为3辆时车辆的网络拓扑结构如图4所示。

紧接着决策层开始工作。适应集群空间分配的间距控制算法给出选取虚拟领导者的条件，若需要，则当前集群的真实领导者L与上一集群的虚拟领导者VL依据PF(Predecessor Following)通信拓扑结构^[18]建立通信，如图4所示。适应集群空间分配的间距控制算法为车辆分配期望间距，以便车辆形成稀疏间距的多集群系统。

此后，控制层在每个更新时刻计算车辆的控制输入。集群内的跟随者车辆依据控制协议(4)更新运动状态，若需要考虑集群间协同，集群内的真实领导者车辆依据控制协议(5)参考上一集群的状态更新控制输入。

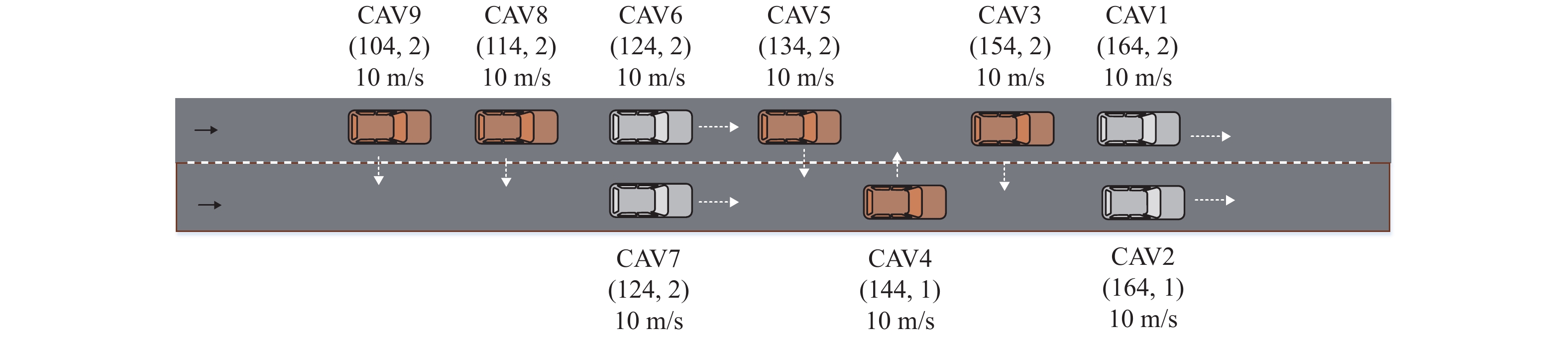
如图5所示，当稀疏纵向间距的多集群系统速度收敛一致，车间间距收敛为期望安全间距并稳定行驶后，进入换道阶段。从稀疏队形开始，换道车辆根据角色选择对应的控制协议，即跟随者应用控制协议(4)，领导者应用控制协议(5)保持纵向速度不变，维持期望间距。同时换道CAVs开始执行横向控制器，选择目标车道并依据控制协议(16)，完成换道操作。

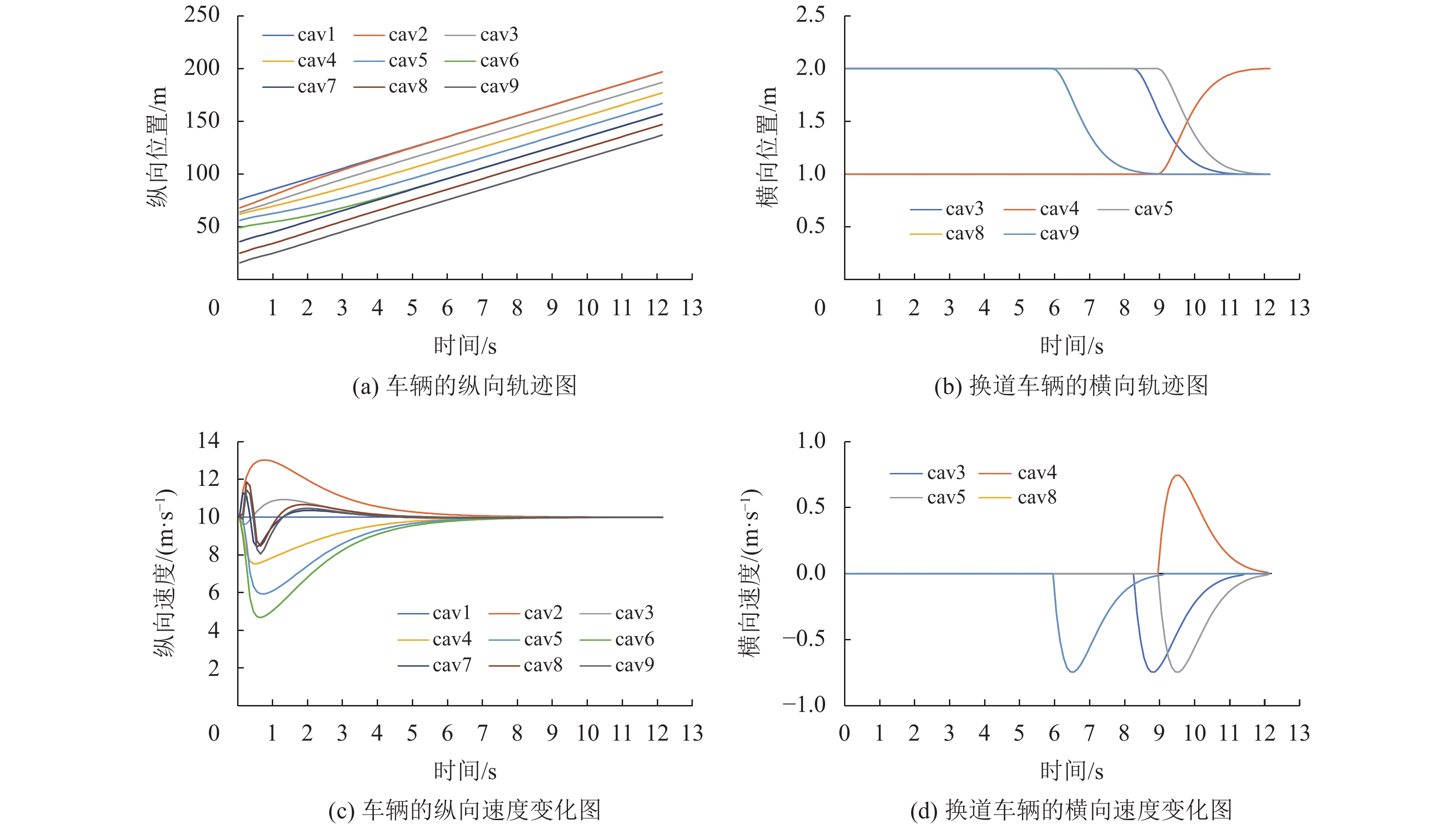
图6是集群内最大车辆数目为3辆时车辆的位置、速度曲线图，其中CAV1-3属于集群1，CAV4-6属于集群2，CAV7-9属于集群3。在稀疏间距阶段，集群1中跟随者与L1的期望间距分别为 $ {\left(0,-1\right)}^{\rm{T}},{(-{10,0})}^{\rm{T}} $ 。集群2中L2与VL2、跟随者与L2的期望间距分别为 $ {\left(-10,-1\right)}^{\rm{T}},{\left(-{10,1}\right)}^{\rm{T}},{\left(-{20,1}\right)}^{\rm{T}} $ ，集群3中L3与VL3、跟随者与L3的期望间距分别为 $ {\left(0,-1\right)}^{\rm{T}},{\left(-{10,1}\right)}^{\rm{T}} $ , $ {(-{20,1})}^{\rm{T}} $ 。图6(a)表明CAVs之间的纵向间距逐渐收敛为期望安全间距稳定行驶。CAV1和CAV2由于没有换道需求并且行驶在不同车道上，根据2.3节算法，两辆CAV纵向间距为0，因此二者的纵向轨迹会有所重合。图6(c)表明CAVs纵向速度最终会收敛一致，其中CAV4作为集群2的领导者且存在换道需求，需要避免与集群1车辆发生交叉碰撞，会执行减速操作扩大间距。图6(b)(d)表明换道车辆以平滑的轨迹成功换道，并且横向速度最终收敛为0。由于换道车辆纵向方向维持换道安全间距，因此整个换道过程是安全的。

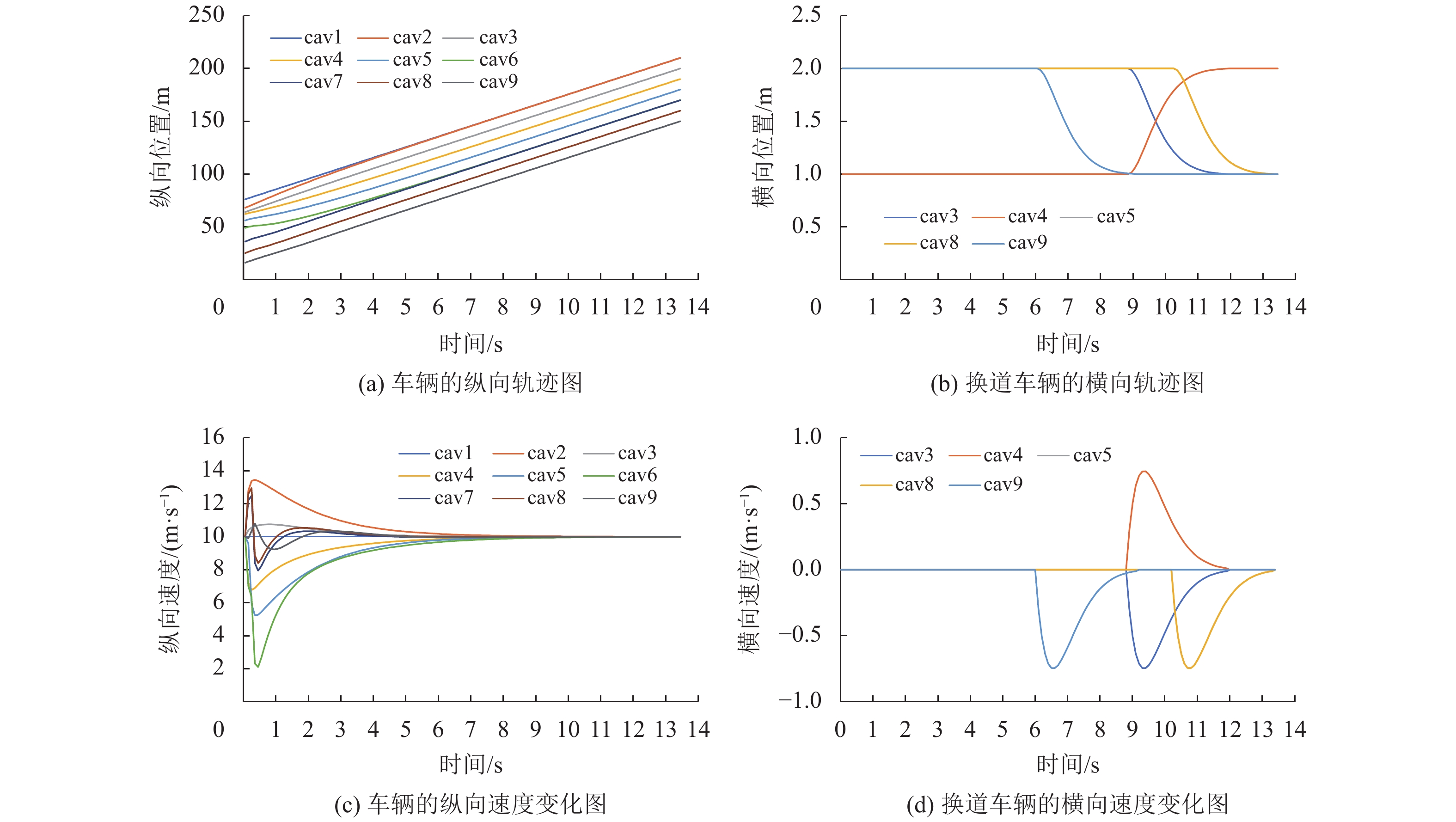
图7是集群内最大车辆数目为4辆时车辆的位置、速度曲线图。其中CAV1-4属于集群1, CAV5-8属于集群2,CAV9属于集群3。在稀疏纵向距离阶段，集群1中跟随者与L1的期望间距分别为 $ {\left(0,-1\right)}^{\rm{T}}, {\left(-10,0\right)}^{\rm{T}}, $ $ {\left(-20,-1\right)}^{\rm{T}} $ 。集群2中L2与VL2、跟随者与L2期望间距分别为 $ {\left(-{10,1}\right)}^{\rm{T}},{\left(-{10,0}\right)}^{\rm{T}},{\left(-10,-1\right)}^{\rm{T}},{\left(-{20,0}\right)}^{\rm{T}} $ ，集群3中L3与VL3的期望间距为 $ {(-{10,0})}^{\rm{T}} $ 。图7(a)(c)表明CAVs最终达到期望间距，纵向速度收敛一致，形成稀疏纵向间距的队形稳定行驶。图7(c)体现所提一致性控制协议能自适应调整车辆状态，如CAV4与CAV3初始间距较小，CAV4减速以扩大到所需换道安全间距；在后续状态中当二者距离过大时，CAV4调整为加速运动。图7(b)(d)换道CAVs横向位置收敛为目标车道，横向速度收敛为0，实现成功换道。但集群1中的车辆在t=9.0 s才开始执行车道变更操作，换道耗时比图6所示情况有所增加。

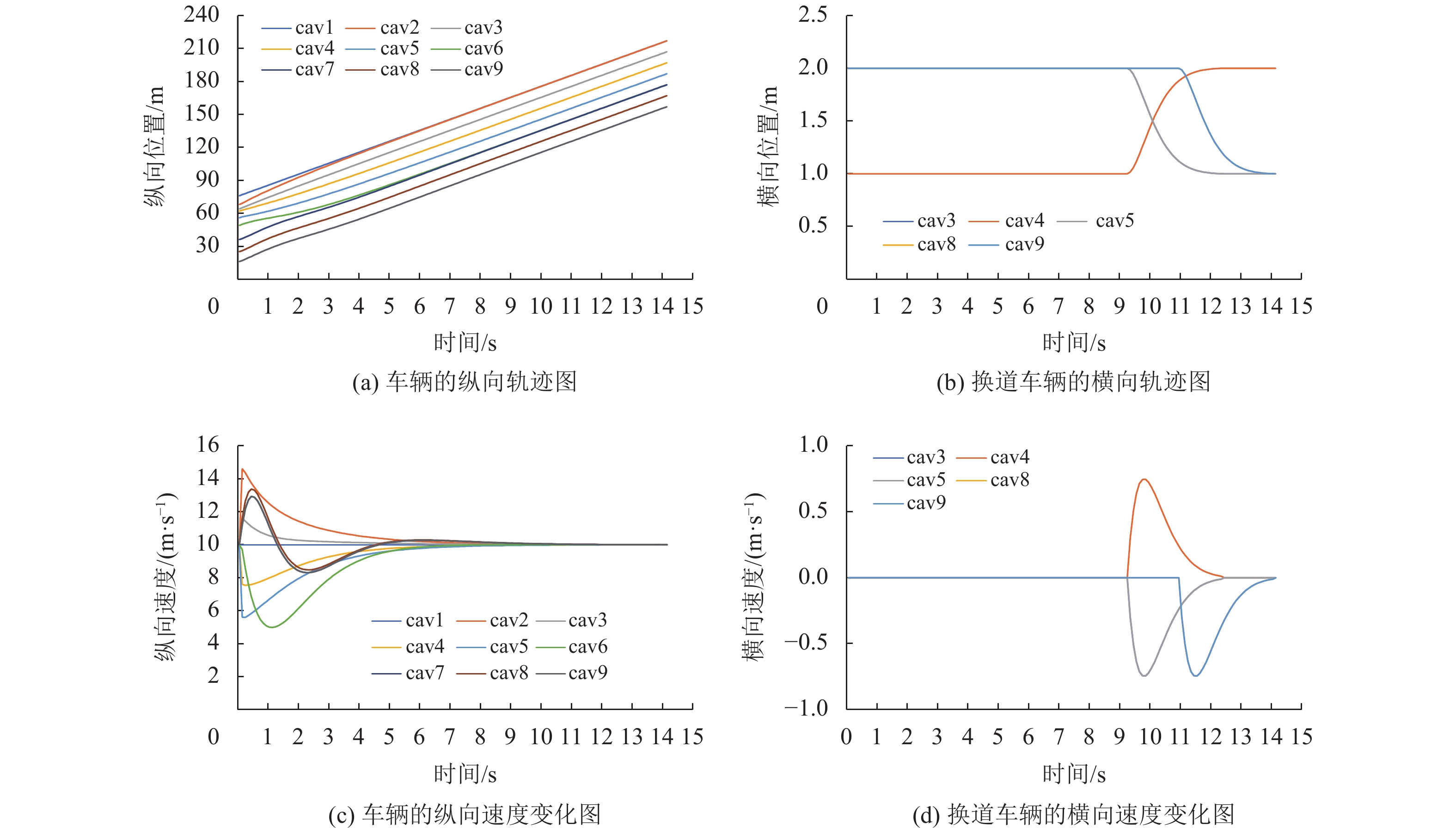
图8是集群内最大车辆数目为5辆时车辆的位置、速度曲线图，CAV1-5属于集群1，CAV6-9属于集群2。在稀疏纵向间距阶段，集群1中跟随者与L1的期望间距为 $ {\left(0,-1\right)}^{\rm{T}},{(-{10,0})}^{\rm{T}},{(-20,-1)}^{\rm{T}},{(-30,0)}^{\rm{T}} $ ,集群2中L2与VL2、跟随者与L2的期望间距分别为 $ {\left(-{10,0}\right)}^{\rm{T}},{\left(0,-1\right)}^{\rm{T}},{\left(-{10,0}\right)}^{\rm{T}},{\left(-{20,0}\right)}^{\rm{T}} $ 。图8(a)(c)速度收敛一致，达到给定的期望间距，先形成稀疏纵向间距的队形行驶再进行换道操作，从而保证换道过程的安全性。图8(b)(d)表示换道CAVs以平滑曲线成功换道到目标车道上，体现出横向控制器的舒适性，横向速度最终收敛0。对比图6和图7所示情况，图8情况下车辆开始换道耗时更长，这是由集群内车辆数目增加，集群内协同耗时更长导致的。根据图8(b)所示，集群1内的车辆在t=9.4 s开始执行换道操作，集群2内的车辆则在t=11.2 s时才执行车道变更。

当集群内最大车辆数目 $ N $ 分别为3、4、5辆时车辆换道所需时间如表1所示。从表1得知，集群内最大车辆数目 $ N $ 为3辆时集群1开始换道耗时、完成换道总耗时均小于其余两种情况。当 $ N $ 为4辆时，集群1开始换道耗时、完成换道总耗时小于 $ N $ 为5辆的情况。从表1的结果并结合图6、图7、图8得知，随着集群内最大车辆数目 $ N $ 的增大，由于控制协议需要参考更多邻居车辆的状态信息以达到期望间距和速度一致，集群内协同耗时更长。

4 总结

本文研究了在智能联网环境下的多车协同控制问题，并以高速公路的出口匝道区域作为研究背景，参考多智能体系统理论，提出一个基于多集群系统的车辆协同框架用于实现出口匝道的强制换道。本文根据所提分布式集群划分算法，将其与适用于集群空间分配的间距控制算法和基于领导者跟随者的集群一致性控制协议结合，应用于多车协同换道的场景。理论分析利用对非齐次微分方程的求解，证明所提控制协议能达到集群内领导者跟随者的局部一致性和集群间主从领导者的群一致性。仿真实验表明，车辆首先收敛一致形成稀疏纵向间距的多集群系统，换道车辆从稀疏队形开始换道直至成功。理论证明结合仿真实验表明所提策略的有效性。