在土建行业中,河砂短缺及河砂价格持续上涨,导致建筑砂浆和商品混凝土单价大幅上涨[1],采用合适的材料代替河砂是目前建筑行业亟需解决的问题。而在石材制品行业,石材加工厂对石材制品进行切割、打磨、抛光等一系列工艺步骤时会产生大量石材污泥废料,通常将其简单掩埋处理,但对生态环境产生严重破坏[2],因而,如何有效处置石材污泥是石材行业亟需解决的难题。
为妥善解决上述行业中存在的难题,将石材污泥加工成石材废渣粉掺入砂浆或混凝土中置换砂石材料为一举两得的低耗减废的可行办法。李古等[3-4]实验表明用石粉代替水泥浆体可以改善砂浆的流动性及强度,有部分学者认为用废石粉部分取代砂可以改善砂浆的和易性,提高力学性能并有助于施工[5-7]。郭育霞等[8]实验表明在混凝土中外掺15%~20%废石粉时,混凝土的力学性能及耐久性最好,代替20%砂时,混凝土的粘聚性和保水性较好[9],研究发现复掺石粉时,自密实混凝土表现出更优异的性能[10]。究其原因,孙虎等[11-12]认为用废石粉作为混凝土掺和料时,优化了混凝土中细集料颗粒级配,提高了混凝土的各项性能。也有研究表明石粉的颗粒形貌是主要因素[13],石粉在砂浆和混凝土中发挥晶核、填充、化学和稀释作用,从而提高水泥基材料的工作性能[14]。
聚丙烯纤维作为一种常见、廉价的纤维制品,掺入到砂浆或混凝土中对其性能有显著影响。有研究表明聚丙烯纤维的掺量及纤维长度对砂浆的流动性和粘附性有负面作用,对粘聚性有正面作用[15-17],而往再生混凝土中掺入聚丙烯纤维能够有效提升其力学性能及耐久性[18-19]。
阅读文献发现,研究人员已开展矿物掺和料和纤维在砂浆中应用的探索,但用石材废渣粉置换标准砂对纤维砂浆流变性能的影响的相关研究尚未展开。有研究表明砂浆的流变性主要受到固体材料比表面积、表面积、固体材料之间空隙率以及水含量等诸多因素的影响[20]。为探索掺入石材废渣粉置换标准砂的纤维砂浆流变性能的控制因素,测量了纤维砂浆的填充密度,并综合考虑固体材料比表面积、表面积、固体材料之间空隙率和液体体积,计算出砂浆的平均液层厚度和平均泥浆层厚度,探索平均液层厚度与平均泥浆层厚度与纤维砂浆流变性能的关系。
1 实验方案 1.1 原材料水泥采用42.5普通硅酸盐水泥,密度为3 127 kg/m3,比表面积为0.364 m2/g;细集料采用标准砂,细度模数为2.48,密度为2 476 kg/m3,比表面积为5.52×10–3 m2/g;石材废渣粉(简称废渣粉)由广东省佛山市利铭蜂窝复合材料有限公司提供的石材污泥在实验室干燥箱100 ℃条件下干燥至恒重,用粉碎机将泥渣块体粉碎,最后经筛分实验得到粒径小于1.25 mm的废渣粉,如图1所示,经测试密度为2 400 kg/m3,比表面积为0.364 m2/g;纤维采用长度为6 mm,直径为31 μm,密度为910 kg/m3的聚丙烯纤维;减水剂采用聚羧酸高效减水剂。从扫描电子显微镜(Scanning Electron Microscope,SEM)图像观察到水泥、废渣粉和标准砂的几何形状极不规则,形貌复杂,如图2所示。经激光粒度分析仪测试,固体颗粒粒径分布见图3,其中废渣粉的粒径最小,远远小于标准砂的粒径。

|
图 1 石材废渣粉图 Figure 1 Images of waste stone powder |

|
图 2 原材料SEM图 Figure 2 SEM images of raw material |
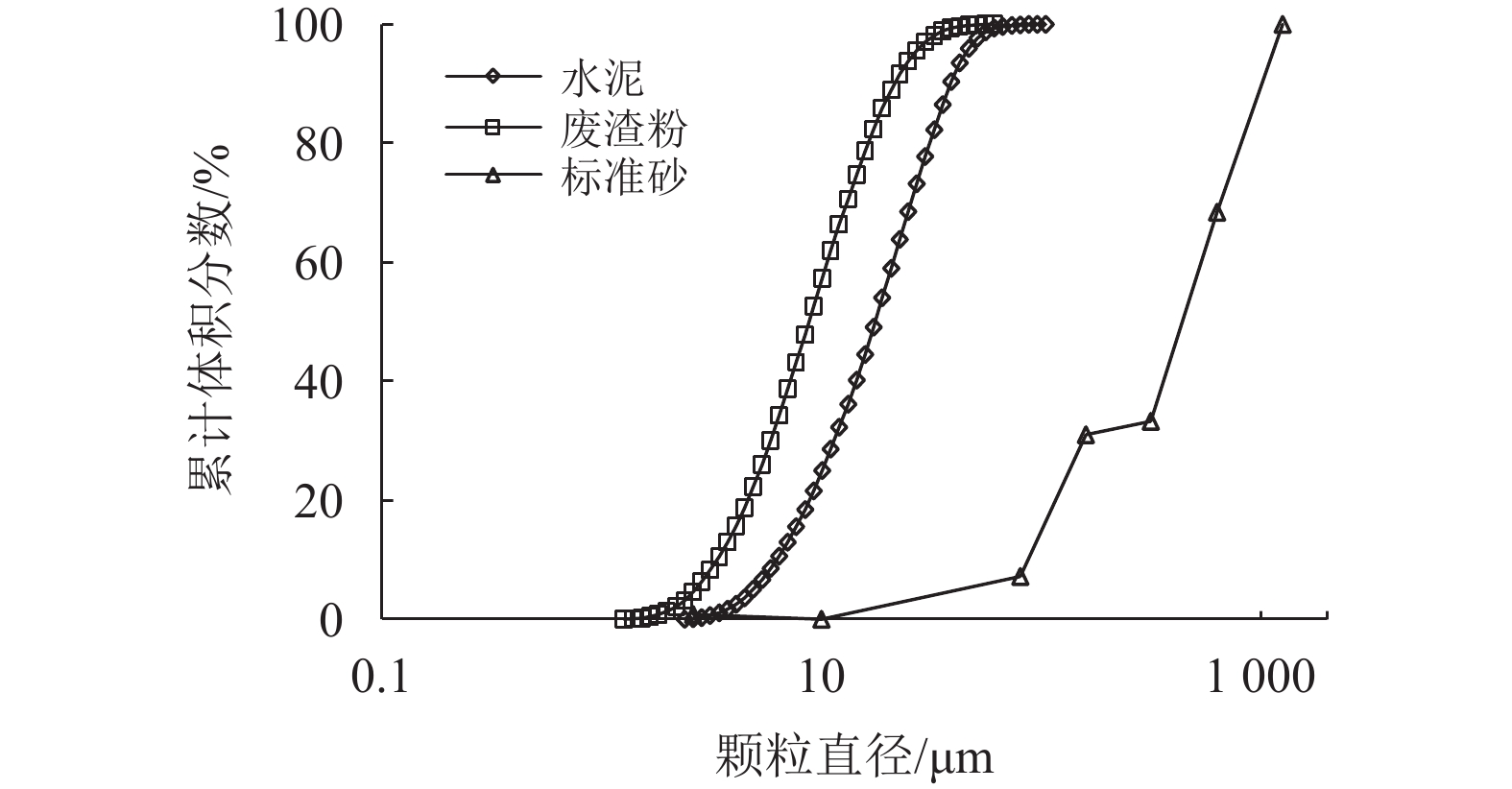
|
图 3 水泥、标准砂和废渣粉的颗粒分布 Figure 3 Particle size distributions of cement, standard sand and waste stone powder |
配制20组不同水灰比、不同废渣粉置换量的纤维砂浆进行测试。纤维掺量为水泥质量的0.2%,减水剂掺量根据水泥和废渣粉颗粒表面积计算,水泥和废渣粉颗粒单位面积上减水剂的质量为2.6×10–5 kg;水泥浆体积比(水泥、水、减水剂的总体积占砂浆总体积比例)为50%,纤维砂浆的水灰比(水与水泥的体积比)从1.0到1.6,以0.2为级差递增,骨料体积比(标准砂和废渣粉的总体积占砂浆总体积的比例)为50%,废渣粉置换标准砂的体积分数为0%~20%,以5%为级差递增。由于在砂浆流变性能中起决定作用的是体积而非质量,水灰比和废渣粉置换量均按体积计算。试块用“X-Y”编号表示,X表示废渣粉置换量(废渣粉置换标准砂的体积分数),Y表示水灰比,具体配比见表1。
| 表 1 砂浆试样配合比 Table 1 Mix design of mortar samples |
砂浆动态流动性采用V型漏斗作流速测试,静态流动性采用小型塌落度筒作扩展度测试。流速为漏斗装满砂浆的体积与砂浆流出时间(流出时间为测量开始至漏斗下端出口初次看见光的时间)的比值;扩展度为装满砂浆的塌落度筒慢慢提起后浆体在两个垂直方向的直径平均值减去筒底的直径。流动性测量在砂浆搅拌完成后5 min内进行。
1.3.2 粘聚性测量砂浆粘聚性采用过筛率的大小来表示。将约300 g砂浆试样倒入型号为1.25 mm的孔筛中,静置2 min后测量孔筛下方托盘中收集的试样质量,则过筛率用托盘中收集的试样质量与倒入孔筛中试样质量的比值来表示。粘聚性测量在砂浆搅拌完成后5 min内进行。
1.3.3 粘附性测量粘附性是指试样粘附在石棒表面的能力,将石棒浸入装有砂浆试样的容器中,然后提起静置2 min后测量石棒的质量,则粘附性为石棒增加的质量与石棒浸入容器中表面积的比值。粘附性测量在砂浆搅拌完成后5 min内进行。
2 测量结果及分析纤维砂浆的流速、扩展度、过筛率和粘附性的测量结果见表2,并在图4中分别绘制了流速、扩展度、过筛率、粘附性与水灰比的变化关系。从图4中可观察到,无论废渣粉置换量如何变化,当水灰比由1.0上升到1.6时,纤维砂浆的流速、扩展度和过筛率均明显提高,而粘附性则一直减小,因此,纤维砂浆的流速、扩展度、过筛率和粘附性均受到水灰比的影响。主要原因是当水灰比较大时,纤维砂浆中液体体积增加,扩大了固体材料间空隙导致纤维砂浆的密实度下降;而多余的液体在纤维砂浆中发挥润滑作用,有助于改善纤维砂浆的性能。
| 表 2 砂浆试样的测量结果 Table 2 Test results of mortar samples |
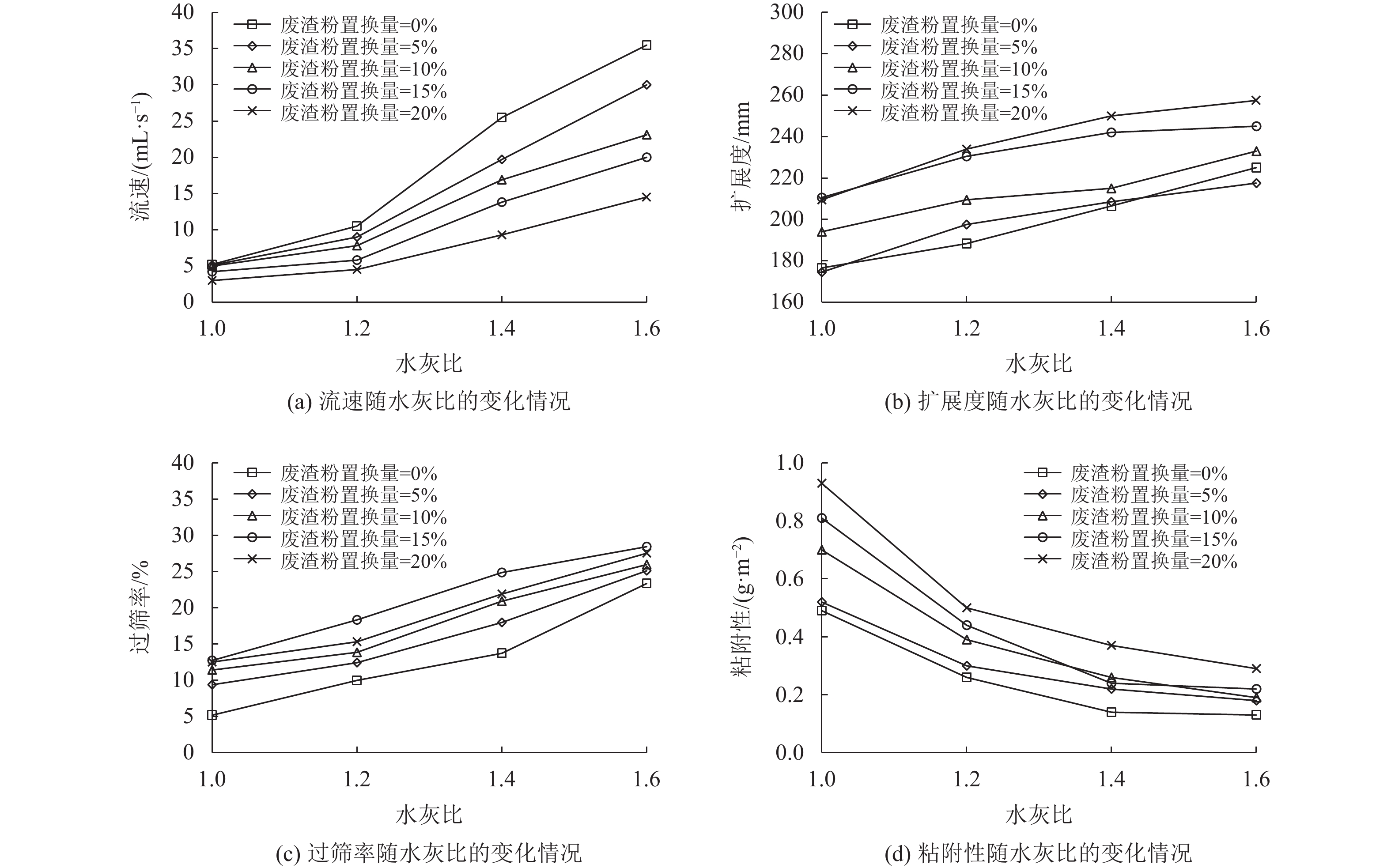
|
图 4 纤维砂浆性能随水灰比变化情况 Figure 4 Variation of properties with water/cement ratio |
观察图4还发现,当水灰比保持不变时,随着废渣粉置换量的提高,纤维砂浆的流速、扩展度、过筛率和粘附性均发生显著变化。当废渣粉置换量由0%提高到20%时,纤维砂浆的流速逐渐变小,而扩展度和粘附性逐渐增大,过筛率则先上升后下降,在15%时达到最大。这主要是因为废渣粉粒径小于水泥和标准砂粒径,随着废渣粉置换量的提高,纤维砂浆中的泥浆体积(水泥和废渣粉浆体的体积)大幅增加,泥浆在纤维砂浆中能够充当润滑剂,改善纤维砂浆的性能。
3 平均液层厚度与平均泥浆层厚度计算方法及结果分析 3.1 填充密度测量固体材料的填充密度采用水测紧密值法[21-23]。首先将固体材料装入搅拌锅中搅拌2 min,然后加入适量水和减水剂再次搅拌2 min,将搅拌完成的纤维砂浆填满体积固定的容器中,则有
| $ \begin{split} m =& {m_{\rm{c}}} + {m_{\rm{p}}} + {m_{\rm{s}}} + {m_{\rm{f}}} + {m_{\rm{w}}} = PV{R_{\rm{c}}}{\rho _{\rm{c}}} + \\& PV{R_{\rm{p}}}{\rho _{\rm{p}}} + PV{R_{\rm{s}}}{\rho _{\rm{s}}} + PV{R_{\rm{f}}}{\rho _{\rm{f}}} + PV{U_{\rm{w}}}{\rho _{\rm{w}}} \end{split}$ | (1) |
式(1)中,m、V分别为纤维砂浆的质量和体积,P为填充率,mc、mp、ms、mf、mw分别为水泥、废渣粉、标准砂、纤维和水的质量,Rc、Rp、Rf、Rs分别为水泥、废渣粉、纤维和标准砂体积与固体材料总体积的比值,Uw为水灰比,ρc、ρp、ρs、ρf、ρw分别为水泥、废渣粉、标准砂、纤维和水的密度。则由式(1)可推导出填充率P的表达式为
| $ P=\frac{m/V}{{R}_{\mathrm{c}}{\rho }_{\mathrm{c}}+{R}_{\mathrm{p}}{\rho }_{\mathrm{p}}+{R}_{\mathrm{s}}{\rho }_{\mathrm{s}}{+R}_{\mathrm{f}}{\rho }_{\mathrm{f}}+{U}_{\mathrm{w}}{\rho }_{\mathrm{w}}} $ | (2) |
逐渐增加水量,重复操作,直至测出最大填充率Pmax,则Pmax即为固体材料的填充密度。水测紧密值法能有效模拟出固体材料在纤维砂浆中的紧密悬浮状态,综合考虑了空气、水、减水剂等影响因素。
3.2 填充密度测量结果填充密度测量结果见表3第2列并在图5中绘制了与废渣粉置换量的变化关系,结果显示在不同水灰比的情况下,随着废渣粉置换量的增加,固体材料的填充密度的变化先增加后减少,当废渣粉置换10%的标准砂时,能够有效改善固体颗粒间级配,提升了砂浆的密实度,固体材料之间空隙体积最小,填充密度达到最大值,进一步增加废渣粉的置换量对填充密度产生负面影响,造成填充密度下降。
| 表 3 砂浆试样填充密度、平均液层厚度及平均泥浆层厚度计算结果 Table 3 Test results of packing density, average liquid thickness and average paste thickness of mortar samples |
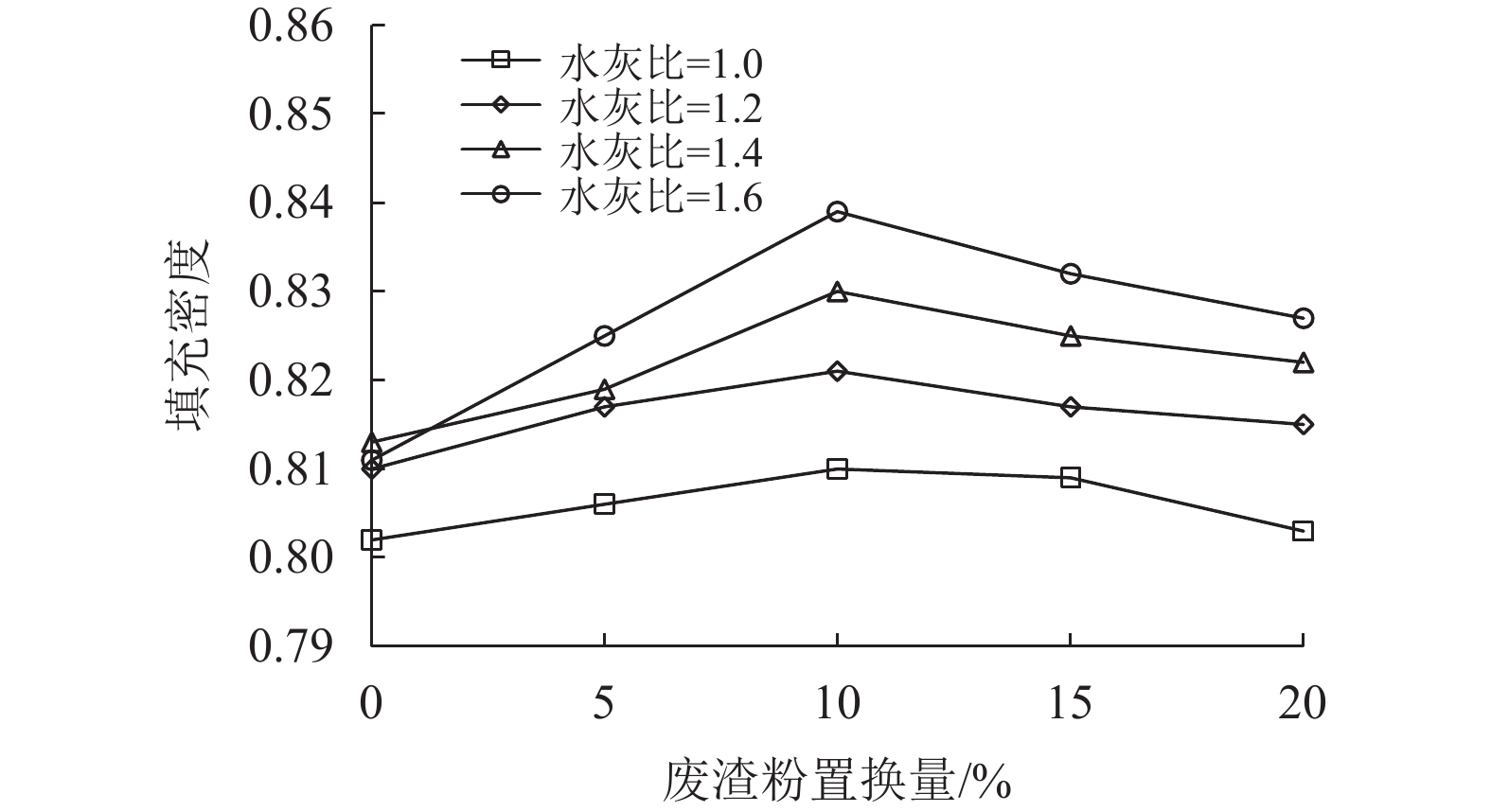
|
图 5 填充密度随废渣粉置换量变化情况 Figure 5 Variation of packing density with waste stone powder content |
测得各组纤维砂浆的填充密度后,结合固体材料的比表面积、剩余液体体积和固体材料间空隙体积可推导出平均液层厚度和平均泥浆层厚度的表达式
| $ h=\frac{{V}_{\mathrm{e}}}{A_{\rm{g}}} $ | (3) |
| $ {V}_{\mathrm{e}}={V}_{\mathrm{n}}-{V}_{\mathrm{k}}$ | (4) |
| $ \mu =\frac{1-{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{P}_{\mathrm{m}\mathrm{a}\mathrm{x}}} $ | (5) |
| $ {V}_{\mathrm{k}}=\mu \left(\frac{{m}_{\mathrm{c}}}{{\rho }_{\mathrm{c}}}+\frac{{m}_{\mathrm{p}}}{{\rho }_{\mathrm{p}}}+\frac{{m}_{\mathrm{s}}}{{\rho }_{\mathrm{s}}}+\frac{{m}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}}\right) $ | (6) |
| $ A_{\rm{g}}=\frac{{m}_{\mathrm{c}}{A}_{\mathrm{c}}}{{\rho }_{\mathrm{c}}}+\frac{{m}_{\mathrm{p}}{A}_{\mathrm{p}}}{{\rho }_{\mathrm{p}}}+\frac{{m}_{\mathrm{s}}{A}_{\mathrm{s}}}{{\rho }_{\mathrm{s}}}+\frac{{m}_{\mathrm{f}}{A}_{\mathrm{f}}}{{\rho }_{\mathrm{f}}} $ | (7) |
其中h为平均液层(泥浆层)厚度,Ve为剩余液体(泥浆)体积,Ag为固体颗粒的比表面积,Vn为实际使用液体(泥浆)体积,Vk为固体材料间空隙体积,μ为空隙比率,mc、mp、ms、mf分别为水泥、废渣粉、标准砂和纤维的质量,ρc、ρp、ρs、ρf分别为水泥、废渣粉、标准砂和纤维的密度,Pmax为填充密度,Ac、Ap、As、Af分别为水泥、废渣粉、标准砂和纤维的比表面积。
3.4 平均液层厚度与平均泥浆层厚度计算结果平均液层厚度和平均泥浆层厚度的计算结果见表3第3、4列并在图6中分别绘制了平均液层厚度、平均泥浆层厚度与水灰比的变化关系。观察图6(a)可发现,当水灰比保持不变时,随着废渣粉置换量的增加,平均液层厚度呈减小趋势。这是由于废渣粉的比表面积远远大于标准砂的比表面积,采用废渣粉置换标准砂之后,固体材料的总比表面积增大,固体材料单位表面积上附着的液体厚度减小,即平均液层厚度减小。
平均泥浆层厚度随水灰比变化情况见图6(b),当水灰比由1.0提高到1.6时,平均泥浆层厚度没有明显变化,然而,随着废渣粉置换量由0%上升到20%,纤维砂浆的平均泥浆层厚度明显增加。这是因为用废渣粉置换标准砂增大了砂浆中的泥浆体积(水泥和废渣粉浆体的体积),同时标准砂体积减小,导致包裹标准砂和聚丙烯纤维的浆体厚度大幅增加,即平均泥浆层厚度增大。
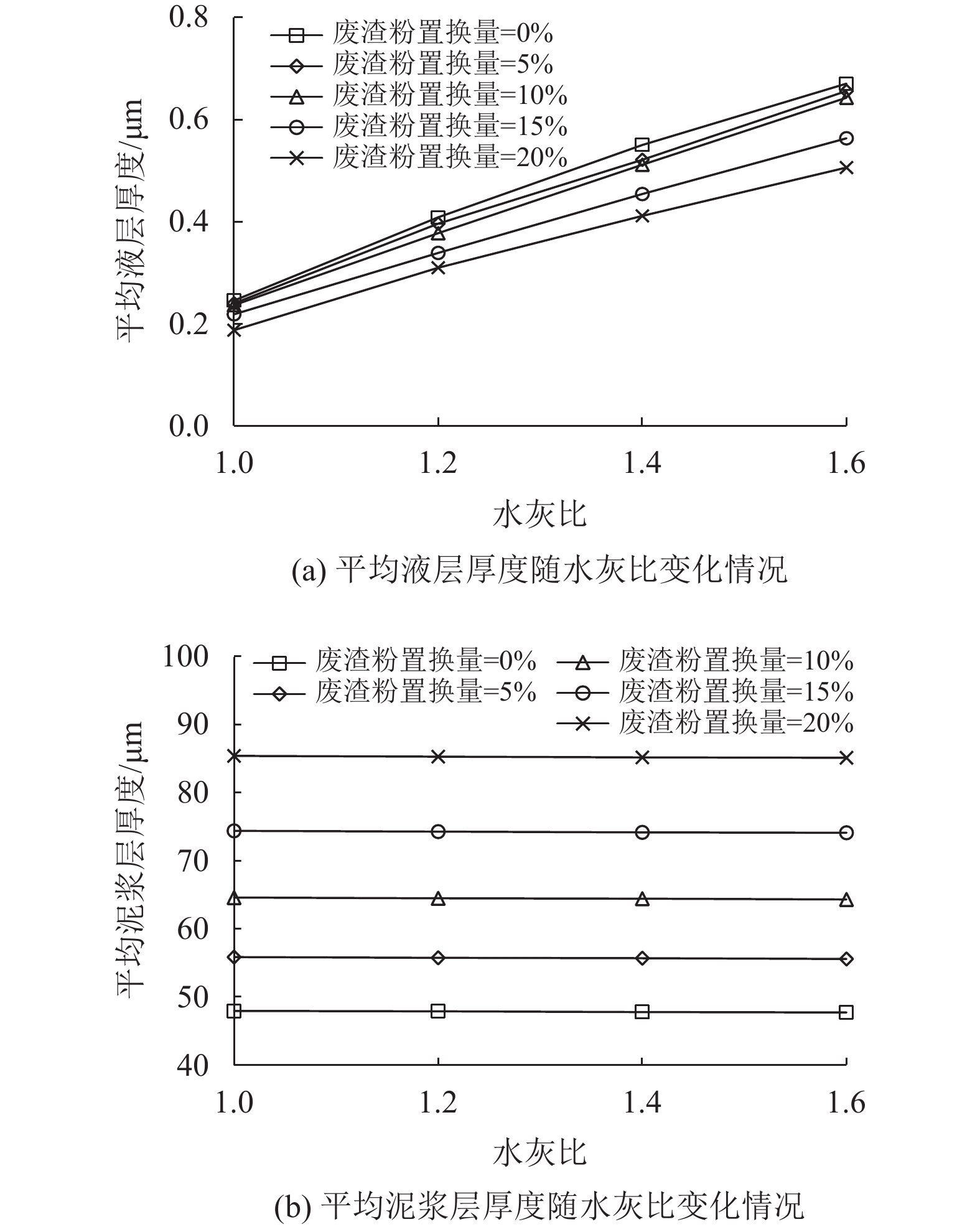
|
图 6 平均液层厚度与平均泥浆层厚度随水灰比变化情况 Figure 6 Variation of average liquid thickness and average paste thickness with water/cement ratio |
纤维砂浆的流速测量结果随平均液层厚度(Average Liquid Thickness,ALT)变化情况见图7。从图中的数据点可观察到,平均液层厚度越大纤维砂浆的流速随之越大,而当平均泥浆层厚度(Average Paste Thickness,APT)提高时,纤维砂浆的流速并没有明显变化。由此可见,纤维砂浆的流速仅受平均液层厚度的影响。
为了定量分析平均液层厚度与平均泥浆层厚度对纤维砂浆流速的控制作用,通过回归分析,拟合曲线及公式见图7。结果显示纤维砂浆的流速随着平均液层厚度的增加而增加,并且增速不断增大,这是因为固体材料表面附着的液层厚度增大,减少了固体材料之间的摩擦力,提高了砂浆的流速。平均液层厚度单一参量与流速的相关系数R2值达到0.940,在拟合公式中加入平均泥浆层厚度参量,结果发现相关系数R2值并没有进一步提高。因此,平均液层厚度是纤维砂浆流速的控制因素,而平均泥浆层厚度没有明显的控制作用。
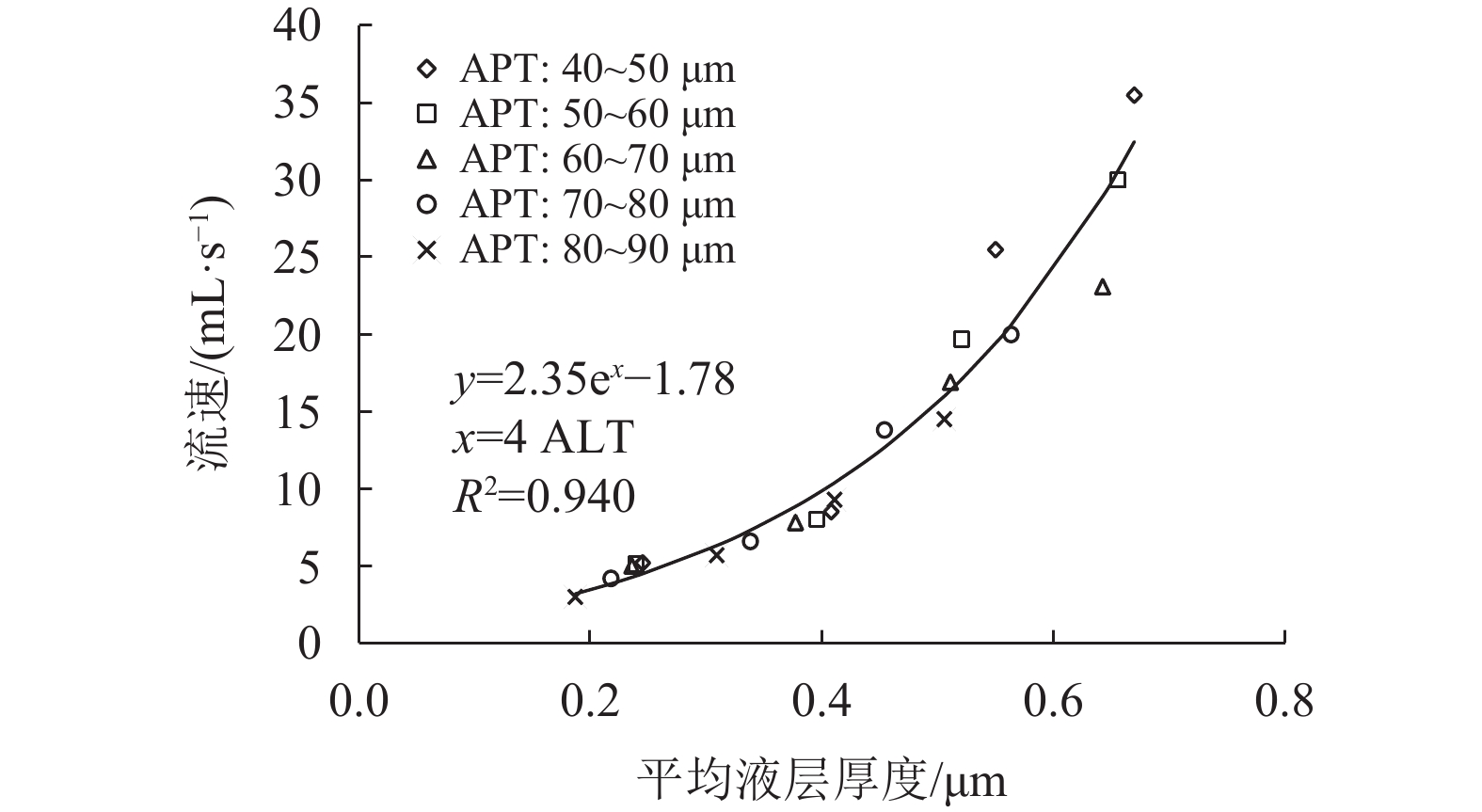
|
图 7 流速随平均液层厚度、平均泥浆层厚度的变化情况 Figure 7 Variation of flow rate with ALT and APT |
纤维砂浆的扩展度随平均液层厚度变化情况见图8。从图8中的数据点可以发现,随着平均液层厚度的提高,纤维砂浆的扩展度逐渐变大,因此,与流速结果相似,纤维砂浆的扩展度也受到平均液层厚度的影响。但是,当纤维砂浆的平均液层厚度保持不变时,随着平均泥浆层厚度的提高,纤维砂浆的扩展度则会进一步增大,所以,纤维砂浆的扩展度也受到平均泥浆层厚度的影响。
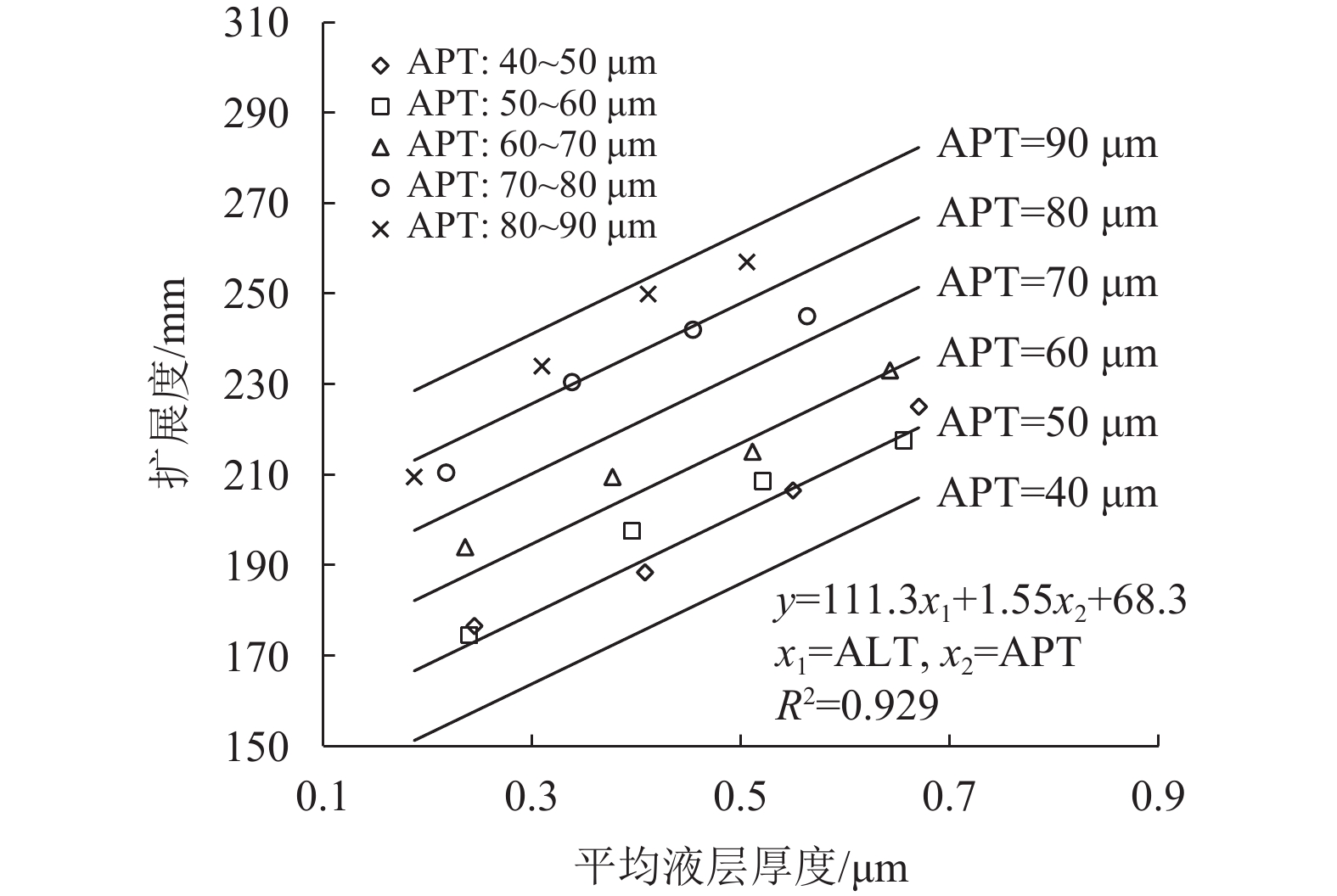
|
图 8 扩展度随平均液层厚度、平均泥浆层厚度的变化情况 Figure 8 Variation of flow spread with ALT and APT |
为了定量研究平均液层厚度与平均泥浆层厚度对纤维砂浆扩展度的共同控制作用,采用回归分析,最佳拟合曲线及公式见图8。结果显示纤维砂浆的扩展度与平均液层厚度呈正比关系,当平均泥浆层厚度由40 μm增加到90 μm时,拟合曲线向上平移产生更大的扩展度。究其原因,采用废渣粉置换等体积的标准砂会显著增加泥浆体积,提高了标准砂和纤维表面的泥浆层厚度,同时,标准砂体积减小使其骨架作用减弱,较厚的平均泥浆层厚度更加有利于减小固体材料之间相互作用力,提高纤维砂浆的扩展度。平均液层厚度和平均泥浆层厚度与扩展度的相关系数R2值达到0.929,因此,纤维砂浆的扩展度受平均液层厚度和平均泥浆层厚度的共同控制。
4.3 对粘聚性的作用过筛率随平均液层厚度变化情况见图9。从图9中数据点发现,纤维砂浆的平均液层厚度越大往往会有更高的过筛率,所以,粘聚性受到平均液层厚度的影响。同时,图9中的数据点还显示,在平均液层厚度保持不变时,平均泥浆层厚度越大,纤维砂浆的过筛率则越高,因此,粘聚性也会受到平均泥浆层厚度的影响。
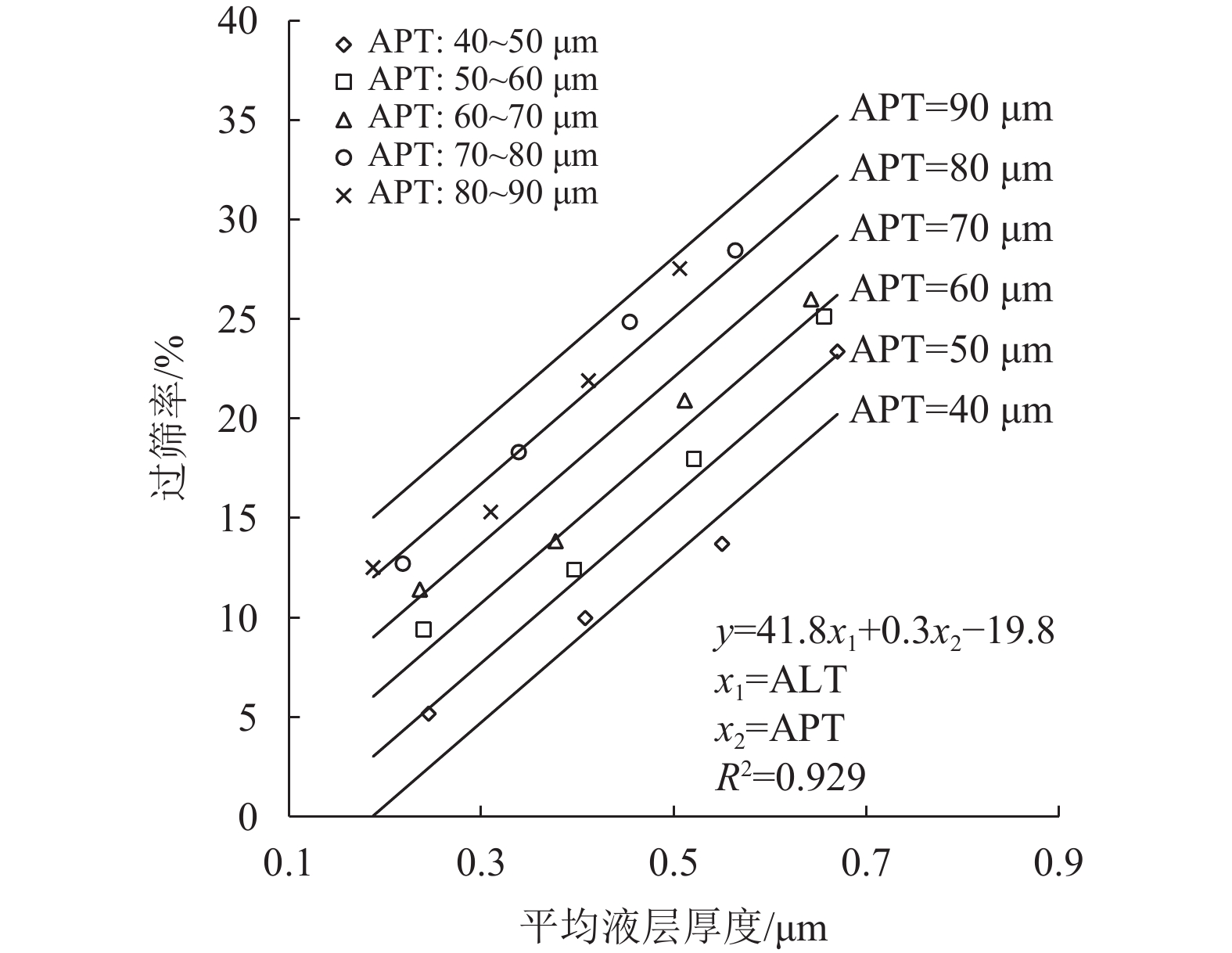
|
图 9 过筛率随平均液层厚度、平均泥浆层厚度的变化情况 Figure 9 Variation of sieve segregation index with ALT and APT |
为了定量研究平均液层厚度与平均泥浆层厚度对纤维砂浆过筛率的共同控制作用,采用回归分析,最佳拟合曲线及拟合公式见图9。结果显示纤维砂浆的粘聚性与平均液层厚度呈正比关系,当平均泥浆层厚度由40 μm提高到90 μm时,拟合曲线向上平移产生了更大的过筛率,因此,平均液层厚度和平均泥浆层厚度对纤维砂浆的粘聚性产生不利的影响。这是因为采用废渣粉置换等体积的标准砂提高了标准砂和纤维表面的泥浆层厚度,泥浆能够更好地发挥润滑作用,加速固体材料穿过孔筛,提高过筛率,降低了砂浆的粘聚性。平均液层厚度和平均泥浆层厚度与过筛率的相关系数R2值达到0.929,因此,纤维砂浆的粘聚性受平均液层厚度和平均泥浆层厚度的共同控制。
4.4 对粘附性的作用石棒粘附性随平均液层厚度变化情况见图10。图10中数据点显示,随着纤维砂浆平均液层厚度变大,粘附性逐渐降低,但是,无论平均泥浆层厚度如何变化,纤维砂浆的粘附性并没有显著的变化。所以,纤维砂浆粘附性仅受平均液层厚度的影响。
为了定量分析平均液层厚度与平均泥浆层厚度对纤维砂浆粘附性的共同控制作用,通过曲线拟合分析,最佳拟合曲线及拟合公式见图10。结果表明随着平均液层厚度提高,纤维砂浆的粘附性呈逐渐减小的趋势,主要原因是随着固体材料表面附着的液层厚度提高,有利于减小固体材料与石棒表面的摩擦力。平均液层厚度单一参量与粘附性相关系数R2值已经达到0.921。在拟合公式中加入平均泥浆层厚度参量,相关系数R2值并未有明显提高,因此,纤维砂浆的粘附性主要受到平均液层厚度的控制作用,而平均泥浆层厚度并没有明显的控制作用。
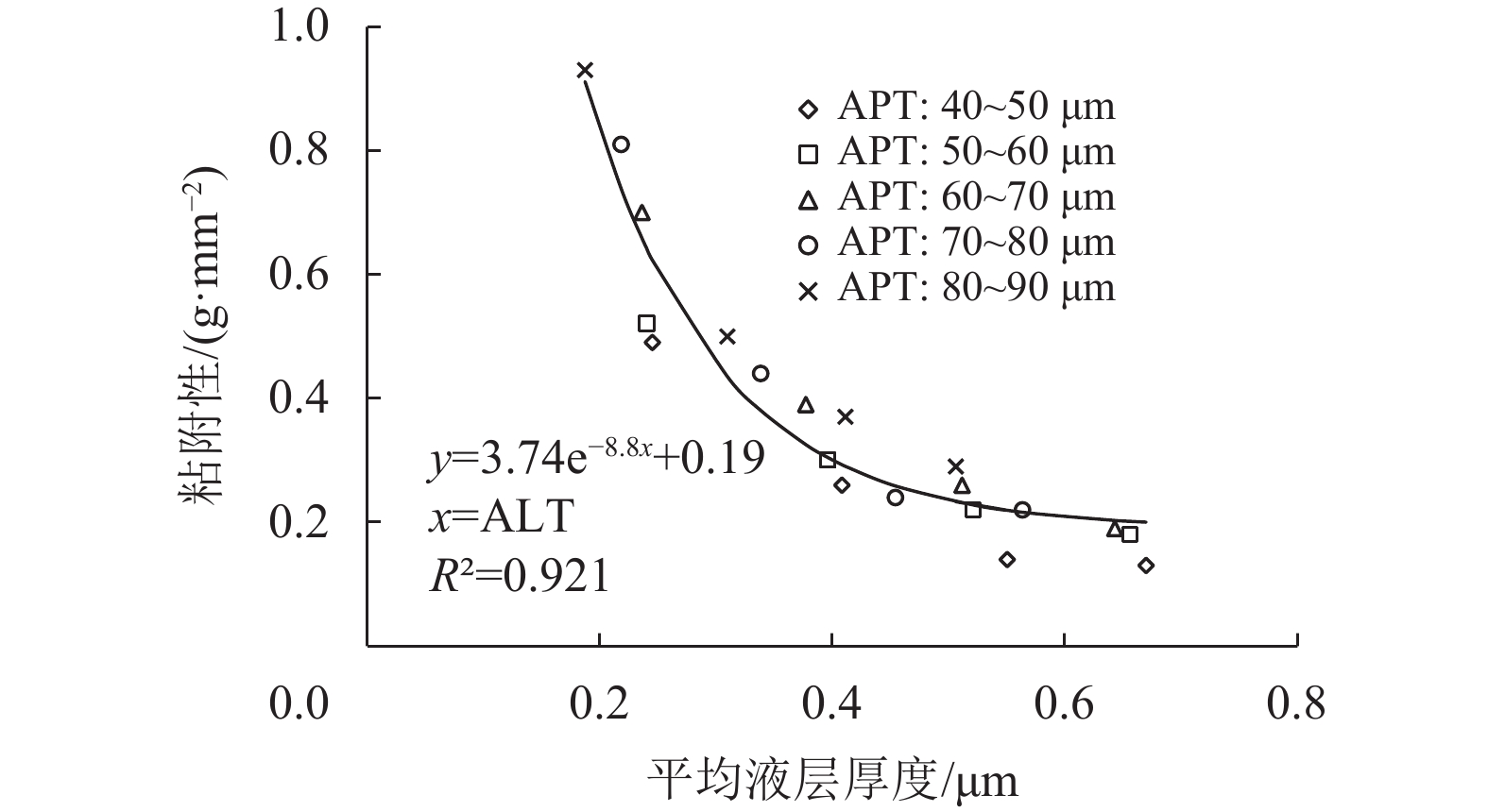
|
图 10 粘附性随平均液层厚度、平均泥浆层厚度的变化情况 Figure 10 Variation of adhesion with ALT and APT |
通过测量20组不同水灰比、不同置换量的废渣粉对纤维砂浆流动性、粘聚性、粘附性和填充密度的影响,以及计算各组砂浆的平均液层厚度和平均泥浆层厚度,得到以下的主要结论。
(1) 随着废渣粉置换量的增加,纤维砂浆的扩展度和粘附性的测量结果呈上升趋势,而流速呈下降趋势,过筛率则先增加后减少,当废渣粉置换量在15%的时候过筛率最大,即粘聚性最差。
(2) 用废渣粉置换等体积的标准砂可以有效提高固体材料的填充密度,10%是最佳置换体积。
(3) 纤维砂浆的流速和粘附性根本控制因素是平均液层厚度,流速和粘附性与平均液层厚度的相关系数R2值分别达到0.940、0.921;而扩展度和粘聚性的根本控制因素是平均液层厚度和平均泥浆层厚度,扩展度和粘聚性与平均液层厚度和平均泥浆层厚度的相关系数R2值均为0.929。
| [1] |
中国砂石协会. 全国各地砂石价格和供需关系分析及对混凝土价格的影响[J]. 商品混凝土, 2018(7): 9-10.
|
| [2] |
王刚. 工业设计视角下石材工业余料的升级利用探析[J].
装饰, 2017(11): 130-131.
WANG G. Exploration on upgrading of leftover material in stone industry from the industrial design perspective[J]. Art and Design, 2017(11): 130-131. DOI: 10.3969/j.issn.0412-3662.2017.11.031. |
| [3] |
LI L G, WANG Y M, TAN Y P, et al. Adding granite dust as paste replacement to improve durability and dimensional stability of mortar[J].
Powder Technology, 2018, 333: 269-276.
DOI: 10.1016/j.powtec.2018.04.055. |
| [4] |
王宇谋. 花岗岩石粉对砂浆性能的影响研究[D]. 广州: 广东工业大学, 2018.
|
| [5] |
鞠丽艳, 张雄. 废石粉在商品砂浆中的应用研究[J].
新型建筑材料, 2002(12): 42-43.
DOI: 10.3969/j.issn.1001-702X.2002.12.019. |
| [6] |
周鹏. 切割花岗岩石粉对干混砌筑砂浆性能的影响[J].
福建建材, 2015(12): 13-14.
|
| [7] |
杨舜龙, 张春成, 栾亚红, 等. 石粉对机制砂自密实砂浆性能的影响[J].
商品混凝土, 2018(11): 41-44.
YANG S L, ZHANG C C, LUAN Y H, et al. Effect of stone powder on the performance of manufactured-sand self-compacting mortar[J]. Ready-Mixed Concrete, 2018(11): 41-44. |
| [8] |
郭育霞, 贡金鑫, 李晶. 石粉掺量对混凝土力学性能及耐久性的影响[J].
建筑材料学报, 2009, 12(3): 266-271.
GUO Y X, GONG J X, LI J. Influence of mass fractions of limestone powder on mechanical property and durability of concrete[J]. Journal of Building Materials, 2009, 12(3): 266-271. DOI: 10.3969/j.issn.1007-9629.2009.03.003. |
| [9] |
霍曼琳, 王娅丽, 肖瑜, 等. 采石场废弃石粉对混凝土基本性能影响的试验研究[J].
兰州交通大学学报, 2015, 34(4): 57-61.
HUO M L, WANG Y L, XIAO Y, et al. A Study on the influencing of waste stone powder produced in quarries on concrete basic performance[J]. Journal of Lanzhou Jiaotong University, 2015, 34(4): 57-61. DOI: 10.3969/j.issn.1001-4373.2015.04.011. |
| [10] |
SADEK D M, EL-ATTAR M M, ALI H A. Reusing of marble and granite powders in self-compacting concrete for sustainable development[J].
Journal of Cleaner Production, 2016, 121: 19-32.
DOI: 10.1016/j.jclepro.2016.02.044. |
| [11] |
孙虎. 石材加工业废料在水泥混凝土工业中的应用研究[D]. 广州: 华南理工大学, 2010.
|
| [12] |
陈家珑. 合理利用人工砂中的石粉[J].
新型建筑材料, 2004(5): 48-50.
DOI: 10.3969/j.issn.1001-702X.2004.05.020. |
| [13] |
任静. 石屑对混凝土性能影响的研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
|
| [14] |
史才军, 王德辉, 贾煌飞, 等. 石灰石粉在水泥基材料中的作用及对其耐久性的影响[J].
硅酸盐学报, 2017, 45(11): 1582-1593.
SHI C J, WANG D H, JIA H F, et al. Role of limestone powder and its effect on durability of cement-based materials[J]. Journal of the Chinese Ceramic Society, 2017, 45(11): 1582-1593. |
| [15] |
LI L G, ZHAO Z W, ZHU J, et al. Combined effects of water film thickness and polypropylene fibre length on fresh properties of mortar[J].
Construction and Building Materials, 2018, 174: 586-593.
DOI: 10.1016/j.conbuildmat.2018.03.259. |
| [16] |
LI L G, ZHAO Z W, ZHU J, et al. Roles of water film thickness and polypropylene fibre content in fresh properties of mortar[J].
Advances in Cement Research, 2017, 29(2): 71-80.
DOI: 10.1680/jadcr.16.00102. |
| [17] |
LI L G, CHU S H, ZENG K L, et al. Roles of water film thickness and fibre factor in workability of polypropylene fibre reinforced mortar[J].
Cement and Concrete Composites, 2018, 93: 196-204.
DOI: 10.1016/j.cemconcomp.2018.07.014. |
| [18] |
刘华新, 杨剑伟, 王学志, 等. 纤维材料与再生混凝土组合应用研究进展[J].
硅酸盐通报, 2017, 36(2): 507-514.
LIU H X, YANG J W, WANG X Z, et al. Research progress on fiber materials and recycled concrete combination application[J]. Bulletin of The Chinese Ceramic Society, 2017, 36(2): 507-514. |
| [19] |
冯玲. 聚丙烯纤维再生混凝土的力学性能试验研究[D]. 西安: 西安建筑科技大学, 2012.
|
| [20] |
KWAN A K H, LI L G. Combined effects of water film thickness and paste film thickness on rheology of mortar[J].
Materials and Structures, 2012, 45(9): 1359-1374.
DOI: 10.1617/s11527-012-9837-y. |
| [21] |
温梦丹, 陈嘉健, 高御审, 等. 基于水膜厚度假设分析磨细高炉矿渣对水泥浆性能影响[J].
广东工业大学学报, 2018, 35(4): 119-126.
WEN M D, CHEN J J, GAO Y S, et al. Effect of ground granulated blast furnace slag on properties based on analysis of water film thickness hypothesis[J]. Journal of Guangdong University of Technology, 2018, 35(4): 119-126. |
| [22] |
WONG H H C, KWAN A K H. Packing density of cementitious materials: part 1—measurement using a wet packing method[J].
Materials and Structures, 2008, 41(4): 689-701.
DOI: 10.1617/s11527-007-9274-5. |
| [23] |
KWAN A K H, WONG H H C. Packing density of cementitious materials: part 2—packing and flow of OPC+PFA+CSF[J].
Materials and Structures, 2008, 41(4): 773-784.
DOI: 10.1617/s11527-007-9281-6. |
 2021, Vol. 38
2021, Vol. 38

