自1980年至今，SLAM(即时定位与地图构建)^[1-3]一直都是计算机视觉和机器人领域的热门研究方向，广泛应用于需要实时定位的设备比如移动机器人、无人机^[4]、自动驾驶汽车^[5-6]以及增强现实/虚拟现实^[7]等。现有的SLAM算法中涵盖了多种不同类型的传感器，比如相机、激光雷达、GPS或者惯性测量单元(Inertial Measurement Unit, IMU)等。由于相机具有成本低、普及率高并且可被动地获取丰富的环境信息等优点，因此基于相机的视觉SLAM研究成为热点。

视觉SLAM主要由前端和后端两部分组成：前端实现对相机的跟踪，根据当前地图全局定位相机^[7-10]，也可以根据视觉里程计本地定位相机^[11-12]。后端创建和维护关键帧地图并通过闭环检测和地图优化减少全局误差。

现有的视觉SLAM算法可以分为间接法和直接法，其中间接法通过对图像提取特征点，实现对相机的定位和环境地图的构建，但只用少量的特征点代替一整幅图像导致重建的环境地图非常稀疏，无法用于机器人等设备导航^[8-9]。尽管ORB-SLAM3^[10]采用IMU和相机紧耦合的方式提高了定位精度^[8-9]，并且利用新的回环方式减少系统整体的累积误差，但是其纯双目版本的性能并无改善。此外，特征点的SLAM方法会耗费大量时间进行特征提取，并且对于弱纹理场景不具备很好的鲁棒性。鉴于特征点这些缺点，文献[12]提出了一种直接法的SLAM算法，直接基于图像所有像素点和边缘进行处理，实现对相机的定位和环境地图构建，并且构建出非常稠密的环境地图。然而，重建非常稠密的环境地图需要消耗大量的计算资源，不适用于一般的移动设备，比如增强现实、虚拟现实、无人机等。因此，文献[13]提出一种基于直接法的稀疏里程计方法(Direct Sparse Odometry, DSO)，通过提取图像中梯度较大的点进行相机定位，在后端采用滑动窗口和边缘化技术对相机位姿和环境点云进行优化，实现相对稠密的环境重建以及定位，同时达到较高的帧率。然而，采用直接法、滑动窗口和边缘化技术的直接稀疏里程计目前仍然存在许多挑战，比如在室内环境中运行时无法产生具有绝对尺度的定位结果和环境重建，在室外场景中运行时会产生严重的尺度漂移问题。双目DSO通过引入双目约束，解决了单目DSO中的尺度不确定性和大尺度环境下漂移的问题，但其深度初始化效率低，且并未在运动估计初值时引入双目约束，无法得到较好的绝对尺度信息^[14]。

针对上述问题，本文提出一种基于双目强约束的直接稀疏视觉里程计。主要的工作如下：

(1) 提出一种新的双目初始化方案，通过对梯度点提取快速描述子，采用绝对误差和算法(Sum of Absolute Differences, SAD)在极线方向搜索最优匹配点，利用归一化积相关算法(Normalized Cross Correlation, NCC)进行验证，实现了快速的双目初始化。

(2) 基于双目相机固定基线长度设置阈值，根据梯度点的初始深度值将所有点划分为近点和远点两种类型。对远点和近点分别赋予不同的深度范围，深度滤波器在帧间滤波时可以快速收敛到其真实值。

(3) 在估计移动机器人运动初值时，引入双目约束，增强运动估计阶段的绝对尺度信息，使得移动机器人在定位精度上得到显著提高。

(4) 与现有方法相比，本文所提出的方法无需提取特征点，对于弱纹理场景具有较好的鲁棒性。优化目标函数包含所有远点和近点，极大提高了移动机器人定位的旋转准确率。实验结果表明，本文提出的方案在直接法SLAM中，如Stereo DSO与LSD-SLAM2，定位精度上达到了先进水平，而相比特征点法的SLAM方案，本文方案达到了与ORB-SLAM3相近的水平。

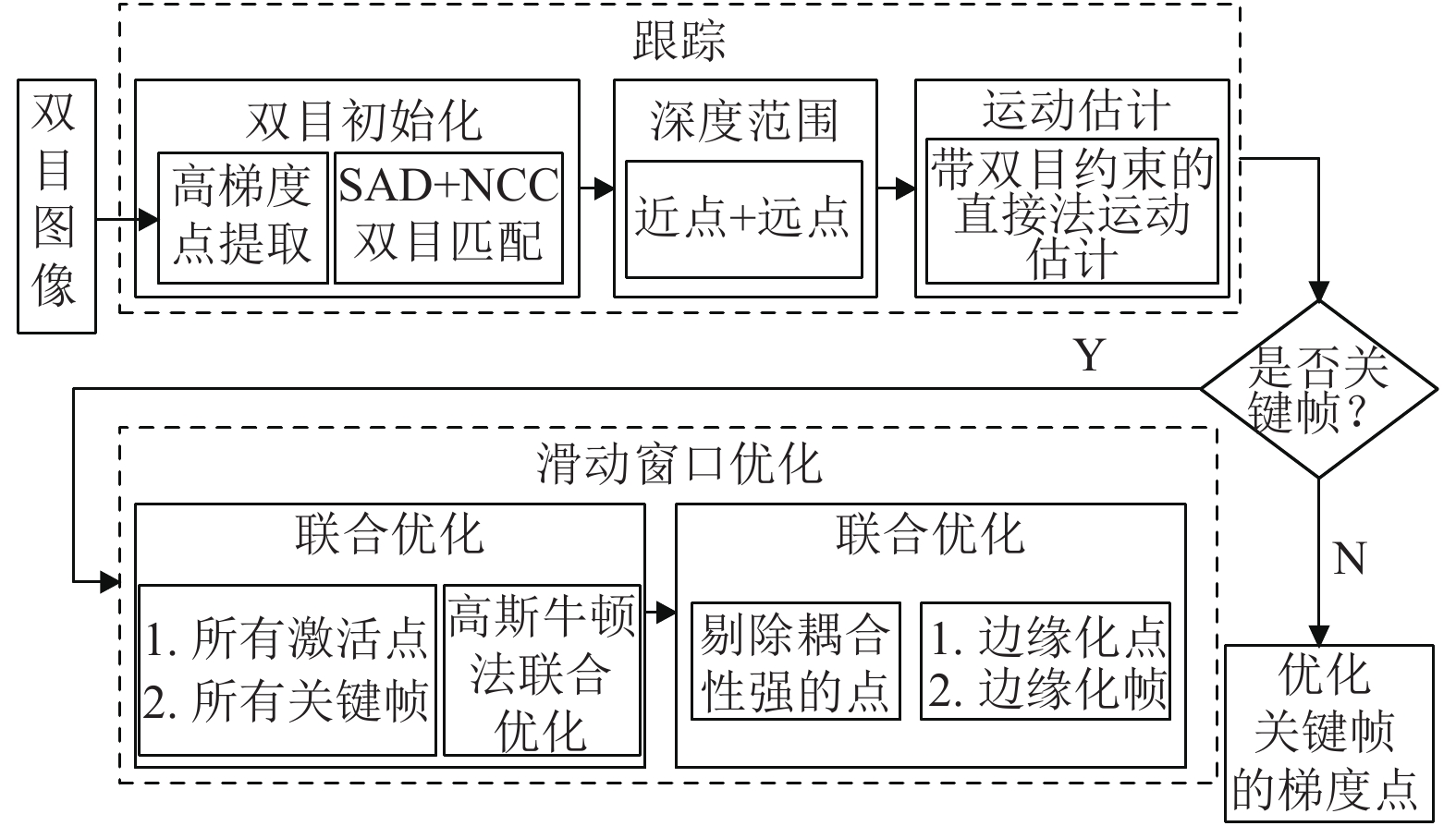
1 本文方法 1.1 系统框架

本文提出的基于双目强约束的直接稀疏视觉里程计系统流程如图1所示。

系统的输入是双目图像对，通过对左帧图像网格化，并在每个网格中计算梯度信息，得到期望的关键点。结合SAD以及NCC双步骤验证的方式进行双目图像初始化，得到每个关键点的初始深度值。

基于图像双目固定基线长度设置参考阈值，根据初始深度值将所有关键点划分成近点和远点。由于双目相机的固定基线长度较短，对于近距离的点深度估计较为准确，因此近距离的点初始深度范围被限制得比较小。远距离的点深度直接由双目相机估计会产生较大的误差，需要融合较多相邻帧的信息做深度优化，因此远距离的点初始化深度范围设置得相对比较大。

在估计相对运动初值时，引入双目相机约束，从而更准确地估计绝对尺度。

在系统后端，所有模型参数包括相机固有参数、所有关键帧的相机位姿以及所有关键点的深度值，都在一个滑动窗口中联合优化。为了在滑动窗口中保持固定数量的关键帧和激活点，系统采用了边缘化的操作，以保持数据关联的一致性。

1.2 Two-stages双目初始化

为了获得跟踪阶段需要的初始深度图像，文献[14]采用NCC的双目匹配方式^[15]实现双目初始化。对于左帧图像 ${I_{\rm{L}}}$ 中检测到的每个关键点 $p$ ，沿着极线方向在右帧图像 ${I_{\rm{R}}}$ 计算NCC匹配分数，搜索最优匹配点 $q$ 。对于每一个 ${\rm{3}} \times {\rm{5}}$ 的图像块M，NCC度量相似性的计算方法如式(1)所示。

$ {S_{{\rm{NCC}}}} = \frac{{\displaystyle \sum\limits_{{p_i} \in {M_p}} {\displaystyle \sum\limits_{{q_j} \in {M_q}} {({I_{\rm{L}}}[{p_i}] - I_{\rm{L}}^{{\rm{avg}}}[p])({I_{\rm{R}}}[{q_j}] - I_{\rm{R}}^{{\rm{avg}}}[q])} } }}{{\sqrt {\displaystyle \sum\limits_{{p_i} \in {M_p}} {{{({I_{\rm{L}}}[{p_i}] - I_{\rm{L}}^{{\rm{avg}}}[p])}^2}} } \sqrt {\displaystyle \sum\limits_{{q_j} \in {M_q}} {{{({I_{\rm{R}}}[{q_j}] - I_{\rm{R}}^{{\rm{avg}}}[q])}^2}} } }} $

(1)

其中， ${M_p}$ 和 ${M_q}$ 分别表示左帧图像中的点 $p$ 和右帧图像中的点 $q$ 对应的 ${\rm{3}} \times {\rm{5}}$ 的匹配块， ${I_{\rm{L}}}[{p_i}]$ 和 ${I_{\rm{R}}}[q{}_j]$ 分别表示左帧图像块 ${M_p}$ 中的点 ${p_i}$ 与右帧图像块 ${M_q}$ 中的点 ${q_j}$ 对应的图像光度值， $I_{\rm{L}}^{{\rm{avg}}}[p]$ 和 $I_{\rm{R}}^{{\rm{avg}}}[q]$ 分别表示对应图像块光度平均值。

由于每一次匹配，NCC都必须计算公式(1)，显然是非常耗时的。为了提高双目初始化的效率，并保持与Stereo DSO^[14]深度滤波器误差方程的一致性，本文提出Two-stages的双目初始化方式。采用图2所示的描述子^[16]对SAD进行搜索匹配^[17]，如式(2)所示。

$ {S_{{\rm{SAD}}}} = \sum\limits_{{p_i} \in {Q_p},{q_i} \in {Q_q}} {\left| {{I_{\rm{L}}}[{p_i}] - {I_{\rm{R}}}[{q_i}]} \right|} $

(2)

其中， ${Q_p}$ 和 ${Q_q}$ 分别表示左帧图像中的点 $p$ 和右帧图像中的点 $q$ 对应的描述子。

显然，本文采用的描述子的大小为 $16$ 维，与NCC匹配块大小接近，但度量相似性的计算步骤更简单，可以极大提高匹配效率。为了保证匹配结果可靠性，NCC被用于验证SAD的匹配结果。通过这种双步骤验证的方式，降低双目初始化的计算量，在不损失定位精度的情况下提高了匹配速度。

1.3 深度范围初始化

由于双目相机固定基线的长度固定，距离相机中心比较远的关键点深度值无法准确测量，因此得到的初始深度图像并不完全可靠。

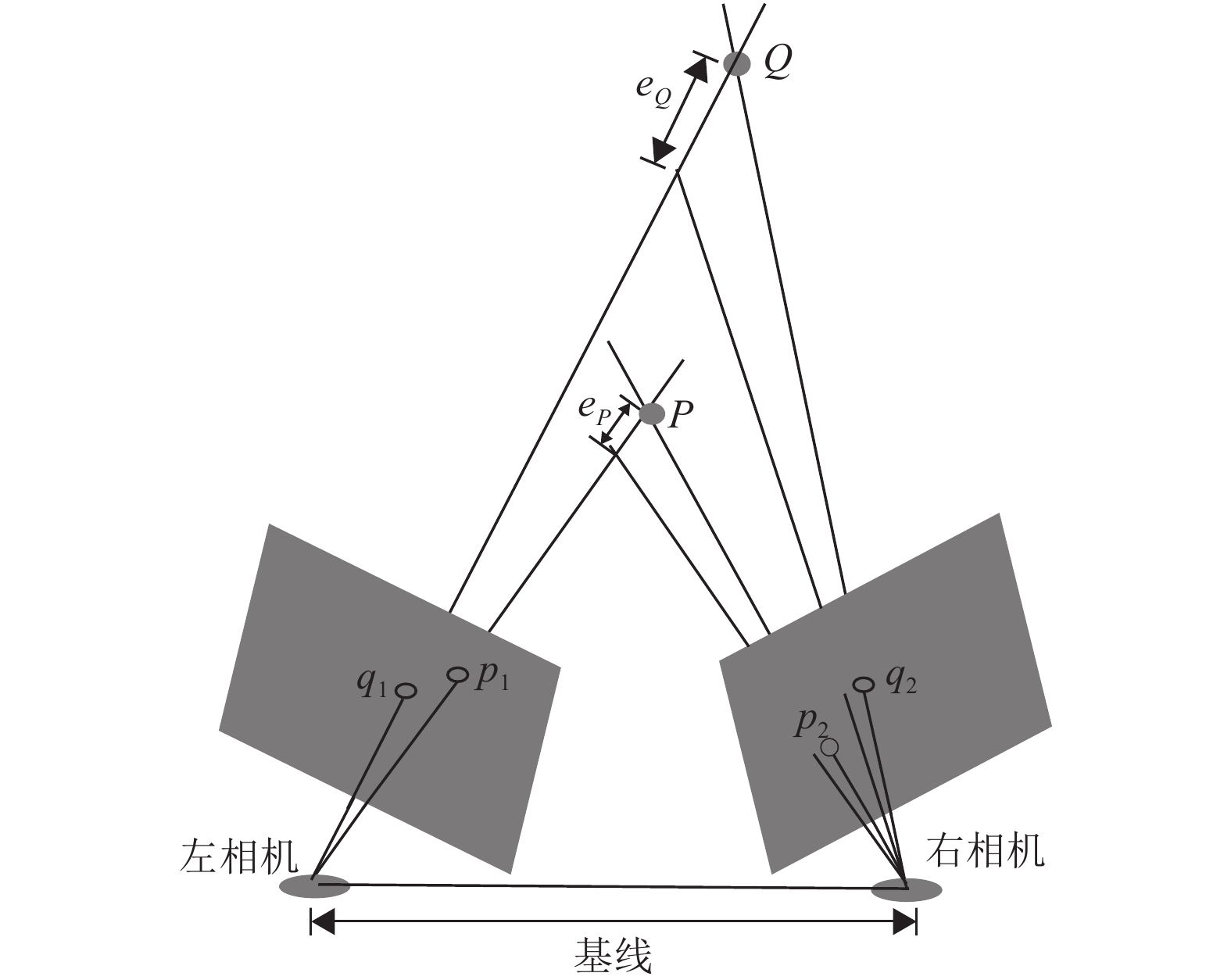
如图3所示，假设世界坐标系下有两个点 $P$ 和 $Q$ ，它们在左、右帧图像中的投影分别用 ${p_1}$ 、 ${p_2}$ 和 ${q_1}$ 、 ${q_2}$ 表示，根据多视图几何约束，可以通过三角化得到其对应空间深度值。值得注意的是，由于测量存在误差，对于距离相机中心较近的点，当测量存在一个像素误差时，估计的深度值误差为 ${e_P}$ ，而距离相机中心较远的点，一个像素误差导致的深度值误差为 ${e_Q}$ ，显然 ${e_P} < {e_Q}$ 。距离相机中心越远的点，其深度值不确定性会越大，即测量误差越大。

在本文中，参考文献[9]将区分近点和远点的阈值设置为40倍双目相机固定基线长度。初始深度值小于40倍基线的点被定义为近点，否则定义为远点。Stereo DSO^[14]采用深度滤波器^[18]对关键点的深度进行估计，但其对所有的点都采用同样的深度范围，并未考虑三角测量不确定性。本文通过区分近点和远点，对近点赋予较小的深度范围，对远点赋予较大的深度范围。通过相邻帧约束，使关键点的深度范围快速收敛到真实值。

1.4 基于双目约束的运动估计

在跟踪线程中，滑动窗口中的所有激活点被投影到最新的关键帧构建参考帧深度图。通过将参考帧中的点反投影到当前帧并优化能量函数(3)，可以获得当前帧 ${I_{\rm{c}}}$ 相对于参考帧 ${I_{\rm{r}}}$ 的相对运动。

$ {E_{{\rm{cr}}}} = {\sum\limits_{p \in {P_{\rm{r}}}} {\sum\limits_{\tilde p \in {N_p}} {{\omega _p}\left\| {{I_{\rm{c}}}[\tilde q] - {b_{\rm{c}}} - \frac{{{e^{{a_{\rm{c}}}}}}}{{{e^{{a_{\rm{r}}}}}}}({I_{\rm{r}}}[\tilde p] - {b_{\rm{r}}})} \right\|} _\gamma } } $

(3)

其中， ${P _{\rm{r}}}$ 表示参考帧图像中的点， ${N_p}$ 采用与DSO^[13]一样的图像块， ${\omega _p}$ 表示点的权重，并且 ${N_p}$ 中所有的点均采用同样的权重， ${\left\| \cdot \right\|_\gamma }$ 为核函数，防止畸形点破坏优化结构。 $({a_{\rm{r}}},{b_{\rm{r}}})$ 和 $({a_{\rm{c}}},{b_{\rm{c}}})$ 分别表示参考帧和当前帧的光度仿射参数，用于建模光度变化。对于投影点 $\tilde q$ ，由公式(4)计算得出。

$ \tilde q = \pi ({T_{{\rm{cr}}}}{\pi ^{ - 1}}(\tilde p,{d_p})) $

(4)

其中， $\pi ( \cdot )$ 表示将相机坐标系的三维点投影到相机平面，同理， ${\pi ^{ - 1}}( \cdot )$ 表示将相机平面的点反投影到相机坐标系中。 ${T_{{\rm{cr}}}}$ 表示参考帧到当前帧的相对位姿， ${d_p}$ 为点 $p$ 的逆深度， ${N_p}$ 中的所有点均采用同样的深度值。

实际上，具有固定基线的双目图像可以为绝对尺度估计提供更多的约束，但Stereo DSO^[14]并未引入这个约束。因此，在本文中，通过引入双目约束，将能量函数(3)拓展为公式(5)。

$ \begin{split} {E_{{\rm{cr}}}} =& \sum\limits_{{p^{\rm{L}}} \in P_{\rm{r}}^{\rm{L}}} {\sum\limits_{{{\tilde p}^{\rm{L}}} \in {N_{{p^{\rm{L}}}}}} {\omega _p^{\rm{L}}} } {\left\| {I_{\rm{c}}^{\rm{L}}[{{\tilde q}^{\rm{L}}}] - b_{\rm{c}}^{\rm{L}} - \frac{{{e^{a_{\rm{c}}^{\rm{L}}}}}}{{{e^{a_{\rm{r}}^{\rm{L}}}}}}(I_{\rm{r}}^{\rm{L}}[{{\tilde p}^{\rm{L}}}] - b_{\rm{r}}^{\rm{L}})} \right\|_\gamma } {\rm{ + }}\\& \sum\limits_{{p^{\rm{R}}} \in P_{\rm{r}}^{\rm{R}}} {\sum\limits_{{{\tilde p}^{\rm{R}}} \in {N_{{p^{\rm{R}}}}}} {\omega _p^{\rm{R}}} } {\left\| {I_{\rm{c}}^{\rm{R}}[{{\tilde q}^{\rm{R}}}] - b_{\rm{c}}^{\rm{R}} - \frac{{{e^{a_{\rm{c}}^{\rm{R}}}}}}{{{e^{a_{\rm{r}}^{\rm{R}}}}}}(I_{\rm{r}}^{\rm{R}}[{{\tilde p}^{\rm{R}}}] - b_{\rm{r}}^{\rm{R}})} \right\|_\gamma } \end{split} $

(5)

其中， ${p^{\rm{L}}}$ 和 ${p^{\rm{R}}}$ 分别表示参考帧中左图和右图匹配的关键点， $(a_{\rm{r}}^{\rm{L}},b_{\rm{r}}^{\rm{L}},a_{\rm{r}}^{\rm{R}},b_{\rm{r}}^{\rm{R}})$ 和 $(a_{\rm{c}}^{\rm{L}},b_{\rm{c}}^{\rm{L}},a_{\rm{c}}^{\rm{R}},b_{\rm{c}}^{\rm{R}})$ 分别表示参考帧和当前帧的左右图像光度仿射参数。

通过最小化公式(5)，当前帧的参数包括相机位姿、左右帧图像的光度仿射参数被有效初始化，随后传入后端滑动窗口^[19]中进一步优化。

2 实验分析 2.1 数据集

本文使用KITTI数据集^[20]对所提出的算法进行验证与分析。KITTI数据集是车载双目相机在街区和高速公路等地区同步采集，并经过校正得到的高分辨率双目图像，是视觉SLAM测试算法在大场景环境下的定位性能常用的数据集。为了验证本文算法的有效性，在该数据集上进行了定位与建图实验，同时与Stereo DSO^[14]、LSD-SLAM2^[21]以及ORB-SLAM3^[10]分别进行了对比，其中Stereo DSO、LSD-SLAM2是目前公开性能最优的直接法SLAM方案，ORB-SLAM3是目前公开性能最优的特征点法SLAM方案。本文算法的实验平台为：Intel i5 4200H处理(2.8 GH)，12 GB RAM，64位Ubuntu16.04操作系统。

2.2 定位精度比较

由于本文所提出的方案是基于直接法的SLAM，因此为了验证本文方案的性能，首先将本文方案与基于直接法的视觉SLAM方案(LSD-SLAM2以及Stereo DSO)在位移误差、旋转误差上进行定位精度对比。由于Stereo DSO并未开源代码，我们无法直接与其进行对比实验。通过复现Stereo DSO提出的方法，与本文方案进行对比。从表1的实验结果可以看出，本文提出的基于双目强约束的直接稀疏里程计系统通过增强双目约束条件，实现了比Stereo DSO与LSD-SLAM2更好的定位效果。特别是，本文的平均位移误差和平均旋转误差分别为0.89%和0.23%，而LSD-SLAM2为1.14%和0.4%，Stereo DSO为0.95%和0.25%，均是本文提出的方案最优。相比LSD-SLAM2和Stereo DSO，本文采用快速双目初始化的策略，提高梯度点深度值初始化效率，同时根据初值深度值区分近远点，为深度滤波器提供较为准确的深度初始范围，使梯度点可以快速收敛到其真实值。在估计运动初始阶段，引入双目约束，可以有效克服尺度误差，提高定位精度。

为了进一步验证本文算法的可靠性，还与特征点法SLAM方案ORB-SLAM3进行比较。由于本文算法是纯双目视觉里程计，因此为了公平比较，关闭了ORB-SLAM3的回环模块与全局优化模块等功能。实验结果如表2所示，显然本文的直接法SLAM与基于特征点法的ORB-SLAM3取得相近的性能，在平均位移误差上，本文算法弱于ORB-SLAM3，主要原因是KITTI数据集帧间距离较远，相邻帧图像同一位置的像素偏差较大，对直接法SLAM方案挑战较大，此外，光照强度变化较大时也会对直接法的定位精度产生一定影响。特别是，在KITTI序列03和序列09，本文提出的方案在位移误差上与ORB-SLAM3相差较大，原因在于这两个序列的光照强度较大，强弱变化也非常频繁，直接法很难对这样的光照变化进行非常准确的建模。但在旋转误差上，本文算法几乎完全优于ORB-SLAM3。这是由于ORB-SLAM3在估计运动时只考虑近点，而本文算法同时考虑远点和近点两类点，其中近点可以提高位移估计的准确度，而远点可以更好地估计旋转变化，特别是表2中的序列01和序列10，旋转误差明显远小于ORB-SLAM3。从实验结果也可以明显看出，同时融合远点和近点的策略可以极大提高旋转估计的精度。在绝对轨迹误差上，本文算法在大部分序列中都优于ORB-SLAM3，本文算法的绝对轨迹误差为3.21 m，而ORB-SLAM3的绝对轨迹误差为3.44 m。从综合结果来看，本文提出的算法与ORB-SLAM3性能相近，为无人驾驶汽车/移动机器人提供一个较优的解决方案，特别是在弱纹理以及窄基线的场景环境中。

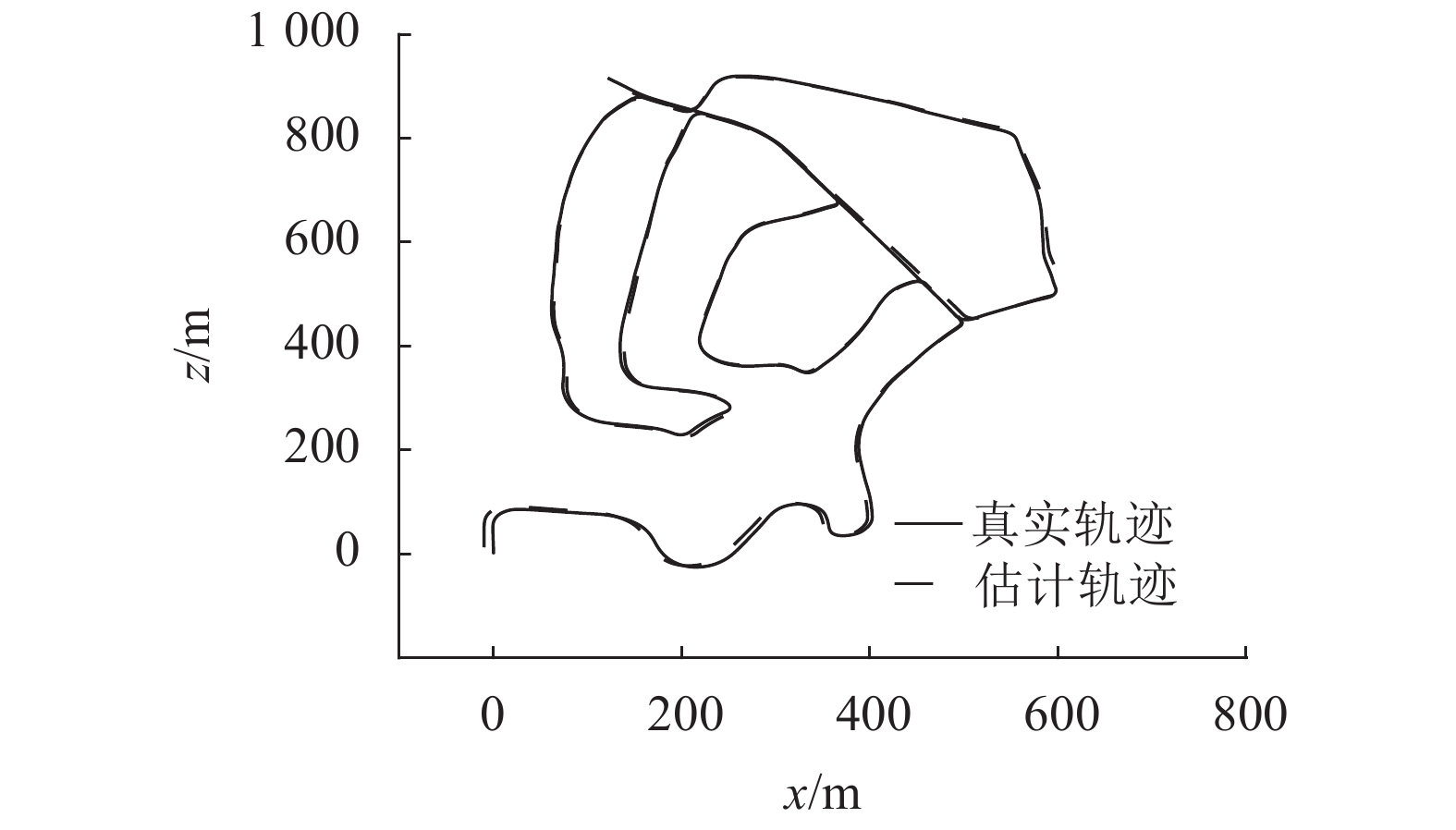
图4是本文算法在KITTI 02序列估计的轨迹与真实轨迹的对比图，可以看出本文提出的算法定位精度是非常高的。

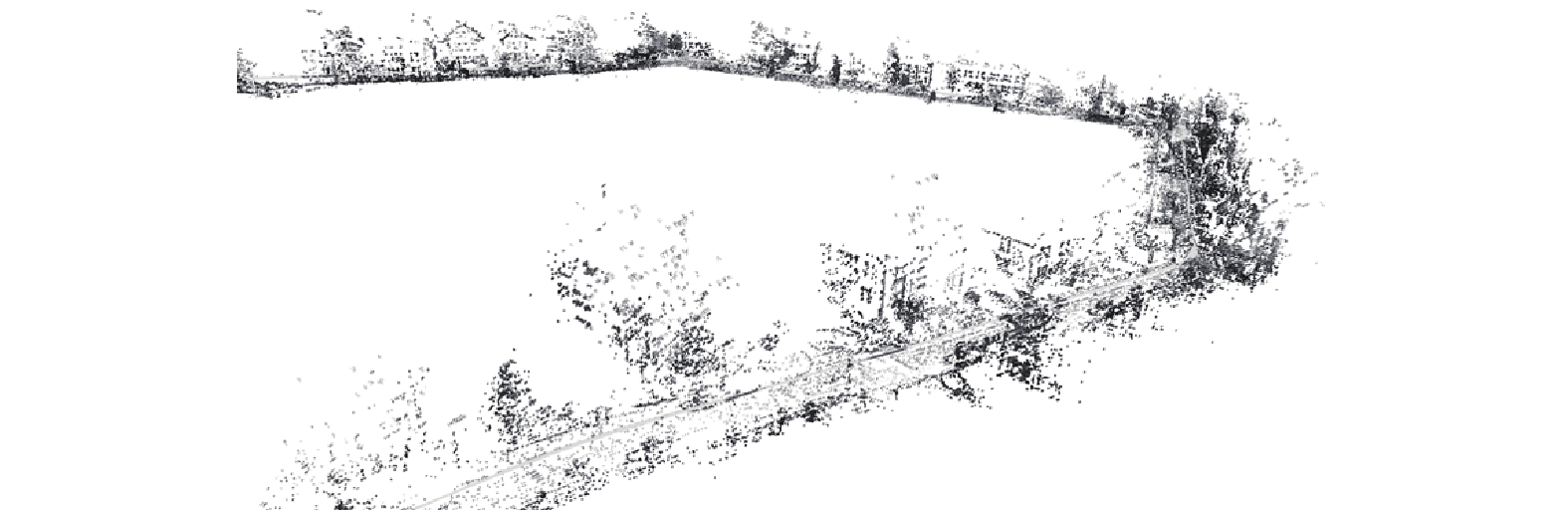
图5是本文算法在KITTI 00序列重建的环境地图，相比于基于特征点法的ORB-SLAM3，本文算法重建的环境地图更加稠密，能更好地实现机器人/无人驾驶汽车的导航功能。

由上述实验结果可知，本文通过增强双目约束，在公开的直接法SLAM方案中定位精度达到了先进水平，并实现了与最优的特征点法SLAM系统ORB-SLAM3相近的定位精度。

3 结语

本文提出了基于双目强约束的直接稀疏视觉里程计系统进行SLAM应用研究，为直接法SLAM提供一种改进方案。通过引入SAD与NCC双步骤的双目匹配方案，实现了快速的双目初始化。基于双目相机固定基线长度设置阈值条件，将观测点划分成远点和近点，由于三角化不确定性随观测点的观测深度变化而变化，因此对两类点分别初始化不同的深度范围，后续深度滤波估计时可以快速收敛到其真实值。在估计相对运动初值时，添加双目约束可以为估计绝对尺度信息提供更多约束信息。本文分别与目前性能最优的直接法SLAM系统Stereo DSO和LSD-SLAM2以及性能最优的特征点法SLAM系统ORB-SLAM3在KITTI数据集11个序列上进行了对比试验，实验结果验证了双目强约束的有效性并证明本文提出的方案在直接法SLAM中达到了先进水平，相比于目前最优的基于特征点法的ORB-SLAM3，本文方案实现了与其相近的定位精度。

本文提出的基于双目强约束的直接稀疏视觉里程计，仅是一个直接法视觉SLAM前端，随着系统长时间长距离的运动，会产生累积误差，导致定位精度下降。因此，为了使本文提出的方案在大场景环境下更加鲁棒，未来需要进一步为系统添加回环检测和全局优化模块。