随着信息时代的快速发展,无人机凭借自身独特的优势被广泛地应用到诸多领域,比如空中侦察、航空影像以及灾后紧急救援等。在无线通信领域中,无人机因其高度灵活性、造价低廉等特点备受欢迎,其主要应用在3个方向,移动基站、移动中继和数据搜集[1-3]。在无人机协作的无线通信系统中,无人机在空中的高度优势使得其与地面通信时的链路极大概率是视距信道(Light-of-Sight,LoS),很大程度上提高了通信质量。然而无人机的参与也带来了新的安全挑战,由于无线信道具备广播的开放特性,无人机与地面通信在提高通信质量的同时也提高了潜在窃听者接收信息的强度,增加了信息传输时的安全隐患。如何确保机密信息在传输过程中不被窃听是一个很重要的应用技术。物理层安全作为一个有效的防窃听技术被广泛研究[4],本文通过研究物理层安全提高无人机无线通信的安全性能。
根据窃听信道模型可知,当合法信道的通信质量优于窃听信道时,可以实现安全通信性能的提升[5]。保密率是物理层安全中一个极为重要的概念,当合法链路的通信质量比窃听链路的通信质量高时,可以得到一个非零的保密率。因此,物理层安全研究的关键就是考虑如何在提高合法链路通信质量的同时降低窃听链路的通信质量。在已有的物理层安全相关文献中,根据是否利用到无人机的高度机动性可以分为两种类型,即通信节点是静态(或准静态)的无线通信和无人机协作的无线通信。当通信节点固定时,物理层安全的研究主要集中在信道、功率控制以及信号检测等技术手段[6-7]。例如文献[8-9]提出利用人工噪声在避开合法接收者的情况下降低窃听链路的通信质量。在多输入多输出系统中,可以利用波束成形的技术方法改善合法链路的通信质量,降低窃听链路的通信质量[10-11]。相对于将通信节点布置在地面的传统方法,无人机协作的物理层安全研究充分利用了无人机的机动灵活性,使其在三维空间内部署,可以明显提高合法链路的通信质量,提高保密率。文献[12-13]提出联合优化无人机轨迹和通信资源分配以提高物理层安全。文献[14]将无人机作为空中基站,通过有效分配带宽、功率等资源提高无线通信系统的通信质量。文献[15-16]提出通过可移动的无人机发出噪声干扰窃听者,从而提高通信安全的方法。此外,考虑到单个无人机的活动范围较小,对系统通信质量的提升有限,文献[17-18]对多无人机进行部署以提高系统的通信质量和吞吐量。值得注意的是,以上所述文献的无线通信系统是基于视距信道模型的,将通信环境视为完全已知。若无人机和地面用户的坐标确定,可以在无人机出发前完成整个飞行路径的设计,轨迹优化策略也是离线的。若通信环境发生变化,离线策略得到的无人机轨迹不能做出相应变动,其弊端在于忽略了由于存在障碍物位置的随机性造成无人机与地面节点间信道衰落的随机性,真实的信道应是视距信道和非视距信道(Non-Light-of-Sight,NLoS)的混合,故信道增益也是随机的。
针对这个问题,本文研究无人机轨迹的在线优化策略,提出一种基于强化学习Q-learning算法的优化方法[19]。动态规划(Dynamic Programming,DP),蒙特卡洛方法(Monte Carlo Methods,MC)和时序差分学习(Temporal-Difference Learning,TD)是强化学习中常用的方法,而Q-learning算法是TD方法中一个重要突破。相比于DP方法,TD方法的最大优势在于其可以直接从与环境互动的经验中学习,不需要构建环境模型。相比于MC方法,TD方法不需要等待与环境交互的最终结果,而是基于已得到的其他状态的估值以在线、完全增量的方式更新当前状态的动作价值函数,可用于连续任务。
相比于已有的无人机轨迹设计算法,本文提出的算法不需要环境完全已知,借助无人机在飞行过程中每个位置得到的反馈信号作为收益值可以不断训练、更新无人机的轨迹,最终实现路径优化。若是环境发生变化,无人机也可以通过与环境的自主交互实现轨迹重新优化。算法的目标是通过优化无人机的飞行轨迹使得平均保密率达到最大。此外,本文的空地信道模型采用更符合实际的视距/非视距混合信道模型,由文献[20]可知,空地通信链路是视距链路或者是非视距链路的概率大小与无人机到地面节点的仰角以及环境因素有关。由仿真结果可知,当无线通信系统的通信环境处于动态变化时,本文提出的算法可以在线优化无人机飞行路径,并取得优于基准策略的平均保密率性能。
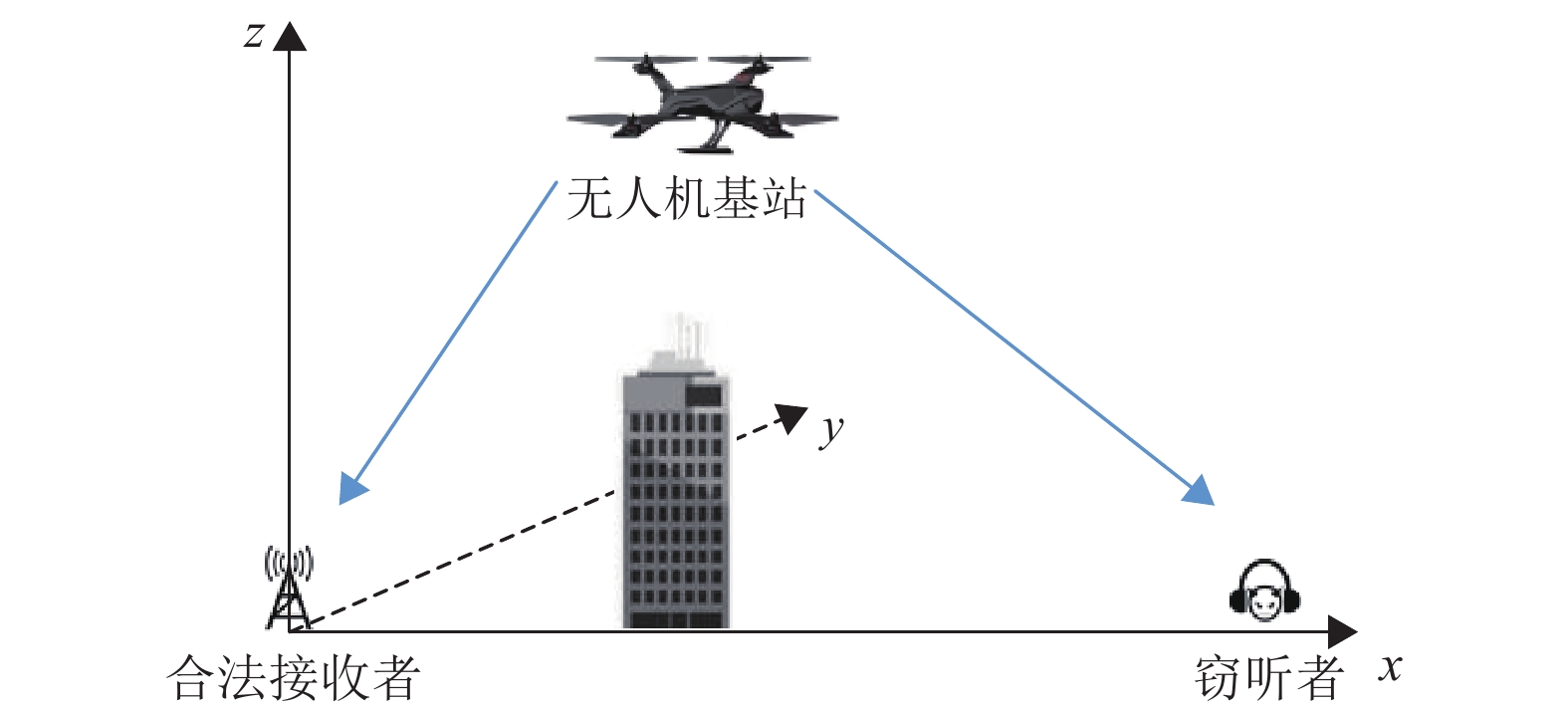
1 系统模型本文考虑一个无人机基站通信系统,该系统由一个无人机基站和一个地面合法接收节点组成,同时地面存在一个窃听节点,系统模型如图1所示。地面窃听者的位置可借助雷达扫描定位等技术手段探得[12, 21],所以本文设定合法接收节点和窃听节点的位置已知,两者之间的距离为
|
图 1 一个基于无人机的无线通信系统 Figure 1 A UAV-enabled wireless communication |
| $ D\left(t\right)=\left\| \varOmega \left(t\right)-{\varOmega }_{{\rm{F}}} \right\|,\forall t $ | (1) |
本文采用文献[22]中的视距/非视距混合信道模型,对无人机基站到地面两个节点的链路进行建模。其信道增益包含大尺度的路径损耗和小尺度的瑞利衰落。用
| $ {h}_{k}\left(t\right)=\frac{{\rho }_{k}\left(t\right)}{\sqrt{{\mathrm{P}\mathrm{L}}_{k}\left(t\right)}} $ | (2) |
其中,
| $ {{\rm{pr}}}_{k}^{{\rm{LoS}}}\left(t\right)=\frac{1}{1+{\omega }_{1}\exp\left(-{\omega }_{2}\left({\theta }_{k}\left(t\right)-{\omega }_{1}\right)\right)} $ | (3) |
其中,
| $ {\rm{P}}{{\rm{L}}_k}( t ) = {\rm{pr}}_k^{{\rm{LoS}}}( t ){\rm{P}}{{\rm{L}}^{{\rm{LoS}}}}( t ) + ( {1 - {\rm{pr}}_k^{{\rm{LoS}}}( t )} ){\rm{P}}{{\rm{L}}^{{\rm{NLoS}}}}( t )$ | (4) |
其中,
| $ {\mathrm{P}\mathrm{L}}^{\mathrm{L}\mathrm{o}\mathrm{S}}\left(t\right)={\left(\frac{4{\text{π}}f{d}_{k}\left(t\right)}{c}\right)}^{2}\times {\eta }^{\mathrm{L}\mathrm{o}\mathrm{S}} $ | (5) |
其中,无人机在t时刻到节点k的距离表示为
| $ {\mathrm{P}\mathrm{L}}^{\mathrm{N}\mathrm{L}\mathrm{o}\mathrm{S}}\left(t\right)={\left(\frac{4{\text{π}}f{d}_{k}\left(t\right)}{c}\right)}^{2}\times {\eta }^{\mathrm{N}\mathrm{L}\mathrm{o}\mathrm{S}} $ | (6) |
其中,
| $ {\varGamma }_{k}\left(t\right)={\mathrm{l}\mathrm{o}\mathrm{g}}_{2}\left(1+\frac{P{g}_{k}\left(t\right)}{{\sigma }^{2}}\right) $ | (7) |
其中,
| $ {\varGamma }_{\mathrm{s}\mathrm{e}\mathrm{c}}\left(t\right)={{[\varGamma }_{1}\left(t\right)-{\varGamma }_{2}\left(t\right)]}^+ $ | (8) |
无人机完成一次飞行的时间为
| $ {\varGamma }_{k}\left[n\right]={\mathrm{l}\mathrm{o}\mathrm{g}}_{2}\left(1+\frac{P{g}_{k}\left[n\right]}{{\sigma }^{2}}\right) $ | (9) |
其中,n=1,2,···,N,由式(8)可知,在无人机从出发点到终点飞行的
| ${\varGamma _{{\rm{ave}}\_{\rm{sec}}}} = \frac{1}{N}\sum\nolimits_{n = 1}^N {{{\left[ {{\varGamma _1}\left[ n \right] - {\varGamma _2}\left[ n \right]} \right]}^ + }} $ | (10) |
其中,
本文的目标是通过对无人机轨迹优化使得式(10)中的平均保密率
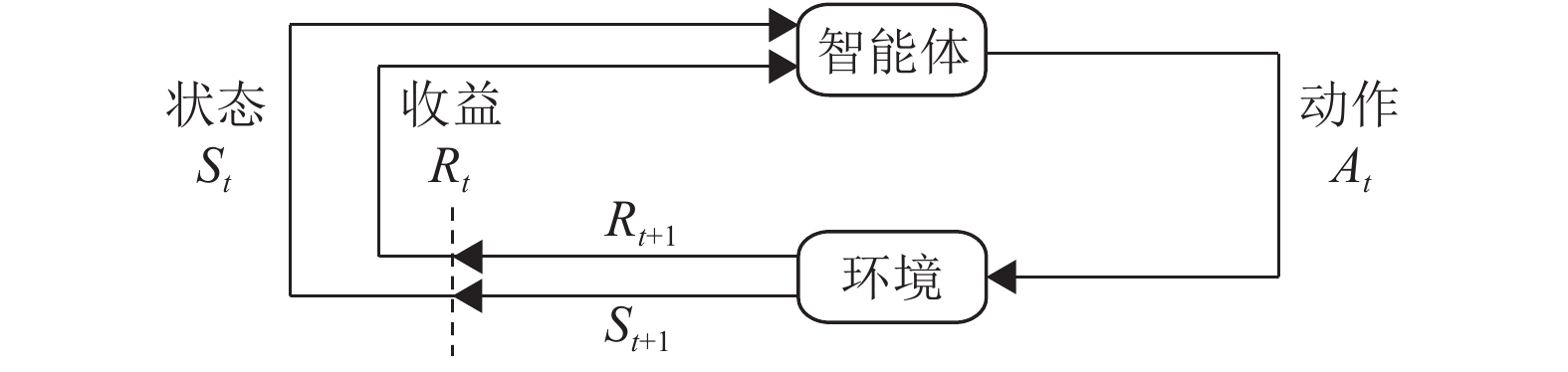
强化学习明确考虑了目标导向的智能体与未知环境之间的交互问题。马尔可夫决策过程(Markov Decision Process,MDP)是一种通过交互式学习来实现目标的理论框架,也是强化学习问题在数学上的理想形式。智能体是进行环境学习和实施决策的个体,与智能体相互作用的事物被称为环境,也可以将环境理解为智能体要经历的状态集合。智能体做出决策,即选择一个合适的动作
|
图 2 马尔可夫决策过程中智能体与环境的交互 Figure 2 The agent-environment interaction in a Markov decision process |
使用收益来形式化目标是强化学习最显著的特征之一,智能体的目标不是最大化当前收益,而是最大化长期收益
Q-learning算法是一种使用时序差分求解强化学习控制问题的方法,是不基于环境状态转化模型的求解方法。该算法以迭代的方式计算最优动作价值函数,即通过动作价值函数更新策略,由策略产生新的状态和收益,进而更新动作价值函数,直到动作价值函数和策略都收敛。动作价值函数的更新表示为
| $ \begin{split} & Q\left( {{S_t},{A_t}} \right) = Q\left( {{S_t},{A_t}} \right) + \\&\qquad \alpha \left[ {{R_{t + 1}} + \gamma \mathop {{\rm{max}}}\nolimits_a Q\left( {{S_{t + 1}},a} \right) - Q\left( {{S_t},{A_t}} \right)} \right] \end{split}$ | (11) |
其中,步长
根据提出的模型,本文将无人机飞行过程分为两个阶段。设定时间
智能体:无人机
状态
动作
收益
算法如下:
参数:幕数
(1) 初始化两个
(2) 设定2个飞行阶段的终点位置的状态分别是
(3) 开始迭代以下步骤,直到幕值为
a) 初始化无人机起飞位置;
b) 用
c) 执行动作
d) 按照下式更新动作价值函数
e)
f) 如果
转到步骤b)。
4 仿真结果此节将通过仿真结果对文中提出的无人机轨迹优化算法的优越性进行验证,并且与两种基准算法进行比较。
(1) 直线飞行轨迹(标记为Line)。此算法考虑视距/非视距混合信道,无人机从出发位置以恒速飞向合法接收节点的位置,到达后并在该节点悬停,最后在飞行时间结束前飞向终点位置。
(2) 凸近似方法优化轨迹(标记为Convex)。此算法只考虑视距信道,即忽略了信道衰落的随机性,利用连续凸近似法和块坐标下降法对无人机的离线轨迹进行优化[12]。
此文中合法接收节点和窃听节点之间的距离设为
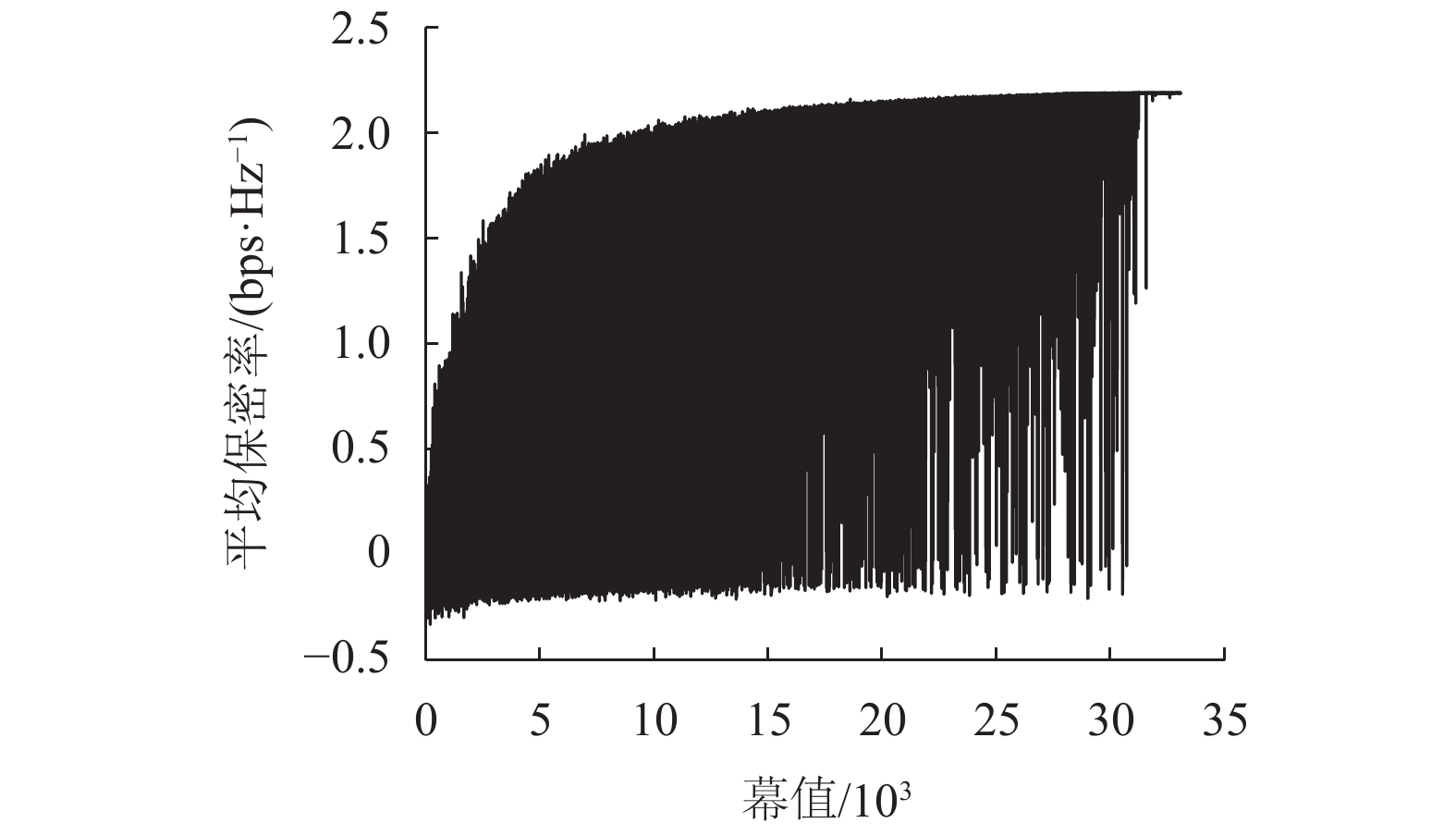
图3显示的是在利用Q-learning算法训练过程中,每幕的平均保密率值随着幕数的增加而收敛。训练开始的时候,无人机因为对未知环境探索,平均保密率有很大的波动。随着迭代次数增加,动作价值函数和策略逐渐收敛,无人机飞行的优化路径逐渐明晰,相应的平均保密率也开始收敛。由于利用
|
图 3 每幕平均保密率的收敛图 Figure 3 Convergence of average secrecy rate versus episode |
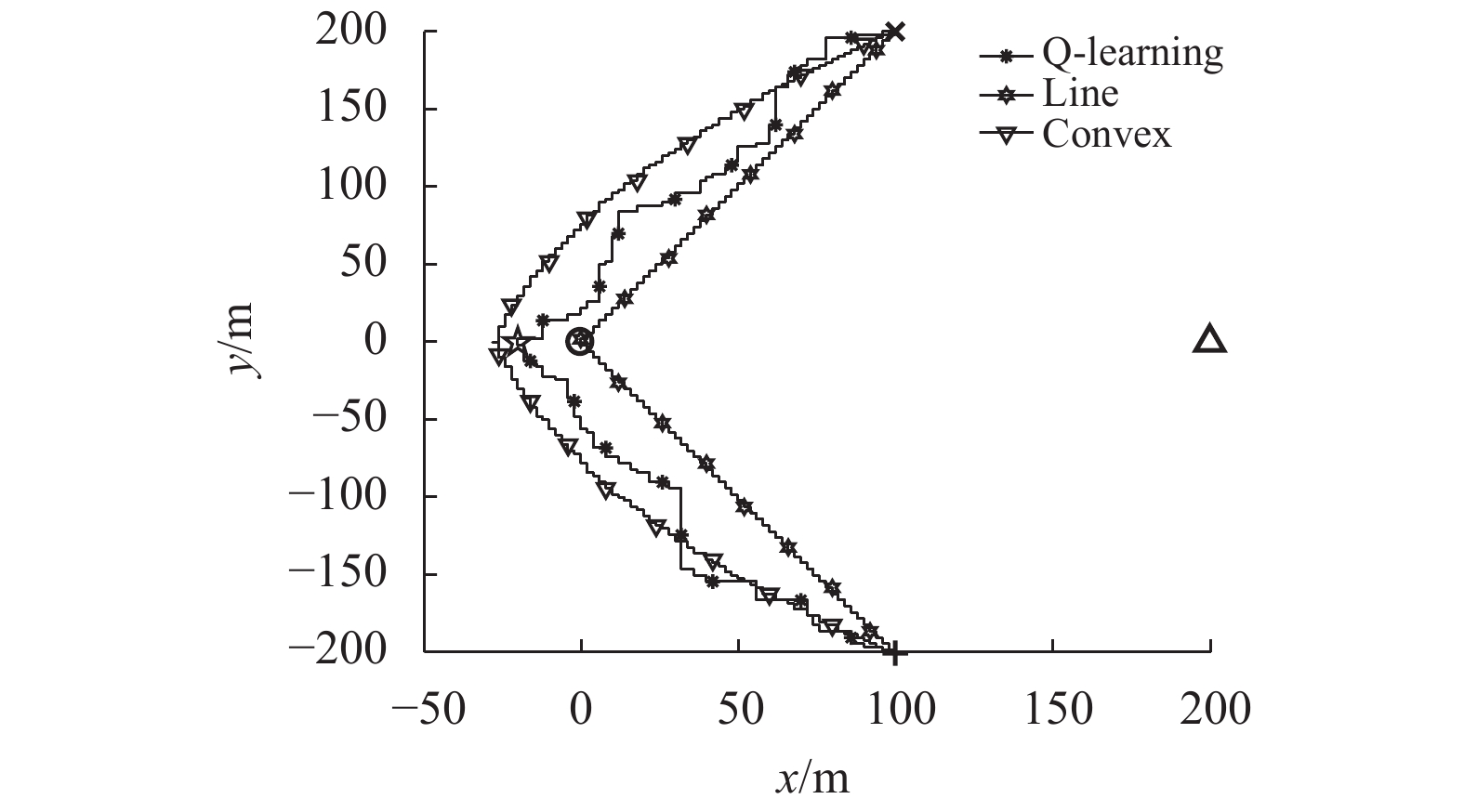
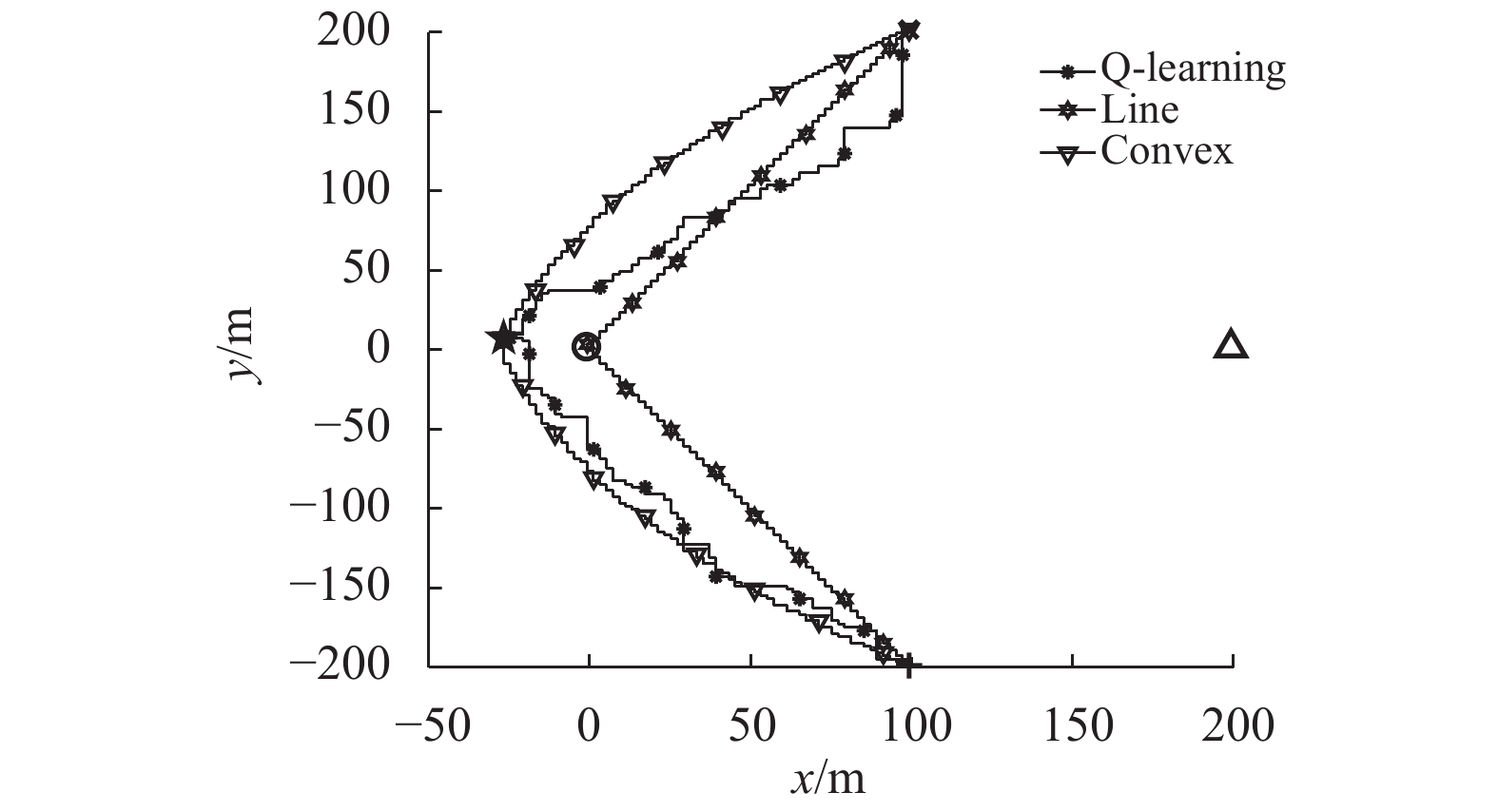
图4和图5分别展示了文中提出的算法和基准算法在因信道增益随机性而造成的2种不同通信环境下的无人机飞行轨迹。其中合法接收节点、窃听节点的位置以及无人机初始、终点位置分别用○,Δ,×,+,这4种符号标记。为了限制无人机的状态数目,文中将其飞行区域离散化并分割成一定数目的格子,因此图中无人机的飞行轨迹是曲折的。由于图4和图5中显示的2种基准算法是离线策略,所以得到的无人机路径是固定不变的。而Q-learning算法是在线策略,其轨迹图(标记为Q-learning)是随着不同通信情况而变化的,此算法使得无人机飞行时会避开窃听节点的位置,先飞到保密率最大的位置保持悬停状态,最后在飞行时间结束前飞向终点位置。保密率最大的位置在图4和图5中分别用五角星☆标记。
|
图 4 3种算法的轨迹对比图(环境I) Figure 4 Trajectories of different algorithms (Environment I) |
|
图 5 3种算法的轨迹对比图(环境II) Figure 5 Trajectories of different algorithms (Environment II) |
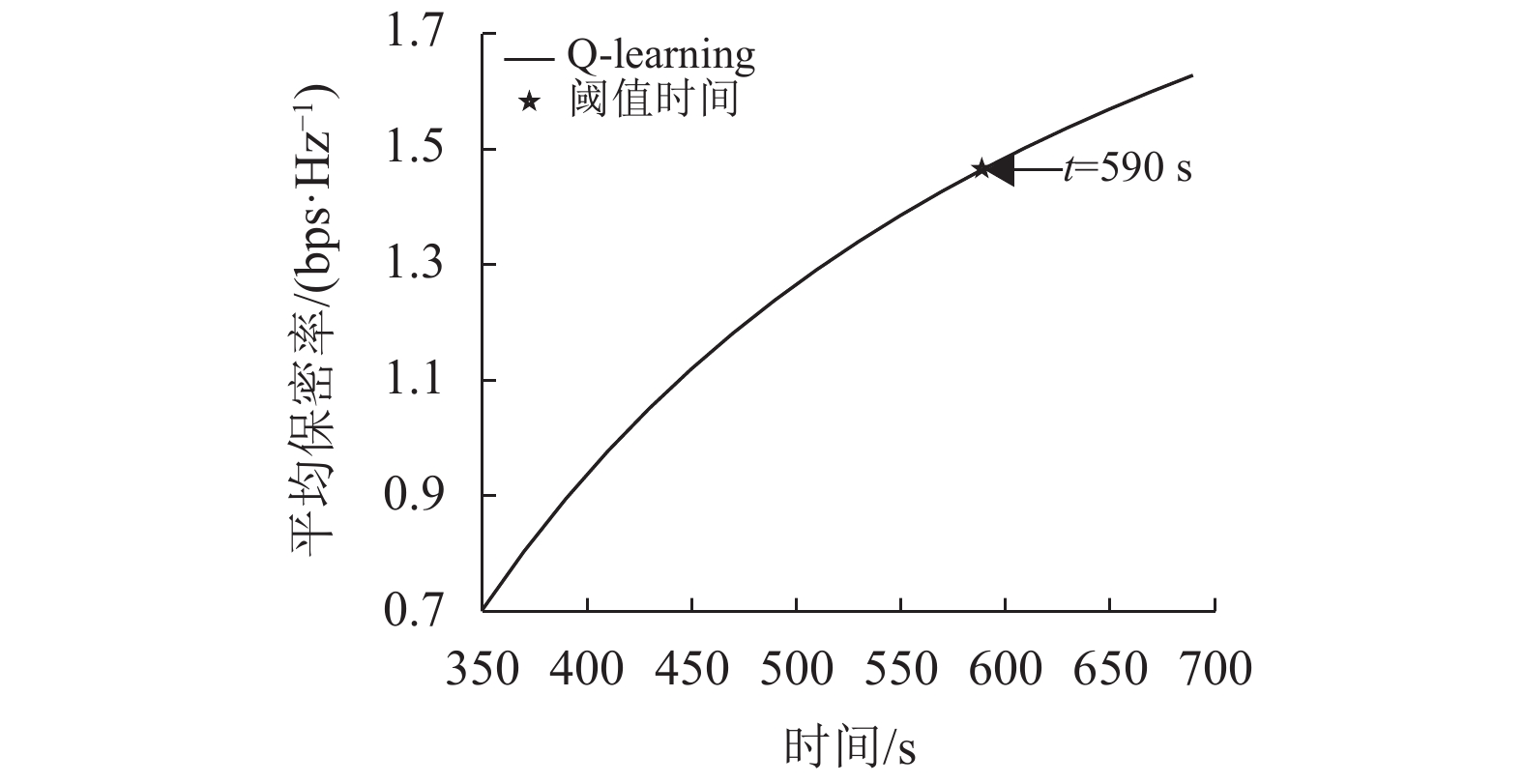
随着无人机在保密率最大位置停留的时间增加,平均保密率也是增加的。图6是在飞行环境Ⅰ的情况下无人机的平均保密率随着悬停时间增加的变化曲线。当平均保密率的增长率低于设定的阈值时(阈值=
|
图 6 平均保密率随时间变化图 Figure 6 Average secrecy rate versus flight time |
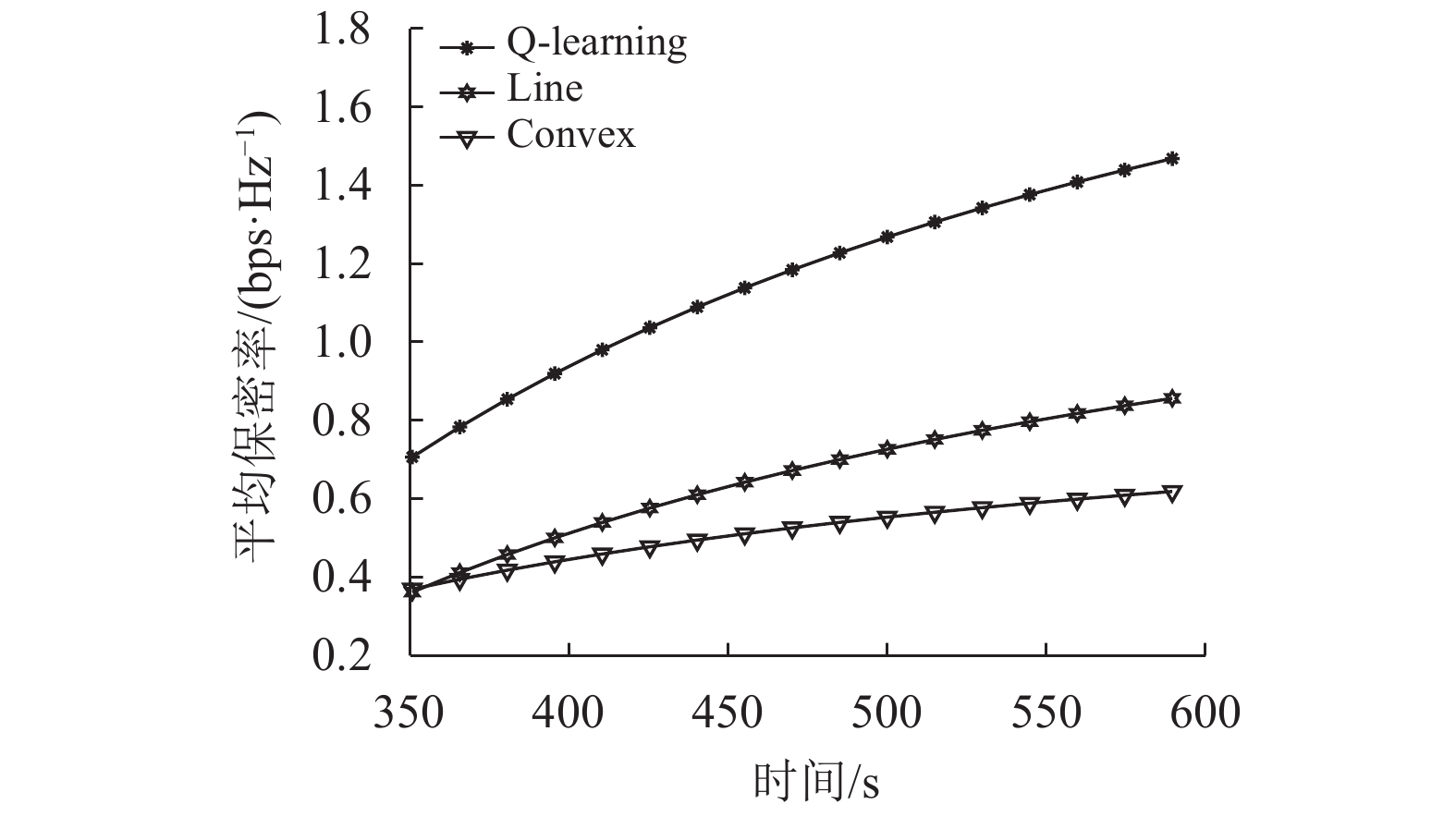
图7展示的是在
|
图 7 不同算法的平均保密率变化图 Figure 7 Average secrecy rates of different algorithms |
本文基于强化学习中的Q-learning算法提出了一种无人机与环境自主交互、可在线优化无人机飞行轨迹的保障物理层通信安全的方法,目的是在存在窃听者的情况下使得无人机基站发送的机密信息被安全地传输,最大化平均通信保密率。由仿真结果可知,在视距/非视距混合信道下,利用Q-learning算法能够对无人机进行有效训练使得其飞行轨迹实现在线优化,所提算法的平均保密率性能优于已有的离线基准算法。
| [1] |
ZENG Y, ZHANG R, LIM T J. Wireless communications with unmanned aerial vehicles — opportunities and challenges[J].
IEEE Communications Magazine, 2016, 54(5): 36-42.
DOI: 10.1109/MCOM.2016.7470933. |
| [2] |
LYU J, ZENG Y, ZHANG R. Cyclical multiple access in UAV-aided communications — a throughput-delay tradeoff[J].
IEEE Wireless Communications Letters, 2016, 5(6): 600-603.
DOI: 10.1109/LWC.2016.2604306. |
| [3] |
SOTHEARA S, ASO K, AOMI N, et al. Effective data gathering and energy efficient communication protocol in wireless sensor networks employing UAV[C]//Wireless Communications & Networking Conference. Istanbul: IEEE, 2014: 2342-2347.
|
| [4] |
ZHENG G, KRIKIDIS I, LI J, et al. Improving physical layer secrecy using full-duplex jamming receivers[J].
IEEE Transactions on Signal Processing, 2013, 61(20): 4962-4974.
DOI: 10.1109/TSP.2013.2269049. |
| [5] |
WYNER A D. The wire-tap channel[J].
Bell System Technical Journal, 1975, 54(8): 1355-1387.
DOI: 10.1002/j.1538-7305.1975.tb02040.x. |
| [6] |
SHIU Y S, CHANG S Y, WU H C, et al. Physical layer security in wireless networks — a tutorial[J].
IEEE Wireless Communications, 2011, 18(2): 66-74.
DOI: 10.1109/MWC.2011.5751298. |
| [7] |
童辉志, 张广驰, 周绪龙, 等. 具有能量获取基站的相邻多蜂窝小区的能量与频谱分配研究[J].
广东工业大学学报, 2018, 35(4): 72-78.
TONG H Z, ZHANG G C, ZHOU X L, et al. Joint energy and spectrum allocation in multiple adjacent cells with energy harvesting base stations[J]. Journal of Guangdong University of Technology, 2018, 35(4): 72-78. |
| [8] |
GOEL S, NEGI R. Guaranteeing secrecy using artificial noise[J].
IEEE Transactions on Wireless Communications, 2008, 7(6): 2180-2189.
DOI: 10.1109/TWC.2008.060848. |
| [9] |
GOPALA P K, LAI L, EL GAMAL H. On the secrecy capacity of fading channels[J].
IEEE Transactions on Information Theory, 2008, 54(10): 4687-4698.
DOI: 10.1109/TIT.2008.928990. |
| [10] |
WANG H, YIN Q, XIA X. Distributed beamforming for physical layer security of two-way relay networks[J].
IEEE Transactions on Signal Processing, 2012, 60(7): 3532-3545.
DOI: 10.1109/TSP.2012.2191543. |
| [11] |
ZHANG G, LI X, CUI M, et al. Signal and artificial noise beamforming for secure simultaneous wireless information and power transfer multiple-input-multiple-output relaying systems[J].
IET Communications, 2016, 10(7): 796-804.
DOI: 10.1049/iet-com.2015.0482. |
| [12] |
ZHANG G, WU Q, CUI M, et al. Securing UAV communications via joint trajectory and power control[J].
IEEE Transactions on Wireless Communications, 2019, 18(2): 1376-1389.
DOI: 10.1109/TWC.2019.2892461. |
| [13] |
ZHANG J, ZENG Y, ZHANG R. Spectrum and energy efficiency maximization in UAV-enabled mobile relaying[C]//International Conference on Communications. Paris: IEEE, 2017: 1-6.
|
| [14] |
HUANG Y, CUI M, ZHANG G, et al. Bandwidth, power and trajectory optimization for UAV base station networks with back haul and user QoS constraints[J].
IEEE Access, 2020(8): 67625-67634.
DOI: 10.1109/ACCESS.2020.2986075. |
| [15] |
ZHOU Y, YEOH P L, CHEN H, et al. Secrecy outage probability and jamming coverage of UAV-enabled friendly jammer[C]//2017 11th International Conference on Signal Processing and Communication Systems. Gold Coast: IEEE, 2017: 1-6.
|
| [16] |
LIU J, LIU Z, ZENG Y, et al. Cooperative jammer placement for physical layer security enhancement[J].
IEEE Network the Magazine of Global Internetworking, 2016, 30(6): 56-61.
DOI: 10.1109/MNET.2016.1600119NM. |
| [17] |
FAN J, CUI M, ZHANG G, et al. Throughput improvement for multi-hop UAV relaying[J].
IEEE Access, 2019(7): 147732-147742.
DOI: 10.1109/ACCESS.2019.2946353. |
| [18] |
ZHANG G, YAN H, ZENG Y, et al. Trajectory optimization and power allocation for multi-hop UAV relaying communications[J].
IEEE Access, 2018(6): 48566-48576.
DOI: 10.1109/ACCESS.2018.2868117. |
| [19] |
SUTTON R, BARTO A. Reinforcement learning — an introduction[M]. 2nd ed. Cambridge: MIT Press, 2018.
|
| [20] |
FENG Q, TAMEH E, NIX A R, et al. Modelling the likelihood of line-of-sight for air-to-ground radio propagation in urban environments[C]// Globecom2006. San Francisco: IEEE, 2007: 1-5.
|
| [21] |
CUI M, ZHANG G, WU Q, et al. Robust trajectory and transmit power design for secure UAV communications[J].
IEEE Transactions on Vehicular Technology, 2018, 67(9): 9042-9046.
DOI: 10.1109/TVT.2018.2849644. |
| [22] |
AL HOURANI A, KANDEEPAN S, LARDNER S. Optimal lap altitude for maximum coverage[J].
Wireless Communications Letters IEEE, 2014, 3(6): 569-572.
DOI: 10.1109/LWC.2014.2342736. |
 2021, Vol. 38
2021, Vol. 38

