2. 辽宁工程技术大学 安全科学与工程学院,辽宁 葫芦岛 125105
2. College of Safety Science and Engineering, Liaoning Technical University, Huludao 125105, China
在任何项目构成的管理系统中,都存在博弈问题。系统中各参与者都在使用各种行为,力求使己方收益最大化,同时平衡各方收益,满足各方要求。就最简单工程系统而言,直接劳动者往往是被雇佣的,是直接操作系统的人。他们以自己收益最大化为目标,同时采用简便、易行且成本最低的行为完成系统赋予的工作,一般是片面的收益最大化。但往往操作者的这些行为综合在一起导致系统发生故障或事故,给系统整体收益带来不利影响。另一角度,系统管理者往往是系统的所有者和受益人。他们以系统整体收益最大化为目标,一般不可考虑操作者群体的收益情况。因此当操作者和管理者成为系统运行的参与者时,他们的行为为各自收益最大化服务。同时,作为系统运行参与者,他们要考虑对方行为,从而调整己方行为,在获得收益最大化的同时满足对方要求。因此操作者和管理者组成了具有博弈特征的系统,而如何在管理者角度分析和保障系统收益成为研究的关键问题。
关于各类系统博弈和收益问题的研究已有很多。风险收益动态视角下政府与社会资本合作演化博弈[1];动态激励视角下建筑工人不安全行为演化博弈[2];资源投入不确定情形下的合作博弈策略[3];网络博弈合作剩余收益分配[4];新零售模式下供应链收益博弈优化[5];三方博弈视角下项目安全行为策略分析[6];进化博弈的矿工不安全行为研究[7];多方博弈下起重作业人员有意不安全行为分析[8];基于动态博弈的矿工不安全行为研究[9]和干预[10];风险管理合作中的演化博弈分析[11];建设工程管理的合作博弈决策[12]。这些研究一般专注于各自领域,并取得了良好效果,作者也在相关领域进行了一些研究等[13-15]。但缺乏对多事件组成系统的收益情况研究。操作者和管理者对系统中各事件可能采取各种行为,那么对两者而言这些事件收益是不同的。进一步,如果这些事件间存在逻辑关系,共同演化导致了系统收益的变化,则是一个复杂的演化过程。现有分析方法难以胜任。
针对上述问题,论文使用SFN[16-20]对演化过程进行表示和处理,将操作者和管理者不同行为作用于事件后的收益,定义为事件综合收益,作为SFN边缘事件。确定边缘事件演化过程逻辑关系和处理方法,演化后得到最终事件,即系统收益,并判断胜出者。
1 操作者与管理者行为任何系统,特别是实际工程建设过程作为系统研究时,可从人、机、环、管4个方面对系统需要的各种目标进行评价和分析,当然还有更细分类。这里人是系统的实际操作者,是系统中付出劳动的,操作各类机器的人。人存在不安全行为,这主要是对机器、环境及管理的不适应。机是系统中人的主要操作对象,在机发生物理破坏和不可逆破坏前一般不发生故障。机存在不安全状态,该状态一般是由人的不安全行为和环境因素干扰造成的。环境在系统中对人和机都有影响,但主要是对人的干扰。适合和不适合的环境对人的不安全行为有明显影响。管是系统中对人的约束,也是对机器操作的规范,使人避免不安全行为,管的具体实施者仍是人。因此上述系统可视为由操作系统的人和管理操作者的人,即操作者和管理者作为参与者的系统。
操作者是系统的使用者,具有安全行为和不安全行为。例如施工现场电焊过程中,焊工对于穿绝缘鞋这个事件可以采取安全和不安全行为。安全行为包括穿符合要求的绝缘鞋等;不安全行为包括不穿绝缘鞋或穿损坏的绝缘鞋等。操作者选择安全行为或不安全行为的动机是考察行为后该事件给己方带来的收益。安全行为往往投入更大,需满足繁琐的规章制度;不安全行为往往是方便快捷的,根据直观而定。还需考虑行为后管理者对操作者行为的反应,可能对操作者收益有利或不利。操作者会综合考量,在一定概率条件下选择安全或不安全行为。
管理者是系统的管理或拥有者,系统整体收益可以说是管理者的收益。因此他们往往从系统收益最大化出发考虑行为策略,对操作者进行管理,包括惩罚和奖励行为。例如施工现场电焊过程,管理者对操作者穿绝缘鞋或不穿绝缘鞋可采取不同的行为或无行为。对穿符合要求绝缘鞋的操作者进行奖励,一般情况下管理者没有奖励行为;对不穿或穿不符合绝缘鞋的操作者进行惩罚,一般都对这种情况进行惩罚。管理者从系统和项目整体出发考量收益,并确保最大化;一般不考虑操作者的收益最大。基于此,管理者根据操作者行为在一定概率条件下选择惩罚和奖励行为。
因此,系统中管理者行为和操作者行为都力求己方收益最大化,同时满足对方的基本要求使对方妥协,两方策略构成了博弈系统。该系统在生产生活中普遍存在,只要存在管理者和操作者就存在这样的博弈系统,因此,研究参与者行为博弈和导致的系统收益具有重要意义。
2 SFN与博弈过程系统存在两个参与者相互博弈时,对系统中一个事件,操作者和管理者可执行不同行为满足己方收益。例如上节的穿绝缘鞋事件,双方都有一定概率采取各自的不同行为。系统中另一事件,比如焊枪接地线接触位置选择,理论上可接在任何金属构件上。但不可接在脚手架、钢筋笼或周围设备金属外壳上,例如操作者的安全行为是接在专用地线上,不安全行为是接在上述构件上。但由于现场条件限制,地线时常接在上述构件而不接地。操作者有一定概率选择安全或不安全行为;同样管理者也根据实际情况对操作者的接地事件进行管理,有一定概率采取惩罚和奖励行为。
穿绝缘鞋事件和焊接接地事件操作者都采取了一定行为,同时管理者也采取了对应行为。这时出现另一捆扎钢筋事件,使得操作者必须徒手捆扎钢筋,当然操作者和管理者对该事件也要采取适当行为。这3个事件组合在一起,最坏的情况是操作者触电,操作者收益下降,导致停工,管理者收益下降;或者不发生触电事故,操作者蒙混过关,管理者并未发现,两者收益不变。可见操作者和管理者组成了以收益为目标的博弈系统。
可见系统层面的收益取决于使系统发生故障的基本原因,即基本事件在受到操作者和管理者综合行为处理后,两者得到的收益情况。这些原因事件收益相互交织,因果演化成为一连串的事件组合,最终形成系统收益。该过程与系统故障过程发生机理类似,且系统中发生意外和故障是导致这些事件和系统功能效用变化的主要原因,而功能直接影响收益。作者提出使用SFN研究操作者和管理者博弈系统的收益问题。
博弈论源于20世纪初,又称对策论。主要研究参与者之间对抗和合作交织情况下,如何决策从而使己方获得较大收益,并使对方接受。博弈是两个或多个参与者组成系统的局势,至少应包括参与者、策略和收益。参与者是博弈存在的基础,参与者不一定是人,可以是任何与其他系统存在竞争合作关系的系统;策略是参与者根据系统局势和各方情况在采取具体行为前进行的分析与考量。收益指各参与方在经过一系列竞争合作采用各种行为后,己方获得的目标方面的收益。那么操作者与管理者行为导致系统收益变化是博弈问题。
作者将系统故障过程中各种事件及其逻辑关系抽象为系统故障演化过程(System Fault Evolution Process,SFEP),用SFN表示SFEP[16-20]。SFN包括节点和有向线段。节点代表事件,包括SFEP起始原因的边缘事件,经历的过程事件和系统最终故障情况的最终事件。有向线段表示事件之间的传递关系,从原因事件指向结果事件;传递概率表示原因事件导致结果事件的可能性。过程事件和最终事件是结果事件,它们有多个原因事件时下角标标注原因事件间逻辑关系。这样SFN可表示复杂的SFEP、事件间逻辑关系及演化流程。由操作者和管理者组成博弈系统,由于操作者和管理者的不同行为会导致不同的收益,那么对同一事件的不同行为得到的事件收益就可作为SFN的边缘事件,通过SFN分析得到最终系统收益情况。使用SFN表示操作者与管理者行为的事件综合收益与演化所得系统收益的关系,并通过博弈论思想解决是可行的。
3 系统层面收益分析方法 3.1 基本参数定义根据文献[2],基于SFN的综合操作者与管理者行为博弈的系统收益分析方法的基本参数定义如下:
r1:操作者安全行为己方收益,
I:边缘事件数量,i=1,···,I。
r2:操作者安全行为对方(管理者)收益,
r3:操作者不安全行为己方收益,
r4:操作者不安全行为对方收益,
h:操作者不安全行为系统损失,H={h1,···,hi,···,hI}。
b1:管理者对对方不安全行为罚金,
b2:管理者对对方安全行为奖金,
上述安全与不安全行为,惩罚和奖励行为都针对同一个事件ei,所有边缘事件的集合e={e1,···,ei,···,eI}。
根据文献[2],操作者各行为给己方带来的收益
| $\left\{ \begin{aligned} & {{C_{{\rm{avg}}}} = P{C_A} + (1 - P){C_U}} \\ & {{C_A} = Q{R_1} + (1 - Q)({R_1} + {R_2})} \\ & {{C_U} = Q({R_3} - {B_1}) + (1 - Q)({R_3} - {B_2})} \end{aligned} \right.$ | (1) |
其中,
同理管理者各行为给己方带来的收益
| $\left\{ \begin{split} & {{X_{{\rm{avg}}}} = Q{X_F} + (1 - Q){X_Z}} \\ & {{X_F} = P{R_2} + (1 - P)({R_4} + {B_1} - H)} \\ & {{X_Z} = P({R_2} - {B_2}) + (1 - P)({R_4} + {B_2} - H)} \end{split} \right.$ | (2) |
其中,
对单一事件而言,操作者和管理者行为后得到的事件综合收益CXavg是操作者采取的安全和不安全行为给操作者带来的收益
| $ \begin{split} & {\rm{C}}{{\rm{X}}_{{\rm{avg}}}} \!\!=\!\! {X_{{\rm{avg}}}} \!\!-\!\! {C_{{\rm{avg}}}} \!\!=\!\! Q{X_F} \!\!+ \!\!(1 - Q){X_Z} - (P{C_A} + (1 - P){C_U}) = \\&\quad Q(P{R_2} + (1 - P)({R_4} + {B_1} - H)) + (1 - Q)(P({R_2} - {B_2}) + \\&\quad(1 - P)({R_4} + {B_2} - H)) - (P(Q{R_1} + (1 - Q)({R_1} + {R_2})) +\\&\quad (1 - P)( Q({R_3} - {B_1}) + (1 - Q)({R_3} - {B_2}))) \\[-12pt] \end{split} $ | (3) |
将式(3)展开,分别根据基本参数合并同类项,得到这些基本参数和对应行为概率与事件综合收益的关系,如表1所示。
| 表 1 基本参数与事件综合收益关系 Table 1 Relationship between basic parameters and comprehensive event profit |
从表1可知,由于基本参数在事件综合收益计算的设定都是正值,且综合收益是站在管理者角度确定的,因此它代表了管理者收益最大,操作者收益最小的情况。例如,R4对CXavg的影响来源于操作者的不安全行为收益和管理者奖励行为收益,当这两种行为发生的概率变化时,R4对CXavg的影响也发生变化。同理可确定其余基本参数与各行为的收益关系。对事件ei的事件综合收益如式(4)所示,CXavg是
| $\begin{split} {\rm{cx}}_{{\rm{avg}}}^i =& {\rm-}{p^i}r_1^i + {p^i}{q^i}r_2^i - (1 - {p^i})r_3^i + (1 - {q^i})(1 - {p^i})r_4^i - \\&(1 - {p^i}){h^i} + 2{q^i}(1 - {p^i})b_1^i + (1 - {q^i})(2 - 3{p^i})b_2^i \end{split}$ | (4) |
对应于操作者和管理者的博弈过程,边缘事件相当于操作者行为和管理者行为产生的事件综合收益。系统最终收益可能取决于操作者和管理者对多个事件采取的不同行为,因此这些行为对所有事件e1~i处理后产生的事件综合收益
| $ \begin{split} & {{\text{乐观后继事件综合收益为}}}\\&\left\{ \begin{array}{l}{\rm{cx}}_{\rm{avg}}^{i}+{\rm{cx}}_{\rm{avg}}^{j}={\rm{max}}\{{\rm{cx}}_{\rm{avg}}^{i},{\rm{cx}}_{\rm{avg}}^{j}\},{{\text{或关系}}}\\ {\rm{cx}}_{\rm{avg}}^{i}\cdot {\rm{cx}}_{\rm{avg}}^{j}={\rm{Sum}}\{{\rm{cx}}_{\rm{avg}}^{i},{\rm{cx}}_{\rm{avg}}^{j}\},{{\text{与关系}}}\end{array} \right. \end{split}$ | (5) |
| $ \begin{split} & {{\text{悲观后继事件综合收益为}}}\\&\left\{ \begin{array}{l}{\rm{cx}}_{\rm{avg}}^{i}+{\rm{cx}}_{\rm{avg}}^{j}={\rm{min}}\{{\rm{cx}}_{\rm{avg}}^{i},{\rm{cx}}_{\rm{avg}}^{j}\},{{\text{或关系}}}\\ {\rm{cx}}_{\rm{avg}}^{i}\cdot {\rm{cx}}_{\rm{avg}}^{j}={\rm{Sum}}\{{\rm{cx}}_{\rm{avg}}^{i},{\rm{cx}}_{\rm{avg}}^{j}\},{{\text{与关系}}}\end{array} \right. \end{split}$ | (6) |
结合SFN网络结构,各边缘事件的事件综合收益
如下给出一个SFEP的SFN,如图1所示。
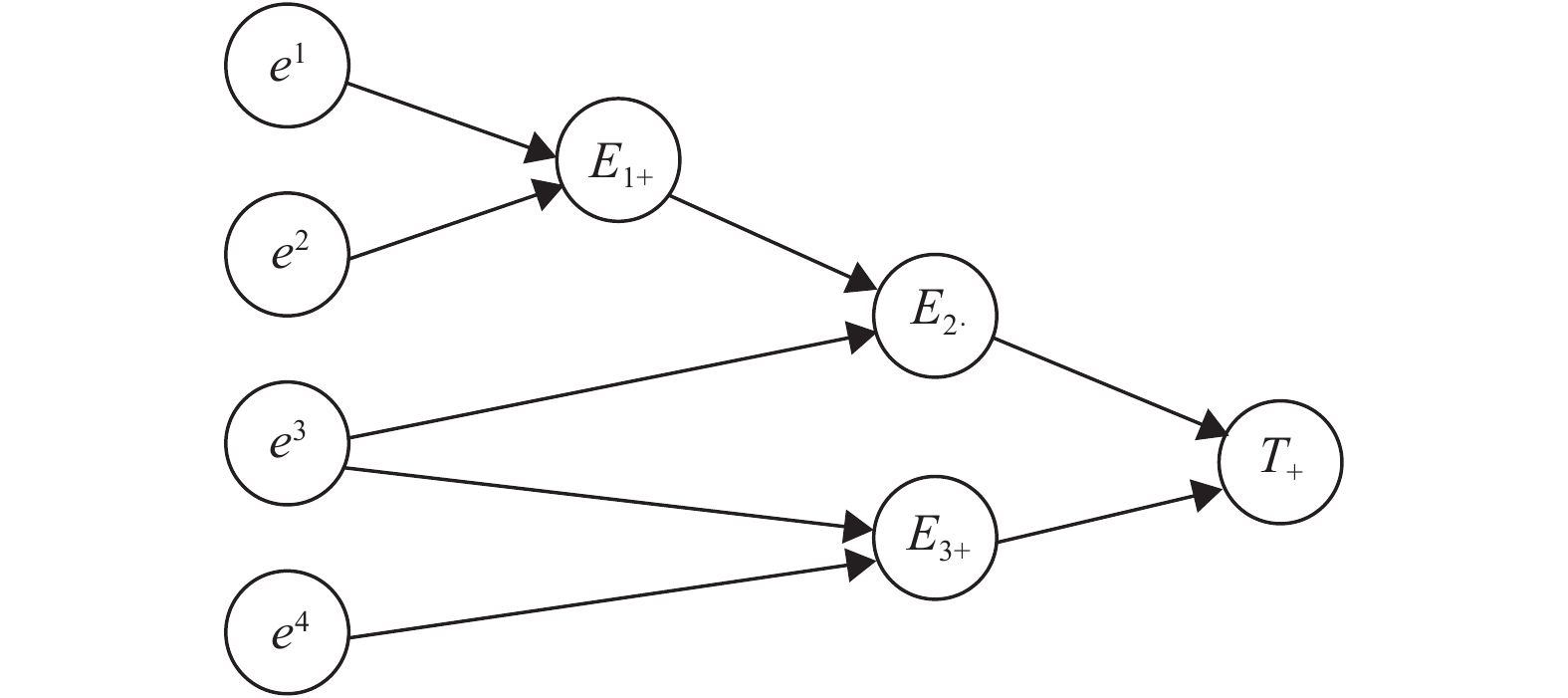
|
图 1 SFN的模型 Figure 1 Model of SFN |
图1是某工程项目中事故的SFEP。边缘事件包括e1、e2、e3、e4,代表导致事故的基本原因;E1、E2、E3表示过程事件,是边缘事件相互作用后的中间事件;T表示最终事件,是系统最终事故状态。
由3.3节可知,事件之间的演化和逻辑关系可等同于事件综合收益的演化和逻辑关系。因此,e1、e2、e3、e4可代表操作者和管理者行为后产生的事件综合收益。过程事件和最终事件下角标的“·”和“+”分别表示与关系和或关系。根据图1和SFN的化简方法[16-20]得到系统收益
| ${\rm{CXT}}_{{\rm{avg}}}^{} = {\rm{cx}}_{{\rm{avg}}}^1{\rm{cx}}_{{\rm{avg}}}^3 + {\rm{cx}}_{{\rm{avg}}}^2{\rm{cx}}_{{\rm{avg}}}^3 + {\rm{cx}}_{{\rm{avg}}}^3 + {\rm{cx}}_{{\rm{avg}}}^4$ | (7) |
基于乐观和悲观角度,将式(5)~(6)分别代入式(7)得到系统收益
| $ \begin{split} & \quad\;{{\text{乐观系统收益}}}\\&\left\{ \begin{array}{l}{\rm{CXT}}_{\rm{SFN}}=\rm{Max}\left\{\rm{Sum}\right\{\rm{Max}\{{\rm{cx}}_{\rm{avg}}^{1},{\rm{cx}}_{\rm{avg}}^{2}\},{\rm{cx}}_{\rm{avg}}^{3}\},\\ \qquad\qquad \rm{Max}\{{\rm{cx}}_{\rm{avg}}^{3},{\rm{cx}}_{\rm{avg}}^{4}\left\}\right\}\\ {\rm{CXT}}_{\rm{SFN}}>0,{{\text{管理者胜出}}}\\ {\rm{CXT}}_{\rm{SFN}}<0,{{\text{操作者胜出}}}\end{array} \right. \end{split}$ | (8) |
| $ \begin{split} & \quad\;{{\text{悲观系统收益}}}\\&\left\{ \begin{array}{l}{\rm{CXT}}_{\rm{SFN}}=\rm{Min}\left\{\rm{Sum}\right\{\rm{Min}\{{\rm{cx}}_{\rm{avg}}^{1},{\rm{cx}}_{\rm{avg}}^{2}\},{\rm{cx}}_{\rm{avg}}^{3}\},\\\qquad\qquad\rm{Min}\{{\rm{cx}}_{\rm{avg}}^{3},{\rm{cx}}_{\rm{avg}}^{4}\left\}\right\}\\ {\rm{CXT}}_{\rm{SFN}}>0,{{\text{管理者胜出}}}\\ {\rm{CXT}}_{\rm{SFN}}<0,{{\text{操作者胜出}}}\end{array} \right. \end{split}$ | (9) |
各事件e1、e2、e3、e4确定对应的基本参数代入式(4)求得
上述过程完成了系统收益的分析。该系统的参与者是操作者和管理者,操作者有安全和不安全行为,管理者有惩罚和奖励行为。对于任何一个导致系统故障的边缘事件,操作者和管理者都可采取这些行为。因此,经过这些行为处理后的事件对于参与者将得到收益。不同边缘事件之间逻辑关系不同,最终演化为系统的最终事件。可使用SFN方法研究事件综合收益和系统收益关系,进而判断系统中参与者的胜出方。为类似的施工安全管理、组织管理、工程管理等的参与者提供博弈方案,使己方利益最大化。
5 结论在系统中,对各事件操作者和管理者都有概率采取不同行为导致各事件综合收益变化,进而导致系统收益变化。对事件综合收益表达式进行化简,重新组合得到各基本参数在事件综合收益中出现的概率。给出了与或关系的事件综合收益与后继事件收益逻辑关系表达式,从而确定系统收益和博弈胜出者。通过实例说明方法分析流程,得到了实例系统的各事件综合收益和系统收益。说明了方法的适用性和正确性。
| [1] |
徐杰, 李果林. 风险收益动态视角下政府与社会资本合作演化博弈分析[J].
软科学, 2020, 34(6): 126-130.
XU J, LI G L. An evolutionary game analysis of government and social capital cooperation under the dynamic perspective of risk-benefit[J]. Soft Science, 2020, 34(6): 126-130. |
| [2] |
陈艳, 吕云翔, 柴访, 等. 动态激励视角下建筑工人不安全行为演化博弈分析[J].
安全与环境工程, 2020, 27(1): 197-203.
CHEN Y, LYU Y X, CHAI F, et al. Evolutionary game analysis of unsafe behavior of construction workers from the perspective of dynamic incentives[J]. Safety and Environmental Engineering, 2020, 27(1): 197-203. |
| [3] |
于晓辉, 杜志平, 张强, 等. 一种资源投入不确定情形下的合作博弈形式及收益分配策略[J].
运筹学学报, 2019, 23(4): 71-85.
YU X H, DU Z P, ZHANG Q, et al. A generalized form of fuzzy cooperative game and its solution[J]. Operations Research Transactions, 2019, 23(4): 71-85. |
| [4] |
刘佳, 王先甲. 网络博弈合作剩余收益分配的协商方法[J].
系统工程理论与实践, 2019, 39(11): 2760-2770.
LIU J, WANG X J. A bargaining method for cooperative surplus income allocation in network game[J]. Systems Engineering-Theory & Practice, 2019, 39(11): 2760-2770. DOI: 10.12011/1000-6788-2018-2282-11. |
| [5] |
杨柏林. 基于博弈论的新零售模式下供应链收益优化研究[D]. 吉林: 吉林大学, 2019.
|
| [6] |
何长全, 贾广社, 孙继德. 三方博弈视角下项目安全行为治理策略分析[J].
软科学, 2019, 33(1): 87-90.
HE C Q, JIA G S, SUN J D. Governance strategy analysis of project safety behavior from the perspective of three-party game theory[J]. Soft Science, 2019, 33(1): 87-90. |
| [7] |
杨雪, 田阳, 仝凤鸣. 基于进化博弈的矿工情绪监管与不安全行为研究[J].
煤矿安全, 2018, 49(8): 299-302.
YANG X, TIAN Y, TONG F M. Research on miners' emotional supervision and unsafe behavior based on evolutionary game[J]. Safety in Coal Mines, 2018, 49(8): 299-302. |
| [8] |
郑霞忠, 史高阳, 陈述. 多方博弈下起重作业人员有意不安全行为致因分析[J].
中国安全生产科学技术, 2017, 13(5): 175-181.
ZHENG X Z, SHI G Y, CHEN S. Causation analysis on intentional unsafe behavior of crane operator under multi-parties game[J]. Journal of Safety Science and Technology, 2017, 13(5): 175-181. |
| [9] |
盖丽丽. 基于动态博弈的矿工不安全行为研究[J].
煤矿安全, 2016, 47(9): 251-253.
GAI L L. Research on miners' unsafe behavior based on dynamic game theory[J]. Safety in Coal Mines, 2016, 47(9): 251-253. |
| [10] |
田水承, 赵雪萍, 黄欣, 等. 基于进化博弈论的矿工不安全行为干预研究[J].
煤矿安全, 2013, 44(8): 231-234.
TIAN S C, ZHAO X P, HUANG X, et al. Research on miner unsafe behavior intervention based on evolutionary game theory[J]. Safety in Coal Mines, 2013, 44(8): 231-234. |
| [11] |
高云莉, 王庆春, 王楠楠. 工程项目主体在风险管理合作中的演化博弈分析[J].
数学的实践与认识, 2012, 42(9): 33-37.
GAO Y L, WANG Q C, WANG N N. An evolutionary game model for the risk management cooperation among the project management parties[J]. Mathematics in Practice and Theory, 2012, 42(9): 33-37. DOI: 10.3969/j.issn.1000-0984.2012.09.006. |
| [12] |
王敏, 王卓甫, 肖建红. 建设工程管理的合作博弈决策[J].
统计与决策, 2007(16): 65-67.
WANG M, WANG Z F, XIAO J H. Cooperative game decision of construction project management[J]. Statistics and Decision, 2007(16): 65-67. DOI: 10.3969/j.issn.1002-6487.2007.16.024. |
| [13] |
李莎莎, 崔铁军. 基于SFN故障模式的最终事件故障概率分布确定方法[J].
广东工业大学学报, 2020, 37(6): 9-16.
LI S S, CUI T J. The determination method for fault probability distribution of target event based on fault mode of SFN[J]. Journal of Guangdong University of Technology, 2020, 37(6): 9-16. DOI: 10.12052/gdutxb.200078. |
| [14] |
崔铁军, 李莎莎. 基于因素驱动的东方思维人工智能理论研究[J].
广东工业大学学报, 2021, 38(1): 1-4.
CUI T J, LI S S. Research on the intelligent science theory of oriental thinking based on factor driven[J]. Journal of Guangdong University of Technology, 2021, 38(1): 1-4. DOI: 10.12052/gdutxb.200123. |
| [15] |
崔铁军, 李莎莎. 系统故障演化过程的可拓学原理[J].
广东工业大学学报, 2020, 37(5): 1-6.
CUI T J, LI S S. An extension theory of system fault evolution process[J]. Journal of Guangdong University of Technology, 2020, 37(5): 1-6. DOI: 10.12052/gdutxb.200053. |
| [16] |
崔铁军. 系统故障演化过程描述方法研究[J].
计算机应用研究, 2020, 37(10): 3006-3009.
CUI T J. Research on description method of system fault evolution process[J]. Application Research of Computers, 2020, 37(10): 3006-3009. |
| [17] |
CUI T J, LI S S. Research on complex structures in space fault network for fault data mining in system fault evolution process[J].
IEEE Access, 2019, 7(1): 121881-121896.
|
| [18] |
崔铁军, 李莎莎. 空间故障树与空间故障网络理论综述[J].
安全与环境学报, 2019, 19(2): 399-405.
CUI T J, LI S S. A Survey of space fault tree and space fault network[J]. Journal of Safety and Environment, 2019, 19(2): 399-405. |
| [19] |
崔铁军, 李莎莎, 朱宝岩. 含有单向环的多向环网络结构及其故障概率计算[J].
中国安全科学学报, 2018, 28(7): 19-24.
CUI T J, LI S S, ZHU B Y. Multidirectional ring network structure with one-way ring and its fault probability calculation[J]. China Safety Science Journal, 2018, 28(7): 19-24. |
| [20] |
CUI T J, LI S S. System movement space and system mapping theory for reliability of IoT[J].
Future Generation Computer Systems, 2020, 107: 70-81.
DOI: 10.1016/j.future.2020.01.040. |
| [21] |
何华灿. 重新找回人工智能的可解释性[J].
智能系统学报, 2019, 14(3): 393-412.
HE H C. Refinding the interpretability of artificial intelligence[J]. CAAI Transactions on Intelligent Systems, 2019, 14(3): 393-412. |
| [22] |
何华灿. 泛逻辑学理论——机制主义人工智能理论的逻辑基础[J].
智能系统学报, 2018, 13(1): 19-36.
HE H C. Universal logic theory — logical foundation of mechanism-based artificial intelligence theory[J]. CAAI Transactions on Intelligent Systems, 2018, 13(1): 19-36. |
 2021, Vol. 38
2021, Vol. 38

