2. 辽宁工程技术大学 理学院,辽宁 阜新 123000;
3. 广东工业大学 可拓学及创新方法研究所,广东 广州 510006;
4. 国家高性能计算中心 成都分中心,四川 成都 610094
2. College of Science, Liaoning Technical University, Fuxin 123000, China;
3. Institute of Extenics and Innovation Methods, Guangdong University of Technology, Guangzhou 510006, China;
4. Chengdu Sub Center, National High Performance Computing Center, Chengdu 610094, China
人工智能所面临的一个迫切问题是要有统一的人工智能理论[1-3];知识图谱是当前人工智能发展的热点[4-5],在肯定其重大意义的同时,要看到它在理论上的不完善,以及发展方向上的不明确。知识图谱发展的最终目标是要把数据库构建成为人脑知识生长的同构体,它不是被动的僵化储存所,而是主动生长的拓展体。本文提出了智能拓展库的构想,这是知识图谱的升级版,是多层次的嵌入式图数据库系统。因素牵引的知识增长表达式是知识谱系多支图的基元,由此建成一个概念谱系图网络,勾画出有关领域的知识本体结构。基于因素表达事实作基元所生成的另外一个图网络则是进行智能生成与工作的系统,利用因素空间的理论和方法来辅助智能的开拓。本文的结构:第1节对知识图谱进行简评;第2节介绍因素空间对知识图谱的拓展问题的帮助;第3节对智能拓展库进行构想,并介绍因素查询语言;第4节说明问题和展望。
1 知识图谱简评人工智能有2个截然不同的任务:(1) 把人类已有的知识从图书、文件、信函中转移给机器;(2) 让机器模拟人脑认识和改造世界。前者似乎是容易且该先做的事情,但事实恰好相反,它比后者更难而被长期拖延。在2012年前后,“知识图谱”的名称在谷歌叫响,掌握互联网资源的几家巨头公司竞相用此技术来开发新的搜索引擎。互联网是传递信函的渠道,知识图谱必须理解自然语言,因而也必然会加速自然语言理解的研究进程,它的历史贡献首先是实现图书、文件、信函的数字化。现在,它已使自然语言理解从数据驱动的字频统计方法转向知识连同数据驱动的研究途径。图数据网络模型已经在跨越同义字、反义字等类歧义鸿沟方面取得了明显成效。知识图谱必会在机器模拟人脑认识和改造世界方面取得卓越成效,它为智能化提供了网络传输的翅膀,其前景不可限量。
在肯定其意义的同时,也要看到其在基础理论方面的不足。知识图谱与传统的知识表示的分界线在于它们所采用语言的分离:关系数据库的查询靠SQL语言(Structured Query Language);知识图谱的查询要靠SPARQL语言(Simple Protocol and RDF Query Language)。SQL叫做表库语言,SPARQL叫做图库语言,图数据库的名称便由此而来。
知识表示的每一种方法都要表达事实,无论差异如何,都要在语言上符合主、谓、宾的SPO表达形式,把主语和宾语视为节点,把谓语视为有向边,它们都是图的基元。知识图谱的数学定义是一个有向图,有向图的定义是在一组前节点H、一组有向边G和一组后节点T之间所建立的特定关系,也就是笛卡尔乘积空间H×G×T中的一个特定子集。一张关系数据库表是由对象、属性名、属性值所建立的一个三元关系,设三者所构成集合分别是H,G,T,表中每个格子点所对应的三元组就是H×G×T中的一个点,一个用属性名作边的图基元;整个表就是H×G×T中的一个子集,就是一个知识图谱。所以,表数据库与图数据库并没有本质的差别;数学上的“图”并非生活当中的图,生活当中的图是看得见的绘制品,称SPARQL为图数据库语言,是因为Web是生活中的图,有节点和边。但Web图其实并不符合图的数学定义,SPARQL图中的节点与Web节点的域名毫无关系。所以,知识图谱从基础上说理论尚欠严谨。现在人们误以为图数据的特征是直观可见,这适用于小数据,当节点稍多时,复杂一点的图谱就不再直观,这使可视化研究变得格外重要。
SPARQL语言并不是理想的语言,它的程序在阅读和编写上极其繁琐,它的查询功能不像SQL语言那样可进行是非判断和推理,只是回答给定的一个基元在不在库中,进而回答给定的一组基元是否与某个子库同构。SPARQL语言的推理功能更是无法与SQL语言相比,只能发现“叔侄”是“兄弟”和“父子”关系的叠加这一类规则,尽管这种推理有其独特作用,但都需要进行提升和改进。
SPARQL语言打破了人们的惯性思维,给编程带来新的研究前景,开源的知识图谱可以在短短几周的时间内就发展到节点过亿的规模。各种限制都可以考虑取消,新的设想和构思不断涌现,但也要保持头脑清醒,在大潮中求实求稳。图谱要大而不乱,活而不杂。现在已经发现有错,也有纠错的算法,但是在庞大的图谱中要搜寻迴路,可能是一个NP(Nondeterminism Polynomial)难问题。图谱要计算代价、讲求效率、防止浪费,更要防止对环境可能带来的污染。
在知识图谱的发展方面,实践一直发展在理论的前头,现在需要加强基础理论,尤其是数学理论。
2 因素空间的知识谱系理论 2.1 因素是智能数学的元词人脑面对事物的第一反应就是要回答“这是什么?”的问题。神经中枢把对象信息传递到记忆单元,查找该对象的存储位置,或建立新档,或用旧档进行对比判断,迅速做出应答。这是最基本的思维活动环节,其数学形式可表达为
这里
因素在数学上被定义成一个映射
例如,因素
知元表达式:
| $ f(e) = p $ | (1) |
例如,“这辆车的颜色是红的”。
从对象
可拓学[6]早就睿智地提出了“物元”和“事元”的概念,并在这方面做了很好的研究[7]。“知元”是对“物元”和“事元”的一种承袭,只是特别强调了因素的地位和作用。
记因素
关系也可以用因素来表示。例如,“张三是李四的妻子”表达的是李四和张三之间有夫妻关系。取因素
因素的定义域
单一对象也可以被视为概念,例如,“北京”只有一个,也可以当作概念。所以,关系因素也是谱系因素。
概念定义因素,因素导出概念,因素与概念是否一样多?的确,同一个因素在对象的层次结构中会产生众多的后裔因素,例如,
因素的相是表示属性、情感和意向的词汇,也可以是表示形态或程度的数。相域
人的智能活动不靠条件反射,而是靠人脑所具有的因果分析的能力。因素是因果分析的要素。因素非因,乃因之素。“雨量充沛”是取得“好收成”的原因,但却不是因素,这里的因素是降雨量。它是一个变量,其变化可以使农作物丰收,也可以使之颗粒无收,显示了它对收成有重要影响,这才使人断定“雨量充沛”是取得“好收成”的原因。因果分析的核心思想不是从属性或状态层面孤立静止地去寻找原因,而是要先从更深层面上去寻找对结果最有影响的因素,只有找到了这组因素,才能找到最佳的原因。从找原因到找因素是人脑认识的一种升华,也是因果性科学的思想核心。
因素是定性的变项,是广义的变量。它可以把定性的相域嵌入殴氏空间的定量相域中去,转化为普通的变量。前提是要把相域按一定目标有序化。例如职业相域={工人,农民,士兵,企业主,雇员,教师,医生,律师,官员,···},这些职业之间没有次序。但是在高考生报考志愿时就要对未来的职业排序。工资待遇、社会需要、兴趣爱好、综合加权各有不同排法。当
因素有几种特殊的叫法:(1) 两极叫法,如“美丑”;(2) 后面加问号,如“美丽?”;(3) 前面加“有无”或“是否”,如“是否美丽”;(4) 后面加“性”字,如“美丽性”。
因素与属性不能混淆。属性能问是非:“这花是紫的吗?”因素不能问是非:“这花是颜色吗?”。属性是被动描述的静态词;因素是主动牵引思维的动态词。“Attribute”在形式概念分析(Formal Concept Analysis,FCA)[8]中代表属性值,如“红”“黄”等;但在粗糙集(Rough Sets,RS)[9]中代表属性名,如“颜色”等。在术语上出现了混乱。FCA和RS都是在1982年与因素空间(Factor Space,FS)[10]同年创立,协调的约定是:FCA中的“Attribute”=FS中的“属性”;RS中的“Attribute”=FS中的“因素”。
因素比属性高一个层次,因素统帅属性。人脑是高效率的信息处理器,按因素来组织感觉神经元。孟德尔在遗传学研究中苦于生物属性的杂乱,在1865年提出了基因的概念,他所使用的英文名字就是Factor(约翰森在1909年才改名为Gene),基因就是生物属性的质根,因素是广义的基因。基因打开了生命科学的大门,因素是从数学上帮助打开信息科学大门的一把钥匙。
2.2 因素/概念谱系概念是一个二元组
每个内涵描述句都是由因素所表达的知元表示句,见式(1)。它们被外延中全体对象所满足,也就是说,团粒中的所有对象在有关因素下的相值均相同。当目标需求不满足时,知识就需要更新了。这时,人的注意力就会根据目标需求而确定一个新的因素,它在团粒中能取不同的相值,按照它的不同相值来分类,概念团粒就分裂了。因素就是概念团粒细化的分化器,这是知识增长的关键环节,需要设立一种统一的表达形式。
知增表达式:
| $ U = D(f) \to I(f) = \left\{ {{\alpha _1}, \cdots ,{\alpha _k}} \right\} $ | (2) |
式(2)中,
例1
这是一个知增表达式,简称概念分化式。被分化的是零概念,它的概念团粒是宇宙。“虚实”是定义在宇宙万事万物上的一个因素。除了虚实之外是否能找到以宇宙为定义域的因素?“身高”是因素,但只对能直立起来的动物有意义,对石头则没有意义。“重量”是因素,但只对物质有意义,对精神界则没有意义。因此能找到最普遍、最抽象的因素寥寥无几。在某种意义,甚至是唯一的。例如“阴阳”,它也是最具普遍意义的一个因素,但和虚实可以相互转化。虚实这个因素把宇宙划分成两大类,零概念被分化为物质与精神2个概念。
精神=D(文理)
例1说明了因素是怎样牵引着概念分化和知识增长的。因素在划分概念的过程中,也塑造出自己发展的谱系。因素被定义域所制约,在定义域之外,因素会失去意义。于是,在因素与因素之间出现了生与被生的关系:没有虚实因素的划分,就没有物质的概念,没有物质的外延,就没有因素生命性的定义域,生命性就失去了生存的土壤。所以,因素虚实生出了因素生命性。
定义1[3] 如果因素
对谱系因素来说,一个因素
显然,祖裔关系具有传递性,构建
为了能画出祖裔关系图,需要先把祖裔表变为父子关系表,具体做法是:对
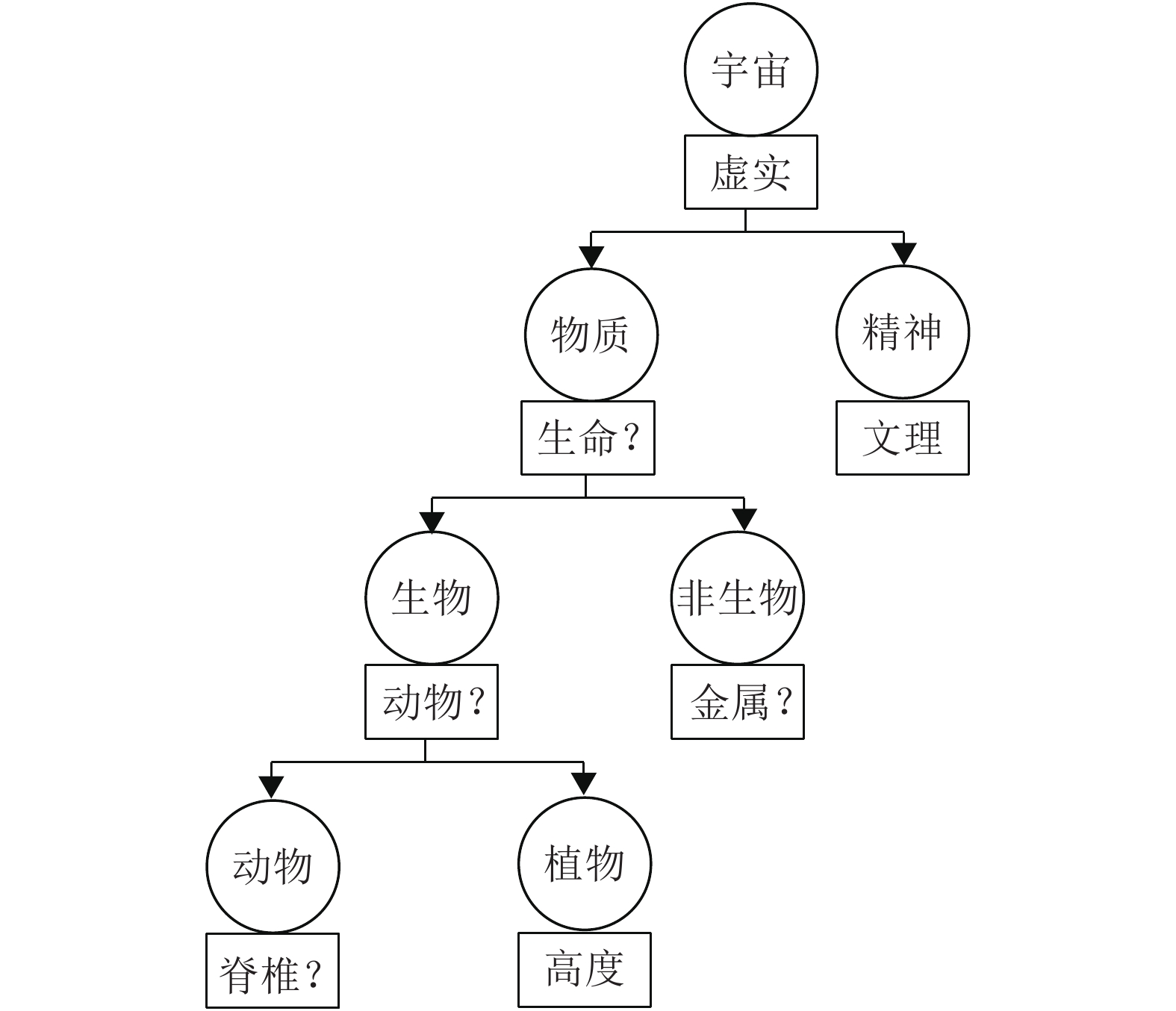
|
图 1 因素/概念谱系 Figure 1 Factor/concept spectrum |
用记号“
定义2 称
记号
因素空间是智能活动的平台,它在同定义域的因素之间定义了逻辑、数学和注意力权重等多方面的运算,可以快捷地进行识别、判断、归纳、推理、预测、控制、评价、决策等智能活动[10-15]。
如果说粗糙集为关系数据库提供了样本理论,那么,因素空间就为粗糙集提供了母体理论。如前所述,粗糙集的属性名就是因素,信息系统表就是因素分析表,表的每一行就是因素空间中的一个样本点。信息决策表就是因果分析表,粗糙集的决策分析和分类学习都在因果分析与决策方法之中。因素空间能完成粗糙集能做的事,而且做得更快,粗糙集不能做而因素空间能做的事情有6类。
(1) 对因素(包括属性名)的逻辑运算给出了明确的数学定义。
(2) 提出了背景关系和背景分布的概念。给定因素空间
定义3 给定因素空间
| $R = F(E) = \{ {f_1}(e), \cdots , {f_n}(e)|e \in E\} $ | (3) |
背景关系反映了因素之间的相互影响。当背景关系没有去掉任何格子点时,因素就是独立的。粗糙集没有引进背景关系,就只能表现独立因素,而独立因素之间不存在因果联系,这就先天制约了它进行因果分析的能力。
(3) 背景关系决定了因素之间的一切归纳与推理,它一般是凸集,可以由少数个顶点生成。这一组顶点的集合叫做背景基
(4) 将概率逻辑引入因果分析。
定义4 给定联合相空间中的一组样本点
这个定义把概率逻辑引入了因素空间,贝叶斯的逆向推理可以从目标倒逼条件,为问题求解提供了便利。
(5) 将模糊逻辑引入识别与推理。
定义5 设背景分布的最大值为
| ${A_{i(1) \cdots i(n)}} = (1/L){r_{i(1) \cdots i(n)}}$ | (4) |
因素空间是模糊数学的升级版,它所导出的模糊落影理论,把模糊度定义为随机集的覆盖概率,把模糊现象转化为幂上的随机现象。为主观性测度建立了坚实的理论基础和可行的实践方法。
(6) 通过定性坐标的定量化、线性规划等优化理论可以进入智能孵化的过程。
2.3 用因素对子库名进行编码对概念名词进行编码是自然语言理解最重要的工程。这一工程进展不易的原因是没有聘用因素。内涵都是靠因素来叙述的,只有因素才能确定内涵,靠因素来编码就能看准同义字、近义字和反义字,并确立国际语言的范本。
任何表名或图名都是一个概念名词,这些名词必定组成一个概念谱系。下面涉及8个因素和它们所生出的19个概念,按祖裔的世代排列见图2。
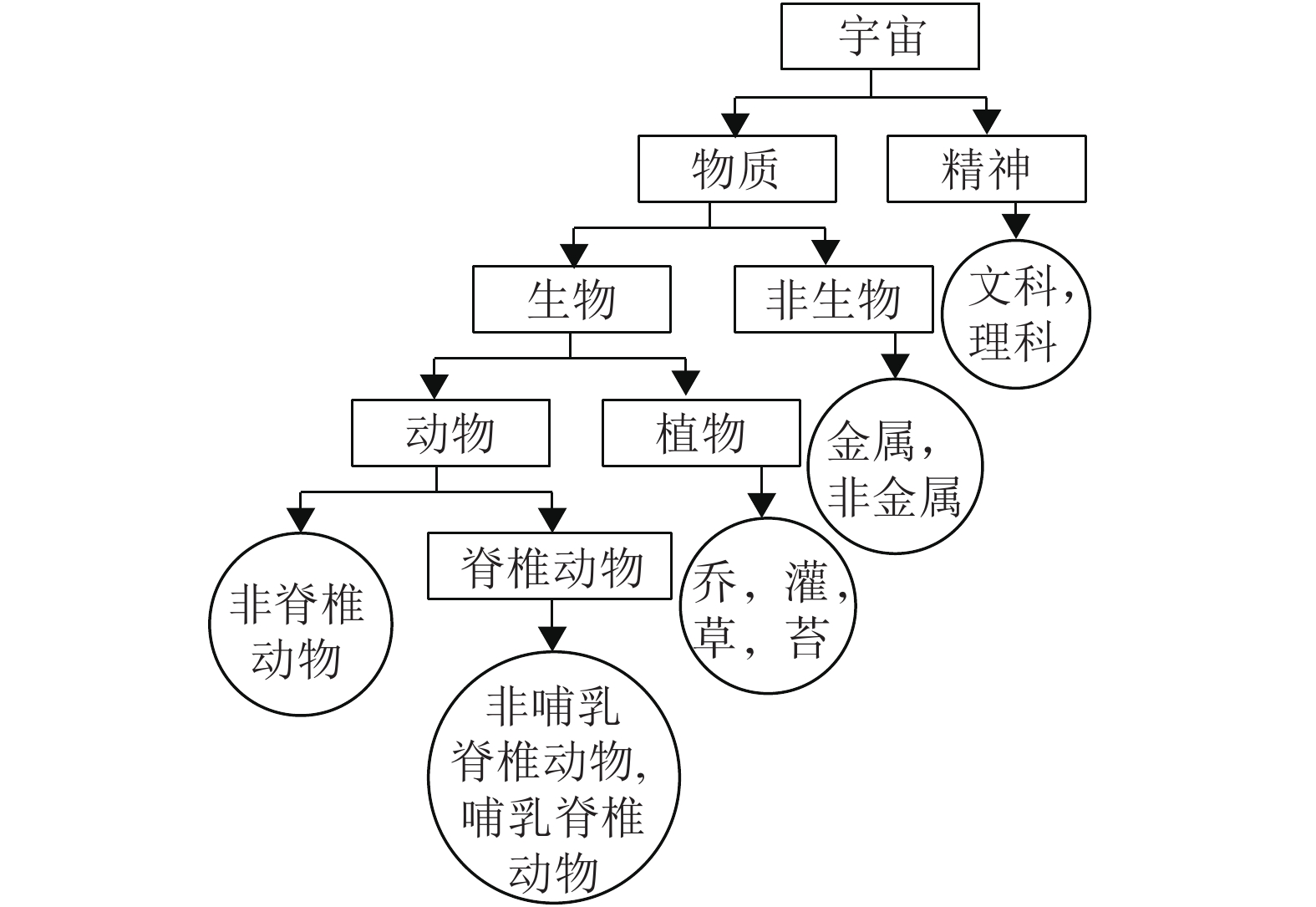
|
图 2 祖裔世代排列谱系 Figure 2 Pedigree of ancestral generation arrangement |
在始祖概念“宇宙”之下,18个概念按世代排成5行。
预备步骤为将所有因素的相分别编码,加到括号中。
它们的编码为
物质:1;精神:0;
生物:1I; 非生物:10;文科:00;理科:01;
动物:111; 植物:110;金属:101; 非金属:100;
脊椎:1111;非脊椎:1110;乔:1101;灌:1102; 草:1103;苔:1104;
哺乳动物:11111;非哺乳的脊椎动物:11110。
宇宙是始祖,不编码。其他概念的编码原则是:以概念的世代来定码位,再按各因素相域的编码来填入码值。码的位数越少,码字越短,概念的辈分越高,概念团粒越大。子概念必须继承父概念的编码,在父码之后加上自己对其生出因素的相值码。
例如,排在第一行的精神由宇宙的被定义因素“虚实”所分出,在虚实相域中的编号为0。因它是宇宙的第一代子概念,就把0排在第一位。又如,理科是因素“文理”所分,它在相域中的编号为0,因属于第2代,将0填入第2位。因它是精神的子概念,第一位照写0,故其编码为00。又如,苔是因素“植物高度”所分,它在相域中的编号为4,因属于第4代,将4填入第4位。因它是植物的子概念,前3位照写110,故其编码为1104。
编码根本意义在于把内涵数字化,这蕴含着难以想见的应用。最显眼的应用是查询。在包含大量概念的图中要找出其中的一个,先按第一足码缩小搜索范围,再查第二足码缩小范围,直到该概念被查出,这是最快的方式。值得指出的是,例1的概念谱系图是一颗倒树,由于目标的不同,会得到不同的倒树,这样所得到的林,会打乱世代次序,两树的交点会有不同的编码。但就像图书目录有多种查号一样,能有多种编码,但不能一个编码对应着多个不同义的概念,如果是那样,就需要寻找新的因素增加码位。
编码的意义除了快速查询之外,另一个重要应用是快速进行演绎推理。
命题1 若概念乙的编码是概念甲编码的前一部分,则推理句“
证明 若概念乙的编码是概念甲编码的前一部分,则概念乙必是概念甲的祖先,概念甲的外延必被概念乙的外延所包含,按集合论中著名的Stone表现定理知,逻辑的蕴含就是外延的被包含,故推理句“
树状图编码有明确的世代,多树成林,会出现乱代现象,编码不唯一,但像人的家谱一样,没有害处。
3 智能拓展库的构建 3.1 库的结构智能拓展库是由一系列知识谱系图所构成的系统。每张知识谱系图的基元就是一个多支图。图与图之间存在着层次关系,形成嵌套结构。
(1) 子库的嵌入和编码。以图1为例,“理科”位于图的末端,称为足概念。它在主库中有码01,但若不满足这个概念,还想知道有多少不同的理科,这就可以把理科当做按键,一按就开出一个窗口,里面亮出一个以理科为始祖的子库。由数、理、化、代数、几何、分析等6个概念组成。编码原则是层层负责,子库要对它所属的全部6个节点进行编码:数1、理2、化3、代数11、几何12、分析13。
但是,子表不能给自己的表名编码。因为子表名就是上级足概念节点之名,都叫做“理科”,所以子表表名的编码已经被上级定为01,子表中各节点全名等于子表名下接表内名:数 011、理012、化013、代数0111、几何0112、分析0113。这就叫做图的嵌入和编码的层层负责制。
(2) 概念查询。假定有一概念,已知其编码,要在总库中查出来,则在总表中寻找具有该概念码的第一位码的节点,直到无法下移,点击按键进入下层子表。继续查询,直到查获为止。
(3) 因素空间藤。知识谱系图中有一些带花的节点,在那些概念上同时定义多个因素形成因素空间。带有因素空间的谱系就叫做因素空间藤。对每个花苞,都必须在窗口下存放一张因果分析表。因果分析图的职责是实现因素空间所能做的一切工作:识别、归纳、推理、预测、评价、决策、规划等智能活动。
3.2 因素查询语言FQL(Factorial Query Language)FQL和SQL语言一样,具有4种功能:数据定义、数据操纵、数据控制和数据查询。下文分述不同之处。
1) 数据定义语言
数据定义的任务是根据目标从主库中建立子库的知识谱系图。
生成知识谱系图的前提是要靠专家先给编程员一张因素词表,表上用自然语言写出所有要用到的因素名称,并在每一个因素
字号(周瑜)=公瑾,字号(关羽)=云长,······
则必须由专家输入:因素“字号”,
在这份表中还要注明定义域之间的包含关系,例如:[人]
如果输入的名单足够充分,编程员就可以操作如下:(1) 在因素之间定义祖裔关系:
写出因果分析表的过程与关系数据库表的一样。
2) 数据的查询
规定1 对于给定的子库,数据查询的基本任务是:给定一个域名,要写出子库的因素谱系图;对任意一个输入的因素,要回答它在不在主库中。若在,则找到所在的因果分析表进行查询,其查询方式同于关系数据库的查询。
给定因果分析表
FQL概念生成器要实现的功能是:(1) 给定多因素的因果分析表,生成原子概念集;(2) 按因素的分辨度从高到低,对论域进行划分,得到概念格。
框架中的槽,就是一组因素,一个侧面就是一个因素,到了侧面就没法再往下走了。因素谱系把框架思想发展了。
因素库语言可以描写状态空间,可以与图数据库的知识图谱相互转化,只不过把传统的知识图谱划分为非关系因素表和关系图谱,这样才能提高数据库的效能;盲目的混合开源扩张不宜渲染。FQL能融合SQL和知识表示的各种语言。
4 问题和展望知识图谱构建的目标是为系统性、全面性认识事物、提高决策水平和解决问题等服务。从被动的凝固储存体到智能拓展、主动生长是知识图谱发展的内在要求。本文提出了知识图谱智能孵化库的基本概念和构想,并用因素空间理论探讨实现智能判断、推理、评价、决策、规划等问题的基本策略,使知识图谱数据库变为智能孵化、智能拓展的活体。
后续的研究将进一步与可拓学理论结合,进行知识图谱智能拓展的交叉研究,研究大数据环境下知识图谱拓展库的的拓展、变换算法,研究知识图谱的基元−因素化表达及其运算,进一步提升知识图谱在问题处理等领域的智能化程度。本文提到的拓展还很不成熟,离可拓学的拓展还有一定距离,需继续努力。
展望未来,希望智能拓展库可以进一步实现智能孵化器的作用,自上而下与自下而上相结合地开展智能孵化的全民工程。实现分布式多智能体想实现的系列功能。
| [1] |
钟义信. 机制主义人工智能理论——一种通用人工智能理论[M]. 北京: 北京邮电大学出版社, 2021.
|
| [2] |
何华灿. 泛逻辑学理论——机制主义人工智能理论的逻辑基础[M]. 北京: 北京邮电大学出版社, 2021.
|
| [3] |
汪培庄. 因素空间理论——机制主义人工智能理论的数学基础[M]. 北京: 北京邮电大学出版社, 2021.
|
| [4] |
刘峤, 李杨, 段宏, 等. 知识图谱构建技术综述[J].
计算机研究与发展, 2016, 53(3): 582-600.
LIU Q, LI Y, DUAN H, et al. Knowledge graph construction techniques[J]. Journal of Computer Research and Development, 2016, 53(3): 582-600. DOI: 10.7544/issn1000-1239.2016.20148228. |
| [5] |
HIBA A, SHADY E. Effective searching of RDF knowledge graphs[J].
Web Semantics: Science, Services and Agents on the World Wide Web, 2018(48): 66-84.
|
| [6] |
蔡文, 杨春燕. 可拓学的基础理论和方法体系[J].
科学通报, 2013, 58(13): 1190-1199.
CAI W, YANG C Y. Basic theory and method system of topology[J]. Chinese Science Bulletin, 2013, 58(13): 1190-1199. DOI: 10.1360/972012-1472. |
| [7] |
李兴森, 许立波, 刘海涛. 面向问题智能处理的基元—因素空间模型研究[J].
广东工业大学学报, 2019, 36(1): 1-9.
LI X S, XU L B, LIU H T. A research on problem oriented intelligent processing model by basic-element and factor space[J]. Journal of Guangdong University of Technology, 2019, 36(1): 1-9. DOI: 10.12052/gdutxb.180135. |
| [8] |
WILLE R. Restructuring lattice theory: an approach based on hierarchies of concepts[J].
Ordered Set, 1982: 445-470.
DOI: 10.1007/978-3-642-01815-2_23. |
| [9] |
PAWLAK Z. Rough sets[J].
International Journal of Computer and Information Sciences, 1982, 11(5): 341-356.
DOI: 10.1007/BF01001956. |
| [10] |
汪培庄, 李洪兴. 知识表示的数学理论[M]. 天津: 天津科技出版社, 1994.
|
| [11] |
WANG P Z, SUGENO M. The factors field and background structure for fuzzy subsets[J].
Fuzzy Math, 1982, 2(2): 45-54.
|
| [12] |
汪培庄. 模糊集与随机集落影[M]. 北京: 北京师范大学出版社, 1985.
|
| [13] |
任思行, 曾繁慧, 郭嗣琮. 结构元理论下的模糊Markov决策过程[J].
辽宁工程技术大学学报(自然科学版), 2020, 39(2): 180-183.
REN S H, ZENG F H, GUO S Z. Fuzzy markov decision process based on structural element theory[J]. Journal of Liaoning Technical University (Natural Science), 2020, 39(2): 180-183. |
| [14] |
蒲凌杰, 曾繁慧, 汪培庄. 因素空间理论下基点分类算法研究[J].
智能系统学报, 2020, 15(3): 528-536.
PU L J, ZENG F H, WANG P Z. Base point classification algorithm based on factor space theory[J]. CAAI Transactions on Intelligent Systems, 2020, 15(3): 528-536. |
| [15] |
孙慧, 曾繁慧, 蒲凌杰. 因素空间理论下多目标因果分析的降维算法研究[J].
辽宁工程技术大学学报(自然科学版), 2021, 40(5): 466-472.
SUN H, ZENG F H, PU L J. Research on dimension reduction algorithm of multiple targets causal analysis based on factor space theory[J]. Journal of Liaoning Technical University (Natural Science), 2021, 40(5): 466-472. |
 2021, Vol. 38
2021, Vol. 38

