数字高程模型(Digital Elevation Model, DEM)是地表形态的数字化模拟，被广泛应用于测绘、水文、军事、工程建设、自然灾害监测等领域^[1-3]，分析其高程精度对相关应用领域具有重要参考价值。目前，对DEM进行高程精度检核的数据来源主要有GNSS (Global Navigation Satellite System)静态/动态测点、水准仪和全站仪测点、机载激光扫描测点、ICESat (Ice, Cloud, and land Elevation Satellite)等雷达测高、地形图提取点、航空摄影测量生成DEM与其他高精度DEM等^[4-7]，其中车载动态PPP(Precise Point Positioning)技术具有廉价、高效、作业范围广、精度高等特点，本文将车载动态PPP技术结合重力场模型采集到的正常高数据作为DEM高程检核的外部数据。

近年来，全球数字高程模型发展迅猛，其中典型代表主要有2003年美国国家航空航天局(National Aeronautics and Space Administration, NASA)和美国国家地理空间情报局(National Geospatial-Intelligence Agency, NGA)联合发布的SRTM(Shuttle Radar Topography Mission)、2009年美国国家航空航天局和日本经济产业省(METI, Ministry of Economy, Trade and Industry)共同研制的ASTER GDEM (Advanced Spaceborne Thermal Emission and Reflection Radiometer Global Digital Elevation Model)、2015年日本航空航天局(JAXA, Japan Aerospace Exploration Agency)公开的AW3D30(ALOS World 3D)。本文以广东部分地区为研究区域，对上述3种数字高程模型进行了外部精度检核，并着重分析了各模型在不同的海拔区间的精度差异。

精密单点定位技术(PPP)指利用载波相位观测值以及由IGS(International GNSS Service)等组织提供的高精度的卫星星历及卫星钟差来进行精密单点定位的方法，伪距及相位的线性化观测方程可写为^[8]。

式中： ${\tilde \rho _i}$ 为伪距观测值， ${l_i}{\rm{ = }}\dfrac{{{X_i} - {X_{\rm{0}}}}}{{\rho _i^{\rm{0}}}}{\rm{,}}{m_i}{\rm{ = }}\dfrac{{{Y_i} - {Y_{\rm{0}}}}}{{\rho _i^{\rm{0}}}}{\rm{,}}{n_i}{\rm{ = }}\dfrac{{{Z_i} - {Z_{\rm{0}}}}}{{\rho _i^{\rm{0}}}}$ ，其中(X_i, Y_i, Z_i)为第i颗卫星的坐标，(X₀, Y₀, Z₀)为近似坐标，V_x、V_y、V_z为坐标改正数， ${\varphi _i}$ 为卫星i的载波相位观测值； ${V_{\rm{tR}}}$ 为接收机钟差改正； ${N_i}$ 为整周模糊度； ${V_{\rm{tsi}}}$ 第i颗卫星的钟差改正数； $\rho _i^0$ 为卫星到接收机的近似距离； ${{\rm{(}}{V_{\rm{ion}}}{\rm{)}}_i}$ 为电离层延迟项； ${({V_{\rm{trop}}}{\rm{)}}_i}$ 为对流层延迟项； $\displaystyle\sum {{\delta _i}} $ 为各项改正数，包括天线相位中心偏差改正、地球固体潮改正、海潮负荷改正、引力延迟改正等。

利用PPP技术获得的动态点高程为大地高H，而DEM的高程采用正常高h，为了统一高程系统，需要对动态点的大地高H扣除其高程异常 $\zeta $ 。

根据Bruns公式，地球表面上任意点P的模型高程异常可由下式获得^[9]。

式中： $ r$ 、 $ \theta $ 、 $ \lambda $ 分别为计算点P的地心向径、地心余纬和经度， $ GM$ 为地心引力常数， $ \gamma $ 为计算点P的正常重力值，a为参考椭球的长半轴， $ {{{\bar C}_{nm}}}$ 、 $ {{{\bar S}_{nm}}}$ 为完全规格化位系数， $ {{{\bar P}_{nm}}(\cos \theta )}$ 为完全规格化缔合勒让德函数，N为地球重力场模型展开的最高阶数。

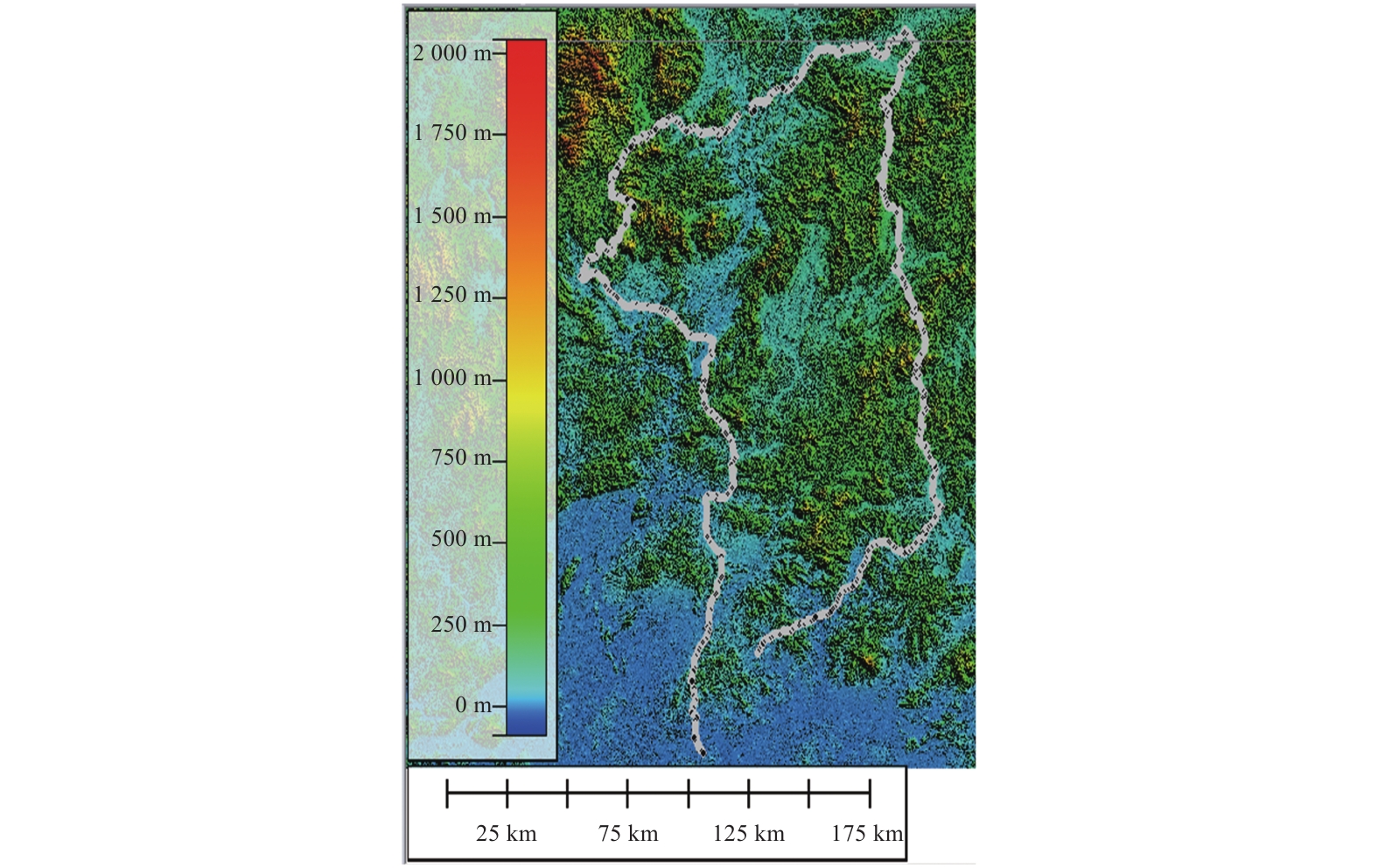
研究区域为广东省部分地区(不同地形条件)，介于23.0° N—25.1° N，112.9° E—114.3° E之间，如图1所示，主要地形为丘陵、山地，整体地势北高南低，其海拔基本在1000 m以下。利用车载Trimble 5700接收机对沿广州、惠州、韶关、清远约730 km的线路进行了数据采集，线路方向为图1中的逆时针方向，主要经过了增城、龙门、翁源、始兴、乳源、英德、从化、白云等15个区县。

图 1(Figure 1)

图 1 研究区域及数据采集线路 Figure 1 Research area and data collection line

数字高程模型采用AW3D30、SRTM3 V4.1和ASTER GDEM V3，其中AW3D30的水平分辨率达到1弧秒(约30 m)，标称高程精度优于5 m^[10]；SRTM3 V4.1的水平分辨率为3弧秒(约90 m)，标称高程精度为16 m^[11]，有学者研究表明，SRTM3 V4.1的高程精度远优于其标称精度^[12]；ASTER GDEM V3由美国国家航空航天局和日本经济产业省共同研制，并于2019年8月进行更新发布，第3版的ASTER GDEM剔除了第2版的高程异常值并扩充了其地理覆盖范围，ASTER GDEM V3的水平分辨率为1弧秒(约30 m)，其标称高程精度为10 m~16 m。

精密单点数据处理系统主要有APPS (The Automatic Precise Positioning Service)、CSRS (Canadian Spatial Reference System Precise Point Positioning service)、GAPS (GNSS analysis and positioning software)、magicGNSS及AUSPOS等^[13]，本文采用加拿大自然资源部PPP数据处理软件系统CSRS，另外，重力场模型采用德国地学研究中心GFZ (German Research Centre for Geosciences)发布的EIGEN-6C4。

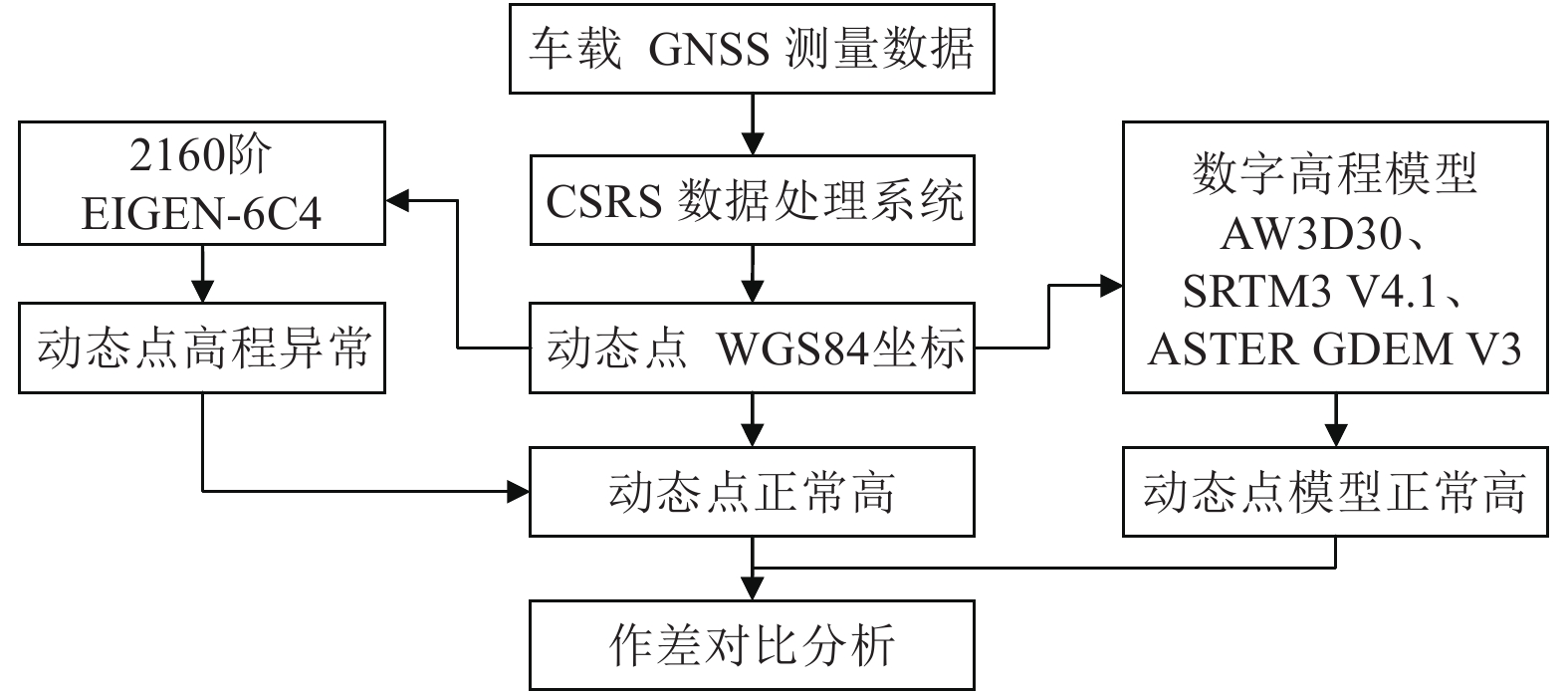
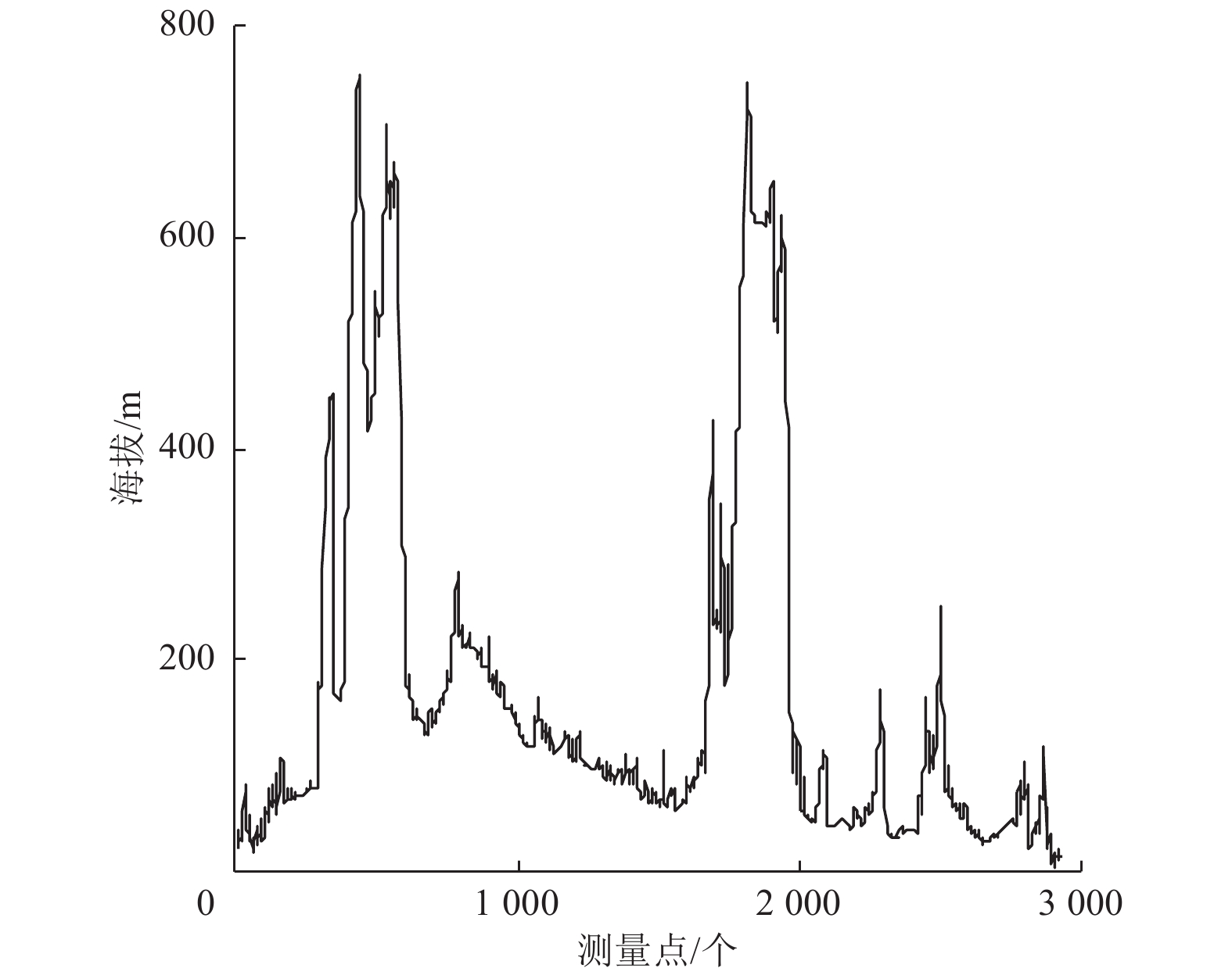
数据处理流程如图2所示：(1) 将采集到的数据通过数据处理系统CSRS进行解算，获得动态点的WGS84坐标；(2) 利用EIGEN-6C4重力场模型(截断至2160阶次)求得动态点的高程异常；(3) 将动态点的大地高与重力场模型高程异常作差获得正常高；(4) 利用数字高程模型AW3D30、SRTM3 V4.1和ASTER GDEM V3内插得到动态点的模型正常高；(5) 将测得的动态点正常高与数字高程模型正常高进行比较分析。本次实验共采集到2937个有效GNSS动态点，其海拔情况如图3所示。

图 2(Figure 2)

图 2 数据处理流程 Figure 2 Data processing flow

图 3(Figure 3)

图 3 GNSS动态测量点的海拔 Figure 3 Altitude of GNSS dynamic measurement point

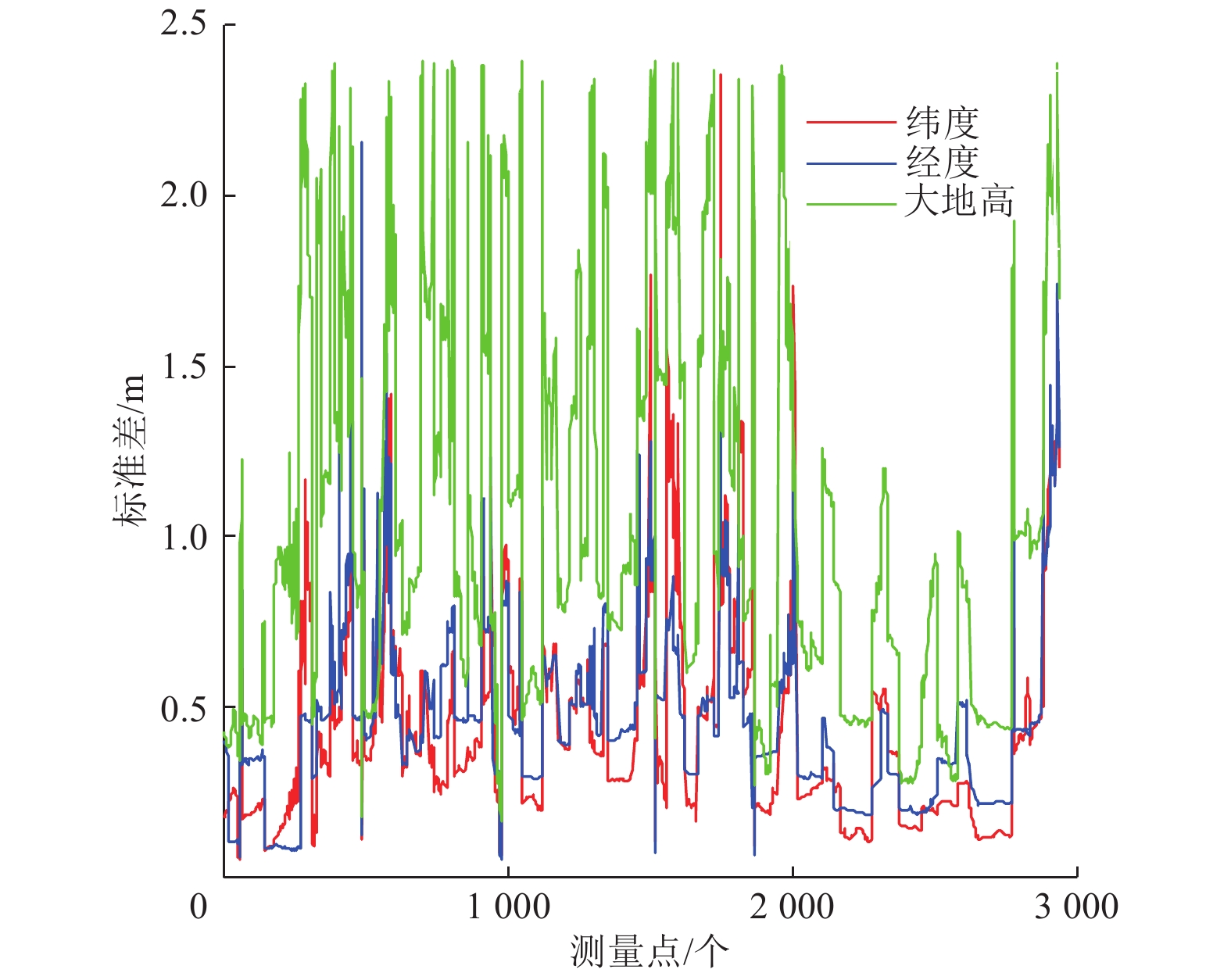
利用CSRS对采集的数据进行解算，可以获得动态点的WGS84坐标，其纬度、经度和大地高的内符合精度如图4所示，由图4可知，动态点的纬度和经度标准差基本在1 m以内，大地高标准差基本在2 m以内。以标准差平均值作为动态点整体的精度衡量指标，则纬度、经度和大地高的精度分别为0.42、0.45和1.03 m。进一步地，将动态点的大地高与重力场模型EIGEN-6C4计算得到的高程异常作差可以得到动态点的正常高。文献[14]研究表明：EIGEN-6C4在广东省内的模型高程异常精度为0.07 m^[14]，综合动态点的大地高精度与模型高程异常精度，本文采集到的动态点正常高精度为1.10 m，远优于上文提到的三种数字高程模型标称精度，满足对其进行高程精度检核的要求。

图 4(Figure 4)

图 4 GNSS动态点的内符合精度 Figure 4 Internal coincidence accuracy of GNSS dynamic points

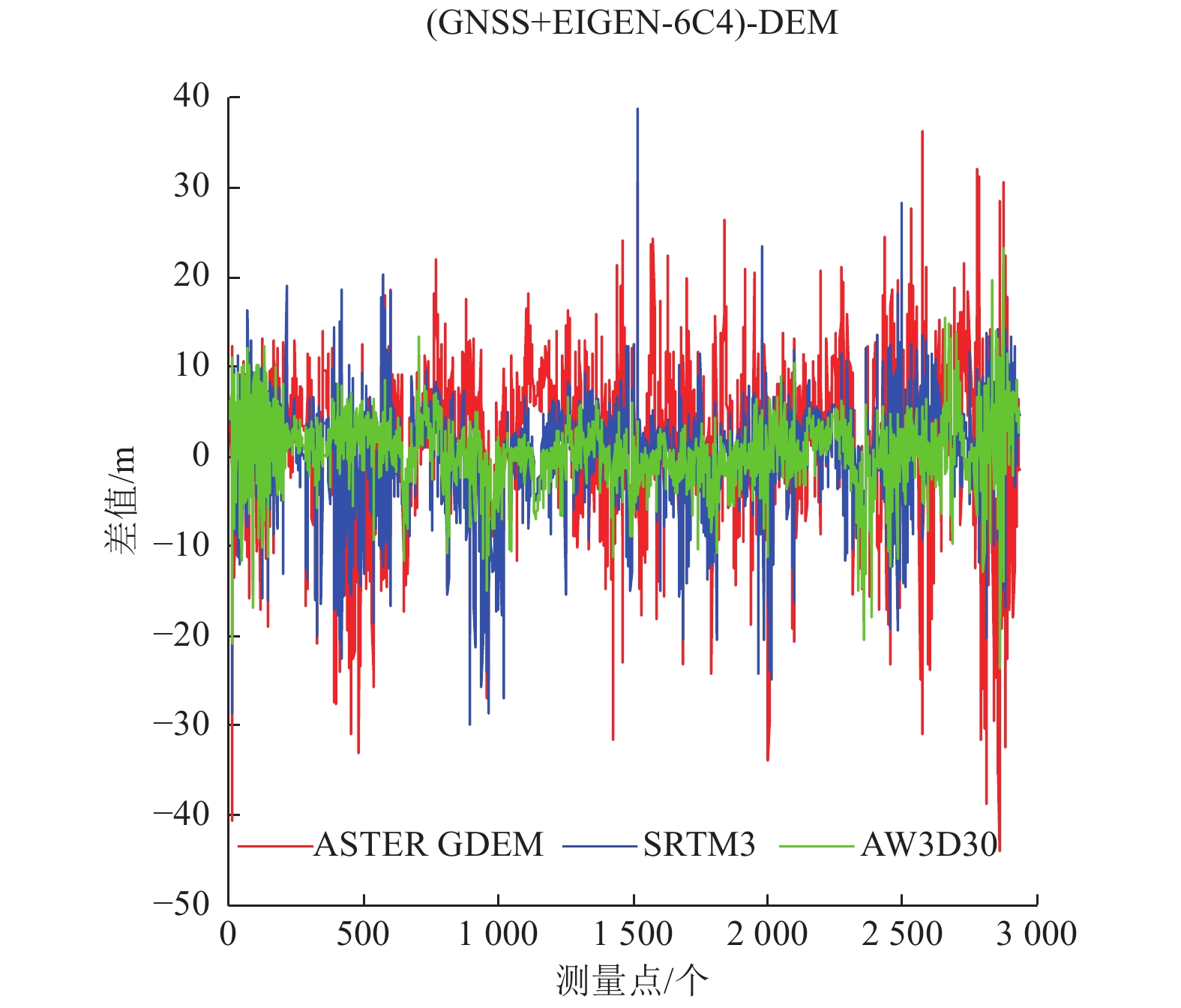
以GNSS大地高与EIGEN-6C4高程异常作为DEM高程精度检核标准，将采集到的动态点正常高分别与AW3D30、SRTM3 V4.1和ASTER GDEM V3三种模型正常高进行作差，结果如图5所示。由图5可知，AW3D30最优，SRTM3 V4.1次之，而ASTER GDEM V3的结果明显要差于前两者。利用差值的最大值、最小值、平均误差、均方根误差和标准偏差作为统计参数对上述3种DEM模型进行统计，结果如表1所示。其中平均误差反映了DEM数据的系统差，均方根误差反映了DEM误差的整体大小，标准偏差反映了DEM误差的离散程度。由表1可知，AW3D30的最大偏差在20 m量级，SRTM3 V4.1和ASTER GDEM V3的最大偏差在40 m量级；SRTM3 V4.1的系统偏差最小，为0.17 m，AW3D30的系统偏差为0.55 m，ASTER GDEM V3的系统偏差较大为1.59 m；AW3D30、SRTM3 V4.1和ASTER GDEM V3的均方根误差分别为3.78、5.84、8.88 m，标准偏差分别为3.74、5.84、8.74 m，均优于3种DEM模型的高程标称精度。综上所述，AW3D30的精度最高，SRTM3 V4.1次之，ASTER GDEM V3最差。

图 5(Figure 5)

图 5 动态点正常高与DEM正常高差值 Figure 5 Difference between dynamic point normal height and DEM normal height

表 1(Table 1)

表 1 AW3D30、SRTM3 V4.1和ASTER GDEM V3误差统计表 Table 1 Error statistics of AW3D30, SRTM3 V4.1 and ASTER GDEM V3 m 模型 最大值 最小值 平均误差 均方根误差 标准偏差 AW3D30 23.22 –23.59 0.55 3.78 3.74 SRTM3 V4.1 38.78 –29.98 0.17 5.84 5.84 ASTER GDEM V3 36.29 –43.93 1.59 8.88 8.74

表 1 AW3D30、SRTM3 V4.1和ASTER GDEM V3误差统计表 Table 1 Error statistics of AW3D30, SRTM3 V4.1 and ASTER GDEM V3

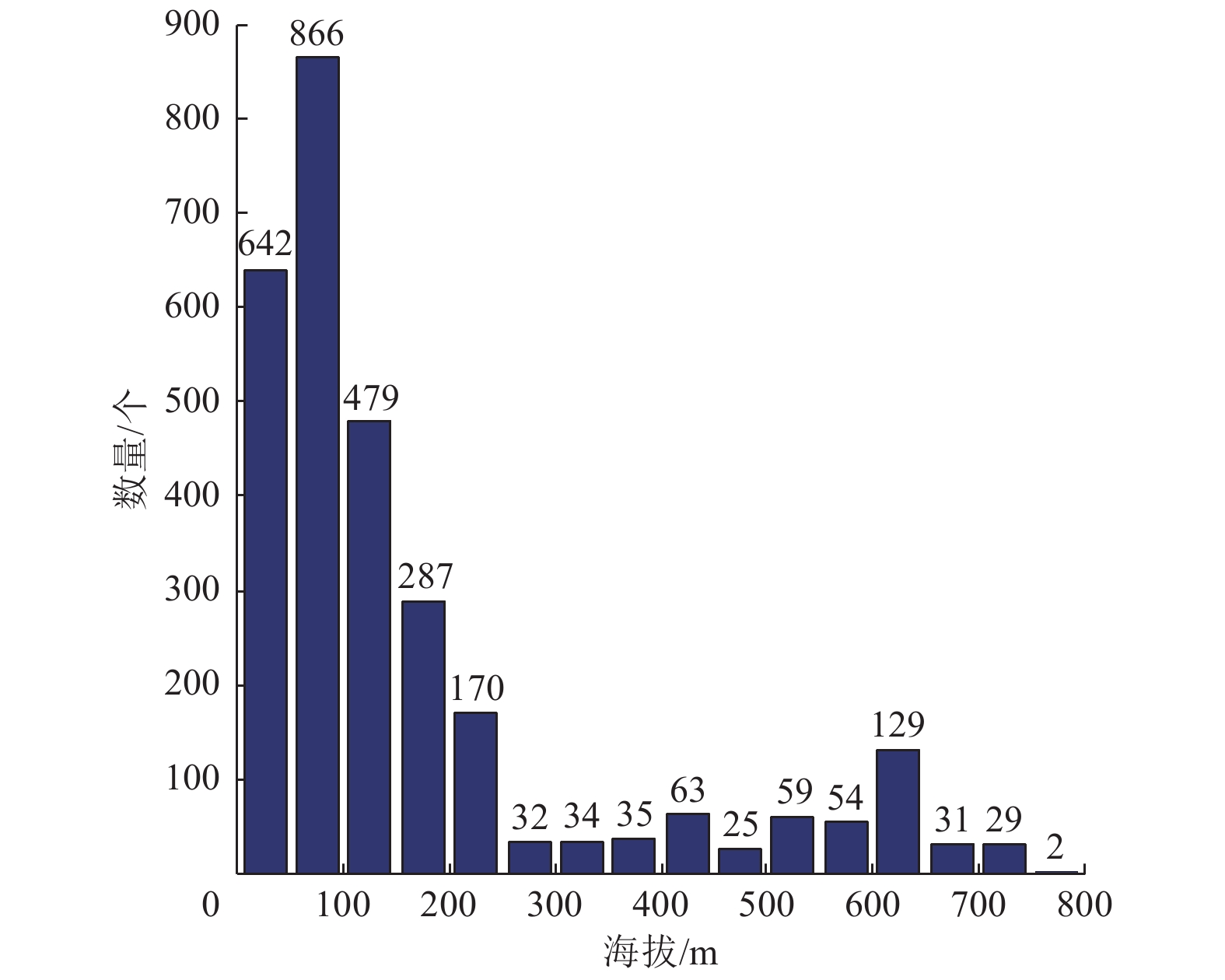
DEM模型精度受多种因素综合影响，包括海拔、坡度、地形起伏度、土地利用类型、植被密度等^[15]，由于本次实验所收集的数据呈线型分布，较难对各因素进行逐一分析，故本文仅对海拔因素进行展开研究。为了分析DEM数据在不同海拔下的高程精度，将采集到的数据按海拔分多个区间进行分析。图6为GNSS动态测量点的海拔直方图，由图6可知，海拔250 m以上的动态点较少，按50 m的区间长度对其进行统计分析，容易因为采样点过少而导致统计结果失真，故将数据按海拔分为以下5个区间：(0 m, 50 m]、(50 m, 100 m]、(100 m, 150 m]、(150 m, 250 m]、(250 m, 800 m]，采样点数量分别为642、866、479、457、493个。

图 6(Figure 6)

图 6 动态测量点的海拔直方图 Figure 6 Elevation histogram of dynamic measurement points

由表2可知，AW3D30在不同海拔区间的系统差(平均误差)振幅较小，在2.18 m以内，系统差只在(100 m, 150 m]区间为负值(DEM高程比实际高程高)，在其他区间内均为正值(DEM高程比实际高程低)，其中在(0 m, 50 m]区间系统差绝对值最大，为1.41 m，在(150 m, 250 m]区间系统差绝对值最小，为0.25 m；SRTM3 V4.1的系统差在(0 m, 250 m]的区间呈线性相关，随着海拔的增加，系统差由正值逐渐转为负值，在(0 m, 100 m]区间为正值，在(100 m, 800 m]区间为负值；ASTER GDEM V3的系统差在(0 m, 250 m]的区间内较为稳定，均为正值，整体上随着海拔的升高而逐渐增大，但在(250 m, 800 m]的区间内出现突变，由(150 m, 250 m]区间的2.67 m降为–2.28 m，说明ASTER GDEM V3的高程在(0 m, 250 m]区间内整体比实际高程低2 m左右，在(250 m, 800 m]区间内比实际高程高2 m左右。AW3D30的均方根误差及标准偏差整体上随着海拔的升高而减小，分别由(0 m, 50 m]区间的4.89、4.69 m降为(250 m, 800 m]的2.97、2.93 m；SRTM3 V4.1的均方根误差及标准偏差在(0 m, 50 m]区间与AW3D30相当，并整体上随着海拔的升高而增大，其中在(0 m, 250 m]的区间内较为稳定，在5.16-5.60 m的范围内；ASTER GDEM V3的均方根误差及标准偏差与海拔无明显的线性关系，其中在(100 m, 250 m]的区间内较小，分别在7.69 m和7.17 m以内，在其他区间内偏大，均在9 m左右。

表 2(Table 2)

表 2 不同海拔区间的DEM高程精度统计表 Table 2 DEM elevation accuracy statistics table for different altitude ranges m 模型 区间 Mean RMSE STD AW3D30 (0, 50] 1.41 4.89 4.69 (50, 100] 0.85 3.57 3.46 (100, 150] –0.77 3.63 3.55 (150, 250] 0.25 3.28 3.27 (250, 800] 0.48 2.97 2.93 SRTM3 V4.1 (0, 50] 2.71 5.16 4.40 (50, 100] 0.96 5.23 5.14 (100, 150] –0.66 5.60 5.56 (150, 250] –2.21 7.29 6.95 (250, 800] –1.49 6.40 6.23 ASTER GDEM V3 (0, 50] 1.83 9.09 8.91 (50, 100] 2.38 9.86 9.58 (100, 150] 2.79 7.69 7.17 (150, 250] 2.67 7.38 6.89 (250, 800] –2.28 9.14 8.86

表 2 不同海拔区间的DEM高程精度统计表 Table 2 DEM elevation accuracy statistics table for different altitude ranges

本文以广东省部分地区为研究区域，利用车载动态PPP技术测定了沿广州、惠州、韶关、清远约730 km线路的大地高，经EIGEN-6C4重力场模型转换为正常高，分别对AW3D30、SRTM3 V4.1和ASTER GDEM V3 3种高程数据模型进行了高程精度检核。研究结果表明，AW3D30、SRTM3 V4.1和ASTER GDEM V3在本文研究区域的高程平均误差分别为0.55、0.17、1.59 m，均方根误差分别为3.78、5.84、8.88 m，标准偏差分别为3.74、5.84、8.74 m。

AW3D30的高程在海拔(0 m, 100 m]与(150 m, 800 m]的区间内整体比实际高程低0.25~1.41 m，在(100 m, 150 m]区间内整体比实际高程高0.77 m；SRTM3 V4.1的系统差在(0 m, 250 m]的区间呈线性相关，随着海拔的增加，其整体高程由比实际高程低2.71 m到比实际高程高出2.21 m；ASTER GDEM V3的高程在(0 m, 250 m]的区间内整体比实际高程低1.83~2.67 m，在(250 m, 800 m]的区间内整体比实际高程高2.28 m。

以均方根误差作为精度衡量标准。AW3D30的精度整体上随着海拔的升高而逐步升高，在2.97~4.89 m之间；SRTM3 V4.1的精度整体上随着海拔的升高而降低，在5.16~7.29 m之间；ASTER GDEM V3的精度在(100 m, 250 m]区间较高，优于7.69 m，在其余区间为9.09~9.86 m。

综上所述，AW3D30的高程精度在不同海拔和不同地形中均优于另外2种模型，在实际应用中可优先考虑，其次为SRTM3 V4.1，ASTER GDEM V3的各项精度则相对于前两者较差。