2. 中国能源建设集团 广东省电力设计研究院有限公司,广东 广州 510663
2. Guangdong Electric Power Design Institute Co., Ltd., China Energy Engineering Group, Guangzhou 510663, China
随着日益严峻的环境污染与化石能源问题,世界各国大力推进汽车电气化,把禁售燃油汽车提上日程,如荷兰、挪威禁售时间是2025年,印度是2030年,法国是2040年。我国采用分区域、分车类、分阶段的方案,有望于2050年全面退出燃油汽车[1]。随着电动汽车数量快速增多,充电站数量也迅速增长。截止2019年9月,我国充电设施数量达到111.5万座,是国内加油站数量的10倍[2]。尽管充电站数量庞大,但是充电难问题依然存在。充电站分布不合理、“跑马圈地”式建设导致充电站要么不堪重负,要么闲置率极高。因此充电站的合理规划非常必要。
电动汽车充电站选址定容问题是多变量、多约束、高维度的非线性优化问题。目前,该问题的研究仍处在起步阶段,尚未形成完整的理论体系。文献[3]提出交通满意度模型,结合加权Voronoi图和遗传算法,进行多场景分析;文献[4]提出目标为最大充电网络服务能力和最小配电系统网络损耗的多目标优化模型,模糊化处理后采用遗传算法进行求解;文献[5]综合考虑充电站建设成本与用户广义充电成本,引入便捷系数概念,提出多种规划目标的取值建议;文献[6]提出以最大化满足路径中需求与最小化平均等待时间为目标的混合整数规划模型,求解后得出选址定容问题的3大关键要素;文献[7]通过分析用户出行行为和充电习惯,提出兼顾运营商利益与用户充电需求的规划模型;文献[8]把用户碳排放量作为充电站规划考核指标之一,并采用帕累托最优前沿分析可选的方案;文献[9]依据城市道路信息,确定充电站最优位置分布,再运用Voronoi图划分充电站所服务的负荷区,确定其容量。上述研究成果均片面考虑用户或运营商的利益,考虑的因素不够全面,在实际推行过程中可能会遇到较大阻力。文献[10]建立的模型虽考虑了充电站运营商、电动汽车用户以及电网企业三者的综合利益,但电网侧利益是通过设备损耗来简单折算,与实际运行情况存在较大差距。文献[11]建立的模型选中了多个交通节点作为最优站址;文献[12]建立的模型是在规划范围内随机生成站点,运用改进PSO算法求得最优站址。上述研究得出的最优站址在现实中不一定具备建站条件,实用性偏低。
本文综合多种约束条件,建立以建设运行成本、用户充电时间成本、配网损耗成本为目标的电动汽车充电站选址定容多目标决策模型;针对多目标决策难问题,引入层次分析熵权法进行决策;针对标准引力搜索算法收敛速度慢,求解高维度问题精度不足的缺点,引入混沌理论以及全局最优来引导粒子速度更新;针对选址定容模型的求解,引入Voronoi图划分充电站服务区域,与改进引力搜索算法联合求解。小区几何分布与IEEE30节点系统的算例表明本模型及算法具有较高的可行性。
1 电动汽车充电站选址定容数学模型电动汽车充电站属于公共服务设施,在进行规划时不仅要考虑运营商的效益,还应考虑用户便利程度等多个因素。本文在考虑潮流、充电站规模等约束条件下,提出以建设运行成本、用户充电时间成本及配网损耗成本为目标的电动汽车充电站选址定容数学模型。
1.1 目标函数 1.1.1 建设运行成本建设运行成本包括建设成本和运行成本[13]。建设成本Ccon
| ${C_{\rm{con}}} = \frac{{{r_0}{{( {1 + {r_0}} )}^{n_{{\rm{year}}}}}}}{{{{( {1 + {r_0}} )}^{n_{{\rm{year}}}}} - 1}}( {{C_{\rm{g}}} + \varphi n_{{\rm{char}}}^2 + \varepsilon {n_{{\rm{char}}}}} )$ | (1) |
其中,r0为贴现率;nyear为折旧年限;Cg为固定投资成本;nchar为站内充电桩数量;φ是配电变压器和输电线路等相关设备成本的等效投资系数;ε为充电桩的单价。运行成本Cop主要有人力成本、设备维护成本等,如式(2)所示。
| ${C_{\rm{op}}} = ( {{C_{\rm{g}}} + \varphi n_{{\rm{char}}}^2 + \varepsilon {n_{{\rm{char}}}}} )\gamma $ | (2) |
其中,γ
| ${f_1} = \sum\limits_{i = 1}^I {\left( {{C_{{\rm{con}}i}} + {C_{{\rm{op}}i}}} \right)} $ | (3) |
其中,I为充电站合集;i为充电站;Cconi和Copi分别为充电站i的建设成本和运行成本。
1.1.2 用户充电时间成本用户充电时间成本包括电动汽车前往充电站的时间成本及站内排队等待的时间成本[12]。假设用户在充电站内的排队过程符合M/M/s排队模型,充电站i 的排队等待期望Wi为
| ${W_{{i}}} = \frac{{{n_{{\rm{char}}}}{\rho ^{{n_{{\rm{char}}}} + 1}}{p_0}}}{{D \cdot {n_{{\rm{char}}}}!{{\left( {{n_{{\rm{char}}}} - \rho } \right)}^2}}}$ | (4) |
其中
| ${p_0} = {\left[ {\sum\limits_{i = 0}^{{n_{{\rm{char}}}} - 1} {\frac{{{\rho ^i}}}{{i!}} + \frac{{{n_{{\rm{char}}}}{\rho ^{{n_{{\rm{char}}}}}}}}{{{n_{{\rm{char}}}}!\left( {{n_{{\rm{char}}}} - \rho } \right)}}} } \right]^{ - 1}}$ | (5) |
其中,ρ=D/ψ为充电桩服务强度,D为充电需求量,ψ为充电桩服务效率;p0为充电桩全部闲置概率。
用户前往充电站的行驶时间tDA与站内排队等待时间tWA如式(6)与式(7)所示。
| ${t_{\rm{DA}}} = \frac{{\displaystyle\sum\limits_{i = 1}^I {\displaystyle\sum\limits_{j = 1}^J {\mu {D_j}{E_{ij}}{d_{ij}}} } }}{v_{\rm{q}}}$ | (6) |
| ${t_{\rm{WA}}} = \sum\limits_{i = 1}^I {{W_i}\Bigg( {\sum\limits_{j = 1}^J {{D_j}{E_{ij}}} } \Bigg)} $ | (7) |
其中,I为充电站合集;J为需求点合集;μ为道路曲折系数;Dj为需求点j的充电需求量;Eij为0或1,若需求点j选择充电站i充电,则Eij为1,反之为0;dij为需求点j与充电站i的欧氏距离;vq为汽车平均行驶速度;Wi为充电站i的排队等待期望。
则用户充电时间成本f2的目标函数为
| ${f_2} = 365{C_{\rm{cut}}}\left( {{t_{\rm{DA}}} + {t_{\rm{WA}}}} \right)$ | (8) |
其中,Ccut为用户单位时间成本。
1.1.3 配网损耗成本电动汽车充电站的大规模接入会对电网产生一定影响,如网损增加、频率下降、电压下降。为降低电动汽车充电负荷对电网的影响,提高电网公司效益,本文在充电站选址定容中计算配网损耗[14]。其计算公式为
| ${P_{{\rm{LOSS}}}} = \sum\limits_{h = 1}^N {\sum\limits_{k = 1}^N {{G_{hk}}{U_h}{U_k}\cos {\delta _{hk}}} } $ | (9) |
其中,PLoss为配网损耗,用功率表示;N为节点集合;Ghk为节点h,k之间的电导;Uh为节点h电压;Uk为节点k电压;δhk为节点h,k的功角差。
所以配网损耗年成本f3的目标函数为
| ${f_3} = 365{t_{{\rm{CH}}}}{C_{\rm{fa}}}{P_{{\rm{LOSS}}}}$ | (10) |
其中,tCH为充电站日运行时间;Cfa为电价。
1.2 约束条件 1.2.1 潮流约束| $ \begin{split} & {P_{{\rm{GE}}h}} - {P_{{\rm{CH}}h}} - {U_h}\displaystyle\sum\limits_{k = 1}^N {{U_k}({G_{hk}}\cos {\theta _{hk}} + {B_{hk}}\sin {\theta _{hk}})} = 0 \\& {Q_{{\rm{GE}}h}} - {Q_{{\rm{CH}}h}} - {U_h}\displaystyle\sum\limits_{k = 1}^N {{U_k}({G_{hk}}\cos {\theta _{hk}} + {B_{hk}}\sin {\theta _{hk}})} = 0\\ & \quad\qquad\qquad\qquad(\forall hk \in Y,\forall h \in [1,N]) \end{split} $ | (11) |
其中,Bhk为
| $ \left| {{S_{hk}}} \right| \leqslant S_{hk}^{\max },\forall hk \in Y,\forall h \in [1,N]$ | (12) |
其中
| ${S_{hk}} = \sqrt {P_{hk}^2 + Q_{hk}^2} $ | (13) |
其中,
| $U_h^{\min } \leqslant {U_h} \leqslant U_h^{\max },\begin{array}{*{20}{c}} {} \end{array}\forall h \in [1,N]$ | (14) |
其中,Uhmin和Uhmax分别是节点h的电压下限和上限。
1.2.4 充电站数量约束| ${n_{{\rm{CH}},\min }} \leqslant {n_{{\rm{CH}}}} \leqslant {n_{{\rm{CH}},\max }}$ | (15) |
其中,nCH,min和nCH,max分别是候选充电站最小和最大数量。
1.2.5 站内充电桩数量约束| ${n_{{\rm{char}},\min }} \leqslant {n_{{\rm{char}}}} \leqslant {n_{{\rm{char}},\max }}$ | (16) |
其中,nchar,min和nchar,max分别是充电站内允许安装充电桩的最小和最大值。
1.3 基于层次分析熵权法的多目标决策在对多目标问题进行决策时,采用层次分析法得到的权值虽反映了专家的经验和决策者的意向和偏好等主观因素,但不能反映各个目标函数之间的客观博弈结果,主观随意性较大。如采用熵权法决策,虽得到的权值较为客观,但不能反映专家的经验和决策者的意见,得到的权重可能与实际情况有偏差,甚至相违背。因此,本文综合上述2种决策方法的优缺点,提出了层次分析熵权法[15],该方法可以避免过度依赖主观权值或客观权值而导致的决策偏差。
假定现有目标数为Z的决策问题,采用层次分析法计算得到权值矩阵为
| ${\lambda _z} = \frac{{{F _z} {M _z}}}{{\displaystyle\sum\limits_{z = 1}^Z {{F _z} {M _z}} }}$ | (17) |
综上,本文采用层次分析熵权法把电动汽车充电站选址定容的多目标问题转化为单目标问题,目标函数如式(18)所示。
| ${\rm{fit}} = {\lambda _{\rm{1}}}{f_{\rm{1}}}{\rm{ + }}{\lambda _{\rm{2}}}{f_{\rm{2}}}{\rm{ + }}{\lambda _{\rm{3}}}{f_{\rm{3}}}$ | (18) |
引力搜索算法(GSA)于2009年由Esmat Rashedi提出,是一种受万有引力定律以及牛顿第二定律启发的优化算法[16]。引力搜索算法与粒子群算法相似,通过不断改变种群粒子的位置来寻找最优解。GSA算法在迭代过程中,把粒子看作存在一定质量的物体,相互之间存在引力。粒子的适应度越大,其惯性质量越大,引力就越大;适应度越小的粒子惯性质量越小,引力也越小。质量小的粒子容易被质量大的粒子吸引并移动。因此,每代可能接近全局最优的粒子质量最重,其吸引力也最大。随着算法的循环,粒子靠它们之间的万有引力在搜索空间内不断运动,当粒子移动到最优位置时,最优解便找到了。其速度和位置更新公式为
| $\left\{ \begin{array}{l} {v_e}\left( {\pi + 1} \right) = R \times {v_e}\left( \pi \right) + {a_e}\left( \pi \right) \\ {x_e}\left( {\pi + 1} \right) = {x_e}\left( \pi \right) + {v_e}\left( {\pi + 1} \right) \end{array} \right.$ | (19) |
其中,π为当前代数;ve(π)表示粒子e的速度;x(π)为第π次更新后的状态值;R是区间[0,1]间的随机数,ae(π)是粒子e的加速度。
2.2 改进引力搜索算法(IGSA) 2.2.1 引入组合混沌映射策略GSA算法在初始化阶段随机生成初始种群,不利于种群的多样性和遍历性,因此本文采用Logistic映射与Tent映射相结合,将其应用于种群初始化与寻优过程,增加粒子遍历性,提高收敛性能,其表达公式为
| $\left\{ \begin{array}{l} {y_0} = {x_0} \\ {\rm{if}}\begin{array}{*{20}{c}} {} \end{array}{y_0} < 0.5,{y_{\pi + 1}} = 2{y_0} \\ {\rm{ else}}\begin{array}{*{20}{c}} {} \end{array}{y_{\pi + 1}} = 2( {1 - {y_0}} ) \\ {\rm{temp}} = \xi {x_0}\left( {1 - {x_0}} \right) + | {{y_{\pi + 1}}}| \\ {x_{\pi + 1}} = od (t,1) \end{array} \right.$ | (20) |
其中,x0, y0是粒子初始值,xπ+1, yπ+1是更新后状态值,temp为待求余状态值,ξ是Logistic混沌系数,mod()为取余函数。
2.2.2 引入全局最优点引导的自适应移动策略标准GSA算法在粒子移动阶段仅考虑了当前位置信息,缺少记忆性,寻优效率及效果较差,特别是在求解高维优化问题时容易陷入局部最优。受粒子群算法启发,在粒子移动阶段,引入全局最优点GB来引导速度更新[17],其更新公式为
| $ {v_e}\left( {\pi + 1} \right) = R \times {v_e}\left( \pi \right) + {c_1} \times {a_e}\left( \pi \right) + {c_2} \times \left( {{\rm{GB}} - {x_e}\left( \pi \right)} \right) $ | (21) |
其中,GB是全局最优点,c1和c2是加速因子,其表达式为
| ${c_1} = - \frac{{{t^3}}}{{{{\varPhi}^3}}} + {\rm{1}}$ | (22) |
| ${c_2} = \frac{{{t^3}}}{{{\varPhi^3}}}$ | (23) |
其中,Φ为最大迭代次数。
3 基于Voronoi图和改进引力搜索算法的选址定容 3.1 Voronoi图及服务区域划分Voronoi图,又名泰森(Thiessen)多边形,于1908年由M. G. Voronoi提出,由一组连接两邻点直线的垂直平分线形成的连续多边形组成。Voronoi图生成方法如图1所示。设生长点集合H={H1,H2,H3,···,HL}, 3≤L≤∞,则Voronoi图的数学表述为
| $ {\rm{Vor}}({H}_{b})=\{u\in {\rm{Vor}}({H}_{b})丨d(u,{H}_{b})\leqslant d(u,{H}_{l})\}$ | (24) |
其中,

|
图 1 Voronoi图生成方法 Figure 1 Voronoi diagram generation method |
利用Voronoi图,进行服务区域划分。把充电站的选址集合视为二维平面上的点集,需求点视为平面上的点。以充电站点集为生长点作Voronoi图,由Voronoi图特点可知,充电站服务区域内的需求点到该充电站的距离应小于等于到其他充电站的距离,满足车主就近选择充电站原则。
3.2 求解步骤步骤1:初始化数据,输入规划区的面积、人口密度、需求点和候选点的具体坐标、需求点的负荷信息、配网结构等参数信息,根据式(25)折算各需求点电动汽车数量。
| ${n_{{\rm{car}}i}} = \left| {A\alpha \beta \eta \frac{{{O_i}}}{{{O_\Sigma }}}} \right|$ | (25) |
其中,ncari是需求点i的电动汽车数量;A是规划区占地面积;α是人口密度;β是人均汽车保有量;η是电动汽车占比;Oi为需求点i的电荷,OΣ为需求点总电荷。
步骤2:生成初始种群,粒子具体编码方式为
| ${{x}} = \left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_{\rm{2}}}}& \cdots &{{x_{\omega}}}&{{y_1}}&{{y_2}}& \cdots &{{y_{\omega}}} \end{array}} \right]$ | (26) |
例如当ω=3,x=[1 5 8 10 20 30]指选取了1、5、8号候选站,对应站内充电桩数目分别为10、20、30。如种群粒子数为m,则初始种群编译为
| ${{X}} = \left[ {\begin{array}{*{20}{c}} {x_1^1}&{x_2^1}& \cdots &{x_{\omega}^1}&{y_1^1}&{y_2^1}& \cdots &{y_{\omega}^1} \\ {x_1^2}&{x_2^2}& \cdots &{x_{\omega}^2}&{y_1^2}&{y_2^2}& \cdots &{y_{\omega}^2} \\ \vdots & \vdots &{}& \vdots & \vdots & \vdots &{}& \vdots \\ {x_1^m}&{x_2^m}& \cdots &{x_{\omega}^m}&{y_1^m}&{y_2^m}& \cdots &{y_{\omega}^m} \end{array}} \right]$ | (27) |
步骤3:对步骤2生成的初始种群归一化处理,再进行m–1次混沌操作,然后反归一处理。
步骤4:依据建站数量和建站规模,由式(3)得到建设运行成本f1。
步骤5:把候选站址坐标作为生长点作Voronoi图,划分各充电站服务范围。由式(4)和式(8)计算出用户充电时间成本f2。
步骤6:将候选站址接入配网后并进行潮流计算,由式(10)得到配网损耗成本f3。
步骤7:依据改进策略更新粒子位置和速度,并对粒子按步骤3进行混沌操作。
步骤8:由层次分析熵权法得到的λ1、λ2、λ3代入式(18),将多目标函数变为单目标函数,记录个体最优和全局最优。
步骤9:重复步骤4~8,直至满足收敛条件,输出全局最优值。
4 算例分析以某市规划区为例进行分析,该区占地面积为12.1 km2,人口密度为7000人/km2,人均汽车保有量为19%,其中电动汽车占30%。规划区包含21个小区位置重心(需求点)和根据实际情况确定的9个候选站址(候选点),假设其对应IEEE30节点系统,需求点、候选点具体坐标和对应接入的节点号如表1所示。其中,1~34号为需求点,35~43号为候选点。
| 表 1 需求点、候选点坐标和节点号 Table 1 Demand point, candidate point coordinates and node number |
假设该规划区电动汽车型号为比亚迪E2,电池容量为35.2 kW;充电站固定投资成本为300 万元/座;折算到充电桩的等效投资系数为2 万元/台;充电桩价格为10 万元/台;站内允许安装充电桩的最小数量为8台;站内允许安装充电桩的最大数量为45台;人工、设备运行维护成本折算系数为0.1;贴现率为0.08;折旧年限为20年;道路曲折系数为1.3;车辆平均行驶速度为35 km/h;用户单位时间成本为20 元/h;充电桩额定功率为120 kW;充电效率为0.9;充电站日运行时间为12 h;电价为0.6 元/kW·h。IGSA算法参数设置为:种群规模为20,迭代次数最大值为500,引力常数初始值为100,引力系数衰减因子为30。
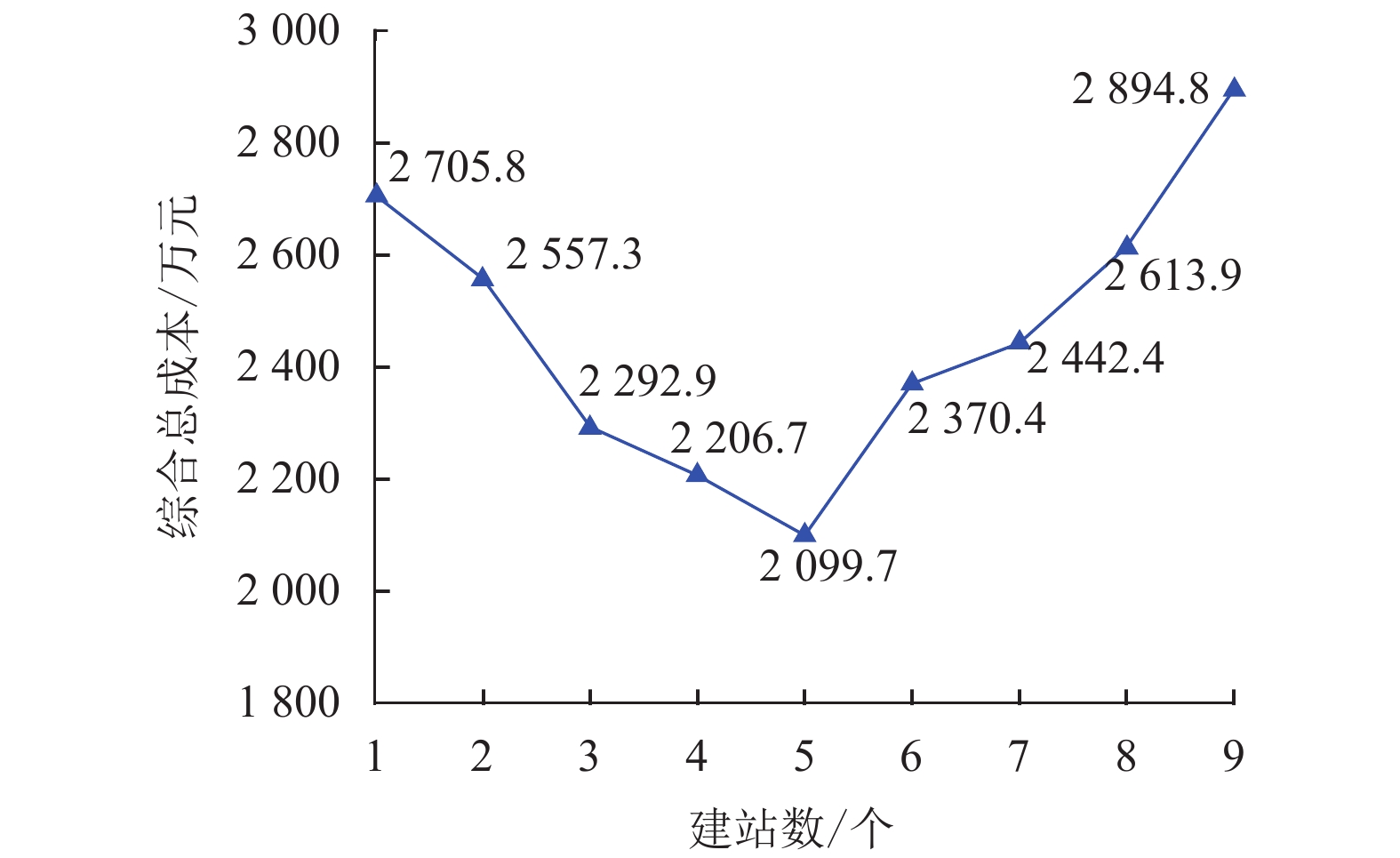
根据3.2节求解步骤,建不同数量候选站的计算成本如图2所示。由图2可知,若建站数量过少会由于用户时间成本的增加而导致综合总成本过高;而建站数量过多又会由于建设运行成本和配网损耗成本的增加导致综合成本过高。
|
图 2 不同建站数量的综合成本 Figure 2 Calculation result of selecting different number of candidate stations |
由图2可知,当建站数量为5个时,综合总成本最低,为2099.7 万元。具体站点分布、服务区域划分以及配置的充电桩数量如图3所示,图中圆点为需求点,方形为候选点,其中实心方形为被选中的候选点,实心方形旁的数值为选中充电站安装的充电桩数量,网状直线由Voronoi图生成,即服务区域划分边界。由图3可知,规划区由5个充电站划分为5个服务区域,具体划分情况为:有8个充电桩的充电站覆盖了2个需求点;有16个充电桩的充电站分别覆盖了8个和5个需求点;有24个充电桩的充电站覆盖了8个需求点;有32个充电桩的充电站覆盖了11个需求点。

|
图 3 最优方案及服务区域划分 Figure 3 Optimal plan and service area division |
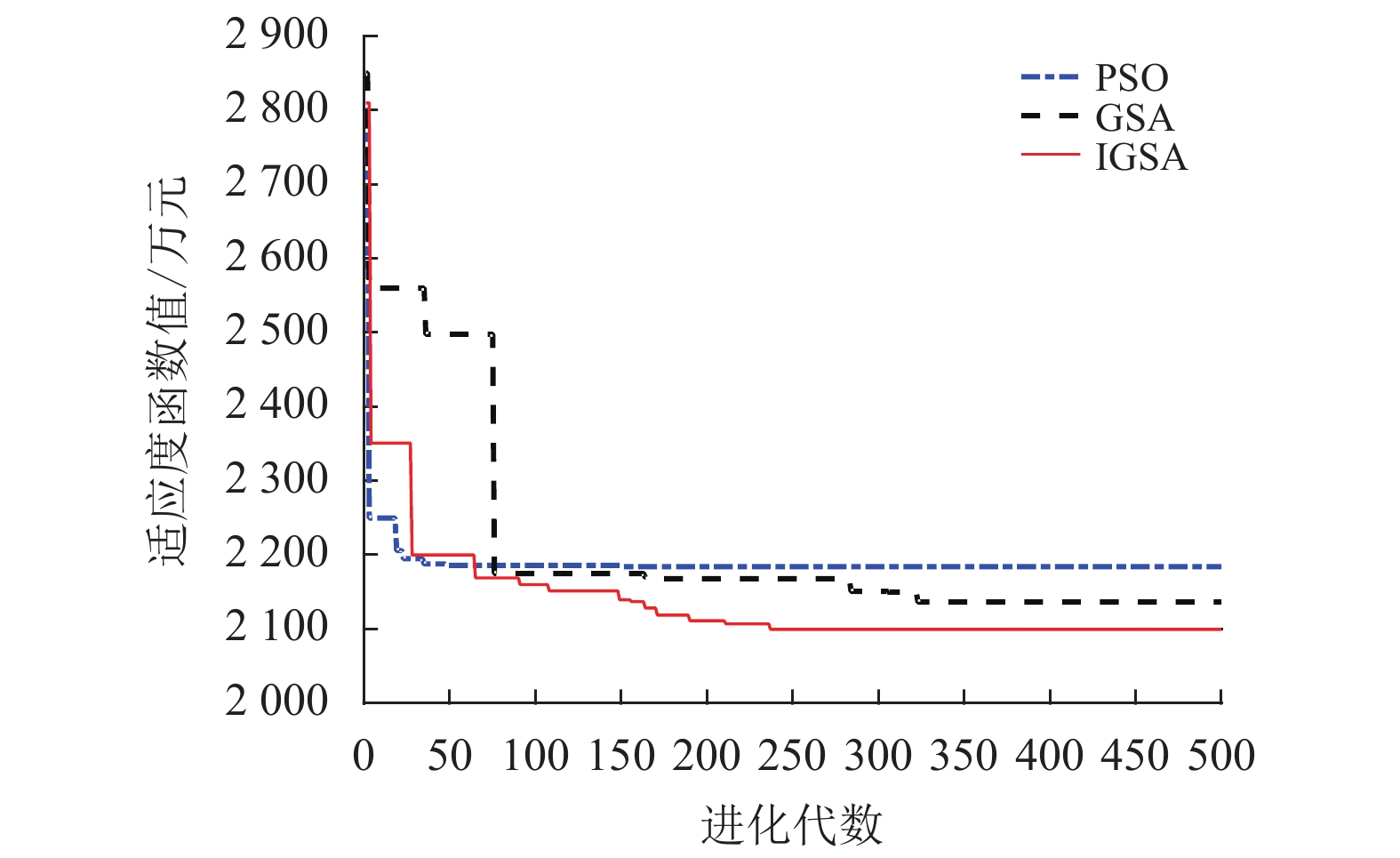
本文分别采用IGSA、GSA和PSO 3种算法进行仿真,其收敛曲线对比如图4所示。由图4可知,PSO前期收敛速度很快,但在中期陷入了局部最优;GSA前期收敛速度较慢,中期缓慢收敛,后期陷入了局部最优;IGSA前期收敛速度跟GSA相比有了一定提升,中期平稳收敛逐渐趋于最优。优化结果如表2所示,结果显示,IGSA求得的方案综合总成本最低,GSA求得的方案充电桩数量较少,因此建设运行成本和配网损耗成本较低,但用户充电时间成本大大增加,综合总成本较高;PSO求得的方案由于充电桩数量过多导致建设运行成本和配网损耗成本激增,综合总成本最高。求解时间方面,IGSA运算效率虽不如PSO,但较GSA有了一定改善,效率提高了16%。
|
图 4 3种算法收敛曲线对比 Figure 4 Comparison of convergence curves of three algorithms |
| 表 2 3种算法优化结果对比 Table 2 Comparison of four algorithm optimization results |
随着电动汽车的推广普及,电动汽车充电站的选址定容非常重要。本文考虑了多方面因素,建立了以建设运行成本、用户充电时间成本、配网损耗成本为目标的电动汽车充电站选址定容多目标决策模型,通过对某市规划区的算例进行仿真,得出以下结论。
(1) 提出的IGSA算法是在GSA算法基础上,引入混沌理论以及自适应移动策略,提高了算法的收敛速度和跳出局部最优能力,与GSA、PSO算法相比,IGSA在电动汽车充电站规划方面具有较高的效率和更强的寻优能力。
(2) 运用Voronoi图划分充电站服务区域,配合IGSA对模型进行联合求解,为电动汽车充电站规划提出新思路。
本文未考虑电动汽车类型、电动汽车换电站、用户充电习惯等因素,需日后继续研究完善。
| [1] |
安锋, 康利平, 秦兰芝, 等. 中国传统燃油车退出时间表研究[R]. 北京: 能源与交通创新中心, 2019.
|
| [2] |
张帆, 李康, 秦雪亮, 等. 2019—2020年度中国充电基础设施发展年度报告[R]. 北京: 中国电动汽车充电基础设施促进联盟, 2020.
|
| [3] |
李逸欣, 林勇, 杨军. 基于改进加权Voronoi图的多场景电动汽车充电网络规划方法[J].
广东电力, 2019, 32(8): 43-50.
LI Y X, LIN Y, YANG J. Research on multi-scenario planning method for EV charging network based on improved weighted voronoi diagram[J]. Guangdong Electric Power, 2019, 32(8): 43-50. |
| [4] |
丁丹军, 戴康, 张新松, 等. 基于模糊多目标优化的电动汽车充电网络规划[J].
电力系统保护与控制, 2018, 46(2): 43-50.
DING D J, DAI K, ZHANG X S, et al. Network planning for electric vehicle charging based on fuzzy multi-objective optimization[J]. Power System Protection and Control, 2018, 46(2): 43-50. DOI: 10.7667/PSPC162073. |
| [5] |
罗清玉, 田万利, 贾洪飞. 考虑通勤需求的电动汽车充电站选址与定容模型[J].
吉林大学学报(工学版), 2019, 49(5): 1471-1477.
LUO Q Y, TIAN W L, JIA H F. Location and capacity model of electric vehicle charging station considering commuting demand[J]. Journal of Jilin University (Engineering Edition), 2019, 49(5): 1471-1477. |
| [6] |
朱书研, 杨斌, 朱小林. 考虑偏差路径的电动汽车充电站选址和定容[J].
上海海事大学学报, 2019, 40(1): 44-50.
ZHU S Y, YANG B, ZHU X L. Location and capacity of electric vehicle charging station considering deviation path[J]. Journal of Shanghai Maritime University, 2019, 40(1): 44-50. |
| [7] |
陈静鹏, 艾芊, 肖斐. 基于用户出行需求的电动汽车充电站规划[J].
电力自动化设备, 2016, 36(6): 34-39.
CHEN J P, AI Q, XIAO F. EV charging station planning based on travel demand[J]. Electric Power Automation Equipment, 2016, 36(6): 34-39. |
| [8] |
陈光, 毛召磊, 李济沅, 等. 计及碳排放的电动汽车充电站多目标规划[J].
电力系统自动化, 2014, 20(17): 49-53.
CHEN G, MAO Z L, LI J Y, et al. Multi-objective planning of electric vehicle charging stations considering carbon emissions[J]. Automation of Electric Power Systems, 2014, 20(17): 49-53. DOI: 10.7500/AEPS20140505005. |
| [9] |
赵书强, 李志伟, 党磊. 基于城市交通网络信息的电动汽车充电站最优选址和定容[J].
电力自动化设备, 2016, 36(10): 8-15.
ZHAO S Q, LI Z W, DANG L. Optimal EV charging station siting and sizing based on urban traffic network information[J]. Electric Power Automation Equipment, 2016, 36(10): 8-15. |
| [10] |
艾欣, 李一铮, 王坤宇, 等. 基于混沌模拟退火粒子群优化算法的电动汽车充电站选址与定容[J].
电力自动化设备, 2018, 38(9): 9-14.
AI X, LI Y Z, WANG K Y, et al. Locating and sizing of electric vehicle charging station based on chaotic simulated annealing particle swarm optimization algorithm[J]. Electric Power Automation Equipment, 2018, 38(9): 9-14. |
| [11] |
裴文杰, 汪沨, 谭阳红, 等. 含光伏分布式电源配电网的电动汽车充电站机会约束规划[J].
电力系统及其自动化学报, 2017, 29(6): 45-52.
PEI W J, WANG F, TAN Y H, et al. Chance-constrained programming for electric vehicle charging stations in distribution network containing photovoltaic distributed generations[J]. Journal of Electric Power System and Automation, 2017, 29(6): 45-52. DOI: 10.3969/j.issn.1003-8930.2017.06.007. |
| [12] |
熊虎, 向铁元, 祝勇刚, 等. 电动汽车公共充电站布局的最优规划[J].
电力系统自动化, 2012(23): 65-70.
XIONG H, XIANG T Y, ZHU Y G, et al. Electric vehicle public charging station location optimal planning[J]. Automation of Electric Power Systems, 2012(23): 65-70. |
| [13] |
闫天泽, 邱晓燕, 刘延博, 等. 基于引入模拟退火思想的改进粒子群算法的电动汽车充电站最优规划[J].
电测与仪表, 2017, 54(6): 11-16.
YAN T Z, QIU X Y, LIU Y B, et al. Optimal planning of electric charging station based on PSOSA algorithm[J]. Electric Measurement and Instrumentation, 2017, 54(6): 11-16. DOI: 10.3969/j.issn.1001-1390.2017.06.003. |
| [14] |
张娟. 电动汽车有序充电策略及充电设施规划研究[D]. 太原: 太原理工大学, 2018, 52-53.
|
| [15] |
叶珍. 基于AHP的模糊综合评价方法研究及应用[D]. 广州: 华南理工大学, 2010.
|
| [16] |
范炜锋. 万有引力搜索算法的分析与改进[D]. 广州: 广东工业大学, 2014.
|
| [17] |
唐俊杰, 陈璟华, 邱明晋. 基于动态模糊混沌粒子群算法的含电动汽车微电网多目标优化调度研究[J].
广东工业大学学报, 2018, 35(3): 100-106.
TANG J J, CHEN J H, QIU M J. Multi-objective dispatch of microgrid based on dynamic fuzzy chaotic particle swarm algorithm[J]. Journal of Guangdong University of Technology, 2018, 35(3): 100-106. |
 2021, Vol. 38
2021, Vol. 38

