在信号处理领域，为了实现信号的分类、存储、识别等目的，通常需要将信号分解为不同的原子，研究它们的不同表示形式。而稀疏表示的目的就是用尽可能少的原子来表示信号，以获得信号更为简洁的表示形式和更容易地获取信号所蕴含的信息，实现信号的压缩、存贮等目标^[1-3]。经典的信号分解模型有Fourier分解、短时Fourier分解、小波分解等^[4-5]。在1998年，N.E.Huang等人提出了经验模式分解算法(Empirical Mode Decomposition，简称EMD)，它能将任意复杂信号 $f(t)$ 分解为数目有限的本征模态函数之和

$f(t) = \sum\nolimits_{k = 1}^n {{f_k}(t)} + {r_{n + 1}}(t)$

(1)

其中 ${f_k}(t)$ 为本征模态函数(Intrinsic Mode Functions，简称IMF)^[6]， ${r_{n + 1}}(t)$ 为余量。借助于D.Gabor在1947年提出的用解析信号的方法来定义IMF的瞬时频率的结论^[7]，通过对每一个IMF的 ${f_k}(t)$ 做Hilbert变换H，可得到其对应的解析信号为

${z_k}(t) = {f_k}(t) + {\rm{j}} \left( {H{f_k}} \right)\left( t \right) = {a_k}(t){{\rm{e}} ^{{\rm{j}} {\theta _k}(t)}}$

(2)

其中 ${a_k}(t) = \sqrt {{{\left| {{f_k}(t)} \right|}^2} + {{\left| {\left( {H{f_k}} \right)\left( t \right)} \right|}^2}} $ 称为信号 ${f_k}(t)$ 的幅度，而 ${\theta _k}(t) = \arctan \left[ {\dfrac{{H{f_k}(t)}}{{{f_k}(t)}}} \right]$ 及 $\dfrac{{\rm{d}} }{{{\rm{d}}t }}[{\theta _k}(t)]$ 分别被称为信号 ${f_k}(t)$ 的相位和瞬时频率。这样，原始信号 $f(t)$ 表示为时频平面上的一个能量−频率−时间分布，称为Hilbert谱，它具有极高的时频局部性^[6]。该方法不仅具有适应非线性、非平稳过程的能力，同时含有很高的分解效率，已被成功地用于海洋波动数据分析、损伤监测、模式识别以及血压变化、心率不整等研究领域^[8-11]。然而，与传统的时频分析方法相比，该方法仅是算法型、操作性的，缺乏进行严格理论分析的数学基础，具有模式混叠效应而且存在满足条件的IMF，其对应的解析信号并不满足瞬时频率为正的物理条件^[12]。

为了建立IMF和EMD算法的相关理论基础以及推广和改进现有的非平稳数据处理方法，研究者们根据HHT(Hilbert-Huang transform)提出的理论背景，希望刻画出满足瞬时频率为正的解析信号的特征，并最终实现将复杂信号 $f(t)$ 分解为如下模型的可能

$f(t) = \sum\nolimits_{k = 0}^n {{a_k}(t)} \cos {\theta _k}(t) + r(t)$

(3)

其中 $r(t)$ 为余量，分量 ${f_k}(t) = {a_k}(t)\cos {\theta _k}(t)$ 满足

$ H({a_k}( \cdot )\cos {\theta _k}( \cdot ))(t) = {a_k}(t)\sin {\theta _k}(t), {a_k}(t) \geqslant 0, \theta _k'(t) \geqslant 0 $

为了从理论上实现上述分解目标，研究者们根据解析信号空间 ${H^2}(T)$ 与Hardy函数空间 ${H^2}(D)$ 边值之间的一一对应关系，刻画了瞬时频率为正的解析信号与Blaschke积和Bedrosian等式的关系，构造出了一系列满足瞬时频率为正的解析信号字典^[13-16]。进一步，从这些字典出发，构造出了一组经典的满足瞬时频率为正的有理解析正交基 $\left\{ {{\phi _k}({{\rm{e}} ^{{\rm{i}} t}})} \right\}_{k = 0}^\infty $ ，可表示为

$ \begin{split} & {\phi _0}({{\rm{e}} ^{{\rm{i}} t}}) = \frac{{\sqrt {1 - {{\left| {{\alpha _0}} \right|}^2}} }}{{1 - {{\overline \alpha }_0}{{\rm{e}} ^{{\rm{i}} t}}}} , \\& {\phi _k}({{\rm{e}} ^{{\rm{i}} t}}) = \frac{{\sqrt {1 - {{\left| {{\alpha _k}} \right|}^2}} }}{{1 - {{\overline \alpha }_k}{{\rm{e}} ^{{\rm{i}} t}}}}\prod\limits_{j = 1}^{k - 1} {\frac{{{{\rm{e}} ^{{\rm{i}} t}} - {\alpha _j}}}{{1 - {{\overline \alpha }_j}{{\rm{e}} ^{{\rm{i}} t}}}}} , k \geqslant 1 \end{split} $

(4)

其中 $\left| {{\alpha _k}} \right| < 1$ ， $\overline {{\alpha _k}} $ 表示 ${\alpha _k}$ 的共轭。这组有理解析正交基 $\left\{ {{\phi _k}({{\rm{e}} ^{{\rm{i}} t}})} \right\}_{k = 0}^\infty $ 也被称为Takenaka-Malquist系(简称TM系)，它是由Hardy空间对应的的Szego再生核 $\dfrac{1}{{1 - \overline \alpha z}}$ 在一组离散点 $\left\{ {\dfrac{1}{{1 - \overline \alpha z}}} \right\}_{k = 0}^\infty$ 取值经过Gram-Schimit正交化过程而得到的。当所有的 ${\alpha _k} = 0$ 时，有理解析正交基 $\left\{ {{\phi _k}({{\rm{e}} ^{{\rm{i}} t}})} \right\}_{k = 0}^\infty $ 就变为经典的Fourier级数 $\left\{ {{{\rm{e}} ^{{\rm{i}} kt}}} \right\}_{k = 0}^\infty $ ，而当 ${\alpha _k}$ 满足超不可分条件时 $\displaystyle\sum\limits_{k = 0}^\infty {(1 - |{\alpha _k}|)} = \infty$ ，对任意的 $f({{\rm{e}} ^{{\rm{i}} t}}) \in {H^2}(T)$ ，在 ${L^2}[{\rm{ - {\text{π}} }},{\rm{{\text{π}} }}]$ 的范数的定义下可实现推广的Fourier分解为

$ \begin{split} & f({{\rm{e}} ^{{\rm{i}} t}}) = \left\langle {f({{\rm{e}} ^{{\rm{i}} t}}),{\phi _0}({{\rm{e}} ^{it}})} \right\rangle {\phi _0}({{\rm{e}} ^{it}}) + \cdots + \\& \left\langle {f({{\rm{e}} ^{it}}),{\phi _k}({{\rm{e}} ^{it}})} \right\rangle {\phi _k}({{\rm{e}} ^{it}}) + \cdots = \left\langle {f({{\rm{e}} ^{it}}),\frac{{\sqrt {1 - |{\alpha _0}{|^2}} }}{{1 - {{\overline \alpha }_0}{{\rm{e}} ^{it}}}}} \right\rangle + \cdots + \\& \left\langle{f({{\rm{e}} ^{it}}),\frac{{\sqrt {1 - |{\alpha _0}{|^2}} }}{{1 - {{\overline \alpha }_0}{{\rm{e}} ^{it}}}}\prod\limits_{j = 0}^{k - 1} {\frac{{{{\rm{e}} ^{it}} - {\alpha _j}}}{{1 - {{\overline \alpha }_j}{{\rm{e}} ^{it}}}}} }\right\rangle\frac{{\sqrt {1 - |{\alpha _0}{|^2}} }}{{1 - {{\overline \alpha }_0}{{\rm{e}} ^{it}}}}\prod\limits_{j = 0}^{k - 1}{\frac{{{{\rm{e}} ^{it}} - {\alpha _j}}}{{1 - {{\overline \alpha }_j}{{\rm{e}} ^{it}}}}} + \cdots \end{split} $

(5)

其中 $\left\langle {f({{\rm{e}} ^{{\rm{i}}t}}),g({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle $ 的内积被定义为

$ \left\langle {f({{\rm{e}} ^{{\rm{i}}t}}),g({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle = \frac{1}{{2{\rm{{\text{π}} }}}}\int\limits_0^{2{\rm{{\text{π}} }}} {f({{\rm{e}} ^{{\rm{i}}t}})\overline {g({{\rm{e}} ^{{\rm{i}}t}})} } {\rm{d}} t = \frac{1}{{2{\rm{{\text{π}} i}}}}\oint\limits_{|z| = 1} {f(z)\overline {g\left(\frac{1}{{\overline z }}\right)} } \frac{{{\rm{d}} z}}{z} $

(6)

关于有理Fourier级数的研究已经被成功应用到系统辨识、信号处理等领域^[17-20]。

事实上，当令 ${f_0}({{\rm{e}} ^{{\rm{i}}t}}) = f({{\rm{e}} ^{{\rm{i}}t}})$ ， ${f_{k + 1}}({{\rm{e}} ^{{\rm{i}}t}}) = {f_k}({{\rm{e}} ^{{\rm{i}}t}}) - $ $ \left\langle {{f_k}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _k}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle {\phi _k}({{\rm{e}} ^{{\rm{i}}t}})$ 。由于 ${\rm{\{ }}{\phi _k}{\rm{(}}{{\rm{e}}^{{\rm{i}}t}}{\rm{)\} }}_{k = 0}^\infty $ 是规范正交基，知

$ \begin{split} \left\langle {{f_{k + 1}}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}}),{\phi _{k + 1}}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}})} \right\rangle =& \left\langle {{f_k}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}}),{\phi _{k + 1}}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}})} \right\rangle = \cdots =\\& \left\langle {{f_0}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}}),{\phi _{k + 1}}({{\mathop{\rm{e}}\nolimits} ^{{\rm{i}}t}})} \right\rangle \end{split} $

因此，上述分解也可进一步表示为

$ \begin{split} {f_0}({{\rm{e}} ^{{\rm{i}}t}}) =& {{{f}}_1}{\rm{(}}{{\rm{e}}^{{\rm{i}}t}}{\rm{) + }}\left\langle {{f_0}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _0}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle {\phi _0}({{\rm{e}} ^{{\rm{i}}t}}){\rm{ = }} \cdots = \\& \sum\limits_{j = 1}^k {\left\langle {{f_k}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _k}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle } {\phi _k}({{\rm{e}} ^{{\rm{i}}t}}){\rm{ + }}{f_{k + 1}}({{\rm{e}} ^{{\rm{i}}t}}) = \\& \sum\limits_{j = 1}^k {\left\langle {{f_0}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _k}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle } {\phi _k}({{\rm{e}} ^{{\rm{i}}t}}){\rm{ + }}{f_{k + 1}}({{\rm{e}} ^{{\rm{i}}t}}) \end{split} $

(7)

为了实现上述模型的快速分解，在2011年，钱涛教授及合作者结合分解算法的能量守恒原则

$ {\rm{|}}f{\rm{(}}{{\rm{e}} ^{{\rm{i}}t}}{\rm{)|}}{{\rm{|}}^2} = |\left\langle {{f_{0,}}{\phi _0}} \right\rangle {|^2} + |\left\langle {{f_{1,}}{\phi _1}} \right\rangle {|^2}{\rm{ + }} \cdots {\rm{ + }}|\left\langle {{f_{k,}}{\phi _k}} \right\rangle {|^2} + ||{f_{k + 1}}({{\rm{e}} ^{{\rm{i}}t}})|{|^2} $

及正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)的思想^[21]，给出了解析信号 $f({{\rm{e}} ^{{\rm{i}}t}})$ 快速分解为瞬时频率为正的原子的自适应Fourier分解算法(Adaptive Fourier Decomposition，简称AFD)^[22]，即参数 ${\alpha _k}$ 要求逐步根据能量最大(贪婪)的原则选取，算法具体流程如下。

令 ${f_0}({{\rm{e}} ^{{\rm{i}}t}}) = f({{\rm{e}} ^{{\rm{i}}t}})$ ，先求最优值 ${{\alpha}} _0^ * \in D$ 使得

$ \begin{split} \alpha _0^* =& \mathop {\arg \max }\limits_{{\alpha _0} \in D} |\left\langle {{f_0},{\phi _0}} \right\rangle {|^2} = \mathop {\arg \max }\limits_{{\alpha _0} \in D} |\left\langle {f,\frac{{\sqrt {1 - |{\alpha _0}{|^2}} }}{{1 - {{\overline \alpha }_0}{{\rm{e}} ^{{\rm{i}}t}}}}} \right\rangle {|^2} = \\& \mathop {\arg \max }\limits_{{\alpha _0} \in D} (1 - |{\alpha _0}{|^2}){\rm{|}}f\left( {{\alpha _0}} \right){{\rm{|}}^2}\\[-18pt] \end{split} $

(8)

令 ${f_1}({{\rm{e}} ^{{\rm{i}}t}})={f_0}({{\rm{e}} ^{{\rm{i}}t}})-\left\langle {{f_0}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _0}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle {\phi _0}({{\rm{e}} ^{{\rm{i}}t}}),$ 其中 ${\phi }_{0}({\rm{e}}^{\rm{i}t})= $ $ \dfrac{\sqrt{1-|{\alpha }_{0}^{\rm{*}}{|}^{2}}}{1-\overline{{\alpha }_{0}^{*}}{\rm{e}}^{\rm{i}t}}$ 。再求最优值 $\alpha _1^ * \in D $ 使得

$ \begin{split} \alpha _1^* = &\mathop {\arg \max }\limits_{{\alpha _1} \in D} |\langle {{f_1}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _1}({{\rm{e}} ^{{\rm{i}}t}})} \rangle {|^2} = \\& \mathop {\arg \max }\limits_{{\alpha _1} \in D} \left|\left\langle {{f_1}({{\rm{e}} ^{{\rm{i}}t}}),\frac{{\sqrt {1 - |{\alpha _1}{|^2}} }}{{1 - \overline {{\alpha _1}} {{\rm{e}} ^{{\rm{i}}t}}}}\frac{{{{\rm{e}} ^{{\rm{i}}t}} - \alpha _0^{\rm{*}}}}{{1 - \overline {\alpha _0^ * } {{\rm{e}} ^{{\rm{i}}t}}}}} \right\rangle \right|^2 = \\& \mathop {\arg \max }\limits_{{\alpha _1} \in D} (1 - |{\alpha _1}{|^2}){\rm{|}}{{\rm{g}}_1}\left( {{\alpha _1}} \right){{\rm{|}}^2} \end{split} $

(9)

其中 ${g_1}({{\rm{e}} ^{{\rm{i}}t}}) = {f_1}({{\rm{e}} ^{{\rm{i}}t}})\dfrac{{1 - \overline {\alpha _0^*} {{\rm{e}} ^{{\rm{i}}t}}}}{{{{\rm{e}} ^{{\rm{i}}t}} - \alpha _0^*}}$ 。

依次迭代下去，令 ${f_k}({{\rm{e}} ^{{\rm{i}}t}}) = {f_{k - 1}}({{\rm{e}} ^{{\rm{i}}t}}) - $ $\langle {f_{k - 1}}({{\rm{e}} ^{{\rm{i}}t}}), \;{\phi _{k - 1}}({{\rm{e}} ^{{\rm{i}}t}}) \rangle $ $ {\phi _{k - 1}}({{\rm{e}} ^{{\rm{i}}t}})$ ，其中， ${\phi }_{k-1}({\rm{e}}^{\rm{i}t})=\dfrac{\sqrt{1-|{\alpha }_{{}_{k-1}}^{\rm{*}}{|}^{2}}}{1-\overline{{\alpha }_{k-1}^{\rm{*}}}{\rm{e}}^{\rm{i}t}}{\displaystyle \prod _{j=0}^{k-2}\dfrac{{\rm{e}}^{\rm{i}t}-{\alpha }_{j}^{*}}{1-\overline{{\alpha }_{j}^{*}}{\rm{e}}^{\rm{i}t}}}$ ，求最优值 $\alpha _k^ * \in D$ 使得

$ \begin{split} \alpha _k^* = &\mathop {\arg \max }\limits_{{\alpha _k} \in D} |\left\langle {{f_k}({{\rm{e}} ^{{\rm{i}}t}}),{\phi _k}({{\rm{e}} ^{{\rm{i}}t}})} \right\rangle |^2 = \\[-3pt]& \mathop {\arg \max }\limits_{{\alpha _k} \in D} \left|\left\langle {{f_k}({{\rm{e}} ^{{\rm{i}}t}}),\frac{{\sqrt {1 - |{\alpha _k}{|^2}} }}{{1 - \overline {{\alpha _k}} {{\rm{e}} ^{{\rm{i}}t}}}}\prod\limits_{j = 0}^{k - 1} {\frac{{{{\rm{e}} ^{{\rm{i}}t}} - \alpha _j^*}}{{1 - \overline {\alpha _j^*} }}} } \right\rangle \right|^2 {\rm{ = }}\\[-3pt]& \mathop {\arg \max }\limits_{{\alpha _k} \in D} \left|\left\langle {{g_k}({{\rm{e}} ^{{\rm{i}}t}}),\frac{{\sqrt {1 - |{\alpha _k}{|^2}} }}{{1 - {{\overline \alpha }_k}{{\rm{e}} ^{{\rm{i}}t}}}}} \right\rangle \right|^2 \end{split} $

其中 ${g_k}({{\rm{e}} ^{{\rm{i}}t}}) = {f_k}({{\rm{e}} ^{{\rm{i}}t}})\displaystyle\prod\limits_{j = 1}^{k - 1} {\dfrac{{1 - \overline {\alpha _j^*} {{\rm{e}} ^{{\rm{i}}t}}}}{{{{\rm{e}} ^{{\rm{i}}t}} - \alpha _j^*}}}$ 。

当 $\| {{f_{k + 1}}({{\rm{e}} ^{{\rm{i}}t}})} \| < \varepsilon$ 停止。

关于这个算法极大值选取的存在性及算法的收敛性证明具体参见文献[22]。围绕这个分解，钱涛教授及合作者^[23-26]开展了一系列的工作，他们不仅从理论上证明了AFD算法的快速收敛性，而且实现了在系统辨识、图像去噪等领域的应用，并将AFD分解的相关结论推广到矩阵值函数、高维复分析、Clifford分析等领域。

由于自适应Fourier分解是基于Hardy空间的性质建立的分解模型，而Hardy空间本质上是一个再生核空间。为了拓宽其应用范围，本文将研究再生核空间 $W_2^1[a,b]$ ^[27-29]的自适应Fourier分解算法，利用能量下降最快的原理自适应性地构造出最佳 $n$ 项逼近函数，从理论上证明其收敛性及极大选择原理成立。最后用实验验证在 $W_2^1[a,b]$ 再生核空间中利用自适应Fourier分解原理构造的 $n$ 项最佳数值原函数的逼近效果要优于用等分节点构造的 $n$ 项最佳数值原函数。并且随着节点数的增加，两个方法的逼近误差都会逐步变小。

1 $W_2^1$ 空间的介绍 1.1 $W_2^1$ 空间的基础介绍

定义1 　 $W_2^1[a,b] = \{ u(x)|u(x)$ 在 $[a,b]$ 上是绝对连续函数，而且 $u'(x) \in {L^2}[a,b]\} $ 。

对于任意的 $u(x) , v(x) \in W_2^1$ ，其内积定义为

$(u,v) = \int_a^b {[u(x)v(x) + u'(x)v'(x)]{\rm{d}}x} $

故其范数为 $\| u \|={{\| u \|}_{W_{2}^{1}}}={{(u,u)}^{{}^{1}\diagup{}_{2}\;}}(u\in W_{2}^{1})$ 。

在文献[27-29]，已证明 $W_2^1[a,b]$ 空间是完备的再生核空间，即对任意的 $u(x) \in W_2^1[a,b]$ ，存在再生核 $R(x,y)$ ，使得 $u(x) = \left\langle {u(y),R(x,y)} \right\rangle $ 。借助再生核空间的定义和 $W_2^1[a,b]$ 空间中内积的定义可知其再生核的表达式为

$ R(x,y)=\frac{{\rm{e}}^{x+y}+{\rm{e}}^{2a+2b-(x+y)}+{\rm{e}}^{2a+|x-y|}+{\rm{e}}^{2b-|x-y|}}{2({\rm{e}}^{2b}-{\rm{e}}^{2a})}$

(10)

设 $\{ {x_i}\} _1^n$ 是给定的一组实数，定义 $W_2^1[a,b]$ 空间上的一组泛函 $\{ {I_j}\} _1^n $

${I_j}u = u({x_j}), \;\;(u \in W_2^1,j = 1,2,\cdots,n) $

则 $\{ {I_j}\} _1^n$ 是 $W_2^1$ 上一组有界线性泛函。

$ | {{I_j}u} | = | {u({x_j})} | \leqslant {\| u \|_c} \leqslant M\| u \| (u \in W_2^1,j = 1,2,\cdots,n), $

其中 $ {{\left\| \centerdot \right\|}_{c}}$ 表示 $C[a,b]$ 的最大值范数。表明 $\| {{I_j}} \| \leqslant M$ 。由Riesz泛函表示定理知，存在 ${\varphi _j}(x) \in W_2^1$ ，使

$ \begin{split} & {I_j}u = (u(x), {\varphi _j}(x)), \;\;\;\;(u(x) \in W_2^1)\\& \| {{I_j}} \| = \| {{\varphi _j}} \|,\;\;\;\;(j = 1,2,\cdots,n) \end{split}$

对于 $x \in [a,b]$ ，作 $W_2^1$ 上的泛函 ${Q_x}$

$u(x) = {Q_x}u = (u(y),R(x,y)), \;\;(u(x) \in W_2^1)$

因此有

$ \begin{split} {\varphi _j}(x) =& {Q_x}{\varphi _j} = ({\varphi _j}(y),R(x,y)) = (R(x,y),{\varphi _j}(y)) = \\& {I_j}R(x,y) = R(x,{x_j}) \end{split} $

2 AFD在 $W_2^1[a,b]$ 空间的应用 2.1 最佳 $n$ 项逼近及其性质

设 $u \in W_2^1[a,b]$ ，已知 $u(x)$ 在给定 $n$ 个点 $\{ {x_i}\} _1^n$ 处的函数值 $\{ u({x_i})\} _1^n$ 。设 ${u_n}(x)$ 是根据 $\{ u({x_i})\} _1^n$ 构造出来的逼近函数，假定它具有如下形式

${u_n}(x) = \sum\nolimits_{j = 1}^n {{a_j}(x){R_{{x_j}}}(x)} $

(11)

根据最小均方误差原理有

$ \begin{split} & \mathop {\min }\limits_{{a_k}} {\left\| {u(x) - \sum\nolimits_{j = 1}^n {{a_j}(x){R_{{x_j}}}(x)} } \right\|^2} = \\& {\left\| {u(x) - \sum\nolimits_{j = 1}^n {\left\langle {u(x)} \right.,\left. {\widetilde {{\varphi _j}}(x)} \right\rangle \widetilde {{\varphi _j}}(x)} } \right\|^2} \end{split} $

(12)

其中 $R(x,{x_i})={R_{{x_i}}}(x)={\varphi _i}(x)$ ， $\widetilde {{\varphi _j}}(x)=\displaystyle \sum\limits_{k = 1}^j {{\beta _{kj}}{\varphi _k}(x)}$ 是由 $\{ {\varphi _k}(x)\} _{_{k = 1}}^j$ 根据Gram-Schmidt正交化过程得到的规范正交函数系。

根据规范正交函数系的性质，知

$ \left\langle {\widetilde {{\varphi _n}}(x)} \right.,\left. {\widetilde {{\varphi _j}}(x)} \right\rangle = \sum\nolimits_{i = 1}^j {\beta _{ij}^*{{\tilde \varphi }_n}} ({x_i}) = 0, j = 1,2, \cdots ,n - 1 $

从而推得 ${x_i} ,i = 1,2, \cdots n - 1$ 为 $\widetilde {{\varphi _n}}(x)$ 的零点，即 $\widetilde {{\varphi _n}}({x_i}) = 0, $ $ \;i = 1,2, \cdots ,n - 1$ 。

根据最佳平方逼近原理，最佳 $n$ 项逼近函数 $u_n^*(x)$ 可表示为 $u_n^*(x) = \displaystyle \sum\nolimits_{j = 1}^n {\left\langle {u(x)} \right.,\left. {\widetilde {{\varphi _j}}(x)} \right\rangle \widetilde {{\varphi _j}}(x)}$ 。

根据再生核的性质，上述公式也可以表示为

$u_n^*(x) = \sum\nolimits_{j = 1}^n {a_j^*{\varphi _j}(x)} $

$a_j^*$ 可以由下面的线形方程组确定

$ \left( {\begin{array}{*{20}{c}} {\left\langle {{\varphi _1},\left. {{\varphi _1}} \right\rangle } \right.}&{\left\langle {{\varphi _1},\left. {{\varphi _2}} \right\rangle } \right.}& \cdots &{\left\langle {{\varphi _1},\left. {{\varphi _n}} \right\rangle } \right.}\\ {\left\langle {{\varphi _2},\left. {{\varphi _1}} \right\rangle } \right.}&{\left\langle {{\varphi _2},\left. {{\varphi _2}} \right\rangle } \right.}& \cdots &{\left\langle {{\varphi _2},\left. {{\varphi _n}} \right\rangle } \right.}\\ \vdots & \vdots & {} & \vdots \\ {\left\langle {{\varphi _n},\left. {{\varphi _1}} \right\rangle } \right.}&{\left\langle {{\varphi _n},\left. {{\varphi _2}} \right\rangle } \right.}& \cdots &{\left\langle {{\varphi _n},\left. {{\varphi _n}} \right\rangle } \right.} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {a_1^*}\\ {a_2^*}\\ \vdots \\ {a_n^*} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {u({x_1})}\\ {u({x_2})}\\ \vdots \\ {u({x_n})} \end{array}} \right)$

因此，很容易知道最佳的 $n$ 项逼近 $u_n^*(x)$ 满足插值条件

$u_n^*({x_i}) = f({x_i}), \;\;i = 1,2, \cdots n$

而且，利用再生核的性质， $u_n^*(x)$ 还可以进一步写成拉格朗日插值的形式。

定理1 　最佳 $n$ 项逼近 $u_n^*(x)=\displaystyle \sum\nolimits_{j = 1}^n{\left\langle {u(x)} , {\widetilde {{\varphi _j}}(x)} \right\rangle \widetilde {{\varphi _j}}(x)}$ 也可以写成

$u_n^*(x) = \sum\nolimits_{j = 1}^n {l{}_j(x)u({x_j})} $

其中，拉格朗日基函数 $l{}_j(x)$ 可以表示为

$l{}_j(x) = \sum\nolimits_{i = j}^n {{\beta _{ij}}\widetilde {{\varphi _i}}(x)} = \sum\nolimits_{i = j}^n {{\beta _{ij}}\sum\nolimits_{k = 1}^i {{\beta _{ki}}{\varphi _k}(x)} } $

(13)

并且满足 ${l_j}({x_k}) = \left\{ {\begin{array}{*{20}{c}} {1\;,\;j = k} \\ {0\;,\;j \ne k} \end{array}} \right.$ 。

证明 　因为

$\widetilde {{\varphi _j}}(x) = \sum\limits_{k = 1}^j {{\beta _{kj}}{\varphi _k}(x)} {\rm{ = }}\sum\limits_{k = 1}^j {{\beta _{kj}}{R_{{x_k}}}(x)} $

而

$ \begin{split} u_n^*(x) =& \sum\nolimits_{j = 1}^n {\left\langle {u(x)} \right.,\left. {\widetilde {{\varphi _j}}(x)} \right\rangle \widetilde {{\varphi _j}}(x)} {\rm{ = }}\\& \sum\nolimits_{j = 1}^n {\sum\nolimits_{i = 1}^j {{\beta _{ij}}u({x_i})} \widetilde {{\varphi _j}}(x)} = \\& \sum\nolimits_{j = 1}^n {\left[ {\sum\nolimits_{i = j}^n {{\beta _{ij}}} \widetilde {{\varphi _i}}(x)} \right]u({x_j})} \end{split} $

因此，拉格朗日基函数 $l{}_j(x)$ 可以表示为

$ l{}_j(x) = \sum\nolimits_{i = j}^n {{\beta _{ij}}\widetilde {{\varphi _i}}(x)} = \sum\nolimits_{i = j}^n {{\beta _{ij}}\sum\nolimits_{k = 1}^i {{\beta _{ki}}{\varphi _k}(x)} } $

接下来简单讨论一下 $l{}_j(x)$ 的性质，验证。

$ {l_j}({x_k}) = \left\{ {\begin{array}{*{20}{c}} {1 , j = k} \\ {0 , j \ne k} \end{array}} \right. $

(1) 当 $j = k$ 时，由于 ${x_i} ,i = 1,2, \cdots n - 1$ 为 $\widetilde {{\varphi _n}}(x)$ 的零点，故而

${l_k}({x_k}) = \sum\nolimits_{i = k}^n {{\beta _{ki}}\widetilde {{\varphi _i}}({x_k})} = \sum\nolimits_{i = k}^n {{\beta _{ki}}\left\langle {\widetilde {{\varphi _i}}} \right.,\left. {{\varphi _k}} \right\rangle } $

再由 $\widetilde {{\varphi _k}}(x) = \displaystyle \sum\nolimits_{j = 1}^k {{\beta _{jk}}{\varphi _j}}$ 可解出 ${\varphi _k} = \displaystyle \sum\nolimits_{j = 1}^k {{\gamma _{kj}}\widetilde {{\varphi _j}}}$ ，所以 ${\gamma _{kk}}{\rm{ = }}\widetilde {{\varphi _k}}({x_k}) = \dfrac{1}{{{\beta _{kk}}}}$ ，则有

${l_k}({x_k}) = \sum\nolimits_{i = k}^n {{\beta _{ki}}\left\langle {\widetilde {{\varphi _i}}} \right.,\left. {{\varphi _k}} \right\rangle } = {\beta _{kk}}{\gamma _{kk}} = 1$

(2) 当 $ j \ne k$ 时

① $j > k$ 时 ${l_j}({x_k}) = \displaystyle \sum\nolimits_{i = j}^n {{\beta _{ji}}\left\langle {\widetilde {{\varphi _i}}} \right.,\left. {{\varphi _k}} \right\rangle } = 0$ 。

② $j < k$ 时，可用数学归纳法证明，具体过程参见文献[28]。

引理1 　设 $u \in W_2^1[a,b],u({x_i}) = {u_i}$ 是 $u(x)$ 在给定点 ${x_i}$ 处的值 $ i = (1,2, \cdots, n)$ 。当 $\left\{ {{x_i}} \right\}$ 在 $[a,b]$ 区间稠密时，最佳 $n$ 项逼近函数 $u_n^{\rm{*}}(x)$ 是

$u_n^{\rm{*}}(x) = \sum\limits_{i = 1}^n {\left\langle {u(x),{{\tilde \varphi }_i}(x)} \right\rangle } {\tilde \varphi _i}(x){\rm{ = }}\sum\nolimits_{i = 1}^n {{l_i}(x){u_i}} $

(14)

一致收敛于原函数 $u(x)$ ，其中 ${l_i}(x)$ 由式(13)给出。

证明 　若 $\left\{ {{x_i}} \right\}_{i = 1}^\infty $ 在 $\left[ {a,b} \right]$ 中稠密，则 $\left\{ {\widetilde {{\varphi _i}}(x)} \right\}_{i = 1}^\infty $ 是 $W_2^1 $ $ [a,b]$ 中的完全正交系。事实上，若 $\left\langle {u(x),\widetilde {{\varphi _i}}(x)} \right\rangle = 0, \; $ $ u(x) \in W_2^1[a,b]$ ，有

$0 = \sum\nolimits_{k = 1}^i {{\beta _{ki}}} \left\langle {u(x),{\varphi _k}(x)} \right\rangle = \sum\nolimits_{k = 1}^i {{\beta _{ki}}} u({x_k}) (i = 1,2, \cdots )$

(15)

因此

$u({x_i}) = 0,\;\;(i = 1,2, \cdots )$

(16)

由 $\left\{ {{x_i}} \right\}_{i = 1}^\infty $ 在区间 $\left[ {a,b} \right]$ 中的稠密性及 $u(x)$ 的连续性，有

$u(x) \equiv 0 ,\;\;(x \in \left[ {a,b} \right])$

(17)

因此，对任何 $ u(x) \in W_2^1$ ，有

$ \begin{split} & \left\| {u(x) - u_n^{\rm{*}}(x)} \right\| = \left\| {u(x) - \sum\nolimits_{i = 1}^n {{l_i}(x){u_i}} } \right\| = \\& \left\| {u(x) - \sum\nolimits_{i = 1}^n {\left\langle {u(x),\widetilde {{\varphi _i}}(x)} \right\rangle \widetilde {{\varphi _i}}(x)} } \right\| \to 0 \;\;(n \to \infty ) \end{split}$

(18)

再根据 $ {\left\| u \right\|_c} \leqslant M{\left\| u \right\|_{W_2^1}}$ ，知

$ u_{n}^{*}(x)\xrightarrow{{\text{一致}}}u(x), \;\;(n\to \infty ) $

证毕。

定理2 　设 $\left\{ {{x_i}} \right\}_{i = 1}^n \in \Omega $ 是一组互异的节点， $B = \{ u| \| u \| \leqslant $ $ 1 \}$ ，则有

$\mathop {\sup }\limits_{\left\| u \right\| \leqslant 1} \left| {u\left( x \right) - {u_n}\left( x \right)} \right| \leqslant M\sqrt d $

(19)

其中 $M = 2{\left[ {\dfrac{{{\rm{ch}} (b - a)}}{{1 + {\rm{ch}} (b - a)}}} \right]^{1/2}}$ ， $d = \mathop {\min }\limits_{1 \leqslant i \leqslant n} \left| {x - {x_i}} \right|$ 。

证明 　令

$ \begin{split} & {d_B}(x) = \mathop {\inf }\limits_{{X_n} \in W_2^1} \mathop {\inf }\limits_{\left\{ {{l_i}} \right\}_{i = 1}^n \in {X_n}} \mathop {\sup }\limits_{\left\| u \right\| \leqslant 1} \left| {u(x) - \sum\nolimits_{i = 1}^n {{l_i}(x){u_i}} } \right| = \\& \mathop {\inf }\limits_{{X_n} \in W_2^1} \mathop {\inf }\limits_{\left\{ {{l_i}} \right\}_{i = 1}^n \in {X_n}} \mathop {\sup }\limits_{\left\| u \right\| \leqslant 1} \left| {\left\langle {u( \cdot ),{R_x}( \cdot )} \right\rangle - \sum\nolimits_{i = 1}^n {{l_i}(x)\left\langle {u( \cdot ),{R_{{x_i}}}( \cdot )} \right\rangle } } \right| = \\& \rho \mathop {\inf }\limits_{{X_n} \in W_2^1} \mathop {\inf }\limits_{\left\{ {{l_i}} \right\}_{i = 1}^n \in {X_n}} \mathop {\sup }\limits_{\left\| u \right\| \leqslant 1} \left| {\left\langle {u( \cdot ),{R_x}( \cdot )} \right\rangle - \sum\nolimits_{i = 1}^n {{l_i}(x){\varphi _i}( \cdot )} } \right| = \\& \rho \mathop {\inf }\limits_{{X_n} \in W_2^1} \mathop {\inf }\limits_{\left\{ {{l_i}} \right\}_{i = 1}^n \in {X_n}} \left| {{R_x}( \cdot ) - \sum\nolimits_{i = 1}^n {{l_i}(x){\varphi _i}( \cdot )} } \right| \end{split} $

设 ${X_n} = {\rm{span}} \left\{ {{\varphi _i}(x)} \right\}_{i = 1}^n$ ， ${P_n}$ 是 $W_2^1[a,b]$ 空间到 ${X_n}$ 投影算子。由于 $\displaystyle\sum\nolimits_{i = 1}^n {{l_i}(x){\varphi _i}(x)} = \left( {{P_n}{R_x}} \right)(x)$ ，知

$\mathop {\sup }\limits_{\left\| u \right\| \leqslant 1} \left| {u\left( x \right) - {u_n}\left( x \right)} \right| = {d_B}(x) = \left\| {{R_x}( \cdot ) - \left( {{P_n}{R_x}} \right)( \cdot )} \right\|$

(20)

由于，对于每一个 $i, {\varphi _i} \in X_n^B$ ，故 ${R_x}( \cdot )$ 到 ${X_n}$ 的距离小于等于 ${R_x}( \cdot )$ 到 ${\rm{span}} \left\{ {{\varphi _i}(x)} \right\}$ 的距离。进一步，由 ${R_{{x_i}}}({x_i}) = {\left\| {{\varphi _i}} \right\|^2}$ ，得

$ \begin{split} & d_B^2(x) \leqslant {\left\| {{R_{{x_t}}}( \cdot ) - \left\langle {{R_{{x_t}}}(x),{\varphi _i}(x)} \right\rangle {\varphi _i}( \cdot )/{{\left\| {{\varphi _i}} \right\|}^2}} \right\|^2} = \\& {R_{{x_t}}}(x) - {\varphi _i}(x){\varphi _i}(x)/{\left\| {{\varphi _i}} \right\|^2} = \left[ {{R_{{x_t}}}(x){R_{{x_i}}}({x_i}) - R_{{x_i}}^2(x)} \right]/{\left\| {{\varphi _i}} \right\|^2} = \\& [{R_{{x_t}}}(x)\left( {{R_{{x_i}}}({x_i}) - {R_{{x_i}}}(x)} \right) + {R_{{x_i}}}(x)\left( {{R_{{x_t}}}(x) - {R_{{x_i}}}(x)} \right)]/{\left\| {{\varphi _i}} \right\|^2} \end{split} $

(21)

再生核 ${R_s}(x)$ 有

$ \left\{ \begin{aligned} & {R_s}(x) = {R_r}(s), \left| {{R_s}({x_1}) - {R_s}({x_2})} \right| \leqslant \left| {{x_1} - {x_2}} \right| \\ & \mathop {\max }\limits_{s,x} \left| {{R_s}(x)} \right| = \frac{{{\rm{ch}} (b - a)}}{{{\rm{sh}} (b - a)}}, \mathop {\min }\limits_x \left| {{R_x}(x)} \right| = \frac{{1 + {\rm{ch}} (b - a)}}{{2{\rm{sh}} (b - a)}} \end{aligned} \right. $

故 ${\left\| {{\varphi _i}} \right\|^2} = {R_{{x_i}}}({x_i}) \geqslant \dfrac{{1 + {\rm{ch}} (b - a)}}{{2{\rm{sh}} (b - a)}}$ ， ${R_{{x_i}}}(x) \leqslant \dfrac{{{\rm{ch}} (b - a)}}{{{\rm{sh}} (b - a)}}$ ， ${R_{{x_t}}}(x) \leqslant \dfrac{{{\rm{ch}} (b - a)}}{{{\rm{sh}} (b - a)}}$ ，则有

$ \left| {{R_{{x_i}}}({x_i}) - {R_{{x_i}}}(x)} \right| \leqslant \left| {{x_i} - x} \right|,\left| {{R_{{x_t}}}(x) - {R_{{x_i}}}(x)} \right| \leqslant \left| {{x_t} - {x_i}} \right| $

综上可得

$d_B^2(x) \leqslant 4 \cdot \frac{{{\rm{ch}} (b - a)}}{{1 + {\rm{ch}} (b - a)}} \cdot d$

(22)

其中 $d = \mathop {\min }\limits_i \left| {x - {x_i}} \right|$ 。得 ${d_B}(x) \leqslant M \cdot \sqrt d $ 。证毕。

2.2 AFD的最佳 $n$ 项逼近收敛性

接下来，进一步论证逐步按能量最大的原理选取 $\left\{ {{x_i}} \right\}_{i = 1}^\infty $ ，用预正交自适应分解算法求得 ${u_n}(x)$ 也可收敛到 $u(x)$ 。具体过程如下。

(1) 令 $u_1^a(x) = u(x)$ ， ${\varphi _y}(x) = {R_y}(x){\rm{ = }}R(x,y)$ ，首先找最优的 $x_1^*$

$ \begin{split} x_1^* = & \mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\left\langle {u(x),\frac{{{\phi _y}(x)}}{{\sqrt {\left\langle {{\phi _y}(x),{\phi _y}(x)} \right\rangle } }}} \right\rangle } \right|^2} = \\& \mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\left\langle {u(x),\frac{{{R_y}(x)}}{{\sqrt {\left\langle {{R_y}(x),{R_y}(x)} \right\rangle } }}} \right\rangle } \right|^2} = \\& \mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\frac{{u(y)}}{{R(y,y)}}} \right|^2} \end{split} $

(2) 令 $u_2^a(x) = u_1^a(x) - \langle {u_1^a(x), {{\tilde\phi _{x_1^*}}}(x)} \rangle {{\tilde\phi _{x_1^*}}}(x)$ ，可知 $\langle u_{^2}^a(x), $ $ {{\tilde\phi _{x_1^*}}}(x)\rangle = 0$ ，其中 $ {{\tilde\phi _{x_1^*}}}(x){\rm{ = }}\dfrac{{{R_{x_1^*}}(x)}}{{\sqrt {R(x_1^*,x_1^*)} }}$ 是由 ${\phi _{x_1^*}}(x)$ 经过G-M正交得到的。然后按照如下方式寻找最优的 $x_2^*$ 。

$ \begin{split} x_2^{\rm{*}} = &\mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\left\langle {u_2^a(x),\frac{{{\phi _y}(x) - \left\langle {{\phi _y}(x), {{\tilde\phi _{x_1^*}}}(x)} \right\rangle {{\tilde\phi _{x_1^*}}}(x)}}{{\sqrt {R{\rm{(}}y{\rm{,}}y{\rm{)}} - {{\left| {\left\langle {{\phi _y}(x), {{\tilde\phi _{x_1^*}}}(x)} \right\rangle } \right|}^2}} }}} \right\rangle } \right|^2} = \\& \mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\left\langle {u_2^a(x),\frac{{{R_y}(x)}}{{\sqrt {R(y,y) - {{\left| {\left\langle {{R_y}(x), {{\tilde\phi _{x_1^*}}}(x)} \right\rangle } \right|}^2}} }}} \right\rangle } \right|^2} = \\& \mathop {\arg \max }\limits_{y \in [a,b]} \frac{{{{\left| {u_2^a(y)} \right|}^2}}}{{R(y,y) - {{\left| {\left\langle {{R_y}(x), {{\tilde\phi _{x_1^*}}}(x)} \right\rangle } \right|}^2}}} \end{split} $

(3) 逐步重复上述步骤，令

$u_k^a(x) = u_{k - 1}^a(x) - \left\langle {u_{k - 1}^a(x),{\tilde {\phi} _{x_{k - 1}^*}}(x)} \right\rangle {\tilde{\phi} _{x_{k - 1}^*}}(x) $

按照能量下降最快原理，可得最优的 $x_k^*$ ，

$ \begin{split} x_k^*=&\mathop {\arg \max }\limits_{y \in [a,b]} {\left| {\left\langle {{u_k}(x),\frac{{{\phi _y}(x) - \displaystyle\sum\nolimits_{j = 1}^{k - 1} {\left\langle {{\phi _y}(x), {{\tilde\phi _{x_j^*}}}(x)} \right\rangle {{\tilde\phi _{x_j^*}}}(x)} }}{{\sqrt {R{\rm{(}}y{\rm{,}}y{\rm{)}} - \displaystyle\sum\nolimits_{j = 1}^{k - 1} {{{\left| {\left\langle {{\phi _y}(x), {{\tilde\phi _{x_j^*}}}(x)} \right\rangle } \right|}^2}} } }}} \right\rangle } \right|^2} = \\& \mathop {\arg \max }\limits_{y \in [a,b]} \frac{{{{\left| {{u_k}(y)} \right|}^2}}}{{R(y,y) - \displaystyle\sum\nolimits_{j = 1}^{k - 1} {{{\left| {\left\langle {{R_y}(x), {{\tilde\phi _{x_j^*}}}(x)} \right\rangle } \right|}^2}} }} \end{split} $

其中 ${\tilde {\phi} _{x_j^*}}(x)$ 是由 ${\rm{\{ }}{\phi _{x_k^*}}(x){\rm{\} }}_{k = 1}^j$ 经过Gram-Schmit正交化而得到的。

接下来，证明在AFD原则得到的 $u_{_k}^a(x)$ 会收敛到 $u(x)$ 。

定理3 　假设 $u(x) \in W_2^1[a,b]$ ，当 $k \to \infty $ 时，通过AFD思想求得的 $u_{_k}^a(x)$ 会一致收敛到 $u(x)$ 。

证明 　因为 $u_{_{k + 1}}^a(x) = u_k^a(x) -\langle {u_{_k}^a(x),{\tilde {\phi} _{x_k^*}}(x)} \rangle {\tilde {\phi} _{x_k^*}}(x)$ ，所以

$ \begin{split} & {\left\| {u_{k + 1}^a(x)} \right\|^2} = {\left\| {u_k^a(x)} \right\|^2} - {\left| {\left\langle {u_k^a(x),{\tilde {\phi} _{x_k^*}}(x)} \right\rangle } \right|^2} =\\& {\left\| {u(x)} \right\|^2}-\displaystyle\sum\nolimits_{j = 1}^k {{{\left| {\left\langle {u_j^a(x),{\tilde {\phi} _{x_j^*}}(x)} \right\rangle } \right|}^2}} {\rm{ = }}{\left\| {u(x)} \right\|^2} - \\& \displaystyle\sum\nolimits_{j = 1}^k {{{\left| {\left\langle {u_j^a(x),\frac{{{\phi _{_{x_j^*}}}(x) - \displaystyle\sum\nolimits_{i = 1}^{j - 1} {\left\langle {{\phi _{x_j^*}}(x), {{\tilde\phi _{x_i^*}}}(x)} \right\rangle } {{\tilde\phi _{x_i^*}}}(x)}}{{\sqrt {\left\langle {{\phi _{x_j^*}}(x),{\phi _{x_j^*}}(x)} \right\rangle-\displaystyle\sum\nolimits_{i = 1}^{j - 1} {{{\left| {\left\langle {{\phi _{x_j^*}}(x), {{\tilde\phi _{x_i^*}}}(x)} \right\rangle } \right|}^2}} } }}} \right\rangle } \right|}^2}} \end{split} $

因此有

$ \begin{split} & {\left\| {u(x)} \right\|^2} ={\left\| {u_{k + 1}^a(x)} \right\|^2} + \sum\nolimits_{j = 1}^k {{{\left| {\left\langle {u_j^a(x),{\tilde {\phi} _{x_j^*}}(x)} \right\rangle } \right|}^2}} = \\& {\left\| {u_{k + 1}^a(x)} \right\|^2} + \sum\nolimits_{j = 1}^k {\frac{{{{\left| {u_j^a(x_j^*)} \right|}^2}}}{{R(x_j^*,x_j^*) - \displaystyle\sum\nolimits_{i = 1}^{j - 1} {{{\left| {\left\langle {{\phi _{x_j^*}}(x),{\tilde {\phi} _{x_i^*}}(x)} \right\rangle } \right|}^2}} }}} \end{split} $

由于 $ u(x) \in {L^2}[a,b]$ ，则有

$ \sum\nolimits_{j = 1}^\infty {\frac{{{{\left| {u_j^a(x_j^*)} \right|}^2}}}{{R(x_j^*,x_j^{\rm{*}}) - \displaystyle\sum\nolimits_{i = 1}^{j - 1} {{{\left| {\left\langle {{\phi _{x_j^*}}(x),{\tilde {\phi} _{x_i^*}}(x)} \right\rangle } \right|}^2}} }}} \leqslant {\left\| u \right\|^2} < \infty $

根据无穷级数收敛原理，有

$\mathop {\lim }\limits_{j \to \infty } \frac{{{{\left| {u_j^a(x_j^*)} \right|}^2}}}{{R(x_j^*,x_j^*) - \displaystyle\sum\nolimits_{i = 1}^{j - 1} {{{\left| {\left\langle {{\phi _{x_j^*}}(x),{\tilde {\phi} _{x_i^*}}(x)} \right\rangle } \right|}^2}} }} = 0$

因为 $x_j^*$ 是按极大原理选取的，故対任意的 $y \in [a,b]$ ，有

$ \begin{split} & \frac{{{{\left| {u_j^a(y)} \right|}^2}}}{{R(y,y)}} \leqslant \frac{{{{\left| {u_j^a(y)} \right|}^2}}}{{R(y,y) - \displaystyle\sum\nolimits_{i = 1}^{j - 1} {{{\left| {\left\langle {{\phi _y}(x),{\tilde {\phi} _{x_i^*}}(x)} \right\rangle } \right|}^2}} }} \leqslant \\& \frac{{{{\left| {u_j^a(x_j^*)} \right|}^2}}}{{R(x_j^*,x_j^*) - \displaystyle\sum\nolimits_{j = 1}^{k - 1} {{{\left| {\left\langle {{\psi _{x_k^*}}(x),{\tilde {\psi} _{x_j^*}}(x)} \right\rangle } \right|}^2}} }} \end{split} $

再根据 $R(y,y) \leqslant \dfrac{{{\rm{ch}} (b - a)}}{{{\rm{sh}} (b - a)}}$ 的有界性，知，对任意的 $y \in [a,b]$ ，有 $\mathop {\lim }\limits_{j \to \infty } {u_j}(y) = 0$ 。证毕。

3 $W_2^1[a,b]$ 空间中的最佳数值原函数

设 $u \in W_2^1[a,b]$ ，假设 $u(x)$ 在给定 $n$ 个点 $\{ {x_i}\} _1^n$ 处的函数值为 $\{ u({x_i})\} _1^n$ 。很神奇的，无论是由给定节点得到的最佳平方 $n$ 项逼近函数 $u_n^ * (x)$ 还是根据AFD思路得到的 $u_n^a(x)$ ，它们都可进一步表示为拉格朗日插值基函数的形式

$ \begin{split} u_n^c(x) = &\sum\nolimits_{j = 1}^n {\left\langle {u(x),\widetilde {{\varphi _j}}(x)} \right\rangle } \widetilde {{\varphi _j}}(x) = \sum\nolimits_{j = 1}^n {[{l_j}(x)]u({x_j})} {\rm{ = }}\\& \sum\nolimits_{j = 1}^n {\left[ {\sum\nolimits_{i = j}^n {\beta _{ji}^*\sum\nolimits_{k = 1}^i {{\beta _{ki}}R({x_k},x)} } } \right]} u({x_j}) \end{split} $

(23)

其中 $c$ 表示 $ * $ 或者 $a$ ， ${{\tilde\varphi _j}}(x) = \displaystyle \sum\nolimits_{k = 1}^j {{\beta _{kj}}R} ({x_k},x)$ 是由 $R({x_k},x)$ 经过Gram-Schmidt正交化得到的， ${\beta _{kj}}$ 为其对应的正交化系数。写成拉格朗日插值形式的优点是，可以用它来求 $u(x)$ 的近似数值原函数 $f(x)$

定理4 　设 $u \in W_2^1[a,b],u({x_i}) = {u_i}$ 是 $u(x)$ 在给定点 ${x_i}$ 处的值 $ i = (1,2, \cdots ,n)$ 。则用上述两种方式求得的最佳数值原函数 $f_n^c(x)$ 可表示为

$ \begin{split} & f_n^c(x) = \int_a^x {u_n^c(t){\rm{d}} t} = \\& \sum\nolimits_{j = 1}^n {\left[ {\sum\nolimits_{i = j}^n {\beta _{ji}^*\sum\nolimits_{k = 1}^i {{\beta _{ki}}\int_a^x {R({x_k},t){\rm{d}} t} } } } \right] } u({x_j}) \end{split} $

(24)

当 $\left\{ {{x_i}} \right\}$ 在 $[a,b]$ 中稠密时或者 $\{ {x_i}{\rm{\} }}$ 按AFD原理选择出来时，都有 $\mathop {\lim }\limits_{n \to \infty } f_n^c(x) = f(x)$ ，其中 $c$ 表示 $ * $ 或者 $a$ ， $\displaystyle\int_a^x {R({x_k},t){\rm{d}} t}$ 可表示为

$ \begin{split} & \int_a^x {{R_{{x_k}}}(t){\mathop{\rm{d}}\nolimits} t} {\rm{ = }}\\& \frac{{{{\mathop{\rm{e}}\nolimits} ^{{x_k} + x}} - {{\mathop{\rm{e}}\nolimits} ^{2a + 2b - {x_k} - x}} - 2{{\mathop{\rm{e}}\nolimits} ^{2a}} + {{\mathop{\rm{e}}\nolimits} ^{2a - {x_k} + x}} + 2{{\mathop{\rm{e}}\nolimits} ^{2b}} - {{\mathop{\rm{e}}\nolimits} ^{2b + {x_k} - x}}}}{{2\left( {{{\mathop{\rm{e}}\nolimits} ^{2b}} - {{\mathop{\rm{e}}\nolimits} ^{2a}}} \right)}} \end{split} $

(25)

证明 　由于

$ \begin{split} u_n^c(x) = &\sum\nolimits_{j = 1}^n {\left\langle {u(x), {{\tilde \varphi _j}}(x)} \right\rangle } {{\tilde \varphi _j}}(x) = \sum\nolimits_{j = 1}^n {[{l_j}(x)]u({x_j})} {\rm{ = }}\\& \sum\nolimits_{j = 1}^n {\left[ {\sum\nolimits_{i = j}^n {\beta _{ji}^*\sum\nolimits_{k = 1}^i {{\beta _{ki}}R({x_k},x)} } } \right]} u({x_j}) \end{split} $

一致收敛于 $u{\rm{(}}x{\rm{)}}$ 。对两边同求积分，知其具有如下表达形式

$f_n^c(x) = \sum\nolimits_{j = 1}^n {\left[ {\sum\nolimits_{i = j}^n {\beta _{ji}^*\sum\nolimits_{k = 1}^i {{\beta _{ki}}\int_a^x {R({x_k},t){\rm{d}} t} } } } \right]} u({x_j})$

(25)

再根据再生核的表达式

$ {R_x}(t){\rm{ = }} \dfrac{{{{\mathop{\rm{e}}\nolimits} ^{x + t}} + {{\mathop{\rm{e}}\nolimits} ^{2a + 2b - (x + t)}} + {{\mathop{\rm{e}}\nolimits} ^{2a + |x - t|}} + {{\mathop{\rm{e}}\nolimits} ^{2b - |x - t|}}}}{{2\left( {{{\mathop{\rm{e}}\nolimits} ^{2b}} - {{\mathop{\rm{e}}\nolimits} ^{2a}}} \right)}} $

知其为

$ \begin{split} & {\lambda _k}(x) = \int_a^x {{R_{{x_k}}}(t){\mathop{\rm{d}}\nolimits} t} {\rm{ = }}\\&\frac{{\left\{ {{{\mathop{\rm{e}}\nolimits} ^{{x_k} + x}} - {{\mathop{\rm{e}}\nolimits} ^{2a + 2b - {x_k} - x}} - 2{{\mathop{\rm{e}}\nolimits} ^{2a}} + {{\mathop{\rm{e}}\nolimits} ^{2a - {x_k} + x}} + 2{{\mathop{\rm{e}}\nolimits} ^{2b}} - {{\mathop{\rm{e}}\nolimits} ^{2b + {x_k} - x}}} \right\}}}{{2\left( {{{\mathop{\rm{e}}\nolimits} ^{2b}} - {{\mathop{\rm{e}}\nolimits} ^{2a}}} \right)}} \end{split} $

证毕。

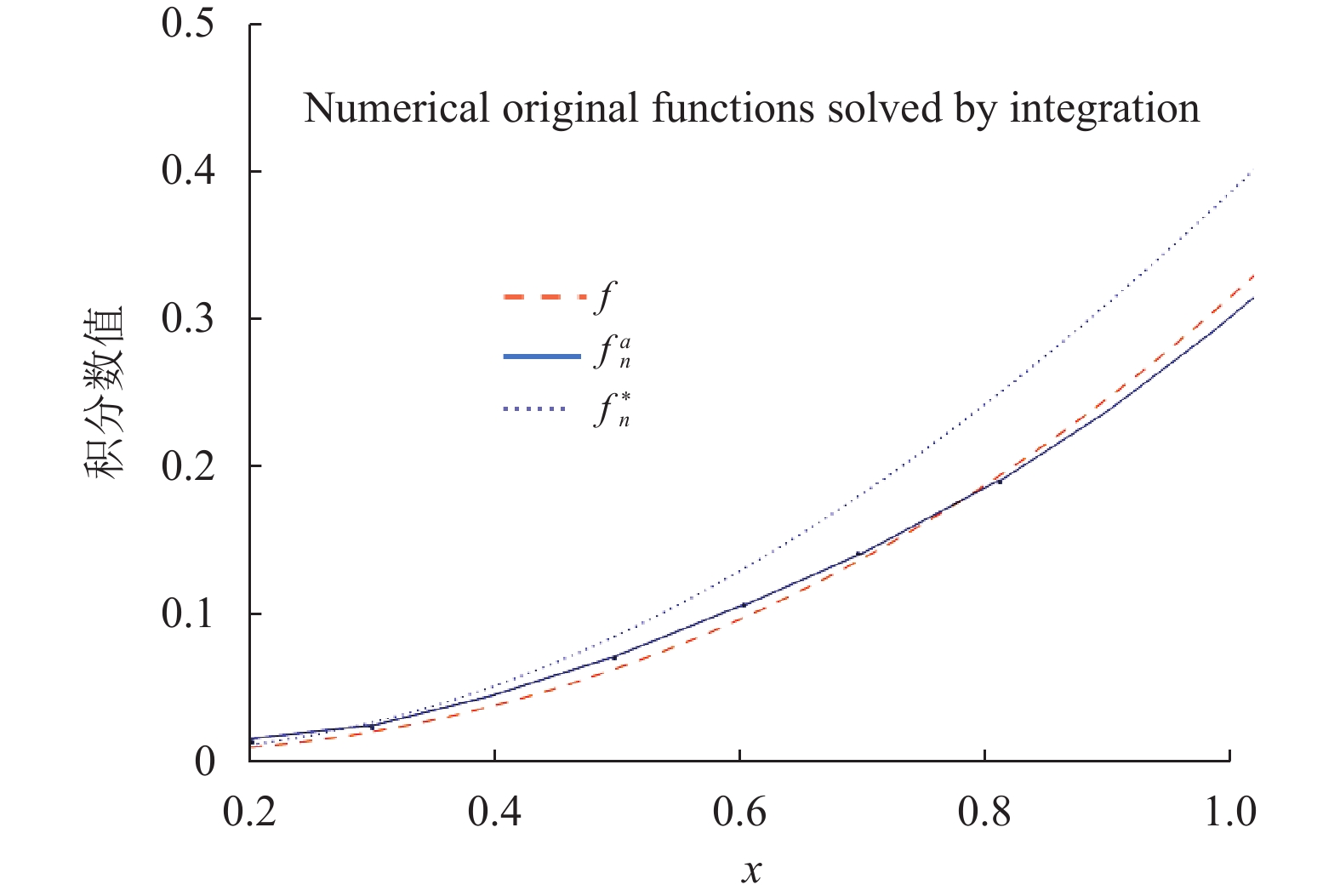
算例：用简单的函数来验证用两种方式求得的最佳数值原函数的逼近效果，取 $u(x) =\sin (x)$ $x \in [0,1]$ 。根据积分公式，我们知其原函数为

$f(x) = \int_0^x {\sin t{\rm{d}} t} = - \cos x{\rm{ + 1}}$

在[0，1]区间上分别按等分方式和AFD思想取5个节点，分别得到最佳数值逼近原函数 $f_n^*(x)$ 和 $f_n^a(x)$ ，如图1所示。从图1可以看出，用AFD思想求得的最佳 $n$ 项函数 $f_n^a$ 逼近原函数 $f$ 的效果要优于用等分节点求得的最佳 $n$ 项函数 $f_n^{\rm{*}}$ 逼近 $f$ 的效果。