2. 广东农工商职业技术学院 智能工程学院,广东 广州 510507
2. School of Intelligent Engineering, Guangdong AIB Polytechnic, Guangzhou 510507, China
近年来,复杂网络引起了学界越来越多的关注。多变复杂的系统可以用复杂网络加以描述,如神经网络、电力网络、通信网络等。同步作为复杂网络的典型集群动力学行为备受关注,现有相关理论研究已被应用在保密通讯[1]、信号处理[2]、机器人列队[3]等诸多实际领域。复杂网络的同步可以简单理解为网络中或者网络之间的节点系统通过相互作用或外部调控,使状态逐步接近,最后达到同一状态。
在实际应用中,复杂网络不可避免地会受到各种因素的影响,如环境中的外部干扰、通讯时延等,这些因素可以使原来稳定的系统变得不稳定[4]。对于如何衡量外部干扰对系统的影响,鲁棒H∞控制则具有较好的描述与处理方法,其控制思想是把系统输出控制在外部干扰的某一特定范围之内,所以对鲁棒H∞同步的研究尤为重要。文献[5]考虑切换复杂网络的鲁棒H∞同步问题,文献[6]通过分布式脉冲控制方法,得到了时滞复杂网络实现鲁棒H∞同步的充分条件,文献[7]考虑复杂网络的鲁棒H∞有限时间同步问题, 文献[8]在文献[7]的基础上考虑复杂网络结构不确定时的鲁棒H∞有限时间同步问题,需要指出的是,上述文献只针对单权重复杂网络。
现实中,由于复杂网络节点间的连接具有非单一性,如人际网络中,个体间的通讯可以通过网络、电话、传真等多种方式实现。每种方式具有各自的特点,多权重复杂网络可以更精确地描述这类系统的动态特性,即网络的节点间存在多个连接边(权重)。文献[9-12]研究了多权重时滞复杂网络的同步和鲁棒H∞同步问题,文献[13]研究了多权重复杂网络存在自适应状态耦合时的鲁棒H∞同步问题,文献[14-15]通过运用牵引控制方法,得到了多权重复杂网络的实现鲁棒H∞同步的充分条件。
如上所述,已有众多方法用于处理多权重复杂网络的鲁棒H∞同步问题,如反馈控制、牵引控制、自适应控制。在众多控制方法中,脉冲控制作为一种非连续控制,能有效降低控制成本,增强系统抗干扰性能,具有很强的实用性[16]。本文将通过脉冲控制方法考虑一类多权重复杂网络的鲁棒H∞同步问题。受文献[5-6]启发,本文设计了新颖的分布式脉冲控制器,通过在分布式脉冲控制器中添加误差状态反馈项,以保证网络实现鲁棒H∞同步。通过模型变换, 利用Lyapunov稳定性理论分析网络的鲁棒H∞同步特性, 以线性矩阵不等式(LMIs)的形式给出了多权重复杂网络实现鲁棒H∞同步的充分条件,仿真结果验证了结论的正确性。
1 问题描述与预备知识考虑一类含有
| $\left\{ \begin{split} & {{\dot {{x}}}_i}(t) = {{f}}(t,{{{x}}_i}(t)) + \sum\limits_{h = 1}^g {\sum\limits_{j = 1}^N {{a_h}b_{ij}^h{{{\varGamma }}_h}{{{x}}_j}(t - \tau (t))} } +\\&\qquad\quad {{{u}}_i}(t)+ {{{D}}_i}{{w}}(t),{\rm{ }}t \geqslant {t_0} \\& {{{y}}_i}(t) = {{C}}{{{x}}_i}(t),{\rm{ }}i \in \tilde N \\& {{{x}}_i}({t_0} + \theta ) = {{{\eta}} _i}(\theta ),{\rm{ }} - \bar \tau \leqslant \theta \leqslant 0 \end{split} \right.$ | (1) |
其中,
假设1 连续非线性向量函数
假设2 外部干扰
引理1[17] 符号“
| $(a{{A}}) \otimes {{B}} = {{A}} \otimes (a{{B}})$ |
| $\;\;\;\;({{A}} + {{B}}) \otimes {{C}} = {{A}} \otimes {{C}} + {{B}} \otimes {{C}}$ |
| $({{A}} \otimes {{B}})({{C}} \otimes {{D}}) = ({{AC}}) \otimes ({{BD}})\;\;\;\,$ |
| ${({{A}} \otimes {{B}})^{\rm{T}}} = {{{A}}^{\rm{T}}} \otimes {{{B}}^{\rm{T}}}$ |
引理2[18] (Schur补引理)对给定的实对称矩阵
| ${{S}} < 0$ |
| ${{{S}}_{11}} < 0,{\rm{ }}{{{S}}_{22}} - {{S}}_{12}^{\rm{T}}{{S}}_{11}^{ - 1}{{{S}}_{12}} < 0$ |
| ${{{S}}_{{\rm{22}}}}{\rm{ < 0, }}{{{S}}_{{\rm{11}}}}{\rm{ - }}{{{S}}_{{\rm{12}}}}{{S}}_{{\rm{22}}}^{{\rm{ - 1}}}{{S}}_{{\rm{12}}}^{\rm{T}}{\rm{ < 0}}$ |
本文的主要目标是通过脉冲控制令网络式(1)中各节点状态
| $ \dot {{s}}(t) = {{f}}(t,{{s}}(t)),{\rm{ }}t \geqslant {t_0},\;\;{{s}}(t) \in {{\bf{R}}^n} $ |
其中
设计如下分布式脉冲控制器
| ${{{u}}_i}(t) ={{H}} \sum\limits_{k = 1}^\infty {\delta (t - {t_k})} ,{\rm{ }}i \in \tilde N$ | (2) |
| ${{H}} = \sum\limits_{j \in {{{{\tilde N}}}_i}} {{v_{ij}}({{{x}}_j}(t) - {{{x}}_i}(t))} + z_i({{{x}}_i}(t) - {{s}}(t))$ |
其中
将式(2)代入式(1),结合狄拉克函数
| $ \left\{ \begin{aligned} & {{\dot {{x}}}_i}(t) = {{f}}(t,{{{x}}_i}(t)) + \sum\limits_{h = 1}^g {\sum\limits_{j = 1}^N {{a_h}b_{ij}^h{{{\varGamma }}_h}{{{x}}_j}(t - \tau (t))} } + \\&\qquad\quad {{{D}}_i}{{w}}(t),{\rm{ }}t \ne {t_k} \\& \Delta {{{x}}_i}({t_k}) = \sum\limits_{j \in {{{{\tilde N}}}_i}} {{v_{ij}}({{{x}}_j}(t_k^ - ) - {{{x}}_i}(t_k^ - ))} + z_i({{{x}}_i}(t_k^ - ) - \\&\qquad\qquad {{s}}(t_k^ - )),k \in {{\bf{N}}^ + } \\& {{{y}}_i}(t) = {{C}}{{{x}}_i}(t),{\rm{ }}i \in \tilde N \\& {{{x}}_i}({t_0} + \theta ) = {{{\eta}} _i}(\theta ),{\rm{ }} - \bar \tau \leqslant \theta \leqslant 0 \end{aligned} \right. $ | (3) |
其中
令误差状态变量
| $ \left\{ \begin{aligned} & {{\dot {\tilde {{x}}}}_i}(t) = \tilde {{f}}(t,{{\tilde {{x}}}_i}(t)) + \sum\limits_{h = 1}^g {\sum\limits_{j = 1}^N {{a_h}b_{ij}^h{{{\varGamma }}_h}{{\tilde {{x}}}_j}(t - \tau (t))} } + \\ &\qquad\quad {{{D}}_i}{{w}}(t),{\rm{ }}t \ne {t_k} \\ & \Delta {{\tilde {{x}}}_i}({t_k}) = \sum\limits_{j \in {{{{\tilde N}}}_i}} {{v_{ij}}({{\tilde {{x}}}_j}(t_k^ - ) - {{\tilde {{x}}}_i}(t_k^ - ))} + z_i{{\tilde {{x}}}_i}(t_k^ - ),k \in {{\bf{N}}^ + } \\ & {{\tilde {{y}}}_i}(t) = {{C}}{{\tilde {{x}}}_i}(t),{\rm{ }}i \in \tilde N \\ & {{\tilde {{x}}}_i}({t_0} + \theta ) = {{{\phi}} _i}(\theta ),{\rm{ }} - \bar \tau \leqslant \theta \leqslant 0 \end{aligned} \right. $ | (4) |
令
由引理1,同步误差系统式(4)可重写成式(5)。
| $\left\{ \begin{split} & \dot {\tilde {{x}}}(t) = \tilde {{F}}(t,\tilde {{x}}(t)) + \sum\limits_{h = 1}^g {{a_h}({{{B}}^h} \otimes {{{\varGamma }}_h})} \tilde {{x}}(t - \tau (t))+ \\[-5pt]&\qquad\quad {{D}}{{w}}(t),{\rm{ }}t \ne {t_k} \\& \Delta \tilde {{x}}({t_k}) = ({{M}} \otimes {{{I}}_n})\tilde {{x}}(t_k^ - ),{\rm{ }}k \in {{\bf{N}}^ + } \\& \tilde {{y}}(t) = ({{{I}}_N} \otimes {{C}})\tilde {{x}}(t) \\& \tilde {{x}}({t_0} + \theta ) = \;{{\phi}}\; (\theta ),{\rm{ }} - \bar \tau \leqslant \theta \leqslant 0 \end{split} \right.$ | (5) |
当
| $\left\{ \begin{split} & \dot {\tilde {{x}}}(t) = \tilde {{F}}(t,\tilde {{x}}(t)) + \sum\limits_{h = 1}^g {{a_h}({{{B}}^h} \otimes {{{\varGamma }}_h})} \tilde {{x}}(t - \tau (t)),{\rm{ }}t \ne {t_k} \\& \Delta \tilde {{x}}({t_k}) = ({{M}} \otimes {{{I}}_n})\tilde {{x}}(t_k^ - ),{\rm{ }}k \in {{\bf{N}}^ + } \\& \tilde {{y}}(t) = ({{{I}}_N} \otimes {{C}})\tilde {{x}}(t) \\& \tilde {{x}}({t_0} + \theta ) = \;{{\phi}}\; (\theta ),{\rm{ }} - \bar \tau \leqslant \theta \leqslant 0 \end{split} \right.$ | (6) |
系统初始值
备注1 通过构建同步误差系统,将网络式(1)的鲁棒H∞同步问题转化为同步误差系统式(5)的稳定性和有限
为推导本文结论,给出定义1和定义2。
定义1
| $||\tilde {{x}}(t,{t_0},\;{{\phi}}\; )|| \leqslant K{{\rm{e}}^{ - c(t - {t_0})}}||\;{{\phi}}\; ||,{\rm{ }}t \geqslant {t_0}$ |
成立,其中
定义2 当下列2个条件同时满足时,称多权重复杂网络式(1)实现鲁棒H∞同步。
条件1为同步误差系统式(5)是内部全局指数稳定的。
条件2是在零初始条件下,对任意
| $\int_{\;{t_0}}^{{t_p}} {||\tilde {{y}}(t)|{|^2}{\rm{d}}t \leqslant {\gamma ^2}\int_{\;{t_0}}^{{t_p}} {||{{w}}(t)|{|^2}} } {\rm{d}}t,$ |
定理1 考虑满足假设1的同步误差系统式(6)。若对于给定常量
| $ \left[ {\begin{array}{*{20}{c}} {{\varTheta }}&{{{PS}}}&{{P}}\\ * &{ - \mu {{P}}} & 0 \\ * &*&{ - \alpha {{I}}} \end{array}} \right]< 0 $ | (7) |
| $\left[ {\begin{array}{*{20}{c}} { - \vartheta {{P}}} &{{{({{I}} + ({{M}} \otimes {{{I}}_n}))}^{\rm{T}}}{{P}}} \\ * & { - {{P}}} \end{array}} \right] < 0$ | (8) |
其中
| ${{\varTheta }} = \left(\frac{\mu }{\vartheta } + \frac{{\ln \vartheta }}{\rho }\right){{P}} + \alpha ({{{I}}_N} \otimes {{{L}}^{\rm{T}}}{{L}})$ |
| ${{S}} = \sum\limits_{h = 1}^g {{a_h}({{{B}}^h} \otimes {{{\varGamma }}_h})} $ |
证明 对于足够小的数
| ${{\varXi }} = \left[ {\begin{array}{*{20}{c}} {{{\varTheta '}}} & {{{PS}}} & {{P}} \\ * & { - \mu {{\rm{e}}^{ - 2c\bar \tau }}{{P}}} & 0 \\ * & * &{ - \alpha {{I}}} \end{array}} \right] < 0$ | (9) |
其中
| ${{\varTheta '}} = \left(\frac{\mu }{\vartheta } + \frac{{\ln (\vartheta + \ell )}}{\rho } + 2c\right){{P}} + \alpha ({{{I}}_N} \otimes {{{L}}^{\rm{T}}}{{L}})$ |
用
| $V(t) = {\tilde {{x}}^{\rm{T}}}(t){{P}}\tilde {{x}}(t)$ | (10) |
令
| $\bar V({t_0} + \theta ) \leqslant {{\lambda} _1}||\;{{\phi}}\; |{|^2} < \vartheta {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2} < {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2}$ | (11) |
下文证明式(12)成立。
| $\bar V(t) < {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2},{\rm{ }}\forall t > {t_0}$ | (12) |
首先证明
| $ \bar V(t) < {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2},{\rm{ }}t \in ({t_0},{t_1}) $ | (13) |
假设式(13)不成立, 存在时刻
令
| $\bar V({t^ * }) = {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2},{\rm{ }}\bar V(t) < {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2},{\rm{ }}\forall t \in [{t_0} - \bar \tau ,{t^ * })$ | (14) |
令
| $\bar V(t') = \vartheta {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2} $ |
当
| $\bar V(t) \geqslant \vartheta {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2} \geqslant \vartheta \bar V(t + \theta ),\;\theta \in [ - \bar \tau ,0] $ |
可得
| $0 < [{\tilde {{x}}^{\rm{T}}}({t^ * }){{P}}\tilde {{x}}({t^ * }) - \vartheta {{\rm{e}}^{ - 2c\bar \tau }}{\tilde {{x}}^{\rm{T}}}({t^ * } - \tau ({t^ * })){{P}}\tilde {{x}}({t^ * } - \tau ({t^ * }))]$ |
鉴于
| $ 0<\left[\frac{\mu }{\vartheta }{{\tilde {{x}}}^{\rm{T}}}({t^ * }){{P}}\tilde {{x}}({t^ * })-\mu {{\rm{e}}^{ - 2c\bar \tau }}{{\tilde {{x}}}^{\rm{T}}}({t^ * }-\tau ({t^ * })){{P}}\tilde {{x}}({t^ * }-\tau ({t^ * }))\right] $ | (15) |
另一方面,由
| $0 \leqslant \alpha [{\tilde {{x}}^{\rm{T}}}(t)({{{I}}_N} \otimes {{{L}}^{\rm{T}}}{{L}})\tilde {{x}}(t) - {\tilde {{F}}^{\rm{T}}}(t,\tilde {{x}}(t))\tilde {{F}}(t,\tilde {{x}}(t))]$ | (16) |
沿着同步误差系统式(6)的轨迹对
| $ \begin{split} \dot {\bar V}(t) =& 2{{\rm{e}}^{2c(t - {t_0})}}{{\tilde {{x}}}^{\rm{T}}}(t)\{ [c{{P}}\tilde {{x}}(t) + {{P}}[\tilde {{F}}(t,\tilde {{x}}(t))+ \\& {{S}}\tilde {{x}}(t - \tau (t))]\} \end{split} $ | (17) |
令
| $\dot {\bar V}(t) \leqslant {{\rm{e}}^{2c(t - {t_0})}}[{{{\xi}} ^{\rm{T}}}(t){{\varXi }}{{\xi}} (t) + \varphi V(t)] < \varphi \bar V(t)$ |
可得
| $\bar V({t^*}) \leqslant {{\rm{e}}^{\varphi ({t^*} - t')}}\bar V(t') < \vartheta {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2}{{\rm{e}}^{\varphi \rho }} < {{\lambda} _0}\varsigma ||\;{{\phi}}\; |{|^2}$ |
显然,这与式(14)矛盾,故式(13)成立。通过引理2,式(8)等价于
| ${({{I}} + ({{M}} \otimes {{{I}}_n}))^{\rm{T}}}{{P}}({{I}} + ({{M}} \otimes {{{I}}_n})) < \vartheta {{P}}$ |
可得
| $ \begin{split} & \bar V({t_1}) = {{\rm{e}}^{2c({t_1} - {t_0})}}{{\tilde {{x}}}^{\;\rm{T}}}({t_1}){{P}}\tilde {{x}}({t_1})= \\& {{\rm{e}}^{2c({t_1} - {t_0})}}{{\tilde {{x}}}^{\;\rm{T}}}(t_1^ - ){({{I}} + ({{M}} \otimes {{{I}}_n}))^{\;\rm{T}}}{{P}}({{I}} + ({{M}} \otimes {{{I}}_n}))\tilde {{x}}(t_1^ - )< \\& {{\rm{e}}^{2c({t_1} - {t_0})}}\vartheta {{\tilde {{x}}}^{\;\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - ) < {{\rm{e}}^{2c({t_1} - {t_0})}}{{\tilde {{x}}}^{\;\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - ) < \bar V(t_1^ - ) \end{split} $ | (18) |
结合式(13)、式(18),得
由
| $||\tilde {{x}}(t)|| \leqslant \sqrt {\frac{\varsigma }{\vartheta }} {{\rm{e}}^{ - c(t - {t_0})}}||\;{{\phi}}\; ||,{\rm{ }}\forall t \geqslant {t_0}$ |
由此,同步误差系统式(6)在脉冲时刻序列
备注2 当
定理2 考虑满足假设1、2的同步误差系统式(5)。若对于给定常量
| $ {\tilde{ \varXi }} = \left[ {\begin{array}{*{20}{c}} {{\tilde{ \varTheta }}}&{{{PS}}}&{{P}}&{{{PD}}}&{{{({{{I}}_N} \otimes {{C}})}^{\rm{T}}}}\\ * &{ - \mu {{P}}}&0&0&0\\ * & * &{ - \alpha {{I}}}&0&0\\ * & * & * &{ - \vartheta \;{\gamma ^2}{{{I}}_m}}&0\\ * & * & * & * &{ - {{{I}}_{qN}}} \end{array}} \right] < 0 $ | (19) |
| $\left[ {\begin{array}{*{20}{c}} { - \delta {{P}}}&0&{{{({{{I}}_N} \otimes {{C}})}^{\rm{T}}}}\\ * &{ - \vartheta \;{\gamma ^2}{{{I}}_m}}&0\\ * & * &{ - {{{I}}_{qN}}} \end{array}} \right] < 0$ | (20) |
其中
| ${\tilde{ \varTheta }} = \left(\frac{\mu }{{\vartheta (1 - \delta \bar \tau )}} + \frac{{\ln \vartheta }}{\rho }\right){{P}} + \alpha ({{{I}}_N} \otimes {{{L}}^{\rm{T}}}{{L}})$ |
| ${{S}} = \sum\limits_{h = 1}^g {{a_h}({{{B}}^h} \otimes {{{\varGamma }}_h})} $ |
证明 当式(19)成立时,有式(7)成立。通过定理1可知,同步误差系统式(5)在脉冲时刻序列
| ${{\tilde{ \varXi }}_1} = \left[ {\begin{array}{*{20}{c}} {{\varDelta }}&{{{\varSigma }}_1^{\rm{T}}} \\ * &{ - {{{I}}_{qN}}} \end{array}} \right] < 0$ | (21) |
其中
| ${{{\varSigma }}_1} = [\begin{array}{*{20}{c}} {({{{I}}_N} \otimes {{C}})}&0&0&0 \end{array}]$ |
| ${{\varDelta }} = \left[ {\begin{array}{*{20}{c}} {{\tilde{ \varTheta }}}&{{{PS}}}&{{P}}&{{{PD}}} \\ * &{ - \mu {{P}}}&0&0 \\ * & * &{ - \alpha {{I}}}&0 \\ * & * & * &{ - \vartheta {\gamma ^2}{{{I}}_m}} \end{array}} \right]$ |
通过引理2,式(21)等价于
| ${{\varDelta }} + {{\varSigma }}_1^{\rm{T}}{{{\varSigma }}_1} < 0$ | (22) |
同理,式(20)等价于
| $\left[ {\begin{array}{*{20}{c}} { - \delta {{P}}}&0 \\ 0&{ - \vartheta {\gamma ^2}{{{I}}_m}} \end{array}} \right] + {{\varSigma }}_2^{\rm{T}}{{{\varSigma }}_2} \leqslant 0$ | (23) |
其中
在不等式(23)左右两边分别乘以
| $||\tilde {{y}}(t)|{|^2} - \vartheta {\gamma ^2}||{{w}}(t)|{|^2} \leqslant \delta V(t)$ | (24) |
对于给定的脉冲时刻序列
当
| $\bar \rho (t) = \frac{1}{{{t_k} - {t_{k - 1}}}}$ |
| $ {\rho _1}(t) = (t - {t_{k - 1}})\bar \rho (t),\;\;\varepsilon (t) = \left\{ \begin{array}{l} {\vartheta ^{{\rho _1}(t)}},\;\;t \geqslant {t_0} \\ 1,\;\;\;\;\;\;\;\;t < {t_0} \end{array} \right. $ |
易知
定义辅助函数
| $J(t) = \left\{ \begin{split} & \varepsilon (t)V(t) + \int_{{t_0}}^t {\varepsilon (\psi)(||\tilde {{y}}(\psi)|{|^2} - \vartheta {\gamma ^2}||{{w}}(\psi)|{|^2}){\rm{d}}\psi} , \\&\qquad t > {t_0} \\& \varepsilon (t)V(t),{\rm{ }}{t_0} - \bar \tau \leqslant t \leqslant {t_0} \end{split} \right.$ |
可知
证明下式(25)成立。
| $J(t) \leqslant 0,{\rm{ }}\forall t > {t_0}$ | (25) |
首先证明
| $J(t) \leqslant 0,{\rm{ }}\forall t \in ({t_0},{t_1})$ | (26) |
假设式(26)不成立,存在一个特定的
| $J({t^ * }) > 0,{\rm{ }}J({t^ * }) > J(t),{\rm{ }}t \in ({t_0} - \bar \tau ,{t^ * })$ | (27) |
且
| $\dot J({t^ * }) \geqslant 0$ | (28) |
对于任意
| $ \begin{split} & \varepsilon ({t^ * } + \theta )V({t^ * } + \theta ) \leqslant \varepsilon ({t^ * })V({t^ * }) + \\ &\quad \int_{{t^ * } + \theta }^{{t^ * }} {\varepsilon (\psi)(||\tilde {{y}}(\psi)|{|^2} - \vartheta {\gamma ^2}||{{w}}(\psi)|{|^2}){\rm{d}}\psi} = \\ &\quad \varepsilon ({t^ * })V({t^ * }) + \delta \int_{{t^ * } + \theta }^{{t^ * }} {\varepsilon (\psi)V(\psi){\rm{d}}\psi}+ \\ &\quad \int_{{t^ * } + \theta }^{{t^ * }} {[\varepsilon (\psi)(||\tilde {{y}}(\psi)|{|^2} - \vartheta {\gamma ^2}||{{w}}(\psi)|{|^2}) - \delta \varepsilon (\psi)V(\psi)]{\rm{d}}\psi} \end{split} $ |
由式(24),可得
| $ \begin{split} & \varepsilon ({t^ * } + \theta )V({t^ * } + \theta )\leqslant \\ &\qquad \varepsilon ({t^ * })V({t^ * }) + \delta \int_{{t^ * } + \theta }^{{t^ * }} {\varepsilon (\psi)V(\psi){\rm{d}}\psi} \leqslant \\ &\qquad \varepsilon ({t^ * })V({t^ * }) + \delta \bar \tau \mathop {\sup }\limits_{\theta \in [ - \bar \tau ,0]} \varepsilon ({t^ * } + \theta )V({t^ * } + \theta ) \end{split} $ |
进而
| $\mathop {\sup }\limits_{\theta \in [ - \bar \tau ,0]} \varepsilon ({t^ * } + \theta )V({t^ * } + \theta ) \leqslant \frac{1}{{1 - \delta \bar \tau }}\varepsilon ({t^ * })V({t^ * })$ |
鉴于
| $ 0 \leqslant \Bigg[\frac{\mu }{{\vartheta (1 - \delta \bar \tau )}}{{\tilde {{x}}}^{\rm{T}}}({t^ * }){{P}}\tilde {{x}}({t^ * }) - \Bigg.\Bigg. \mu {{\tilde {{x}}}^{\rm{T}}}({t^ * } - \tau ({t^ * })){{P}}\tilde {{x}}({t^ * } - \tau ({t^ * }))\Bigg] $ | (29) |
沿着同步误差系统式(5)的轨迹对
| $ \begin{split} & \dot J(t) = \varepsilon (t)\{ (\bar \rho (t)\ln \vartheta ){{\tilde {{x}}}^{\rm{T}}}(t){{P}}\tilde {{x}}(t) + 2{{\tilde {{x}}}^{\rm{T}}}(t){{P}}[\tilde {{F}}(t,\tilde {{x}}(t)) + \\&\qquad {{S}}\tilde {{x}}(t - \tau (t)) + {{D}}{{w}}(t)] + ||\tilde {{y}}(t)|{|^2} - \vartheta {\gamma ^2}||{{w}}(t)|{|^2}\} \end{split} \;$ | (30) |
又
| $ \begin{split} & \dot J(t) \leqslant \varepsilon (t)\Bigg\{ \frac{{\ln \vartheta }}{\rho }{{\tilde {{x}}}^{\rm{T}}}(t){{P}}\tilde {{x}}(t) + 2{{\tilde {{x}}}^{\rm{T}}}(t){{P}}[\tilde {{F}}(t,\tilde {{x}}(t)) + \Bigg.\\&\quad\Bigg. {{S}}\tilde {{x}}(t - \tau (t)) + {{D}}{{w}}(t)] + ||\tilde {{y}}(t)|{|^2} - \vartheta {\gamma ^2}||{{w}}(t)|{|^2}\Bigg\} \end{split}\;\;\;\;\;\;\;\;$ | (31) |
当
| $\dot J({t^ * }) \leqslant \varepsilon ({t^*})\;{\mathchar'26\mkern-10mu{{{\lambda}}} ^{\rm{T}}}({t^ * })({{\varDelta }} + {{\varSigma }}_1^{\rm{T}}{{{\varSigma }}_1})\;\mathchar'26\mkern-10mu{{{\lambda}}} ({t^ * })$ |
其中
| $ \begin{split} & J({t_1}) - J(t_1^ - ) = \varepsilon ({t_1}){{\tilde {{x}}}^{\rm{T}}}({t_1}){{P}}\tilde {{x}}({t_1}) - \varepsilon (t_1^ - ){{\tilde {{x}}}^{\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - )= \\&\qquad {{\tilde {{x}}}^{\rm{T}}}(t_1^ - ){({{I}} + ({{M}} \otimes {{{I}}_n}))^{\rm{T}}}{{P}}({{I}} + ({{M}} \otimes {{{I}}_n}))\tilde {{x}}(t_1^ - ) - \\&\qquad {\rm{ }} \vartheta {{\tilde {{x}}}^{\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - ) < \vartheta {{\tilde {{x}}}^{\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - ) - \vartheta {{\tilde {{x}}}^{\rm{T}}}(t_1^ - ){{P}}\tilde {{x}}(t_1^ - ) < 0 \end{split} $ |
可知
重复上述证明步骤可得式(25)成立。进而可得
| $\int_{{t_0}}^t {||\tilde {{y}}(\psi)|{|^2}{\rm{d}}\psi} \leqslant \vartheta {\gamma ^2}\int_{{t_0}}^t {||{{w}}(\psi)|{|^2}{\rm{d}}\psi} $ |
注意到
| $\int_{{t_0}}^t {||\tilde {{y}}(\psi)|{|^2}{\rm{d}}\psi} \leqslant {\gamma ^2}\int_{{t_0}}^t {||{{w}}(\psi)|{|^2}{\rm{d}}\psi} $ |
即在脉冲时刻序列
备注3 定理2给出了多权重复杂网络式(1)在受到外部干扰影响时实现鲁棒H∞同步的充分条件,网络的鲁棒H∞同步性能由同步误差系统式(5)的稳定性和
本节将对多权重复杂网络式(1)进行数值仿真,验证上述结论的有效性,给定如下参数。
| ${{{B}}^1} = 0.1\left[ {\begin{array}{*{20}{c}} { - 1}&0&1&0&0 \\ 0&{ - 1}&0&1&0 \\ 0&1&{ - 1}&0&0 \\ 0&1&0&{ - 1}&0 \\ 0&0&1&0&{ - 1} \end{array}} \right]$ |
| ${{{B}}^2} = 0.1\left[ {\begin{array}{*{20}{c}} { - 2}&1&1&0&0 \\ 1&{ - 3}&0&2&0 \\ 0&1&{ - 3}&2&0 \\ 0&0&1&{ - 2}&1 \\ 1&0&1&0&{ - 2} \end{array}} \right]$ |
| ${{{B}}^3} = 0.1\left[ {\begin{array}{*{20}{c}} { - 2}&0&1&0&1 \\ 0&{ - 2}&0&2&0 \\ 0&0&{ - 1}&0&1 \\ 1&1&0&{ - 2}&0 \\ 0&1&1&0&{ - 2} \end{array}} \right]$ |
进一步,验证定理2的有效性。取脉冲时刻序列
给定
| ${{Q}} = \left[ {\begin{array}{*{20}{r}} { - 0.3}&{0.1}&{0.1}&0.0&{0.1} \\ {0.1}&{ - 0.2}&0.0&{0.1}&0.0 \\ 0.0&{0.1}&{ - 0.3}&{0.1}&{0.1} \\ {0.1}&{0.1}&{0.1}&{ - 0.4}&{0.1} \\ {0.1}&{0.1}&{0.1}&0.0&{ - 0.3} \end{array}} \right]$ |
令
用Matlab工具对LMIs式(8)、(19)、(20)进行求解,可求得存在一组正定矩阵
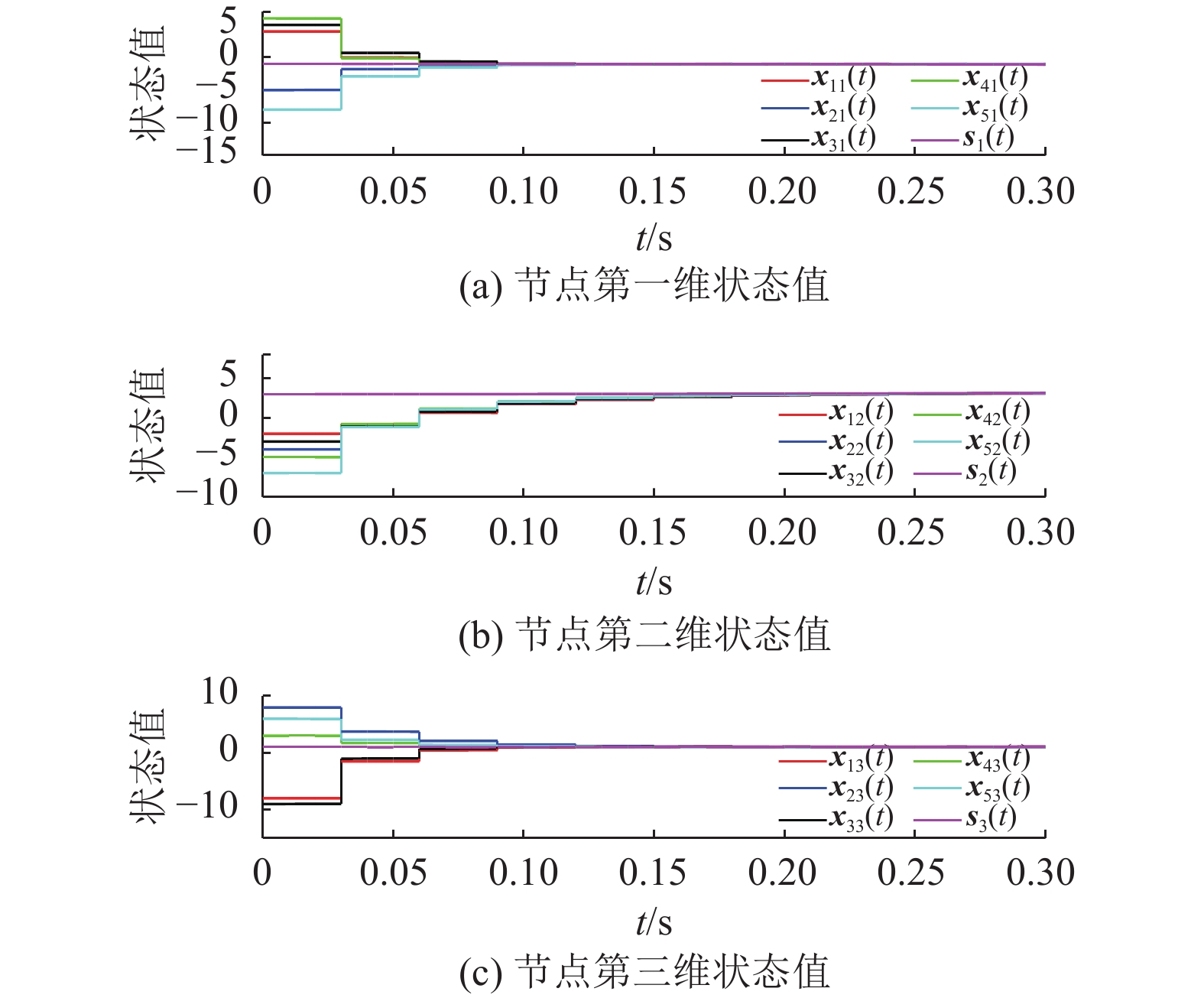
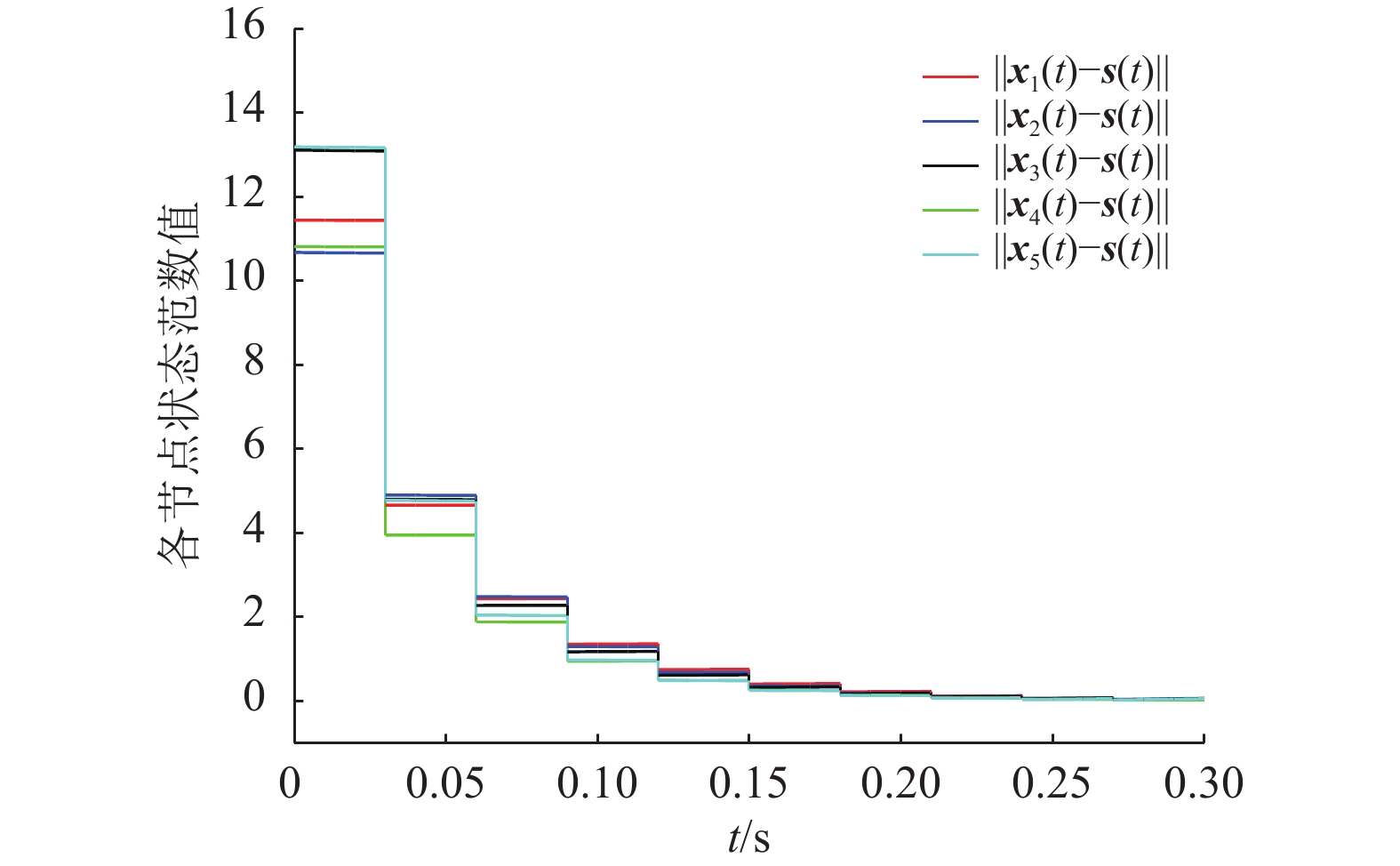
当外部干扰w(t)=0时,对多权重复杂网络式(1)施加脉冲控制,各节点状态变量
|
图 1 脉冲控制下,网络式(1)各节点状态曲线 Figure 1 State curves of each node in the network formula (1) under impulsive control |
|
图 2 脉冲控制下,同步误差系统式(4)各节点的状态范数曲线 Figure 2 The state norm curve of each node in synchronization error system formula (4) under impulsive control |
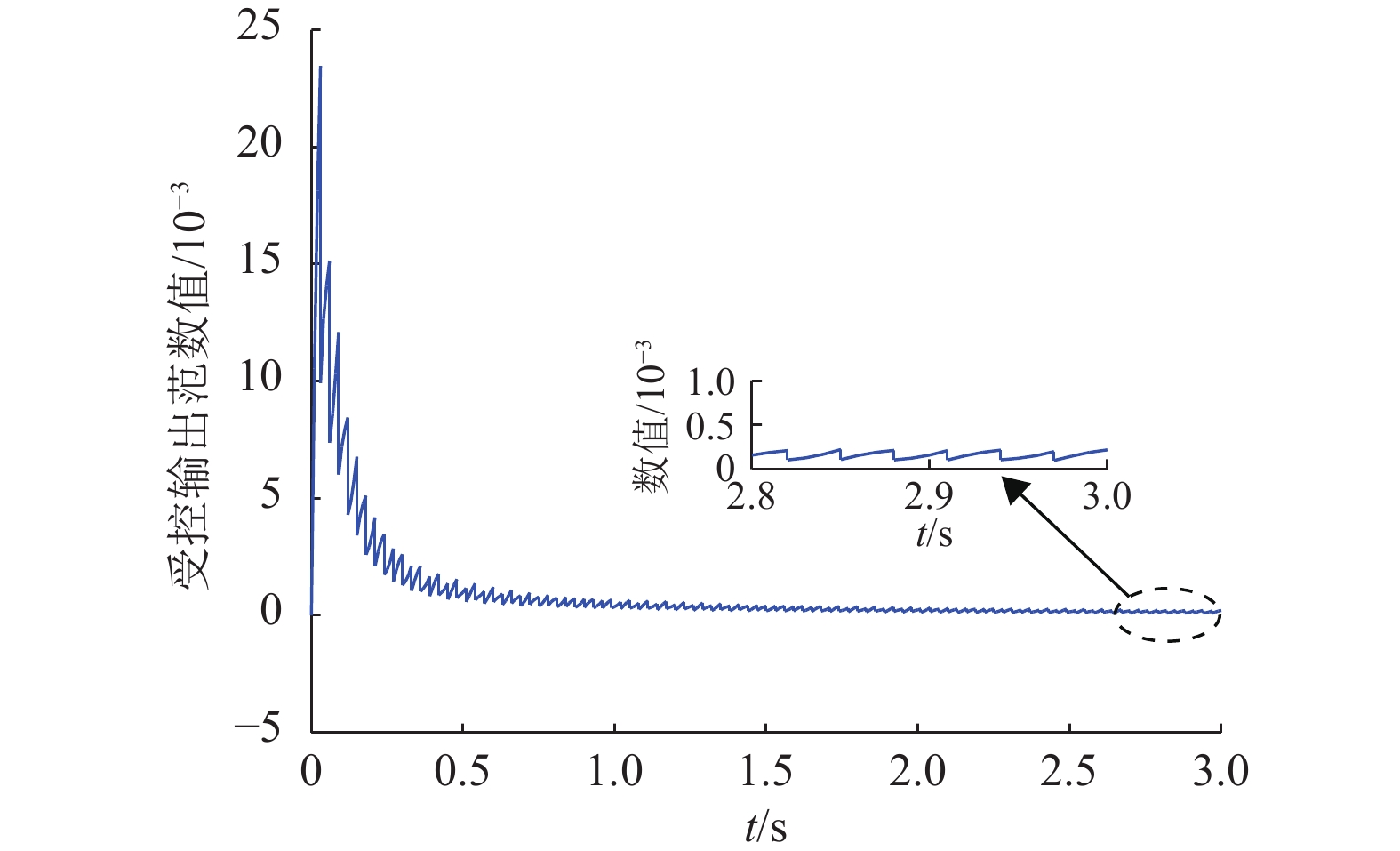
当外部干扰
|
图 3 脉冲控制下,同步误差系统式(5)的受控输出范数曲线 Figure 3 The controlled output norm curve of synchronization error system formula (5) under impulsive control |
本文基于脉冲控制方法,对一类多权重复杂网络的鲁棒H∞同步问题进行了研究,给出了多权重复杂网络实现鲁棒H∞同步的充分条件,并用Matlab软件实例仿真验证了结论的有效性。研究结果表明,通过在分布式脉冲控制器中添加节点状态变量与同步状态间的误差状态反馈项,可以保证同步误差系统是内部全局指数稳定的且具有有限的
| [1] |
ZHU S, XU S, SETIA S, et al. Establishing pairwise keys for secure communication in ad hoc networks: a probabilistic approach[C]//International Conference on Network Protocols. Atlanta: IEEE, 2003: 326-335.
|
| [2] |
ZHOU Z, PLISHKER W, BHATTACHARYYA S S, et al. Scheduling of parallelized synchronous dataflow actors for multicore signal processing[J].
Signal Processing Systems, 2016, 83(3): 309-328.
DOI: 10.1007/s11265-014-0956-2. |
| [3] |
LI Y, GE S S. Force tracking control for motion synchronization in human-robot collaboration[J].
Robotica, 2016, 34(6): 1260-1281.
DOI: 10.1017/S0263574714002240. |
| [4] |
WU Y, FU S, LI W, et al. Exponential synchronization for coupled complex networks with time-varying delays and stochastic perturbations via impulsive control[J].
Journal of The Franklin Institute-engineering and Applied Mathematics, 2019, 356(1): 492-513.
DOI: 10.1016/j.jfranklin.2018.11.003. |
| [5] |
ZONG G, YANG D. H∞ synchronization of switched complex networks: a switching impulsive control method
[J].
Communications in Nonlinear Science and Numerical Simulation, 2019(77): 338-348.
|
| [6] |
CHEN W H, JIANG Z Y, LU X M, et al. H-infinity synchronization for complex dynamical networks with coupling delays using distributed impulsive control
[J].
Nonlinear Analysis Hybrid Systems, 2015(17): 111-127.
|
| [7] |
SHEN H, PARK J H, WU Z, et al. Finite-time H∞ synchronization for complex networks with semi-Markov jump topology
[J].
Communications in Nonlinear Science and Numerical Simulation, 2015, 24(1): 40-51.
|
| [8] |
LI F, SHEN H. Finite-time H∞ synchronization control for semi-Markov jump delayed neural networks with randomly occurring uncertainties
[J].
Neurocomputing, 2015(166): 447-454.
|
| [9] |
QIU S, HUANG Y, REN S, et al. Finite-time synchronization of multi-weighted complex dynamical networks with and without coupling delay[J].
Neurocomputing, 2018(275): 1250-1260.
|
| [10] |
LI N, SUN H, JING X, et al. Exponential synchronisation of united complex dynamical networks with multi-links via adaptive periodically intermittent control[J].
Iet Control Theory and Applications, 2013, 7(13): 1725-1736.
DOI: 10.1049/iet-cta.2013.0159. |
| [11] |
QIN Z, WANG J, HUANG Y, et al. Synchronization and H∞ synchronization of multi-weighted complex delayed dynamical networks with fixed and switching topologies
[J].
Journal of The Franklin Institute-engineering and Applied Mathematics, 2017, 354(15): 7119-7138.
DOI: 10.1016/j.jfranklin.2017.08.033. |
| [12] |
PENG H, WEI N, LI L, et al. Models and synchronization of time-delayed complex dynamical networks with multi-links based on adaptive control[J].
Physics Letters A, 2010, 374(23): 2335-2339.
DOI: 10.1016/j.physleta.2010.03.052. |
| [13] |
WANG J, QIN Z, WU H, et al. Finite-time synchronization and H∞ synchronization of multiweighted complex networks with adaptive state couplings
[J].
IEEE Transactions on Cybernetics, 2020, 50(2): 600-612.
DOI: 10.1109/TCYB.2018.2870133. |
| [14] |
WANG J, QIN Z, WU H, et al. Analysis and pinning control for output synchronization and H∞ output synchronization of multiweighted complex networks
[J].
IEEE Transactions on Cybernetics, 2018, 49(4): 1-13.
|
| [15] |
SUN H, ZHANG Q, LI N, et al. Pinning synchronization of directed complex dynamical networks with multi-links[J].
International Workshop on Chaos Fractals Theories and Applications, 2010(49): 24-28.
|
| [16] |
张振华, 彭世国. 二阶多智能体系统拓扑切换下的领导跟随一致性[J].
广东工业大学学报, 2018, 35(2): 75-80.
ZHANG Z H, PENG S G. Leader-following consensus of second-order multi-agent systems with switching topology[J]. Journal of Guangdong University of Technology, 2018, 35(2): 75-80. DOI: 10.12052/gdutxb.170125. |
| [17] |
HORN R A, HORN R A, JOHNSON C R. Topics in matrix analysis[M]. Cambridge: Cambridge University Press, 1991.
|
| [18] |
BOYD S, El GHAOUI L, FERON E, et al. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial & Applied Mathematics, 1994: 28-29.
|
 2021, Vol. 38
2021, Vol. 38
