同时定位与地图构建^[1](Simultaneous Location And Mapping，SLAM)是指搭载传感器的主体，在没有环境先验信息的情况下，于运动过程中跟踪主体的位置，并同时构建环境结构一致性地图的技术。近年来视觉同时定位与地图构建技术已经在室内服务机器人、自动驾驶汽车、无人机导航定位以及增强现实设备中得到一定的应用。

视觉里程计^[2](Visual Odometry，VO)可分为两类：基于特征的方法和直接方法。基于特征的方法在每个图像中提取显著的图像特征，使用不变的特征描述符在连续帧中进行匹配，使用极线几何约束恢复相机位姿和结构，通过最小化投影误差来优化位姿和结构提取的特征也可以用于闭环和重定位，从而使视觉里程计成为一个完整的SLAM。

Klein和Murray^[2]于2007年开发出实时的PTAM(Parallel Tracking and Mapping)。该算法对于单目SLAM的发展具有里程碑式的意义。算法将SLAM框架中的位姿跟踪和建图分离成两个线程单独运行，让离线的SFM(Structure From Motion)算法可以在设备上实时的运行。Gomez-Ojeda等^[3]使用联合点线特征进一步提升精确度。UcoSLAM^[4]在图像中提取特征点和分布大量的标记，然而，特征提取和匹配非常耗时，因此基于特征的方法比直接方法慢。

直接方法通过光度误差直接恢复相机的位姿和结构，不需要特征提取。不同于PTAM、ORB_SLAM(Oriented FAST and Rotated BRIEF-Simultaneous Localization and Mapping)^[5]的低帧率，由Forster^[6]开源的SVO(Semi-direct Visual Odometry)系统采用直接法或特征法来获取场景中的特征信息。对于其中深度估计问题，岑仕杰^[7]结合了注意力与无监督深度学习方法，但是在远景的部分泛化能力不够好，估计的深度比实际要近。然而，直接SLAM的闭环检测仍然是一个开放的课题。长期移动的累积漂移是直接法所遇到的主要问题之一。

闭环检测算法在过去十几年里取得卓越的进展，对解决自主定位中的漂移和丢失跟踪时的重定位至关重要。Angeli^[8]首次提出将闭环检测算法模块加入视觉SLAM算法系统，并成功运用词袋模型解决当移动机器人运行于大型室内环境中，视觉特征的差异使得算法能有效地寻找出场景间的不同，并识别出之前曾访问过的视觉场景，进而消除累积误差。近年来何元烈等^[9]尝试使用神经网络方法检测闭环，但受环境光照影响较大。

为保持直接方法的快速性和基于特征的方法的高精度和闭环检测优化，本文提出一种新的基于稀疏直接方法的混合型梯度−特征点，该方法提取两种特征：梯度点和ORB(Oriented FAST and Rotated BRIEF)特征^[10]。首先，使用梯度点和少量ORB特征点对齐图像序列。然后，选取关键帧中ORB特征点，这些特征点在普通帧中动态更新深度，收敛后加入地图。并且ORB特征还用来检测和闭环优化。本文方法相比特征法节省时间；与直接方法相比，该方法具有导航必须的闭环检测功能。此外，本文对所提出的稀疏直接法视觉里程计闭环定位系统与最新方法在开放数据集中进行了比较。

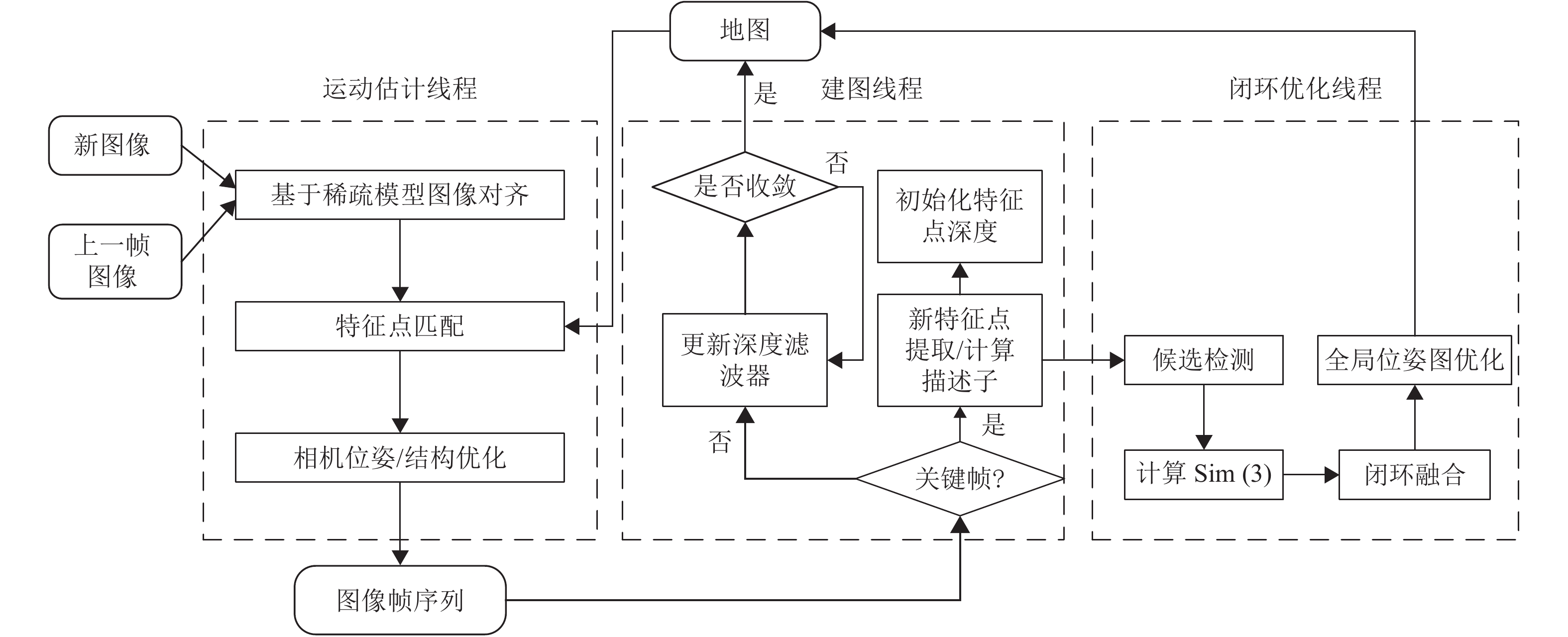
1 系统概述

本文方法流程图如图1所示。该系统使用3个并行线程，分别用于估计相机运动、建图和闭环检测优化。

运动估计线程使用稀疏直接方法实现相对位姿估计。(1) 通过基于稀疏模型的图像对齐初始化位姿：通过最小化与相同3D点的投影位置相对应的像素之间的光度误差来找到相对于前一帧的相机位姿。(2) 通过对齐相应的特征块，对于重新投影点对应的2D坐标进行细化。运动估计是通过最小化前一个特征对齐步骤中引入的重投影误差细化位姿。

在建图线程中，图像帧被分为关键帧和普通帧，在关键帧上选取特征点，作为种子，并且初始化一个非常不确定深度估计^[6]。在传入新的普通帧时，融合更新这些种子的深度。当种子深度收敛时，把这个特征点插入到地图，用于运动估计。否则继续等待下一次深度更新。传入新的关键帧时，再次提取新的种子，整个过程处于动态更新。

最后是闭环优化线程，每一关键帧成为候选检测帧。这样，如果检测并验证闭环候选，则计算其相对于当前关键帧的相似变换群Sim(3)约束并将其添加到全局位姿图中，然后对全局位姿图进行优化以获得更精确的长期相机位姿估计。

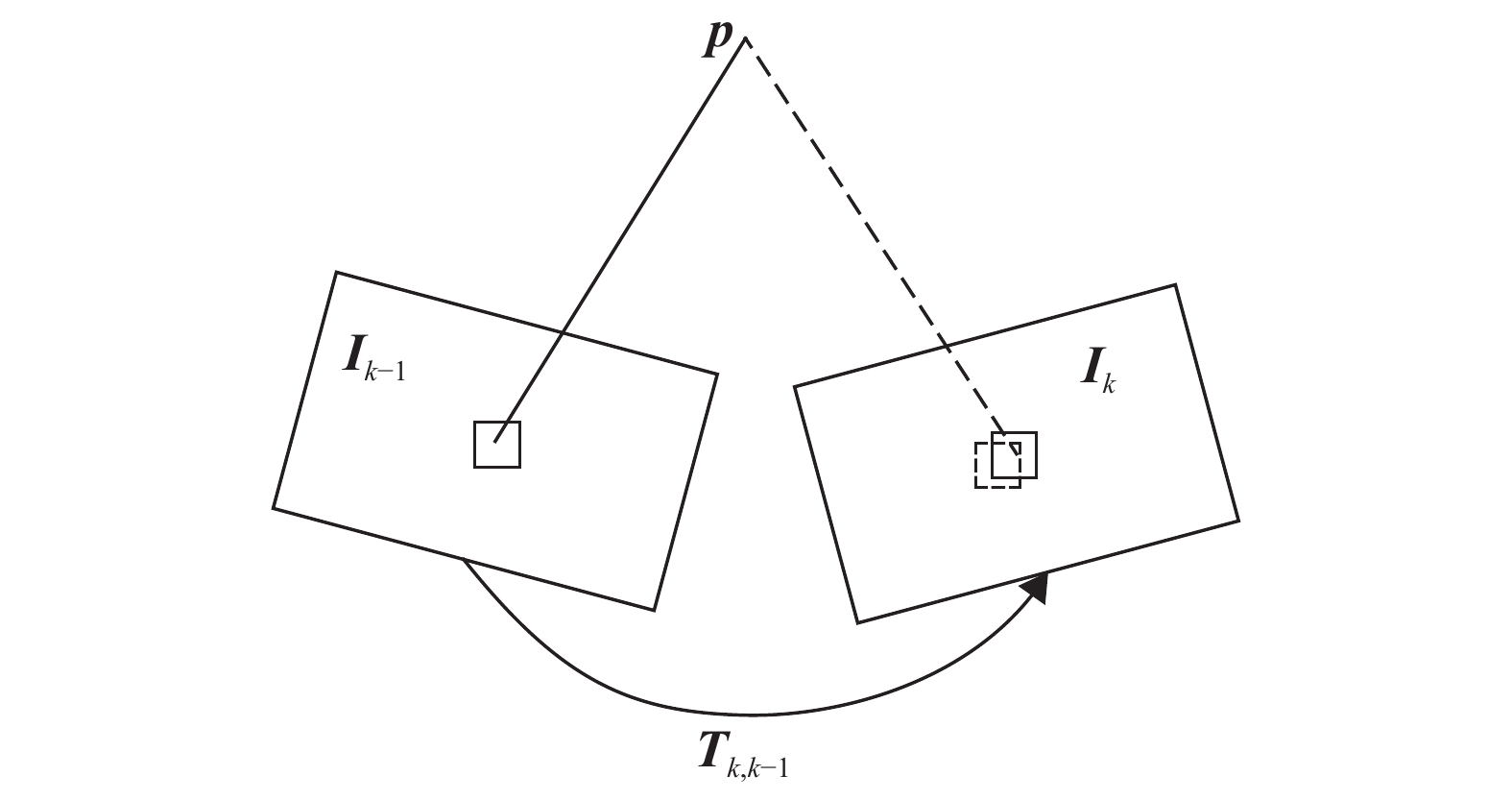
2 稀疏直接法视觉里程计中的闭环 2.1 运动估计

利用直接法对相机的相对运动和特征对应关系进行初始估计，最后得到基于特征的非线性重投影误差。如图2所示，在运动估计线程中，相机运动到当前帧 ${{{I}}_k}$ 时，已知上一帧 ${{{I}}_{k - 1}}$ 、上一帧的特征点 ${{u}}$ 形成的图像区域 ${\cal R}$ ，和u投影到三维空间的地图点p，计算相机从 ${{{I}}_{k - 1}}$ 到 ${{{I}}_k}$ 的位姿变换 ${{{T}}_{k,k - 1}}$ ：

${{{T}}_{k,k - 1}} = \mathop {\arg \min }\limits_{{T}} \iint_{\cal R} {\rho [\delta {{I}}({{T}},{{u}})]{\rm{d}}{{u}}}$

(1)

像素强度残差 $\delta {{I}}\left( {{{T}},{{u}}} \right)$ 被定义为地图点 ${{u}}$ 投影在上一帧与投影到当前相机平面 ${{T}}$ 的光度差。式(1)用负对数似然最小化解最小二乘问题： $\rho [ \cdot ]\stackrel{\wedge}{=}\dfrac{1}{2}{\Vert \cdot \Vert }^{2}$ ，将相机位姿在两图像间对齐，由于单目相机存在尺度不确定性，为了减少偏移，相机位姿应该与地图对齐，而不是与前一帧对齐。

将式(1)估计的相机位姿所观察到的所有地图点投影到 ${{{I}}_k}$ 中，从而估计出相应的二维特征位置 ${{u}}_i^\prime $ 。用最近的关键帧 $r$ 观察这些投影点。然后，特征对齐步骤通过最小化 ${{{I}}_k}$ 投影图像块相对于关键帧 $r$ 中的参考图像块的光度误差，分别优化新图像中的所有二维特征点位置 ${{u}}_i^\prime $ ：

${{u}}_i^\prime = \mathop {\arg \min }\limits_{{{u}}_i^\prime } \frac{1}{2}{\left\| {{{{I}}_k}\left( {{{u}}_i^\prime } \right) - {{{A}}_i} \cdot {{{I}}_r}\left( {{{{u}}_i}} \right)} \right\|^2},\forall i$

(2)

这里使用逆合成Lucas-Kanade算法来解决这种对齐问题。与前面的步骤相反，对参考特征块应用仿射变换 ${{{A}}_i}$ ，因为关键帧通常比上一帧图像更远，使用较大的图像块( $8 \times 8$ )易于观察。

在前面的步骤中，建立了亚像素精度的特征对应关系。特别是生成平均约为0.3像素的重投影残差 $\left\| {\delta {{{u}}_i}} \right\| = \left\| {{{{u}}_i} - \pi \left( {{{{T}}_{k,w}}{}_w{{{p}}_i}} \right)} \right\| \ne 0$ ，其中 $ \pi ( \cdot )$ 是投影函数，p表示世界坐标系中点，w表示世界坐标系。在最后一步中，再次优化相机位姿 ${{{T}}_{k,w}}$ ，以最小化重投影残差：

${{{T}}_{k,w}} = \mathop {\arg \min }\limits_{{{{T}}_{k,w}}} \frac{1}{2}\sum\limits_i {{{\left\| {{{{u}}_i} - \pi \left( {{{{T}}_{k,w}} {}_w{{{p}}_i}} \right)} \right\|}^2}} $

(3)

使用约束调整和迭代非线性最小二乘最小化算法求解，如高斯牛顿迭代，这样就可以得到基于直接法的相机位姿估计。一般来说，在相机缓慢运动时，此估计较为准确，但环境剧烈变化时跟踪的相机轨迹容易丢失，因此在2.2节介绍本文提出的特征点提取策略弥补这一不足。

2.2 混合梯度−特征点

当相机运动剧烈时，采用基于特征的方法来保证鲁棒性。即使是基于直接的方法也提取一些像素点，直接方法不考虑这些点在未来的图像中能否再次出现，为了有效解决直接方法选取的点不具有可重复性的问题，本文提出一种新的特征点提取方法：混合型梯度−特征点。混合型梯度−特征点由两部分组成，分别是图像梯度点和ORB特征点。梯度点指的是该图像中梯度明显的像素，用于直接法的相机追踪；另一部分是ORB特征点，它在图像队列中多次出现，用来检测闭环和跟踪。

对于梯度点的选取，算法模型将图像转换成图像金字塔，本文为4层。每一层划分成多个图像块，从顶层每个图像块中使用像素差平方和求光度误差的方法提取梯度较大的点作为特征点 ${{{U}}_{{\rm{grad}}}}$ ，依次传递到底层。如果图像块中没有梯度明显的像素，比如墙面等纹理稀疏的环境，则降低梯度要求直到选取足够的点，这样可以提升系统的鲁棒性，避免系统在跟踪时丢失。

混合型梯度−特征还提取一些ORB特征，ORB特征由FAST(Features from Accelerated Segment Test)角点和BRIEF(Binary Robust Independent Elementary Features)描述子组成，具有256位描述符，特征提取和匹配速度快，具有较高的鲁棒性、高效性，可应对平移、旋转、光照变化等情况。FAST角点本身不具有方向性和尺度，系统构建图像金字塔，在每一层检测角点实现尺度不变性；通过指定灰度质心为旋转方向可得到具有旋转不变性的oFAST(oriented FAST)描述符。假设灰度质心偏移图像重心，根据偏移构建向量定义为特征点方向。连接图像块 ${{S}}$ 的几何中心与质心，构成一个方向向量 ${{c}}$ ，定义特征点方向 $\theta $ 为

$\theta = \arctan \left( {{m_{{\rm{01}}}},{m_{{\rm{10}}}}} \right)$

(4)

其中 $m$ 是图像的矩。

BRIEF描述子是一种没有方向信息的二进制编码，利用oFAST角点的方向信息 $\theta $ 可以计算出Steer BRIEF，使其具有旋转不变性。

${{{R}}_{\theta}} = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta } \\ { - \sin \theta }&{\cos \theta } \end{array}} \right]$

(5)

${{{G}}_n}(i,\theta ): = {f_{{n_d}}}({{I}})|\left( {{x_i},{y_i}} \right) \in {{{S}}_\theta }$

(6)

${{{R}}_\theta }$ 为方向矩阵， ${{{S}}_\theta }$ 是由 ${{{R}}_\theta }{{S}}$ 得到的具有方向特征的点集，所以本文使用改进的ORB特征点集 ${{{G}}_n}\left( {i,\theta } \right)$ 由特征函数 ${f_{{n_d}}}$ 提取得到， ${n_d}$ 为特征描述符维数，本文中是256。

最后得到混合型梯度−特征点集 ${{U}}$ ：

${{U}} = {{{U}}_{\rm{grad}}} + {{G}}{ _n}\left( {i,\theta } \right)$

(7)

视觉里程计前端使用梯度点和ORB特征点跟踪相机，这样闭环线程的特征提取步骤的开销保持在最小。

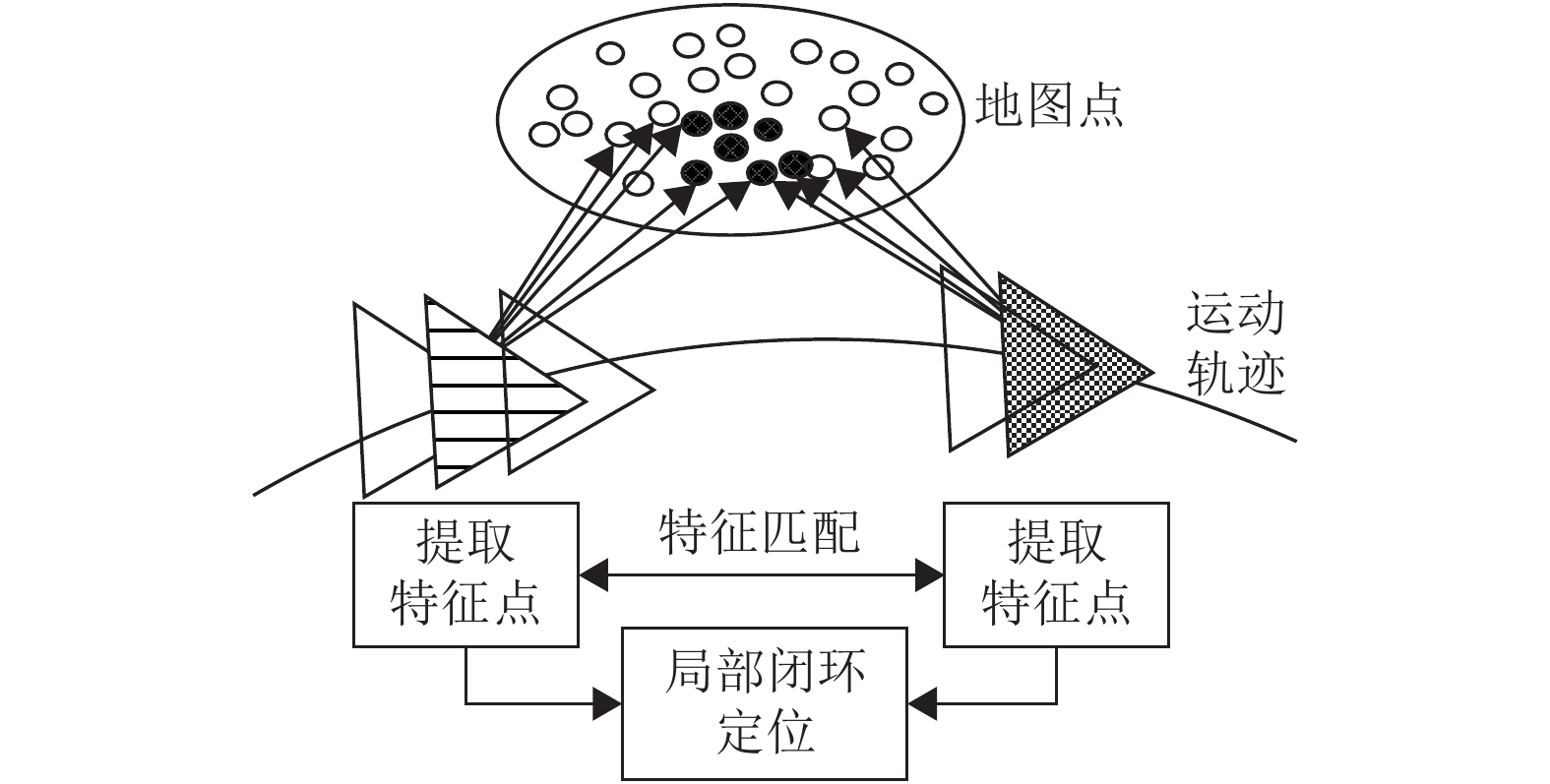
2.3 闭环帧检测

本文通过在图像帧中选择符合条件的帧为关键帧，并以其作为闭环检测的图像帧进行检索、对比、匹配，减少地图生成累计误差，校正位姿估计误差。如图3所示，模型使用稀疏直接法视觉里程计的选择关键帧策略^[6]，用稀疏直接法粗略估计图像帧的位姿，并判断是不是关键帧。另外再增加两条关键帧选择的条件：相机旋转大于30度、当前帧与上一关键帧间隔30帧，这两个条件保证在快速运动时跟踪的鲁棒性和在非关键帧下跟踪的准确性。

闭环检测算法计算每个关键帧的特征描述子时，使用最新DBoW3库构建视觉词袋模型^[11]。前端视觉里程计筛选出的关键帧组成候选队列，候选检测是当前关键帧与候选队列中的帧寻找相匹配，这里优先选择远离当前帧的关键帧。如图3所示，当前关键帧(右侧深色图像帧)与候选队列中某个(左侧横线条纹图像帧)关键帧有一定数量的共视特征点(图中黑色地图点)，相匹配的关键帧数目大于阈值，执行RANSAC(RANdomSAmple Consensus，随机抽样一致)算法解PnP(Perspective-n-Point)得到相机位姿的初始估计，利用高斯牛顿法对Sim(3)优化，使3D和2D几何约束最小化。本文使用文献[12]计算位姿从闭环候选到当前关键帧 ${{{S}}_{cr}}$ 的Sim(3)转换估计：

$ \begin{split} {{{E}}_{{\rm{loop}}}} =& \sum\limits_{{{{q}}_i} \in {{ {{Q}}}_1}} {{w_1}} {\left\| {{{{S}}_{cr}}{\pi ^{ - 1}}\left( {{{{G}}_i},{d_{{{{p}}_i}}}} \right) - {\pi ^{ - 1}}\left( {{{{q}}_i},{d_{{{{q}}_i}}}} \right)} \right\|_2} + \\& \sum\limits_{{{{q}}_j} \in {{{{Q}}}_2}} {{w_2}} {\left\| {\pi \left( {{{{S}}_{cr}}{\pi ^{ - 1}}\left( {{{{G}}_j},{d_{{{{G}}_j}}}} \right)} \right) - {{{q}}_j}} \right\|_2} \end{split} $

(8)

其中， ${{{G}}_i}$ 是候选帧的特征， ${d_{{{{G}}_i}}}$ 为其深度估计， ${{{{Q}}}} = \left\{ {{{{q}}_i}} \right\}$ 为当前关键帧中的匹配特征， $ {\pi }^{-1}( \cdot )$ 是反投影函数， ${w_1}$ 和 ${w_2}$ 是用于平衡不同测量单位的权重。在实际应用中，尺度只能由3D部分估计，但如果没有2D重投影误差，在估计的深度值有噪声的情况下，旋转和平移估计将是不准确的。

2.4 位姿图优化

在上一步闭环检测得到的闭环帧以及闭环候选中的关键帧可以看作是一个位姿图，顶点是待优化的相机位姿，边表示误差项。采用图优化库g2o^[13]对位姿进行优化。

本文的闭环检测方法是计算闭环候选帧和当前帧之间的相对位姿约束，所以还利用两两相对位姿之间的观测值来近似为候选关键帧之间的约束。具体来说，优化算法计算从前端的当前全局位姿估计这些观测值。另外，在位姿图优化中将修改当前帧的位姿估计，但全局优化不能干扰包含绝对位姿信息的闭环优化结果。因此，位姿图优化将倾向于修改闭环以外部分的全局位姿。在位姿图优化后，不更新闭环内相机的全局位姿，以进一步确保闭环内相机位姿的约束调整不受全局优化的影响。

3 实验结果

为验证混合梯度−特征点和闭环优化给稀疏直接里程计的影响，设计实验运行EuRoC数据集和TUM数据集评估系统性能。本文实验所用计算机CPU为AMD 2600，主频3.4 GHz，内存8 GB，搭载Ubuntu16.04。实验主要分为两部分：(1) 比较本文混合特征梯度−特征点算法、SVO的对视觉里程计前端时间、特征点数、精确度的影响；(2) 利用EuRoC数据集及测试工具，比较本文方法、SVO、ORB_SLAM2^[14]等的估计轨迹与真实轨迹误差。

为减少计算机系统的不确定性对算法的影响，每个序列运行5次记录平均值。通过测试工具(evaluation of odometry and SLAM)对齐所有轨迹，再与真实轨迹进行比较计算出均方根误差(Root Mean Square Error，RMSE)。

3.1 特征点选取对比

将本文方法(无回环)与SVO进行均方根误差、前端平均每帧运行时间做对比试验，使用TUM数据集中的RGB-D数据集。均方根误差和平均每帧运行时间如表1所示。

从表1中看出，测试同样的数据集序列，本文方法的每帧运行时间只比SVO略微增加2~7 ms，但均方根误差小于SVO。fr1_xyz和fr2_xyz序列仅包含沿运动主轴的平移运动，而相机的朝向保持固定，属于简单数据集，SVO处理这种场景的误差已经足够小，因此提升很有限。fr1_floor序列扫过的办公室地板上有几个结洞，本文方法提取ORB特征点很容易追踪轨迹。此外，地板都是纹理稀疏的平面，视觉里程计易于陷入局部最优的情况。fr2_desk序列记录一个典型的办公室场景，本文方法相较SVO精度有所提高，代价是运行时间略微提升。

3.2 轨迹对比

轨迹对比实验使用公共数据集EuRoC^[15]，EuRoC收集自20 Hz的微型飞行器。数据集分为两部分，第一部分记录在一个工业机器大厅中，其中包含由激光跟踪仪测量的毫米级精度位置坐标。数据集的第二部分记录在具有两个不同场景的室内。根据轨迹长度、光照和飞行动态，所有序列分为3个级别：简单、中等和困难。表2列出了本文方法、SVO、DSO^[16](Direct sparse odometry)和ORB_SLAM2的均方根误差、每帧运行时间。

表2中本文方法、SVO和ORB保存了关键帧轨迹，根据DSO开源代码保存所有帧轨迹的特性，为了进行有效的比较，DSO每帧的阈值数设置为800。

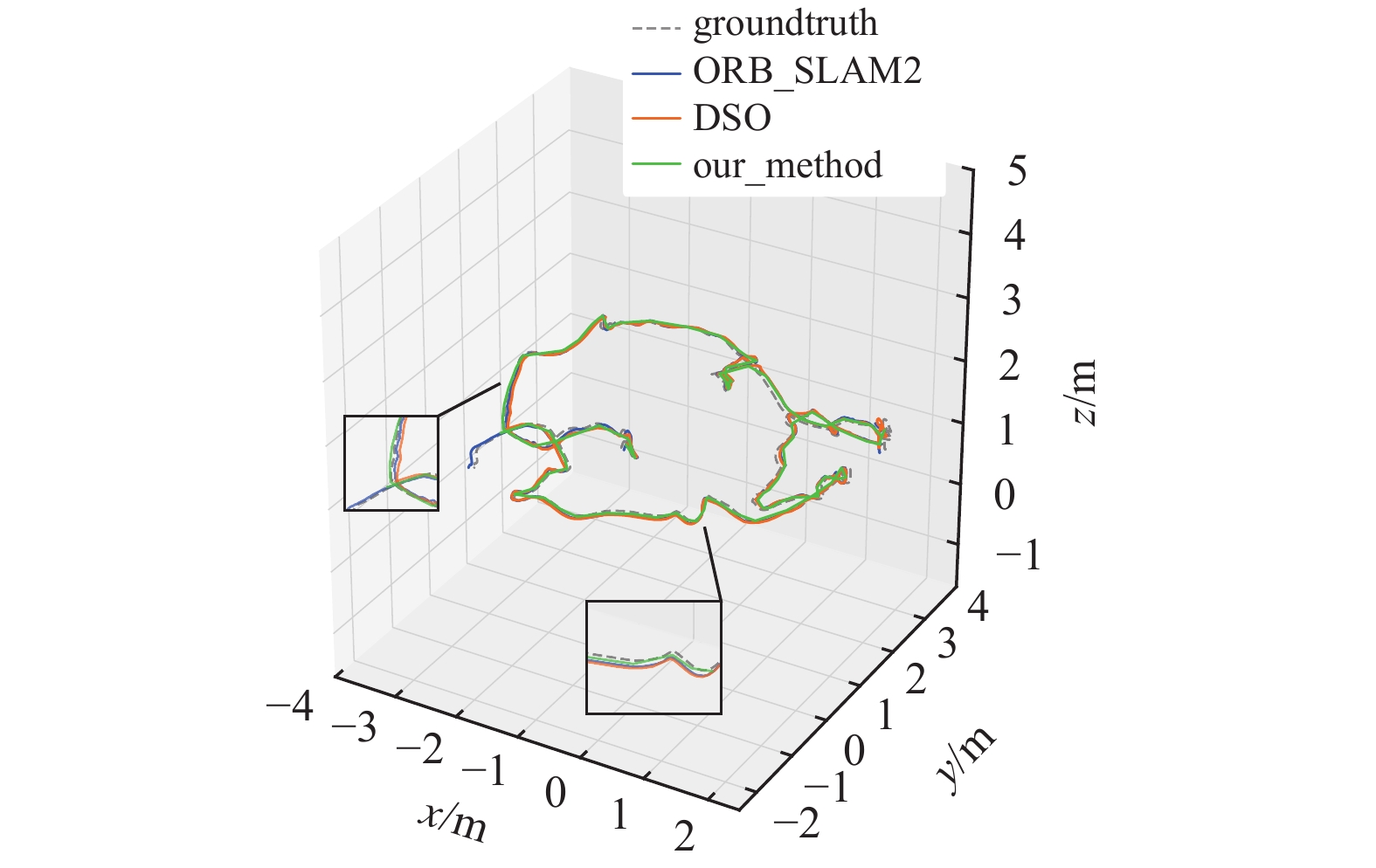
图4展示了本文方法运行MH_02和MH_04的关键帧轨迹图与关键帧轨迹误差图，图5展示本文方法与ORB_SLAM2运行V1_01_easy的关键帧轨迹对比。

EuRoC数据集中有相机快速旋转导致的严重运动模糊和光照不足的环境，SVO追踪时丢失相机轨迹，无法运行大部分序列。本文方法使用混合型梯度−特征点策略提取梯度点和ORB特征具有较强的鲁棒性，因而可以运行。

由于加入回环检测，本文方法相较于SVO有着很大的提升，特别是V1_01_easy和V2_01_easy两个标记简单的序列，本文方法性能优于ORB_SLAM2，而有相机快速运动和光照不足的MH_03_medium、MH_04_difficult和MH_05_difficult序列也能够运行。在每一个序列开始时有极不稳定的相机运动，对DSO的影响比本文方法或ORB的影响更大。因此，DSO(特征数目为800)的精度低于其他两种方法。本文方法不匹配非关键帧中的特征，精度低于ORB。然而，在相似的精度下，本文方法比其他两种方法要快得多，ORB_SLAM2平均处理一帧图像需要32.06 ms，DSO为23.66 ms，本文方法仅需要13.21 ms，图像的处理速度约为ORB_SLAM2的2倍，实时性优于ORB_SLAM2和DSO，因此本文方法更适合于轻型飞行器或机器人。

表3对比本文方法和Richard Elvira的ORBSLAM-Atlas^[17]，使用了地图集合存储了多张子图。从表中看出MH_02_easy简单序列ORBSLAM-Atlas更占优势，本文方法在复杂的序列中较优。

本文方法可以认为是直接法和特征点法的结合，追踪使用直接法，闭环优化使用特征点法。实际实验对原模型进行改进，以完成两种方法的结合。混合型梯度−特征点提取两种点，增加相对较少的时间，在纹理稀疏和复杂的环境中也能提升视觉里程计的精度。又结合闭环检测，大幅提升直接法的精度，由于间接点法需要大量时间计算特征点描述子和特征匹配，本文方法的处理时间少于ORB_SLAM2的处理时间。相比之下，大部分帧将采用直接方法来估计相机运动，当相机快速运动时，采用基于特征的方法保证鲁棒性。

4 结束语

本文介绍一种新的特征点提取策略，即混合型梯度−特征点，在快速运动中使系统保持稳定性。本文基于稀疏直接法加入闭环检测和位姿优化，明显提升系统的定位精度。利用图像像素强度来估计相机位姿。通过关键帧匹配ORB特征，使用视觉词袋模型检测闭环，再使用位姿图优化得到精确的轨迹。在实际环境中特征选择策略非常重要，因为更多的有用特征可以提高系统的鲁棒性和准确性，本文实验结果为其他SLAM方法的设计和改进提供有价值的参考，未来还可以扩展包括通过减少关键帧的数量提高速度，提高运动模糊的鲁棒性等。