光栅作为位移、速度和加速度测量器件，也是高精度高速数控机床和半导体晶圆生产设备上的标准配置器件之一，在高精度、高速自动化数控反馈闭环系统^[1-2]有广泛应用。

光栅技术^[3]发展主要有以下两个方向。一是基于现场可编程逻辑门阵列 (Field Programmable Gate Array, FPGA)、数字信号处理器 (Digital Signal Processor，DSP)等新数字器件的数字数据处理^[4-5]，需要超过现有半导体器件技术水平的高精度、高速AD转换器，以及超高速数字信号处理器。不适用于只有数字增量式编码器接口的典型伺服控制器，如西门子可编程逻辑控制器 (Programmable Logic Controller, PLC)和可编程多轴控制器 (Programmable Multi-Axis Controller, PMAC)高级运动控制卡。由于校正参数必须离线标定，比较麻烦复杂，因此这种方法在自动化装备大规模应用受到很大限制。二是光电编码与解码，使用新光栅设计和新莫尔条纹产生方法及多个光电探测器新型排列方式。

我国光栅研究和生产可以追溯到20世纪60年代，但是我国光栅产品普遍是基于传统的教科书式的测量原理，不适合高速、高精度和高稳定性反馈自动控制系统，只适合低速平缓，微米级精度反馈自动控制系统。而且2000年以后，我国在这方面新研究比较少，且主要集中在使用FPGA、DSP等新数字器件的数据处理上，光电编码与解码研究几乎是空白。

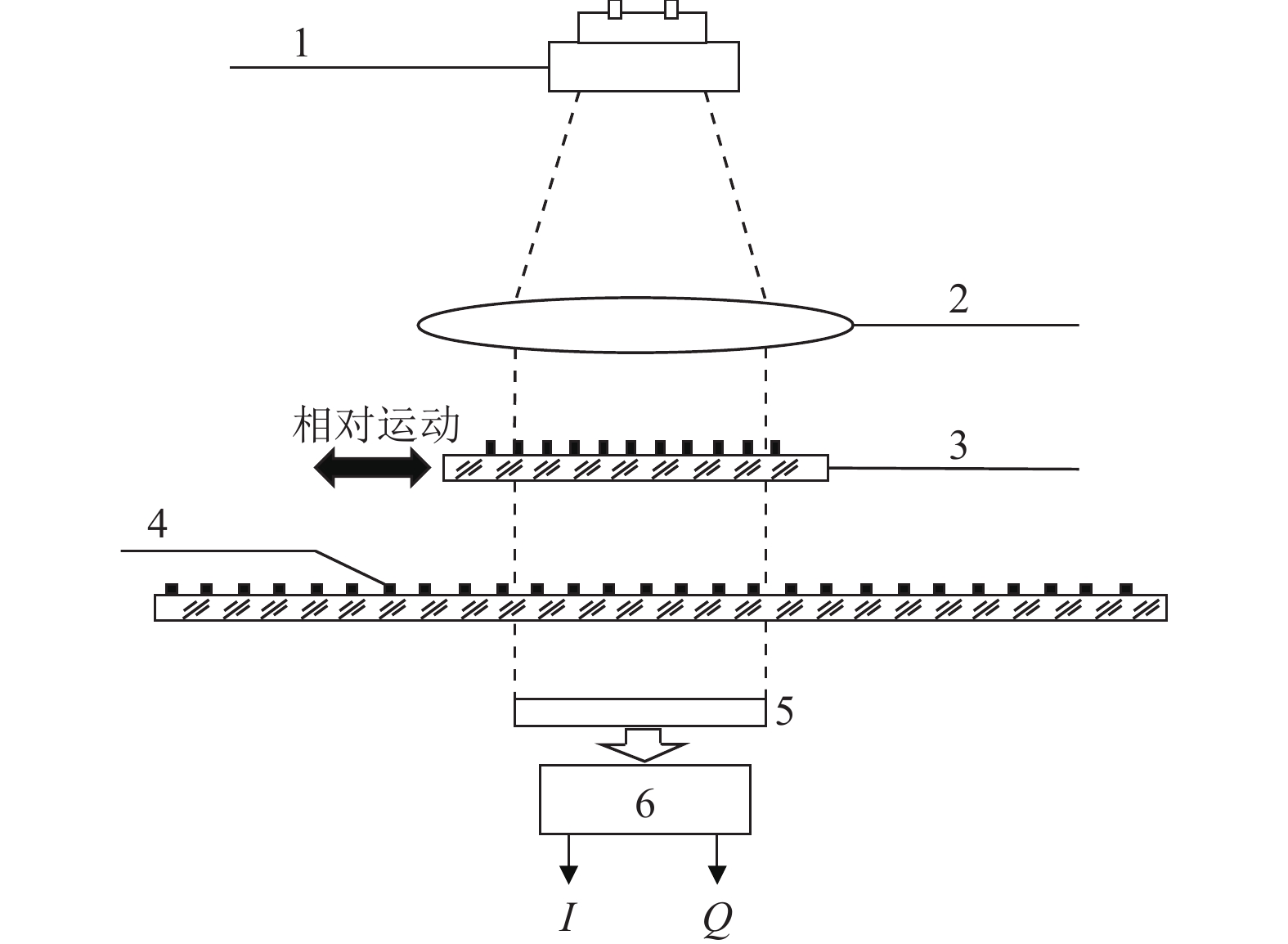
1 光栅尺结构

本文涉及的光栅尺结构如图1所示。LED光源1发出的光经过扩束准直透镜2变为平行光，并透射穿过指示光栅3和主光栅4，最后成像在光电二极管阵列5上^[6-7]。指示光栅和主光栅平行放置，刻线之间夹角为0º。两者之间有间隙，主光栅固定不动，指示光栅左右移动。主光栅与指示光栅的刻线面对齐，叠合在一起。在两光栅刻线重合处，光从缝隙透过形成亮带；在两光栅刻线错开处，由于相互挡光作用，形成暗带，这就是莫尔条纹^[8]。主光栅与指示光栅移动一个光栅间距，莫尔条纹滚动一个周期。

主光栅的空间频率为 ${f_m}$ ，指示光栅的空间频率为 ${f_s}$ 。主光栅和指示光栅在光路内重叠，形成莫尔条纹如图2所示。

莫尔条纹的空间频率 $f$ 可表示为

${f_{}} = {f_m} - {f_s}$

(1)

亮带与亮带之间的距离，或暗带与暗带之间的距离为莫尔条纹间距 $P$ ，可表示为

$P = \frac{1}{f}$

(2)

在图1光栅尺结构中，光电探测器为光电二极管阵列。每个莫尔条纹间距均匀放置 $N$ 个光电二极管，共计 $M$ 个。光电二极管分布相位间距 $\Delta \phi $ 为

$\Delta \phi = 2{\text{π}} /N$

(3)

光电二极管分布覆盖莫尔条纹周期T可表示为

$T = \frac{{2{\text{π}} \cdot M}}{N}$

(4)

光电二极管阵列上每个光电二极管为2个独立检测通道的输入，其光电流分别经过相对应的直流运放电路放大转换为电压信号后，送入两路直流运放电路加法器，其输出为两路频率相同，相位相差90º的载波调制信号，即两路正交信号： $I$ 和 $Q$ ，这就是信号调节与解码处理电路的功能。以传统4场扫描莫尔条纹光栅尺为例，在一个莫尔条纹周期内的0º、90º、180º和270º位置分别布置4个独立的光电二极管，经过放大倍数为1、–1的直流放大后，使用直流运放电路加法运算得

$I(\theta ) = V({90^\circ }) - V({270^\circ })$

(5)

$Q(\theta ) = V({0^\circ }) - V({180^\circ })$

(6)

其中 $V$ 表示光电探测器信号AD转换后的数值。相位角 $\theta $ 即两光栅形成的莫尔条纹相位角，与位移相关；或伺服电机码盘角度，与角度相关。在控制器内做类似 $\theta = \arctan (I,Q)$ 实时计算，求出 $\theta $ 和跨越周期数目，最后对应位移量。两路正交信号 $I$ 和 $Q$ 是自动化控制器位置反馈标准信号，本质上是2组正交三角函数信号，其振幅、频率相同，仅仅是相位角 $\theta $ 的函数。 $I(\theta )$ 和 $Q(\theta )$ 具有通用性，送入自控系统运动控制器或信号解调器，完成鉴向、加减脉冲计数和细分等功能，最后给出指示光栅和主光栅相对位移的高精度数据。标准运动控制器这样设计的优点是， $I(\theta )$ 和 $Q(\theta )$ 偏移90°正交，成了它产生误差的唯一来源。

但是传统4场扫描的莫尔条纹光栅尺的两路正交信号 $I$ 和 $Q$ 易于受到LED照明分布不均匀、污染物和振动等外界干扰，测量稳定性不好，基本上不能应用于自动化装备上，仅能做低速手动位置指示。

2 基于直线光栅尺的I-Q调制与解调原理

本文提出一个I-Q平衡式莫尔条纹相位分析理论。莫尔条纹相位分析任务^[9-11]是解调一个与位移有关的周期信号 $g(\theta ,d)$ ，计算出与位移一一对应的相位 $\theta $ 。

$g(\theta ,d) = R( 1 + K\cos (\theta + \phi (d))) \cdot w(d)$

(7)

其中 $\theta $ 是指示光栅和主光栅相对位移一一对应的莫尔条纹相移位移， $d$ 是光电二极管阵列分布； $R$ 为莫尔条纹直流分量， $K$ 为莫尔条纹对比度， $\phi (d)$ 为光电二极管阵列分布的空间相移， $w(d)$ 为光电二极管阵列的分布系数。信号 $g(\theta ,d)$ 的频域表达式 $G(\theta ,f)$ 为

$ \begin{split} G(\theta ,f) =& Q( W(f) + 0.5(W(f - {f_0})){{\rm{e}}^{{\rm{i}}\theta }} + \\& {(W(f + {f_0})){{\rm{e}}^{ - {\rm{i}}\theta }}) } \end{split} $

(8)

其中 $W(f)$ 是 $w(d)$ 的频域表达式， ${f_0}$ 是测量时刻光电二极管阵列分布的空间频率， ${\rm{e}}$ 表示自然常数，一旦光电二极管阵列空间分布确定，这个频率为常数。在实践中，光电二极管阵列 $j(0, \cdot \cdot \cdot ,M - 1)$ 是离散分布检测莫尔条纹信号，因此光电二极管空间分布可以按固定空间频率莫尔条纹信号的相移 $\phi (j)$ 分布。每个光电二极管有两个独立的输出通道 $s$ ， $c$ ，其放大倍数 $s(j)$ 和 $c(j)$ 为

$s(j) = \operatorname{Im} (w(j){{\rm{e}}^{ - {\rm{i}}\phi (j)}})$

(9)

$c(j) = \operatorname{Re} (w(j){{\rm{e}}^{ - {\rm{i}}\phi (j)}})$

(10)

如果要求直流分量的影响在调制频率处归零，则满足条件一

$\left\{ \begin{split} & \sum\limits_{j = 0}^{M - 1} {s(j) = 0} \\& \sum\limits_{j = 0}^{M - 1} {c(j) = 0} \end{split} \right.$

(11)

如果要求负频率影响在调制频率处归零，则满足条件二

$ \left\{ \begin{split} & {\sum\limits_{j = 0}^{M - 1} {s(j)\sin ( - {\phi _j}) = \sum\limits_{j = 0}^{M - 1} {c(j)\cos ({\phi _j})} } }\\& {\sum\limits_{j = 0}^{M - 1} {s(j)\cos ({\phi _j}) = - \sum\limits_{j = 0}^{M - 1} {c(j)\sin ( - {\phi _j})} } } \end{split}\right. $

(12)

满足上述条件一和二的4个方程是莫尔条纹相位分析I-Q平衡式编码与解码方程。光栅尺数据解调不良，误差过大，通常可追溯到参数偏离上述2个条件的4个方程。

光电二极管阵列每个独立测量通道测量结果分别经过 $s(j)$ 和 $c(j)$ 放大后，送入两路加法器电路，输出2路频率相同，相位相差90º的正交信号 $I$ 和 $Q$

$I(\theta ) = \sum\limits_{j = 0}^{M - 1} {s(j) \cdot g(j)} $

(13)

$Q(\theta ) = \sum\limits_{j = 0}^{M - 1} {c(j) \cdot g(j)} $

(14)

3 光栅M场扫描算法

传统光栅4场扫描系统是I-Q平衡式编码与解码的一个特例^[12-14]。在 $f = {f_0}$ 和 $f = 2{f_0}$ 处有适当零点。但这些点邻域中存在强导数，这个方法对调制频率的变化和低频强度噪声敏感。

本文提出莫尔条纹相位分析I-Q平衡式编码与解码条件，将传统的光栅4场扫描系统扩充到光栅M场扫描系统，莫尔条纹相位分析I-Q平衡式编码与解码方程是多解方程，求解可以得出一系列光栅M场扫描算法，如表1~表3所示。

7场π/2法的数据如表1所示，表中光电二极管阵列空间分布相移 $\phi (j)$ 有两套数据，对应相应的分布系数 $w(j)$ ，可以分别使用，因此有两套7场π/2扫描法。

15场π/4扫描法的数据如表2所示，表中 $\phi (j)$ 有两套数据，对应相应的 $w(j)$ ，可以分别使用，因此有两套15场π/4扫描法。

31场π/4扫描法的数据如表3所示，表中 $\phi (j)$ 有两套数据，对应相应的 $w(j)$ ，可以分别使用，因此有两套31场π/4扫描法。

将上述表1~表3数据代入 $s(j)$ 和 $c(j)$ 表达式求出，并以二者分别为每个光电二极管的直流放大电路的发大倍数，最后按I-Q表达式分别接入两路直流加法器电路；两路直流加法器电路输出信号即I-Q信号。正交的I-Q信号符合市面上流行的所有运动控制器位移反馈接入标准^[15]。

4 光栅相移扫描算法性能对比

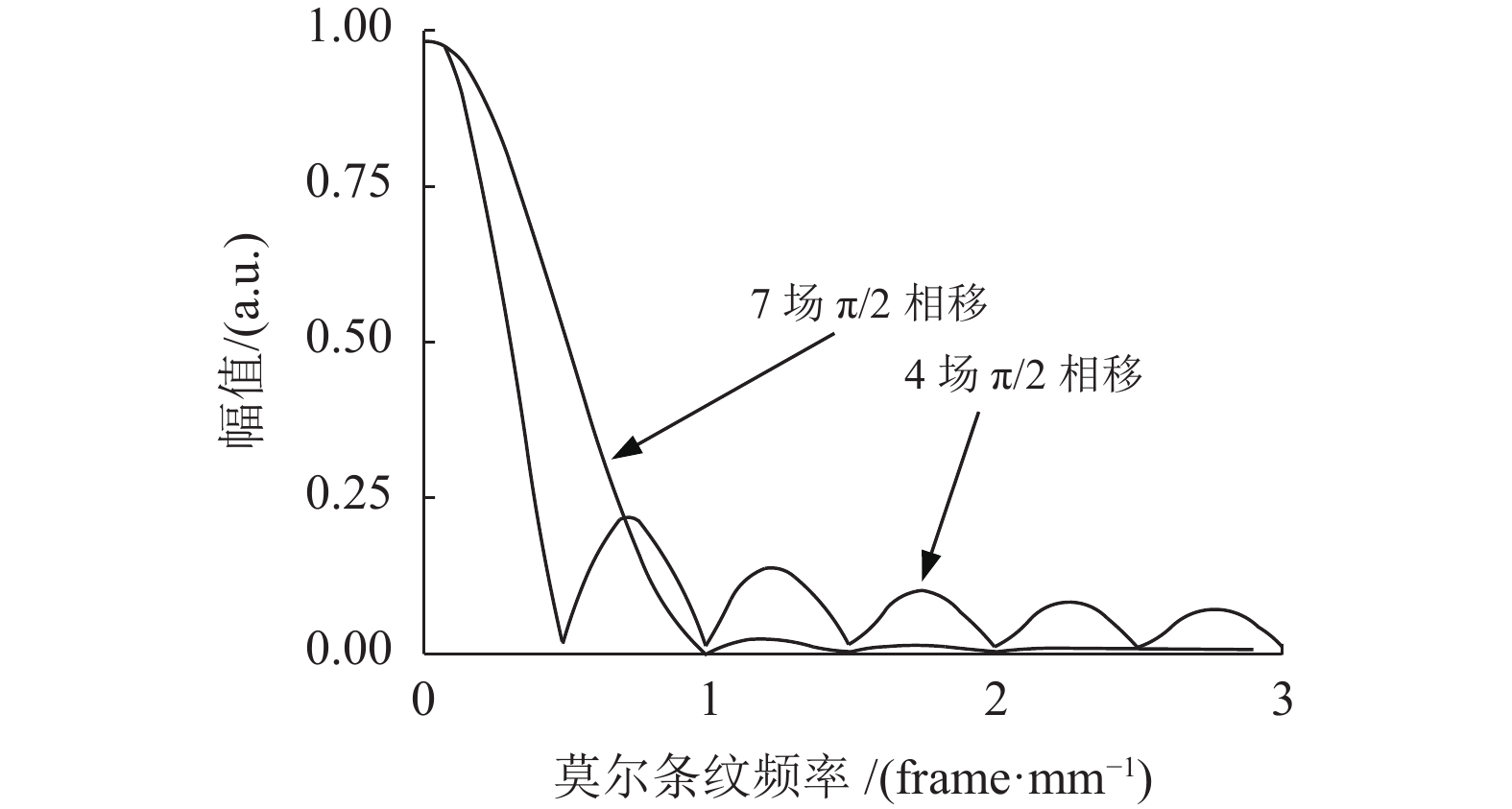
现采用7场π/2相移扫描算法与传统的4场π/2扫描算法进行对比研究，对 $I(\theta )$ 和 $Q(\theta )$ 偏移90°正交进行了分析和抑制，仿真。其中7场π/2相移扫描算法采用的光电二极管阵列空间分布相移 $\phi (j)$ ，以及对应相应的分布系数 $w(j)$ 如表1所示。

图3所示的傅里叶变换正频率^[16-17]部分。设莫尔条纹空间频率为 ${f_0} = 1$ ，传统4场π/2相移扫描方法在 $f = {f_0}$ 、 $f = 2{f_0}$ 附近幅值快速变化，光电二极管空间分布误差对莫尔条纹幅值测量结果影响大^[18]。而7场π/2相移扫描方法，在 $f = {f_0}$ 、 $f = 2{f_0}$ 附近相对平坦，光电二极管空间分布误差对幅值影响相对较小，从而使用7场π/2相移扫描方法，光电二极管空间分布误差对于位移测量结果影响较小。

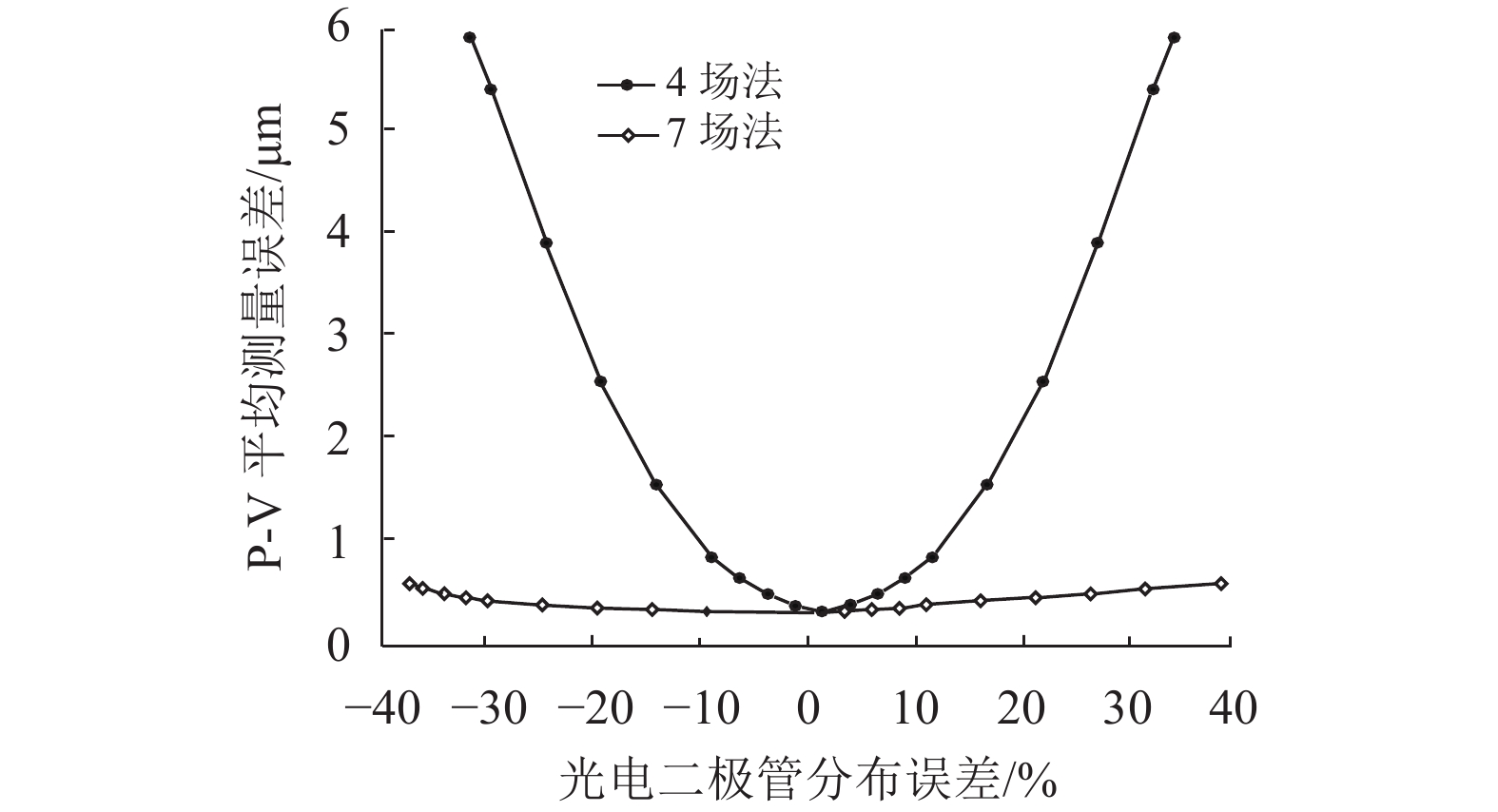
图4所示是光电二极管分布误差导致位移测量误差。水平轴是相对误差：光电二极管分布误差与π/2比值的百分比。光电二极管分布误差导致光栅尺位移误差呈现交变特性，其P-V(Peak-Valley，峰值与谷值的差值)值是纵轴。从图上看，即使光电二极管分布误差达到π/2的30%(30º角)，7场π/2相移扫描方法的P-V位移误差0.5 μm，对于大部分测量情况仍然可以使用，而4场π/2相移扫描方法的P-V位移误差大于5.5 μm，基本不能使用。

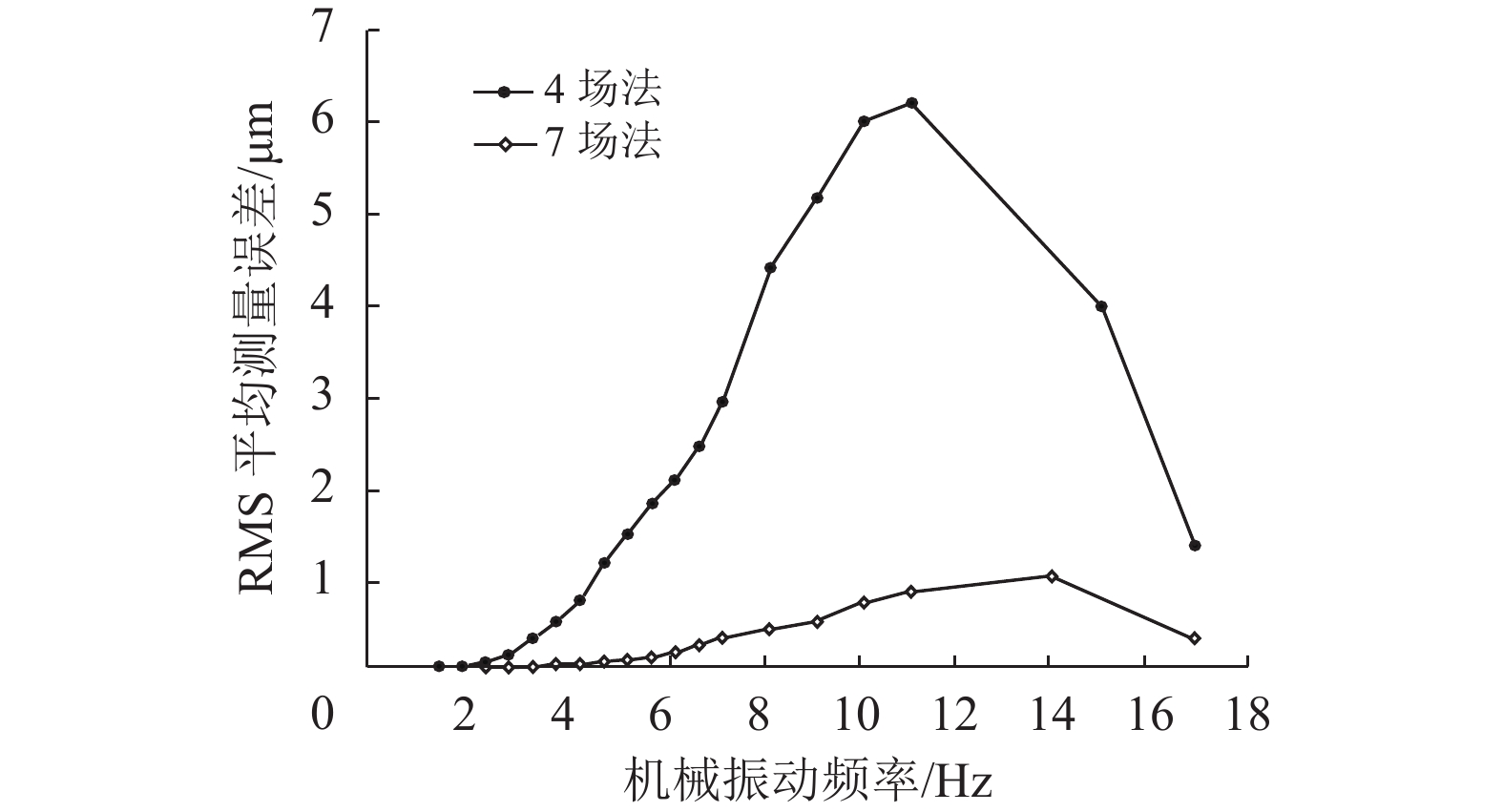
图5所示外界机械振动对4场π/2扫描和7场π/2扫描方法的位移测量结果的影响。对于频率大于18 Hz的外界机械振动，两种方法误差趋于相同。然而实际使用中，自动化装备的温和气流扰动、平台振动、热变形和地面振动都在小于18 Hz的低频范围内，7场π/2相移扫描方法显著改善了光栅尺位移测量系统的低频特性。

综上所述，7场π/2算法最重要的优点是对相移误差、振动和强度噪声引起的畸变具有良好的抵抗能力。

5 结论

本文研究并分析了基于直线型光栅尺的I-Q平衡式光电编码与解码方法原理，并提出通过莫尔条纹相位分析I-Q平衡式编码与解码条件，将传统的扫描系统扩充到光栅M场扫描系统。首先分析了光栅尺的结构设计方案，并推导了直线光栅尺的I-Q调制与解调原理，在此基础上提出了I-Q平衡式莫尔条纹相位分析理论。通过7场π/2扫描法与传统的4场π/2扫描法的性能对比发现，该方法使得自动化闭环系统在抗光栅表面污染、抗光电二极管分布位置误差和抗低频振动等方面的性能大大改善，是可靠、实用性强的光栅技术。

本方法专门针对自动化设备位置反馈使用，与现有技术相比具有以下的优点：

(1) 抗LED照明不均引起的I-Q正交信号幅值和相位变化误差；

(2) 抗光栅表面污染引起的I-Q正交信号幅值和相位变化误差；

(3) 抗光电二极管分布位置误差引起的I-Q正交信号幅值和相位变化误差；

(4) 抗低频振动引起的I-Q正交信号幅值和相位变化误差。

因此，在高速测量时，本方法光栅尺的精度保持性和可靠性大幅优于现有技术。虽然光电探测器通道增加，但是每个通道都是直流放大与加法器模拟电路，在技术层面，本方法与传统技术相同。考虑到光电探测及其放大电路使用定制集成电路芯片，多通道光电探测器没有增加复杂度，空间尺寸和成本变化不大，可见本方法具有很强的实用性。