在数据分析领域,经常会遇到一些数据集的预测问题,如:5G网络数据[1]、房屋价格[2]、股票价格[3]、出生率[4]、公交车客流[5]等的预测问题。有些数据统计的时间周期较长(比如按周、月或年等进行统计),或数据样本统计时间比较短等原因,使得可以获得的数据样本数量很少。对这种只包含少量数据的场合,准确预测相对较难,而在实际应用中对于决策部门却有着重要的参考意义。
数据预测问题通常输出一个连续值,属于回归问题,对于小样本数据的预测往往采用线性回归,已有一些文献在该领域作出研究。文献[6]讨论了不同分布模型阈值选择和准确性对小样本数据及样本偏差的影响。文献[7]比较了使用小样本数据进行随机分组设计的方法,认为当样本量极小时,传统方法都将失效。文献[8]提出了一种简单实用的特征提取方法来减少小样本量的影响。文献[9]对小样本集提出了一种扩展样本数量的方法。文献[10]提出一种基于一致性估计的方法,这是关于小样本数据置信区间的新方法。文献[11]则提出了一种基于超像素分割和距离加权线性回归分类器的光谱空间高光谱图像分类方法来解决小标签训练样本集问题。文献[12]从理论上提出了一种没有对应关系的线性回归的代数几何方法,是一种有效适应于小样本值的解决方案。
本文将线性回归应用于广州车牌竞拍价格数据集[13],以探索小样本数据集的预测方法。广州车牌竞拍是每月一次,从2012年8月首次竞拍开始,到2020年7月为止,共96个月。将其制作为一个数据集,该数据集总共有96个样本,每个样本包含竞拍的主要特征,如:投放指标数、有效编码数、第一次播报均价、第二次播报均价等,输出的主要指标为最低报价和平均报价,本文主要预测平均报价。
1 算法基本原理 1.1 模型设投放指标数为x1,有效编码数为x2,第一次播报均价为x3,第二次播报均价为x4,输出平均报价为y,线性回归假设输出与各输入之间是线性关系,则输出y的预测值与各输入之间的关系可用式(1)表示。
| $\hat y = {x_1}{w_1} + x{}_2{w_2} + {x_3}{w_3} + {x_4}{w_4} + b$ | (1) |
其中,w1、w2、w3和w4是权重,b是偏差,且均为标量。它们是模型的参数,整个算法的目的是找到合适的参数值,使预测值尽可能接近真实值。
由于数据集样本数较少,为尽可能通过训练获得准确的参数,将前90个样本作为训练集,后6个样本作为测试集。对于训练集样本逐一预测输出均价,将得到式(2)。
| $ \begin{split} & {{\hat y}^{(1)}} = x_1^{(1)}{w_1} + x_2^{(1)}{w_2} + x_3^{(1)}{w_3} + x_4^{(1)} + b \\& {{\hat y}^{(2)}} = x_1^{(2)}{w_1} + x_2^{(2)}{w_2} + x_3^{(2)}{w_3} + x_4^{(2)} + b \\& \vdots \\& {{\hat y}^{(n)}} = x_1^{(n)}{w_1} + x_2^{(n)}{w_2} + x_3^{(n)}{w_3} + x_4^{(n)} + b \end{split} $ | (2) |
其中,n为训练集的样本总数,即90。
将式(2)表示为矩阵的形式,如式(3)所示。
| ${\hat {{y}}} = {{Xw}} + b$ | (3) |
其中,
| $ \begin{array}{l} {\hat {{y}}} = \left[ \begin{array}{c} {{\hat y}^{(1)}} \\ {{\hat y}^{(2)}} \\ \vdots \\ {{\hat y}^{({\rm{n}})}} \end{array} \right],\;{{X}} = \left[ {\begin{array}{*{20}{c}} {x_1^{(1)}}&{x_2^{(1)}}&{x_3^{(1)}}&{x_4^{(1)}} \\ {x_1^{(2)}}&{x_2^{(2)}}&{x_3^{(2)}}&{x_4^{(2)}} \\ {\vdots}&{\vdots}&{\vdots}&{\vdots} \\ {x_1^{({\rm{n}})}}&{x_2^{(n)}}&{x_3^{(n)}}&{x_4^{(n)}} \end{array}} \right]\\ {{w}} = \left[ {\begin{array}{*{20}{c}} {{w_1}} \\ {{w_2}} \\ {{w_3}} \\ {{w_4}} \end{array}} \right] \end{array} $ |
同时,式(3)中的加法运算使用了广播机制[14]。
1.2 损失函数和优化算法为衡量平均报价的预测值与真实值之间的误差,本算法采用平方误差函数作为损失函数。设模型参数θ=[w1, w2, w3, w4, b]T,则损失函数
| $\ell ({{\theta }}) = \frac{1}{{2m}}{({\hat {{y}}} - {{y}})^{\rm{T}}}({\hat {{y}}} - {{y}})$ | (4) |
其中,m为用于计算损失函数的样本数。
通过模型训练,需要找出一组模型参数,以使训练样本平均损失最小。随机梯度下降(stochastic gradient descent, SGD)[15]在深度学习算法中被广泛用作优化算法以减小训练样本的平均损失,本文也采用此算法。随机梯度下降的迭代更新用式(5)表示。
| ${{\theta }} = {{\theta }}{\rm{ - }}\frac{\eta }{{\left| { B} \right|}}\sum\limits_{{\rm{i}} \in B} {{\nabla _\theta }{\ell ^{(i)}}} ({{\theta }})$ | (5) |
其中,|B|为每个小批量中的样本个数,在此处用于代替式(4)中的m;η为学习率,均为算法中的超参数,需要通过不断尝试以找到合适的值;样本i的梯度是与损失有关5个标量参数的偏导数组成的向量,结合式(4),可推导得式(6),如下所示。
| $ \begin{split} & {\nabla }_{{{\theta}} }{\ell }^{(i)}({{\theta}} )=\left[\begin{array}{c}\dfrac{\partial {\ell }^{(i)}({w}_{1},{w}_{2},{w}_{3},{w}_{4},b)}{\partial {w}_{1}}\\ \dfrac{\partial {\ell }^{(i)}({w}_{1},{w}_{2},{w}_{3},{w}_{4},b)}{\partial {w}_{2}}\\ \dfrac{\partial {\ell }^{(i)}({w}_{1},{w}_{2},{w}_{3},{w}_{4},b)}{\partial {w}_{3}}\\ \dfrac{\partial {\ell }^{(i)}({w}_{1},{w}_{2},{w}_{3},{w}_{4},b)}{\partial {w}_{4}}\\ \dfrac{\partial {\ell }^{(i)}({w}_{1},{w}_{2},{w}_{3},{w}_{4},b)}{\partial b}\end{array}\right]=\\& \left[\begin{array}{c}{x}_{1}^{(i)}({x}_{1}^{(i)}{w}_{1}+{x}_{2}^{(i)}{w}_{2}+{x}_{3}^{(i)}{w}_{3}+{x}_{4}^{(i)}{w}_{4}+b-{y}^{(i)})\\ {x}_{2}^{(i)}({x}_{1}^{(i)}{w}_{1}+{x}_{2}^{(i)}{w}_{2}+{x}_{3}^{(i)}{w}_{3}+{x}_{4}^{(i)}{w}_{4}+b-{y}^{(i)})\\ {x}_{3}^{(i)}({x}_{1}^{(i)}{w}_{1}+{x}_{2}^{(i)}{w}_{2}+{x}_{3}^{(i)}{w}_{3}+{x}_{4}^{(i)}{w}_{4}+b-{y}^{(i)})\\ {x}_{4}^{(i)}({x}_{1}^{(i)}{w}_{1}+{x}_{2}^{(i)}{w}_{2}+{x}_{3}^{(i)}{w}_{3}+{x}_{4}^{(i)}{w}_{4}+b-{y}^{(i)})\\ {x}_{1}^{(i)}{w}_{1}+{x}_{2}^{(i)}{w}_{2}+{x}_{3}^{(i)}{w}_{3}+{x}_{4}^{(i)}{w}_{4}+b-{y}^{(i)}\end{array}\right]=\\& \left[\begin{array}{c}{x}_{1}^{(i)}\\ {x}_{2}^{(i)}\\ {x}_{3}^{(i)}\\ {x}_{4}^{(i)}\\ 1\end{array}\right]({\hat{y}}^{(i)}-{y}^{(i)}) \end{split}$ | (6) |
针对数据集中样本少的情况,可以采用k折交叉验证(k-fold cross-validation)[15]的方法。具体地,是将原始训练集分成k个互不重叠的子集,然后做k次模型训练和验证,其中k–1个子数据集来训练模型,另外1个子数据集来验证模型。通过k次训练和验证,每次用来验证的子数据集都不同,最后对k次训练误差和验证误差求平均。这样通过选择不同参数进行验证,最终找到合适的一组参数。
通过k折交叉验证可以调优算法中的超参数,以找到最合适的超参数。为了评价一组超参数的交叉验证误差,本文使用基于对数的均方根误差,假定预测值为
| ${\rm{rmse}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{(\ln ({y_i}) - \ln ({{\hat y}_i}))}^2}} } $ | (7) |
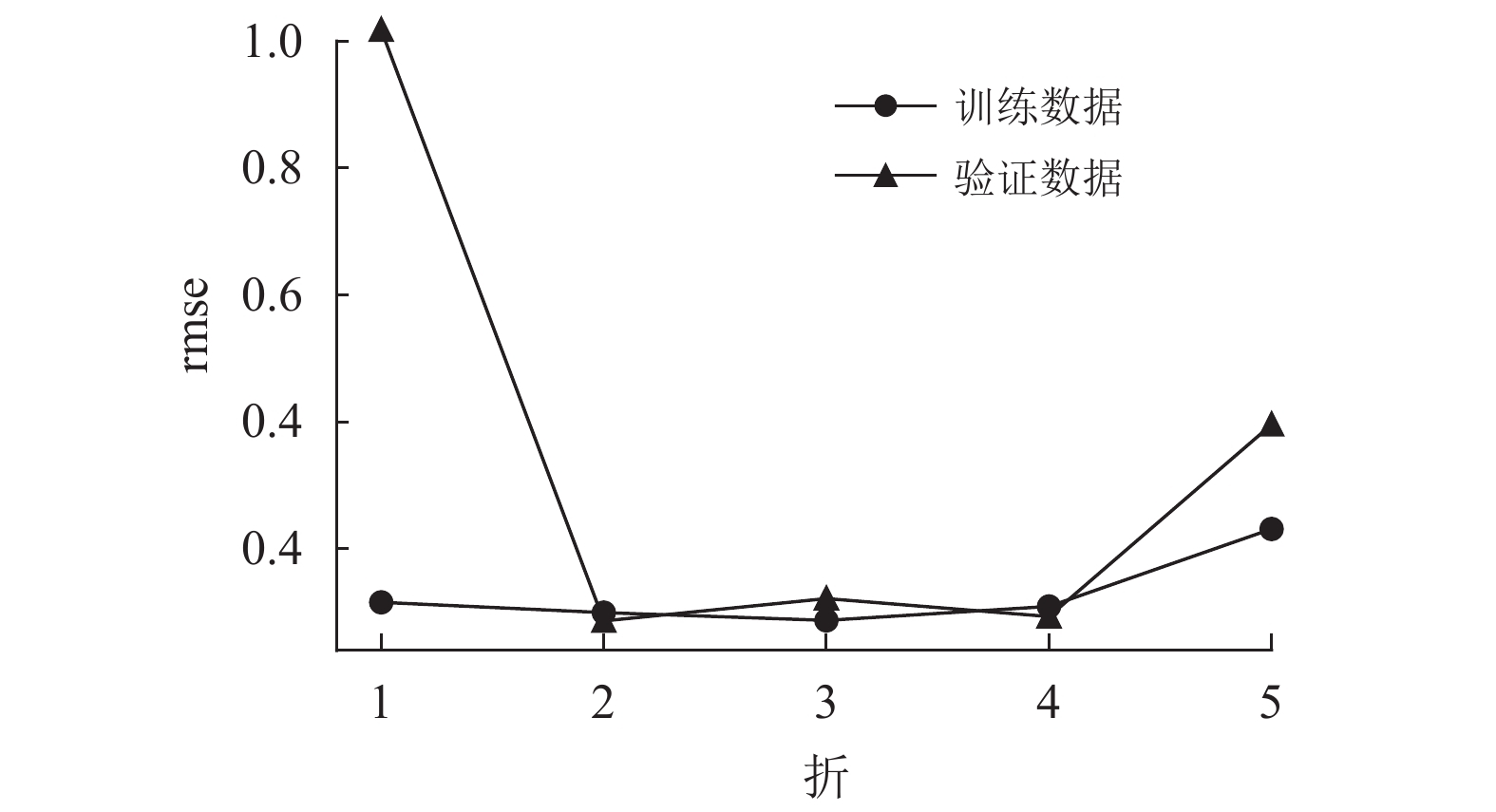
对本文的训练集数据进行k折交叉验证(这里取k值为5),即将训练集分成5组,每次取4组用于训练,1组用于验证,结果如图1所示。
由图1可见,第1折验证时,由于第1组数据作为验证数据,rmse值为1.018,比第1折的训练数据rmse的值0.116几乎大了一个数量级,其他4折两者的结果基本在同一个数量级。5折平均后,训练数据的rmse平均值为0.129,而验证数据的rmse平均值为0.343,验证数据rmse均值明显增大,主要由于第1折的较大值所导致。本文的目标是找到一组超参数,使得测试数据和验证数据的平均rmse值尽可能小且趋于相等,以确保最终测试结果既不会过拟合,也不会欠拟合。而上述的平均误差结果的差异,主要源于第1组验证数据,并非超参数设置所引起的,因此很难判断某一组超参数的设置是否恰当。
|
图 1 k折交叉验证的rmse Figure 1 rmse of k-fold cross-validation |
经过不断实验和分析,发现问题出在混洗(Shuffling)策略上。所谓混洗,就是在对数据进一步处理之前,随机打乱数据的顺序。在本文所研究的车牌竞拍数据中,就是把原本按照竞拍时间顺序排列的样本数据随机打乱,然后再处理。
通常作k折交叉验证将原始训练集分成k组后,在每折验证时,只对该折的训练组数据和验证组数据分别进行混洗,即局部混洗,然后再分别进行训练和验证,图1的实验结果正是采用了这种方法。
在所研究的广州车牌竞拍数据中,发现所选取的第1组数据与其他组有明显的区别:在第1组数据样本的输入特征中,有很多样本的有效编码数小于投放指标数,即参与竞标的人数少于所提供的标的,而这种现象在后面几组数据中很少出现。这种现象源于竞价早期阶段,愿意参与的人数较少(大部分人希望通过车牌摇号或上外地牌等方式低成本地获得车牌),但随着时间推移,车牌的获取难度越来越大,参与人数越来越多。
这种局部数据特异性现象在其他数据集中都是常见的。只是由于大样本数据集数据量非常大,特异性数据相对于其所在数据组的数据总量来说数量极少,以致于迭代过程其对结果不会产生可观的影响。而小样本数据集由于样本数量太少,当选取的样本组中包含较多的特异性数据,就会对结果产生难以忽略的影响。
针对该问题,本文在进行k折交叉验证之前,先对整个原始训练集数据进行混洗,即全局混洗,使潜在的特异性数据随机分布到整个数据集中,这样作k折交叉验证时,就不会有大量特异性数据集中在某一组的情况。
2 实验验证本文算法通过Pytorch框架[16]实现,所有输入特征进行了标准化的预处理,即每个特征值先减去均值再除以标准差得到标准化后的特征值;式(2)中的权重和偏差均初始化为均值0,标准差0.01的正态随机数。首先对训练集数据进行全局混洗,然后通过多组实验来寻找合适的超参数,最后验证所选择的一组参数的预测效果。在本算法实现中,超参数有3个,分别是每个小批量中的样本个数(|B|)、学习率(η)和迭代周期次数(λ)。
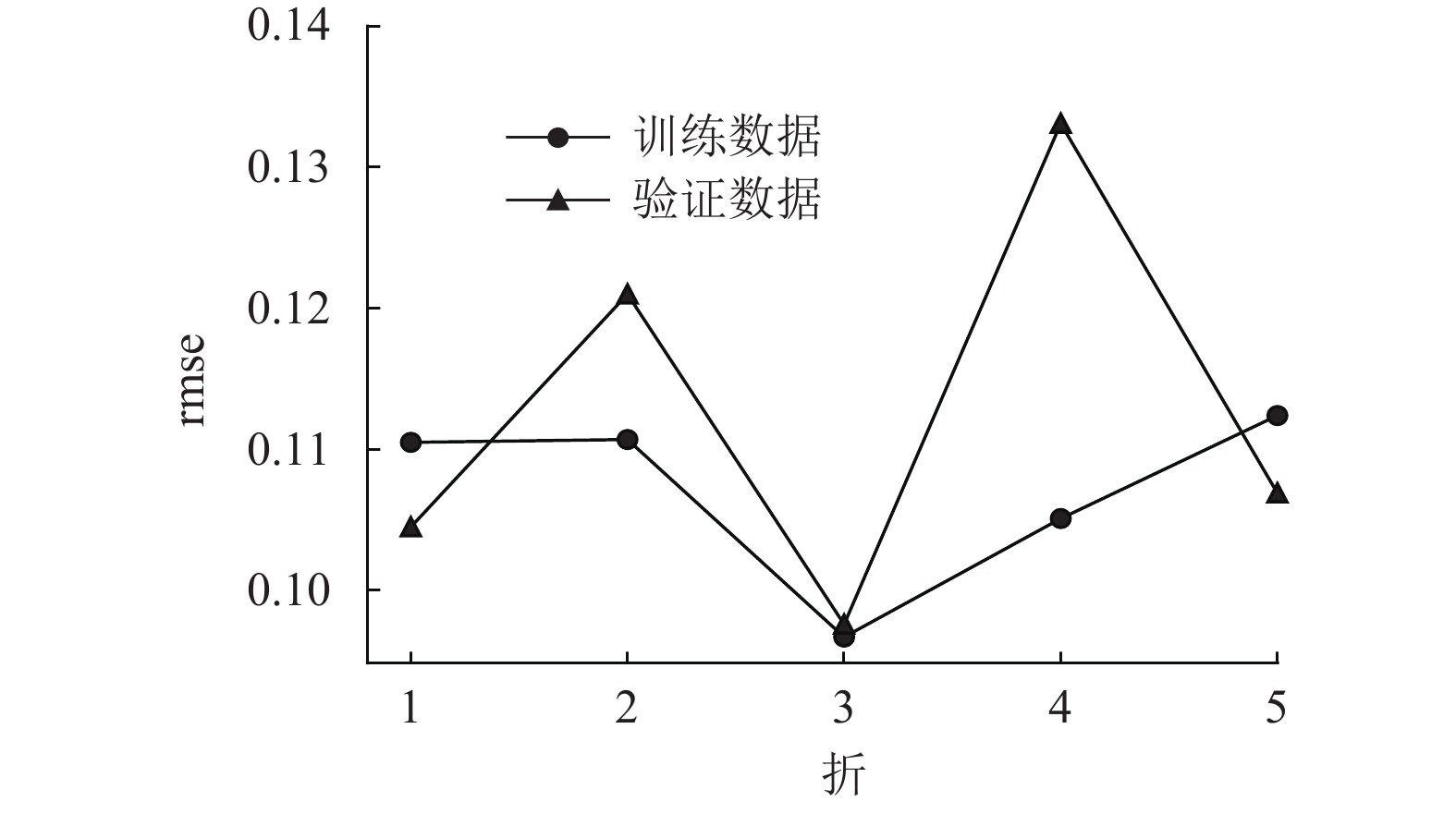
2.1 采用全局混洗策略的k折交叉验证本节首先对原始训练集数据进行全局混洗,然后再进行k折交叉验证(其中k设为5),如图2所示。
|
图 2 采用全局混洗策略的k折交叉验证的rmse Figure 2 rmse of k-fold cross-validation with global shuffling strategy |
由图可见,经过混洗后,每折的rmse值没有显著差异,测试数据rmse均值0.107,验证数据的rmse均值为0.112,均值比较接近。
下面进一步通过k折交叉验证优化超参数,以选择最适合样本集的一组超参数。对超参数的选择可以针对某个超参数,选择一组不同值,而保持其他参数的值不变,然后评价得到的平均rmse。
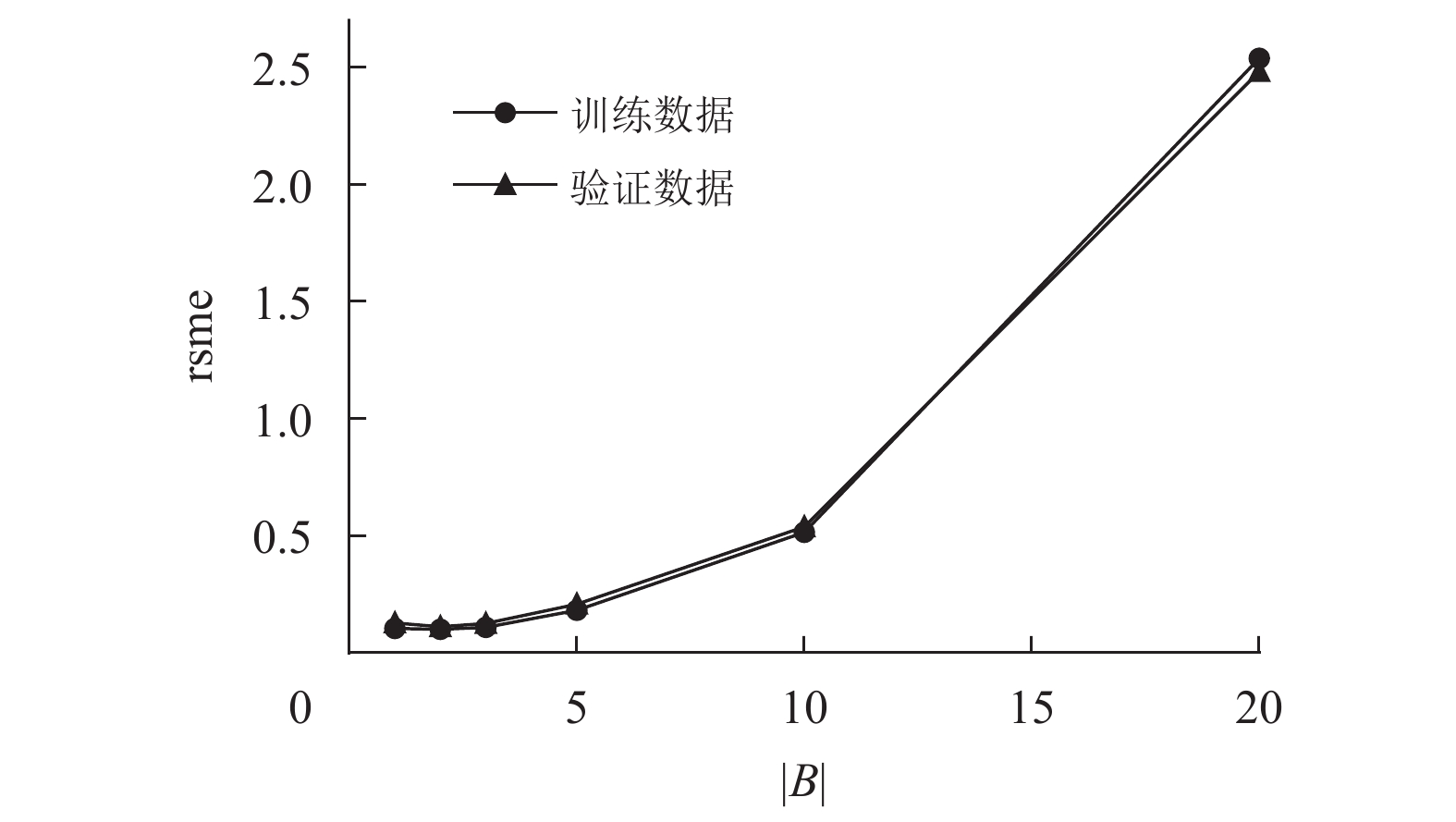
2.2 确定批量样本个数|B|本文通过比较不同的|B|以确定最合适的值。实验中,训练集样本90个,λ为10次,学习率η为0.01。除了|B|,其他给定的超参数也是经过大量反复实验找到的较合适的值,限于论文篇幅原因,无法展示所有实验。图3是输入批量样本个数|B|取值分别为1、2、3、5、10和20时rmse的结果。
|
图 3 不同批量样本个数时的rmse比较 Figure 3 Comparison of rmse for different batch size |
图3中给出了k折交叉验证的训练数据和验证数据的5折平均rmse,可见,|B|为1、2、3时的rmse比较小,可考虑作为选择值。
2.3 确定学习率η本文通过比较不同的η以确定最合适的值。实验中训练集样本90个,λ为10次,|B|为3。图4是学习率分别为0.001、0.005、0.01、0.03、0.05、0.1、0.2时rmse的结果。

|
图 4 不同学习率时的rmse比较 Figure 4 Comparison of rmse for different learning rates |
由图4可见,η为0.01、0.03、0.05、0.1时的rmse比较小,可考虑作为选择值。
2.4 确定迭代周期次数λ迭代周期决定了数据训练的次数,并非迭代次数越多越好,一般样本集训练若干次即能收敛,继续训练只不过额外耗费算力,对于获得更好的结果几乎没有帮助。另外,如果其他超参数选的不好,也可能导致迭代结果无法收敛,甚至可能发散为极大的值。本实验通过比较不同的λ以确定最合适的值。实验中训练集样本90个,|B|为3,学习率η为0.01。图5是λ分别为1、2、3、5、10、20、30、50、100时的rmse的结果。

|
图 5 不同迭代周期次数时的rmse比较 Figure 5 Comparison of rmse for different number of iteration cycles |
由图5可见,λ为10以后的rmse已经收敛,进一步迭代,结果没有明显的变化。因此通过此实验,可以确定10作为λ的值。
2.5 选定超参数通过2.2~2.4节的k折交叉验证实验,本文找到了超参数一些较合适的值,其中|B|的可选值为1、2、3,η的可选值为0.01、0.03、0.05、0.1,λ的可选值为10,为了进一步确定它们的最优组合,我们进一步比较不同组合的训练集和测试集的平均正确率,其中训练集样本90个,测试集样本6个。实验结果如表1所示,表中分别选择|B|、η和λ的不同组合,以验证平均正确率。
| 表 1 平均正确率 Table 1 Average correctness rates |
从表中可见,(|B|, η, λ)取值为(3, 0.01, 10)时,无论训练集还是测试集的平均正确率都比较高,且很接近。由于实验初始参数是随机数,且数据随机混洗,每次训练结果都会有一定差异,但经过多次实验,发现(3, 0.01, 10)这组值的正确率始终保持稳定,因此,最终选择这组值作为竞价样本集的超参数。
2.6 预测值与真实值的比较经过实验,确定了3个超参数的值,即|B|=3,η=0.01,λ=10。基于小样本数据量太少,使用这组值训练出来的w1、w2、w3、w4和b对数据集中的全部数据进行检验,比较计算出来的预测值与真实值之间的拟合程度,结果如图6所示。

|
图 6 样本预测值和真实值的比较 Figure 6 Comparison of sample predicted value and true value |
从图6中可见,预测值和真实值拟合得比较好,只有几处出现了稍大些的差异,总的平均正确率达到约95%,且绝大部分数据的正确率超过90%,其中最低的预测正确率为85.09%。
3 结论本文将线性回归的预测方法应用于广州车牌竞拍均价的预测。基于历史数据的有限性,所能获得的数据量属于小样本数据。在研究过程中,注意到局部数据的特异性会导致k折交叉验证的某组验证数据误差明显增大,通过在验证前采用全局混洗的策略,有效地解决了这个问题,并依此能正确地判断各组算法中的超参数的平均验证误差,从而能找出合适的超参数,通过多组实验,确定了算法的一组最合适的超参数,进而得到了很好的预测结果,最终预测的总平均正确率达到了95%。本文是基于实际数据的预测,预测结果对之后的车牌竞拍有很好的参考意义,预测方法也可以应用于其他场合,故有较好的实际应用价值。本文的全局混洗策略适用于各种小样本数据的情形,故本方法也有较好的理论价值。
| [1] |
SEVGICAN S, TRRAN M, GOKARSLAN K, et al. Intelligent network data analytics function in 5G cellular networks using machine learning[J].
Journal of Communications and Networks, 2020, 22(3): 269-280.
DOI: 10.1109/JCN.2020.000019. |
| [2] |
MADHURI C R, ANURADHA G, PUJITHA M V. House price prediction using regression techniques: a comparative study[C]//2019 International Conference on Smart Structures and Systems (ICSSS). Chennai: IEEE, 2019: 1-5.
|
| [3] |
JAHANDARI S, KALHOR A, ARAABI B N. Online forecasting of synchronous time series based on evolving linear models[J].
IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2020, 50(5): 1865-1876.
DOI: 10.1109/TSMC.2018.2789936. |
| [4] |
HASAN M M, SULTANA M I, SALMA U, et al. Investigation of influential factors towards predicting birth rate in Bangladesh[C]//2020 International Conference on Emerging Trends in Information Technology and Engineering (ic-ETITE). Vellore: IEEE, 2020: 1-6.
|
| [5] |
谢振东, 刘雪琴, 吴金成, 等. 公交IC卡数据客流预测模型研究[J].
广东工业大学学报, 2018, 35(1): 16-22.
XIE Z D, LIU X Q, WU J C, et al. A Study of passenger flow prediction based on IC card data[J]. Journal of Guangdong University of Technology, 2018, 35(1): 16-22. DOI: 10.12052/gdutxb.170143. |
| [6] |
BEAN W T, STAFFORD R, BRASHARES J S. The effects of small sample size and sample bias on threshold selection and accuracy assessment of species distribution models[J].
Ecography, 2012, 35: 250-258.
DOI: 10.1111/j.1600-0587.2011.06545.x. |
| [7] |
ASIRET S, SUNBUL S O. Investigating test equating methods in small samples through various factors[J].
Educational Sciences: Theory & Practice, 2016, 16(2): 647-668.
|
| [8] |
DABBAGHCHIAN S, AGHAGOLZADEH A, MOIN M S. Reducing the effects of small sample size in DCT domain for face recognition[C]//2008 International Symposium on Telecommunications. Tehran: IEEE, 2008: 634-638.
|
| [9] |
ZHANG H, YUAN H, LI P. Estimation method for extremely small sample accelerated degradation test data[C]//First International Conference on Reliability Systems Engineering (ICRSE). Beijing: IEEE, 2015: 21-23.
|
| [10] |
FURSOV V A, GAVRILOV A V, KOTOV A P. Prediction of estimates' accuracy for linear regression with a small sample size[C]//2018 41st International Conference on Telecommunications and Signal Processing (TSP). Athens: IEEE, 2018: 1-7.
|
| [11] |
ZHENG C, WANG N, CUI J. Hyperspectral Image Classification With Small Training Sample Size Using Superpixel-Guided Training Sample Enlargement[J].
IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7307-7316.
DOI: 10.1109/TGRS.2019.2912330. |
| [12] |
TSAKIRIS M C, PENG L, CONCA A, et al. An Algebraic-Geometric Approach for Linear Regression Without Correspondences[J].
IEEE Transactions on Information Theory, 2020, 66(8): 5130-5144.
DOI: 10.1109/TIT.2020.2977166. |
| [13] |
广州产权交易所. 广州市中小客车指标竞价情况表[EB/OL]. [2020-09-21]. http://www.gzqcjj.com/article/gonggao,
|
| [14] |
ZHANG A, LI M, LIPTON Z C. Dive into deep learning[EB/OL]. [2020-09-21]. http://www.d2l.ai.
|
| [15] |
GOODFELLOW I, BENGIO Y, COURVILLE A. Deep Learning[M]. Cambridge: MIT Press, 2016.
|
| [16] |
Torch Contributors. Pytorch documentation [EB/OL]. [2020-09-21]. https://pytorch.org/docs/stable/index.html.
|
 2021, Vol. 38
2021, Vol. 38
