2. 嘉应学院 计算机学院,广东 梅州 514015
2. School of Computer Science, Jiaying University, Meizhou 514015, China
规划就是为了达成某个目标,考虑自身所拥有的资源条件以及所需要的行动,对行动的执行时间及执行次序作出决策。智能规划就是利用计算机实现规划自动化的技术。在研究术语中,针对不同的应用场合,智能规划问题可由领域(domain)和问题(problem)组成。在每个领域下,根据初始条件和目标条件的不同,可实例化出多个问题实例。每个问题实例可由状态命题集合S、行动(或称动作)集合A、初始状态集合I和目标状态集合G组成,即一个规划问题可由<S,A,I,G>这样一个四元组构成。规划的过程就是寻找出一组行动序列,使初始状态I转移到目标状态G。这组行动序列就是一个计划,也被称之为规划解。
1971年,Fikes和Nilsson[1]提出了STRIPS(STanford Research Institute Problem Solver)规划。STRIPS规划克服了早期智能规划使用的纯逻辑方法的缺点,极大地提升了规划系统的求解能力。STRIPS系统是智能规划研究历史上的一个里程碑。此后,智能规划的问题表示通常都是STRIPS规划或是在STRIPS规划基础上的扩展。
现实世界的实际应用需要考虑到时间因素。而STRIPS规划为了限定问题的复杂度作出了诸多严格的假设。其中“动作是瞬时的”这条假设可以表明STRIPS规划并不支持时态动作。为此,STRIPS的扩展版时态规划应运而生。时态规划的出现是智能规划走向现实世界实际应用的需要和必然结果。
1998年举行的第一届国际规划竞赛(International Planning Competition, IPC)统一了关于基准问题的描述,建立了一套领域问题的标准描述方法。此后,国际规划竞赛每两年或三年举行一次。IPC让各个规划器可以同台竞技,极大地促进了智能规划的发展。
智能规划不仅在理论研究上具有重要意义,在现实生活中也具有广泛的应用,在机器人控制、工业制造、物流运输、化学工业、计算机博弈、股票指数模拟中都可以看到其身影。应用的详细内容见下文第4部分。
1 规划表示语言及时态特征的发展要用计算机去求解规划问题,首先要做的就是将规划问题描述成计算机能识别的操作符,即需要一个描述规划的语言来进行知识表示。其次,需要定义描述规划知识的数据结构。最后则是进行规划求解。所以,一个规划器通常由知识表示、数据结构、搜索求解这3个部分组成。
1.1 STRIPS表示和ADL表示1971年,Fikes和Nilson设计了STRIPS规划器。STRIPS定义了“状态(State)”“动作(Action)”“目标(Goal)”等概念以及相应的状态模型、动作模型、状态转移规则。STRIPS的出现使得规划可以轻松地进行描述和操作,是智能规划历史上的一个里程碑。STRIPS规划也被称为经典规划。1989年,Pednault[2]提出了动作描述语言ADL(Action Description Language),这是在STRIPS表达能力的基础上进行扩展的语言,它允许使用全称量词、存在量词、条件效果等特征。ADL的提出让更多类型的问题可以被描述出来,也意味着智能规划技术可以求解更多的问题类型。
1.2 TGP模型(黑盒模型)1999年,Smith[3]设计了一个时态动作模型——TGP(Temporal Graph Planner)模型。TGP模型规定:每个动作都有一个执行时间;一个动作在执行之前以及执行过程中,其所有前提条件必须保持成立;动作的效果命题的真值在动作执行过程中是无定义的,效果命题在动作结束的那一刻开始成立。TGP模型被研究者们称为黑盒模型。
Smith本人的时态规划器TGP,Do和Kambhampati[4]设计的时态规划器SAPA,Fox和Long[5]设计的时态规划器LPGP等都采用黑盒模型作为其动作模型。
1.3 CBI模型2000年,Smith和Frank等[6]提出了一种比黑盒模型表达能力更强大的动作模型,称之为基于约束的区间(Constraint Based Interval, CBI)模型。CBI模型能表达在动作的执行时间区间内任意子区间的前提条件命题,也支持将动作产生的效果命题指定在任意的时间区间内保持成立。在CBI模型下,状态命题通常表示为这样一个二元组Π<P, I >。其中 P是基础命题,I是时间区间。容易看出,CBI模型是一种非常灵活的动作模型,它可以表达出丰富的时态特征。
1.4 规划领域定义语言PDDL规划领域定义语言PDDL(Planning Domain Definition Language)是国际规划竞赛IPC指定的用于规划的知识表示的官方语言。PDDL最早的版本Version1.2由McDermott于1998年提出,并应用于1998年的第一届国际规划竞赛上。PDDL1.2不支持时态动作的表达,其表达能力相当于STRIPS和ADL的结合版。
1.4.1 PDDL2.12002年,Fox和Long[7]提出了PDDL2.1。PDDL2.1被应用于2002年举行的第三届国际规划竞赛。PDDL2.1是一种支持时态规划和度量规划的语言。PDDL2.1的表达能力可以分为5个层次:第1层是STRIPS表达部分。第2层是在STRIPS表达基础上扩充对数值表达的支持。第3层是在STRIPS表达和数值表达的基础上扩充对离散的持续动作的支持。第4层是在STRIPS、数值表达、离散的持续动作的基础上扩充对连续的持续动作的支持。最后的第5层则是在第4层表达的基础上增加对事件和过程的支持。
PDDL2.1可以表达动作的3种时态类型的前提条件,分别是“at-start”条件、“over all”条件和“at-end”条件,以及可以表达2种时态类型的效果,分别是“at-start效果”和“at-end效果”。PDDL2.1语法中,一个持续动作的表示如下:
(:durative-action load-truck
:parameters (?t - truck)
(?l - location)
(?o - cargo)
(?c - crane)
:duration (=?duration 8)
:condition (and (at start (at?t?l))
(at start (at?o?l))
(at start (empty?c)
(over all (at?t?l))
(at end (holding?c?o))
:effect (and (at end (in?o?t)
(at start (holding?c?o))
(at start (not (at?o?l)))
(at end (not (holding?c?o))))
容易看出,该动作的持续时间为8个时间单位。而动作的前提条件是:在动作执行的开始时刻,货车t和货物o都要在同一位置l,并且起重机c要处于空闲状态;然后,在动作的执行期间,货车也必须在位置l保持不移动;在动作执行的结束时刻,起重机c要抓住货物o。而动作的效果则是:在动作开始时刻,货物o离开位置l,货物o被起重机c抓起;在动作的结束时刻,货物o的位置发生改变,不在起重机c上而在货车t上。
此外,PDDL2.1还引入了metric,即规划质量的衡量指标。例如:对于运输领域问题,物流公司考虑的不仅仅是要将货物在指定时间内送达,还要考虑尽可能地减少资源的消耗,降低经济成本;对于看重时间资源的领域问题,则可以将metric指定为total-time,即越早实现目标,规划质量就越高。
1.4.2 PDDL2.22004年,Edelkamp和Hoffmann[8]提出了PDDL2.2。PDDL2.2在支持STRIPS表达、数值表达、离散的持续动作的基础上增加了对派生谓词和时间初始文字的支持。
在规划中,派生谓词是描述动作的非直接效果的一种方式。规划问题的描述是基于一阶谓词逻辑的。谓词可以分为基本谓词和派生谓词两类,基本谓词出现在领域动作的效果中,而派生谓词则不受动作的直接影响,它们在当前状态下的真值是通过领域规则推导得出[9]。
时间初始文字提供了一种表达不需要前提条件就可以发生的外部事件的方式。例如:游戏服务器每天运行的时间、商城每天营业的时间、学生宿舍每天水电供应时段、图书馆每天开放时间等。
下面给出派生谓词的一个例子:
(:derived(plane-usable?p - plane)
(and (plane-has-plane_captain?p)
(plane-has-flight_attendant?p))
)
该例指定飞机仅在有机长和乘务员的情况下才可以使用。“飞机p可以使用”这个派生谓词不由动作决定,而是由“飞机p上有机长”“飞机p上有司机”这两个谓词决定。
下面给出时间初始文字的一个例子:
(:init
(at 9 (mall-open))
(at 22 (not (mall-open)))
)
两个时间初始文字语句表达了“商场的营业时间为早上9点到晚上22点”这样一种状态。
1.4.3 PDDL3.02006年,Gerevini和Long[10]提出了PDDL3.0。PDDL3.0引入了“偏好”“状态轨迹约束”等概念。一直以来,时态规划通常都致力于寻求makespan(总的完工时间)最短的计划。然而,许多现实问题的着重点并不只是要尽快实现目标,还要考虑资源消耗等其他因素。为此,“偏好”应运而生。显然,“偏好”是可以违背的,规划的最终目的是找到从初始状态到目标状态的行动序列,“偏好”只是希望满足但不是必须满足的。所以,与“偏好”相对应的是“软约束”。“偏好”和“软约束”影响的是规划解的好坏,而不能影响规划解的有无。
下面为“偏好”与“规划质量metric”的一个简单示例:
(preference p1 (always (clean truck1)))
(preference p2 (and (at end (at package2 London))
(sometime (clean track1))))
(:metric (+ (* 8 (is-violated p1)) (* 5 (is-violated p2))
偏好p1要求在“always”条件下货车truck1的状态是clean。而偏好p2要求在“at end”条件下包裹package2在London以及在“sometime”条件下track1的状态是clean。而规划质量metric的值为各偏好的违背次数的加权和。
“状态轨迹约束”,表示在规划执行过程中整个状态序列需要满足的条件。它们通过包含状态谓词的时态算子来表示。基本的时态算子有“always”、“sometime”、“at-most-once”、“at end”等。
“状态轨迹约束”的定义方式如下所示:
<con-GD>::=(at end<GD>| (always<GD>) |
(sometime<GD>| (within<num><GD>) |
(at-most-once<GD>) |
(sometime-after<GD><GD>) |
(sometime-before<GD><GD>) |
(always-within<num><GD><GD>) |...
其中num是数值参数,GD是状态谓词参数。PDDL3.0通过加入时态算子的方式给状态谓词加上了时态限定。
“偏好”“状态轨迹约束”的引入大大增强了规划质量衡量标准metric的表达,使PDDL能够表达出更加切合现实的规划问题。
1.4.4 PDDL+Fox和Long提出的PDDL+[11]是对PDDL2.1的第5层表达进行建模,即支持事件和过程。PDDL+中的过程process语法定义如下:
(:process falling
:parameters (?b - basketball)
:precondition (and (not (hold?b))
(<(velocity?b) 11)
)
:effect (and
(increase (velocity?b) (* #t 9.8))
(decrease (distance-to-ground?b) (* #t (velocity?b)))
))
过程process由3个部分组成:parameters、precondition和effect。它们定义了一个process在什么时候对其进行操作,以及该process在作用时具有什么效果。#t代表过程的时间,它用来计算连续数字的影响。事件event的定义和过程process类似,也是由parameters、precondition、effect组成。本质上,事件event是时间上的离散时刻,可看成不可控制的瞬时行为,而过程process是时间区间,可看成不可控制的持续行为。
1.5 小结从时态的不同层次的表达维度上看,时态信息可以分为显式的时态信息和隐式的时态信息。“时间点”“时间区间”等属于显式的时态信息。像“瞬时”“同时”“先后”等则属于隐式的时态信息。所以,经典规划也属于时态规划,是隐式的时态规划。而“同时”“先后”则分别属于并行规划和部分序规划的范畴。目前对时态规划的研究和讨论以显式的时态规划为主。
在PDDL2.1提出之前,TGP模型和CBI模型是主流的显式时态规划的动作模型,被众多时态规划研究者所采用。从PDDL2.1的提出开始,时态领域问题走上了国际规划竞赛IPC的舞台。此后,对时态规划的研究都以PDDL的表达为基础。PDDL2.2对PDDL2.1扩充了派生谓词和时间初始文字。PDDL3.0在PDDL2.2的基础上扩充了软目标和软约束。PDDL+对PDDL2.1扩充了事件和过程。在众多时态规划研究者的努力下,PDDL的表达能力在不断增强,能够描述的问题越来越贴近现实世界实际应用。PDDL各版本所支持的特性如表1所示。
| 表 1 PDDL各版本特性 Table 1 Features of PDDL versions |
状态空间是表示状态的数据结构,它可以是树,也可以是图。状态空间搜索就是对表示状态的树或者图按照一定的搜索规则进行遍历。常用的状态空间搜索有深度优先搜索、广度优先搜索和启发式搜索。深度优先搜索是对每条可能的分支深入搜索到终端顶点的搜索方式。广度优先搜索类似于树的层次遍历,对状态空间进行系统彻底的搜索。启发式搜索是利用问题拥有的启发信息或利用基于人的直观或者经验构造的算法来引导搜索,进而减少搜索范围、降低问题复杂度的搜索方法。
Eyerich、Mattmuller等[12]设计的Temporal Fast Downward (TFD)是采用上下文增强的加法启发式算法来指导搜索的时态规划器。TFD首先将PDDL翻译成SAS+时态规划任务。一个SAS+时态任务是一个五元组Π=<V,s0,s*,A,O >。其中 V是有限的状态变量集合,包含了数值变量、比较变量、逻辑变量;s0是初始状态;s*是目标描述;A是有限的公理集合;O是有限的持续动作集合。然后,TFD对SAS+时态任务进行预处理。最后,TFD将时间戳状态定义为一个五元组S=<t,s,E,C↔,C┥>。其中t是一个值大于0的时间戳,s是一个扩展的状态,集合E是一组预定的效果,C↔和C┥相当于PDDL的over all条件和at end条件。TFD以时间戳状态S为搜索空间,采用上下文增强的加法启发式算法进行状态空间搜索求解。在2008年的国际规划竞赛中,TFD获得了第3名的成绩。TFD也是2018年国际规划竞赛的时态赛道冠军获得者组合时态规划器TemPoRal的组成成员之一。
Vidal[13]设计的YAHSP(Yet Another Heuristic Search Planner)是基于前瞻性计划分析的前向启发式搜索规划器。DAEYAHSP获得了2011年国际规划竞赛的冠军,YAHSP3-MT获得了2014年国际规划竞赛的冠军。YAHSP2和YAHSP3-MT是组合时态规划器(Temporal Portfolio Algorithm, TemPoRal)的组成成员,力助TemPoRal获得2018年国际规划竞赛时态赛道冠军。
2.2 部分序规划部分序规划就是可以将多个动作放在一个计划plan中而不指定它们的执行次序的规划。部分序规划在当前的部分计划plan中通过选择一个求精动作,得到下一个更为接近规划解的部分计划plan,以此方法不断在plan中添加动作,直至得到一个完整的解规划plan。
Schwartz和Pollack[14]设计的Partial-Order Planner (DT-POP)以及Sapena、Marzal、Onaindia等[15]设计的ATemporal Forward Partial-Order Planner (TFLAP)等都是使用部分序规划的时态规划器。其中,TFLAP在2018年的国际规划竞赛的时态赛道中获得了第3名。
2.3 图规划图规划方法是以图为数据结构的搜索方法。以图为数据结构,构造规划图。规划图的顶点分为2类,分别是动作顶点和命题顶点。规划图的边分为3类,分别是前提条件边、添加效果边、删除效果边。规划图是有向无环图。图规划方法以规划图作为搜索空间,即将搜索空间表示为命题层和动作层,其中动作层和命题层交替出现。图规划方法的求解过程分为两部分:在规划图上进行正向的图扩展和反向的解提取。
柴啸龙[16]在规划图的基础上设计了蚁群规划算法,伍丽华[17]在规划图框架下设计了遗传算法求解时态规划问题。
2.4 将时态规划问题转换为STRIPS规划问题求解时态规划的另一种方法是将时态规划问题转换为STRIPS规划问题,再用STRIPS规划的求解方法求解问题。Furelos-Blanco和Jonsson[18]设计的CP4TP就是采用此求解方法的规划器。CP4TP在2018年的国际规划竞赛的时态赛道上大放异彩,夺得了亚军。
2.5 可满足性问题求解可满足性SAT(Satisfiability)问题是计算机领域中的一个重要问题。将时态规划问题形式化成SAT问题,再用求解SAT问题的方法进行求解,这也是求解时态规划的一种方法。Rankoo M和Ghassem-Sani G[19]设计了基于SAT的时态规划器ITSAT (An Effiffifficient SAT-Based Temporal Planner)。在Rankoo和Ghassem-Sani介绍ITSAT的文献中,事件event是一个三元组(pre(e),add(e),del(e))。时态动作a是一个四元组(start(a),end(a),inv(a),dur(a)),其中inv(a)是一组表示不变量a的原子命题。时态状态s是一个二元组(state(s),agenda(s))。时态问题P则是包含了初始状态I、目标状态G和时态动作A的三元组(I,G,A)。而P的有效规划解是一个事件序列π=<e1,···,en>,其中任意一个事件ei是A中某个动作a的开始事件或者结束事件,并且要求π兼容于I,以及G⊆state(succ(s,π)),agenda(succ(s,π))=
约束可满足问题(Constraint Satisfaction Problem,CSP):对于一个变量集合,当每个变量的取值能满足所有关于变量的约束时,问题就得到了解决,这类问题就称为约束可满足问题CSP。一个约束可满足问题CSP由一个变量集合X={x1,x2,···,xn},变量的取值D={D1,D2,···,Dn}以及约束集合C={c1,c2,···,cn}组成。求解CSP问题在于找到一个满足所有约束的对所有变量的赋值。
许多问题都可以自然地形式化为CSP问题,时态规划问题也不例外。CSP问题的求解可以快速消减庞大的搜索空间,许多使用状态空间搜索难以解决的棘手问题,形式化为约束可满足问题后往往能被轻松求解。
伍丽华[20]提出了时态规划中基于CSP技术的时态约束方法。刘越畅[21]在CBI模型下,将时态规划问题形式化为CSP,设计了时态规划算法LP-TPOP。
2.7 基于时间轴的规划基于时间轴的规划( Timeline-based Planning,TP)是在空间任务规划和调度背景下发展起来的方法。其领域由若干个独立但相互作用的组件组成。这些组件由一组状态变量标识。动作随时间的推移而变化,受一组时态约束的控制。与传统的时态规划(以PDDL等基于动作的语言建模的规划)不同的是,TP采用了一种更具声明性的范式,更倾向于关注动作序列为了达到目标而必须满足的约束。
Gigante[22]验证了将传统时态规划问题编码转换为基于时间轴规划问题的求解方案的有效性,并且详细介绍了TP的表达形式和计算特性,为基于时间轴的规划方法提供了详尽的理论理解。
2.8 基于深度学习的智能规划深度学习无疑是当前人工智能领域最热门的一项技术。能否将深度学习用在智能规划领域是值得智能规划研究者探讨的问题。2019年,Liyun B、Xuemin、Sheng等[23]提出了一种基于深层级联神经网络的模型并应用于自动驾驶汽车的运动规划中。2020年6月,Toyer、Trevizan、Thiébaux、Sylvie等[24]提出了面向通用规划的深度学习——动作模式网络,这是将深度学习和智能规划联系起来的首批尝试。文献[24]利用动作模式网络(Action Schema Network, ASNets)对智能规划领域中的概率并行规划和经典规划问题进行学习,可提高规划求解效率。遗憾的是,文中并未涉及对时态领域的处理。但这也足以表明将深度学习技术用于处理时态规划问题具有极大的潜力。
3 主流时态规划器 3.1 YAHSP3和YAHSP3-MTYAHSP3是一种前向的状态空间启发式搜索规划器,它嵌入了基于对松弛计划分析的前瞻性策略。YAHSP3采用了基于Landmark的meta最佳优先搜索算法。YAHSP3-MT是YAHSP3的多线程版本。在2014年的国际规划竞赛中,YAHSP3-MT大放异彩,在10个领域中得到了86.5分,获得第1名。而在求解问题数量上,YAHSP3一共求解了103个问题排第一。而YAHSP3-MT一共求解了97个问题,排名第二。
3.2 TFD(Temporal Fast Downward)TFD是针对时间和数值使用上下文增强的加法启发式引导搜索的时态规划器。TFD采用了Fast Downward架构。TFD将PDDL格式的领域问题转换成时间数值SAS+形式,再对SAS+形式的时间数值进行预处理后再使用上下文增强的加法启发式进行最佳优先搜索求解。在2014年的国际规划竞赛中,TFD表现出色,以79.2分排名第2名,仅次于YAHSP3-MT。
3.3 TFLAPTFLAP是遵循经典的部分序因果链接范式原则的前向链接时态规划器。TFLAP首先将描述领域问题的PDDL格式文件进行解析和预处理,然后将解析、预处理过的文件转换为SAS+形式,最后在前向的部分序规划框架中嵌入启发式方法进行规划求解。在2018年的国际规划竞赛中,TFLAP取得了43.13分的成绩,获得了第3名。
3.4 CP4TPCP4TP (A Classical Planning for Temporal Planning Portfolio)是一个组合时态规划器。时态问题按照并发形式的不同可以分为难度递增的不同类型是作者设计CP4TP的灵感。CP4TP依次运行不同的规划算法直到找到解决方案为止。CP4TP由SEQ、TPSHE、TP、STP共4种规划器组成。SEQ负责求解顺序时态问题,TPSHE负责求解Single Hard Envelope问题,其他并发形式的问题则由TP和STP求解。所有组成的时态规划器都依赖于将时态规划编译成经典规划。CP4TP在2018年的国际规划竞赛中表现出色,拿到43.72分,获得了第2名。
3.5 TemPoRalTemPoRal是一个组合时态规划器。它将可用时间静态均等地分配给组合中的每个规划器。TemPoRal组合了ITSAT、TFD、YAHSP2、YAHSP3-MT一共4个时态规划器。其中的YAHSP3-MT和TFD是2014年国际规划竞赛时态领域的冠亚军。不出所料,在2018年的国际规划竞赛中,TemPoRal以65.8分的成绩轻松斩获冠军。
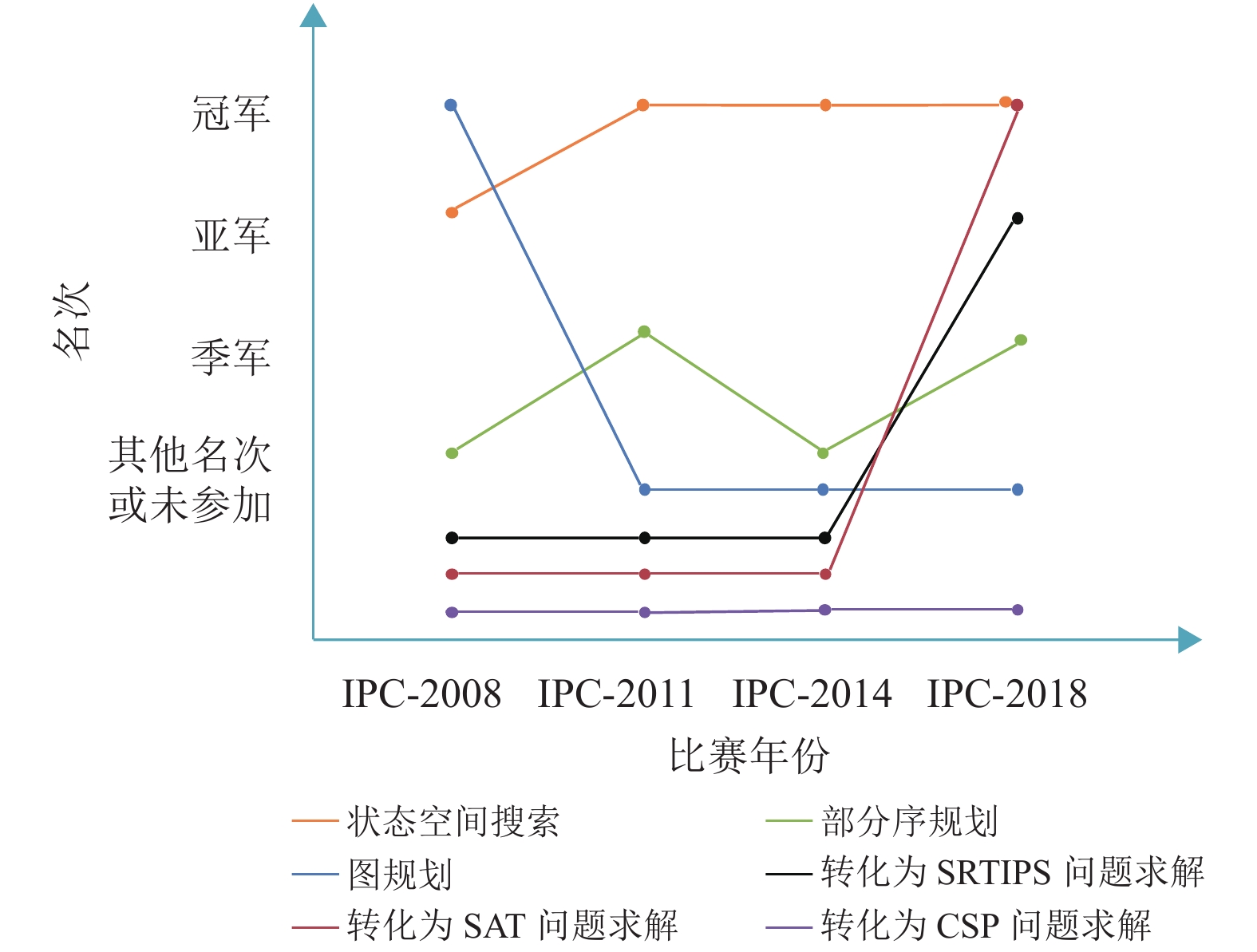
图1展示了采用各种求解方法的时态规划器在最近四届国际规划竞赛中的表现情况。容易看出,求解时态规划问题的主流方法是状态空间搜索、部分序规划、图规划以及转化为STRIPS问题求解。其中,以状态空间搜索为求解方法的时态规划器取得的成绩最为优异。这表明加入启发式算法的状态空间搜索方法是求解时态规划问题最有效的手段。
|
图 1 各求解方法在国际规划竞赛表现情况图 Figure 1 Performance of each method in IPC |
一项技术产生的意义在于应用。在机器人、工业制造、物流运输等领域都可以见到时态规划技术的应用。国际规划竞赛时态赛道的Drivelog领域旨在利用时态规划技术求解物流运输问题。Floortile领域旨在利用时态规划技术让机器人完成在地板瓷砖上绘制图案的工作。Parking领域旨在利用时态规划技术对停车场进行管理。RTAM (Road Traffic Accident Management)领域旨在运用时态规划技术在发生事故时进行道路交通管理。Satellite领域旨在求解卫星观测调度问题,该领域是智能规划研究人员与美国宇航局艾姆斯研究中心的大卫史密斯和杰里米弗兰克斯共同商讨开发的结果。Storage领域旨在运用时态规划技术对起重机、火车的搬运贮藏工作进行调度。
Cooper、Maris等[25]对单调时态规划(Monotone Temporal Planning,MTP)进行深入研究,发现单调时态规划MTP在化学工业、制药和建筑行业都有巨大的应用前景。Nau[26]团队以他们对分层任务网络(Hierarchical Task Network,HTN)的研究为基础,开发了针对桥牌比赛的智能规划系统。Fernandez-Olivares、Perez[27]设计了一个基于HTN的时态规划方法和目标识别应用,为运输公司获取驾驶员的活动轨迹提供服务。
Fernandez-Olivares、Perez的应用首先从事件日志中生成一组以PDDL表示的时间观测值,以此作为HTN问题的初始状态的一部分。第2个步骤是将事件识别表示为时态HTN问题。第3个步骤是将HoS规则形式化为属性语法的产物。第4个步骤是将语法转换为一个时态HTN领域,目的是将事件日志的解析表示为HTN问题。最后,对该领域进行扩展,使其能够识别和标记事件日志中的事件,从而使事件日志易于解释。关于HTN时态规划,冯宇轩[28]在他的博士论文中作了详细的介绍。
2020年,Carreno、Pairet等[29]利用时态规划技术为异构多机器人系统生成支持多机器人执行任务的计划。Carreno、Pairet团队提出了一种新的分散异构机器人任务分配策略。他们从任务空间的分布、执行时间以及机器人的处理能力3个方面出发,在任务分配策略算法中对机器人的目标分配作出优化工作,以此来提高多机器人计划的质量。然后他们将任务分配策略算法与时态规划相结合,为多机器人系统生成计划。
2020年Kiam、Scala等[30]利用时态规划技术为高空伪卫星(High-Attitude Pseudo-Satellite,HAPS)无人机生成执行计划。HAPS是一种为替代具有固定轨道的卫星而生的,用于长时间监测地面活动的太阳能驱动无人机。Kiam、Scala等将HAPS的规划任务问题描述为用PDDL+表示的混合规划问题;并提出了一个结合了PDDL+智能规划器和自适应大领域搜索方法的框架,用于将规划器与启发式方法相结合。最后,用规划器生成出HAPS的执行计划,并利用现实模拟器验证了计划的可行性。
5 总结及展望时态规划是智能规划面向实际应用发展而来的产物。从隐式的时态规划,到显式的以TGP模型、CBI模型为基础的规划,再到以国际规划竞赛官方语言PDDL为基础的时态规划。规划描述语言支持的时态特征越来越丰富,所能表达的问题越来越切合现实应用。在时态规划的求解方法上,众研究者作出了诸多的探索,出现了图规划求解、部分序规划求解、转换为SAT问题求解、转换为CSP问题求解、转换为经典规划问题求解、状态空间搜索、基于时间轴的规划等方法。从历届国际规划竞赛的获奖情况来看,基于启发式的状态空间搜索是求解时态规划问题最主流最有效的方法。在应用方面,虽然在机器人控制、工业制造、物流运输、停车管理、卫星观测调度等领域都有时态规划技术的应用尝试,但大多还是在严格的假设下进行的领域建模,或是基于仿真软件的尝试,与真正的现实应用还有一定的差距。即便如此,时态规划技术研究至今已取得长足的发展,有着深厚的技术基础。近年更是有研究者将深度学习与智能规划联系起来。相信在众多爱好者的努力下,时态规划必将成为人工智能领域中的一项核心技术。
| [1] |
FIKE R E, NILSSON J N. STRIPS: a new approach to the application of theorem proving to problem solving[J].
Artificial Intelligence, 1971, 2(3-4): 189-208.
DOI: 10.1016/0004-3702(71)90010-5. |
| [2] |
PEDNAULT E. ADL: exploring the middle ground between STRIPS and the situation calculus[C]//Proceeding of the First International Conference on Principles of Knowledge Representation and Reasoning. San Francisco: Morgan Kaufmann Publishers Inc, 1989: 324-332.
|
| [3] |
SMITH D, WELD D S. Temporal planning with Mutual exclusion reasoning[C]//Proceeding of the Sixteenth International Joint Conference on Artificial Intelligence. San Francisco: Morgan Kaufmann Publishers Inc, 1999: 326-337.
|
| [4] |
DO M, KAMBHAMPATI S. SAPA: a multi-objective metric temporal planner[J].
Journal of Artificial Intelligence Research, 2003, 20(20): 155-194.
|
| [5] |
FOX M, LONG D. Fast temporal planning in a Graph plan framework. [C]//Proceedings of AIPS-02 Workshop on Planning for Temporal Domains. Palo Alto, CA: AAAI Press, 2002: 9-17.
|
| [6] |
SMITH D E, FRANK J, JONSSON A, et al. Bridging the gap between planning and scheduling[J].
Knowledge Engineering Review, 2000, 15(1): 47-83.
DOI: 10.1017/S0269888900001089. |
| [7] |
FOX M, LONG D. PDDL2.1: an extension to PDDL for expressing temporal planning domains[J].
Journal of Artificial Intelligence Research, 2003, 20: 61-124.
DOI: 10.1613/jair.1129. |
| [8] |
EDELKAMP S, HOFFMANN J. PDDL2.2: The language for the classical part of the fourth international planning competition[R]. Palo Alto, CA: AAAI Press, 2004.
|
| [9] |
饶东宁, 蒋志华, 姜云飞. 规划领域定义语言的演进综述[J].
计算机工程与应用, 2010, 46(22): 23-25.
RAO D N, JIANG Z H, JIANG Y F. Review on evolution of planning domains definition language[J]. Computer Engineering and Applications, 2010, 46(22): 23-25. DOI: 10.3778/j.issn.1002-8331.2010.22.008. |
| [10] |
GEREVINI A, LONG D. Plan constraints and Preferences in PDDL3: the language of the fifth international planning[R]. Italy: University of Brescia, 2005.
|
| [11] |
FOX M, LONG D. PDDL+level5: an extension to PDDL2.1 for modeling planning domains with Continuous time-dependent effects[C]//Proceedings of the Third International NASA Workshop on Planning and Scheduling for Space. Palo Alto, CA: AAAI Press, 2003: 1-48.
|
| [12] |
EYERICH P, MATTMULLER R, ROGER G. Using the context enhanced additive heuristic for temporal and numeric planning[C]//Proceedings of the Nineteenth International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2009: 130-137.
|
| [13] |
VIDAL V. The YAHSP planning system: forward heuristic search with lookahead plans analysis[C]//Proceedings of the Fourth International Planning Competition. Palo Alto, CA: AAAI Press, 2004: 56-58.
|
| [14] |
SCHWARTZ P, POLLACK M E. Planning with Disjunctive temporal constraints[C]//Proceedings of ICAPS-'04 Workshop on Integrating Planning into Scheduling. PaloAlto, CA: AAAI Press, 2004: 67-74.
|
| [15] |
SAPENO O, MARZAL E, ONAINDIA E. TFLAP: a Temporal forward partial-order planner[EB/OL]. (2018-06-29)[2020-11-17]. https://ipc2018.bitbucket.io/#temporal
|
| [16] |
柴啸龙, 姜云飞, 陈蔼祥. 基于规划图的蚁群规划算法[J].
计算机研究与发展, 2009, 46(9): 1471-1479.
CHAI X L, JIANG Y F, CHEN A X. Ant colony planning algorithm based on planning graph[J]. Journal of Computer Research and Development, 2009, 46(9): 1471-1479. |
| [17] |
伍丽华, 姜云飞, 陈蔼祥. 规划图框架下用遗传算法求解时态规划问题[J].
计算机研究与发展, 2008, 45(6): 981-990.
WU L H, JIANG Y F, CHEN A X. Using genetic algorithm to solve temporal planning problems under the framework of the planning graph[J]. Journal of Computer Research and Development, 2008, 45(6): 981-990. |
| [18] |
FURELOS-BALANCO D, JONSSON A. CP4TP: a Classical planning for temporal planning portfolio [EB/OL]. (2018-06-29)[2020-11-17]. https://ipc2018.bit-bucket.io/#temporal
|
| [19] |
RANKOOH M F, GHASSEM-SANI G. ITSAT: an efficient SAT-based temporal planner[J].
Journal of Artificial Intelligence Research, 2015, 53: 541-632.
DOI: 10.1613/jair.4697. |
| [20] |
伍丽华, 姜云飞, 陈蔼祥, 等. 时态规划中基于CSP技术的时态约束方法[J].
计算机学报, 2012, 35(8): 1759-1766.
WU L H, JIANG Y F, CHEN A X, et al. ACSP-based approach for temporal constraints in temporal planning[J]. Chinese Journal of Computer, 2012, 35(8): 1759-1766. DOI: 10.3724/SP.J.1016.2012.01759. |
| [21] |
刘越畅. 基于动态约束满足框架的强表达时态规划算法[J].
计算机科学, 2012, 39(6): 226-230.
LIU Y C. Expressive temporal planning algorithm under dynamic constraint satisfaction framework[J]. Computer Science, 2012, 39(6): 226-230. DOI: 10.3969/j.issn.1002-137X.2012.06.056. |
| [22] |
GIGANTE N. Timeline-based planning: expressiveness and complexity[D]. Udine: University of Udine, 2019.
|
| [23] |
白丽赟, 胡学敏, 宋昇, 等. 基于深度级联神经网络的自动驾驶运动规划模型[J].
计算机应用, 2019, 39(10): 2870-2875.
BAI L Y, HU X M, SONG S, et al. Motion planning model based on deep cascaded neural network for autonomous driving[J]. Journal of Computer Applications, 2019, 39(10): 2870-2875. |
| [24] |
TOYER S, TREVIZAN F, THIEBAUX, SYLVIE, et al. ASNets: deep learning for generalised planning[J].
Journal of Artificial Intelligence Research, 2020, 68: 1-68.
DOI: 10.1613/jair.1.11633. |
| [25] |
COOPER M C, MARIS F, REGNIER P. Monotone temporal planning: tractability, extension and applications[J].
Journal of Artificial Intelligence Research, 2014, 50: 447-485.
DOI: 10.1613/jair.4358. |
| [26] |
SMITH S J J, NAU D S, THROOP T A. Computer bridge: a big win for AI planning[J].
AI Magazine, 1998, 19(2): 93-106.
|
| [27] |
FERNANDEZ-OLIVARES J, PEREZ R. Driver activity recognition by means of temporal HTN planning[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2020: 375-383.
|
| [28] |
冯宇轩. 时间相关的分层任务网络规划[D]. 长春: 吉林大学, 2016.
|
| [29] |
CARRENO Y, PAIRET È, PETILLOT Y, et al. A decentralised strategy for heterogeneous AUV missions via goal distribution and temporal planning[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2020: 431-439.
|
| [30] |
KIAM J J, SCALA E, JAVEGA M R, et al. An AI-based planning framework for HAPS in a time-varying environment[C]//Proceedings of the International Conference on Automated Planning and Scheduling. Palo Alto, CA: AAAI Press, 2020: 412-420.
|
 2021, Vol. 38
2021, Vol. 38

