区块链技术是一种去中心化的新型分布式数据存储技术^[1]，基于共识机制可以使得大量互不认识的节点达成共识^[2]。其具有去中心化、透明、不可篡改、共识信任、跨平台等特性^[3]，在电子货币、供应链物流、知识产权保护等领域已有广泛的应用^[4]。据预测，到2025年，全球10%的GDP可能存储在区块链或区块链相关的技术上^[5]。

然而随着量子计算技术的发展^[6]，区块链技术面临着量子计算机产生的两大威胁^[7]：其一，量子Grover搜索算法^[8]可以使得哈希算法被成功碰撞攻击的概率增加^[9]，由于哈希算法被用于区块链的挖矿流程以及前后区块的关联中，在量子计算时代，会导致现行区块链出现算力不平衡与伪造区块的问题；其二，区块链技术在身份验证中使用了椭圆曲线数字签名(Elliptic Curve Digital Signature Algorithm，ECDSA)和RSA数字签名等算法，这些基于数学计算单向困难性的数字签名算法在面临量子Shor算法^[10]及其变种算法的指数级加速优势下^[11]，也呈现出脆弱性^[12]，导致区块链技术面临着身份伪造的风险^[13]。尽管目前已有一系列抗量子攻击区块链被提出，但这些抗量子攻击区块链要么缺乏坚实的理论安全性证明^[14-17]，要么只是抽象理论的数学概念原型，距离实用化还有相当长的距离。

本文提出的基于委托权益证明(Delegated Proof of Stake，DPoS)扩展的量子加密区块链，是对Kiktenko等^[18-19]所提的量子安全区块链进行的改进，其基于委托权益证明技术，使得所需建设的量子密钥分发(Quantum Key Distribution，QKD)信道数量从 $ O({n}^{2}) $ 降低到 $ O\left(n\right) $ ，并且使得在共识机制中，拜占庭容错协议所需进行的通信轮数上限由 $ n/3+1 $ 降低为 $ k/3+1 $ 。尽管可容纳的错误节点数量上限进行了一定程度的牺牲，但在保证超级节点质量的条件下，本文所提的基于DPoS扩展的量子加密区块链在建设成本、运行效率和经济价值上都具有相当高的实用性。

1 相关工作

对于区块链技术在量子计算时代所暴露出的脆弱性，先后有学者提出了不同思路的抗量子攻击区块链。

1.1 基于后量子密码学的抗量子攻击区块链

后量子密码学为密码学一个新兴的分支，它基于一套能够抵抗量子攻击的算法，主要包括基于编码的加密、基于哈希的加密和基于格的密码等。其中格密码是被研究最多的后量子密码算法，格密码与区块链的结合也是非常具有应用前景的研究方向，已有研究者^[20-22]对格密码与区块链技术的结合做了相当深入的研究。在比特币社区也已经达成一种共识，即：使用一个或多个后量子密码来替代椭圆曲线密码(Elliptic Curve Cryptography，ECC)作为交易的数字签名。

1.2 基于时间纠缠的量子区块链

Del Rajan等^[23]于2018年提出了时间纠缠量子区块链的概念。把经典区块中的记录数据简化为只有2位的字符串，然后将每个区块用临时贝尔态进行编码。再通过融合过程使得临时贝尔态不断迭代映射到一个增长的临时GHZ(Greenberger-Horne-Zeilinger)态。这种前后量子态的关联模拟了区块链中前后区块的关联。

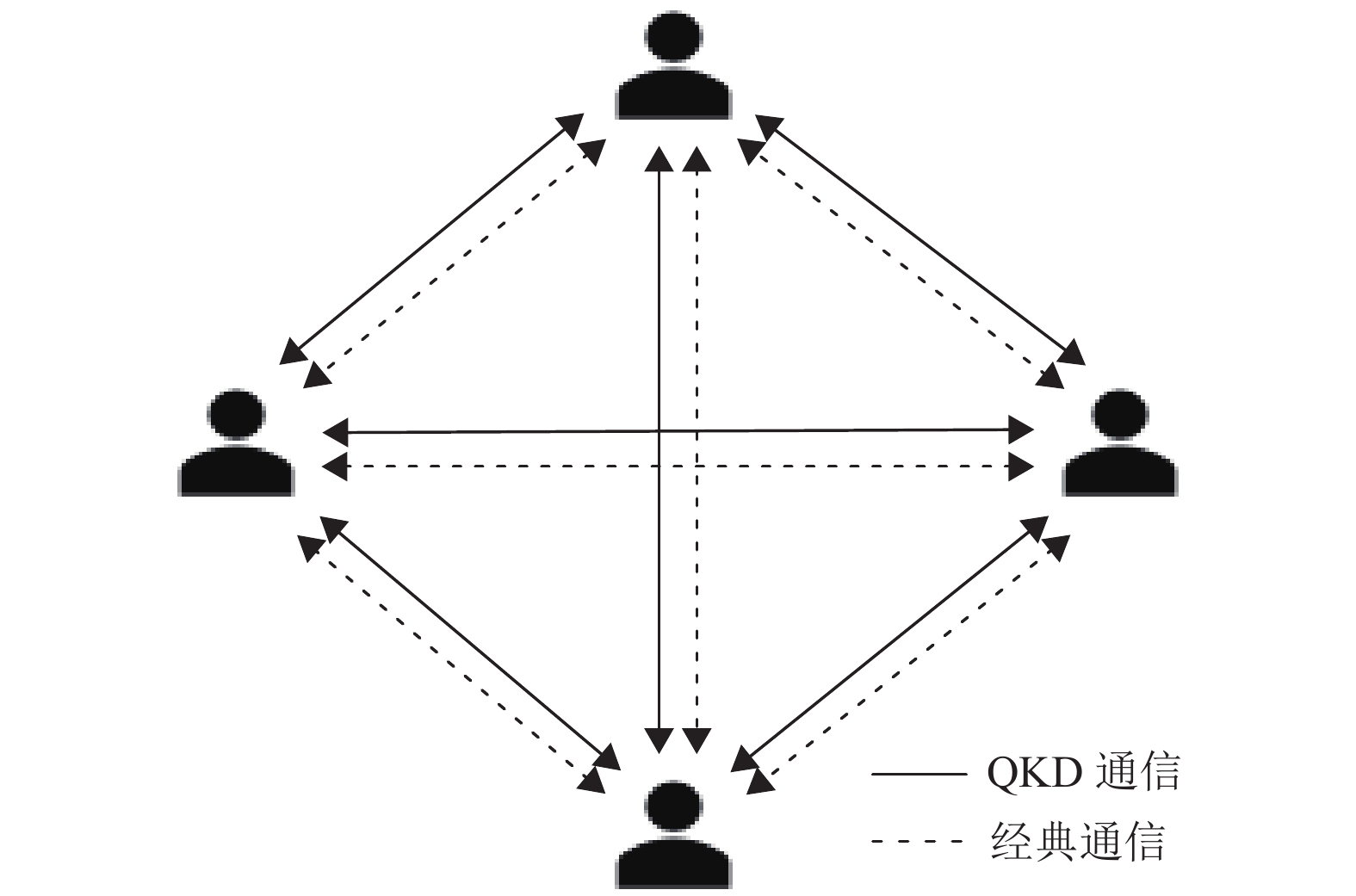
1.3 基于QKD的量子安全区块链

E.O. Kiktenko等^[18]在2017年提出了使用QKD进行签名验证的量子安全区块链。其主要包含了两层网络：第一层是任意两个节点间都可进行保密通信的QKD网络^[19]，主要用于在任意两个节点间共享密钥；第二层为经典网络，用于在第一层QKD网络形成的密钥打上签名标签后，作为交易信息传输。如图1所示，任意两个节点都必须同时建立QKD和经典通信连接。

不同于一般区块链采用的工作量证明(Proof of Work，PoW)或权益证明(Proof of Stake，PoS)的单个节点出块的共识机制，Kiktenko等^[24]建议以分散的方式创建区块，并采用了拜占庭容错重复算法，该算法能在不可信节点少于 $ n/3 $ 的情况下，在成对可信通讯的网络中达成拜占庭共识。用这种算法实现区块链中的广播协议，在某个时间点(例如，每10 min)，网络将协议应用于每一次未确认的交易，就该交易的正确版本达成共识(从而消除了重复支出)，并确定该交易是否可接受。然后，每个节点将所有可接受的事务组成一个块，并根据它们的时间戳进行排序，再将该块添加到数据库中。这样，所有可靠的节点都将形成同一个区块，从而消除了不同矿工同时创建多个不同版本的可能性。这样的区块链设置对某些节点或信道在实施过程中无法正常运行具有显著的容错性。虽然广播协议的数据量相对较大，但数据不必通过量子信道传输，只需要通过量子信道来生成私钥。

数据库在存储时也可能受到恶意伪造的攻击，但攻击者需要同时入侵至少 $ 1/3 $ 的节点才能改变共识，因此造成严重破坏的可能性极小。此外，伪造过去的某一条交易记录后，要对该块中的其他交易记录的变体执行Grover搜索，才能保持其哈希值不变，以使伪造的版本显得合法，但Grover算法相对于经典搜索算法仅提高了平方加速，因此Kiktenko等表示可将块哈希长度增加到其安全非量子值的平方来防止这种情况。

Kiktenko等已经在莫斯科进行了4个节点，6条边的网络的量子安全区块链的实验，完成了一系列的交易过程，并证明了其具有排除少量节点作恶或出错的拜占庭容错能力，其实现细节和参数可参阅文献[18]。

2 基于DPoS扩展的量子加密区块链

在上述一系列抗量子攻击区块链中，基于后量子密码的抗量子攻击区块链的安全性，依赖于目前没有量子算法能对这些后量子密码造成威胁，但后量子密码能抵抗量子攻击只是当前一种暂时的假设，并非是一个已被证明的事实。而且这些后量子密码往往设计过于复杂，实现比较麻烦，计算也相当繁琐。而基于即时纠缠的量子区块链只是抽象概念上的模型，其信息编码能力和实用价值相对比较有限。

基于QKD的量子安全区块链中所采用的QKD技术已经通过了实验的验证，并开始具有普及化的商业价值。Kiktenko等在莫斯科做的实验也验证了量子安全区块链的可行性。然而Kitenko等提出的量子安全区块链存在一个很大的问题，即扩展成本高昂。因为他们提出的量子安全区块链要求任意两个节点间都必须建立QKD通信连接，而QKD信道的建立与使用需制备与传输大量的量子比特。假设有 $ n $ 个节点，那么需要建立的QKD信道就有 ${C}_{n}^{2}=n(n-1)/ 2=O({n}^{2})$ 条。即使只有1万个节点，需要建立的QKD信道也已高达千万条。同时考虑到每条信道都需要制备与传输足够形成可用密钥数量的量子比特串，从而导致新节点的加入门槛过高，限制了整个网络的扩展能力。综上原因，Kiktenko等提出的量子安全区块链只能应用于实验室与极少数场景中。

2.1 协议框架

针对以上分析的问题，本文提出用委托权益证明DPoS对Kiktenko等提出的量子安全区块链进行扩展和改进，协议框架如下：

步骤1：每隔一段时间或一定数量的区块，全网节点根据所持有区块链权益的比例进行投票，选举出 $ k $ 个超级节点，要求 $ k<n $ ，其中 $ n $ 为全网总节点数。

步骤2：每个节点只需与超级节点建立安全的QKD通信连接，普通节点与普通节点之间只需建立普通信道，无需建立QKD信道。

步骤3：意图发布交易的节点通过QKD信道同每个超级节点生成安全密钥。

步骤4：意图发布交易的节点使用第3步中生成的安全密钥，采用信息理论安全的验证算法对交易信息打上所有验证标签，如Kiktenko等原文及实验中所采用的Toeplitz哈希算法。

步骤5：意图发布交易的节点将打上验证标签的交易信息发送出去，同比特币类似，交易信息中包含发送方、接收方、时间戳、转账数目、显示发送方账户具有足够余额的证明等信息。

步骤6：每个超级节点收到交易信息后，对交易信息进行验证，将不合法的交易抛弃。

步骤7：每个超级节点将当前时间窗口内的合法交易按时间戳进行排序，生成区块。

步骤8：所有超级节点之间使用拜占庭容错算法^[24]达成共识，只要出错节点或恶意节点不超过k/3，就能达成共识，完成最终区块的出块过程。

步骤9：超级节点将最终区块广播出去。

步骤10：普通节点收到最终区块后，将其加入到上一个区块之后，接着进入下一轮出块流程。

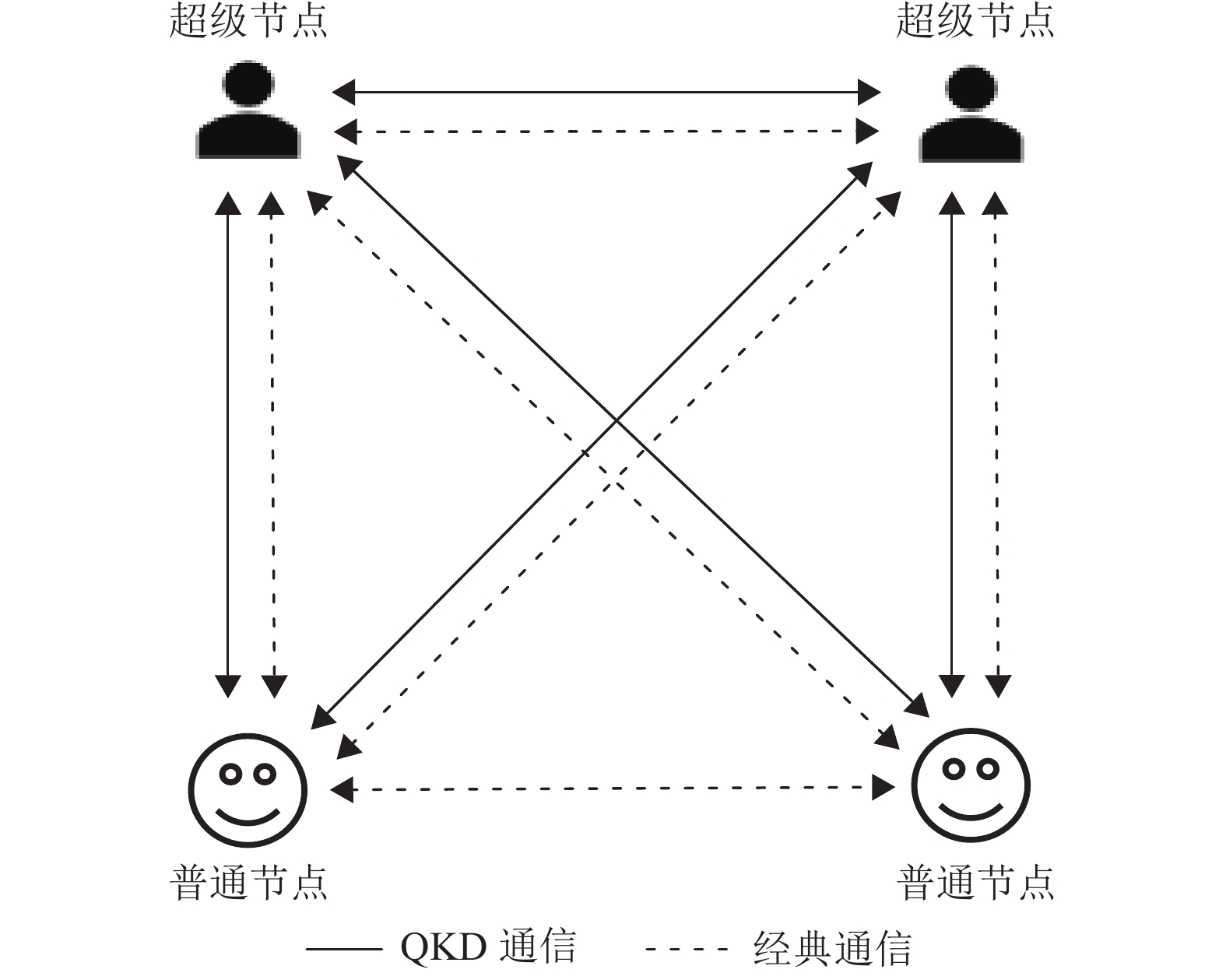
如图2所示，每个节点只需与超级节点建立QKD通信，普通节点与普通节点间只需建立经典通信。

2.2 安全性与可行性分析

(1) QKD已被证明理论上具有无条件安全性，不存在被数学算法攻破的可能，当然也具有抗量子算法攻击的特性。

(2) 由于所有超级节点共同出块，杜绝了单个节点出块可能伪造交易，篡改区块以及交易发起方抵赖交易的可能。

(3) 采用DPoS，无挖矿过程，也就不存在因量子Grover搜索算法可能导致算力不平衡所产生的51%攻击风险。

(4) 具有一定拜占庭容错能力，当不诚实超级节点数不超过 $ k/3 $ 时，都能在超级节点中达成拜占庭共识，完成最终区块的出块过程。

(5) 采用DPoS，不需要所有节点都建立点对点的QKD通信，每个节点只需与选举出的超级节点建立QKD通信即可。这可以将需要建立的QKD信道从平方项数量级降低到了线性数量级，大大降低了量子加密区块链建立QKD信道的成本，提升了其扩展性，使其具有更普及化的实用价值。

(6) 由于所有超级节点共同出块，因此攻击者必须同时攻击至少 $ k/3 $ 个超级节点才能影响共识。同时由于超级节点在每一轮选举可能不同，攻击者攻击成功的难度也会随之增加。

(7) 由于量子Grover算法对传统搜索算法的提升只是二次项数量级，因此通过增加哈希函数输出值的位数，就能够比较有效地抵抗量子Grover搜索算法带来的攻击。例如：如果想达到经典256位哈希的安全性，那么提升到512位哈希，量子Grover搜索算法需要迭代尝试的次数大约为 $ \sqrt{\left({2}^{512}\right)}={2}^{256} $ ，与经典256位哈希难度大致相同。

(8) 采用拜占庭容错算法，所有超级节点都将时间窗口内的交易按时间戳排序生产区块，因此所有诚实可靠的超级节点都会形成一致的区块，这就杜绝了竞争出块可能导致的分叉问题。

3 理论推导与分析

在Kiktenko所提的原始量子安全区块链中，任意两个节点间都需要建立QKD信道，假设整个网络的节点数量为 $ n $ ，显然该QKD网络建立信道的空间复杂度为 $ O({n}^{2}) $ 。

而在本文提出的基于DPoS扩展的量子加密区块链中，所选取的超级节点数量 $ k $ 是一个规定的小于总体网络节点数量 $ n $ 的常数，普通节点数量为 $ n-k $ ，普通节点需要与每个超级节点建立QKD通信，其QKD信道数量为 $ k\left(n-k\right) $ ；而超级节点与超级节点之间需要两两建立QKD通信，其QKD信道数量为 $ k(k-1)/2 $ 。因此本文架构所需建设的QKD信道数量总和为 $ k\left(n-k\right)+k(k-1)/2 $ ，由于 $ k $ 为一个规定的小于 $ n $ 的常数，因此本文基于DPoS扩展的量子加密区块链需建立的QKD信道数量的空间复杂度为 $O(k(n- k)+k(k-1)/2)=O(k(n-k))=O(k(n))= O(n)$ 。

此外，本文同Kiktenko所提的量子安全区块链一样，采用拜占庭容错算法来保证全体网络对所生成的区块内容达成共识。该拜占庭容错算法主要包含两轮步骤：第一轮步骤，所有节点向其他节点广播自己的交易信息；第二轮步骤，所有子程序中的每个节点将其在上一轮接收到的交易信息广播至其他节点。在文献[24]中，Lamport Shostak与Pease证明了在不超过 $ m+1 $ 轮通信后( $ m<n/3 $ )，全体网络会共同认可一个交互一致性的向量，即达成共识。在原始的量子安全区块链中，所有节点都需参与共识机制的通信，需要的通信轮数的上限为 $ n/3+1 $ ，即达成共识的时间复杂度为 $ O(n/3+1)=O\left(n\right) $ 。而在本文改进的基于DPoS扩展的量子加密区块链中，只需要 $ k $ 个超级节点进行拜占庭容错算法，需要的通信轮数上限为 $ k/3+1 $ ，由于 $ k $ 是一个已规定的小于 $ n $ 的常数，因此达成共识的时间复杂度为 $ O(k/3+1)=O(k/3)=O\left(k\right)= O\left(1\right) $ 。

Kiktenko的原始量子安全区块链与本文改进的基于DPoS扩展的量子加密区块链的具体性能对比如表1所示。

由表1可看出，本文方案在QKD信道数量的空间复杂度与广播共识协议通信轮数的时间复杂度方面，较Kiktenko的原始量子安全区块链具有显著优势。但在可容纳的错误节点数量上限方面存在劣势，在提升了方案效率性能的同时，不可避免地产生了安全性能的些许降低。在实际应用场景中可根据具体情况对超级节点的数量进行调节，以实现对效率性能与安全性能的权衡与调节。

4 结论

本文针对Kiktenko等提出的基于QKD的量子安全区块链，因其任意两个节点间都需建立QKD通信，从而导致扩展成本高、难以推广普及的问题，提出了基于DPoS扩展的量子加密区块链。通过选举小于全网总节点个数的超级节点，每个节点只需与超级节点建立安全的QKD通信连接，普通节点与普通节点之间只需建立普通信道，无需建立QKD信道。从而使需要建立的QKD信道数量由 $ O({n}^{2}) $ 降低到了 $ O\left(n\right) $ ，所需进行的通信轮数上限由 $ n/3+1 $ 降低为 $ k/3+1 $ ，使得量子加密区块链的建设成本显著降低，也提升了其运行效率与拓展能力，更进一步地推动了区块链同量子领域的结合发展。

从安全性和可行性分析上来看，本文提出的基于DPoS扩展的量子加密区块链能有效地通过区块链和量子计算技术加以实现并得到优于原方法的数据结果，但区块链与量子计算技术的融合发展当前仍处于相对初步的阶段，本文的改进方法目前也处于初步的研究阶段。虽然目前有关区块链领域、行业管理等工作也在有序推进，区块链技术在金融领域的落地场景和实践案例比较丰富^[25]，但在量子等其他领域的适用场景，通常比较大型且商业化，成本较高，实践案例也较少。目前来说，开展这个实验研究的条件有限，相关的实验应用探索有待深入研究。