高等教育的普及程度不断加大,教育部数据显示,2020年全国高考报名人数1017万,录取率有望达到85%。随着高等教育的普及,优质的教育资源就会供不应求。为了适应教育发展的新需要,近年来教育部陆续出台了一系列的高考改革政策。高考改革带来的是机遇还是挑战,改革会给学生带来怎样的影响,改革是否真的有利于学生的发展,只有科学地回答了这样的问题,改革才能稳步推进。学者们分别从培养理念[1],学生对未来学业的适应[2],教育资源配置[3]等角度对此进行了分析。本文通过调查问卷的形式,从学生自身发展的角度选取评价指标,建立适当的关联函数,将高考改革视为一个可拓变换,计算变换前后的关联度,进而定量分析出改革对学生考前和未来成长发展等方面均有正向促进作用,高考改革利大于弊。
对于研究生入学招生工作,学者们分别从招生信息化[4],招生的管理措施[5],招生计划分配和优化[6]等角度提出了研究生招生工作中的策略。据教育部数据统计,2020年考研报考人数达到了341万,实际录取人数111.4万,录取率32.7%。由于报考人数的大幅增长,导致大量的考生由于招生计划的限制,需要调剂到其他院校。本文根据教育部《2020年全国硕士研究生招生工作管理规定》,利用德尔菲法进行指标的选取,然后利用可拓层次分析法建立了招收调剂生的决策模型。以大连海事大学招收调剂生为例,探讨了研究生调剂择优录取的定量化评价和决策。
1 高考改革的可拓关联度分析 1.1 高考改革矛盾问题转化的条件是变换,变换是解决矛盾问题的核心、基本手段和方法[7]。因此解决原先的高考和教育环境所产生的矛盾问题,必然要涉及到变换——也就是高考改革。在2014年,国务院发布《关于深化考试招生制度改革的实施意见》以来,改革任务扎实推进。2017年,第一批高考综合改革试点在上海、浙江平稳落地,随后北京等地作为第二批改革的试点启动。2018年教育部先后确定了辽宁、福建等8个省市启动高考综合改革。改革主要涉及到以下几个方面。
(1) 入学考试制度的改革。
由于之前的考试制度存在一些问题,如:考试的科目分为文理两大类,在高考中将选择对应的“文综”或“理综”科目来进行考试,而“文综”和“理综”的科目是固定的,使学生的自主选择性降低且易出现偏科的现象,影响学生的全面发展。因此在新高考的改革中,实行文理不分科,即实行“3+1+2”的考试制度,“3”为统考科目语数外,不分文理使用全国卷,“1”为在物理和历史两门课程中必选的一门考试科目,以原始分计入总分,“2”为在政治、地理、化学、生物中任选两门课程,实行等级赋分制计入总分。
之前的高考“一考定终生”,导致许多平时成绩原本很好的学生,由于紧张焦虑等心理因素的影响,高考发挥失常,从而影响到升学。而现行新高考的改革,在部分省市实行外语有2次考试机会,取成绩较高者计入总成绩,部分省市选考的科目有2次考试机会,且均在高考前进行考试。
(2) 招生录取机制的改革。
新高考逐步取消批次的设定。部分省市将一本、二本批次合并为本科普通批。
新高考将基本参照“两依据,一参考”的原则录取,不再将分数作为唯一录取标准,不仅依据高考统考成绩,依据学生选考的科目等级赋分,还参考学生的综合素质测评等因素。
1.2 特征选择和物元模型从新高考改革内容可以看出改革的目的在于通过科目的自主选择、职业规划教育来强化高中阶段的素质教育,促进学生的全面发展。同时旨在通过多次考试、等级赋分等政策减轻学生的备考压力和心理负担。
通过以上分析,本文主要从以下5个方面考察高考改革前后对学生的影响,分别是自主选择性(c1),职业规划能力(c2),全面发展水平(c3),集中备考多科的负担(c4),备考的心理压力(c5)。以c1,c2,c3,c4和c5为特征建立关于学生的物元模型。
| ${{M}} = \left[ {\begin{array}{*{20}{c}} {O,}&{{c_1},}&{{v_1}} \\ {}&{{c_2},}&{{v_2}} \\ {}&{{c_3},}&{{v_3}} \\ {}&{{c_4},}&{{v_4}} \\ {}&{{c_5},}&{{v_5}} \end{array}} \right]$ |
根据教育学专家和心理学专家的认定,关于特征c1,c2,c3,c4和c5的正域X,满意区间(即标准正域)X0以及最优点x0如表1所示。
| 表 1 正域X,满意区间X0以及最优点x0 Table 1 Positive interval X, satisfactory interval X0 and the optimal value x0 |
向参加过2014年以前高考的10名考生发放网络调查问卷,收回5份有效问卷。通过考生的打分情况可以得到高考改革前关于5个特征指标的打分情况,如表2所示。
| 表 2 高考改革前特征值 Table 2 Values of indexes before reform |
在可拓学中,用关联函数[8-10]来刻画论域中的对象具有某种性质的程度,关联函数的取值范围为
| $ k( x ) = \left\{ \begin{aligned} & {\frac{{\rho ( {x,{x_0},X} )}}{{D( {x,{x_0},{X_0},X} )}},}\;\;\;{D( {x,{x_0},{X_0},X} ) \ne 0,x \in X}\\& { - \rho ( {x,{x_0},X} ) + 1,}\;\;{D( {x,{x_0},{X_0},X} ) = 0,x \in {X_0}}\\& {0,}\qquad\qquad\quad\;\;\;\;{D( {x,{x_0},{X_0},X} ) = 0,x \notin {X_0},x \in X}\\& {\frac{{\rho ( {x,{x_0},X} )}}{{D( {x,{x_0},X,\hat X} )}},}\;\;\;\;{D( {x,{x_0},X,\hat X} ) \ne 0,x \in R - X}\\& { - \rho ( {x,{x_0},\hat X} ) - 1,}\;\;{D( {x,{x_0},X,\hat X} ) = 0,x \in R - X} \end{aligned} \right.$ | (1) |
其中
根据固定点x0在区间中的位置不同,可分为左侧可拓距、中点可拓距和右侧可拓距,计算公式分别为
若
| ${\rho _l}(x,{x_0},X) = \left\{ \begin{aligned} & a - x,x \leqslant a \\& \frac{{b - {x_0}}}{{a - {x_0}}}(x - a),x \in \left\langle {a,{x_0}} \right\rangle \\& x - b,x \geqslant {x_0} \end{aligned}\right.$ |
若
| $ {\rho }_{l}(x,a,X)=\left\{ \begin{aligned} & a-x,x<a\\& a-b,x=a{\text{且}}a\in X\\& x-b,x>a \end{aligned}\right.$ |
若
| ${\rho _r}(x,{x_0},X) = \left\{ \begin{aligned} & a - x,x \leqslant {x_0} \\& \frac{{a - {x_0}}}{{b - {x_0}}}(b - x),x \in \left\langle {{x_0},b} \right\rangle \\& x - b,x \geqslant {x_0} \end{aligned} \right.$ |
若
| $ {\rho }_{r}(x,b,X)=\left\{ \begin{aligned} & a-x,x<b\\& a-b,x=b{\text{且}}b\in X\\& x-b,x>b \end{aligned}\right.$ |
同理可计算出可拓距
式(1)中,点x关于x0与X0和X组成的区间套的位值为
| $D(x,{x_0},{X_0},X) = \rho (x,{x_0},X) - \rho (x,{x_0},{X_0})$ |
点x关于x0与
| $D(x,{x_0},X,\hat X) = \rho (x,{x_0},\hat X) - \rho (x,{x_0},X)$ |
(1) 计算关联度。从表1可以看出,特征c1,c2,c3,c4和c5的最优点x0在区间X0的右端点或左端点。根据式(1),可以计算得到关联度(见表3)。
| 表 3 高考改革前的关联度 Table 3 The correlation degree before reform |
(2) 计算特征权重。利用层次分析法确定各特征的权重。首先,根据专家打分,得到两两比较判断矩阵(见表4),矩阵中的标度值释义见表5。
| 表 4 两两比较矩阵 Table 4 Pairwise comparison matrix |
| 表 5 标度值释义 Table 5 Interpretation of values |
利用matlab对表4的两两比较矩阵求最大特征向量,得出5个特征的权重(见表6)。
| 表 6 特征的权重 Table 6 Weights of characteristic indexes |
两两比较判断矩阵(表4)的最大特征值为
(3) 计算综合关联度。根据表3中的关联度和表6中各个特征的权重系数,利用式(2)计算综合关联度,结果见表7。
| $K = \sum\limits_{i = 1}^n {{\lambda _i}{k_i}} $ | (2) |
其中
| 表 7 高考改革前的综合关联度 Table 7 The comprehensive correlation degree before reform |
向对参加过2014年以后高考的5名考生发放网络调查问卷。通过考生的打分情况可以得到高考改革后关于5个特征指标的打分情况,如表8所示。
| 表 8 高考改革后的特征值 Table 8 Values of indexes after reform |
(1) 计算关联度。利用式(1)计算实行高考改革变换后特征的关联度,结果见表9。
| 表 9 改革变换后的关联度 Table 9 The correlation degree after reform |
(2) 计算综合关联度。根据表9中的关联度和表6中各特征的权重,利用式(2)计算高考改革后的综合关联度
| 表 10 高考改革后的综合关联度 Table 10 The comprehensive correlation degree after transform |
从表10可以看出,实施新高考改革后,学生的综合关联度差均为正值,说明改革对学生的发展起到了很好的促进效果。饱受争议的改革虽然在许多方面都发生了较大的变动,可能会使得学校的教学管理以及学生的备考计划做出相应的调整。面临的挑战肯定是存在的,但是改革确实会增强学生的自主选择性,全面发展以及职业规划,会有利于减轻学生的学习压力和心理负担,以及对社会人才的选拔均有积极的促进作用,高考改革机遇大于挑战,改革势在必行。
2 硕士调剂生录取的可拓决策在硕士研究生录取中,由于招生计划的限制,有些考生虽然达到分数线,但并不能被报考的学校录取,这些考生就要调剂到其他学校。在学校招收调剂生的过程中,需要综合各项因素和指标对备选考生进行考察,例如综合考生的专业知识、科研潜力、综合素质、英语水平能力、第一志愿院校等。在备选考生中,其各种能力往往不可能同时具备,经常会有诸如专业成绩高而英语成绩低这样的考生。如何在众多的各有所长各有所短的备选考生中择优录取,是一个复杂的矛盾问题。解决这类矛盾问题可以将矛盾问题分解为对指标和因素的量化评价问题[11]。
2.1 可拓层次分析法在层次分析法中,构造两两比较判断矩阵是由专家打分给出的。为了弱化专家打分的主观性,可以用区间[12]表示两两比较的相对重要程度,此时称为可拓层次分析法[13]。
可拓层次分析法的基本步骤如下:
(1) 根据实际问题,构建关于评价指标的递阶层次结构。
(2) 根据专家给出的区间数,构造相应的区间数判断矩阵。区间数判断矩阵定义为
(3) 计算综合判断矩阵和权重向量。将步骤(2)中的矩阵
| $ k = \sqrt {\sum\limits_{j = 1}^{{n_k}} {\frac{1}{{\displaystyle \sum\limits_{i = 1}^{{n_k}} {a_{ij}^ + } }}} } ,m = \sqrt {\sum\limits_{j = 1}^{{n_k}} {\frac{1}{{\displaystyle \sum\limits_{i = 1}^{{n_k}} {a_{ij}^ - } }}} } $ |
(4) 层次单排序。由步骤(3)可得第
| $V({{S}}_i^K \geqslant {{S}}_j^K) = \frac{{2({{S}}_i^{K + } - {{S}}_j^{K - })}}{{({{S}}_j^{K + } - {{S}}_j^{K - }) + ({{S}}_i^{K + } - {{S}}_i^{K - })}}$ |
计算出区间数
(5) 层次总排序。第
以大连海事大学2020年调剂生录取中对其中3名调剂生进行优选为例,阐述在调剂生录取中如何建立基于可拓层次分析法的决策模型。
2.2.1 德菲尔法选取指标和建立递阶层次结构根据教育部《2020年全国硕士研究生招生工作管理规定》招收硕士研究生的要求:要求掌握本学科坚实的理论基础和系统的专业知识,具有从事科学研究的能力等,因此选取“本科院校”“一志愿院校”“专业课成绩”和“考研总成绩”作为调剂生录取的参考指标。依据教育部办公厅《关于进一步规范和加强研究生培养管理的通知》,应当优化人才培养体系,加强研究生创新意识,因此,本文将“英语成绩”和“专业相关的竞赛奖项”也作为调剂生录取的参考指标。研究生作为高素质人才,他们将会面临或多或少的心理压力与焦虑,而心理状况堪忧将会影响到研究生的健康发展和国家人才培养的质量,因此“心理状况”也是调剂生录取的参考指标。
在初步选取的“本科院校”“一志愿院校”“专业课成绩”“考研总成绩”“英语成绩”“专业相关的竞赛奖项”和“心理状况”7个指标中,可能会存在对最终的评价目标影响很小的指标。本文利用德尔菲法筛选得出最终录取时的评价指标。德尔菲法[14-15],本质是一种反馈匿名函询法。基本过程为:针对所要预测的问题,征得专家意见后,进行归纳统计,整理出综合意见,再将综合意见匿名反馈给各专家,再次征询意见,各个专家根据综合意见来修改自己原有的意见,然后再整理汇总。反复执行多轮,直到取得基本一致的意见,具体操作流程如图1所示。
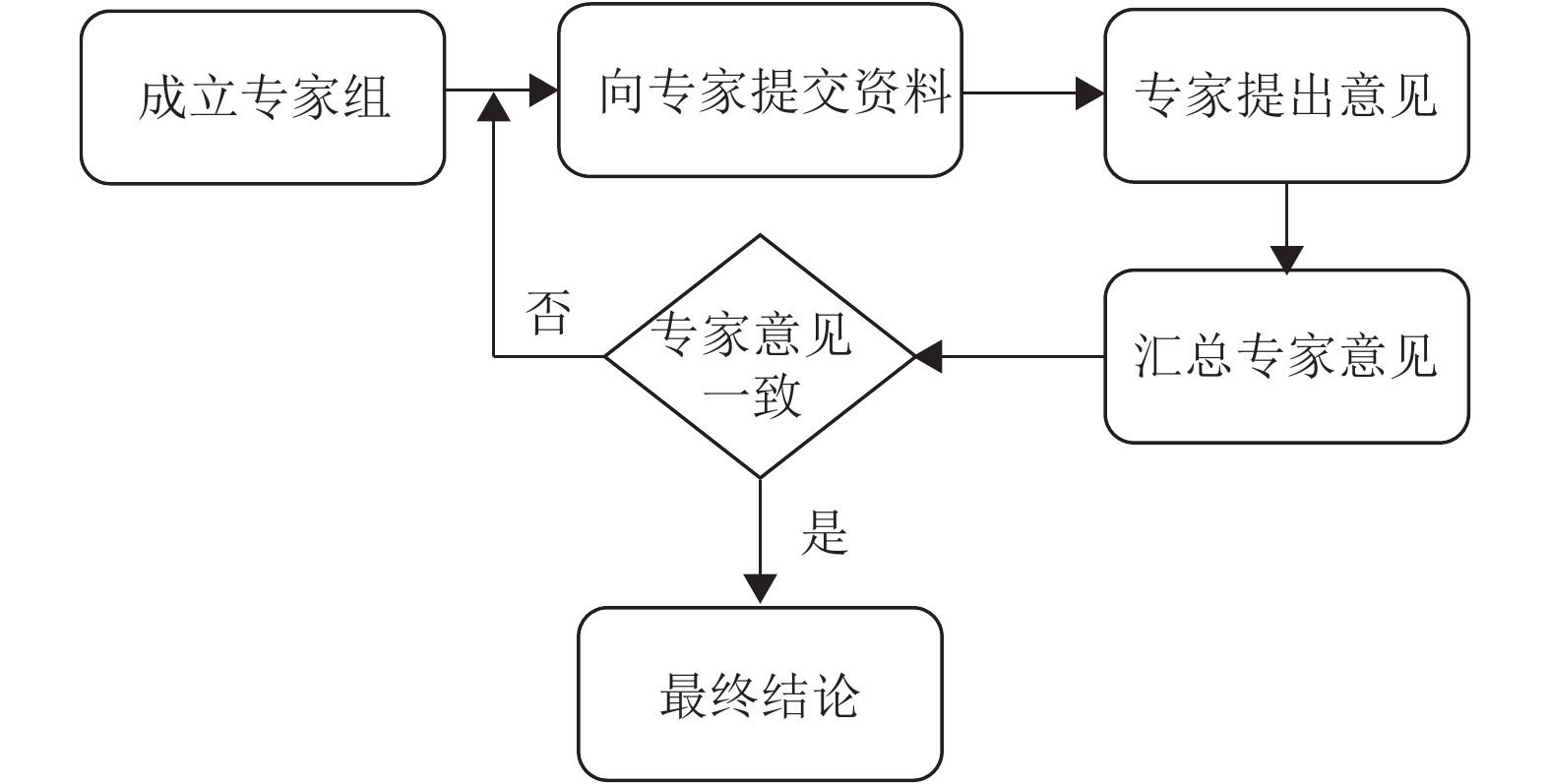
|
图 1 德尔菲流程图 Figure 1 Flow chart of Delphi method |
具体操作是:(1) 成立专家组。选择10名经验丰富的高校教师,5名研究生招生办教师组成专家组。(2) 向专家提交资料。向15名教师提交预选的7个评价指标及相关背景资料。以问卷的形式发放到教师手中,问卷内容为7个预设评价指标的重要性:很重要,比较重要,一般,不太重要,不重要。(3) 专家提出意见。专家完成问卷中各个预设指标的重要性选择,并给出选择的理由。(4) 汇总专家意见:回收问卷,统计7个指标每个选项的选择人数,若意见不一致,将整理后的意见连同选择理由再次发放至各教师。由教师参考整理后的意见再次修改自己的选择,多次反复,直至不再修改意见,此时各个指标的重要性意见基本一致。
对最终结果经过检验以及数据处理,对问卷选项赋予分值:很重要(5分),比较重要(4分),一般(3分),不太重要(2分),不重要(1分)。通过上述德尔菲法,可获得专家对调剂录取各个指标的分值,最终取所有专家意见的平均数即可得到各指标的重要性分值。总结意见,专家认为在总成绩和各科成绩通过国家录取分数线和录取名额的120%参加复试的前提下预设指标中“专业课成绩”和“考研总成绩”重要性不大,可将其忽略。调剂的考生的报考院校不同,专业课的难易程度不同,因此专业课的成绩与考研总成绩都不能完全说明考生学习成绩的优劣。
通过上述筛选,最终选取的指标为:本科院校(
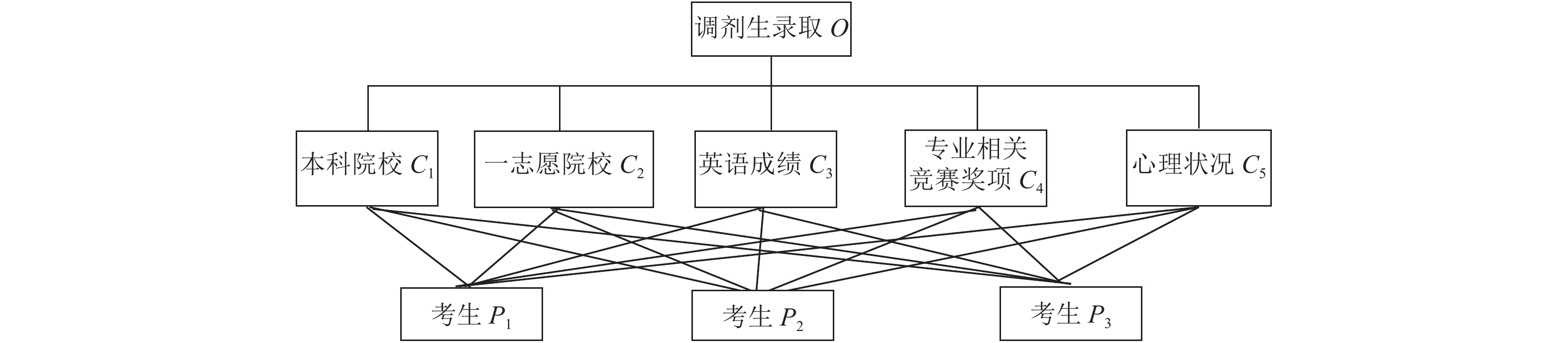
|
图 2 层次结构图 Figure 2 Hierarchy chart |
其中目标层是调剂生的录取决策,准则层是5个评价指标,方案层是3个候选调剂生。
2.2.2 区间数判断矩阵邀请我校研究生院负责招生的一位教师和一位研究生指导教师对准则层的5项指标,根据总目标调剂录取的要求,进行两两比较打分,得到评价准则的区间数判断矩阵A1和A2。
| $ {{{A}}_{{1}}} = \left[ {\begin{array}{*{20}{c}} {\langle 1.00,1.00\rangle }&{\langle 2.42,3.58\rangle }&{\langle 0.40,0.68\rangle }&{\langle 0.27,0.44\rangle }&{\langle 0.58,0.79\rangle } \\ {\langle 0.28,0.41\rangle }&{\langle 1.00,1.00\rangle }&{\langle 0.26,0.47\rangle }&{\langle 0.46,0.55\rangle }&{\langle 0.60,0.75\rangle } \\ {\langle 1.47,2.53\rangle }&{\langle 2.15,3.85\rangle }&{\langle 1.00,1.00\rangle }&{\langle 0.36,0.79\rangle }&{\langle 1.13,1.87\rangle } \\ {\langle 2.26,3.74\rangle }&{\langle 1.83,2.17\rangle }&{\langle 1.26,2.74\rangle }&{\langle 1.00,1.00\rangle }&{\langle 1.42,1.58\rangle } \\ {\langle 1.27,1.73\rangle }&{\langle 1.34,1.66\rangle }&{\langle 0.53,0.88\rangle }&{\langle 0.63,0.70\rangle }&{\langle 1.00,1.00\rangle } \end{array}} \right] $ |
| $ {{{A}}_{{2}}} = \left[ {\begin{array}{*{20}{c}} {\langle 1.00,1.00\rangle }&{\langle 2.42,3.58\rangle }&{\langle 0.36,0.79\rangle }&{\langle 0.27,0.44\rangle }&{\langle 0.46,0.55\rangle } \\ {\langle 0.28,0.41\rangle }&{\langle 1.00,1.00\rangle }&{\langle 0.26,0.47\rangle }&{\langle 0.46,0.55\rangle }&{\langle 0.65,0.68\rangle } \\ {\langle 1.26,2.74\rangle }&{\langle 2.15,3.85\rangle }&{\langle 1.00,1.00\rangle }&{\langle 0.36,0.79\rangle }&{\langle 1.13,1.87\rangle } \\ {\langle 2.26,3.74\rangle }&{\langle 1.83,2.17\rangle }&{\langle 1.26,2.74\rangle }&{\langle 1.00,1.00\rangle }&{\langle 1.36,1.64\rangle } \\ {\langle 1.83,2.17\rangle }&{\langle 1.46,1.54\rangle }&{\langle 0.53,0.88\rangle }&{\langle 0.61,0.74\rangle }&{\langle 1.00,1.00\rangle } \end{array}} \right] $ |
依据2.1节中可拓层次分析法步骤(3)~(5)中的算式,计算出准则层各评价指标对于目标层的相对重要性的综合权重向量。
| ${{{A}}^ - } = \left[ {\begin{array}{*{20}{c}} 1&{2.42}&{0.38}&{0.27}&{0.52} \\ {0.28}&1&{0.26}&{0.46}&{0.63} \\ {1.37}&{2.15}&1&{0.36}&{1.13} \\ {2.26}&{1.83}&{1.26}&1&{1.39} \\ {1.55}&{1.4}&{0.53}&{0.62}&1 \end{array}} \right]$ |
| ${{{A}}^ + } = \left[ {\begin{array}{*{20}{c}} 1&{3.58}&{0.74}&{0.44}&{0.67} \\ {0.41}&1&{0.47}&{0.55}&{0.72} \\ {2.64}&{3.85}&1&{0.79}&{1.87} \\ {3.74}&{2.17}&{2.74}&1&{1.61} \\ {1.95}&{1.6}&{0.88}&{0.72}&1 \end{array}} \right]$ |
利用matlab对左矩阵
| ${{{x}}^ - } = (0.153,0.107,0.224,0.316,0.201)'$ |
| ${{{x}}^ + } = (0.149,0.093,0.255,0.331,0.172)'$ |
由步骤(3)中的算式计算
| $ k = \sqrt {\sum\limits_{j = 1}^5 {\frac{1}{{\displaystyle \sum\limits_{i = 1}^5 {a_{ij}^ + } }}} } = 0.901,\;m = \sqrt {\sum\limits_{j = 1}^5 {\frac{1}{{\displaystyle \sum\limits_{i = 1}^5 {a_{ij}^ - } }}} } = 1.069 $ |
根据步骤(4)中算式得出
| $ \begin{split} & {{{S}}_1} = \langle 0.138,0.159\rangle ,{{{S}}_2} = \langle 0.096,0.099\rangle ,{{{S}}_3} = \langle 0.202,0.273\rangle ,\\ & {{{S}}_4} = \langle 0.285,0.354\rangle ,{{{S}}_5} = \langle 0.181,0.184\rangle \end{split} $ |
| $ V({{{S}}_1} \geqslant {{{S}}_2}) = \frac{{2(0.159 - 0.096)}}{{(0.099 - 0.096) + (0.159 - 0.138)}} = \frac{{0.126}}{{0.024}} = 5.25 $ |
| $ V({{{S}}_3} \geqslant {{{S}}_2}) = \frac{{2(0.273 - 0.096)}}{{(0.099 - 0.096) + (0.273 - 0.202)}} = \frac{{0.354}}{{0.074}} = 4.78 $ |
| $ V({{{S}}_4} \geqslant {{{S}}_2}) = \frac{{2(0.354 - 0.096)}}{{(0.099 - 0.096) + (0.354 - 0.285)}} = \frac{{0.516}}{{0.072}} = 7.17 $ |
| $ V({{{S}}_5} \geqslant {{{S}}_2}) = \frac{{2(0.184 -0.096)}}{{(0.099 - 0.096) + (0.184 - 0.181)}} = \frac{{0.176}}{{0.006}} = 29.33 $ |
因此可得
| ${p_1}=5.25, {p_2}{\rm{ = 1,}} {p_3}{\rm{ = 4}}{\rm{.78,}} {p_4}{\rm{ = 7}}{\rm{.17,}} {p_5}{\rm{ = 29}}{\rm{.33}}$ |
归一化后评价指标相对于总目标的单排序为
| $P = (0.110,0.021,0.101,0.151,0.617)$ |
表11是方案层3名考生
| 表 11 考生对于评价指标的分值 Table 11 Candidate’s scores for evaluation index |
根据表9中3名调剂生在各项指标上的分值进行两两比较打分,得到待选考生相对于准则层评价指标C1, C2, C3, C4, C5的判断矩阵分别为
| $ {{{B}}_{{1}}} = \left[ {\begin{array}{*{20}{c}} 1&1&{1.67} \\ 1&1&{1.67} \\ {0.6}&{0.6}&1 \end{array}} \right],\;\;{{{B}}_{{2}}} = \left[ {\begin{array}{*{20}{c}} 1&2&1 \\ {0.5}&1&{0.5} \\ 1&2&1 \end{array}} \right] $ |
| $ {{{B}}_{{3}}} = \left[ {\begin{array}{*{20}{c}} 1&{1.06}&{0.97} \\ {0.94}&1&{0.92} \\ {1.03}&{1.09}&1 \end{array}} \right],\;\;{{{B}}_{{4}}} = \left[ {\begin{array}{*{20}{c}} 1&{0.6}&{0.75} \\ {1.67}&1&{1.25} \\ {1.33}&{0.8}&1 \end{array}} \right] $ |
| ${{{B}}_{{5}}} = \left[ {\begin{array}{*{20}{c}} 1&1&{1.17} \\ 1&1&{1.17} \\ {0.85}&{0.85}&1 \end{array}} \right]$ |
然后计算出待选考生相对于评价指标的权值,如表12所示。
| 表 12 方案层单排序 Table 12 Single ranking weight of decision layer |
结合2.2.3节得出的准则层对目标层的单排序,以及2.2.4节得出的方案层对准则层的单排序,依据2.1节中可拓层次分析法的步骤(5),可得出总权重。
| $\begin{split} & {{W}} = \left[ {\begin{array}{*{20}{c}} {0.384\;7}&{0.4}&{0.336\;3}&{0.250\;0}&{0.350\;7} \\ {0.384\;7}&{0.2}&{0.317\;4}&{0.416\;9}&{0.350\;7} \\ {0.230\;7}&{0.4}&{0.346\;3}&{0.333\;1}&{0.298\;6} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {0.110} \\ {0.021} \\ {0.101} \\ {0.151} \\ {0.617} \end{array}} \right] = \\&\left[ {\begin{array}{*{20}{c}} {0.338\;8} \\ {0.357\;9} \\ {0.303\;3} \end{array}} \right] \end{split} $ |
最终,考生
本文利用关联函数对高考改革进行了定量分析,并对硕士研究生调剂录取建立了基于可拓层次分析法的决策模型。
在高考改革方面,从近年来实施的高考改革出发,建立了关于学生的物元模型。将高考改革视为可拓变换,通过比较变换前后学生与指标的关联度变化,定量地衡量了高考改革确实会对学生发展等方面起到正向的促进作用,可以打消改革的顾虑,促使高考改革稳步推进。
在研究生调剂生录取决策中,通过德尔菲法建立了恰当的层次结构,利用可拓层次分析法实现了对调剂生的录取决策,对高校定量地实施调剂生的录取工作提供了思路和理论指导。
| [1] |
贺腾飞, 寇福明. 我国高等教育人才培养理念七十年的创新与展望[J].
当代教育科学, 2020(4): 7-12.
HE T F, KOU F M. 70 years' innovation and prospect of talent training concept in China's higher education[J]. Contemporary Education Sciences, 2020(4): 7-12. DOI: 10.3969/j.issn.1672-2221.2020.04.003. |
| [2] |
鲍威, 金红昊. 新高考改革对大学新生学业适应的影响: 抑制还是增强?[J].
华东师范大学学报(教育科学版), 2020(6): 20-33.
BAO W, JIN H H. The influence of the college entrance examination reform on freshman’s academic adaptation: inhibition or promotion?[J]. Journal of East China Normal University (Educational Sciences), 2020(6): 20-33. |
| [3] |
姜柳, 陈培智, 沈霄菡, 等. 新高考改革落地的教育资源配置问题研究[J].
数学建模及其应用, 2020, 9(2): 53-64.
JIANG L, CHEN P Z, SHEN X H, et al. Research on the allocation of educational resources in the reform of college entrance examination[J]. Mathematical Modeling and Its Application, 2020, 9(2): 53-64. |
| [4] |
刘小艳, 黄静, 陈铁军, 等. 新形势下研究生招生信息化的思考与探索[J].
中国教育信息化, 2020(13): 37-39.
LIU X Y, HUANG J, CHEN T J, et al. Thinking and exploration on the informatization of graduate enrollment in the new situation[J]. The Chinese Journal of ICT in Education, 2020(13): 37-39. |
| [5] |
陶玉萍, 叶安发, 刘延卿. 加强高校研究生招生工作管理探析[J].
辽宁工业大学学报(社会科学版), 2020, 22(3): 59-61.
TAO Y P, YE A F, LIU Y Q. Analysis on strengthening the management of postgraduate enrollment in universities[J]. Journal of Liaoning University of Technology (Social Science Edition), 2020, 22(3): 59-61. |
| [6] |
罗洪川. 高校研究生招生计划分配及其优化策略初探[J].
黑龙江科学, 2020, 11(7): 126-127.
LUO H C. On the distribution of graduate enrollment plan and its optimization strategy[J]. Heilongjiang Science, 2020, 11(7): 126-127. DOI: 10.3969/j.issn.1674-8646.2020.07.061. |
| [7] |
杨春燕, 蔡文. 可拓学[M]. 北京: 科学出版社, 2014.
|
| [8] |
杨春燕. 可拓创新方法[M]. 北京: 科学出版社, 2017.
|
| [9] |
高红, 徐晓明, 刘巍. 可拓分类在港口与后方物流园区发展关系中的应用[J].
数学的实践与认识, 2018, 48(8): 1-10.
GAO H, XU X M, LIU W. Application of Extension classification in the relationship of a port and its rear logistics parks[J]. Mathematics in Practice and Theory, 2018, 48(8): 1-10. |
| [10] |
陈智斌, 余永权. 以层次结构形式实现可拓分类的研究[J].
广东工业大学学报, 2005, 22(4): 124-128.
CHEN Z B, YU Y Q. Research on extension classification based on hierarchical structure[J]. Journal of Guangdong University of Technology, 2005, 22(4): 124-128. DOI: 10.3969/j.issn.1007-7162.2005.04.027. |
| [11] |
杨春燕, 蔡文, 涂序彦. 可拓学的研究、应用与发展[J].
系统科学与数学, 2016, 36(9): 1507-1512.
YANG C Y, CAI W, TU X Y. The research, application and development of Extenics[J]. Journal of Systems Science and Mathematical Sciences, 2016, 36(9): 1507-1512. |
| [12] |
张钊, 张韧志. 区间数型水环境质量综合评价云物元模型及其应用[J].
数学的实践与认识, 2019, 49(8): 269-276.
ZHANG Z, ZHANG R Z. Cloud matter element model for comprehensive evaluation of water environment quality based on interval number and its application[J]. Mathematics in Practice and Theory, 2019, 49(8): 269-276. |
| [13] |
高洁, 盛昭瀚. 可拓层次分析法研究[J].
系统工程, 2002, 20(5): 6-11.
GAO J, SHENG Z H. Research on extension analytic hierarchy process[J]. Systems Engineering, 2002, 20(5): 6-11. DOI: 10.3969/j.issn.1001-4098.2002.05.002. |
| [14] |
MEESAPAWONG P, REZGUI Y, LI H J. Planning innovation orientation in public research and development organizations: using a combined Delphi and Analytic Hierarchy, Process approach[J].
Technological Forecasting & Social Change, 2014, 87(9): 245-256.
|
| [15] |
BOUZON M, GOVINDAN K, RODRIGUEZ C M T, et al. Identification and analysis of reverse logistics barriers using fuzzy Delphi method and AHP[J].
Resources, Conservation & Recycling, 2016, 108: 182-197.
|
 2021, Vol. 38
2021, Vol. 38
