2. 大连海事大学 航运发展研究院,辽宁 大连 116026
2. Shipping Development Research Institute, Dalian Maritime University, Dalian 116026, China
“21世纪海上丝绸之路”旨在通过海上互联互通推动中国与沿线国家的经贸合作,是实现沿线国家经贸互联互通的重要途径,其有两大走向:一是从中国沿海港口过南海,经过马六甲海峡到印度洋,延伸至欧洲;二是从中国沿海港口过南海,向南太平洋延伸。“21世纪海上丝绸之路”沿线国家众多,海上贸易联系密切,航线交通流量大,但沿线海峡众多,自然灾害频发导致主航线船舶交通流结构复杂,对船舶航行、海洋生态环境等造成严重挑战。
由于“21世纪海上丝绸之路”是实现沿线国家多元、可持续发展的关键所在,学者们已经对其进行了诸多方面的研究。贸易方面:张桂梅等[1]基于拓展引力模型对海上丝绸之路西线国家做了国家贸易潜力研究,发现了对贸易量影响较大的正相关因素,并对各个国家进行了潜力型划分;王凤婷等[2]利用随机前沿模型对海上丝绸之路沿线国家农产品出口贸易进行研究,分析了现状和影响因素,估算了贸易效率和出口潜力。港口航线方面:郑崇伟等[3-4]搜集梳理了海上丝绸之路的重要航线、节点和港口的地理水文特征、气候特征、人文背景和商业价值等信息,集中展现了大量背景知识;牟乃夏等[5]从海陆联运视角出发,构建港口区位优势评价模型,对海上丝绸之路沿线港口进行了区位优势度分析。网络方面:李振福等[6]利用复杂网络分析方法,对海上丝绸之路沿线34个集装箱港口的各类中心性进行了测度,结果显示了香港港、深圳港、大连港、新加坡港和上海港在该集装箱海运网络中具有较高的地位。于安琪等[7]分析了海上丝绸之路沿线港口的分布特点和网络特征,并利用班轮连通性指数测度了集装箱海运网络的连通性,指出了海上丝绸之路沿线国家连通性指数普遍较低且增长缓慢的现状。朱小林等[8]针对21个海上丝绸之路沿线国家,建立区域整体贸易运输网络,量化了网络枢纽间规模经济效应和各个国家的物流绩效,通过遗传算法选择出更符合海上丝绸之路沿线区域联动发展的贸易海运网络。文化法律方面:孟夏韵[9]探究了“一带一路”背景下中国文化在拉美的传播路径;杨泽伟[10]研究了建设海上丝绸之路重要节点面临的政治风险和地区法律问题。安全方面:孙海泳[11]研究了“一带一路”背景下,中非海上互通的安全风险,并且提出了防范风险的对策;宫晓婞等[12]利用改进松弛变量模型对海上丝绸之路关键海峡、运河的安全效率进行了排序,指出海盗和船舶事故是影响安全效率的重要因素。海上丝绸之路海上交通流量预测对于提升船舶航行安全性,完善海上交通安全管理制度具有重要意义。但是,目前对海上丝绸之路交通流的研究相对较少。
交通流理论是运用物理和数学的定律来描述交通特性的一门边缘学科[13],广泛应用于交通工程的诸多研究领域。交通流研究最初集中于陆上交通,但随着全球卫星定位、船舶自动识别系统(Automatic Identification System,AIS)等技术的不断成熟,交通流理论逐渐被应用于海上船舶交通流特征统计及交通流量预测等方面。例如,甘浪雄等[14]利用场方法统计了单位时间内某区域的船舶交通流密度;熊振南等[15]利用点统计方法来判断船舶分布类型;金兴赋等[16]、刘敬贤等[17]针对特定水域,利用AIS数据分析船舶交通流特征;文哲等[18]基于交通波理论,分析了枯水期长江中游的船舶流特征。近些年,研究人员在统计分析基础上,开始着手对交通流量预测进行研究,比如,惠子刚等[19]建立自适应模糊推理系统对船舶交通流数据进行了仿真预测;钮浩东等[20]运用优化的广义回归神经网络对东海大桥船舶流量进行了仿真预测;张晓雷等[21]综合季节因素,建立灰色马尔可夫模型对船舶流进行预测;肖进丽等[22]针对船舶交通流时间序列非平稳的特点,使用差分进化算法、BP神经网络等进行了较高精度的组合预测。上述研究均可以较好地预测船舶交通流,但是对交通流规律的解释性不够,不能反映当前船舶交通流会受哪些历史数据的影响。谢振东等[23-24]指出交通流预测可以缓解交通拥堵的问题,Yip[25]指出研究交通流可以更好地进行船舶交通安全管理,所以刻画交通流规律对通航管理具有一定的应用价值。
本文从交通流角度出发,基于2018年海上丝绸之路AIS数据,利用ARIMA模型(Auto-regressive Intergrated Moving Average Model,差分自回归移动平均模型),分别对货船、油轮和货船−油轮3种情形下的船舶交通流进行拟合和预测,探究海上丝绸之路船舶交通流规律。
1 数据和模型描述 1.1 AIS数据描述本文数据来源于《基于卫星组网的“21世纪海上丝绸之路”通道支点检测与保障研究》项目所提供的2018年海上丝绸之路AIS数据,包含以下2类信息:
1) 船舶静态信息。
船舶静态信息包括:MMSI码(Maritime Mobile Service Identify,水上移动通信业务标识码)、船名、船舶类型、IMO编号(International Maritime Organization,国际海事组织,内贸船无该编号)、船长、船宽、船旗国7个字段数据。
2) 船舶动态信息。
船舶动态信息包括:MMSI码、时间、经度、纬度、航向、航速、航行状态7个字段数据。
上述信息中,MMSI码用来识别属于同一船舶的信息,船舶类型用来区分不同类型的船舶,经纬度用来判断船舶的活动位置,时间、航速和航向可以反映船舶活动规律并用来研究交通流。本文根据研究需要,将提取船舶的MMSI码、船舶类型和船舶动态等信息。
1.2 AIS数据筛选2018年全年AIS数据量巨大,并且动态信息记录存在诸多问题,例如,动态信息时间间隔不规范,船舶无有效动态记录(即航速始终为0),船舶航速记录异常等。因此,本文采取以下3个筛选原则:
(1) 筛除无有效动态信息的船舶,即航速始终为0的船舶;
(2) 筛除船舶异常航速信息,即航速明显超出该类型船舶的正常速度范围的船舶记录;
(3) 由于动态数据时间间隔并不规范,所以本文只抽取每小时内的第一条船舶动态数据记录。
此外,船舶静态信息也存在一些问题,例如,船长、船宽和船舶类型等静态信息记录存在错误或缺失。借助船讯网(
经过以上处理,得到31 554条船舶的有效动态信息,其中包含货船、油轮和捕捞船等23个类型的船舶,具体船舶数量见图1,本文重点研究货船和油轮。
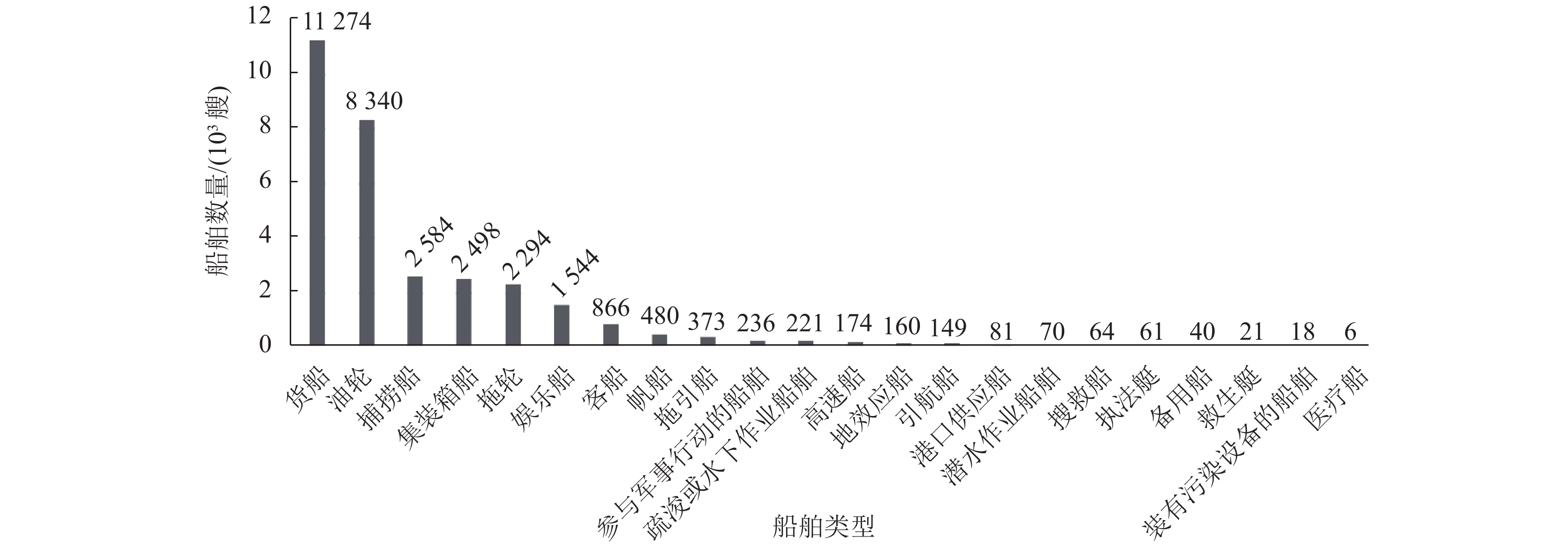
|
图 1 各类型船舶数量 Figure 1 Number of various types of vessels |
船舶交通流时间序列是指在一定时间范围内,以固定时间间隔排列的船舶数量序列。虽然构成该序列的任一序列值具有不确定性,但序列值之间存在一定关联,因此可通过构建数学模型对后续序列值进行预测。常用的时间序列预测模型包括AR模型(Autoregressive Model,自回归模型)、MA模型(Moving Average Model,移动平均模型)、ARMA模型(Autoregressive Moving Average Model,自回归移动平均模型)和ARIMA模型,其中ARMA模型是AR模型和MA模型的组合,ARIMA模型是在ARMA模型的基础上增加了差分处理的改进。
1.3.1 模型简介ARIMA模型由美国统计学家Box和英国统计学家Jenkins提出,是一类预测精度较高的时间序列模型,广泛应用于各类时间序列的预测[26-30],其特点是利用历史数据就可以预测未来响应的时间序列。该模型将具有明显趋势的非平稳数据,经过差分处理使其转化为平稳序列,建立合适的模型,利用历史数据预测下一阶段的数据。ARIMA模型由3部分组成,包括自回归过程AR、差分过程I和移动平均过程MA。
自回归过程的公式:
移动平均过程关注的是自回归模型中误差项的累加,AR与MA结合得到自回归移动平均模型ARMA,其表达式为
差分过程I表示对原始时间序列进行差分处理,一般用
综上,差分自回归移动平均模型一般用
本文利用Python实现ARIMA模型建模过程,调用了Pandas,Numpy和StatsModels库,选取从2018年1月1日起至2018年12月24日止的货船和油轮动态AIS数据,记录每隔7天的2类船舶活动数量,每类船舶有52条数据记录,设置85%的训练集构建模型,15%的测试集来验证模型的准确性。ARIMA模型建模步骤如图2所示。
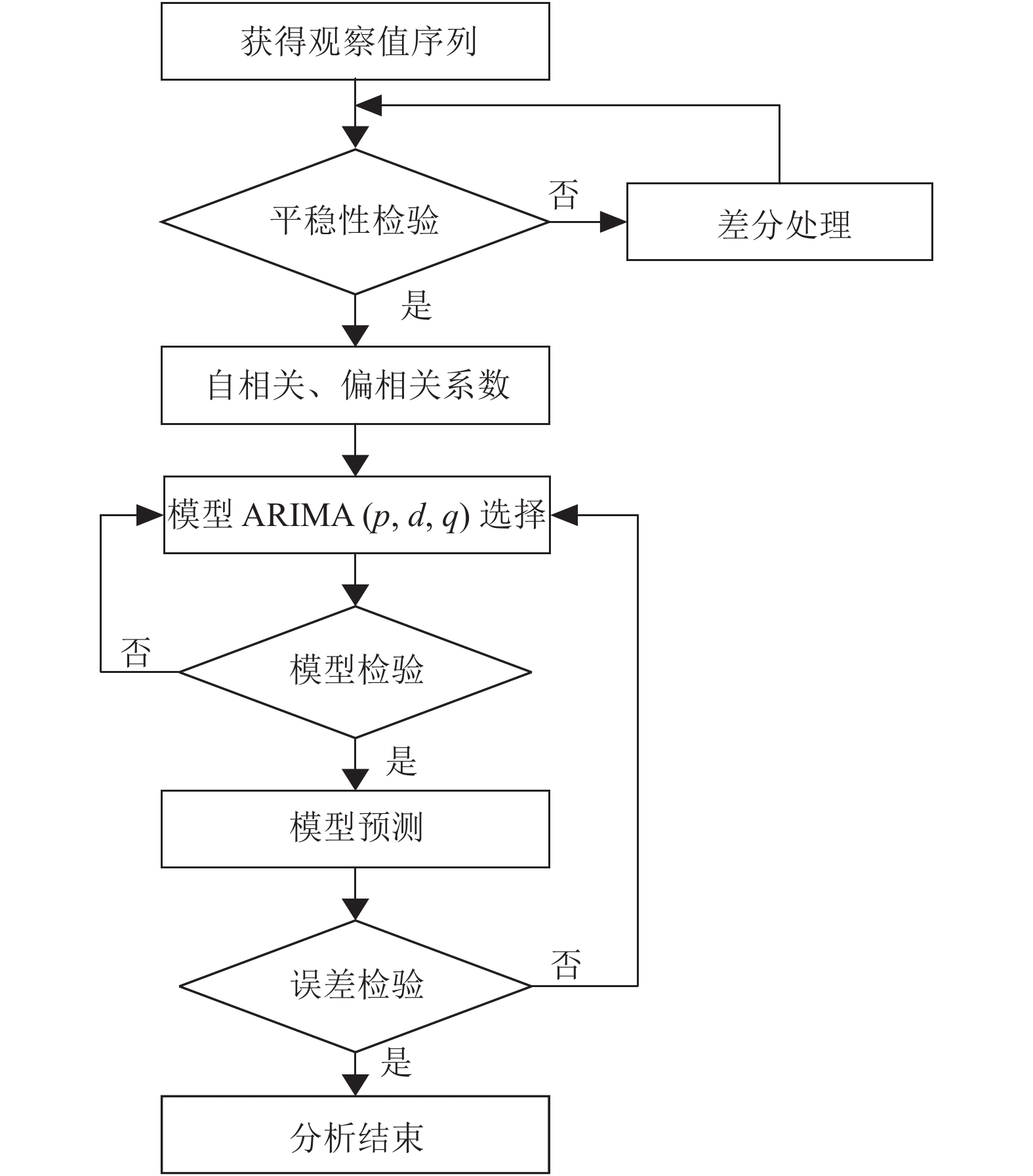
|
图 2 ARIMA建模步骤 Figure 2 ARIMA modeling steps diagram |
本节以货船为例,实现ARIMA预测模型。
2.1 差分平稳化货船交通流原始时间序列数据如图3所示。
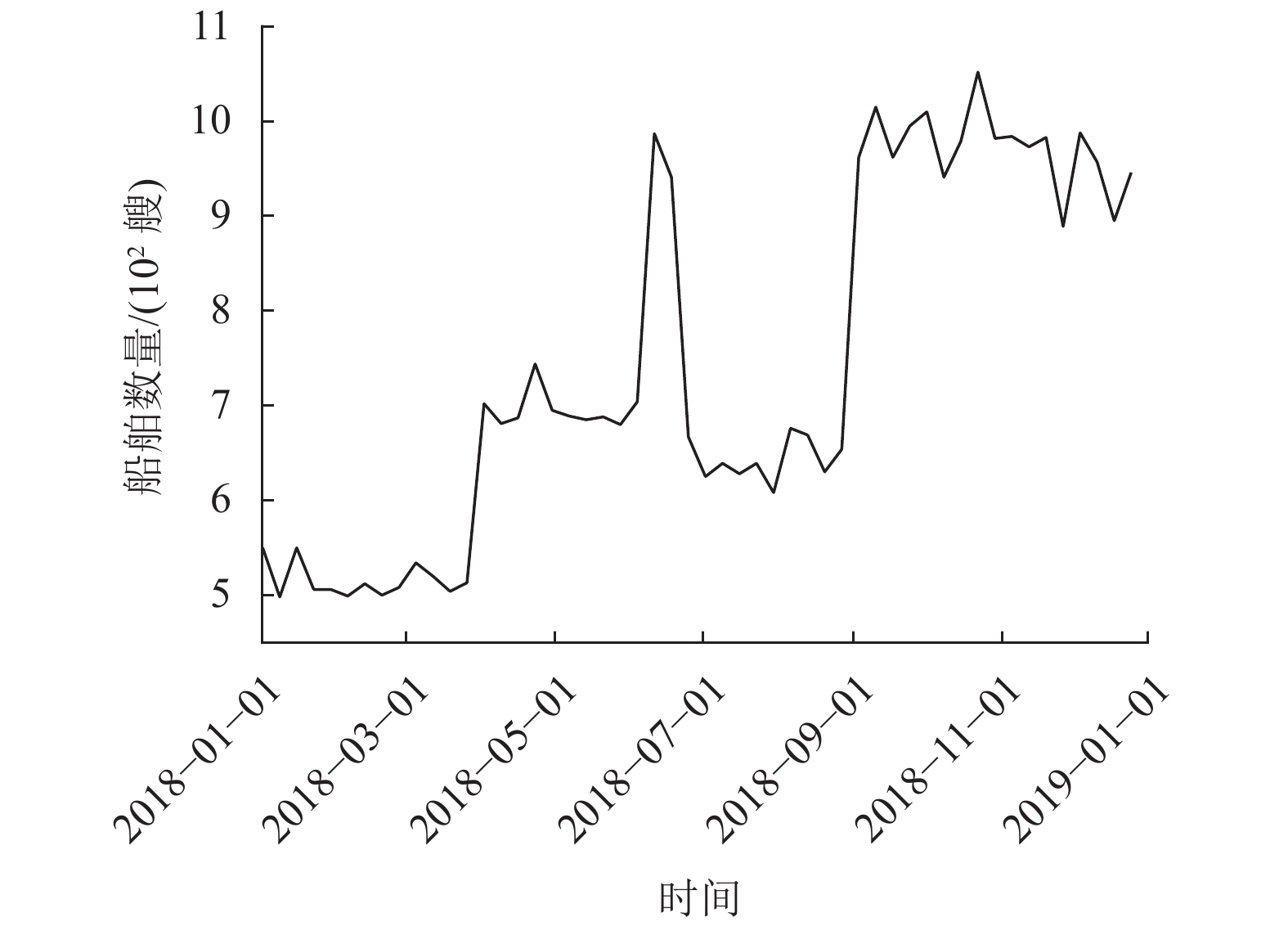
|
图 3 原始时间序列 Figure 3 Original time series |
从图3观察可知,该时间序列是非平稳的,首先对该原始时间序列进行一阶差分处理,得到一阶差分时间序列,如图4所示。
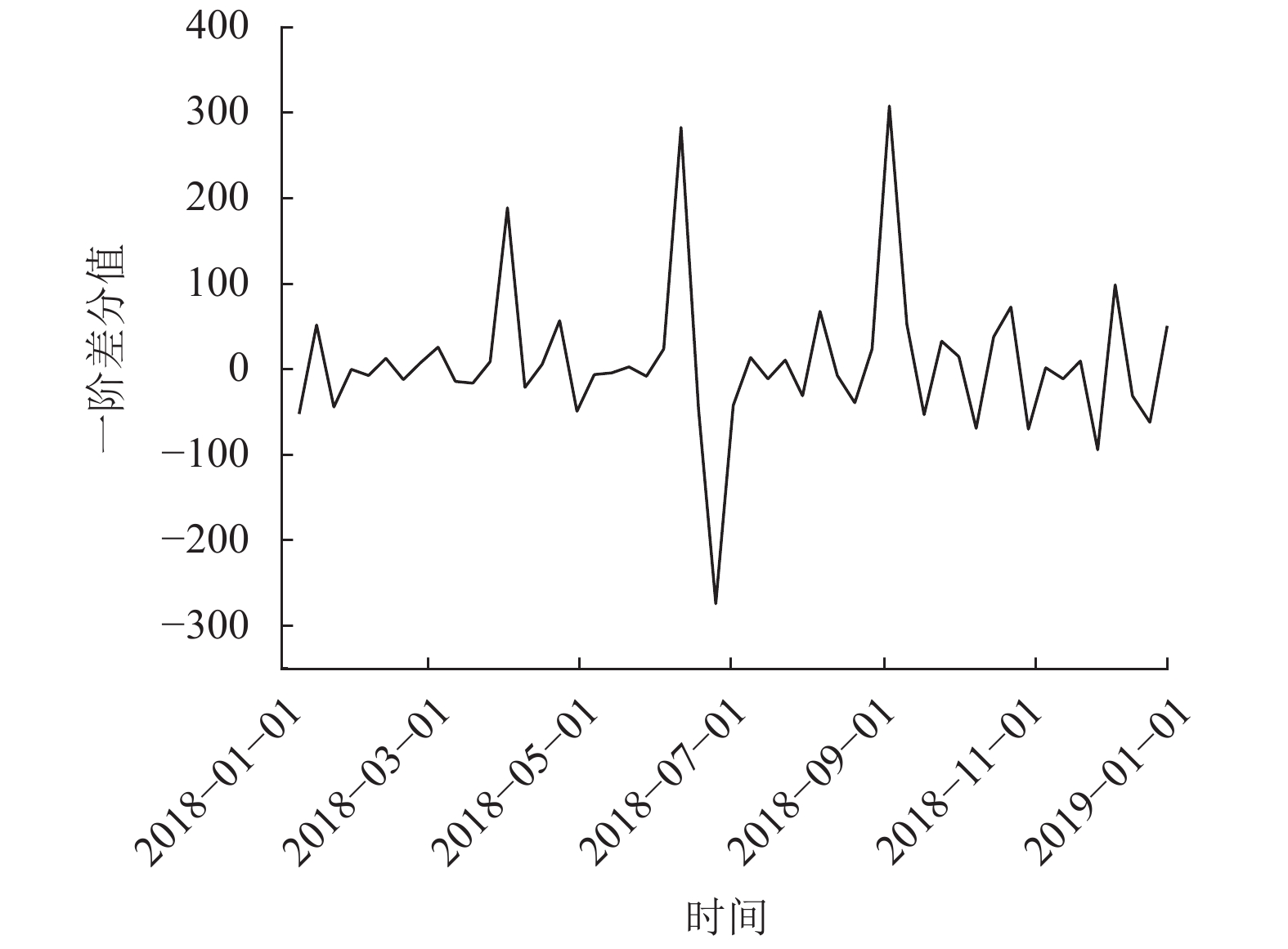
|
图 4 一阶差分时间序列 Figure 4 First order differential time series |
由图4可知,一阶差分时间序列比原始时间序列更趋于平稳。分别对其进行平稳性检验,检验序列中是否存在单位根,若存在单位根就是非平稳时间序列。对比结果见表1。
| 表 1 时间序列的ADF检验 Table 1 Unit root test for time series |
表1中ADF Test值(T值)是对时间序列的检验结果,显著性水平值表示不同显著性水平下拒绝原假设的统计值,ADF检验的原假设是存在单位根,若T值小于1%、5%、10%这3个显著性水平值,即说明非常好地拒绝该假设。Prob(P值)表示T值的概率值,P值要求小于给定的显著性水平,若小于1%就可以极显著地拒绝原假设,表明数据平稳。由表1可知,一阶差分时间序列不存在单位根,为平稳序列。
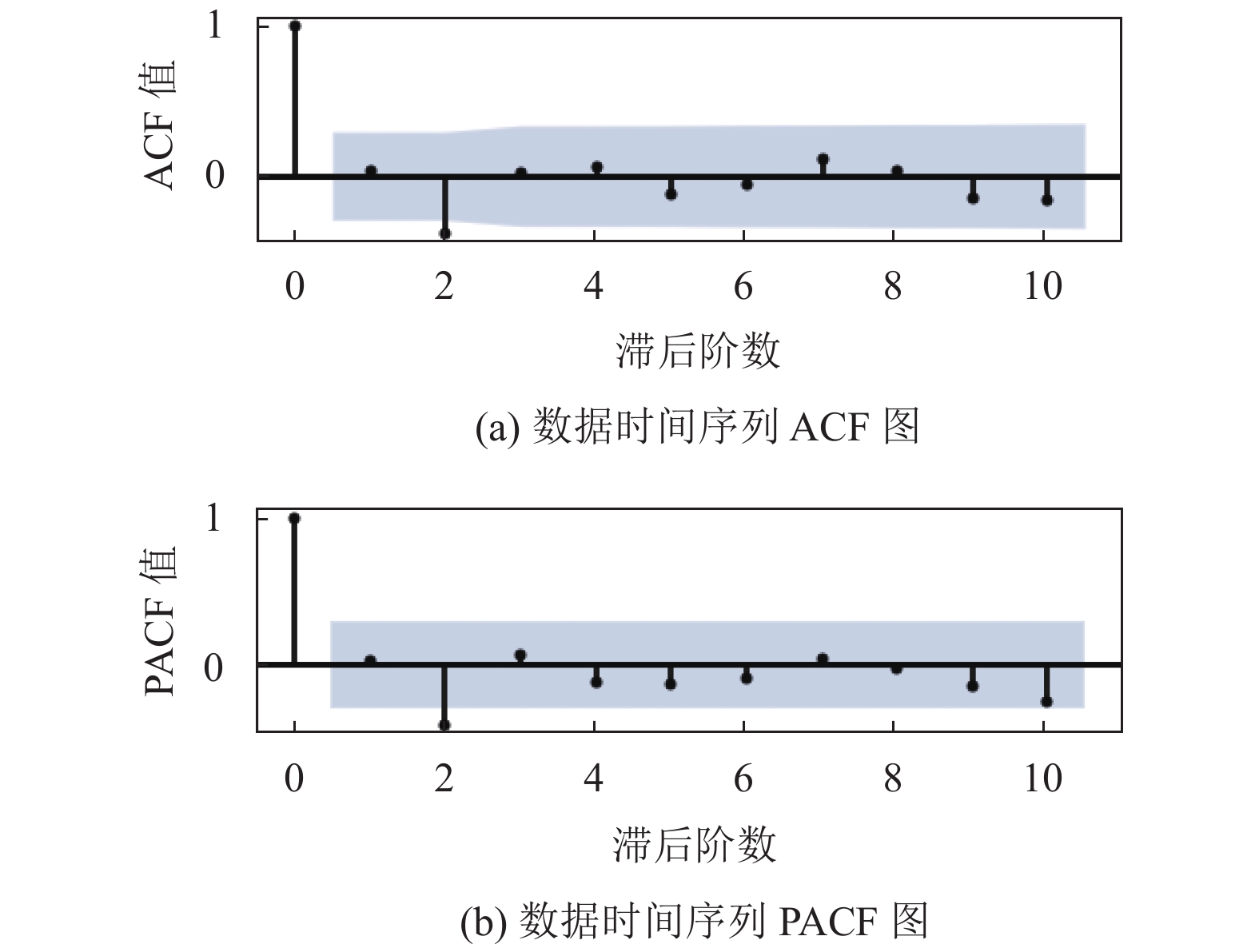
2.2 模型选择取前85%的原始时间序列值作为训练集,进行一阶差分处理后得到数据时间序列,分别计算其自相关函数(Autocorrelation Function,ACF)和偏相关函数(Partial Autocorrelation Function,PACF)。
ACF计算公式为
图5中,横坐标表示滞后阶数,阴影部分表示置信区间,当滞后阶数为2时,ACF和PACF超过了置信区间。
|
图 5 自相关、偏相关图 Figure 5 Autocorrelation and partial autocorrelation diagram |
| 表 2 ARIMA模型选择原则 Table 2 ARIMA model selection principles |
从图5中ACF和PACF图的拖尾性来看,
| 表 3 AIC值 Table 3 AIC value |
| 表 4 BIC值 Table 4 BIC value |
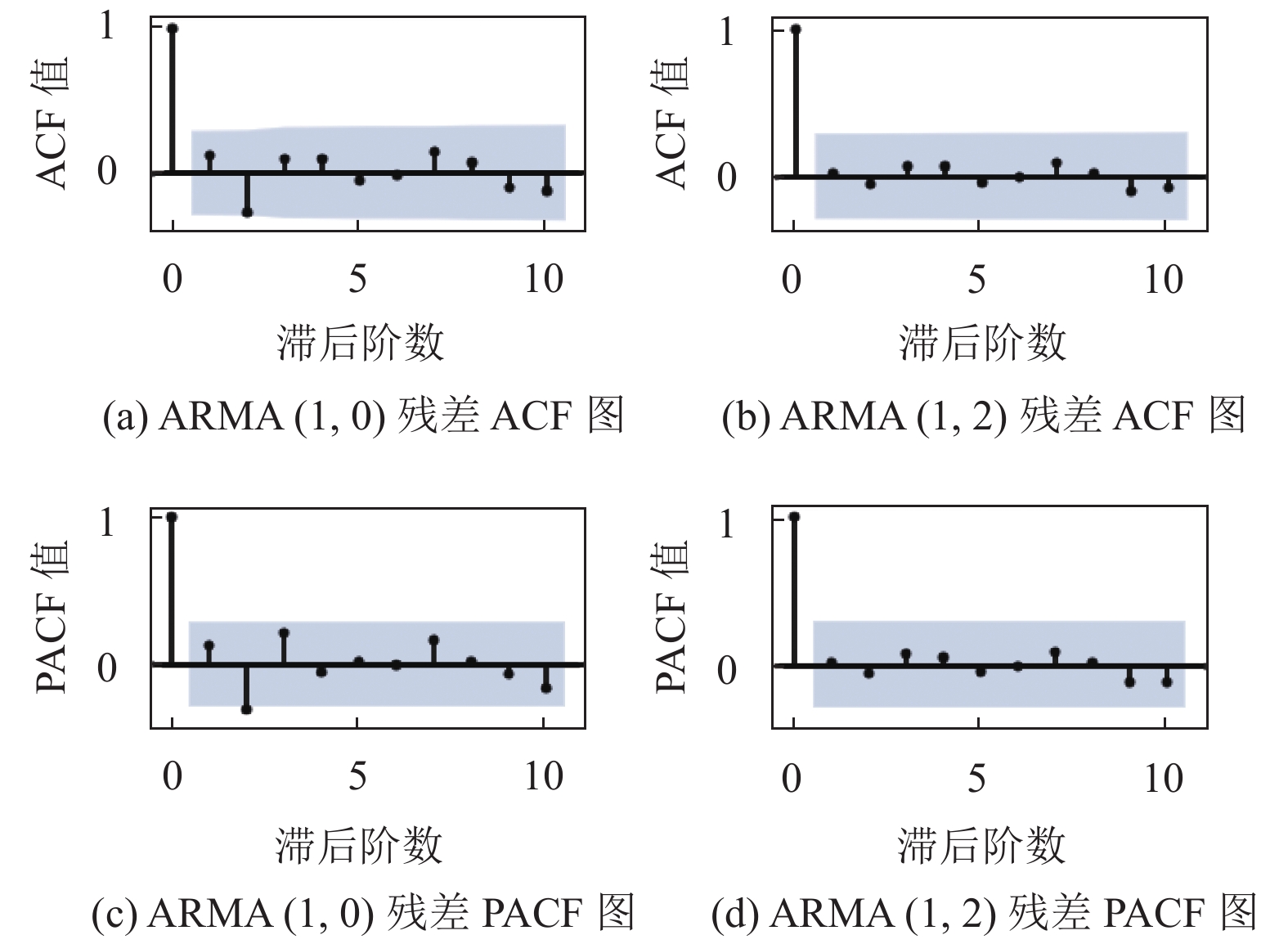
由表3和表4可知,AIC值最小的是ARMA(1,2)模型,BIC值最小的是ARMA(1,0)模型,分别求其残差对应的ACF和PACF,见图6。
图6中显示ARMA(1,2)模型下残差的ACF和PACF均在置信区间内,不存在相关关系。说明在该模型下,数据序列的有效信息已经被全部提取,拟合效果显更优,所以选择ARMA(1,2)模型。
|
图 6 ARMA(1,0),ARMA(1,2)残差自相关、偏相关图 Figure 6 Residual Autocorrelation and Residual Partial Autocorrelation diagram |
对选定的ARMA(1,2)模型进行检验,分为2个步骤:(1) 选用Durbin-Watson检验(D-W检验)来检查模型残差的自相关性,D-W值接于0或4,说明存在自相关性,而D-W值接近于2时,说明不存在相关性;(2) 选用Ljung-Box Q检验(LBQ检验)来判断残差是否为高斯白噪声。在ARIMA模型中残差被假定为高斯白噪声序列,如果检验概率小于给定显著性水平(5%或10%),那么残差就不是高斯白噪声,说明该模型并不是一个合适的模型。
ARMA(1,2)模型下,残差的D-W值为1.8261,接近于2,说明残差不存在自相关性。残差的LBQ检验结果见表5,其中各阶滞后的检验概率均大于5%,说明ARMA(1,2)模型的残差是高斯白噪声序列,即该模型是一个合适的模型。
| 表 5 ARMA(1,2) 残差LBQ检验结果 Table 5 The results of ARMA(1,2) residual LBQ test |
利用ARMA(1,2)模型进行预测,模型表达式为
| $\Delta {y_t} = 9.63 + 0.45\Delta {y_{t - 1}} + {\varepsilon _t} + 0.43{\varepsilon _{t - 1}} + 0.56{\varepsilon _{t - 2}}$ |
将表达式转换后,得到
| $ {y_t} = 9.63 + 1.45{y_{t - 1}} - 0.45{y_{t - 2}} + {\varepsilon _t} + 0.43{\varepsilon _{t - 1}} + 0.56{\varepsilon _{t - 2}} $ |
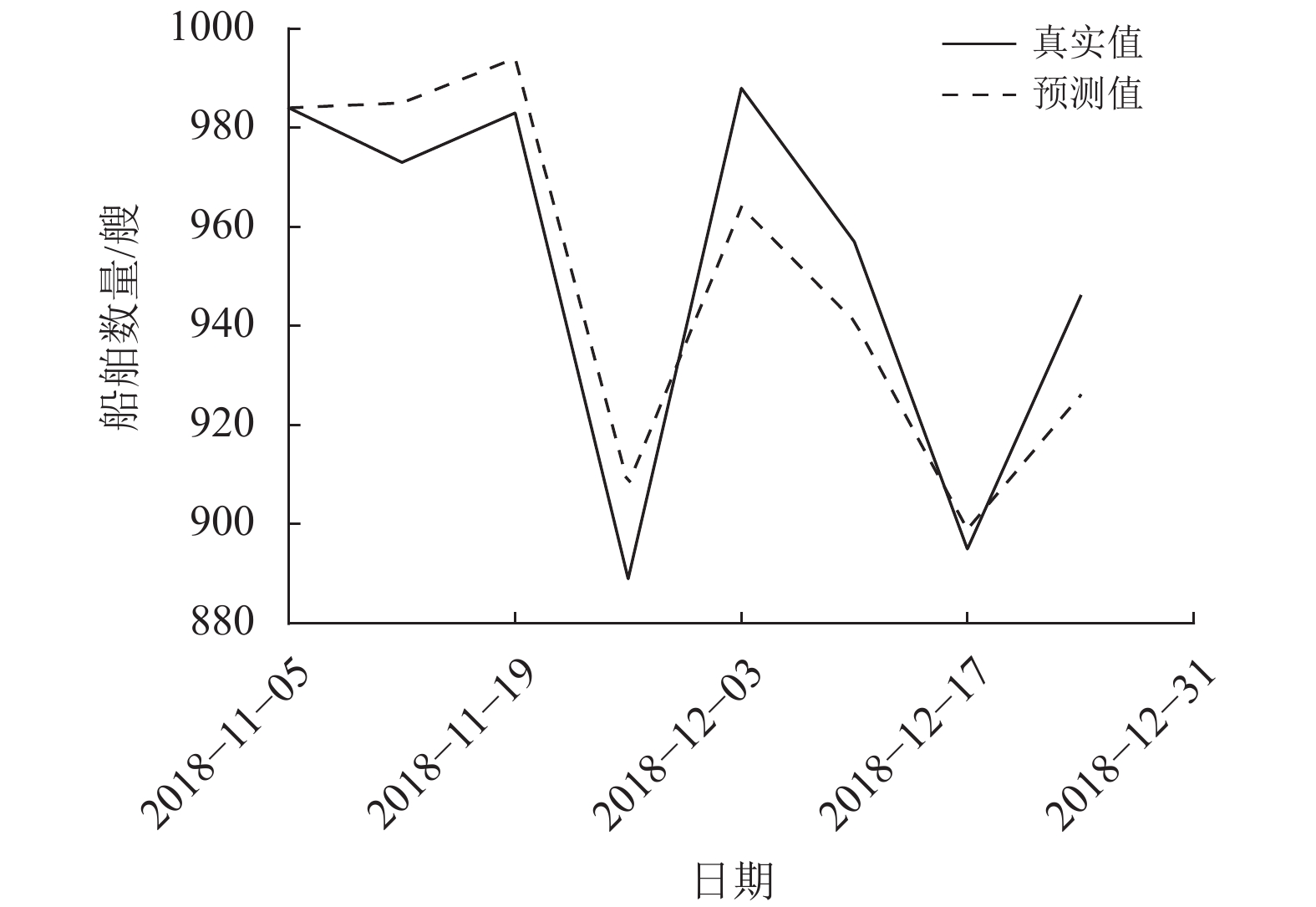
由上述表达式可以看出,当前船舶交通流会受到之前2个时间周期内的船舶交通流的影响,预测结果、真实值及误差见表6。
| 表 6 预测值与误差 Table 6 Forecast values and errors |
常用的回归预测评价方法有均方误差
| $ {R^{\rm{2}}} = 1{\rm{ - }}{{\Bigg( {\displaystyle\sum\limits_{i = 1}^m {{{({y_i} - y_i')}^2}} } \Bigg)} \Big/ {\Bigg( {\displaystyle\sum\limits_{i = 1}^m {{{(\overline y - y_i')}^2}} } \Bigg)}} $ |
其中,
根据表6结果,计算ARMA(1,2)模型的决定系数
|
图 7 预测效果图 Figure 7 Forecast performance diagram |
利用ARIMA模型对油轮和货船−油轮这两类情形的交通流进行预测,建模过程与研究货船时一致,各情形的模型选择和R2值,见表7。
| 表 7 模型和R2值 Table 7 Model and R2 values |
从表7可知,考虑货船、油轮和货船−油轮这3种情形时,最优模型均为ARIMA(1,1,2),表明当前交通流会受到近两周内的交通流的影响。对比不同情形下的R2值,可以发现ARIMA模型对货船和油轮交通流预测效果明显优于对货船−油轮交通流预测效果,表明ARIMA模型更适合用来研究单一船型的交通流。
3 结论本文基于2018年“21世纪海上丝绸之路”AIS数据,针对货船、油轮、货船−油轮3种情形,构建了ARIMA模型拟合船舶交通流并做出预测。结果显示,(1) ARIMA是一个合适的模型,对于不同的情形都可给出较好的拟合预测;(2) 由ARIMA(1,1,2)模型得出的拟合公式可知,当前船舶交通流会受之前2个时间周期内的交通流影响,这为下一周期的船舶水路规划和通航安全管理提供充裕的时间保障;(3) 由本文所求得的R2值可知,ARIMA(1,1,2)模型对单一船型的交通流预测效果明显优于货船−油轮组合船舶。综上表明ARIMA预测模型对“21世纪海上丝绸之路”海上交通流研究具有一定实用价值。建立“21世纪海上丝绸之路”是中国加强与沿线国家贸易联系和打造区域经济一体化的重要战略。沿线的中国港口可以基于船舶到港口数据或AIS数据,利用ARIMA模型对船舶交通流进行预测,确保港口航线通航安全,针对特定船型,通过交通流预测可以预估贸易量,了解其他国家货物需求,这对我国港口发展建设及港口腹地经济研究具有重要意义。
本文不足之处:(1) 项目只包含了2018年的AIS数据,数据量偏少,因此导致预测的精度下降;(2) 影响海上交通流的因素众多,本文利用ARIMA模型研究海上丝绸之路交通流,仅使用了AIS的历史数据作为研究的时间序列,不能反映不确定性因素。
| [1] |
张桂梅, 李晓璇. 中国与“21世纪海上丝绸之路”西线国家贸易潜力研究[J].
山东工商学院学报, 2019, 33(6): 22-35.
ZHANG G M, LI X X. Research on the trade potential between China and the western line countries of the "The 21st-Century Maritime Silk Road"[J]. Journal of Shandong Technology and Business University, 2019, 33(6): 22-35. |
| [2] |
王凤婷, 田园, 程宝栋. 中国与“21世纪海上丝绸之路”沿线国家农产品出口贸易研究[J].
国际经济合作, 2019(2): 80-90.
WANG F T, TIAN Y, CHENG B D. Research on export trade of agricultural products between China and countries along the "21st Century Maritime Silk Road"[J]. Journal of International Economic Cooperation, 2019(2): 80-90. |
| [3] |
郑崇伟, 孙威, 黎鑫, 等. 经略21世纪海上丝路: 重要航线、节点及港口特征[J].
海洋开发与管理, 2016, 33(1): 4-13.
ZHENG C W, SUN W, LI X, et al. Strategy of the 21st Century Maritime Silk Road: on the important routes, crucial nodes and characteristics of ports[J]. Ocean Development and Management, 2016, 33(1): 4-13. |
| [4] |
郑崇伟, 高成志, 高悦. “21世纪海上丝绸之路”波浪能的气候特征及变化趋势[J].
太阳能学报, 2019, 40(6): 1487-1493.
ZHENG C W, GAO C Z, GAO Y. Climate feature and long term trend analysis of wave energy resource of 21st Century Maritime Silk Road[J]. Acta Energiae Solaris Sinica, 2019, 40(6): 1487-1493. |
| [5] |
牟乃夏, 廖梦迪, 张恒才, 等. “海上丝绸之路”沿线重要港口区位优势度评估[J].
地球信息科学学报, 2018, 20(5): 613-622.
MOU N X, LIAO M D, ZHANG H C, et al. Evaluation on location advantages of the ports along the Maritime Silk Road[J]. Journal of Geo-Information Science, 2018, 20(5): 613-622. |
| [6] |
李振福, 李婉莹, 徐梦俏. 新海上丝绸之路集装箱海运网络中心性[J].
中国航海, 2018, 41(3): 123-128.
LI Z F, LI W Y, XU M Q. Centrality of Maritime Silk Road container shipping network[J]. Navigation of China, 2018, 41(3): 123-128. |
| [7] |
于安琪, 王诺. “21世纪海上丝绸之路”集装箱海运网络连通性分析[J].
上海海事大学学报, 2019, 40(4): 72-77.
YU A Q, WANG N. Connectivity analysis of container shipping network of “21st Century Maritime Silk Road”[J]. Journal of Shanghai Maritime University, 2019, 40(4): 72-77. |
| [8] |
朱小林, 陈昌定, 姚婉莹. 考虑物流绩效及规模效益的海上丝绸之路枢纽网络设计与研究[J].
计算机应用与软件, 2018, 35(11): 66-73.
ZHU X L, CHEN C D, YAO W Y. Design and study of Maritime Silk Road hub network considering logistics performance and scale benefits[J]. Computer Applications and Software, 2018, 35(11): 66-73. |
| [9] |
孟夏韵. “一带一路”倡议下中国文化在拉美的传播路径及其改善[J].
江苏大学学报(社会科学版), 2019, 21(6): 27-35.
MENG X Y. The transmission path and improvement of the spread of Chinese culture in Latin America under the "Belt and Road" initiative[J]. Journal of Jiangsu University(Social Science Edition), 2019, 21(6): 27-35. |
| [10] |
杨泽伟. 21世纪海上丝绸之路建设重要节点地区的法律问题研究[J].
法学杂志, 2019, 40(8): 67-75.
YANG Z W. On legal issues of the key connexion in the building the 21st-Century Maritime Silk Road[J]. Law Science Magazine, 2019, 40(8): 67-75. |
| [11] |
孙海泳. “一带一路”背景下中非海上互通的安全风险与防控[J].
新视野, 2018(5): 35-40.
SUN H Y. Security risks in China-Africa maritime exchange and its prevention and control under the background of "the Belt and Road"[J]. Expanding Horizons, 2018(5): 35-40. |
| [12] |
宫晓婞, 吕靖, 李辉. 海上丝绸之路关键海峡运河安全效率研究[J].
运筹与管理, 2019, 28(3): 173-182.
GONG X X, LYU J, LI H. Safety efficiency of strait canal on the Maritime Silk Road[J]. Operations Research and Management Science, 2019, 28(3): 173-182. |
| [13] |
俞洁, 杨成斌. 交通流理论发展分析[J].
合肥工业大学学报(自然科学版), 2004(2): 163-167.
YU J, YANG C B. A general review of the traffic flow theory[J]. Journal of Hefei University of Technology (Natural Science), 2004(2): 163-167. |
| [14] |
甘浪雄, 张磊, 邹早建, 等. 基于场方法的船舶交通流分析[J].
上海交通大学学报, 2014, 48(4): 551-557.
GAN L X, ZHANG L, ZOU Z J, et al. Analysis of vessel traffic flow based on field method[J]. Journal of Shanghai Jiaotong University, 2014, 48(4): 551-557. |
| [15] |
熊振南, 程俊康, 翁跃宗. 点统计法在船舶交通流分析中的应用[J].
中国航海, 2009, 32(1): 64-67.
XIONG Z N, CHENG J K, WENG Y Z. Application of point-statistic method in the analysis of vessel traffic flow[J]. Navigation of China, 2009, 32(1): 64-67. |
| [16] |
金兴赋, 付玉慧, 张连东. 基于AIS数据的成山头水域船舶交通流研究[J].
大连海事大学学报, 2012, 38(1): 33-36.
JIN X F, FU Y H, ZHANG L D. Research on vessel traffic flow at Chengshantou water area based on AIS data[J]. Journal of Dalian Maritime University, 2012, 38(1): 33-36. |
| [17] |
刘敬贤, 韩晓宝. 渤海海峡船舶流的调查与分析[J].
船海工程, 2008(4): 95-98.
LIU J X, HAN X B. Survey and analysis of vessel traffic flow in the Bohai strait[J]. Ship & Ocean Engineering, 2008(4): 95-98. |
| [18] |
文哲, 张培林, 袁子文. 枯水期长江中游船舶交通流特征分析[J].
物流技术, 2018, 37(5): 80-84.
WEN Z, ZHANG P L, YUAN Z W. Characteristics of ship traffic on middle reaches of Yangtze river in dry season[J]. Logistics Technology, 2018, 37(5): 80-84. |
| [19] |
惠子刚, 肖建兵. 基于FCM-ANFIS模型的船舶交通流预测[J].
中国航海, 2018, 41(2): 73-76.
HUI Z G, XIAO J B. Vessel traffic flow prediction based on FCM-ANFIS model[J]. Navigation of China, 2018, 41(2): 73-76. |
| [20] |
钮浩东, 黄洪琼. 基于FOA优化GRNN的船舶交通流预测模型[J].
微型机与应用, 2016, 35(12): 81-83.
NIU H D, HUANG H Q. Ship traffic flow prediction model based on FOA-GRNN algorithm[J]. Information Technology and Network Security, 2016, 35(12): 81-83. |
| [21] |
张晓雷, 黄洪琼. 基于优化的灰色马尔可夫模型对船舶流的预测[J].
计算机技术与发展, 2018, 28(10): 101-104.
ZHANG X L, HUANG H Q. Prediction of ship traffic flow based on optimized grey Markov prediction model[J]. Computer Technology and Development, 2018, 28(10): 101-104. |
| [22] |
肖进丽, 李晓磊. 基于集合经验模态分解和差分进化算法优化BP神经网络的船舶交通流预测[J].
大连海事大学学报, 2018, 44(2): 9-14.
XIAO J L, LI X L. Vessel traffic flow prediction method based on ensemble empirical mode decomposition and back propagation neural network optimized with differential evolution algorithm[J]. Journal of Dalian Maritime University, 2018, 44(2): 9-14. |
| [23] |
谢振东, 刘雪琴, 吴金成, 等. 公交IC卡数据客流预测模型研究[J].
广东工业大学学报, 2018, 35(1): 16-22.
XIE Z D, LIU X Q, WU J C, et al. A study of passenger flow prediction based on IC card data[J]. Journal of Guangdong University of Technology, 2018, 35(1): 16-22. |
| [24] |
谢振东, 何建兵, 何仕晔, 等. 基于IC卡数据的居民出行成本建模分析[J].
广东工业大学学报, 2019, 36(2): 47-53.
XIE Z D, HE J B, HE S Y, et al. Modeling and analysis of residents' travel cost based on IC card data[J]. Journal of Guangdong University of Technology, 2019, 36(2): 47-53. |
| [25] |
YIP T L. A marine traffic flow model[J].
TransNav: International Journal on Marine Navigation and Safety of Sea Transportation, 2013, 7(1).
|
| [26] |
沈彭, 魏峰. ARIMA季节乘积模型在新疆地区细菌性痢疾发病率预测中的应用[J].
重庆科技学院学报(自然科学版), 2019, 21(6): 99-104.
SHEN P, WEI F. Application of multiple seasonal ARIMA model on forecasting incidence of bacillary dysentery in Xinjiang[J]. Journal of Chongqing University of Science and Technology (Natural Sciences Edition), 2019, 21(6): 99-104. |
| [27] |
赵鹏, 李璐. 基于ARIMA模型的城市轨道交通进站量预测研究[J].
重庆交通大学学报(自然科学版), 2020, 39(1): 40-44.
ZHAO P, LI L. Prediction of urban rail transit station inflows based on ARIMA model[J]. Journal of Chongqing Jiaotong University (Natural Science), 2020, 39(1): 40-44. |
| [28] |
耿献辉, 安宁. 基于ARIMA模型的梨果价格波动及市场行情预测[J].
北方果树, 2020(2): 1-4.
GENG X H, AN N. The price fluctuation and market forecast of pear based on ARIMA model[J]. Northern Fruits, 2020(2): 1-4. |
| [29] |
王兴川, 姚恩建, 刘莎莎. 基于AFC数据的大型活动期间城市轨道交通客流预测[J].
北京交通大学学报, 2018, 42(1): 87-93.
WANG X C, YAO E J, LIU S S. Urban rail transit passenger flow forecasting for large special event based on AFC data[J]. Journal of Beijing Jiaotong University, 2018, 42(1): 87-93. |
| [30] |
赵梦鸽, 李林. 基于ARIMA模型的工业生产指数预测分析[J].
经济研究导刊, 2020(3): 30-36.
ZHAO M G, LI L. Industrial production index forecast analysis based on ARIMA model[J]. Economic Research Guide, 2020(3): 30-36. |
 2020, Vol. 37
2020, Vol. 37

