随着科学技术的发展，管道已经成为最经济的运输水工具。然而，供水系统会产生如管道破裂和管道泄漏等问题^[1]。因此，一个可靠的水管道设计是十分必要的。一个合理安全水管道系统的设计是艰难和复杂的，存在许多不确定性，如外部环境，管道内部压力变化等。因此，水管道系统的研究是相当有价值的。

管道系统设计的第一步是清楚地了解流体通过管道的行为特性。计算流体动力学(CFD)技术是从速度剖面、压头损失来研究流动性能的主要方法，是目前研究流体动力学问题的一种省时且准确的方法。准确地理解和处理管道内的流体特性是必要的，特别是在入口区域，因为流体运动是变化的。例如，工业上需要在管道的精确位置安装用于测量流体在管道内变化特性的仪表。为了更加准确地检测流体的特性，仪表需要安装在入口区域之后，即流体从层流状态开始转换为湍流状态，因此工程师应该对入口长度有一个精确的预测^[2]。

分析物理现象有3种方法：理想分析、试验和数学模型。然而，理论分析可能无法接近实际情况，试验成本相对昂贵。因此，数学建模已经成为工程行业中最流行和最有用的技术调查方法。该方法可用于计算机模拟和分析流体流动特性、压力梯度和传热现象，广泛应用于航空航天、水务公司、化工厂等行业。

利用CFD技术解决物理问题有3个核心步骤。首先，物理问题的定义是基于相对流动性质。然后，建立基于一系列控制方程的数学模型。例如，在流体动力学研究中，纳维-斯托克斯方程被用来表示流动行为，但这些偏微分方程很难求出来。因此，适当的预测对简化方程和数值解是必要的。最后，在确定合适的边界条件后，通过有限差分法(Finite Difference Method)、有限元法(Finite Element Method)和有限体积法(Finite Volume Method)对求解过程进行处理。

这个模拟试验假设介质是空气和水。同时，假设流动是不可压缩、温度恒定和稳态的。图1描述了一个二维管道外形，由于几何形状是围绕轴线对称的，所以管道外形是整个管道结构的一半。这种几何结构包括中心线、管壁、进口和出口。先建立管的半径R为0.015 m，长度L为5 m的模型，再设置不同管径进行数值模拟。

图 1(Figure 1)

图 1 管道几何结构 Figure 1 Pipe geometry structure

在仿真过程中，精细网格对精确分析具有重要意义。初始状态下网格划分时是相对粗糙的，所以将对网格独立处理进行优化。网格不断细化，直到仿真结果不受网格优化的影响。图2显示处理后的精细网格。径向和轴向划分别为16和1 900；平均纵横比值为4.491 2。生成网格后，在指定的设置下导入Fluent软件，得到仿真结果。

图 2(Figure 2)

图 2 网格结构 Figure 2 Grids construction

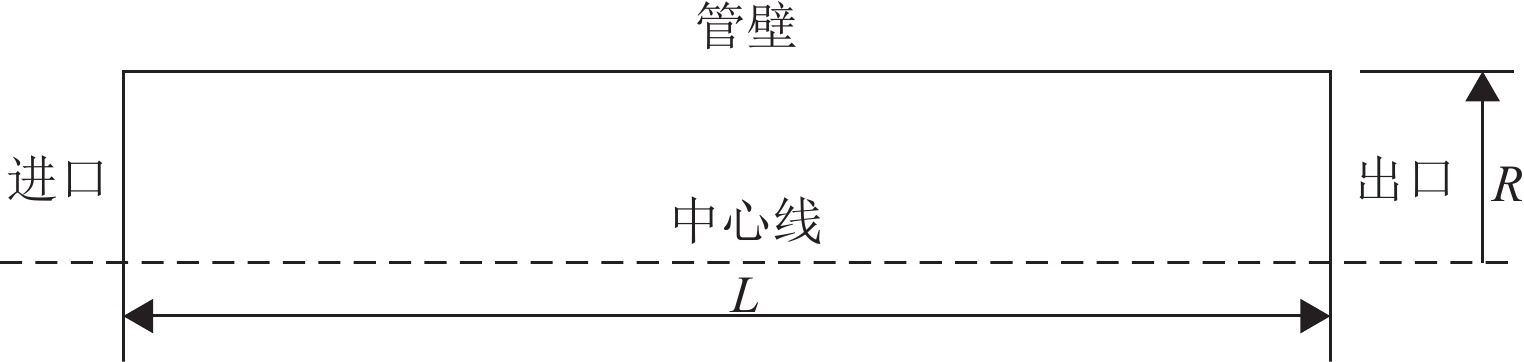
(1) 流体入口长度：流体在管道流动中的速度分布取决于流体的运动特性，包括层流和湍流。通过观察管道内的流体运动变化生成管道截面上的速度分布模式。图3和图4为不同雷诺数下水和空气流动模拟的速度剖面变化，雷诺数值范围为1 000~50 000。横坐标为速度，纵坐标代表管内速度分布点。

图 3(Figure 3)

图 3

图 4(Figure 4)

图 4

从图3和图4可以看出，当雷诺数分别为1 000和2 000时，速度分布呈抛物线形且明显锐化。此外，最大速度是在中心线。同时，在雷诺数分别为5 000、10 000、50 000时，横截面附近的速度色散相对平缓。换句话说，湍流边界层的厚度更小，因为壁面附近剪切应力更大。这与剪切应力公式计算出的结论相吻合。由于壁面附近黏度较高，湍流流型较层流更为平坦。在模拟过程中对98种水流案例进行了测试，以研究入口区的变化情况。在这些模拟中，水是介质。其中48项试验用于研究层流入口区域，其余试验用于湍流研究。模拟的目的是通过改变管道直径和雷诺数来观察入口距离的变化趋势。

图 3(Figure 3)

图 3 对应不同雷诺数的管道水流速度剖面 Figure 3 Velocity profile for water passing a pipe with different Reynolds numbers

图 4(Figure 4)

图 4 对应不同雷诺数的空气在管道内的速度剖面 Figure 4 Velocity profile for air passing a pipe with different Reynolds numbers

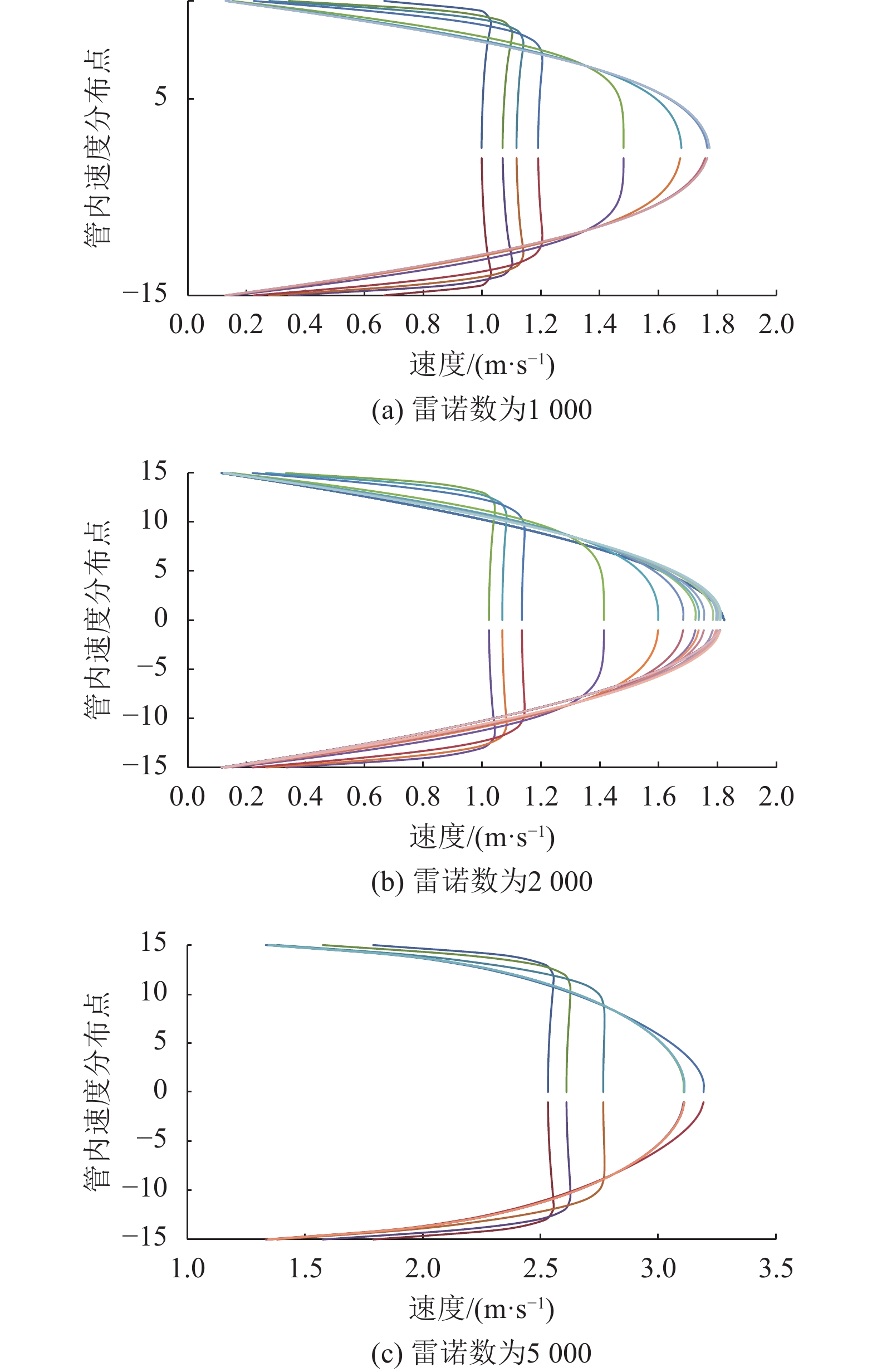
图5(a)、(b)分别为层流和湍流内部流特性示意图，冷色为边界层，暖色为非黏性核心区。根据无滑移边界设置，沿壁面速度为0 m/s。图5(a)中的流体运动特性表明层流运动平稳，没有加速度，同时，图5(b)显示，由于涡流的作用，管里无黏芯内的流动加速。

图 5(Figure 5)

图 5 管口内流体特性示意图 Figure 5 Visualization of laminar pipe-entrance flow

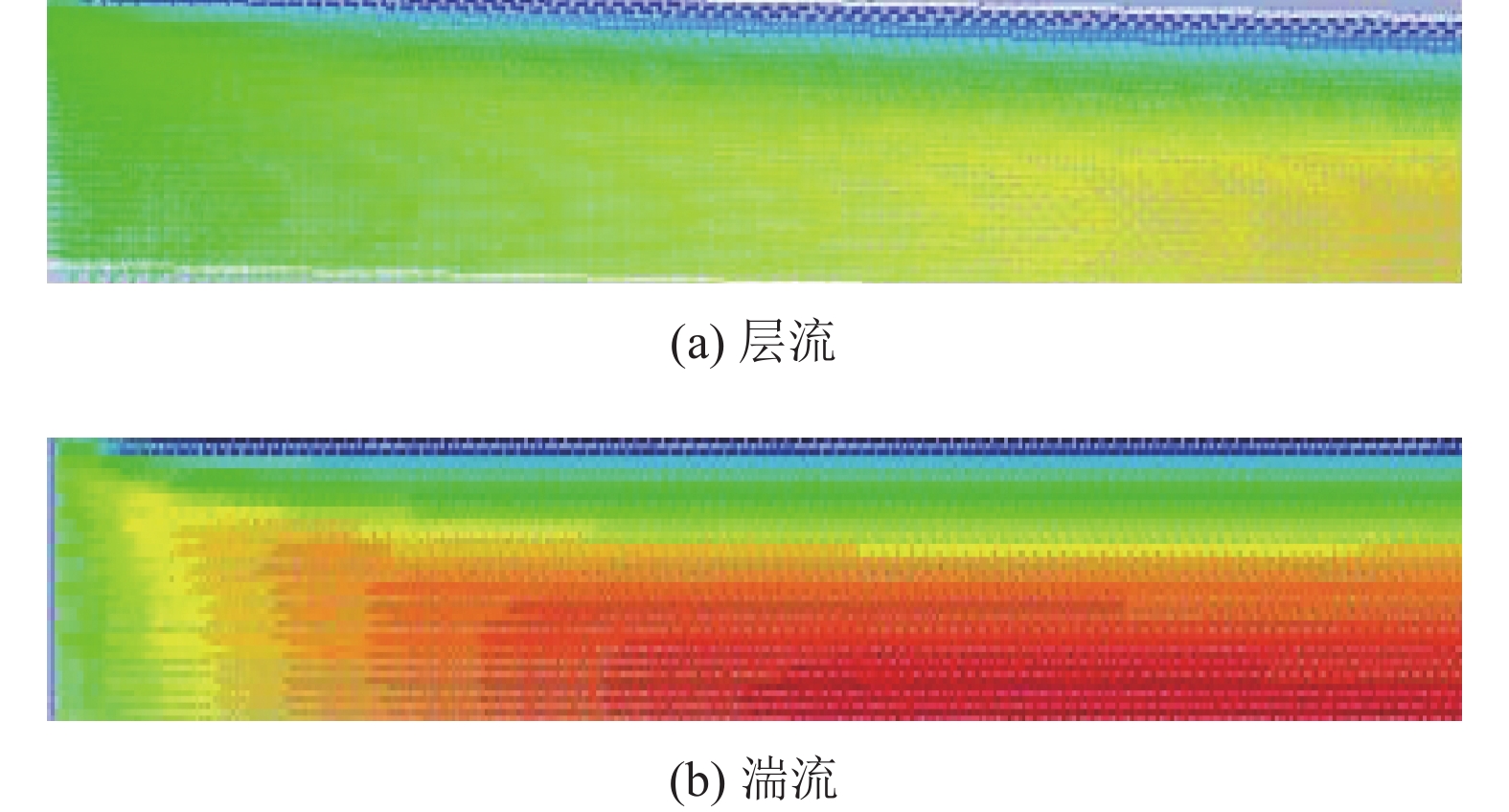
图6展示了管径分别为0.01，0.02，0.03，0.05，0.08，0.10，0.30 m的层流入口长度与雷诺数的对应关系。这表明入口长度随着雷诺数的增加而增加。此外，在雷诺数相同的情况下，直径越大的管道入口区域越长。在小直径管道上，雷诺数对入口长度的影响不明显，尤其是在直径为0.01 m和0.02 m的管道内，入口长度值非常接近。

图 6(Figure 6)

图 6 管径处层流时入口长度与雷诺数的关系 Figure 6 The relationship between entrance length and Reynolds number for laminar flow at pipe diameter

图7所示为湍流进口长度与雷诺数之间的关系。当雷诺数较高时，进口长度几乎是稳定的。结果与理论计算分析结果一致。与层流相比，入口长度对湍流的影响较小。随着管道尺寸的增加，入口长度仅略有增加。在48次湍流试验中，直径为0.03 m时，入口长度是最大的。因此，入口长度几乎取决于管道的尺寸，且最小入口长度约为160d(d为管径)。

图 7(Figure 7)

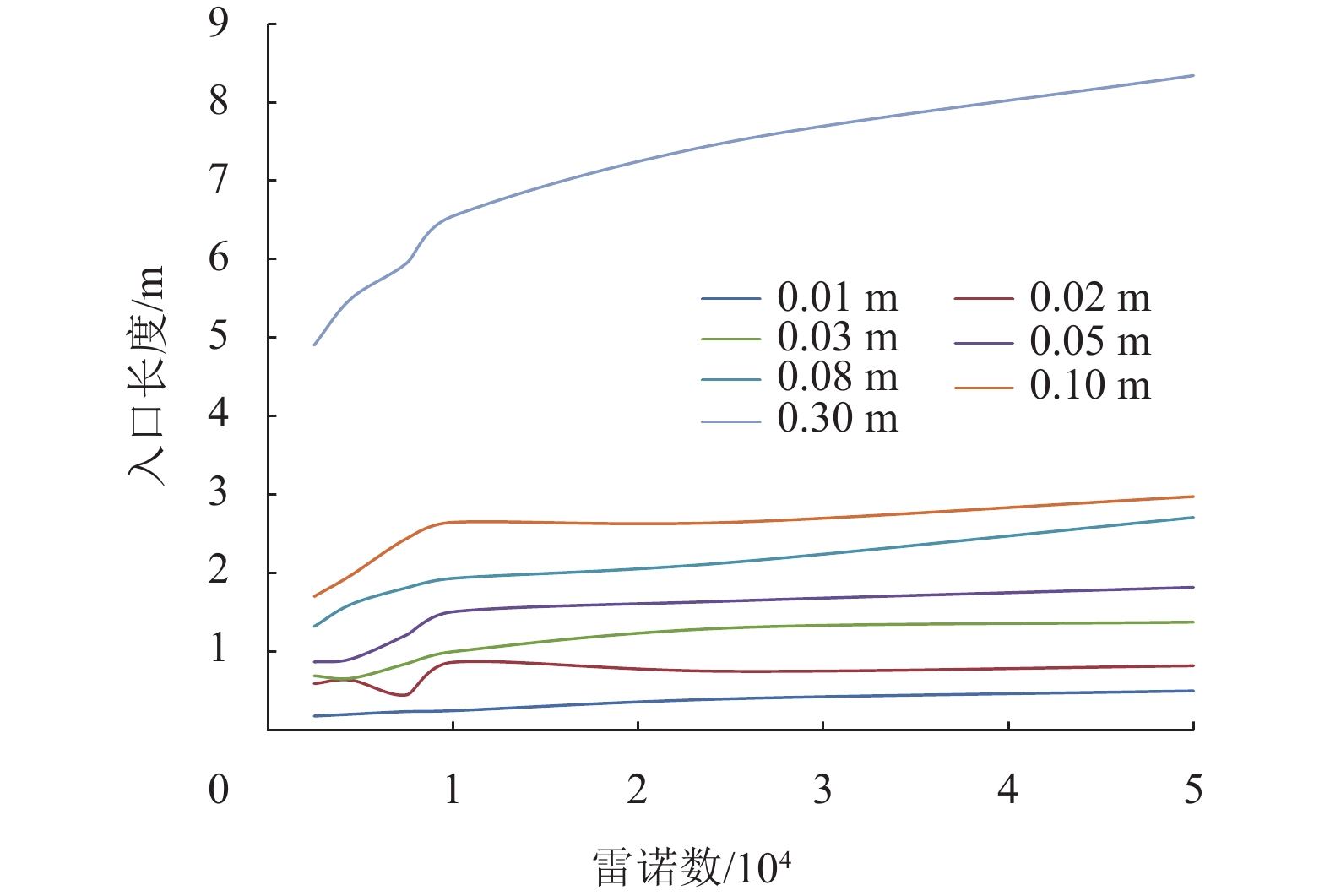
图 7 管径处湍流时入口长度与雷诺数的关系 Figure 7 The relationship between entrance length and Reynolds number for turbulent flow at pipe diameter

(2) 管内流体压降：当流体进入充分发育区域时，剪切应力和速度剖面是恒定的。因此，压力沿管道长度呈线性下降。此外，与层流相比，湍流的压力下降更快。此外，层流和湍流的压降均呈线性变化。图8描述了速度与压降的关系。但是，当速度在大约0.1 m/s到0.2 m/s之间时，会有轻微的波动。这可能是由于从层流过渡到湍流，过渡区流动特性较复杂。

图 8(Figure 8)

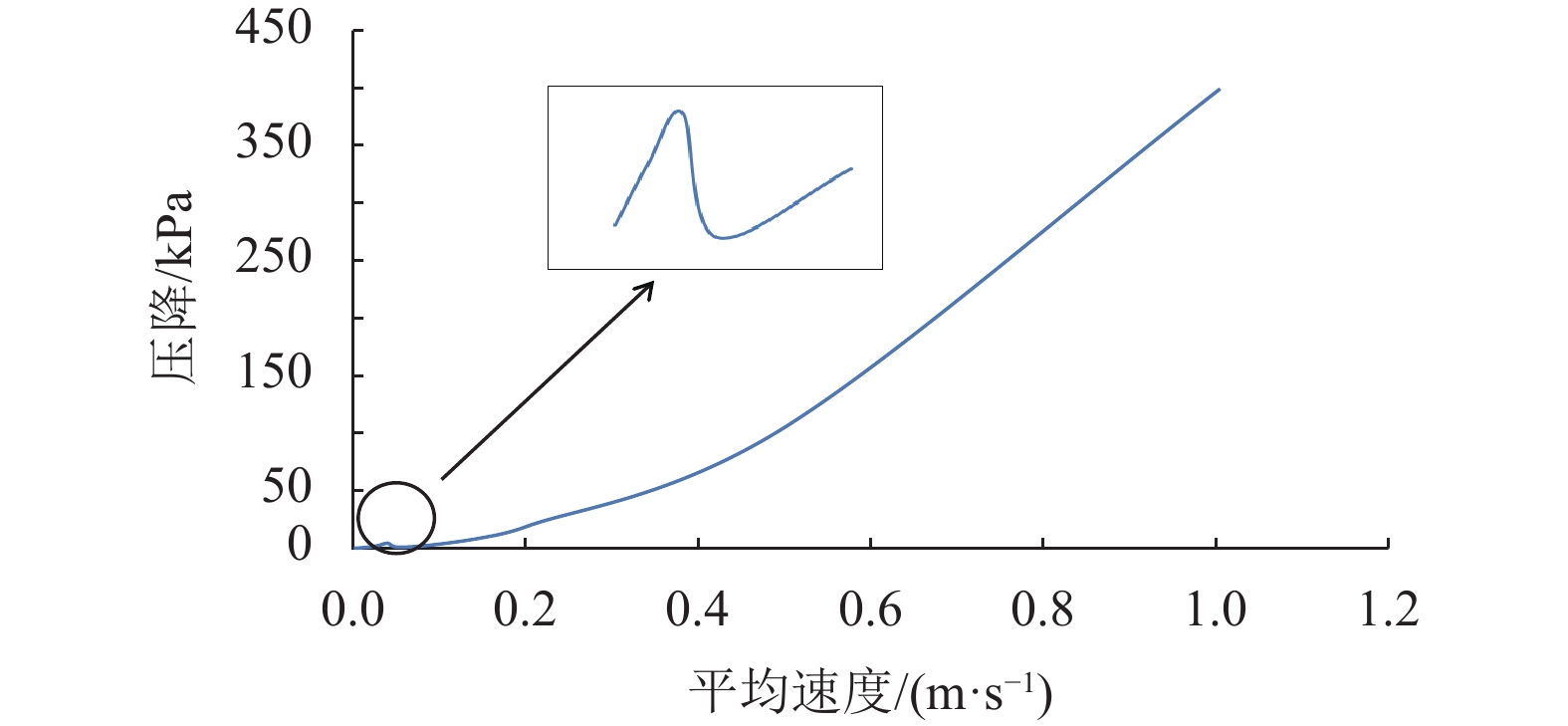
图 8 直径0.08 m管道中水流平均速度与压降的关系 Figure 8 The simulation evidence for transition for water flow in a pipe with diameter 0.08 m

(3) 压头损失：图9显示了雷诺数从50到5 000与摩擦系数之间的关系。摩擦曲线由层流和湍流2部分组成。摩擦曲线表明，湍流区摩擦系数存在差异。由于压头损失部分的摩擦系数取决于剪切应力和速度。湍流的剪切应力比层流大，因为湍流的黏性较大。此外，速度剖面很快就变成常数。因此，摩擦系数在湍流过程中几乎是稳定的。

图 9(Figure 9)

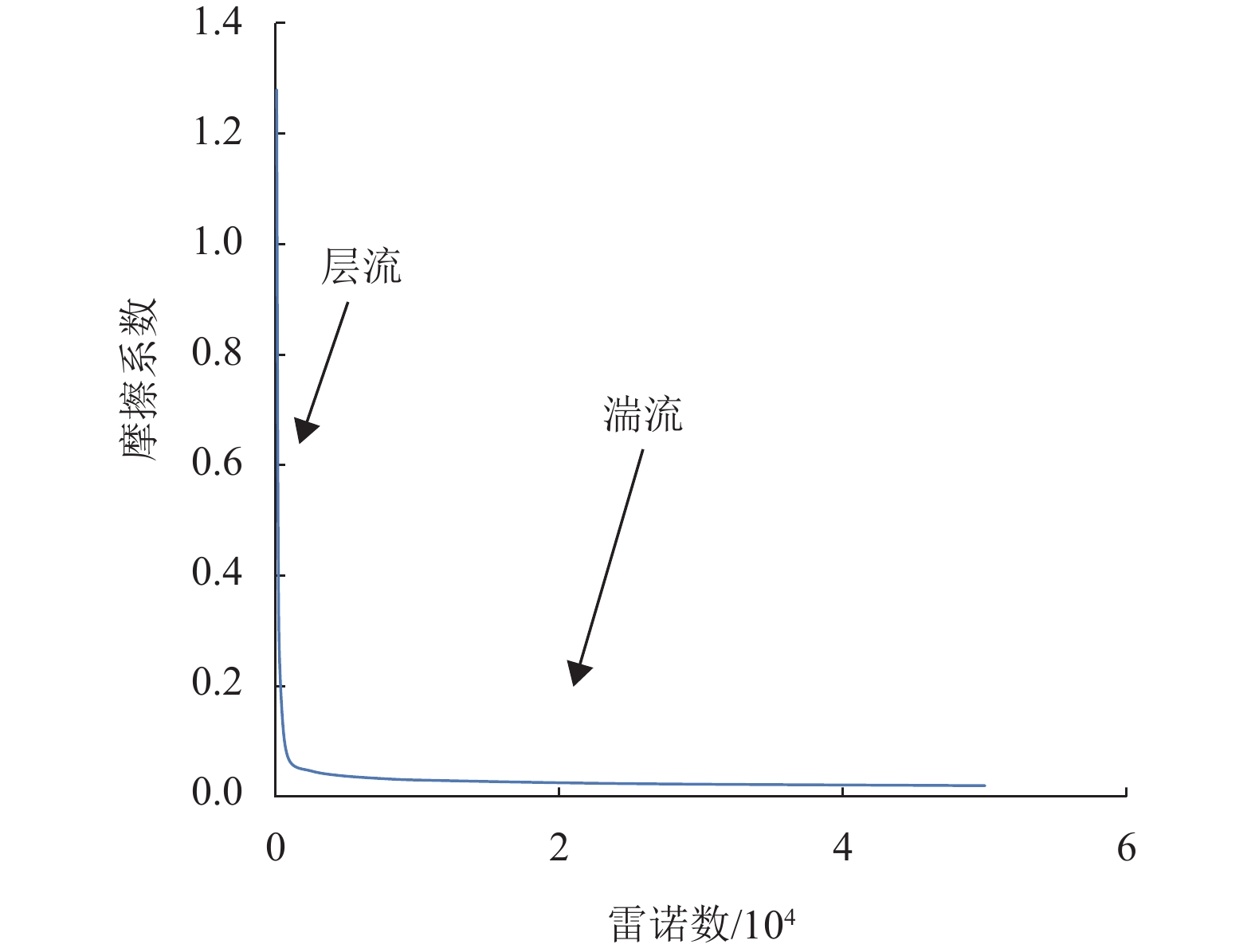
图 9 摩擦系数与雷诺数的关系 Figure 9 The relationship between friction factor and Reynolds number

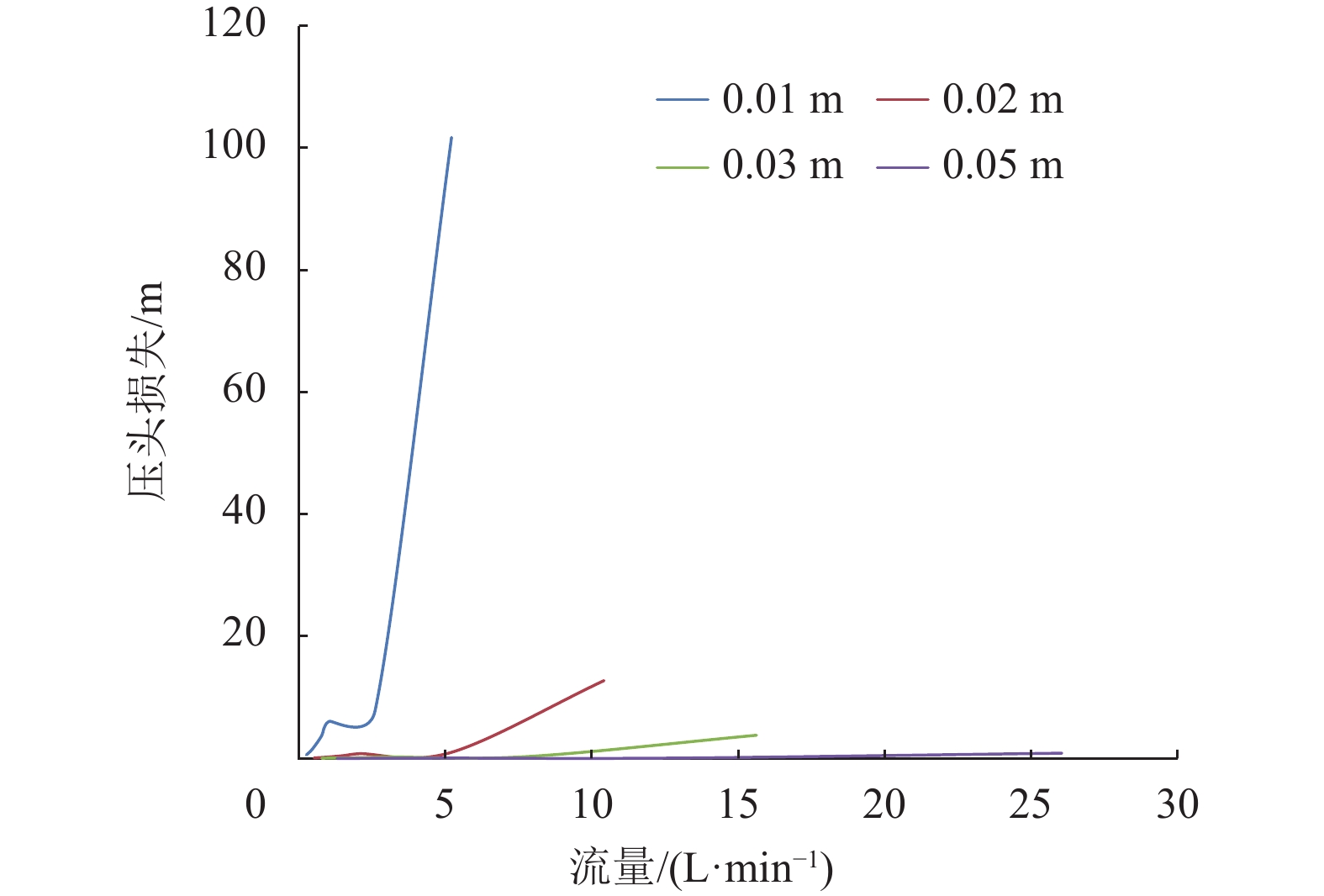
从图10和图11可以看出，在直径为0.01 m、0.02 m、0.03 m和0.05 m的管道中，压头损失随体积流量的变化而变化。2种压头损失数据都表明压头损失随流量的增加而增加。与层流相比，湍流会损失更多的能量。这清楚地表明湍流中存在着巨大的能量损失，特别是直径为0.01 m的管道。截面越大的管道节能效果越好。

图 10(Figure 10)

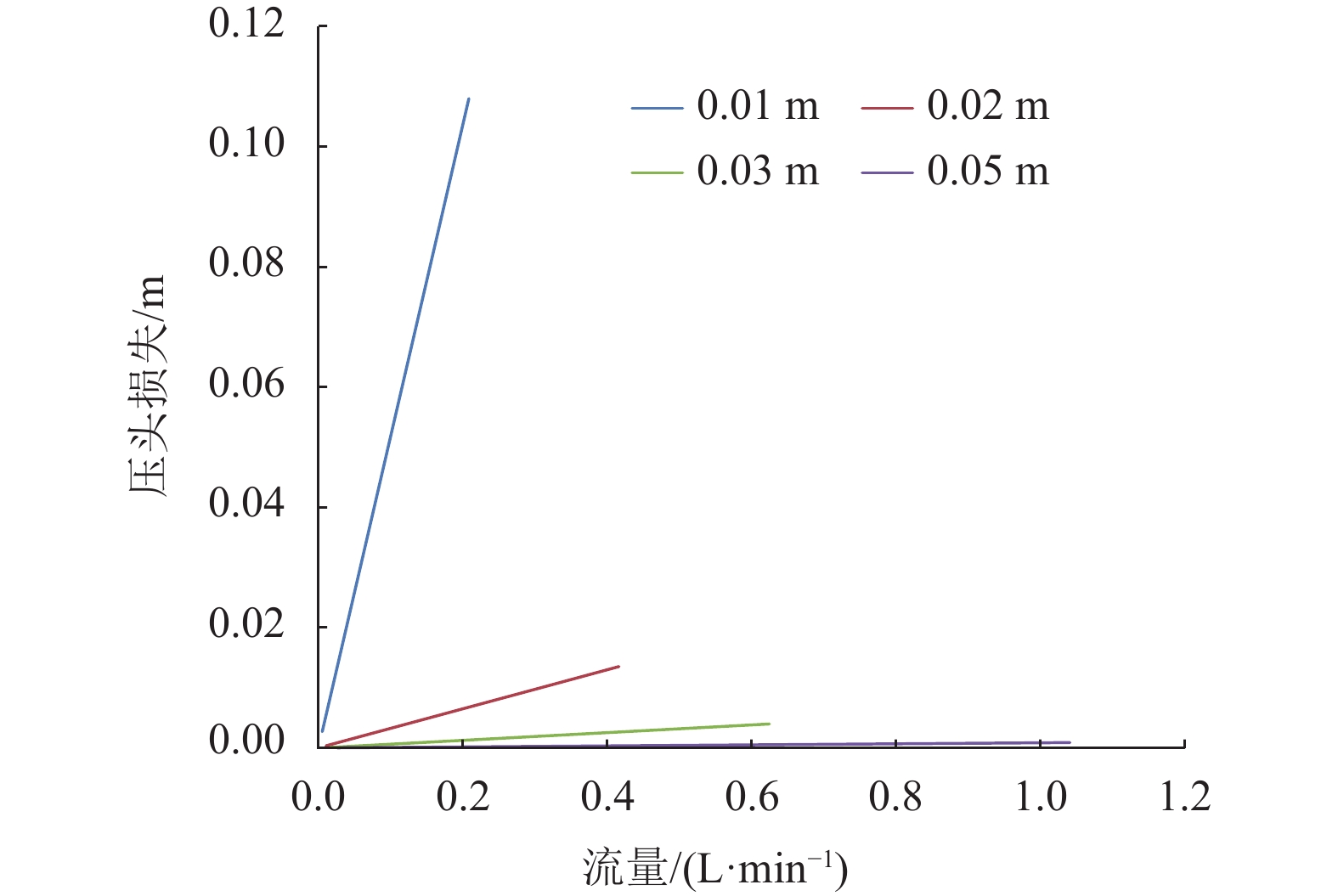
图 10 层流时流量和管径对压头损失的关系 Figure 10 Flow rate and pipe diameter influence on the head loss at laminar flow

图 11(Figure 11)

图 11 湍流时流量和管径对压头损失的影响 Figure 11 Flow rate and pipe diameter influence on the head loss at turbulent flow

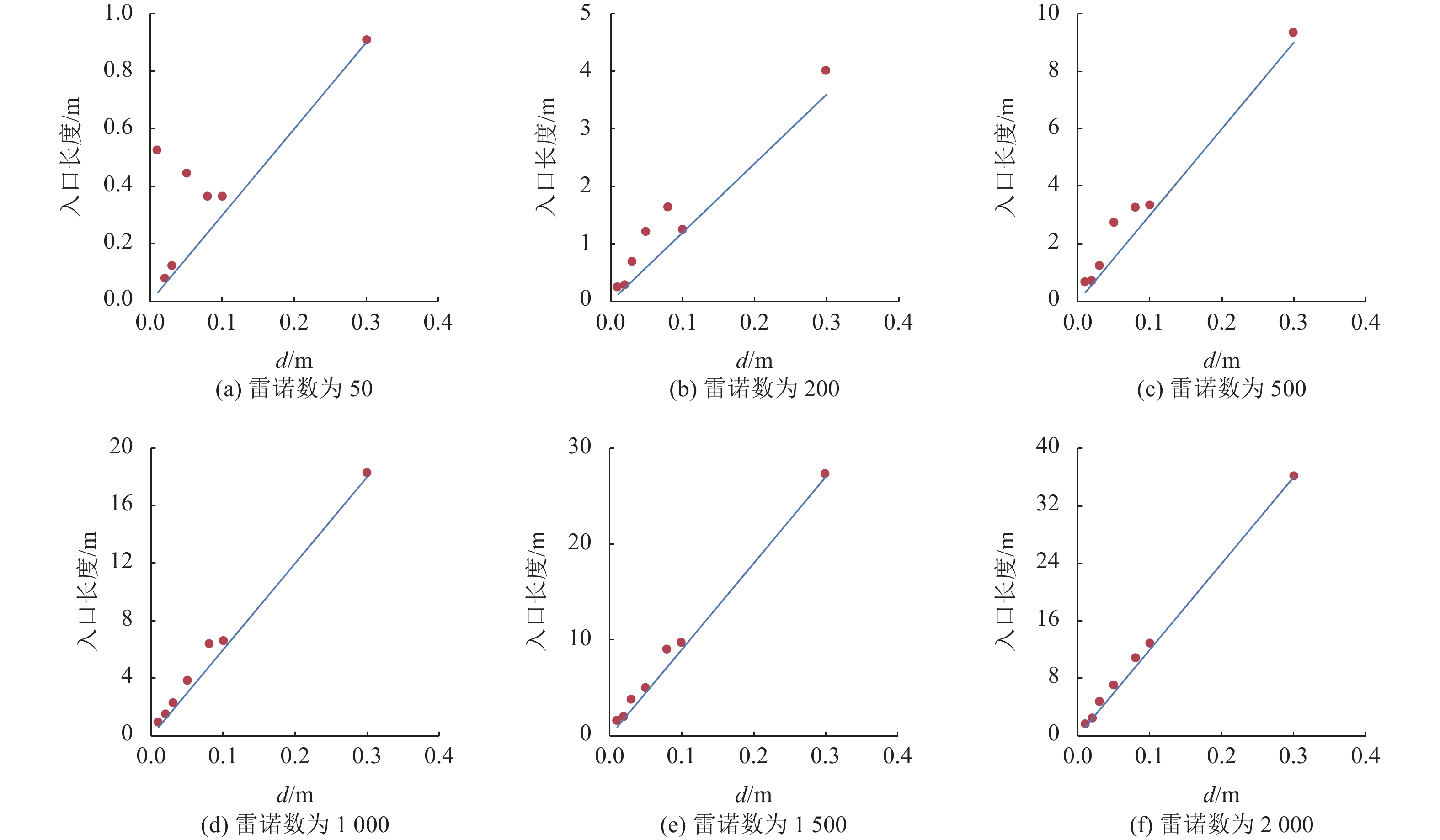
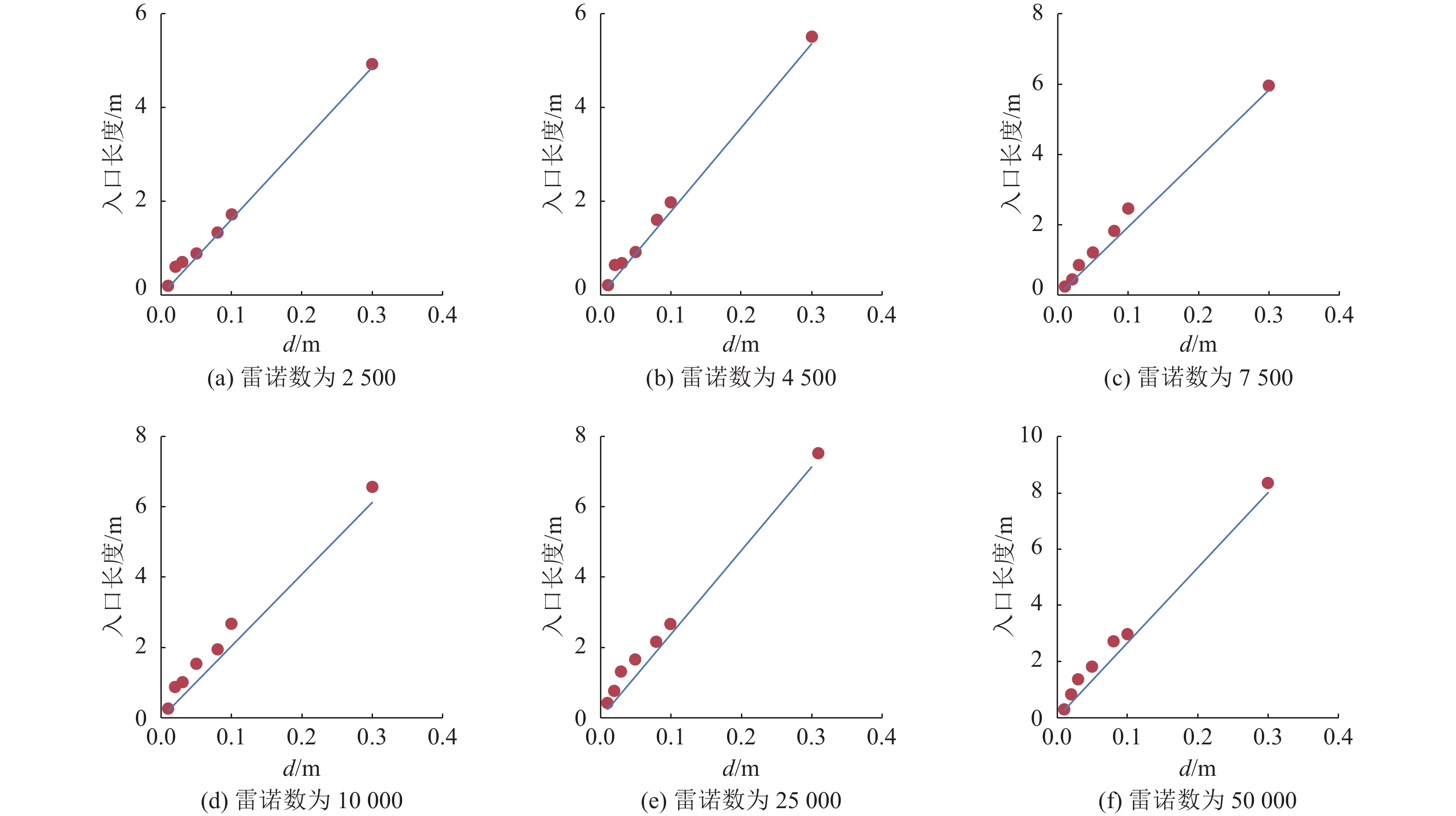
图12和图13为层流和湍流理论计算和CFD模拟计算的入口长度对比。红点表示模拟结果，蓝线表示理论结果。计算结果表明，基于CFD方法的入口长度与理论计算结果吻合较好。然而，湍流模拟结果与理论结果的相关性比层流大，因为低雷诺数的黏度非常高。这种特殊的运动是剧烈的，很难控制沿边界层的流动。因此，模拟层流的精度可能无法保证。入口长度的仿真值仅略大于理论计算结果。因此，这些结果证明CFD是一种准确的流场模拟方法。^[3]

图 12(Figure 12)

图 12 层流模拟中入口长度的验证 Figure 12 Validation for entrance length in laminar flow simulation

图 13(Figure 13)

图 13 湍流模拟中入口长度的验证 Figure 13 Validation for entrance length on turbulent flow simulation

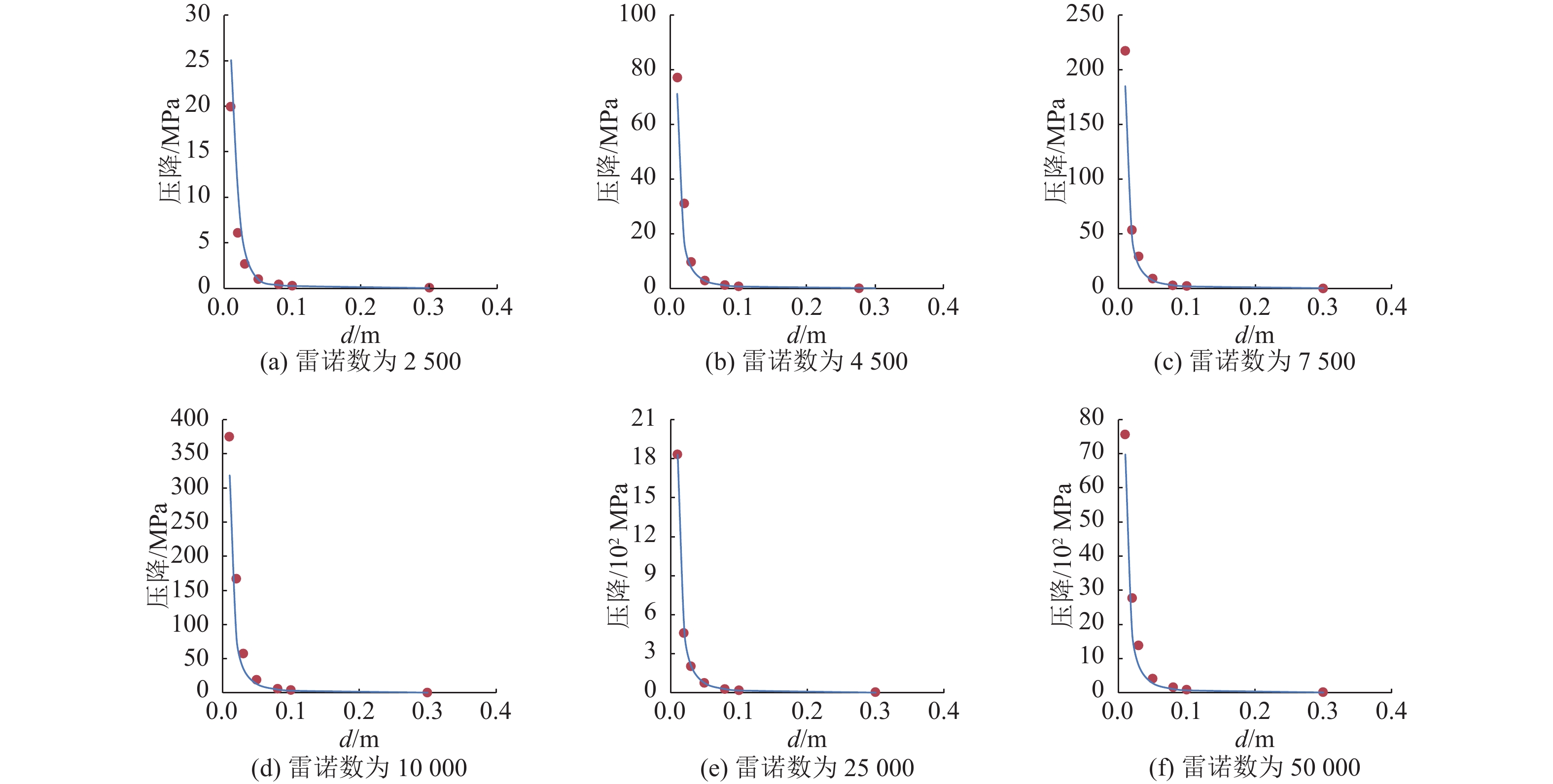
由图14和图15可以看出，通过模型模拟和理论公式计算得出的压降结果比较。红点表示模拟结果，蓝线表示理论结果。横坐标为管径，纵坐标为压降。从图中可以看出，模拟与理论预测的压降相差不大。因此，计算流体力学在该工程中的应用是正确和精确的，具有重要意义。它是研究和分析管道流动现象的一个很好的工具。^[4]

图 14(Figure 14)

图 14 层流模拟压降验证 Figure 14 Validation pressure drop on laminar flow simulation

图 15(Figure 15)

图 15 湍流模拟压降验证 Figure 15 Validation for pressure drop on turbulent flow simulation

为了简化数值模型，模拟湍流运动时可以忽略子层黏度来选择标准壁面函数。基于CFD仿真方法及壁面定律绘制出速度剖面预测图(见图16)。其中黄色直线表示对应壁面定律式(1)的标准变化趋势，其中 $ {u}^{+} $ 和 $ {y}^{+} $ 分别代表无纲量墙距和无纲量速度， $ k $ 和 $ {c}^{+} $ 分别代表卡冯卡曼常数和一个常数，而且黄色的速度曲线是在亚层区域的。为了验证数值的准确性， $ {y}^{+} $ 值应该满足在30到100。由图16可以看出，雷诺数为2 500~50 000时，该模型的模拟 $ {y}^{+} $ 值与试验结果具有较高的一致性，因此，可以证明CFD仿真方法结果是较为准确的。此外，除了雷诺数为2 500和4 500之外，其他雷诺数的 $ {y}^{+} $ 数值大部分都在30到100之间。因此上述速度剖面和压降模拟结果是精确的。然而，雷诺数为2 500和4 500时的 $y^{+}$ 不满足标准壁面函数的条件。由于雷诺数取值范围为2 000~5 000流体流动由层流过渡到湍流，在此范围内是一个复杂的不确定区域。因此， $ {y}^{+} $ 的值不能匹配墙壁定律。综上所述，通过CFD仿真可以保证整个项目的精度^[5]。

图 16(Figure 16)

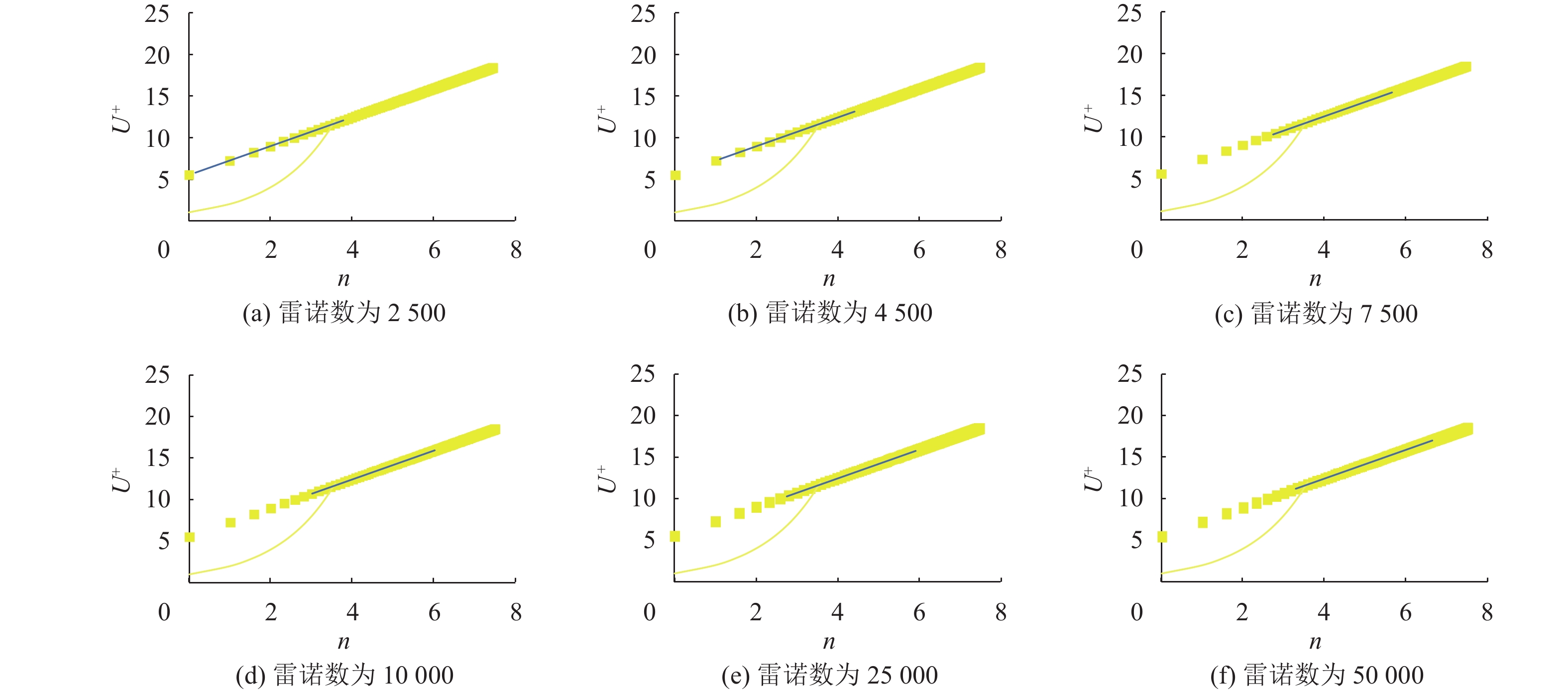
图 16 基于壁面定律的速度剖面预测 Figure 16 Velocity profile prediction based on the wall law

本研究基于CFD技术的Ansys Fluent 15.0软件对直管中空气和水的流动进行模拟，试图了解管道中流体的运动规律。研究假设流体是不可压缩和稳定的，通过一个光滑的圆截面管道。k-ε模型可以模拟流体流动从层流到湍流过渡的过程,应用于解决流体运动问题。

本研究共进行了98项试验。所得到的空气和水的速度剖面图表明，在层流或湍流中，速度剖面是抛物线型的，但在湍流区速度曲线斜率小于层流区的，所以在层流的速度图会更清晰。雷诺数范围在50~2 000之间，流体流动到达完全发达区域。流动压力变化结果表明，随着流量的增加，压力降增大，在直径较大的管道中，压力梯度较小，压力差也更小，特别是当直径为0.3 m时。因此，大直径管道具有更少的压头损失。