2. 广东顺德创新设计研究院,广东 佛山 528300
2. Guangdong Shunde Innovative Design Institute, Foshan 528300, China
随着高新技术的发展,近年来微液滴/微气泡已被广泛用于医学检测、材料合成、环境保护、石油化工、食品安全[1-5]等领域。在众多的应用中,微液滴或微气泡的尺寸和生成频率是两个非常重要的参数,是直接影响其应用效果的技术指标[6]。Tuckerman等[7]在20世纪80年代在集成电路冷却上提出“微通道”的理念,解决了微液滴大小和均匀度问题,开启了微通道内科学问题的研究。十字交叉型微通道在控制微液滴尺寸生成范围和生成的稳定性上体现了优越性,得到了广泛关注[8]。
许多研究人员对十字交叉型微通道内液滴的形成开展了数值模拟。Chen等[9]研究了微通道内Taylor气泡的挤压流型和滴状剪切流的产生机理和流型转变的临界毛细数数。Raj等[10]的研究表明,要使液滴正常产生,接触角应不小于140°。Somasekhara等[11]研究了流变参数对微通道内非牛顿流体液滴形成机制的影响。王维萌[12]对十字交叉型微通道内液滴的形成机理开展了三维数值模拟研究。杨丽等[13]研究表明两相流速和连续相黏度是影响流动聚焦型液滴体积的关键因素。陈珉芮等[14]采用用户自定义(User Defined,UDF)首次用正弦函数定义分散相流速,研究表明液滴尺寸和生成时间也会出现周期性的变化。
液滴形成的关键问题在于微尺度多相流控制。关于三维十字交叉型微通道内液滴的形成机理仍然是当前研究的热点。本文采用Fluent软件中VOF模型对三维十字交叉型微通道内液滴的形成过程进行数值模拟研究,探讨液滴生成的规律。
1 两相流的数值模型与求解 1.1 控制方程本文研究十字交叉型微通道内油包水型液滴的形成,其中连续相为油,分散相为水。油水两相流在微通道内同时存在且互不相溶,存在相界面。VOF模型,又称为体积分数法,是经典的相界面追踪方法。网格单元内某相流体
每个网格单元中两相流体的体积分数之和为1,即有
| $ \frac{\partial {\alpha }_{{\rm{d}}}}{\partial {t}}+\nabla \cdot \left({ U}\cdot {\alpha }_{{\rm{d}}}\right){=0} $ | (1) |
| $ \frac{\partial {\alpha }_{{\rm{c}}}}{\partial {t}}+\nabla \cdot \left({ U}\cdot {\alpha }_{{\rm{c}}}\right){=0} $ | (2) |
其中
| $ \nabla \cdot{ U}{=0} $ | (3) |
| $ \frac{\partial \left(\rho { U}\right)}{\partial {t}}+\nabla \cdot \left(\rho {{{UU}}}\right){=-}\nabla {p}+\nabla \cdot(\mu (\nabla { U}+\nabla {{ U}}^{{{\rm T}}}))+\rho {g}+{{F}}_{{\rm{s}}} $ | (4) |
其中
| $ \rho {=}{\alpha }_{{\rm{c}}}{\rho }_{{\rm{c}}}{+(1-}{\alpha }_{{\rm{c}}}{)}{\rho }_{{\rm{d}}} $ | (5) |
| $ \mu {=}{\alpha }_{{\rm{c}}}{\mu }_{{\rm{c}}}{+(1-}{\alpha }_{{\rm{c}}}{)}{\mu }_{{\rm{d}}} $ | (6) |
表面张力
| $ {{F}}_{{\rm{s}}}{=}\sigma \frac{{2}\rho \kappa }{{\rho }_{{\rm{c}}}+{\rho }_{{\rm{d}}}}\nabla {\alpha }_{{\rm{c}}} $ | (7) |
其中
| $ \kappa = \nabla \hat {{n}} $ | (8) |
| $ \hat {{n}} = {{n}}/\left| {{n}} \right|,\;\;{{n}} = \nabla {\alpha _{\rm{c}}} $ | (9) |
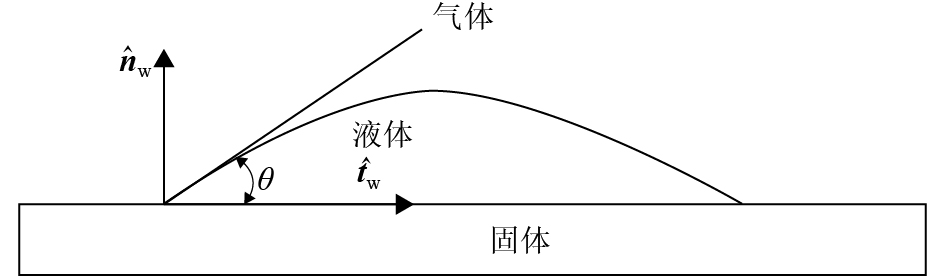
在靠近壁面处,接触角θ定义为气液界面的切线与液固交界线之间的夹角,是壁面润湿性的度量,如图1所示。其中
| $ \hat {{n}} = {\hat {{n}}_{\rm{w}}}{\rm{cos}}\; \theta {{ + }}{\hat {{t}}_{\rm{w}}}{\rm{sin}}\; \theta $ | (10) |
|
图 1 接触角
|
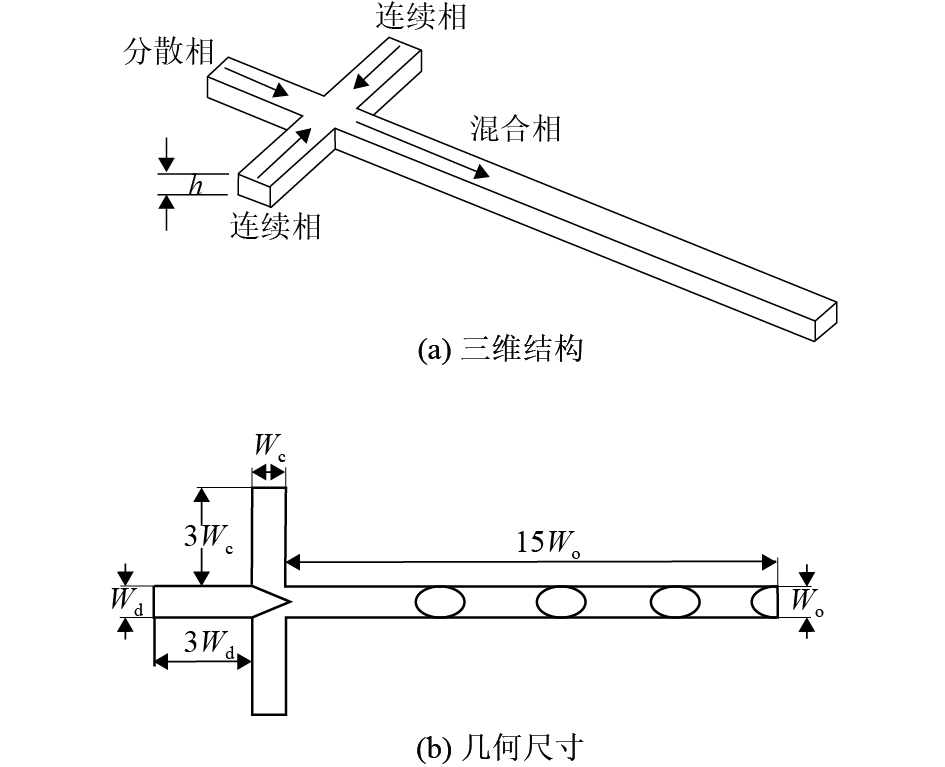
如图2所示,十字交叉型微通道由水平管道和垂直管道组成,其中从水平管道流入的液体为去离子水,作为分散相,从两侧垂直通道流入的液体为氟油HF7500,作为连续相。微通道尺寸由
|
图 2 十字交叉型微通道的三维结构及几何尺寸 Figure 2 Three-dimensional geometry and size of cross focusing micro-channel |
在Fluent软件中选择多相流中的VOF模型,选择层流(Laminar)模型,选用基于压力的非稳态求解器。边界条件设置如下:油相和水相都设置为速度入口,出口设为压力出口,壁面采用无滑移湿润性壁面。对于瞬态求解,选用PISO算法加快收敛,压力方程采用PRESTO!算法离散,动量方程选用二阶迎风格式(Second Order Upwind),体积分数的求解采用几何重构(Geo-Reconstruct)法。计算开始时将水相入口通道初始化为水,其余网格全部初始化成油以减少仿真时间。经验证本文迭代时间步长取
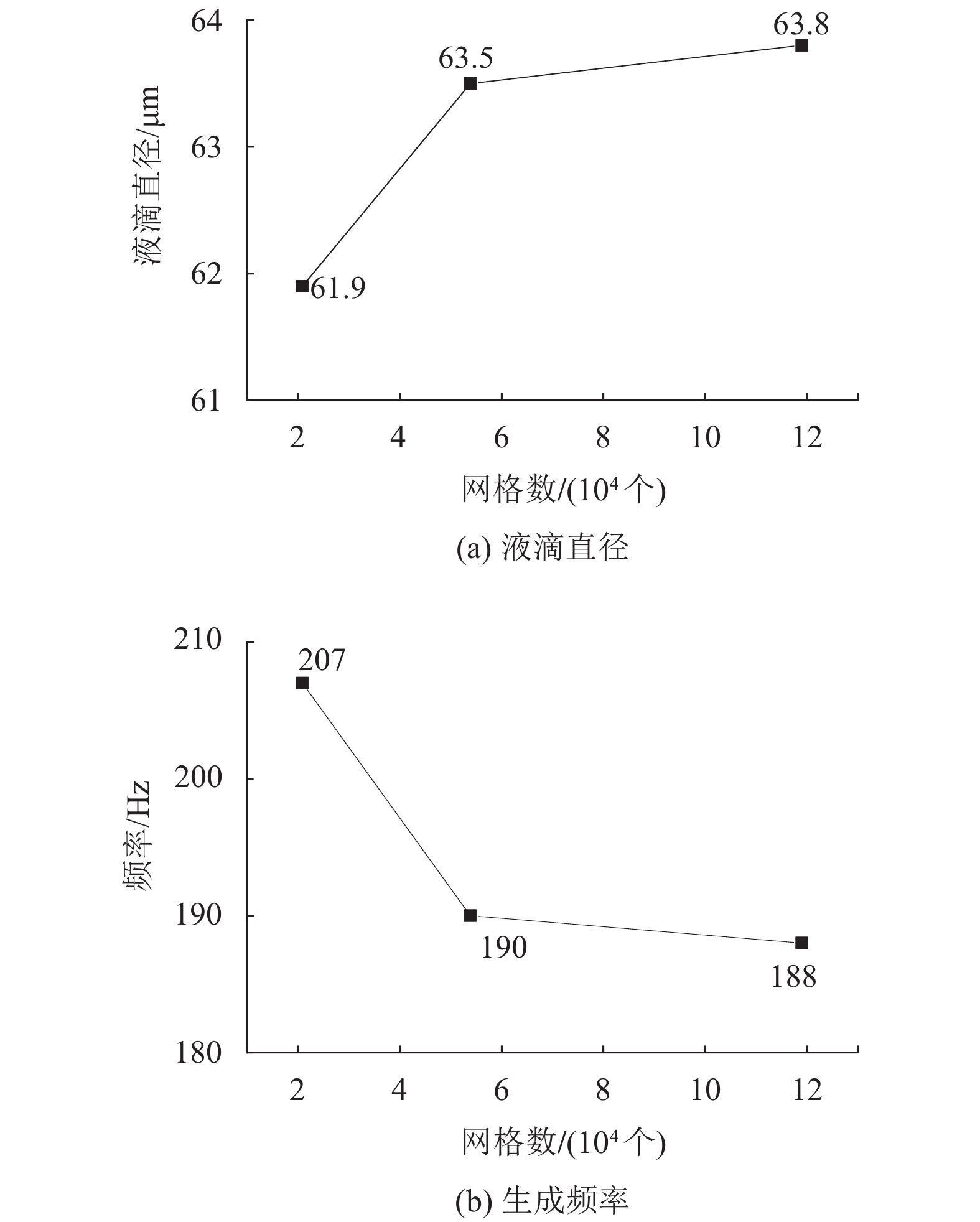
为了消除网格设置的疏密程度对计算结果的影响,采用六面体结构化网格对模型进行离散化时,将网格尺寸分别设置为3 μm、4 μm、5 μm,对应的网格数分别为1.2×105,5.6×104,2.2×104。由于数值模拟结果无法直接获得液滴尺寸和生成频率,考虑到实际中是测量液滴的球形直径,则将球的直径作为液滴尺寸的评价指标。本文通过在Fluent软件中监测通道出口处水相的质量流量以求出单个液滴的质量后,再以球的体积估算出液滴直径,最后通过Matlab软件处理仿真数据间接获得了液滴生成直径和生成频率。油水两相物性参数设置如表1所示,其中连续相选择氟油HF7500,分散相选择去离子水。当两相流速为
| 表 1 两相物性参数 Table 1 Physical properties of two phases |
|
图 3 网格独立性验证 Figure 3 Grid independence verification |
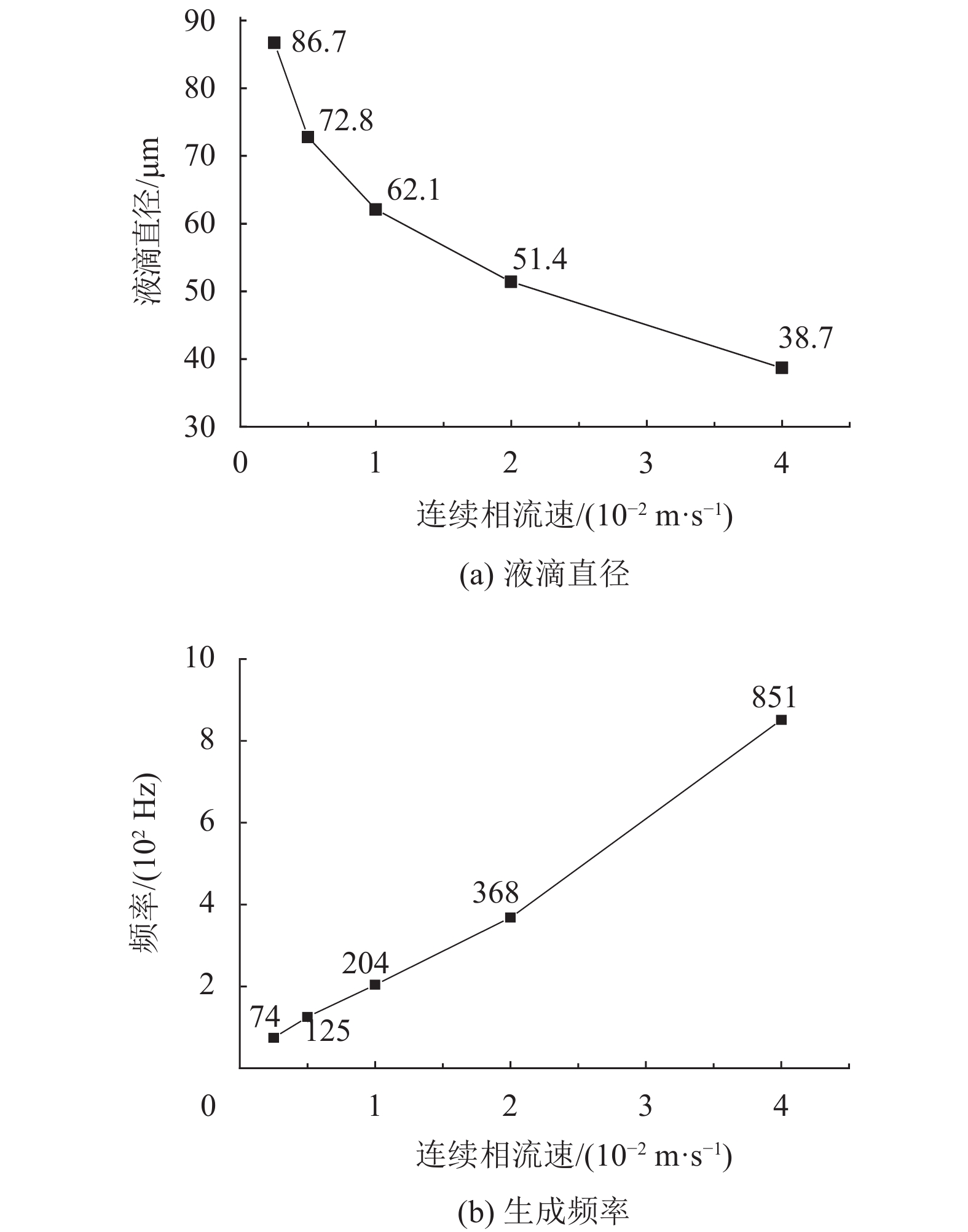
研究连续相流速

|
图 4 不同连续相流速时液滴的体积分数分布云图 Figure 4 Contours of droplet volume fraction at various continuous phase velocities |
|
图 5 连续相流速对液滴生成的影响 Figure 5 Influence of continuous phase flow rate on droplet generation |
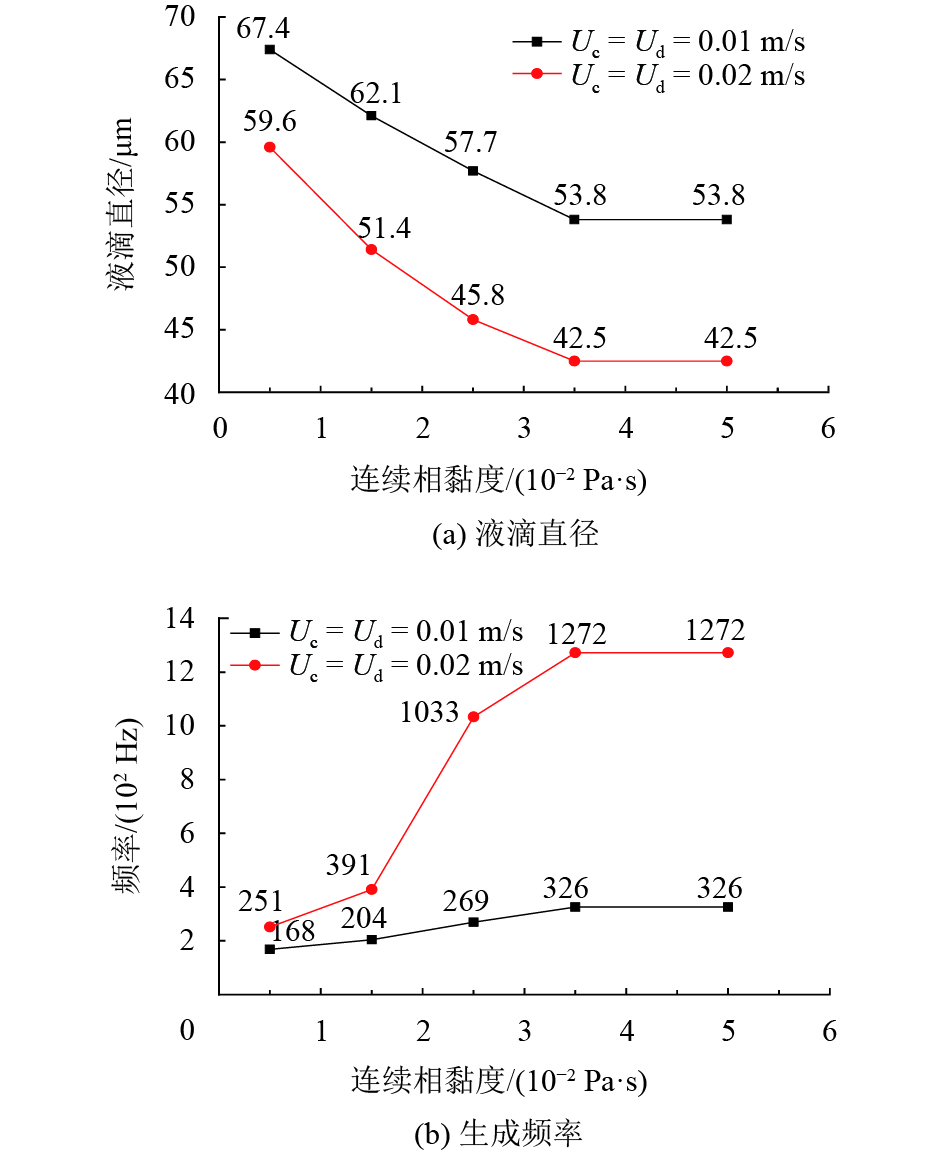
分析连续相黏度对液滴生成的影响时,令连续相流速等于分散相流速,分别设置为
|
图 6 连续相黏度对液滴生成的影响 Figure 6 Influence of continuous phase viscosity on droplet generation |
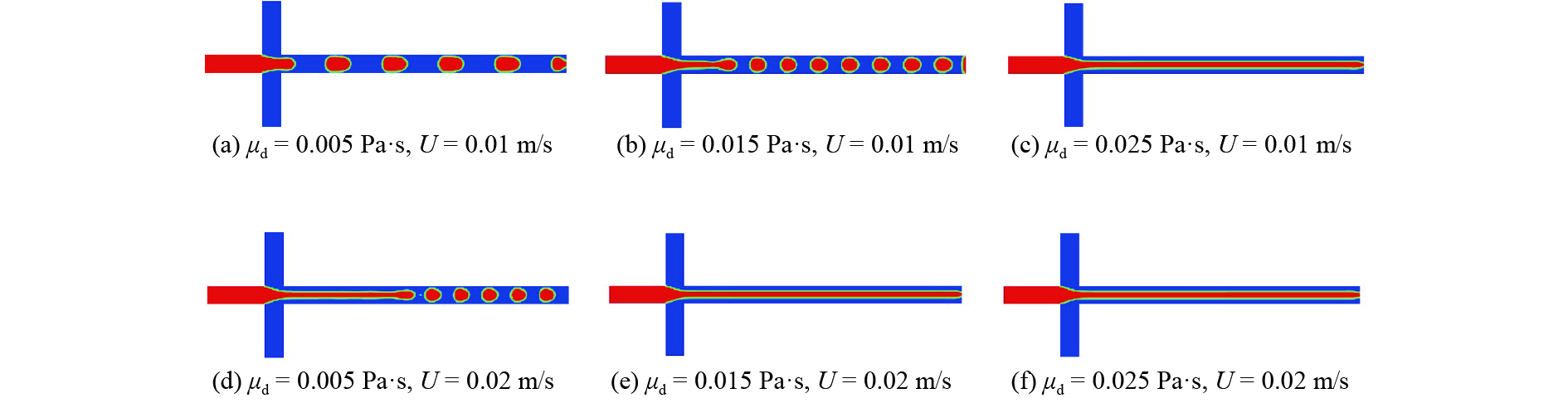
对于同一种连续相试剂,通常需要对多种分散相试剂生成液滴。当取不同分散相时,其黏度会发生变化。研究分散相黏度对液滴生成的影响时,固定连续相黏度
|
图 7 不同分散相黏度时液滴的体积分数分布云图 Figure 7 Contours of droplet volume fraction at various dispersed phase viscosity |
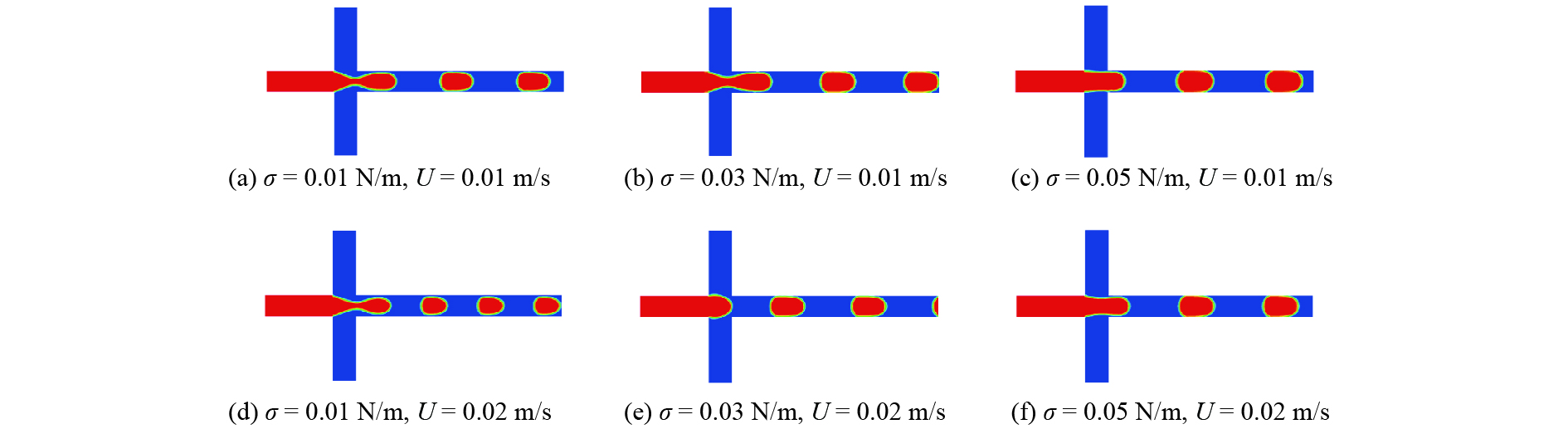
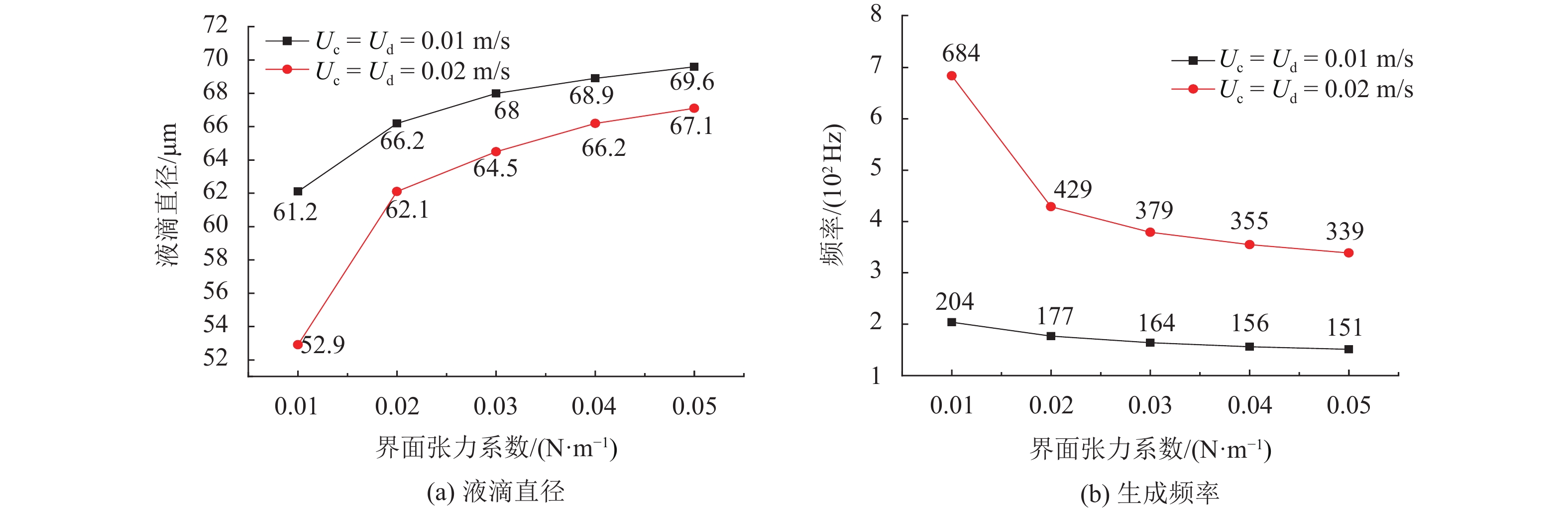
多相流与单相流系统相比存在界面张力。界面张力系数
|
图 8 不同界面张力系数时液滴的体积分数分布云图 Figure 8 Contours of droplet volume fraction at various interfacial tension coefficient |
|
图 9 界面张力系数对液滴生成的影响 Figure 9 Influence of interfacial tension coefficient on droplet generation |
本文最后研究了壁面接触角对液滴形成的影响。仿真中两相流速相等并分别设置为

|
图 10 |

|
图 11 |
本文通过数值模拟方法研究了十字交叉型微通道内液滴的形成过程,得到了以下结论。
(1) 随着连续相流速的增加,液滴生成直径减少,生成频率增高;(2) 液滴生成直径随着连续相黏度的增加而减少,生成频率的变化则相反;(3) 当分散相黏度超过连续相黏度时,出现射流现象而生成不了液滴;(4) 增加两相界面张力系数时,液滴生成直径变大,生成频率降低;(5) 对于油包水液滴的产生,增大壁面接触角有利于液滴的产生,当流速为
由于时间和实验条件的限制,本文虽然通过数值模拟取得了研究成果,但还存在诸多有待完善和深入研究的地方,未来可从以下方面开展研究。
(1) 本文未对数值模型进行实验验证,将数值模拟的动态过程与实验一一对照。后期为了提高研究的可靠性,可先通过实验验证数值模型的准确性再开展下文的研究;实验条件具备时,可将数值模拟与实验结果进行一一对比,提高严谨性。
(2) 仿真结果中液滴生成直径和频率的估算仍然是难点,下一步可采用无量纲化或者图像处理法处理模拟结果,提高研究的可靠性。
(3) 本文通过仿真数据得到了定性研究,后续研究可采用数据拟合的方法建立经验关联式,建立影响因素与液滴直径和频率的表达式,必要时采用实验验证经验关联式的准确性,例如建立接触角与液滴生成直径和频率的关联式指导表面改性处理。
(4) 本文未讨论微尺度多相流中另一个非常重要的概念——
(5) 本文只研究了影响液滴的生成直径和生成频率的各影响因素,未研究液滴形成过程中的动力学特性,未揭示影响趋势的深层机理,后续可深入研究,比如将仿真结果的压力场和流场、速度场同时分析以得出液滴产生的机理。
| [1] |
巩燕, 胡杰, 高彬, 等. 心血管疾病即时检测技术的研究进展[J].
中国科学: 技术科学, 2016, 46(11): 1116-1134.
GONG Y, HU J, GAO B, et al. Advances in real-time detection of cardiovascular diseases[J]. Science in China: Technical Science, 2016, 46(11): 1116-1134. |
| [2] |
林银银, 巫金波. 基于微流控技术的高通量材料合成、表征及测试平台[J].
自然杂志, 2017, 39(2): 103-114.
LIN Y Y, WU J B. High throughput material synthesis, characterization and testing platform based on microfluidic technology[J]. Chinese Journal of Nature, 2017, 39(2): 103-114. |
| [3] |
吴晶, 黄伶慧, 王远航, 等. 微流控芯片电泳在食品安全与环境污染检测中的应用[J].
分析测试学报, 2015, 34(3): 283-288.
WU J, HUANG L H, WANG Y H, et al. Application of microfluidic chip electrophoresis in food safety and environmental pollution detection[J]. Journal of Analytical Testing, 2015, 34(3): 283-288. DOI: 10.3969/j.issn.1004-4957.2015.03.005. |
| [4] |
高克鑫, 范一强, 金志明, 等. 微流控芯片在提高石油采收率技术中的应用[J].
断块油气田, 2018, 25(2): 269-272.
GAO K X, FAN Y Q, JIN Z M, et al. Application of microfluidic chip in enhanced oil recovery[J]. Fault Block Oil and Gas Field, 2018, 25(2): 269-272. |
| [5] |
董亮, 霍丹群, 周军, 等. 微流控芯片在食品安全分析中的应用进展[J].
分析测试学报, 2015, 34(4): 483-487.
DONG L, HUO D Q, ZHOU J, et al. Application progress of microfluidic chip in food safety analysis[J]. Journal of Analytical Testing, 2015, 34(4): 483-487. DOI: 10.3969/j.issn.1004-4957.2015.04.019. |
| [6] |
ZHAO C X, MILLER E, COOPER-WHITE J J, et al. Effects of fluid-fluid interfacial elasticity on droplet formation in microfluidic devices[J].
Aiche Journal, 2011, 57(7): 1669-1677.
DOI: 10.1002/aic.12382. |
| [7] |
TUCKERMAN D B, PEASE R. High-performance heat sinking for VLSI[J].
IEEE Electron Device Letters, 1981, 2(5): 126-129.
DOI: 10.1109/EDL.1981.25367. |
| [8] |
林炳承. 微纳流控芯片实验室[M]. 北京: 科学出版社, 2013.
|
| [9] |
CHEN B, GUO F, LI G J, et al. Three-dimensional simulation of bubble formation through a microchannel t-junction[J].
Chemical Engineering Technology, 2013, 36(12): 1-15.
|
| [10] |
RAJ R, MATHUR N, BUWA V V, et al. Numerical simulations of liquid-liquid flows in microchannels[J].
Industrial & Engineering Chemistry Research, 2010, 49(21): 10606-10614.
|
| [11] |
SOMASEKHARA G S, ARNAB A. CFD analysis of microfluidic droplet formation in non–newtonian liquid[J].
Chemical Engineering Journal, 2017, 330: 245-261.
DOI: 10.1016/j.cej.2017.07.097. |
| [12] |
王维萌, 马一萍, 陈斌. 十字交叉微通道内微液滴生成过程的数值模拟[J].
化工学报, 2015, 66(5): 1633-1641.
WANG W M, MA Y P, CHEN B. Numerical simulation of droplet formation in crossing micro-channels[J]. Journal of Chemical Engineering, 2015, 66(5): 1633-1641. DOI: 10.11949/j.issn.0438-1157.20141899. |
| [13] |
杨丽, 周围, 王学浩, 等. 基于流动聚焦结构的微液滴形成机理[J].
微纳电子技术, 2015, 52(9): 576-580.
YANG L, ZHOU W, WANG X H, et al. Microdroplet formation mechanism based on flow focusing structure[J]. Micro-electronic Technology, 2015, 52(9): 576-580. |
| [14] |
陈珉芮, 钱锦远, 李晓娟, 等. 十字型微通道中非定常分散相速度下液滴生成的数值分析[J].
高校化学工程学报, 2008, 32(3): 522-528.
CHEN M R, QIAN J Y, LI X J, et al. Numerical analysis of droplet formation at unsteady dispersed phase velocity in crossing microchannels[J]. Journal of Chemical Engineering of University of China, 2008, 32(3): 522-528. |
| [15] |
吴梁玉. 双乳液的制备及其流体动力学行为研究[D]. 南京: 东南大学, 2016.
|
| [16] |
吴平. 液滴微流控的实验应用和理论研究[D]. 合肥: 中国科学技术大学, 2014.
|
| [17] |
钟映春, 谭湘强, 杨宜民. 微流体力学几个问题的探讨[J].
广东工业大学学报, 2001, 18(3): 46-48.
ZHONG Y C, TAN X Q, YANG Y M. Discussion on several Issues in microfluid mechanism[J]. Journal of Guangdong University of Technology, 2001, 18(3): 46-48. DOI: 10.3969/j.issn.1007-7162.2001.03.010. |
 2020, Vol. 37
2020, Vol. 37

