作为电力系统“发、输、变、配、用”5大环节之一,配电网起着不可或缺的作用[1]。配电网的正常运行,是保证电力系统的安全性、可靠性、经济性和供电质量的前提。解决配电网故障定位问题对于整个电力系统的安全稳定运行有着重要意义。随着配电网智能化水平的提高,安装在馈线断路器和自动化开关处的配电自动化设备终端可以直接监测到过电流报警信息。因此,实现故障定位主要采用基于馈线自动化技术的故障区段定位方法[2]。
目前,国内外学者已提出众多不同的优化算法,用于配电网故障区段定位的最优解研究,其中大致可分为直接和间接算法。直接算法以统一矩阵算法为主,其本质是利用图论和矩阵论来构建矩阵,概括配电网网络拓扑结构和故障信息,以此还原真实故障状态,不仅原理简单、易于实现,而且实时性好。文献[3]提出了一种改进矩阵算法,能够对配电网末端故障区段进行准确辨识,但在多电源多重故障以及发生信息畸变的情况下,故障定位的准确性和容错性不高。间接算法主要是指人工智能算法,除了早期常用的遗传算法[4]、Petri网[5]和神经网络算法[6]外,文献[7-11]分别提出了应用仿电磁学算法、粒子群算法、蚁群算法、免疫算法以及和声算法等智能仿生算法来解决配电网故障定位问题。此类算法可以适应更为复杂的配电网模型和故障类型,容错性较高,但也有易于陷入局部最优的缺点,导致故障区段定位准确率不够高。
蝙蝠算法(Bat Algorithm, BA)由剑桥大学的Yang教授于2010年首次提出,灵感来自于蝙蝠种群通过回声定位来觅食的行为[12]。已有的研究结果表明,蝙蝠算法比粒子群算法收敛更快,效率更高,但同样也存在精度较低、遍历性差、容易陷入局部最优等缺点。鉴于差分进化算法中变异、交叉和选择操作,拥有帮助种群跳出局部最优解的优势,本文将差分进化算法和自适应理论融合到蝙蝠优化算法中,提出一种改进蝙蝠优化算法,能够改善算法易于陷入局部最优的缺陷,并将其应用于配电网故障区段定位中,仿真结果表明该算法能够解决多种情况下的故障定位问题,与单一算法相比拥有更高准确度和容错性。
1 配电网故障区段定位的数学模型以人工智能算法为基础的配电网故障区段定位是一种典型的含0-1离散约束条件及逻辑求值的最优化问题。根据配电网馈线终端单元(Feeder Terminal Unit, FTU)上传的故障电流信息进行参数编码,根据配电网各个线路区段运行状态进行故障假设,设置合理的评价函数为目标函数,结合故障诊断最小集理论,建立配电网故障区段定位的0-1整数变量逻辑值模型,利用算法找出逼近FTU上传信息的最优解,即为当前故障区段位置。其数学模型[13]为
| $ \begin{array}{l} \min f(x)\\ {\rm{s.t.}}\left\{ \begin{array}{l} x_i = 0{\text{或}}1\\ X \in {{\rm{\bf R}}^{{n}}}\\ {{i}} = 0,1, \cdots ,{{n}} \end{array} \right. \end{array} $ | (1) |
式(1)中,f(x)为所求的目标函数;n是变量的维数,表示候选的故障区段数;xi为第i维变量的取值,表示第i个线路区段的故障状态,0代表正常,1代表故障;X则是配电网线路区段的状态变量。
1.1 参数的确定与编码将配电网中每一个开关(包括进线断路器、分段开关)定义为节点。馈线终端单元FTU是数据采集与监视控制系统SCADA(Supervisory Control And Data Acquisition)的重要组成部分,装设在每一个节点上,主要用于监测和上传各开关的状态信息,为主站控制系统提供数据分析。电网中各开关的状态主要分为正常状态和故障状态两种,因此可以将其对应二进制编码的0或1[14]。将第j号开关处FTU上传的状态信息参数定义为
| $ {{g_j}} = \left\{ \begin{array}{l} {\rm{0}}\;\;\;\;{\text{正常,没有流过故障电流}}\\ {\rm{1}}\;\;\;\;{\text{故障,检测到故障电流}} \end{array} \right. $ | (2) |
在对配电网故障定位的参数进行编码后,还需要将每个FTU上传的开关电流信息转化为相应线路的故障状态值,因此将开关故障电流与线路故障状态之间的逻辑关系定义为开关函数。简单的单电源供电型配电网如图1所示,其开关函数形成规则如表1所示[15],sj表示节点编号为 j 的开关函数,xi表示配电网线路区段编号为 i 的线路状态,

|
图 1 单电源供电型配电网 Figure 1 Single-power-supply distribution network |
| 表 1 开关函数形成规则 Table 1 Rules to switching function |
构建一个函数来描述各开关函数与发生故障时FTU上传的实际电流越限信息的逼近情况,即评价函数。评价函数的解对应当前电网中各个区段的故障期望状态,求评价函数最优解,即可求得与实际故障情况准确对应的每个线路区段的故障状态,从而实现故障定位。针对可能存在一值多解而发生故障误判的情况,可引入权重系数对评价函数fit(x)进行改进[16],如式(3)所示。
| $ {\rm{fit}}(x) = \mu \sum\limits_{i = 1}^{{P}} {\left| {x_i} \right|} + \sum\limits_{j = 1}^{{Q}} {\left| {g_j - s_j} \right|} $ | (3) |
式(3)中,P是配电网线路区段总数;Q是配电网中节点总数;xi为第i号馈线区段的故障状态,0代表正常,1代表发生故障;gj表示第j个节点处的FTU检测到的开关实际状态值;sj的值由设定的开关函数规则可得;
蝙蝠算法是通过模拟蝙蝠种群回声定位的觅食行为而开发出的一种新的群体智能优化方法。其寻优过程首先利用随机分布的蝙蝠种群发射脉冲来搜寻猎物,然后通过比较种群每个蝙蝠位置与当前种群最优蝙蝠的位置,来调整蝙蝠发出脉冲的频率、速率和音强,从而更新自身的飞行速度和飞行轨迹,直到所有的蝙蝠个体都聚集在猎物的附近,即为全局最优位置[17]。
在利用回声定位进行觅食时,蝙蝠种群发出的脉冲频率、飞行速度和位置变化的更新公式为
| $ f_i = f_{\min} + \beta (f_{\max} - f_{\min} ) $ | (4) |
| $ {{v}}_i^t = {{v}}_i^{t - 1} + {f_i}({{x}}_i^t - {{x}}^*) $ | (5) |
| $ {{x}}_i^t = {{x}}_i^{t - 1} + {{v}}_i^t $ | (6) |
其中,
算法起始阶段,先令蝙蝠种群发射小速率、大音强的脉冲,以便扩大搜索范围,提高全局寻优速度;当搜寻到猎物后应适当减小脉冲音强,侧重于逐步增大脉冲速率,从而增加局部搜索的精准度。通过式(7)和式(8)来更新脉冲音强
| $ A_i^{t + 1} = \alpha A_i^t $ | (7) |
| $ R\;_i^{t + 1} = \left[ {1 - {{\rm{e}}^{ - \gamma t}}} \right]R_i^0 $ | (8) |
其中,
差分进化算法(Differential Evolution,DE)由Storn和Price于1995年提出,是一种基于群体的启发式搜索算法,主要用于全局优化[18]。和遗传算法类似,两者都属于进化算法的分支,主要过程都包括变异、交叉和选择3个步骤,区别在于差分进化算法利用随机的父代个体间的差异来产生变异个体,再与父代个体交叉产生新个体,最后通过对种群中的所有个体进行贪婪比较的方法,选择出新一代种群继续进行迭代。差分进化算法原理简单,参数较少,易于实现,变异和交叉操作有助于跳出局部最优,因而考虑将差分进化算法与蝙蝠算法结合,进行优势互补。
差分进化算法的主要操作步骤 [19]如下。
(1) 变异操作。任一变异个体将根据式(9)产生。
| $ {{{q}}_{ij}}(t + 1) = {{{x}}_a}(t) + F({{{x}}_b}(t) - {{{x}}_c}(t)) $ | (9) |
其中,
(2) 交叉操作。通过引入交叉概率因子来提高变异个体在种群中的影响力,从而达到增加种群多样性的目的。父代个体和变异个体通过式(10)交叉操作产生新个体。
| $ {{{v}}_{ij}}(t + 1) = \left\{ \begin{array}{l} {{{x}}_{ij}}(t),{\rm{rand}} > C{\text{或}}{{j}} \ne i\\ {{{q}}_{ij}}(t + 1),{\rm{rand}} \leqslant {{C}}{\text{或}}{{j}} = {{i}} \end{array} \right. $ | (10) |
其中,
(3) 选择操作。采用贪婪策略,根据式(11)比较交叉后的个体vi(t+1)和xi(t)向量的适应度函数值来确定参与种群下一次迭代更新的子代个体。
| $ {{{x}}_i}(t + 1) = \left\{ \begin{array}{l} {{{x}}_i}(t),f({{{v}}_{ij}}(t + 1)) > f({{{x}}_{ij}}(t)) \\ {{{v}}_i}(t + 1),f({{{v}}_{ij}}(t + 1)) \leqslant f({{{x}}_{ij}}(t)) \\ \end{array} \right. $ | (11) |
本文先通过蝙蝠算法进行快速寻优,采用适应度优劣排序策略,将之后得到的种群作为差分进化算法的父代种群,再对父代种群进行相应的变异、交叉和选择操作,使得在每次迭代中寻找到更优的解。
2.3 自适应改进自适应一般指的是通过分析数据的统计分布特征、结构特征和波动规律,设定相应的反馈控制手段约束数据的变化,使其能动态调整自身特性,达到最佳的处理效果。
本文对蝙蝠算法的速度公式进行修改,引入自适应权重参数
| $ \omega = \omega_{\max} - (t - 1)\frac{{\omega_{\max} - \omega_{\min} }}{{t_{\max} - 1}} $ | (12) |
| $ {{v}}_i^t = \omega {{v}}_i^{t - 1} + {f_i}({{x}}_i^t - {{x}}^*) $ | (13) |
其中,
将自适应理论与差分进化算法结合,在分析变异操作和交叉操作的数据特性后,引入柯西分布进行改进,使其能够根据适应度的评估来对需要进行变异交叉的蝙蝠个体进行动态调整,最大化地发挥种群多样性和全局寻优能力的优势。
对差分进化算法的变异公式进行自适应改进后,有
| $ {{{q}}_{ij}}(t + 1) = {{{x}}_a}(t) + {F_i}(t)({{{x}}_b}(t) - {{{x}}_c}(t)) $ | (14) |
| $ \lambda = F_{\min} + \left( {F_{\max} - F_{\min} } \right)\frac{{t - 1}}{{t_{\max} }} $ | (15) |
| $ {F_i}(t) = \lambda + \frac{\delta }{\text{π} }\left( {\frac{{\theta_1}}{{{{\left( {t - {{{x}}_0}} \right)}^2} + \theta_1^2}}} \right) $ | (16) |
其中,Fi(t)为第i个蝙蝠在t迭代时刻的变异因子;
对差分进化算法的交叉公式进行自适应改进后,有
| $ {{ v}_{ij}}(t + 1) = \left\{ \begin{array}{l} {{ x}_{ij}}(t),{\rm{rand}} > {C_i}(t){\text{或}}{{j}} \ne {{i}}\\ {{ x}_{ij}}(t + 1),{\rm{rand}} \leqslant {C_i}(t){\text{或}}{{j}} = {{i}} \end{array} \right. $ | (17) |
| $ \varphi = {\left( {{C_{\max }} - {C_{\min }}} \right)^{\rm{e}}}^{\left( {1 - \frac{{t_{_{\max}} }}{{t + 1}}} \right)} $ | (18) |
| $ {C_i}(t) = \varphi \left( {\frac{1}{\pi }\arctan \left( {\frac{{t - {{{x}}_0}}}{{\theta_2}}} \right) + \frac{1}{2}} \right) $ | (19) |
其中,Ci(t)为第i个个体t迭代时刻的交叉概率;
变异因子F和交叉因子C的自适应处理,有利于优化算法寻优的收敛速度和精度,找到最佳的平衡点达到双赢。在迭代初期,由于种群在空间随机分散,应保证F较大,C较小,让算法侧重于全局搜索,提高寻优收敛速度;在迭代后期,种群朝着最优位置聚拢,应将F值调小,增大C,侧重于局部搜索,提高寻优收敛精度。
3 基于改进蝙蝠算法(Improved Bat Algorithm, IBA)的配电网故障区段定位流程将本文提出的IBA算法应用到配电网故障区段定位的基本寻优流程如下。
(1) 确定算法控制参数,具体有:种群个体数N,脉冲音强和速率初值
(2) 种群初始化,在D维空间中随机分布0-1描述的初始蝙蝠种群。根据蝙蝠种群的初始化位置xi对种群进行评价,计算适应度值,寻找当前的最优解x*。
(3) 根据式(4)、(13)、(6)对蝙蝠的发射脉冲频率、飞行速度和空间位置进行更新。
(4) 根据(rand>ri)条件判断是否对当前最优解x*进行随机扰动产生新解并进行越界处理。
(5) 根据条件(rand<Ai,且 f(xi)<f(x*)),判断是否接受新解并更新脉冲音强Ai和脉冲速率Ri。
(6) 根据群体适应度值优劣排序产生父代种群,并根据式(16)、(19)、(11)来对父代种群进行自适应的交叉、变异和选择操作,产生新的蝙蝠种群,再次比较适应度值的优劣,更新当前最优解和评价函数最优值。否则转到步骤(7)。
(7) 判断是否达到最大迭代次数,满足则输出全局最优解和评价函数最优值,终止程序,否则转到步骤(3)。算法结束时输出的最优解矩阵即为配电网各线路区段的最优状态值,根据状态值可定位出故障线路区段。
4 算例分析基于目前我国配电网主要采用多电源闭环结构、开环运行的模式,区域划分主要以各个常开式的联络开关为界限,配电网区域之间相互独立、互不影响,本文以图2所示的3电源开环运行配电网作为测试算例进行故障区段定位分析。其中,G1、G2、G3为系统电源,S1~S20为分段开关,1~20为馈线对应的定位区段,SL1和SL2是两个常开式的联络开关。
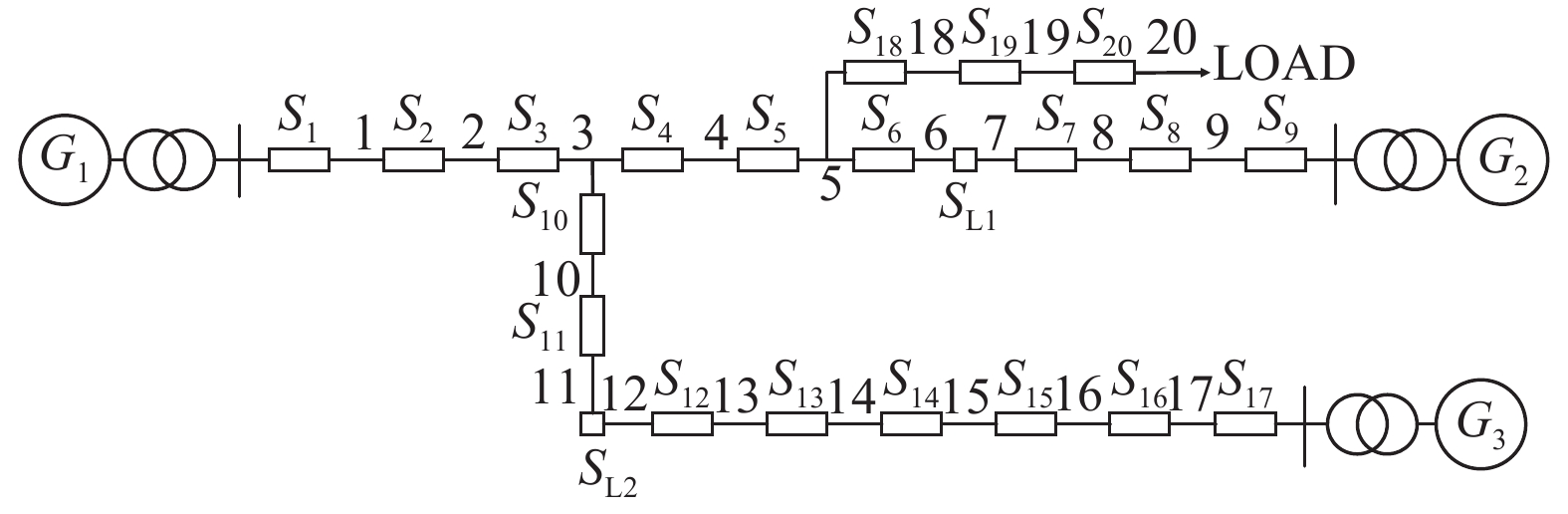
|
图 2 3电源开环供电型配电网 Figure 2 Open-loop power supply distribution network with three sources |
仿真实验所用的硬件是Core(TM)i5-3470 CPU 3.20 GHz,内存为8 GB,软件为MATLAB R2015b。算法基本参数信息:种群个体数N为50,脉冲音强和速率初值
本文通过控制故障发生的位置和信息畸变的有无来组合模拟配电网运行过程中可能发生的各种故障情况。包括线路不同区段的单一故障和多重故障,以及发生单一故障或多重故障的同时伴随有信息畸变等情况。信息畸变指的是某节点上安装的FTU在监测并上传状态信息的过程中发生的信息丢包或者信息突变。利用MATLAB进行相应的仿真实验,以此验证本文提出的改进蝙蝠算法在配电网故障区段定位方面的准确性和容错性。具体的故障区段定位仿真结果如表2所示。
| 表 2 故障区段定位仿真结果 Table 2 Fault section location simulation result |
从表2可看出,在3个独立电源区域发生单一故障时,无论故障的区段是否发生变化,无论上传的开关状态信息是否发生畸变,无论信息畸变位置是否发生变化,本文所构建的算法都能够准确无误地定位出故障线路区段;而即使是在同一电源区域发生多重故障且有多个位置发生信息畸变时,本文提出的改进蝙蝠算法依然能找到线路区段的最优解,定位出正确的故障线路区段,具有良好的容错性和可靠性。
表3给出了IBA、BA、DE、PSO(Particle Swarm Optimization)算法在上述故障区段定位模型的50次仿真结果对比。由仿真结果可知,与PSO算法相比,BA算法在平均迭代次数、平均用时和正确次数上都略胜一筹,证明了BA算法有更好的收敛性和更高的效率,但一样存在“早熟”现象,定位准确率不高;DE算法虽然平均迭代次数和平均用时都最长,但是正确次数也高于PSO和BA算法,表明DE算法能够有效地跳出局部最优,有较强的全局寻优能力;而本文提出的IBA算法在蝙蝠算法中引入差分进化步骤并进行自适应处理后,虽然平均用时有所增加,但算法平均迭代次数远低于其他3种算法且故障区段定位准确率最高,出现错判和漏判的情况大大减少。因此,本文算法更有效率和优势。
| 表 3 算法仿真结果比较 Table 3 Comparison of algorithm Simulation results |
本文针对基于配电自动化终端的配电网故障区段定位问题,提出一种结合蝙蝠算法、差分进化算法和自适应理论的改进优化算法。在蝙蝠算法寻优过程中引入差分进化算法的变异、交叉、选择操作,并对算法参数进行自适应处理后,提高了种群的多样性和全局寻优能力,有利于跳出局部最优。故障区段定位仿真结果表明,与单一算法相比,本文所提算法具有优越的收敛性能,迭代次数少,寻优速度快,效率高;在面对含多位信息畸变的配电网单一故障和多重故障情况,都能准确定位出故障区段,可靠性高,具有良好的应用场景,为解决配电网故障区段定位问题提供了一种新的思路和方法。
| [1] |
何正友. 配电网分析及应用[M]. 北京: 科学出版社, 2014: 1-10.
|
| [2] |
芦兴, 王瑞闯. 配电网故障定位方法研究[J].
电网与清洁能源, 2013, 29(7): 26-30.
LU X, WANG R C. Research on fault location method of distribution network[J]. Grid and Clean Energy, 2013, 29(7): 26-30. DOI: 10.3969/j.issn.1674-3814.2013.07.006. |
| [3] |
唐华, 王玮, 王英男, 等. 一种配电网故障区段定位的改进矩阵算法[J].
科学技术与工程, 2014(11): 196-199.
TANG H, WANG W, WANG Y N, et al. An improved matrix algorithm for fault section location in distribution network[J]. Science Technology and Engineering, 2014(11): 196-199. DOI: 10.3969/j.issn.1671-1815.2014.11.043. |
| [4] |
杜红卫, 孙雅明, 刘弘靖, 等. 基于遗传算法的配电网故障定位和隔离[J].
电网技术, 2000, 24(5): 52-55.
DU H W, SUN Y M, LIU H J, et al. Fault section diagnosis and isolation of distribution network based on genetic algorithm[J]. Grid Technology, 2000, 24(5): 52-55. DOI: 10.3321/j.issn:1000-3673.2000.05.013. |
| [5] |
孙雅明, 吕航. Petri网和冗余纠错技术结合的配电网故障区段定位新方法[J].
中国电机工程学报, 2004, 24(10): 61-67.
SUN Y M, LYU H. A new approach of the fault section locating for distribution system based on Petri nets in combination with redundant correcting technique[J]. Proceedings of the Chinese Journal of Electrical Engineering, 2004, 24(10): 61-67. DOI: 10.3321/j.issn:0258-8013.2004.10.012. |
| [6] |
刘文轩, 严凤, 田霖, 等. 基于LVQ神经网络的配电网故障定位方法[J].
电力系统保护与控制, 2012, 40(5): 90-95.
LIU W X, YAN F, TIAN L, et al. LVQ neural network approach for fault location of distribution network[J]. Power System Protection and Control, 2012, 40(5): 90-95. DOI: 10.3969/j.issn.1674-3415.2012.05.017. |
| [7] |
郭壮志, 吴杰康. 配电网故障区间定位的仿电磁学算法[J].
中国电机工程学报, 2010, 30(13): 34-40.
GUO Z Z, WU J K. Electromagnetism-like mechanism based fault section diagnosis for distribution network[J]. Proceedings of the Chinese Journal of Electrical Engineering, 2010, 30(13): 34-40. |
| [8] |
胡清, 张强. 基于改进二进制粒子群算法的配电网故障定位[J].
南京工程学院学报(自然科学版), 2016(3): 77-81.
HU Q, ZHANG Q. Fault location of distribution networks based on improved binary particle swarm optimization[J]. Journal of Nanjing Institute of Engineering, 2016(3): 77-81. |
| [9] |
邹玙琦, 李瑞. 基于最优个体蚁群算法的配电网故障定位研究[J].
电气传动自动化, 2018, 40(1): 58-62.
ZOU Y Q, LI R. Research on distribution network fault location based on optimal individual ant colony algorithm[J]. Electric Drive Automation, 2018, 40(1): 58-62. DOI: 10.3969/j.issn.1005-7277.2018.01.014. |
| [10] |
陈奎, 张云, 王洪寅, 等. 基于免疫算法的含分布式电源配电网的故障定位[J].
电力系统保护与控制, 2017, 45(24): 57-62.
CHEN K, ZHANG Y, WANG H Y, et al. Fault-section location of distribution network containing distributed generation based on immune algorithm[J]. Power System Protection and Control, 2017, 45(24): 57-62. DOI: 10.7667/PSPC161971. |
| [11] |
陈辉, 周羽生. 基于改进和声算法的含DG配电网故障定位[J].
电力科学与技术学报, 2018, 33(2): 123-128.
CHEN H, ZHOU Y S. Fault location of distribution network with distributed generation based on an improved harmony algorithm[J]. Journal of Electric Power Science and Technology, 2018, 33(2): 123-128. DOI: 10.3969/j.issn.1673-9140.2018.02.017. |
| [12] |
YANG X S. A new metaheuristic bat-inspired algorithm[C]//GONZALEZJ R. Nature Inspired Cooperative Strategies for Optimization (NISCO 2010). Berlin: Spring, 2010, 65-74.
|
| [13] |
卫志农, 何桦, 郑玉平, 等. 配电网故障区间定位的高级遗传算法[J].
中国电机工程学报, 2002, 22(4): 127-130.
WEI Z N, HE H, ZHENG Y P, et al. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002, 22(4): 127-130. DOI: 10.3321/j.issn:0258-8013.2002.04.026. |
| [14] |
郭壮志, 陈波, 刘灿萍, 等. 潜在等式约束的配电网遗传算法故障定位[J].
现代电力, 2007, 24(3): 24-28.
GUO Z Z, CHEN B, LIU C P, et al. Genetic algorithm fault location of distribution network with latent equality constraint[J]. Modern Electric Power, 2007, 24(3): 24-28. DOI: 10.3969/j.issn.1007-2322.2007.03.006. |
| [15] |
郭壮志, 陈波, 刘灿萍, 等. 基于遗传算法的配电网故障定位[J].
电网技术, 2007, 24(11): 88-92.
GUO Z Z, CHEN B, LIU C P, et al. Distribution network fault location based on genetic algorithm[J]. Power Grid Technology, 2007, 24(11): 88-92. DOI: 10.3321/j.issn:1000-3673.2007.11.017. |
| [16] |
付家才, 陆青松. 基于蝙蝠算法的配电网故障区间定位[J].
电力系统保护与控制, 2015, 43(16): 100-105.
FU J C, LU Q S. Fault sections location of distribution network based on bat algorithm[J]. Power System Protection and Control, 2015, 43(16): 100-105. DOI: 10.7667/j.issn.1674-3415.2015.16.015. |
| [17] |
柳岩妮, 公茂法, 王来河, 等. 基于混沌优化蝙蝠算法的含分布式电源配电网故障区段定位[J].
电力科学与工程, 2016, 32(8): 11-14.
LIU Y N, GONG M F, WANG L H, et al. Location of fault section of distributed power distribution network based on chaos optimization bat algorithm[J]. Electric Power Science and Engineering, 2016, 32(8): 11-14. DOI: 10.3969/j.issn.1672-0792.2016.08.003. |
| [18] |
陈璟华, 邱明晋, 唐俊杰, 等. 基于改进差分进化和粒子群混合算法的电力系统最优潮流计算[J].
广东工业大学学报, 2017, 34(5): 24-26.
CHEN J H, QIU M J, TANG J J, et al. A hybrid algorithm based on improved differential evolution and particle swarm optimization for power system optimal power flow calculation[J]. Journal of Guangdong University of Technology, 2017, 34(5): 24-26. |
| [19] |
肖辉辉, 段艳明. 基于DE算法改进的蝙蝠算法的研究及应用[J].
计算机仿真, 2014, 31(1): 272-277.
XIAO H H, DUAN Y M. Research and application of improved bat algorithm based on DE algorithm[J]. Computer Simulation, 2014, 31(1): 272-277. DOI: 10.3969/j.issn.1006-9348.2014.01.061. |
 2020, Vol. 37
2020, Vol. 37