近年来，对自主机器人的研究越来越重视，要想实现自主机器人，室内定位是非常重要的一环。目前高精度的机器人室内定位方法中的硬件主要都是基于激光传感器以及视觉传感器等。激光传感器可以实现高精度的机器人室内定位，但是价格昂贵，硬件成本较高，如文献[1]通过高精度激光雷达进行测距，结合惯性导航系统来实现室内环境下的定位。文献[2]通过机器人上的激光传感器获取室内环境的点云信息，并根据不同位置上的观测得到的约束进行定位。它们的精度都可以达到厘米级别，但是硬件成本昂贵。在采用其他相对廉价的硬件时，所提出的机器人室内定位方法通常含有不同的缺点。如文献[3]先使用惯性导航系统对机器人的位姿进行初始估计，随后利用线段特征之间的匹配关系求出机器人位姿。该方法受环境光影响较严重，运算负荷大，在保证了机器人的高精度定位时会降低稳定性和实时性。文献[4]针对室内环境结构相似的特点，提出了一种基于图像序列拓扑关系的移动机器人全局定位方法，然而对于复杂场景的室内，数据量会过大从而导致机器人定位的实时性受到影响。文献[5]以WiFi位置指纹数据来进行室内定位，通过赋予指纹数据不同的权值之后根据权值的大小划分有效数据并进行滤波处理，从而建立高精度的指纹库来进行室内定位，该方法适用性较广且成本低，但是需要繁琐的指纹数据收集，精度也达不到机器人室内定位的要求。文献[6]通过以蓝牙技术为基础，利用不同蓝牙信标对位置的影响差异以及物体的运动状态来实现室内定位，该方法不需要昂贵的硬件设施，但是在室内环境下，定位精度只能达到2 m左右。

综上可知，当前市面上常见的机器人室内定位方法中，为了实现高精度的定位要求，在采用高精度的传感器如激光雷达时，会使得硬件成本过高。而在采用视觉传感器、路由器及蓝牙等价格相对廉价的硬件时，往往需要处理较多的数据，导致计算成本过高，同时会出现机器人定位稳定性较差、实时性较低以及定位精度达不到要求等缺陷。因此，针对地面含有方格的室内环境下，为了实现高实用性低成本的高精度机器人室内定位，本文在扩展卡尔曼滤波算法的基础上，采用图像处理技术对地面方格直线进行处理，实现单目视觉机器人室内定位。同时为了增强本方法的定位精度，设计并采取线预测算法来排除地面非方格直线的干扰。通过室内环境下机器人移动定位测试验证了该方法的有效性和定位精度。

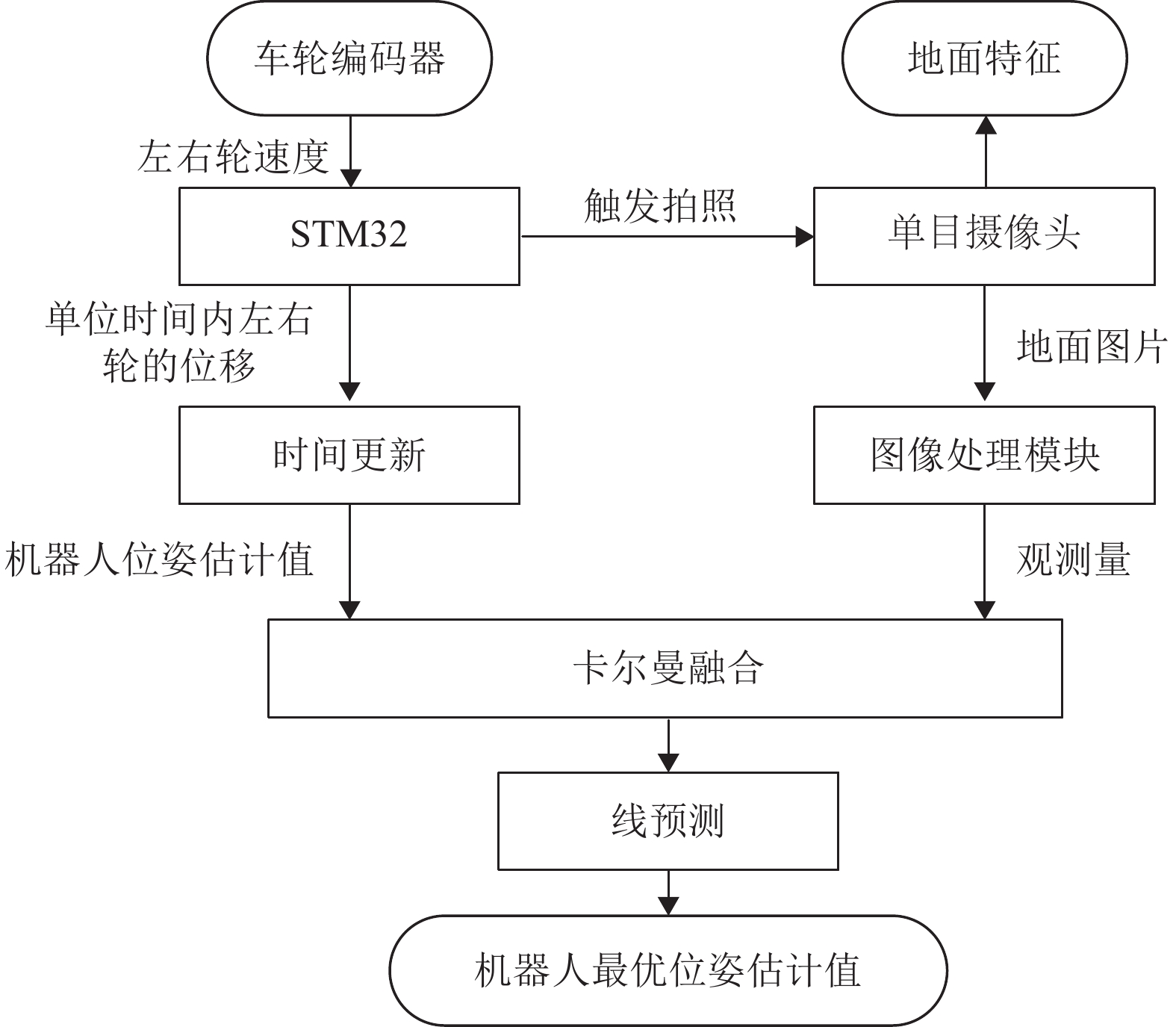
1 系统架构

该定位方法通过STM32串口获取机器人车轮编码器数据，计算出单位时间内左右轮的位移，并通过串口通信传给工控机。然后使用卡尔曼滤波算法时间更新过程，得到机器人的位置以及偏航角。此时得到的机器人位姿由于编码器的累积误差，会随着时间推移逐渐增大^[7]。因此在机器人底部安装一个单目鱼眼摄像头拍摄地面图片，经过一系列图像处理过程，提取出拍摄到的图片中的地面特征即方格直线；计算出方格直线到相机的距离以及倾角，作为观测值给到卡尔曼测量更新部分，推导出观测方程并结合时间更新得到的机器人位姿估计，进行位姿修正，从而得到机器人的最优位姿估计。整个系统架构，如图1所示。

2 图像处理模块

图像处理模块使用机器人底部的相机拍摄地面图片，识别出地面方格线的轮廓，并根据地面方格线的轮廓拟合出地面方格直线，计算出相机中心离地面方格直线的距离和地面方格直线在相机坐标系下的倾角。

2.1 相机标定

本文采用张正友标定法对相机进行标定，可以得到相机内参矩阵和畸变系数，该标定法在OpenCV中有对应的程序工具集可以使用。鱼眼相机拍摄的标定板样例如图2所示。

使用相机从不同角度拍摄标定板，将图片传入到标定程序中，使用的图片越多标定的结果越好。最终程序得到相机内参矩阵 ${{A}}$ ，径向畸变系数 ${k_1}$ 和 ${k_2}$ ，切向畸变系数 ${p_1}$ 和 ${p_2}$ ，相机内参矩阵为

${{A}} = \left[ {\begin{array}{*{20}{c}} {{f_0}}&0&{{u_0}} \\ 0&{{f_1}}&{{v_0}} \\ 0&0&1 \end{array}} \right]$

其中， ${f_0}$ 和 ${f_1}$ 分别表示相机的横向焦距和纵向焦距， ${u_0}$ 和 ${v_0}$ 表示相机主光轴的坐标。

2.2 边缘检测及矫正

机器人底部相机采集的地面图片，如图3所示，图片中的红点是用来标识机器人所处的中心位置，出现的白光是由于机器人底盘安装的LED白光灯带进行补光。图像处理模块会对采集到的图片进行边缘检测，本文采用的方法是使用Canny算子来提取图像的边缘信息。同时采用高斯滤波器来平滑图像，滤除噪声，尽可能减少噪声对边缘检测结果的影响。通过设置合理的Canny阈值，更好地实现对地面图片边缘信息的提取，尽量多地提取出地面方格直线的轮廓。

从图4可以看到，经过Canny边缘检测得到的图片中，地面方格直线是弯曲的，该现象是桶形径向畸变，因此需要对图片进行畸变矫正，对提取出的每个轮廓点进行像素坐标映射计算和像素值插值计算，重建出无畸变的图像^[8]。本文没有采用传统的畸变矫正流程，即先对相机采集的原图立即进行畸变矫正，之后再进行边缘检测。而是采用了先对相机采集的原图进行边缘检测，转化为二值图像，此时已经去除了图片中大量的冗余信息，只需要将二值图像中的所有像素值为(255，255，255)的白点作为轮廓点提取出来即可。接着对得到的几百个轮廓点，运用点矫正的算法进行畸变矫正^[9]，就可以极大地提高运行效率，保证了机器人定位的实时性。

轮廓点畸变矫正图如图5所示。从图5可以看到，点矫正之后的地面方格直线轮廓，已经恢复成直线。

2.3 直线拟合

得到了地面方格直线的轮廓，接下来使用RANSAC算法提取直线内点，RANSAC算法即“Random Sample Consensus(随机抽样一致)^[10]”，RANSAC算法是从观测数据集中，通过迭代方式将观测数据分为内点和外点，内点是符合数学模型参数的点，外点即为噪声点，从而估计出数学模型的参数。

RANSAC需要进行多次迭代，首先从点矫正之后的地面图片轮廓中随机选取两个点生成一条直线，计算所有轮廓点到该直线的距离，大于设定好的阈值的为外点，小于的为内点，并统计内点数。然后从N次迭代中，找到内点数最多的一次，并采用最小二乘法^[11]拟合出直线^[12]，作为地面方格直线。从上述流程可以看出，RANSAC算法具有不确定性，可以通过提高迭代次数来得到一个合理的结果。

图6是通过RANSAC提取内点并采用最小二乘法成功拟合出的直线示意图。

通过相机内参和相机离地高度、相机的俯仰角和偏航角，将图像中的直线映射到物理坐标系下，并消除透视效果^[13]，得到相机坐标系下地面方格直线的方程。并以相机作为原点，求出相机到地面方格直线的距离 $d$ ，以及直线在相机坐标系下的倾角 $\theta $ ， $d$ 和 $\theta $ 都是真实物理值。至此就完成了图像处理部分，将得到的 $d$ 和 $\theta $ 作为观测值，再推导得到观测方程，即可用来修正机器人位姿。

3 机器人位姿计算

通过机器人编码器的数据推导出状态转移方程，并根据图像处理模块得到的观测值，推导出 $d$ 、 $\theta $ 观测方程，该方程为非线性方程，因此采用扩展卡尔曼滤波器进行融合^[14]，得到机器人的最优位姿估计。

3.1 机器人位姿估计

首先选择3个状态变量 $(x,y,\phi )$ 作为系统状态量，向量形式 ${(x,y,\phi )^{\rm{T}}}$ 即为机器人移动的位姿状态向量，其中 $x$ 和 $y$ 表示机器人在世界坐标系下的横坐标和纵坐标， $\phi $ 表示航向角。

工控机每隔 $\Delta t$ 时间间隔，就向STM32开发板发送指令信号，STM32通过串口和电机编码器进行通信，读取电机编码器的数据，即机器人左轮和右轮的速度。并根据时间差和读取到的速度，计算出单位时间内左右轮的位移，分别为 $\Delta {s_l}$ 和 $\Delta {s_r}$ ，发送给工控机。

设机器人当前时刻位姿状态向量为 ${({x_n},{y_n},{\phi _n})^{\rm{T}}}$ ，根据 $\Delta t$ 时间内左右轮移动的距离 $\Delta {s_l}$ 和 $\Delta {s_r}$ ，可以推导出 $n \!+ \! 1$ 时刻机器人的状态方程，见式(1)。

$\left[ \begin{array}{c} {x_{n + 1}} \\ {y_{n + 1}} \\ {\phi _{n + 1}} \\ \end{array} \right] = \left[ \begin{array}{c} {x_n} + \dfrac{{\Delta {s_r} + \Delta {s_l}}}{2}\cos {\phi _n} \\ {y_n} + \dfrac{{\Delta {s_r} + \Delta {s_l}}}{2}\sin {\phi _n} \\ {\phi _n} + \dfrac{{\Delta {s_r} - \Delta {s_l}}}{D} \end{array} \right]$

(1)

式(1)中， $D$ 为左右轮之间的间距， ${\phi _n}$ 是机器人移动的航向角，该状态方程是一个非线性方程，因此采用扩展卡尔曼滤波算法，对其进行局部线性化，得到卡尔曼时间更新过程，见式(2)~(3)。

$\left[ \begin{array}{c} {{\hat x}_{n + 1}} \\ {{\hat y}_{n + 1}} \\ {{\hat \phi }_{n + 1}} \end{array} \right] = \left[ \begin{array}{c} {{\hat x}'}_n + \dfrac{{\Delta {s_r} + \Delta {s_l}}}{2}\cos {{\hat \phi }'}_n \\ {{\hat y}'}_n + \dfrac{{\Delta {s_r} + \Delta {s_l}}}{2}\sin {{\hat \phi }'}_n \\ {{\hat \phi }'}_n + \dfrac{{\Delta {s_r} - \Delta {s_l}}}{D} \end{array} \right]$

(2)

${{{\hat P}}_{n + 1}} = {{{A}}_n}{{\hat P}}_{n}'{{A}}_n^{\rm{T}} + {{{Q}}_n}$

(3)

式(2)~(3)中， ${\hat x_{n + 1}}$ ， ${\hat y_{n + 1}}$ ， ${\hat \phi _{n + 1}}$ 表示 $n + 1$ 时刻卡尔曼时间更新预测得到的先验状态估计值， ${{{\hat P}}_{n + 1}}$ 表示 $n + 1$ 时刻卡尔曼时间更新预测得到的状态估计值的不确定性范围，即先验估计协方差矩阵， ${{\hat P}}_n'$ 是 $n$ 时刻卡尔曼滤波输出的最优估计误差，即后验估计协方差矩阵。 ${{A}}_n$ 是状态方程的雅可比矩阵，即状态方程在上一状态最优估计值处求偏导。 ${{{Q}}_n}$ 是 $n$ 时刻过程激励噪声的协方差矩阵，它是状态转移矩阵与实际过程之间的误差^[15]。

机器人位姿状态向量的估计值，由于编码器的累积误差，这个估计值的误差会越来越大，因此需要对这个状态估计值进行修正。

3.2 $d$ ， $\theta $ 观测方程

根据图像处理模块得到的观测值，即机器人底部相机距离地面方格直线的距离 $d$ ，和地面方格直线在相机坐标系下的倾角 $\theta $ ，推导出关于 $d$ ， $\theta $ 的观测方程。

已知地面方格直线在世界坐标系下的方程，首先需要将该直线方程转换到相机坐标系下，才能求出 $d$ 和 $\theta $ 。图7是机器人移动过程中的世界坐标系和相机坐标系的关系示意图。

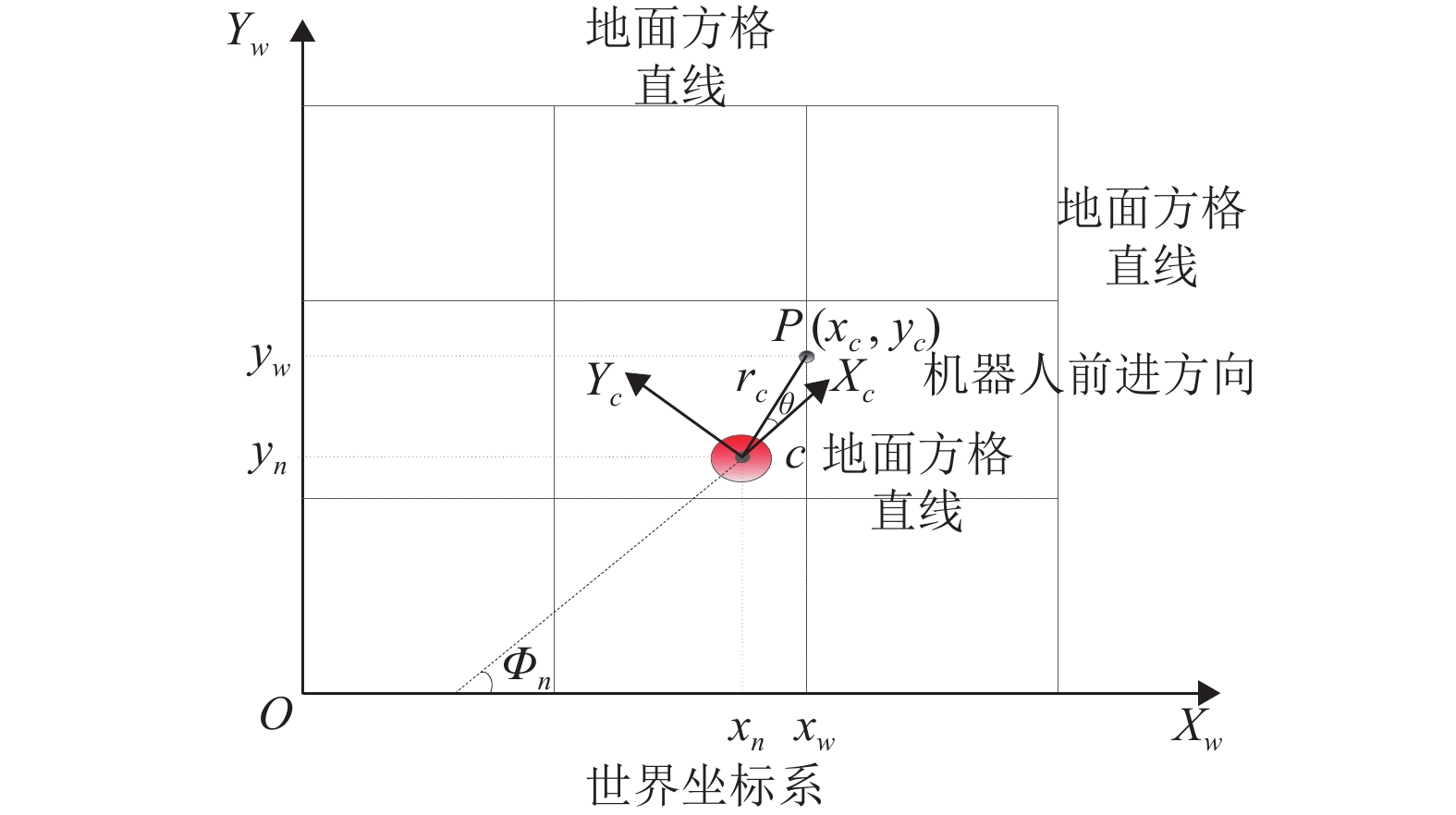
图7中， ${X_w} - {Y_w}$ 表示世界坐标系， ${X_c} - {Y_c}$ 表示机器人底部相机坐标系，机器人当前时刻系统状态向量为 ${({x_n},{y_n},{\phi _n})^{\rm{T}}}$ ，假设一个点P，在相机坐标系下的坐标为 $({x_c},{y_c})$ ，倾角为 ${\theta _c}$ ，离机器人底部相机中心的距离为 ${r_c}$ ，假设其在世界坐标系下的坐标为 $({x_w},{y_w})$ ，可以求得相机坐标系和世界坐标系下点的转换关系，见式(4)。

$\left\{ {\begin{aligned} & {{x_w} = {x_n} + {x_c}\cos {\phi _n} - {y_c}\sin {\phi _n}}\\& {{y_w} = {y_n} + {x_c}\sin {\phi _n} + {y_c}\cos {\phi _n}} \end{aligned}} \right.$

(4)

式(4)中， ${x_c} = {r_c}\cos {\theta _c}$ ， ${y_c} = {r_c}\sin {\theta _c}$ 。

假设机器人底部相机拍摄到的地面方格直线在世界坐标系下的方程如式(5)所示。

${A_w}{x_w} + {B_w}{y_w} + {C_w} = 0$

(5)

对直线方程系数进行归一化处理，即 ${A_w}^2 + {B_w}^2 = 1$ 。

然后，将式(4)代入上述方程，可得地面方格直线在相机坐标系的方程，见式(6)。

$ \begin{aligned} & ({A_w}\cos {\phi _n} + {B_w}\sin {\phi _n}){x_c} + \\&({B_w}\cos {\phi _n} - {A_w}\sin {\phi _n}){y_c} + {A_w}{x_n} + {B_w}{y_n} + {C_w} = 0 \end{aligned} $

(6)

将相机作为原点(0，0)，根据点到直线的公式，最终推导出d， $\theta $ 观测方程，见式(7)。

$\left[ \begin{array}{c} {d_n} \\ {\theta _n} \\ \end{array} \right] = \left[ \begin{array}{c} \left| {{A_w}{x_n} + {B_w}{y_n} + {C_w}} \right| \\ \arctan \left(\dfrac{{{A_w}\cos {\phi _n} + {B_w}\sin {\phi _n}}}{{{A_w}\sin {\phi _n} - {B_w}\cos {\phi _n}}}\right) \\ \end{array} \right]$

(7)

3.3 机器人位姿修正

$d$ 、 $\theta $ 观测方程是一个非线性方程，采用扩展卡尔曼滤波算法，对其局部线性化。并根据扩展卡尔曼滤波算法和位姿估计得到的状态预测值，进行测量更新过程修正预测值^[16]。测量更新过程见式(8)~(10)。

${{K}}_{n + 1} = {{\hat P}}_{n + 1}{{{H}}_{n + 1}}^{\rm{T}}{( {{{{H}}_{n + 1}}{{\hat P}}_{n + 1}{{{H}}_{n + 1}}^{\rm{T}} + {{{R}}_{n + 1}}} )^{-1}}$

(8)

$\hat x_{n + 1}' = \hat x_{n + 1} + {{{K}}_{n + 1}}( {{{{z}}_{n + 1}} - {{h}}({{\hat x}}_{n + 1})} )$

(9)

${{\hat P}}\;_{n + 1}' = \left( {{{I - }}{{{K}}_{n + 1}}{{{H}}_{n + 1}}} \right){{\hat P}}_{n + 1}$

(10)

其中， $K_{n + 1}$ 是卡尔曼增益系数，它的作用是去选择更多的相信估计值还是观测值。 $\hat x_{n + 1}'$ 是卡尔曼融合得到的 $n + 1$ 时刻最优状态估计值， ${{\hat P}}_{n + 1}'$ 是 $n + 1$ 时刻后验估计协方差矩阵，即卡尔曼滤波输出的 $n + 1$ 时刻最优估计误差。 ${{{H}}_{n + 1}}$ 是观测方程的雅可比矩阵，即状态方程在上一状态最优估计值处求偏导。 ${{{R}}_{n + 1}}$ 是观测噪声协方差矩阵，表示在图像处理过程中的噪声误差。 ${{{z}}_{n + 1}} = {(d,\theta )^{\rm{T}}}$ ，是由图像处理模块输出的观测变量 $d$ 和 $\theta $ 组成的观测向量。 ${{h}}({{\hat x}}_{n + 1})$ 是将观测方程泰勒展开式得到的中间矩阵。

至此，根据图像处理模块输出的观测变量 $d$ 和 $\theta $ ，推导出关于 $d$ 、 $\theta $ 的观测方程并进行扩展卡尔曼滤波，从而修正了位姿估计，得到了机器人位姿最优估计值。

3.4 线预测算法

为了保证机器人定位的精度，需要对图像处理模块拟合得到的直线进行判断，当相机采集并拟合出非地面方格直线时，需要作为干扰线段进行排除。因此，设计线预测算法来剔除干扰线段的影响。

在地面方格大小为 $f$ 时，根据时间更新得到的机器人位姿状态估计值( ${\hat x_{n + 1}}$ ， ${\hat y_{n + 1}}$ ， ${\hat \phi _{n + 1}}$ )，即机器人在世界坐标系下 $x$ 方向和 $y$ 方向上行走的距离以及偏航角。可以得到机器人在 $x$ 方向和 $y$ 方向走过的地面方格数 ${n_x} = {\hat x_{n + 1}}/f$ ， ${n_y} = {\hat y_{n + 1}} / f$ 。从而求出 $x$ 方向和 $y$ 方向上机器人会采集到的下一条方格直线的位置 ${x_f}$ 和 ${y_f}$ 。同时机器人移动到任何方格里，都可以等效到起始方格，即机器人周围的4条地面方格直线方程为

$ \begin{array}{l} {l_1}:x = {n_x}f,\;\;\;\;\;\;{l_2}:y = {n_y}f\\ {l_3}:x = {x_f}f,\;\;\;\;\;{l_4}:y = {y_f}f \end{array} $

接下来，通过偏航角推算出相机拍摄到的离机器人最近的一条方格直线，并通过式(7)，分别计算出时间更新得到的位置到地面方格直线的距离 ${d_n}$ 和 ${\theta _n}$ ，以及测量更新得到的位置到图像处理得到的直线的距离 ${\bar d_n}$ 和 ${\bar \theta _n}$ 。距离和角度的差值见式(11)~(12)。

$\Delta d = \left| {{d_n} - {{\bar d}_n}} \right|$

(11)

$\Delta \theta = \left| {{\theta _n} - {{\bar \theta }_n}} \right|$

(12)

将上述距离和角度的差值，结合卡尔曼时间更新得到的估计协方差 ${{{\hat P}}_n}$ 中关于机器人位置的方差 ${\sigma _d}$ 和偏航角的方差 ${\sigma _\theta }$ ，分别得到关于距离的比值 $\Delta d/{\sigma _d}$ 和角度的比值 $\Delta \theta /{\sigma _\theta }$ ，两者都符合正态分布，因此它们的平方和 $X$ 服从自由度为2的 $ {\;\chi ^2} $ 分布，见式(13)。

$X = \frac{{{{\left( {\Delta d} \right)}^2}}}{{\sigma _d^2}} + \frac{{{{\left( {\Delta \theta } \right)}^2}}}{{\sigma _\theta ^2}} \sim \chi _2^2$

(13)

通过上述 ${\;\chi ^2}$ 分布，可以判断测量更新修正得到的机器人偏航角和到图像处理得到的直线的距离，同时间更新得到的机器人偏航角和到地面方格直线的距离的差异程度。自由度为2的 ${\;\chi ^2}$ 分布的概率密度函数曲线是单调递减趋于0的，也就是当上述 $X$ 的值越大， $\Delta d/{\sigma _d}$ 和 $\Delta \theta /{\sigma _\theta }$ 两者的差异程度越显著，那么可以判定是由于错误的采集并拟合出了干扰线，造成测量更新计算出的机器人位置到直线的距离和偏航角，同时间更新得到的值偏差过大。

因此，通过式(13)计算出时间更新和测量更新得到距离和角度差值比的平方和 $X$ ，同时设定最大阈值，当 $X$ 大于阈值，就认为测量更新使用的图像处理得到的直线是干扰线，需要排除干扰线并取消该次测量更新修正得到的位置。

根据机器人当前的位置和航向角，本算法可以提前预测出机器人底部相机将会采集到的下一条地面方格直线，当采集到直线并进行测量更新时，通过判断距离和角度差值比的平方和，能够有效地排除地面干扰线段。这也是本文的一个非常实用的创新点。

4 实验设置与结果分析 4.1 实验设置

实验中使用的机器人小车如图8所示，其中，路由器是作为远程控制设备，机器人底盘下安装有单目鱼眼摄像头，如图9所示，该相机型号为MV-GE31GM-T，帧率为108帧每秒，具备良好的动态采集性能。

按照本文2.1节提到的相机标定方法并使用OpenCV程序工具集对相机进行标定，得到相机内参如下所示。

$ \begin{array}{l} {f_0} \!= \!{\rm{428}}.{\rm{792\;371\;850\;332\;1,}}\;{f_1} \!=\! {\rm{428}}.{\rm{663\;133\;468\;208\;9}},\\ {u_0} \!= \! {\rm{371}}.{\rm{138\;260\;443\;512\;6}},\;{v_0} \!= \! {\rm{230}}.{\rm{377\;519\;821\;157\;5}},\\ {k_1} \!= \!{\rm{ - 0}}.{\rm{019\;418\;7}},\;\;{k_2} = {\rm{ - 0}}.{\rm{112\;524}},\\ {p_1} \!= \! {\rm{0}}.{\rm{197\;063}},\;\;\;{p_2} = {\rm{ - 0}}.{\rm{139\;233}} \end{array} $

计算得到相机距离地面的高度和姿态角为高度h = 71 mm，俯仰角 $\alpha = 88.256\;7^\circ$ ，偏航角 $\beta = {\rm{ }} - 1.412\;7^\circ$ 。

实验中，使用HIAST单点激光测距仪(型号为HI50)测量并输出小车的位置坐标，测量精度为±1 mm，将该激光测距仪得到的小车位置坐标作为本实验的真实数据。

实验测试中，机器人在地面方格大小为50 cm×50 cm的室内环境下移动，在移动过程中，会经过如图10所示的带有干扰线段的方格。

4.2 实验结果分析

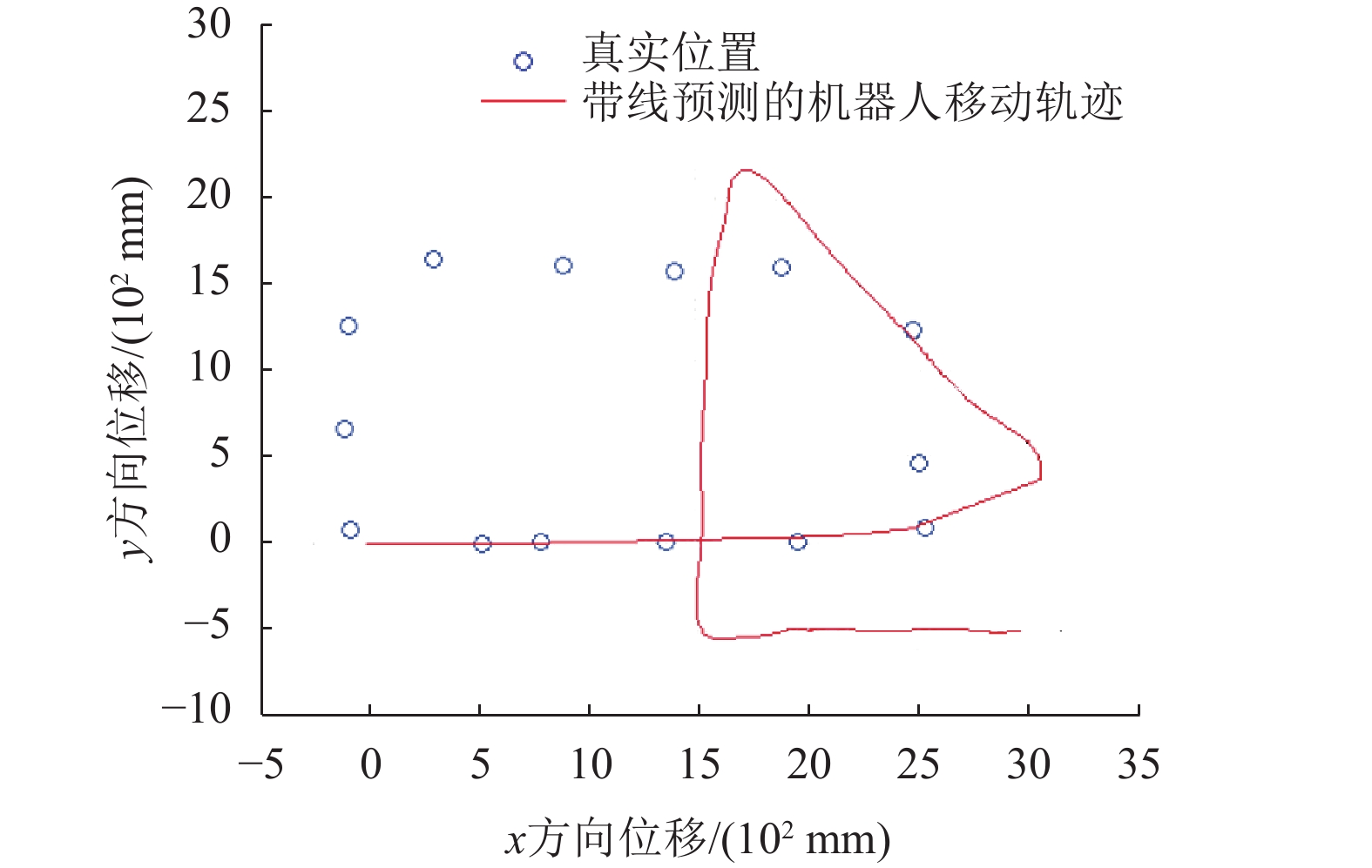
为了充分验证本文提出的带线预测的定位方法的实用性，设置了两组实验进行对比。在第一组实验中，设定机器人按照闭环曲线路线行驶，并在机器人初始前进方向2 500 mm附近经过如图10所示的干扰线段。移动过程中，使用激光测距仪记录机器人的位置数据作为真实值，并通过不带线预测算法的定位程序输出机器人小车的实时位置。为了更直观地呈现出机器人的移动过程，使用MATLAB画出由该不带线预测的定位算法得到的坐标构成的机器人移动轨迹图，以及其中14个真实位置坐标作为参考，如图11所示。

图11中，机器人在初始前进方向2 500 mm附近，经过地面方格中的干扰线段，此时机器人定位程序出现了定位跃迁，使得定位位置及航向角在后续行驶过程中均出现了错误。这是由于机器人在行驶过程中，采集到干扰线段并误认为地面方格直线，会导致机器人定位到错误的方格内，同时在方格内部错误的位置也会导致机器人偏航角出错。

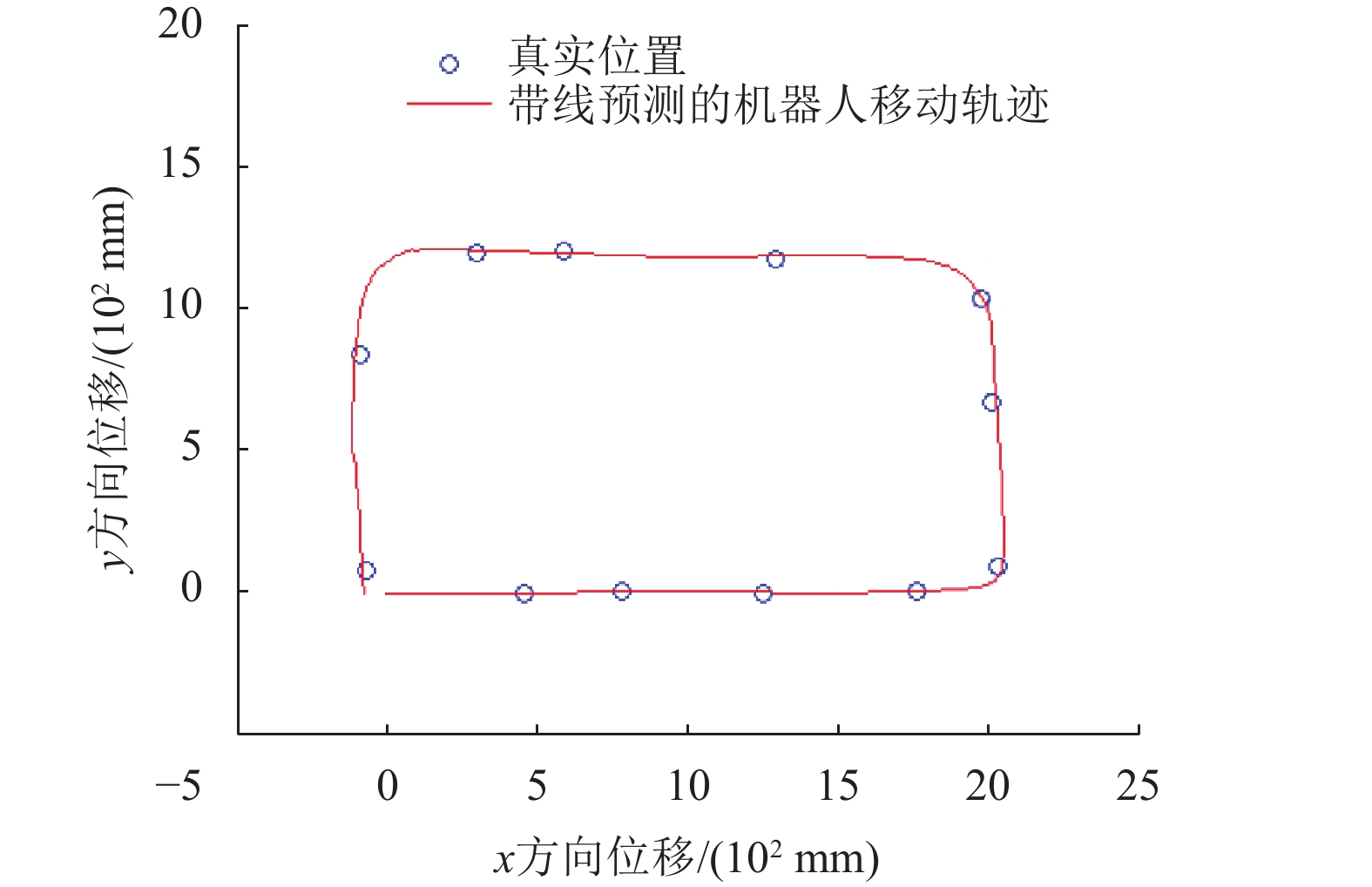
在第二组实验中，机器人在初始前进方向2 000 mm附近经过如图10所示的干扰线段，移动过程中使用带线预测算法的定位程序输出机器人小车的实时位置。同样使用MATLAB画出由带线预测算法的定位程序得到的机器人坐标够成的移动轨迹图，以及移动过程中测得的12个真实位置坐标，如图12所示。可以看到，在机器人的移动过程中，并未受到干扰线段的影响，即采用本文提出的线预测算法能够有效地排除干扰线段的影响。

接下来，对机器人移动过程中的12处位置，使用本文提出的带线预测的定位方法程序得到的坐标和真实坐标进行误差计算，如表1所示。其中 ${x_m}$ 和 ${y_m}$ 为本文带线预测的定位方法得到的机器人位置的横坐标和纵坐标， ${x_l}$ 和 ${y_l}$ 为激光测距仪得到的机器人位置的横坐标和纵坐标，该位置数据作为真实值，误差 ${\varepsilon } = \sqrt {{{({x_m} - {x_l})}^2} + {{({y_m} - {y_l})}^2}} $ 。

从表1中可以看出，通过比较带线预测的卡尔曼滤波输出的机器人位置和激光测距仪得到的真实位置的误差 $\varepsilon $ ，可以看到误差稳定在2 cm左右，有较好的定位精度，同时能够很好地排除干扰线段，保证了测量更新过程修正误差的作用。说明本文提出的带有线预测的单目视觉机器人室内定位系统有较好的定位精度，较好的抗干扰性，基本可以满足机器人室内定位的要求。

5 结 语

本文提出一种基于地面特征的单目视觉机器人室内定位方法。本方法通过对机器人底盘安装的单目鱼眼摄像头拍摄的地面图片进行图像处理，结合车轮编码器的数据进行扩展卡尔曼融合，并通过设计的线预测算法排除干扰线来进行室内定位。该方法仅需要一个单目鱼眼摄像头来辅助定位，程序只需处理含有直线的地面方格图片，拥有较低的硬件成本和计算成本。实验结果表明，机器人通过该方法在具有地面方格的室内场所的定位精度可以达到2 cm，可以应用于低成本的高精度机器人室内定位。下一步的工作主要是针对不同形状的地面方格的室内环境进行定位研究，以及进一步提高该方法的定位精度。