正所谓“不要把所有鸡蛋放在同一个篮子里”，为了规避风险，投资者往往把资金分散地投资在多个资产上。假设资产收益率为随机变量，分别用资产组合的均值和方差度量其收益和风险，Markowitz^[1]提出了均值−方差(MV)投资组合选择模型，为现代投资组合理论奠定了基础。随后，学者们对MV模型进行广泛的推广^[2-5]。

随机投资组合模型利用随机变量刻画资产收益的不确定性，并通过历史数据的统计信息来确定收益率的随机分布。然而，在实际的金融市场中投资决策受到许多非概率因素的影响，如专家观点、投资者情绪等，这些不确定性因素在很大程度上具有模糊性。因此，众多学者开始基于Zadeh^[6]提出的模糊集合理论研究模糊不确定环境下的投资组合问题。Carlsson等^[7]用可能性均值和可能性方差度量资产组合的收益和风险，提出了一个效用最大化的模糊投资组合模型。刘勇军等^[8]考虑现实投资约束，提出了一个以资产组合收益和偏度最大化，以资产组合风险、不确定性和模糊性最小化为目标的多准则模糊投资组合模型。Yue等^[9]提出了一个综合考虑投资组合下半方差风险和下半绝对偏差的多目标模糊投资组合模型。王灿杰和邓雪^[10]提出了一个带融资约束的多目标模糊投资组合模型，并设计了一个改进的多目标粒子群算法进行求解。宋健和邓雪^[11]针对模糊不确定的证券市场提出了一个均值−方差投资组合模型，并综合粒子群算法和人工鱼群算法设计了一个混合智能算法进行求解。

以上模糊投资组合模型假设资产的收益率为模糊变量，在实际应用中还需要对模糊分布的参数进行估计。考虑到线性隶属函数在处理上的便利性，许多学者利用三角模糊数或梯形模糊数来拟合资产的模糊收益率^[12-14]。针对模糊收益率的拟合问题，Zhang等^[15]提出了一个模糊频率估计法。该方法通过统计和分析历史收益率在事先划分好的各个区间上的频数来确定模糊收益率的参数。Vercher等^[16]提出将资产的历史收益率进行排序，然后基于历史收益率的特殊分位点来确定模糊收益率的参数。以上两个简单的估计方法在操作过程中都带有较强的主观性，如划分区间和分位点选择问题，因此在实际应用中不同投资者可能得到差异性较大的结果。此外，以上方式只通过对历史数据的简单分析来确定模糊收益率的参数，并没有考虑专家的观点。

众所周知，在传统的随机投资组合问题中可以通过分散化投资来降低投资风险，因而在追求风险最小化时往往会构建一个分散化的投资组合。然而，在模糊投资组合问题中，传统的风险测度往往在所有资金集中于风险最低的资产上时取得最小，因而传统的投资组合模型往往获得一个集中投资于少数资产的投资组合，这与实际的投资组合管理经验是相悖的^[17]。针对传统模糊投资组合模型过度集中投资的缺陷，主要改进措施有2种：(1) 引入投资比例上下界约束^{[8, 18]}。该方法处理简单，然而分散化的效果并不理想。(2) 引入比例熵的概念作为资产组合的分散化测度^[19-21]。资产组合的比例熵在均匀投资时取得最大值，因而未能体现各个资产之间的差异性。

本文研究模糊环境下考虑交易费用和基数约束的投资组合调整问题。首先，将资产的收益率视为梯形模糊数，并基于资产的历史收益率和专家观点提出一个模糊收益率拟合模型来确定资产模糊收益率的参数。其次，通过提出一个资产组合的分散化测度，以资产组合收益率的可能性均值作为其收益测度，资产组合收益率的下半方差作为其风险测度，构建模糊均值−下半方差−分散化的多准则投资组合调整模型。然后，设计一个改进遗传算法求解所提出的模糊收益率拟合模型及投资组合调整模型。最后，通过真实股票数据对所提出的策略进行实例分析，说明策略的有效性。

1 预备知识

为了便于叙述，首先介绍本文所涉及的模糊数学的相关知识。

定义1^[6] 　若模糊数 $A$ 的隶属度函数具有式(1)的形式

${\mu _A}\left( x \right)=\left\{ {\begin{array}{*{20}{l}} {L\left( {\dfrac{{a - x}}{\alpha }} \right),}\;\;\;\;{a - \alpha < x < a}\\ {1,}\;\;\;\quad\qquad{\;\;a \leqslant x \leqslant b}\\ {R\left( {\dfrac{{x - b}}{\beta }} \right),}\;\;\;\;{b < x < b + \beta }\\ {0,}\;\;\;\quad\qquad{\;\;{\text{其他}}} \end{array}} \right.$

(1)

其中 $\alpha ,\beta > 0$ ， $L,R:\left[ {0,1} \right] \to \left[ {0,1} \right]$ 为单调不增的连续函数且满足 $L\left( 0 \right){\rm{ = }}R\left( 0 \right){\rm{ = }}1$ 和 $L\left( 1 \right){\rm{ = }}R\left( 1 \right){\rm{ = }}0$ ，则称模糊数 $A$ 为 $LR$ 型模糊数。

特别地，当 $L(x){\rm{ = }}R(x){\rm{=}}1 - x$ 时，则称 $A$ 为梯形模糊数，记为 $A{\rm{ = }}\left( {a,b,\alpha ,\beta } \right)$ 。对于任意的 $\gamma \in (0,1]$ ，称集合 $\left\{ {x \in \mathbb{R}:{\mu _A}(x) \geqslant \gamma } \right\}$ 为 $A$ 的 $\gamma {\rm{ - }}$ 截集。易知，它是一个区间，记为 ${[A]^\gamma }{\rm{ = }}[\underline A (\gamma ),\bar A(\gamma )]$ 。

引理1^[22] 　设 ${A_1}{\rm{=}}\left( {{a_1},{b_1},{\alpha _1},{\beta _1}} \right)$ 和 ${A_2}{\rm{=}}\left( {{a_2},{b_2},{\alpha _2},{\beta _2}} \right)$ 为梯形模糊数。对于任意实数 $\lambda \in \mathbb{R}$ ，有

${A_1} + {A_2}=({a_1} + {a_2},{b_1} + {b_2},{\alpha _1} + {\alpha _2},{\beta _1} + {\beta _2})$

(2)

$\lambda {A_1}{\rm{=}}\left\{ {\begin{array}{*{20}{l}} {\left( {\lambda {a_1},\lambda {b_1},\lambda {\alpha _1},\lambda {\beta _1}} \right),}&{\lambda \geqslant 0}\\ {\left( {\lambda {b_1},\lambda {a_1}, - \lambda {\beta _1}, - \lambda {\alpha _1}} \right),}&{\lambda < 0} \end{array}} \right.$

(3)

定义2^[23] 　模糊数 $A$ 的可能性均值定义为其 $\gamma {\rm{ - }}$ 截集中点的加权平均数，即

$E[A]=\dfrac{{\displaystyle\int_0^1 {\gamma ({\underline A} (\gamma ) + \bar A(\gamma )){\rm{d}}\gamma } }}{{2\displaystyle\int_0^1 {\gamma {\rm{d}}\gamma } }}$

(4)

定义3^[24] 　模糊数 $A$ 的可能性上半方差定义为其 $\gamma {\rm{ - }}$ 截集的右端点与其可能性均值之间距离的平方的加权平均数，即

${V^{\rm{ + }}}[A]{\rm{=}}\dfrac{{\displaystyle\int_0^1 {\gamma {{( {\bar A(\gamma ) - E[A]} )}^2}{\rm{d}}\gamma } }}{{\displaystyle\int_0^1 {\gamma {\rm{d}}\gamma } }}$

(5)

定义4^[24] 　模糊数 $A$ 的可能性下半方差定义为其 $\gamma {\rm{ - }}$ 截集的左端点与其可能性均值之间距离的平方的加权平均数，即

${V^ - }[A]{\rm{=}}\dfrac{{\displaystyle\int_0^1 {\gamma {{\left( {{\underline A} (\gamma ) - E[A]} \right)}^2}{\rm{d}}\gamma } }}{{\displaystyle\int_0^1 {\gamma {\rm{d}}\gamma } }}$

(6)

定义5^[24] 　模糊数 $A$ 的可能性方差定义为其可能性上半方差和下半方差的平均数，即

$V[A]{\rm{=}}\dfrac{{\displaystyle\int_0^1 {\gamma ( {{{( {\bar A(\gamma ) - E[A]} )}^2}{\rm{ + }}{{( {\bar A(\gamma ) - E[A]} )}^2}} ){\rm{d}}\gamma } }}{{2\displaystyle\int_0^1 {\gamma {\rm{d}}\gamma } }}$

(7)

特别地，梯形模糊数 $A{\rm{ = }}\left( {a,b,\alpha ,\beta } \right)$ 的可能性均值、下半方差和方差分别为

$E[A]=\frac{{a + b}}{2} + \frac{{\beta - \alpha }}{6}$

(8)

${V^ - }[A]={\left( {\frac{{b - a}}{2} + \frac{{\alpha + \beta }}{6}} \right)^2} + \frac{{{\alpha ^2}}}{{18}}$

(9)

$V[A]={\left( {\frac{{b - a}}{2} + \frac{{\alpha + \beta }}{6}} \right)^2} + \frac{{{\alpha ^2}{\rm{ + }}{\beta ^2}}}{{36}}$

(10)

2 模糊收益率拟合模型

在进行投资决策时，首先需要估计各个风险资产的模糊收益率。考虑到线性隶属度函数便于处理，本文使用梯形模糊数来拟合资产的未来收益率。首先，通过模糊频率量化资产收益率基于历史数据的可能性。其次，考虑到专家观点对于预测资产未来收益具有比较大的价值，综合分析和讨论专家在对所投资资产未来表现的观点，将资产的未来收益率量化为一个三角模糊数。最后，通过整合历史数据信息和专家观点，建立一个模糊收益率拟合模型，将资产的收益率估计为一个梯形模糊数。

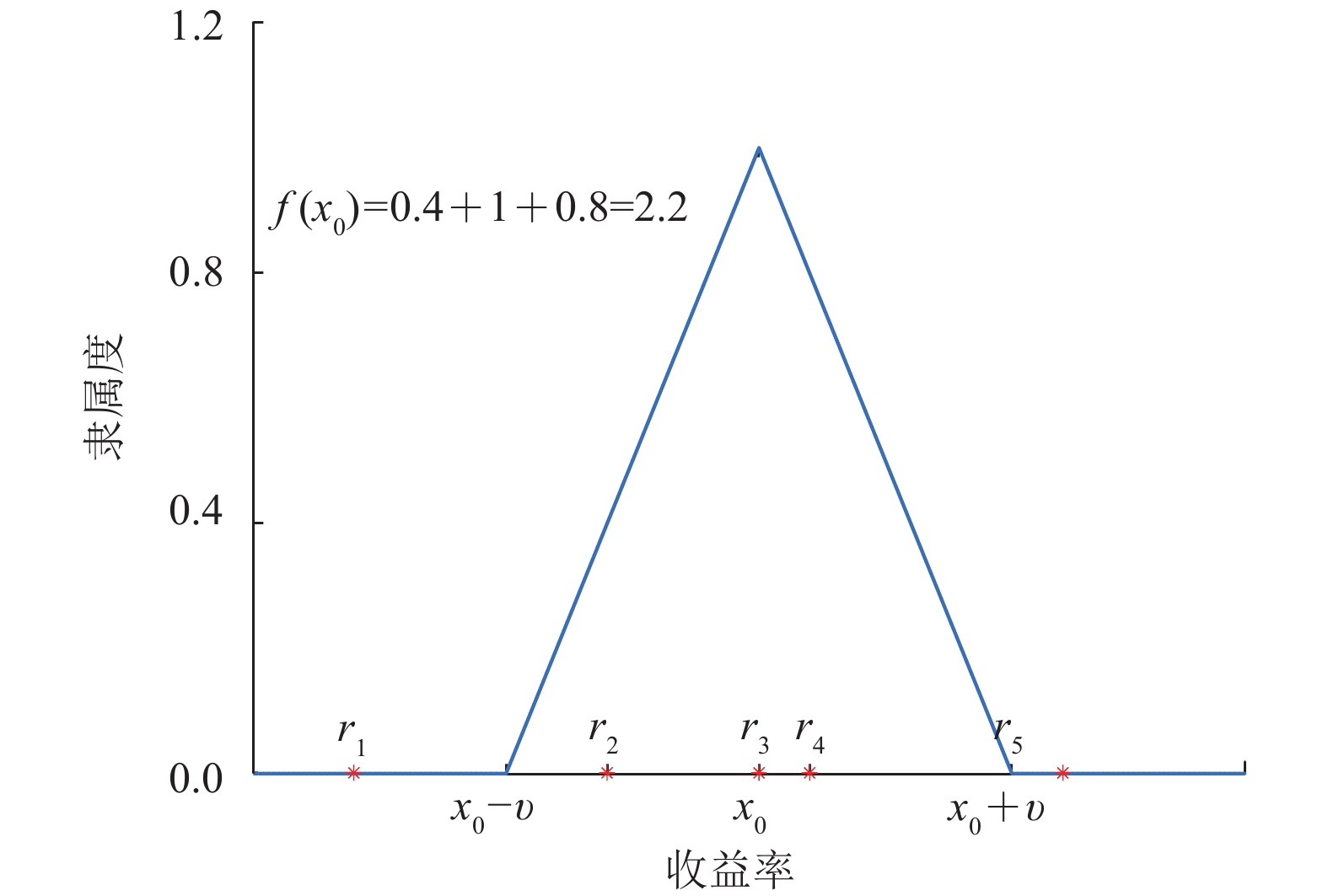
定义6 　记一个资产在 > $T$ 期内的历史收益率为 ${{{r}}^h}{\rm{=}}\left\{ {r_1^h, \cdots ,r_T^h} \right\}$ 。设实数 $\upsilon > 0$ 。对于任意的实数 $x$ ，称为

$f\left( x \right)=\sum\limits_{t=1}^T {\max \left\{ {1 - \frac{{\left| {x - r_t^h} \right|}}{\upsilon },0} \right\}} $

(11)

$x$ 在数据集 ${{{r}}^h}$ 中出现的模糊频数。

模糊频数 $f\left( x \right)$ 表示资产的历史收益率取值在 $x$ 附近的次数，如图1所示。例如，图中 ${x_0}$ 点的模糊频数为2.2。

下面，根据历史数据和专家观点估计一个资产的模糊收益率，假设其为梯形模糊数 $r{\rm{ = }}\left( {a,b,\alpha ,\beta } \right)$ ，隶属函数为 $\mu (x)$ 。需要确定参数 $a,{\rm{ }}b,{\rm{ }}\alpha ,{\rm{ }}\beta $ ，具体过程为给定一个足够大的正整数 $M$ ，令

${z_j}=r_{\min }^h - \upsilon + \frac{{( {j - 1})( {r_{\max }^h - r_{\min }^h + 2\upsilon } )}}{{M - 1}},{\rm{ }}j=1, \cdots ,M$

(12)

其中 $r_{\min }^h{\rm{=}}\mathop {\min }\limits_{1 \leqslant t \leqslant T} r_t^h$ ， $r_{\max }^h{\rm{=}}\mathop {\max }\limits_{1 \leqslant t \leqslant T} r_t^h$ 。根据定义6计算 ${z_j}$ 的模糊频数 $f( {{z_j}} )$ ，并对其进行最大值标准化，即 $\tilde f( {{z_j}} ){\rm{=}} {{f( {{z_j}} )} / {\mathop {\max }\limits_{1 \leqslant j \leqslant M} f( {{z_j}} )}}$ 。 $\tilde f( {{z_j}} )$ 表示基于历史数据的资产收益率取值为 ${z_j}$ 的可能性。

通过咨询相关领域的专家，得到资产收益率常规表现下的预测值 ${a^{\rm{E}}}$ ，较差表现下的预测值 ${r^{\min }}$ 和较好表现下的预测值 ${r^{\max }}$ 。记 ${\alpha ^{\rm{E}}}{\rm{=}}{a^{\rm{E}}} - {r^{\min }}$ 和 $\;{\beta ^{\rm{E}}}{\rm{=}}{r^{\max }} - {a^{\rm{E}}}$ ，则将三角模糊数 ${r^{\rm{E}}}{\rm{=}}({a^{\rm{E}}},{\alpha ^{\rm{E}}},{\beta ^{\rm{E}}})$ 作为专家估计的资产收益率，其隶属度函数为

${\mu _{\rm{E}}}(x)=\left\{ {\begin{array}{*{20}{l}} {\dfrac{{x - {a^{\rm{E}}} + {\alpha ^{\rm{E}}}}}{{{\alpha ^{\rm{E}}}}},}&{{a^{\rm{E}}} - {\alpha ^{\rm{E}}} < x < {a^{\rm{E}}}}\\ {\dfrac{{{a^{\rm{E}}} + {\beta ^{\rm{E}}} - x}}{{{\beta ^{\rm{E}}}}},}&{{a^{\rm{E}}} < x < {a^{\rm{E}}} + {\beta ^{\rm{E}}}}\\ {0,}&{{\text{其他}}} \end{array}} \right.。$

(13)

记 $F( {{z_j}} )=\dfrac{{{\mu _{\rm{E}}}({z_j}){\rm{ + }}\tilde f( {{z_j}} )}}{2}$ ， $j=1, \cdots ,M$ 。求使得 $F( {{z_j}} )$ 取得最大值的 ${z_j}$ ，记为 ${z^*}$ ，即

$F( {{z^{\rm{*}}}} )=\mathop {\max }\limits_{1 \leqslant j \leqslant M} F( {{z_j}} )$

(14)

对 $F( {{z_j}} )$ 进行最大值标准化，得 $\tilde F( {{z_j}} ){\rm{=}}{{F( {{z_j}} )} / {F( {{z^{\rm{*}}}} )}}$ 。 $\tilde F( {{z_j}} )$ 表示资产的收益率取值为 ${z_j}$ 的可能性，它综合考虑了历史数据和专家观点。

估计资产的模糊收益率时，需要保证所得模糊数的容忍区间 $[a,b]$ 包含 ${z^*}$ 且其支集 $[a - \alpha ,b + \beta ]$ 包含于区间 $[{z_1} - \upsilon ,{z_M} + \upsilon ]$ 。以模糊收益率在点 ${z_j}$ 的隶属度 $\mu ({z_j})$ 尽可能地接近 $\tilde F( {{z_j}} )$ 为目标，建立模糊收益率拟合模型。

${P_1}\left\{ \begin{array}{l} \min {\rm{ }}\dfrac{1}{M}\displaystyle\sum\limits_{j=1}^M {| {\mu ({z_j}) - \tilde F( {{z_j}} )} |} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{aligned} & {a \leqslant {z^*}}\\& {b \geqslant {z^*}}\\& {a - \alpha \geqslant {z_1} - \upsilon}\\& {b + \beta \leqslant {z_M} + \upsilon}\\& {\alpha ,\beta > 0} \end{aligned}} \right. \end{array} \right.$

为了便于求解，进行式(15)~(18)的变量替换。

$a={z^ * } - {y_1}\left( {{z^ * } - {z_1}} \right)$

(15)

$b={z^ * }{\rm{ + }}{y_2}\left( {{z_M} - {z^ * }} \right)$

(16)

$\alpha ={y_3}\left( {{z^ * } - {z_1}} \right)\quad\;\;\;$

(17)

$\beta ={y_4}\left( {{z_M} - {z^ * }} \right)\quad\;\;$

(18)

其中 ${y_1},{y_2},{y_3},{y_4}$ 为决策变量，则模型 ${P_1}$ 可以转化为

${P_2}\left\{ \begin{array}{l} \min {\rm{ }}\dfrac{1}{M}\displaystyle\sum\limits_{j=1}^M {| {\mu ({z_j}) - \tilde F( {{z_j}} )} |} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{aligned} & {{y_1} + {y_3} \leqslant 1}\\& {{y_2} + {y_4} \leqslant 1}\\& {0 \leqslant {y_i} \leqslant 1,{\rm{ }}i=1,2,3,4 } \end{aligned}} \right. \end{array} \right.$

本文将在第4节设计一个遗传算法对模型 ${P_2}$ 进行求解，从而估计出资产的模糊收益率。

3 投资组合调整模型

考虑一个包含 $n$ 种风险资产的投资组合问题。假设投资者初始的投资组合为 ${{{x}}^0}{\rm{=}}( {x_1^0, \cdots ,x_n^0} )$ ，其中 $x_i^0$ 表示第 $i$ 种资产的初始投资比例， $i{\rm{=}}1, \cdots ,n$ 。投资者计划在投资期初调整各个资产的头寸，设调整后的投资组合为 ${{x}}{\rm{=}}( {{x_1}, \cdots ,{x_n}} )$ ，其中 ${x_i}$ 表示第 $i$ 种资产调整后的投资比例。为了便于管理，假设投资者要求所投资的资产个数不超过 $K$ ，即 $\displaystyle\sum\nolimits_{i=1}^n {{\rm{sign}}\left( {{x_i}} \right)} \leqslant K$ 。假设投资过程中禁止卖空，即 ${x_i} \geqslant 0$ ，则该投资组合问题的可行域为

$\begin{array}{l} D=\{ {{{x}}=\left( {{x_1}, \cdots ,{x_n}} \right):\displaystyle\sum\limits_{i = 1}^n {{x_i}} = 1,} \\ {\displaystyle\sum\limits_{i = 1}^n {{\rm{sign}}({x_i})} \leqslant K,{x_i} \geqslant 0,i = 1, \cdots ,n} \} \\ \end{array} $

(19)

记买入风险资产的交易费用率为 ${c_b}$ ，卖出风险资产的交易费用率为 ${c_s}$ 。调整过程产生的交易费用为

$C = {c_b}\sum\limits_{i = 1}^n {\max \left\{ {{x_i} - x_i^0,0} \right\} + } {c_s}\sum\limits_{i = 1}^n {\max \left\{ {x_i^0 - {x_i},0} \right\}} $

(20)

设第 $i$ 种资产的收益率为梯形模糊数 ${r_i}{\rm{=}}( {a_i},{b_i}, {\alpha _i},{\beta _i} )$ 。根据引理1，投资组合 ${{x}}$ 的净收益率为

$\begin{aligned} {r_p} =& \displaystyle\sum\limits_{i = 1}^n {{x_i}{r_i}} - C = \Bigg( {\displaystyle\sum\limits_{i = 1}^n {{x_i}{a_i}} ,\displaystyle\sum\limits_{i = 1}^n {{x_i}{b_i}} ,\displaystyle\sum\limits_{i = 1}^n {{x_i}{\alpha _i}} ,\displaystyle\sum\limits_{i = 1}^n {{x_i}{\beta _i}} } \Bigg) - \\ & \Bigg( {{c_s}\displaystyle\sum\limits_{i = 1}^n {\max \{ {x_i^0 - {x_i},0} \}} + {c_b}\displaystyle\sum\limits_{i = 1}^n {\max \{ {{x_i} - x_i^0,0} \}} } \Bigg) \\ \end{aligned} $

(21)

投资组合 ${{x}}$ 的收益测度定义为净收益率的期望值，即

$\begin{aligned} {\rm Re}\left( {{x}} \right) =& E[{r_p}] = \displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\frac{{{a_i} + {b_i}}}{2} + \frac{{{\beta _i} - {\alpha _i}}}{2}} \right)} - \\ &\Bigg( {{c_s}\displaystyle\sum\limits_{i = 1}^n {\max \{ {x_i^0 - {x_i},0} \}} + {c_b}\displaystyle\sum\limits_{i = 1}^n {\max \{ {{x_i} - x_i^0,0} \}} } \Bigg) \\ \end{aligned} $

(22)

投资组合 ${{x}}$ 的风险测度定义为其净收益率的下半方差，即

${\rm Ri}\left( {{x}} \right)\! = \!{V^ - }[{r_p}] \!=\!{\Bigg( {\sum\limits_{i = 1}^n {{x_i}\left( {\frac{{{b_i} - {a_i}}}{2}\!+\!\frac{{{\alpha _i}\! + \!{\beta _i}}}{6}} \right)} } \Bigg)^2}\!+\!\frac{1}{{18}}{\Bigg( {\sum\limits_{i = 1}^n {{x_i}{\alpha _i}} } \Bigg)^2}$

(23)

定义第 $i$ 种资产的回报−波动比例为

${\theta _i} = \frac{{E\left[ {{r_i}} \right]}}{{\sqrt {V\left[ {{r_i}} \right]} }} = \frac{{{{\left( {{a_i} + {b_i}} \right)} / 2} + {{\left( {{\beta _i} - {\alpha _i}} \right)} / 6}}}{{\sqrt {{{\left( {{{\left( {{b_i} - {a_i}} \right)} / 2} + {{\left( {{\alpha _i} + {\beta _i}} \right)} / 6}} \right)}^2} + {{\left( {{\alpha ^2} + {\beta ^2}} \right)} / {36}}} }}$

(24)

定义投资组合 ${{x}}$ 的分散化测度为

$ {\rm Div}\left( {{x}} \right) = {1/ {\mathop {\max }\limits_{1 \leqslant i \leqslant n} \dfrac{{{x_i}}}{{{\theta _i}}}}} = 1 / \mathop {\max }\limits_{1 \leqslant i \leqslant n} \dfrac{{{x_i}\sqrt {{{\left( {{{\left( {{b_i} - {a_i}} \right)} / 2} + {{\left( {{\alpha _i} + {\beta _i}} \right)} / 6}} \right)}^2} + {{\left( {{\alpha ^2} + {\beta ^2}} \right)} /{36}}} }}{{{{\left( {{a_i} + {b_i}} \right)} / 2} + {{\left( {{\beta _i} - {\alpha _i}} \right)} / 6}}} $

(25)

假设投资者追求投资组合的收益最大化、风险最小化和分散化程度最大化。建立如下考虑交易费用的模糊均值−下半方差−分散化(Fuzzy Mean-Semi-Variance-Diversification，FMSVD)投资组合调整模型

${P_3}\left\{ \begin{array}{l} \max {\rm Re}\left( {{x}} \right) = \displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\dfrac{{{a_i} + {b_i}}}{2} + \dfrac{{{\beta _i} - {\alpha _i}}}{2}} \right)} - \Bigg( {{c_s}\displaystyle\sum\limits_{i = 1}^n {\max \left\{ {x_i^0 - {x_i},0} \right\}} + {c_b}\displaystyle\sum\limits_{i = 1}^n {\max \left\{ {{x_i} - x_i^0,0} \right\}} } \Bigg) \\ \min {\rm Ri}\left( {{x}} \right) = {\Bigg( {\displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\frac{{{b_i} - {a_i}}}{2} + \dfrac{{{\alpha _i} + {\beta _i}}}{6}} \right)} } \Bigg)^2} + \dfrac{1}{{18}}{\Bigg( {\displaystyle\sum\limits_{i = 1}^n {{x_i}{\alpha _i}} } \Bigg)^2} \\ \max {\rm Div}\left( {{x}} \right) = {1 / {\mathop {\max }\limits_{1 \leqslant i \leqslant n} \dfrac{{{x_i}\sqrt {{{\left( {{{\left( {{b_i} - {a_i}} \right)} / 2} + {{\left( {{\alpha _i} + {\beta _i}} \right)} / 6}} \right)}^2} + {{\left( {{\alpha ^2} + {\beta ^2}} \right)} /{36}}} }}{{{{\left( {{a_i} + {b_i}} \right)} / 2} + {{\left( {{\beta _i} - {\alpha _i}} \right)} / 6}}}}} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{{x}} \in {\rm D} \end{array} \right.$

定义7 　模型 ${P_3}$ 的一个可行解 ${{{x}}^*}$ 被称为该模型的帕累托有效解，当且仅当不存在其他解 ${{x}} \in D$ ，同时满足 ${\rm Re} \left( {{x}} \right) \geqslant {\rm Re}\left( {{{{x}}^ * }} \right)$ ， ${\rm Ri}\left( {{x}} \right) \leqslant {\rm Ri}\left( {{{{x}}^ * }} \right)$ 和 ${\rm Div}\left( {{x}} \right) \geqslant {\rm Div}\left( {{{{x}}^ * }} \right)$ ，并且至少有一个不等式取严格不等号。

模型 ${P_3}$ 为多目标规划模型，通常情况下同时使所有目标达到最优值的最优解不存在。投资者往往需要根据自己对3个目标的偏好程度选择一个帕累托有效解进行投资。为了求得契合投资者偏好的帕累托有效解，借鉴文献[25]将模型 ${P_3}$ 转化为单目标模型，具体过程如下。

首先，求解以下单目标优化模型

${P_4}\left\{ \begin{aligned} & \max {\rm Re}\left( {{x}} \right) \\ & {{x}} \in {\rm D} \\ \end{aligned} \right.$

${P_5}\left\{ \begin{aligned} & \min {\rm Ri}\left( {{x}} \right) \\ & {{x}} \in {\rm D} \\ \end{aligned} \right.\;\;$

${P_6}\left\{ \begin{aligned} & \max {\rm Div}\left( {{x}} \right) \\ & {{x}} \in {\rm D} \\ \end{aligned} \right.$

所得最优解分别为 ${{x}}_{\rm Re}^ * $ ， ${{x}}_{\rm Ri}^ *$ 和 ${{x}}_{\rm Div}^ *$ 。记3个目标的正理想解分别为 ${\rm R{e}^{\rm{ + }}}{\rm{ = }}{\rm Re}( {{{x}}_{\rm Re}^ * } )$ ， ${\rm R{i}^{\rm{ + }}}{\rm{ = }}{\rm Ri}( {{{x}}_{\rm Ri}^ * } )$ 和 ${\rm Di{v}^{\rm{ + }}}{\rm{ = }}{\rm Div}( {{{x}}_{\rm Div}^ * } )$ ；3个目标的负理想解分别为

${\rm R{e}^ - }{\rm{ = min}}\{ {{\rm Re}( {{{x}}_{\rm Ri}^ * } ),{\rm Re}( {{{x}}_{\rm Div}^ * } )} \}\;\;\;$

(26)

${\rm R{i}^ - }{\rm{ = max}}\{ {{\rm Ri}( {{{x}}_{\rm Re}^ * } ),{\rm Ri}( {{{x}}_{\rm Div}^ * } )} \}\;\;\;\;$

(27)

${\rm Di{v}^ - }{\rm{ = min}}\{ {{\rm Div}( {{{x}}_{\rm Re}^ * } ),{\rm Div}( {{{x}}_{\rm Ri}^ * } )} \}$

(28)

对于任意解 ${{x}} \in D$ ，投资者对于3个目标的满意程度分别表示为

${S_{\rm Re}}\left( {{x}} \right) = \left\{ \begin{array}{l} \dfrac{{{\rm Re}\left( {{x}} \right) - {\rm R{e}^ - }}}{{{\rm R{e}^ + } - {\rm R{e}^ - }}},\;\;{\rm R{e}^ - } \leqslant {\rm Re}\left( {{x}} \right) \leqslant {\rm R{e}^ + } \\ 0,\;\;\;\;\;\;\;\;\qquad{\rm Re}\left( {{x}} \right) < {\rm R{e}^ - } \\ \end{array} \right.$

(29)

${S_{\rm Ri}}\left( {{x}} \right) = \left\{ \begin{array}{l} \dfrac{{{\rm R{i}^ - } - {\rm Ri}\left( {{x}} \right)}}{{{\rm R{i}^ - } - {\rm R{i}^ + }}},\;\;{\rm R{i}^ + } \leqslant {\rm Ri}\left( {{x}} \right) \leqslant {\rm R{i}^ - } \\ 0,\;\;\;\;\;\;\;\;\quad\;\;\;{\rm Ri}\left( {{x}} \right) > {\rm R{i}^ - } \end{array} \right.\;\;\;\;$

(30)

${S_{\rm Div}}\left( {{x}} \right) = \left\{ \begin{array}{l} \dfrac{{{\rm Div}\left( {{x}} \right) - {\rm Di{v}^ - }}}{{{\rm Di{v}^ + } - {\rm Di{v}^ - }}},\;\;{\rm Di{v}^ - } \leqslant {\rm Div}\left( {{x}} \right) \leqslant {\rm Di{v}^ + } \\ 0,\;\;\;\;\;\;\;\;\qquad\;\;\;\;{\rm Div}\left( {{x}} \right) < {\rm Di{v}^ - } \\ \end{array} \right.$

(31)

给定3个目标的权重 ${w_1},{w_2},{w_3}$ ，模型 ${P_3}$ 可以转化为如下单目标规划模型 ${P_7} $ 。

${P_7}\left\{ \begin{array}{l} \max \lambda \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\left\{ {\begin{aligned} & {\dfrac{{{\rm Re}\left( {{x}} \right) - {\rm R{e}^ - }}}{{{\rm R{e}^ + } - {\rm R{e}^ - }}} \geqslant {w_1}\lambda}\\& {\dfrac{{{\rm R{i}^ - } - {\rm Ri}\left( {{x}} \right)}}{{{\rm R{i}^ - } - {\rm R{i}^ + }}} \geqslant {w_2}\lambda}\\& {\dfrac{{{\rm Div}\left( {{x}} \right) - {\rm Di{v}^ - }}}{{{\rm Di{v}^ + } - {\rm Di{v}^ - }}} \geqslant {w_3}\lambda }\\& {{{x}} \in D } \end{aligned}} \right. \end{array} \right.$

引理2^[25] 　模型 ${P_3}$ 的一个可行解 ${{{x}}^ * }$ 为帕累托有效解，当且仅当存在 $\lambda \geqslant 0$ ，使得 $\left( {{{{x}}^ * },\lambda } \right)$ 为模型 ${P_7}$ 的最优解。

4 改进的遗传算法

本节设计一个改进的遗传算法来求解前面建立的模糊收益率拟合模型和投资组合调整模型。对于模糊收益率拟合模型 ${P_2}$ ，采用实数编码将模型的解 ${{y}}{\rm{=}}({y_1},{y_2},{y_3},{y_4})$ 编码为染色体 ${{c}}{\rm{=}}({c_1},{c_2},{c_3},{c_4})$ ，其中基因 ${c_i} \in [0,1]$ ， $i{\rm{=}}1,2,3,4$ 。染色体的解码方式为

${y_i} = \left\{ \begin{array}{l} \dfrac{{{c_i}}}{{\max \left\{ {{c_1} + {c_3},1} \right\}}},\;\;i = 1,3 \\ \dfrac{{{c_i}}}{{\max \left\{ {{c_2} + {c_4},1} \right\}}},\;\;i = 2,4 \\ \end{array} \right.$

(32)

可以看出，由此得到的 ${ y}{\rm{=}}({y_1},{y_2},{y_3},{y_4})$ 是模糊收益率拟合模型的可行解。

对于投资组合调整模型 ${P_4}$ ~ ${P_7}$ ，采用实数编码将模型的解 ${{x}}{\rm{=}}({x_1}, \cdots ,{x_n})$ 编码为染色体 ${{c}}{\rm{=}}({c_1}, \cdots ,{c_n})$ ，其中基因 ${c_i} \in [0,1]$ ， $i{\rm{=}}1, \cdots ,n$ 。染色体的解码方式如下：首先，将最小的 $n - K$ 个基因取值变为0，得 ${\bar {{c}}}{\rm{=}} \left( {{{\bar c}_1}, \cdots ,{{\bar c}_n}} \right)$ ；然后，令

${x_i} = \dfrac{{{{\bar c}_i}}}{{\displaystyle\sum\nolimits_{i = 1}^n {{{\bar c}_i}} }}$

(33)

可以看出，由此得到的 ${{x}} = ({x_1}, \cdots ,{x_n})$ 是投资组合调整模型的可行解。

种群规模记为 $N$ 。随机生成 $N$ 个染色体作为初始种群。接下来介绍种群进化过程的选择、交叉、变异算子及求解算法的主要流程。

4.1 选择算子

选择操作的具体过程为：(1) 复制种群中的 $N$ 个染色体，将 $2N$ 个染色体置入选择池中；(2) 从选择池中不放回地随机抽取4个染色体；(3) 根据所求解模型的目标函数将抽取的4个染色体由差到好进行排序，记为 ${{{c}}_1}$ ， ${{{c}}_2}$ ， ${{{c}}_3}$ 和 ${{{c}}_4}$ ；(4) 保存4个染色体中最好的 ${{ c}_4}$ ，然后根据轮盘赌的方式从其余3个染色体中选择1个保存下来，其中 ${{\bf{c}}_k}$ 被选中的概率为 ${k / 6}$ ， $k{\rm{=}}1,2,3$ ；(5) 重复步骤(2)至(4) ${N / 2}$ 次，得到 $N$ 个新的染色体。它们将作为新种群进入后续的迭代过程。

本文所设计的选择算子具有如下3个优点：(1) 种群中的最优个体必然被保存，避免了最优个体在进化过程中遗失；(2) 任意染色体都有机会被选中，即使是种群中最差的个体，它在组内竞争中也有 ${1 / 6}$ 的概率被选中；(3) 越好的染色体被选中的概率越大，体现了遗传过程中优胜劣汰的本质。

4.2 交叉算子

设交叉概率为 ${P_c}$ ，交叉操作的具体过程如下。

(1) 从种群的 $N$ 个染色体中不放回地随机抽取2个染色体。

(2) 根据所求解模型的目标函数将抽取的2个染色体由差到好进行排序，记为 ${{{c}}_1}{\rm{ = }}\left( {{c_{1,1}}, \cdots ,{c_{1,h}}} \right)$ ， ${{{c}}_2}{\rm{ = }}\left( {{c_{2,1}}, \cdots ,{c_{2,h}}} \right)$ ，其中 $h$ 为染色体长度(求解模糊收益率拟合模型时取 $h = 4$ ，求解投资组合调整模型时取 $h = n$ )。

(3) 在区间 $[0,1]$ 中随机生成1个实数 $v$ ，若 $v \geqslant {P_c}$ ，不对染色体进行交叉操作；否则，以 ${{{c}}_1}$ 和 ${{{c}}_2}$ 作为父代生成2个后代，如式(34)所示：

$\left\{ \begin{array}{l} {{{\bf{c}}_1'}} = {{{c}}_1} + {{d}} \otimes \left( {{{{c}}_2} - {{{c}}_1}} \right) \\ {{{{c}}_2'}} = {{{c}}_2} + {{d}} \otimes \left( {{{b}} - {{{c}}_1}} \right) \\ \end{array} \right.$

(34)

其中 ${{d}}{\rm{ = }}\left( {{d_1}, \cdots ,{d_h}} \right)$ 为区间 $[0,1]$ 上的随机向量，向量 ${{b}}{\rm{ = }}\left( {{b_1}, \cdots ,{b_h}} \right)$ 的分量 ${b_i}{\rm{=}}{\rm{sign}}\left( {\max \left\{ {{c_{2,i}} - {c_{1,i}},0} \right\}} \right)$ ， ${{x}} \otimes {{y}}{\rm{=}} \left( {{x_1}{y_1}, \cdots ,{x_h}{y_h}} \right)$ 。

(4) 比较2个父系染色体与2个后代染色体，保存较好的2个。

(5) 重复步骤 (1) 至步骤 (4) ${N / 2}$ 次，得到 $N$ 个新的染色体。它们将作为新种群进入后续的迭代过程。

4.3 变异算子

设变异概率为 ${P_m}$ ，变异操作的具体过程为：(1) 从种群的 $N$ 个染色体中不放回地随机抽取1个染色体，记为 ${{c}}{\rm{ = }}\left( {{c_1}, \cdots ,{c_h}} \right)$ 。(2) 在区间 $[0,1]$ 中随机生成1个实数 $v$ 。若 $v \geqslant {P_m}$ ，则该染色体不发生变异；否则，在集合 $\left\{ {1, \cdots ,h} \right\}$ 中随机生成1个实数 $k$ ，染色体 ${{c}}$ 中的基因 ${c_k}$ 发生变异，产生1个新的染色体 ${{c'}}{\rm{ = }}\left( {{c_1}, \cdots ,{{c'}_k}, \cdots ,{c_h}} \right)$ ，其中 ${c'_k}$ 为区间 $[0,1]$ 上的随机数。(3) 比较染色体 ${{c}}$ 和 ${{c'}}$ ，保存较好的一个。(4) 重复步骤 (1) ~ (3) $N$ 次，得到 $N$ 个新的染色体。它们将作为新种群进入后续的迭代过程。

4.4 算法流程

求解算法的具体操作流程为：(1) 输入算法的参数：种群规模 $N$ ，交叉概率 ${P_c}$ ，变异概率 ${P_m}$ 和最大迭代次数 ${G_{\max }}$ ；(2) 随机生成 $N$ 个染色体作为初始种群；(3) 通过选择算子更新种群中的染色体；(4) 通过交叉算子更新种群中的染色体；(5) 通过变异算子更新种群中的染色体；(6) 重复步骤(3) ~ (5) ${G_{\max }}$ 次；(7) 输出种群中最优染色体对应的解作为所求模型的满意解。

5 实例分析

为了说明所提出的模型和算法的有效性，本节采用真实的股票数据进行实例分析。假设投资者从上海证券交易所选择了12只股票作为投资对象，其名称和代码如表1所示。不失一般性，假设投资者的初始总财富值1，并均匀地分配在12只股票上，即初始投资组合为 ${{{x}}^0}{\rm{=}}({1 / {12}}, \cdots ,{1 / {12}})$ 。投资者计划调整各只股票的头寸。假设投资者要求调整后持有的股票数目不超过8只，即 $K{\rm{ = }}8$ ；买入和卖出股票的交易费用率分别为 ${c_b}{\rm{ = }}0.003$ 和 ${c_s}{\rm{ = }}0.005$ 。

本文收集了这12只股票102个月(2011年1月~2019年6月)的月收益率数据。将所收集的数据分为2个部分：前96个月(2011年1月~2018年12月)的月收益率为训练集，用于拟合股票收益率的模糊分布；后6个月(2019年1月~2019年6月)的月收益率为测试集，用于检验所提出的策略在金融市场中的实际表现。

在估计风险资产模糊收益率的过程中，需要借鉴专家关于资产未来收益的观点。根据第2节介绍的方法，通过咨询专家对各只股票预期表现的意见，估计了收益率所服从的三角模糊数，具体见表2。

利用第4节设计的遗传算法求解模糊收益率拟合模型 ${P_2}$ 时，模型的参数设置为： $\upsilon {\rm{ = }}0.04$ ， $M{\rm{ = }}3 \;000$ ；遗传算法的参数设置为：种群规模 $N{\rm{ = }}1\;000$ ，交叉概率 ${P_c}{\rm{ = }}0.8$ ，变异概率 ${P_m}{\rm{ = }}0.3$ 和最大迭代次数 ${G_{\max }}{\rm{ = }} 300$ 。各股票模糊收益率的拟合结果如表3所示。

利用第4节设计的遗传算法分别求解最大收益模型 ${P_4}$ 、最小风险模型 ${P_5}$ 和最大分散化模型 ${P_6}$ ，所得最优解如表4所示。

由表3和表4可知，只考虑收益或者风险目标时，所得最优投资组合将大部分资产集中于收益最高或者风险最低的股票上，而只考虑分散化目标时，所得最优投资组合将资产分散地投资于多个资产上。可以看出，模糊投资组合问题中传统的收益和风险测度并不能构建分散化的投资策略，而本文引入的分散化目标可以有效地克服这一缺陷。由表4可知，收益、风险和分散化这3个目标的正理想解分别为 $\rm R{e^ + } {\rm{ = }} 0.037\;5$ ， $\rm R{i^ + } {\rm{ = }} 0.001\;9$ 和 $\rm Di{v^ + } {\rm{ = }} 54.945\;1$ ；负理想解分别为 $\rm R{e^ - } {\rm{ = }} 0.001\;2$ ， $\rm R{i^ - } {\rm{ = }} 0.004\;8$ 和 $\rm Di{v^ - } {\rm{ = }} 4.526\;9$ 。投资者可以通过设定3个目标的权重求解模型 ${P_7}$ ，构建契合自身偏好的投资组合策略。

为了说明本文所提出FMSVD模型的有效性，下面比较其所构建的策略与其他模型所构建策略在实际投资中的表现。对于FMSVD模型，假定投资者对3个目标同等看重，即 ${w_1}{\rm{ = }}{w_2}{\rm{ = }}{w_3}{\rm{ = }}1/3$ ，对应的策略可以通过求解模型 ${P_7}$ 得到。本文选取以下4个模型进行比较。

均匀投资模型( $1/N$ )，即将资金均匀地投资于各个资产上。该策略的收益体现了这12只资产的平均表现。

Markowitz^[1]提出的均值−方差(Mean-Variance，MV)模型：

${P_8}\left\{ \begin{array}{l} \min {\rm{ }}\displaystyle\sum\limits_{i = 1}^n {\displaystyle\sum\limits_{j = 1}^n {{x_i}{x_j}{\sigma _{ij}}} } \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{aligned} & {\displaystyle\sum\limits_{i = 1}^n {{x_i}{\mu _i}} \geqslant \bar \mu}\\& {\displaystyle\sum\limits_{i = 1}^n {{x_i}} = 1}\\& {{\rm{0}} \leqslant {x_i} \leqslant {u_i},{\rm{ }}i = 1, \cdots ,n } \end{aligned}} \right. \end{array} \right.$

其中 ${\mu _i}$ 为第 $i$ 只股票的期望收益率， ${\sigma _{ij}}$ 为第 $i$ 股票和第 $j$ 只股票收益率的协方差， $\bar \mu $ 为给定的收益水平。这里取 $\bar \mu = 0.02$ 。

Zhang等^[24]提出的模糊均值−下半方差投资组合(Fuzzy Mean-Semi-Variance，FMSV)模型

${P_9}\left\{ \begin{array}{l} \min {\rm{ }}{\Bigg( {\displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\frac{{{b_i} - {a_i}}}{2} + \dfrac{{{\alpha _i} + {\beta _i}}}{6}} \right)} } \Bigg)^2} + \dfrac{1}{{18}}{\Bigg( {\displaystyle\sum\limits_{i = 1}^n {{x_i}{\alpha _i}} } \Bigg)^2} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{aligned} & {\displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\dfrac{{{a_i} + {b_i}}}{2} + \frac{{{\beta _i} - {\alpha _i}}}{6}} \right)} \geqslant \bar \mu}\\& {\displaystyle\sum\limits_{i = 1}^n {{x_i}} = 1}\\& {{\rm{0}} \leqslant {x_i} \leqslant {u_i},{\rm{ }}i = 1, \cdots ,n} \end{aligned}} \right. \end{array} \right.$

其中 $\;\bar \mu $ 为给定的收益水平， ${u_i}$ 为投资比例上界。这里 $\;\bar \mu$ 的取值与MV模型相同，即 $\; \bar \mu{\rm{=}}0.02$ ；取 ${u_i}{\rm{=}}0.35$ 。

Vercher等^[16]提出的模糊均值−下半绝对偏差(Fuzzy Mean-Semi-Absolute Deviation，FMSAD)模型为

${P_{10}}\left\{ \begin{array}{l} \min {\rm{ }}\displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\frac{{{b_i} - {a_i}}}{2} + \dfrac{{{\alpha _i} + {\beta _i}}}{6}} \right)} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{aligned} & {\displaystyle\sum\limits_{i = 1}^n {{x_i}\left( {\dfrac{{{a_i} + {b_i}}}{2} + \dfrac{{{\beta _i} - {\alpha _i}}}{6}} \right)} \geqslant \bar \mu}\\& {\displaystyle\sum\limits_{i = 1}^n {{x_i}} = 1}\\& {{\rm{0}} \leqslant {x_i} \leqslant {u_i},{\rm{ }}i = 1, \cdots ,n } \end{aligned}} \right. \end{array} \right.$

其中 $\;\bar \mu$ 为给定的收益水平， ${u_i}$ 为投资比例上界。这里 $\;\bar \mu$ 和 ${u_i}$ 的取值与前两个模型相同，即 $\;\bar \mu{\rm{=}}0.02$ ， ${u_i}{\rm{=}}0.35$ 。

上述5个模型所构建的投资策略如表5所示。接着，通过测试集的数据比较各个投资组合策略在未来半年的实际表现。以每个月最后一个交易日为节点，记录表5中5个策略在测试集中的财富累积情况，结果如表6所示。

由表5可知，本文所提出的FMSVD模型与传统的Markowitz的MV模型可以构建一个较为分散化的投资策略，而传统模糊投资组合模型FMSV和FMSAD所构建的投资策略集中投资于少数几只股票上。可以看到，本文提出的策略可以构建结构合理的投资组合。从表6可以看出，与其他模型相比，本文提出的FMSVD模型在测试集中的财富累积状况一直维持在较高的水平。因此，本文所提出的策略在实际应用中具有较好的表现。

6 结论

本文研究了模糊环境下考虑交易费用和基数约束的投资组合调整问题。首先，基于历史数据和专家观点，通过建立一个模糊收益率拟合模型，确定了各个资产收益率的模糊分布。其次，考虑到传统模糊投资组合模型所构建的投资策略往往集中投资于少数资产，提出了一个模糊均值−下半方差−分散化投资组合调整模型。然后，根据投资者对各个目标的偏好将所提出的多目标规划模型转化为单目标规划模型，并设计了一个改进的遗传算法求解所建立的模型。最后，通过实例分析说明了所提出的策略可以实现较高的收益，较好地满足投资者的分散化要求，具有较强的实用性。在实际投资过程中，影响投资决策的因素和约束很多，本文仅考虑了交易费用与基数约束。因此，考虑更全面的市场因素和现实约束的模糊投资组合调整问题有待进一步探讨。