故障是一种系统状态，对于人而言十分重要。特别是人设计、制造和运行的系统，都消耗了资源，目的是完成人制定的预期目标。该目标就是系统的功能，那么系统在规定时间内，规定条件下完成预定功能的能力即为可靠性。对应的，故障是由于一些事件导致系统不能完成功能或功能降低的状态。人们更关注于系统故障过程的发生发展以及最终结果，因此作者提出了系统故障演化过程(System Fault Evolution Process，SFEP)的概念^[1-2]。对于SFEP的研究正在展开，其目标是面向未来无人化、智能化、信息化和数据化的复杂系统，但适合研究的理论显然并不充分。

对系统故障演化、系统故障及其智能方法研究不多。较新的研究主要包括：故障修复演化研究^[3]、模糊离散和随机离散事件系统的故障预测^[4-5]、大数据统计与故障演化诊断^[6]以及系统连锁故障模型研究^[7]等。国外也进行了基于现场数据的系统故障演化估计^[8]、相互依赖基础设施系统故障演化分析^[9]、机械工程过程故障演化的智能监控^[10]等相关研究。这些方法只限于自身领域的研究，缺乏普适方法论。给SFEP的智能处理和方法研究带来了较大困难。

面对上述问题提出了空间故障网络(Space Fault Network, SFN)理论描述和研究SFEP，虽然在不断发展但其基本理论体系仍缺乏智能方法论和信息方法论。因此提出使用可拓理论，利用可拓原理建立SFEP的分析方法。本文是该研究思路的首篇论文，为该项研究奠定基础。

1 系统功能状态与可拓学

系统建立是为了完成人设想的预定功能。系统可分为人工系统和自然系统。人工系统即是人建立的、按照自然规律完成预定功能的系统。自然系统则是自然形成的系统，与人无关。可以说在哲学层面上，存在即为系统，即万事万物都是系统，只是存在的结构、层析、特征和是否被人观测到的问题。人耗费各种资源建立系统，因此要保证系统功能的功能性和稳定性。系统发展从来都是先满足功能性，然后提高稳定性。但随着具有无人化、智能化、信息化和数据化等特征的复杂系统出现，系统功能的稳定性日渐超越功能性更受到关注。因此保持复杂系统在规定时间内、规定条件下完成预定功能的能力成为关键问题。这是系统可靠性的定义，其对立面是系统的失效性。可总结如下关系：存在即是系统−人建立系统完成功能−系统存在意义−功能可以可靠和失效−系统功能状态包括可靠状态和失效状态，因此系统功能状态代表了系统的存在意义。

系统功能状态有可靠和失效2种状态，其在它们之间徘徊，当然它们的界限是人规定的。系统功能状态最终以何种状态存在取决于人和自然的物质性和意识性^[11]。同时这2种状态组成了系统功能状态的论域空间。就系统功能状态而言，可靠性和失效性是辩证统一、不断转化的对立矛盾关系。遗憾的是这种矛盾关系目前只通过机械唯物主义的机械还原论作为方法论解决^[12-15]。机械还原论将事物之间的联系切断，认为系统与其基本元件或子系统的功能是简单整合的；否认元件与子系统之间存在着物质、能量和信息交换。美国科学院院士南希埃文森等^[16-17]指出，现有方法对系统故障分析结果远小于实际系统故障情况，这正是忽视了子系统之间以外的物质、能量和信息的传递造成的。目前的研究将可靠性和失效性分开研究，或者只研究其一，另一方则按照补集处理。但应该对系统功能性进行全面研究，即可靠性与失效性同时研究，以相互补充认识的不足。

上述过程实际是解决事物矛盾问题的过程，而目前通过可拓学理论研究这类问题较为有效。可拓学是以矛盾问题为研究对象、以矛盾问题的智能化处理为主要研究内容、以可拓方法论为主要研究方法的一门新兴科学^[18]。它能提供形式化模型、定性和定量结合的工具、推理规则和特有方法。文献[18]论述可拓论包括基元理论(拓展分析、共轭分析、开拓变换)、可拓集理论(可拓集和关联函数)、可拓逻辑(可拓模型和可拓推理)3大部分。随着近些年的研究，又形成了可拓创新方法和可拓工程2大部分。虽然在蔡文教授、杨春燕教授和李兴森教授的努力下可拓理论取得了巨大成功，但学界对其与具体学科的结合方面仍存在问题。作者在阅读了近年来的百余篇可拓论文后发现多数研究集中在可拓评价领域，更为有趣的是多是论述系统安全、风险、可靠和失效方面的研究；而且表现出来的思路也是统一的，即物元建立、确定权重、关联函数计算、等级确定；变化集中在权重确定和物元量值的表示。

作为安全科学理论的研究者，认为可拓学有着更为广泛的用途和与安全理论的融合角度。因此使用可拓学来描述SFEP，为可拓学与安全理论结合开辟出另一路径。

2 系统故障演化过程的可拓表示

SFEP是系统功能状态变化的过程，描述过程中系统故障发生、发展、传播和结束。对应于空间故障树理论的第3阶段SFN；也是描述最为广泛的系统故障过程的方法。本节将建立SFEP与可拓之间的联系。

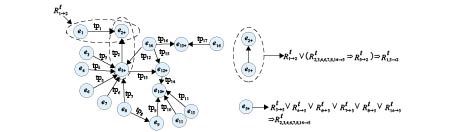
2.1 SFEP描述

为描述SFEP，首先给出简单往复式压缩机的故障过程^[19]，如图1所示。图1中，e代表事件，tp代表传递，→代表传递方向，+表示或关系。符号含义如表1所示。

表1给出了故障过程中涉及的各种事件。事件的来源是对故障过程论述的拆分^[20]。研究过程文本一般可得到2个结果，一是拆分的事件，见表1；二是事件之间的发展过程，如图1所示。事件特征在于以对象和动作的形式完成事件描述。对象一般是客观的物，是动作的接受者。可理解为增加了吸气管线处气压，然后发生了后即结果。表1中事件为了突出状态因此将动作置于对象之后。因此SFEP中的事件是“动作+动作接受对象”。另一方面这些事件组成了对于压缩机系统的SFEP。事件之间存在引起与被引起的关系，即因果关系；也可能存在一个或多个原因对应一个或多个结果的情况。这些对应关系蕴含了复杂的逻辑关系，如“与或”。可见研究SFEP必须能表示和研究其中演化、事件及其因果关系。

2.2 SFEP抽象特征

目前SFEP的研究方法是首先得到事件，然后澄清事件间的联系。基本问题是如何在文本中拆分事件。较为通常的方式是将关系作为核心，加之关系涉及的2个事件组成基本单元，即事件−关系−事件的单元。结构中前者表示原因事件，后者表示结果事件，关系代表原因事件导致结果事件的可能性，是原因事件在具备传递状态时导致结果事件的概率。那么SFEP可抽象为若干关联的基本单元，形式为原因事件−传递条件−结果事件。这些基本单元的有限叠加即可表示SFEP。SFEP抽象的基本结构确定后还应考虑过程中作用的因素。不同因素的不同状态将导致原因事件发生概率、结果事件发生概率及传递概率的不同，甚至导致SFEP改变，产生多样性。

2.3 SFEP基本单元的可拓表示

关于基元的基本概念，见文献[18]论述。这里只给出物元、事元和关系元的最复杂形式。

在物元M=(O_m,c_m,v_m)中，O_m和v_m是参数t的函数，那么M为参变物元，即M(t)=(O_m(t),C_m,V_m(t))。其中，O_m为物，C_m为特征，V_m为量值；t为参数，可理解为影响因素或者它们的集合。

在事元A=(O_a,c_a,v_a)中，O_a和v_a是参数t的函数，那么A为参变事元，即A(t)=(O_a(t),C_a,V_a(t))。其中，O_a为动作，C_a为特征，V_a为量值；t为参数，可理解为影响因素或者它们的集合。

在关系元R=(O_r,c_r,v_r)中，O_r和v_r是参数t的函数，那么R为参变事元，即R(t)=(O_r(t),C_r,V_r(t))。其中，O_r为关系，C_r为特征，V_r为量值；t为参数，可理解为影响因素或者它们的集合。

把物元、事元和关系元统称为基元，即为B=(O,C,V)中，O表示对象，包括物、动作和关系，C代表对象O的特征，V代表对象O关于特征C的量值。

从2.2可知SFEP的基本单元。事件由物和动作组成，那么事件由物元和事元组成的复合元表示。又因为事件是“动作+动作接受对象”的表示形式，因此SFEP的原因事件由物元和事元得到的复合事元表示，如式(1)所示，同理结果事件的复合事元如式(2)所示。传递关系由上述2个复合事元和关系元得到的复合关系元表示，如式(3)所示。按照SFEP对式(3)具体化为式(4)。

$ \left\{ \begin{aligned}\begin{array}{l} {{M^c} = (O_m^c,C_m^c,V_m^c)} \\ {{A^c} = (O_a^c,C_a^c,V_a^c)} \end{array} \Rightarrow \!\!\!\!\! \!\!\!\!\!\!\!\!\begin{array}{*{20}{l}}&{A^c}({M^c}) = (O_a^c,C_a^c,{M^c}) = \\ &(O_a^c,C_a^c,(O_m^c,C_m^c,V_m^c))\end{array} \end{aligned} \right.$

(1)

式(1)中，上角标c代表原因。

$ \left\{ \begin{aligned}\begin{array}{l} {{M^r} = (O_m^r,C_m^r,V_m^r)} \\ {{A^r} = (O_a^r,C_a^r,V_a^r)} \end{array} \Rightarrow \!\!\!\!\! \!\!\!\!\!\!\!\!\begin{array}{*{20}{l}}&{A^r}({M^r}) = (O_a^r,C_a^r,{M^r}) =\\ & (O_a^r,C_a^r,(O_m^r,C_m^r,V_m^r)) \end{array} \end{aligned} \right.$

(2)

式(2)中，上角标r代表结果。

$ \begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{A^c}({M^c}) = (O_a^c,C_a^c,(O_m^c,C_m^c,V_m^c))} \\ {{A^r}({M^r}) = (O_a^r,C_a^r,(O_m^r,C_m^r,V_m^r))} \\ {{R^t} = (O_r^t,C_r^t,({A^c},{A^r})')} \end{array} \Rightarrow } \right.{R^t} = {R^t}(O_r^t,C_r^t,((O_a^c,C_a^c,(O_m^c,C_m^c,V_m^c)),(O_a^r,C_a^r,(O_m^r,C_m^r,V_m^r)))') \end{aligned} $

$ {R^t} = \left[ {\begin{array}{*{20}{c}} {O_r^t,}&{c_{r1}^t,}&{(O_a^c,C_a^c,(O_m^c,C_m^c,V_m^c))} \\ {}&{c_{r2}^t,}&{(O_a^r,C_a^r,(O_m^r,C_m^r,V_m^r))} \end{array}} \right]$

(3)

$ {R^t} = \left[ {\begin{array}{*{20}{c}} {\rm{tp}},&{{\text{前项}},}&{\left[ {\begin{array}{*{20}{c}} {{\text{原因动作}},}&{{\text{施动对象}},}& \cdots \\ {}&{{\text{接受对象}},}& \cdots \\ {}&{{\text{支配对象}},}&{\left[ {\begin{array}{*{20}{c}} {{\text{原因对象}},}&{c_1^c,}&{v_1^c}\\ {}& \vdots & \vdots \\ {}&{c_i^c}&{v_i^c} \end{array}} \right]}\\ {}&{{\text{发生概率}},}&{{\text{量值}}}\\ {}& \vdots &{}\\ \end{array}} \right]}\\ {}&{{\text{后项}},}&{\left[ {\begin{array}{*{20}{c}} {{\text{结果动作}},}&{{\text{施动对象}},}& \cdots \\ {}&{{\text{接受对象}},}& \cdots \\ {}&{{\text{支配对象}},}&{\left[ {\begin{array}{*{20}{c}} {{\text{结果对象}},}&{c_1^r}&{v_1^r}\\ {}& \vdots & \vdots \\ {}&{c_i^r}&{v_i^r} \end{array}} \right]}\\ {}&{{\text{发生概率}},}&{}\\ {}& \vdots &{{\text{量值}}} \end{array}} \right]}\\ {}&{{p_t},}&{{\text{量值}}}\\ {}&\vdots & \cdots \end{array}} \right]$

(4)

式(4)中，p_t表示传递概率。

式(4)即为SFEP基本单元的可拓表示方法。由于SFEP的特点，分析时一般只出现支配对象，为物；接受对象很少出现，一般为人和物；而施动对象不出现。例如事件吸气管线处气压增加，动作是增加，支配对象是吸气管线处气压，没有明显的接受对象和施动对象。传递的属性有很多，如式中给出的前项(原因)、后项(结果)和传递概率p_t，也可以有传递条件等特征。同样动作也可以有很多特征。这些特征可以是事元、物元或关系元。为了进行可拓分析，结合式(3)、(4)得到式(5)，称为SEFP的传递元R^t，即基本单元。

$\begin{aligned} R_{c \to r}^t =& [{\rm{tp}},({e_c},{e_r},{p_t})',(({a_c},({c_c},{p_c})',(({m_c},{C_c},{V_c}),{v_c})'),\\ & ({a_r},({c_r},{p_r})',(({m_r},{C_r},{V_r}),{v_r})'),{v_t})'] \end{aligned} $

(5)

式(5)中， $\rm tp $ 为传递；e_c为原因事件；e_r为结果事件； $p_t $ 为传递概率；a_c为原因动作；c_c为原因动作支配对象；m_c为原因事件对象；C_c为原因事件特征；V_c为量值； $p_c $ 为原因事件概率；v_c为原因事件概率值；a_r为结果动作；c_r为结果动作支配对象；m_r为结果事件对象；C_r为结果事件特征；V_r为量值； $p_r $ 为结果事件概率；v_r为结果事件概率值；v_t为传递概率值。对应的集合用大写表示。

式(5)是SFEP传递元使用复合元表示的最简单形式。该复核元是关系元，因此SFEP可以表示为多个复合关系元(传递元)的复合。通过这样的方式即可表示故障状态的传递过程，即原因事件1−传递1−结果事件1；结果事件1作为原因事件2；原因事件2−传递2−结果事件2，以此类推达到SFEP的最终状态。例如：吸气管线处气压增加的发生概率为0.01%，其导致排气压力增加的概率为0.5%，最终排气压力增加的概率为P(所求值)，表示为R_t=[传递, (吸气管线处气压增加, 排气压力增加, 传递概率)′, ((增加, (支配对象, 发生概率)′, ((吸气管线处气压, 特征, 量值), 0.01%)′), (增加, (支配对象, 发生概率)′, ((排气压力, 特征, 量值), P)′), 0.5%)′]。当传递之间存在逻辑关系时，可用可拓拓展原理进行分析。

3 SFEP的传递元分析原理

上述完成了SFEP中基本单元的可拓表示，如下研究拓展分析原理，以满足分析事件间因果逻辑关系的要求。

3.1 发散分析原理

发散原理是基于一对多情况考虑的，即基元中对象、特征和量值可以在合理范围内无限拓展。包括多个同对象基元、同对象同值基元、同征基元、同征同值基元等。

对SFEP的传递元而言， $\rm tp $ 不具有发散性，因为基本单元属于传递关系。 ${e_c},{e_r}$ 具有发散性，事件可分为原因事件和结果事件，事件是多样的，也可分为边缘事件、过程事件和最终事件^[2]。 $p_t $ 表示传递概率，不具有发散性。原因事件的结构为 $({a_c},({c_c},{p_c})', $ $(({m_c},{C_c},{V_c}),{v_c})')$ ，是事元和物元的复合事元。 ${a_c}$ 表示动作具有发散性。 ${c_c},{p_c}$ 为动作特征和发生概率，前者可发散后者不可。 ${m_c}$ 代表物元对象，具有发散性；对应的 ${C_c},{V_c}$ 具有发散性。同理结果事件也具有同样的特征。 ${v_c}$ 、 ${v_r}$ 和 ${v_t}$ 分别代表原因事件发生概率值、结果事件概率值和传递概率值，它们不具有发散性。式(5)中各量的发散性如式(6)下划线所示。

$\begin{aligned} R_{c \to r}^t =& [tp,(\underline {{e_c}} ,\underline {{e_r}} ,{p_t})',((\underline {{a_c}} ,(\underline {{c_c}} ,{p_c})',((\underline {{m_c}} ,\underline {{C_c}} ,\underline {{V_c}} ),{v_c})'),\\ & (\underline {{a_r}} ,(\underline {{c_r}} ,{p_r})',((\underline {{m_r}} ,\underline {{C_r}} ,\underline {{V_r}} ),{v_r})'),{v_t})'] \end{aligned} $

(6)

3.2 相关分析原理

可拓理论认为一个基元与其他基元关于某一特征的量值之间、同一基元或同族基元关于某一特征量值之间，如果存在一定的依赖关系，则称为相关。

SFEP传递元的相关性指，传递元 ${R^t}$ 中具有发散性的对象、特征和量值，与另一个 ${R^t}'$ 中具有发散性的对应对象、特征和量值具有关系，即可以通过函数关系进行相互表示。相关分为单向相关和互为相关，即 ${R^t} \overset{ \sim }{\mathop{\to }} {R^t}'$ 或 ${R^t}\overset{ \sim }{\mathop{\leftarrow }} {R^t}'$ 和 ${R^t}\sim {R^t}'$ 。进一步分为“与”关系和“或”关系。一个传递元与多个传递元“与”关系表示为 ${R^t}\sim \mathop \wedge \nolimits_{i = 1}^m {R_i}^t$ ；“或”关系为 ${R^t}\sim \mathop \vee \nolimits_{i = 1}^m {R_i}^t$ 。多个传递元与一个传递元的“与”关系 $\mathop \wedge \nolimits_{i = 1}^m {R_i}^t\sim {R^t}$ ；“或”关系为 $\mathop \vee \nolimits_{i = 1}^m {R_i}^t\sim {R^t}$ ；多个传递元与多个传递元之间的关系有四种，这里不再论述。另外单向相关只需将“~”更换为 $\tilde{\to}$ 或 $\tilde{\leftarrow}$ 。

传递元的相关性对SFEP中事件及传递状态的化简非常重要。可通过相关性建立事件与事件、传递与传递之间的关系，化简事件和传递，甚至可进行替代。这将有利于传递元的减少和无关性要求。

3.3 蕴含分析原理

蕴含原理认为2个基元，若基元1实现必将导致基元2实现，则称基元1蕴含基元2，记为 ${B_1} \Rightarrow {B_2}$ ，前者称为上位基元，后者为下位基元。

对于SFEP的传递元存在如下蕴含情况：一个传递元与蕴含多个传递元表示为 ${R^t} \Rightarrow \mathop \wedge \nolimits_{i = 1}^m {R_i}^t$ ；或蕴含为 ${R^t} \Rightarrow \mathop \vee \nolimits_{i = 1}^m {R_i}^t$ 。多个传递元与蕴含一个传递元表示为 $\mathop \wedge \nolimits_{i = 1}^m {R_i}^t \Rightarrow {R^t}$ ；或蕴含为 $\mathop \vee \nolimits_{i = 1}^m {R_i}^t \Rightarrow {R^t}$ 。多个传递元与或蕴含多个传递元有4种。同样蕴含关系具有传递性^[18]。

蕴含分析主要处理传递元之间的关系，这也是SFEP的另一项重要任务。当多个传递元的结果事件相同时，即存在传递元之间的逻辑关系。多个传递元同时存在导致一个结果事件发生是与关系；之一存在是或关系。当然在SFEP中并不限于与或这样的简单关系，详细可参见钟义信教授^[12-15]提出的泛逻辑柔性处理方法。也存在一个原因事件发生同时导致多个传递元存在或者之一传递元存在的情况。但不存在多对多的情况，因为传递元中的原因事件和结果事件唯一。蕴含分析可针对传递元中原因事件相同或结果事件相同的传递元进行分类分析。为满足分析要求，建立以传递元为连接，事件为节点的拓扑网络，如图1所示。图1给出了结果事件e₂发生过程的可拓表示。

3.4 可扩分析原理

可拓学中的事元、物元和关系元均具有可组合性、可分解性和可扩缩性，统称可扩性。同样在SFEP中，可组合性表示存在若干传递元组合成为新的传递元，即 ${R^t} = R_1^t \oplus R_2^t \cdots \oplus R_i^t$ ；可分解性表示一个传递元按照一定条件可分解为若干传递元，即 ${R^t}//\{ R_1^t,R_2^t, \cdots ,R_i^t\} $ ；可扩缩表示传递元在一定条件下可扩大或缩小， $\alpha > 1,\;\alpha {R^t}$ ，则扩大传递元； $0 < \alpha < 1, $ $\;\alpha {R^t}$ ，则缩小传递元。

可扩分析主要用于SFEP的网络拓扑描述。当寻找结果事件的原因事件时可使用可分解性，细化原因事件，建立传递元。当有多个结果事件可共同组成一个确实存在的事件时，可使用可组合性得到传递元。当传递元的传递情况有所加强或减弱时可使用可扩缩性进行调整。由于可扩分析涉及较多定理和公式，请参见文献[18]，在传递元情况下的表示可参照得到。

综上，本文是使用可拓理论表示、分析和研究SFEP的开始。给出了SFEP的3个主要问题，事件、传递和逻辑关系。使用基元表示了SFEP的基本单元，并命名为传递元。同时通过可拓的拓展分析原理对传递元之间的逻辑关系进行表示。另一个SFEP的重要事项是影响因素，但文中并未具体给出影响因素的表示。这是因为基元具有变参基元，即具有参数(影响因素)的基元。可根据影响因素调整传递元中的对象、特征和量值。因此在传递元表达式中并未单独给出影响因素，以便简洁。接下研究将根据文献[18]给出的可拓论框架，逐一将可拓概念引入SFEP，最终形成SFEP的可拓表示和分析原理。

4 结论

本文研究了使用可拓论描述和分析SFEP的可能性，并进行了基础研究。

(1) 论述了系统功能状态与可拓学关系。认为系统功能状态代表了系统存在的意义。系统功能状态只具有两态，即可靠和失效状态。功能状态的变化是两态斗争和博弈的结果，具有矛盾和统一性。因此这符合可拓学研究矛盾问题的本质和特点。因此可使用可拓论研究SFEP。

(2) 实现了可拓方法对SFEP中基本单元的表示。论述了SFEP基本单元的结构，即原因事件−传递条件−结果事件。认为该单元是物元、事元和关系元的组成的复合元。原因事件和结果事件可作为事件由物元和事元复合为复合事元。传递元为关系元和上述两个复合事元组成的复合关系元，作为SFEP的基本单元。

(3) 在SFEP的传递元基础上论述了拓展分析原理。研究了传递元中各对象、特征和状态的发散性。通过相关性可建立事件与事件、传递与传递之间的关系，化简事件和传递。蕴含分析主要处理传递元之间的逻辑关系，即多个传递元指向同一结果事件或一个原因事件指向多个传递元的逻辑关系。可扩分析主要用于SFEP的网络拓扑形成，即原因细化、结果综合及传递程度改变。