非线性延迟微分方程被广泛应用于生物学、物理学、医学、自动化等学科^[1-5]。振动性作为一种重要的定性行为，在生物数学和工业等领域有一些很好的应用^[6-8]。自上世纪70年代起，就有学者开始研究各种非线性延迟微分方程的振动性^[9-12]。1825年，Gompertz^[13]在探讨人类死亡规律时首次提出了Gompertz方程后Winsor^[14]和Laird等^[15]对该数学模型进行了修改并提出了一些在肿瘤方面的应用，后来越来越多的学者对Gompertz型方程的性质^[16-19]与应用^[20-22]展开了大量的研究。

2011年，Piotrowska等^[16]提出了几类带延迟项的Gompertz方程，并研究了延迟项对经典Gompertz方程的影响，2013年，Bodnar等^[17]在其基础上又引入了一项用于反映种群变化过程的外部干扰，并研究了方程的Hopf分支。在此基础上，考虑式(1)和式(2)的延迟Gompertz方程。

$\dot V(t) = - rV(t - \tau )\ln \frac{{V(t - \tau )}}{k} - TV(t - \tau ),t \geqslant 0$

(1)

$ \dot V(t) = - rV(t)\ln \frac{{V(t - \tau )}}{k} - TV(t - \tau ),t \geqslant 0 \;\;\;\;\;\;$

(2)

其中 $r$ ， $k$ ， $T$ 都是大于0的常数，初始条件为

$ V(t) = \varphi (t),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \tau \leqslant t \leqslant 0 $

(3)

其中 $\varphi \in {{\bf{C}}}\left( {\left[ { - \tau ,0} \right],{{{\bf{R}}}^ + }} \right)$ 。本文通过研究极限方程的振动性，从而得到原方程振动性的相关结论。

1 预备知识

定义1^[23] 　设 $x(t)$ 是一个定义在无穷区间 $[ {0, + \infty } )$ 上的连续函数。如果 $x(t)$ 有任意大的零点，则说函数 $x(t)$ 是振动的，即对于每一个 $b > a$ ，都存在点 $c > b$ 使得 $x(c) = 0$ 。否则，如果存在一个 $b > a$ ，使得当 $t > b$ 时，有 $x(t) \ne 0$ ，就说函数 $x(t)$ 是非振动的，即 $x(t)$ 是最终正的或是最终负的。

定义2^[23] 　若 $\left\{ {{x_n} - {y_n}} \right\}$ 既不是最终正的，也不是最终负的，则称 $\left\{ {{x_n}} \right\}$ 是关于 $\left\{ {{y_n}} \right\}$ 振动的，否则称 $\left\{ {{x_n}} \right\}$ 是非振动的。如果 $\left\{ {{y_n}} \right\} = \left\{ y \right\}$ 是常数列，简单地称 $\left\{ {{y_n}} \right\}$ 关于 $y$ 振动。如果 $\left\{ {{y_n}} \right\} = 0$ ，就称 $\left\{ {{x_n}} \right\}$ 关于0振动或简称 $\left\{ {{x_n}} \right\}$ 是振动的。

定义3^[23] 　若方程(1)的所有解都是振动的，则称方程(1)是振动的。

定理1^[23] 　考虑微分方程

$ \dot x(t) + px(t) + qx(t - \tau ) = 0 $

(4)

其中 $p,q,\tau \in {{\bf{R}}}$ ，若 $q\tau {\rm{e}^{p\tau }} > {1}/{\rm{e}}$ ，则称方程(4)的所有解都是振动的。

定理2^[23] 　考虑差分方程

$ {a_{n + 1}} - {a_n} + \sum\limits_{i = - k}^l {{q_i}{a_{n + i}} = 0} $

(5)

其中 $k$ ， $l \in {{\bf{N}}}$ ， ${q_i} \in {{\bf{R}}}$ ， $i = - k,\cdots,l$ ，则以下结论等价：①方程(5)的所有解都是振动的；②特征方程 $\lambda - 1 + \sum\nolimits_{i = - k}^l {{q_i}{\lambda ^i}} = 0$ 无正根。

定理3^[23] 　考虑差分方程

$ {a_{n + 1}} - {a_n} + p{a_{n - k}} + q{a_{n - l}} = 0 $

(6)

其中 $p > 0$ ， $q < 0$ ， $k > 0$ ， $l = 0$ 。若

$p\frac{{{{{\rm{(k + 1}})}^{k + 1}}}}{{{k^k}}} > {{{(1 + q}})^{k + 1}}$

则称方程(6)的所有解都是振动的。

引理1^[24] 　设 $m > M > 0$ ， $M \in {\bf{R}}$ 。

(1)若 $a > 0$ 且 $0 \leqslant \theta \leqslant 1/2$ ，或 $a < 0$ 且 $0 \leqslant \theta \leqslant \phi {\rm{(1}})$ ，则有 $\left( {1 + a/{{(m - \theta a)}^m}} \right) < {{\rm{e}}^a}$ ；(2)若 $a > 0$ 且 $1/2 \leqslant \theta \leqslant 1$ ，或 $a < 0$ 且 $\phi {\rm{( - 1}}) \leqslant \theta \leqslant 1$ ，则有 $\left( {1 + a/{{(m - \theta a)}^m}} \right) \geqslant {{\rm{e}}^a}$ ，其中 $\phi {\rm{(}}x) = 1/x - 1/{\rm{(}}{{\rm{e}}^x} - 1)$ 。

引理2 　若 $x > - 1$ 且 $x \ne 0$ ，则有 $\ln {\rm{(}}1 + x) > \displaystyle\frac{x}{{1 + x}}$ 。

引理3 　若 $x < -1$ 且 $x \ne 0$ ，则有 ${{\rm{e}}^x} < \displaystyle \frac{1}{{1 - x}}$ 。

2 方程(1)和方程(2)的振动行为

定理4 　若

$ \tau (r + T){{\rm{e}}^{ - T\tau }} > \frac{1}{{\rm{e}}} $

(7)

则方程(1)所有的解关于稳定点 ${V^*} = k{\rm{e}}^{- \frac{T}{r}}$ 振动。

证明设 $V(t) = k{{\rm{e}}^{x(t)}}$ ，则 $\dot V(t) = k\dot x(t){{\rm{e}}^{x(t)}}$ ，代入方程(1)得

$k\dot x(t){{\rm{e}}^{x(t)}} = - rk{\rm{e}^{x(t - \tau )}}x(t - \tau ) - Tk{{\rm{e}}^{x(t - \tau )}}$

化简得

$\begin{array}{*{20}{l}} {\dot x(t) = - rx(t - \tau ){{\rm{e}}^{x(t - \tau ) - x(t)}} - T{{\rm{e}}^{x(t - \tau ) - x(t)}}}\\ {\dot x(t) = {{\rm{e}}^{x(t - \tau ) - x(t)}}( - rx(t - \tau ) - T)} \end{array}$

利用泰勒公式得其极限方程为

$ \dot x(t) = Tx(t) - (r + T)x(t - \tau ) - T\qquad \quad\;\;\; $

(8)

再做变换，令 $y(t) = x(t) + \displaystyle\frac{T}{r}$ ，代入式(8)得

$\dot y(t) = T\left( {y(t) - \frac{T}{r}} \right) - (r + T)\left( {y(t - \tau ) - \frac{T}{r}} \right) - T$

化简得　 $\dot y(t) = Ty(t) - (r + T)y(t - \tau ) \qquad\qquad\qquad\;\;(9)$

由定理1知，当式(7)成立时，方程(9)所有的解是振动的，故方程(1)所有的解也是振动的。

定理5 　若式(7)成立，则方程(2)所有的解关于稳定点 ${V^*} = k{\rm{e}}^{ - \frac{T}{r}}$ 振动。

证明 　设 $V(t) = k{{\rm{e}}^{x(t)}}$ ，则 $\dot V(t) = k\dot x(t){{\rm{e}}^{x(t)}}$ ，代入方程(2)得　 $k\dot x(t){{\rm{e}}^{x(t)}} = - rk{{\rm{e}}^{x(t)}}x(t - \tau ) - Tk{{\rm{e}}^{x(t - \tau )}} $

化简得　 $\dot x(t) = - rx(t - \tau ) - T{{\rm{e}}^{x(t - \tau ) - x(t)}} $

利用泰勒公式得其极限方程(8)，后面证明过程同定理4。

接下来通过分析方程(9)的数值解的振动性，从而得出方程(1)和方程(2)数值解振动的充分条件。用线性θ方法对方程(9)进行离散，并得出其数值解的振动的条件。

令 $h = \displaystyle\frac{\tau }{m}$ ， $m \in {{\rm N}^ + }$ ，对方程(1)，方程(2)与方程(9)分别运用线性θ方法得

$\tag{10}\begin{split}{V_{n + 1}} =& {V_n} + h\theta {V_{n + 1 - m}}\left( - r\ln \displaystyle\frac{{{V_{n + 1 - m}}}}{k} - T\right) + \\& h(1 - \theta ){V_{n - m}}\left( - r\ln \displaystyle\frac{{{V_{n - m}}}}{k} - T\right)\end{split} $

(10)

$\tag{11}\begin{array}{l}\displaystyle{V_{n + 1}}\left( {1 + h\theta r\ln \frac{{{V_{n + 1 - m}}}}{k}} \right) = {V_n}\left( {1 - h(1 - \theta )r\ln \frac{{{V_{n - m}}}}{k}} \right) - \\ \qquad \qquad \; \displaystyle T\left( {h\theta {V_{n + 1 - m}} + h(1 - \theta ){V_{n - m}}} \right)\\[-10pt]\end{array}$

(11)

$\tag{12}\begin{aligned} {y_{n + 1}} = &{y_n} + h\theta T{y_{n + 1}} - h\theta (r + T){y_{n + 1 - m}} + h(1 - \theta )T{y_n} - \\ &h(1 - \theta )(r + T){y_{n - m}} \\[-10pt]\end{aligned} $

(12)

式(12)经过变换，得

$\tag{13} \begin{split} {y_{n + 1}} = &\frac{{1 + h(1 - \theta )T}}{{1 - h\theta T}}{y_n} - \frac{{h\theta (r + T)}}{{1 - h\theta T}}{y_{n + 1 - m}} - \quad \;\;\;\; \\ & \frac{{h(1 - \theta )(r + T)}}{{1 - h\theta T}}{y_{n - m}} \end{split} $

(13)

引理4 　方程(12)的特征方程是

$\tag{14} \lambda = R\left( {h(T - (r + T){\lambda ^{ - m}})} \right) $

(14)

其中 $R(x) = \displaystyle\frac{{1 + (1 - \theta )x}}{{1 - \theta x}}$ 是θ方法的稳定函数。

证明 　令 ${y_n} = {\lambda ^n}{y_0}$ ，则方程(12)变为

　 ${\lambda ^{n + 1}}{y_0} = {\lambda ^n}{y_0} + h\theta T{\lambda ^{n + 1}}{y_0} - h\theta (r + T){\lambda ^{n + 1 - m}}{y_0} + $ 　　　　 $ h(1 - \theta )T{\lambda ^n}{y_0} - h(1 - \theta )(r + T){\lambda ^{n - m}}{y_0}$

化简得

$\lambda = 1 + h\theta T\lambda - h\theta (r + T){\lambda ^{1 - m}} + h(1 - \theta )T - h(1 - \theta )(r + T){\lambda ^{ - m}}$

计算得

$( {1 - h\theta (T - (r + T){\lambda ^{ - m}})} )\lambda = 1 + h(1 - \theta )(T - (r + T){\lambda ^{ - m}})$

即

$\begin{aligned}\lambda = \frac{{1 + h(1 - \theta )(T - (r + T){\lambda ^{ - m}})}}{{1 - h\theta (T - (r + T){\lambda ^{ - m}})}} = R(h(T - (r + T){\lambda ^{ - m}}))\end{aligned}$

得证。

引理5 　若 $\tau (r \!+\! T){{\rm{e}}^{ - T\tau }} \! > \! {1}/{{\rm{e}}}$ ，当 $0 \!\leqslant\! \theta \!\leqslant\! 1 \!-\! 1/({\rm{e}} - 1)$ 时，则特征方程(14)无正根。

证明 　不妨令 $f(\lambda ) = \lambda - R(h(T - (r + T){\lambda ^{ - m}}))$ ，由引理1，对任意的 $\lambda > 0$ ，当 $0 \leqslant \theta \leqslant \phi (1) \leqslant 1 \!-\! 1/({\rm{e}} \!- \!1)$ 时，有

$\tag{15} R\left( {h(T - (r + T){\lambda ^{ - m}})} \right) \leqslant \exp \left( {h(T - (r + T){\lambda ^{ - m}})} \right) $

(15)

令 $g(\lambda ) = \lambda - \exp \left( {h(T - (r + T){\lambda ^{ - m}})} \right)$ ，现证对任意的 $\lambda > 0$ ，都有 $g(\lambda ) > 0$ 。假设存在 ${\lambda _0} > 0$ 使得 $g({\lambda _0}) \leqslant 0$ ，即有　 ${\lambda _0} \leqslant \exp \left( {h(T - (r + T){\lambda _0}^{ - m})} \right) $

且有　 ${\lambda _0}^m \leqslant \exp \left( {\tau (T - (r + T){\lambda _0}^{ - m})} \right)\qquad\qquad\quad\;\;\;(16)$

上式两边同乘 $(r + T){{\rm{e}}^{1 - T\tau }}\tau $ ，则有

$\tau (r + T){{\rm{e}}^{1 - T\tau }}\lambda _0^m \leqslant \tau (r + T){{\rm{e}}^{1 - T\tau }}\exp ( {\tau ( {T - (r + T)\lambda _0^{ - m}} )} )$

化简得

$\tag{17} \tau (r + T){{\rm{e}}^{1 - T\tau }} \leqslant \tau (r + T)\lambda _0^{ - m}\exp ( {1 - \tau (r + T)\lambda _0^{ - m}} ) $

(17)

如果 $1 - \tau (r + T)\lambda _0^{ - m} = 0$ ，那么 $\tau (r + T){{\rm{e}}^{1 - T\tau }} \leqslant 1$ ，即

$\tau (r + T){{\rm{e}}^{ - T\tau }} \leqslant {1}/{{\rm{e}}}$

这与式(7)矛盾。

如果 $1 - \tau (r + T)\lambda _0^{ - m} \ne 0$ ，那么由引理3有

$\exp ( {1 - \tau (r + T)\lambda _0^{ - m}} ) \leqslant 1/\tau (r + T)\lambda _0^{ - m}$

即有

$\tau (r + T)\lambda _0^{ - m}\exp ( {1 - \tau (r + T)\lambda _0^{ - m}} ) \leqslant 1$

又由式(16)得

$\tau (r + T)\exp ( {( {1 - \tau (r + T)\lambda _0^{ - m}} ) - T\tau + \tau (r + T)\lambda _0^{ - m}} ) \leqslant 1$

化简得　 $\tau (r + T)\exp \left( {1 - T\tau } \right) \leqslant 1 $

即　 $\tau (r + T){{\rm{e}}^{ - T\tau }} \leqslant {1}/{{\rm{e}}} $

这与式(7)矛盾。

故对任意的 $\lambda > 0$ ，都有 $f(\lambda ) = \lambda - R( {h(T - (r + T)}$ ${\lambda ^{ - m}}) ) \geqslant g(\lambda ) > 0 $ ，也就是说，特征方程(14)没有正根。证毕。

下文讨论 $1 - 1/({\rm{e}} - 1) \leqslant \theta \leqslant 1$ 的情况，不妨设 $m > 1$ 。

引理6 　假设 $1 - T\tau > 0$ 和式(7)成立。当 $1 - 1/$ $({\rm{e}} - 1) \leqslant \theta \leqslant 1$ 且 $h < {h_0}$ 时，特征方程(14)无正根，其中

$\tag{18} {h_0} = \left\{ {\begin{array}{*{20}{l}} {\infty ,}&{(r + T) \geqslant 1}\\ {\displaystyle\frac{{\tau \left( {\ln (r + T)\tau + 1 - T\tau } \right)}}{{1 - T\tau + T\tau \ln (r + T)\tau }},}&{(r + T) < 1} \end{array}} \right. $

(18)

证明当 $\lambda > 0$ 时， $R\left( {h(T - (r + T){\lambda ^{ - m}})} \right)$ 是关于θ的增函数，则当 $1 - 1/({\rm{e}} - 1) \leqslant \theta \leqslant 1$ 时，有

$\begin{array}{c} R\left( {h(T - (r + T){\lambda ^{ - m}})} \right) = \displaystyle\frac{{1 + h(1 - \theta )(T - (r + T){\lambda ^{ - m}})}}{{1 - h\theta (T - (r + T){\lambda ^{ - m}})}} \leqslant \\ \displaystyle\frac{1}{{1 - h(T - (r + T){\lambda ^{ - m}})}}\end{array} $

接下来证明不等式

$\tag{19} \lambda - \frac{1}{{1 - h(T - (r + T){\lambda ^{ - m}})}} > 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda > 0 $

(19)

在一定条件下成立。

$\begin{aligned} &\qquad\qquad\qquad \lambda - \frac{1}{{1 - h(T - (r + T){\lambda ^{ - m}})}} = \\ &\frac{{\lambda - \lambda h(T - (r + T){\lambda ^{ - m}}) - 1}}{{1 - h(T - (r + T){\lambda ^{ - m}})}} \!=\! \frac{{\lambda - \lambda hT - 1 + h(r + T){\lambda ^{1 - m}}}}{{1 - h(T - (r + T){\lambda ^{ - m}})}} \!= \\ & \frac{{{\lambda ^m}(1 \!\!-\!\! hT){\lambda ^{1 \!-\! m}} \!\!-\!\! {\lambda ^{1\! - \!m}}(1 \!\!-\!\! hT)\displaystyle\frac{{{\lambda ^{m \!-\! 1}}}}{{1 \!\!-\!\! hT}} + {\lambda ^{1 \!-\! m}}(1 \!\!-\!\! hT)\displaystyle\frac{{h(r \!\!+\!\! T)}}{{1 \!\!-\!\! hT}}}}{{1 \!\!-\!\! h(T - (r \!\!+\!\! T){\lambda ^{ \!-\! m}})}}= \\ & \frac{{\left( {1 - hT} \right){\lambda ^{1 - m}}}}{{1 - h(T - (r + T){\lambda ^{ - m}})}}\left( {{\lambda ^m} - \frac{1}{{1 - hT}}{\lambda ^{m - 1}} + \frac{{h(r + T)}}{{1 - hT}}} \right) \end{aligned}$

设 $\varphi (\lambda ) = {\lambda ^m} - \displaystyle\frac{1}{{1 - hT}}{\lambda ^{m - 1}} + \displaystyle\frac{{h(r + T)}}{{1 - hT}}$ ，现证当 $\lambda > 0$ ，有 $\varphi (\lambda ) > 0$ 。易知 $\varphi (\lambda )$ 是差分方程

${y_{n + 1}} - {y_n} - \frac{{hT}}{{1 - hT}}{y_n} + \frac{{h(r + T)}}{{1 - hT}}{y_{n + 1 - m}} = 0$

的特征多项式。由定理2和定理3可知， $\varphi (\lambda )$ 无正根当且仅当 $\displaystyle\frac{{h(r + T)}}{{1 - hT}}\frac{{{m^m}}}{{{{(m - 1)}^{m - 1}}}} > {\left( {1 + \frac{{hT}}{{1 - hT}}} \right)^m} $

已知 $1 - T\tau > 0$ ，则 $1 - hT > 1 - T\tau > 0$ ，两边取对数得

$\begin{array}{l} \ln (r \!+\! T)\tau \!+\! (m \!-\! 1)\ln \displaystyle\frac{m}{{m - 1}} \!-\! \ln (1 \!- hT) \!>\! m\ln (1 \!+\! \displaystyle\frac{{hT}}{{1 - hT}})\\ \ln (r \!+\! T)\tau \!+\! (m \!-\! 1)\ln \displaystyle\frac{m}{{m - 1}} - \ln (1 \!-\! hT) > - m\ln (1 - hT) \\ \end{array} $

即

$\ln (r + T)\tau + (m - 1)\left( {\ln \frac{m}{{m - 1}} + \ln (1 - hT)} \right) > 0$

从而有　 $\ln (r + T)\tau + (m - 1)\ln \left( {1 + \displaystyle\frac{{1 - T\tau }}{{m - 1}}} \right) > 0 \quad\;\;\; (20)$

若 $(r + T)\tau \geqslant 1$ ，由假设 $m > 1$ 知对任意的 $h$ ，式(20)都成立；若 $(r + T)\tau < 1$ ，且 $h < \displaystyle\frac{{\tau \left( {\ln (r + T)\tau + 1 - T\tau } \right)}}{{1 - T\tau + T\tau \ln (r + T)\tau }}$ ，则式(20)成立。由引理2得

$\begin{array}{c}\ln (r + T)\tau + (m - 1)\ln \left( {1 + \displaystyle\frac{{1 - T\tau }}{{m - 1}}} \right) > \\\ln (r + T)\tau + \displaystyle \frac{{(m - 1)(1 - T\tau )}}{{m - T\tau }}\end{array} $

现证

$\begin{array}{c}\ln (r + T)\tau + \displaystyle \frac{{(\tau - h)(1 - T\tau )}}{{\tau - hT\tau }} = \\ \displaystyle \frac{{(\tau - hT\tau )\ln (r + T)\tau + (\tau - h)(1 - T\tau )}}{{\tau (1 - hT)}} > 0\end{array} $

即证

$\tau \ln (r + T)\tau + \tau (1 - T\tau ) > hT\tau \ln (r + T)\tau + h(1 - T\tau )$

即

$h < \frac{{\tau \left( {\ln (r + T)\tau + 1 - T\tau } \right)}}{{1 - T\tau + T\tau \ln (r + T)\tau }}$

从而证明不等式(20)成立。

综上得知对任意的 $\lambda > 0$ ，当 $h < {h_0}$ 时，都有

$\begin{aligned} f(\lambda ) =& \lambda - R\left( {h(T - (r + T){\lambda ^{ - m}})} \right) \geqslant \\ & \lambda - \exp (h(T - (r + T){\lambda ^{ - m}})) > 0 \end{aligned} $

即特征方程(14)无正根。

由引理5和引理6，可得如下方程(1)和方程(2)的数值解的振动性结论。

定理6 　当 $0 \leqslant \theta \leqslant 1 - 1/({\rm{e}} - 1)$ 时，有 $h < \infty $ ，当 $1 - 1/({\rm{e}} - 1) \leqslant \theta \leqslant 1$ ， $1 - T\tau > 0$ 时，有 $h < {h_0}$ ，其中 ${h_0}$ 定义如式(18)，且式(3)和式(7)成立，则方程(1)和方程(2)的数值解振动。

3 数值实验

这一部分将举例验证前文所证得的结果。前3个例子验证方程(1)的相关结论，后3个例子用于验证方程(2)的相关结论。其中 $1 - 1/({\rm{e}} - 1) \approx 0.418\;0$ 。

首先给出方程(1)中 $\theta \in \left[ {0,1 - 1/({\rm{e}} - 1)} \right]$ 的数值实验。考虑方程(21)。

$\tag{21}\left\{ \begin{array}{l} \dot V(t) = - \displaystyle\frac{1}{3}V(t - 2)\ln \displaystyle\frac{{V(t - 2)}}{5} - \displaystyle\frac{1}{3}V(t - 2),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - 2 \leqslant t \leqslant 0 \\ \end{array} \right.\\[-10pt] $

(21)

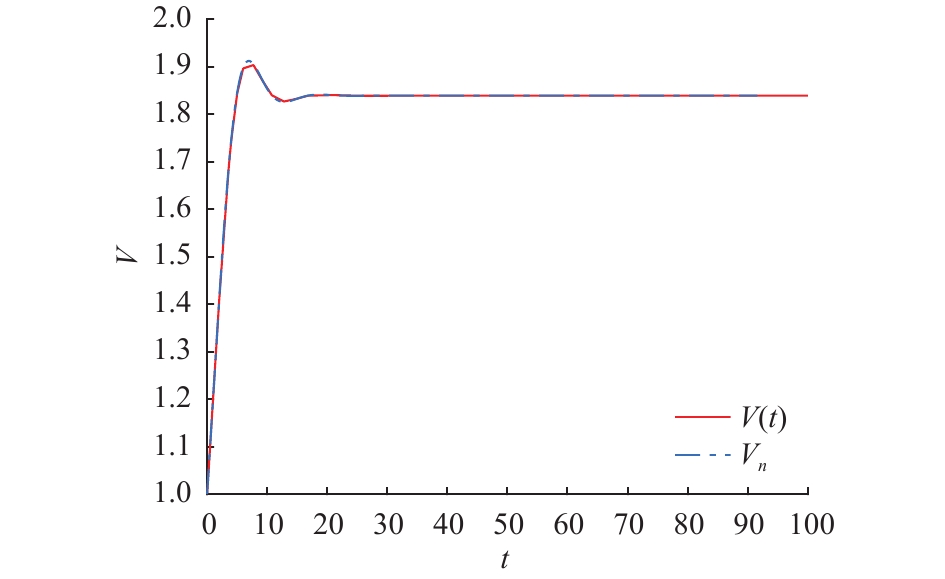
在方程(21)中，易知 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 2.597\;9 > 1/{\rm{e}}$ ，由定理4得，方程(21)的解析解是关于平衡点 ${V^*} = $ $k{{\rm{e}}^{ - \frac{T}{r}}}{\rm{ = }}5{{\rm{e}}^{ - 1}} \approx 1.839\;4$ 振动的。取 $\theta = 0.4 \in \left[ {0,1 \!-\! 1/({\rm{e}} \!-\! 1)} \right]$ ， $m = 16$ ，则 $h = \tau /m = 0.125\;0$ ，由定理6知，对任意的 $h \in {{\bf{R}}}$ ，方程(21)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图1)。

讨论方程(1)中 $\theta \in \left[ {1 - 1/({\rm{e}} - 1),1} \right]$ 的数值实验，考虑方程(22)。

$\tag{22}\left\{ \begin{array}{l} \dot V(t) = - 2V(t - \displaystyle{1}/{6})\ln \displaystyle\frac{{V(t - \displaystyle{1}/{6})}}{3} - 2V(t - \displaystyle{1}/{6}),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 20, - 1/6 \leqslant t \leqslant 0 \\ \end{array} \right. $

(22)

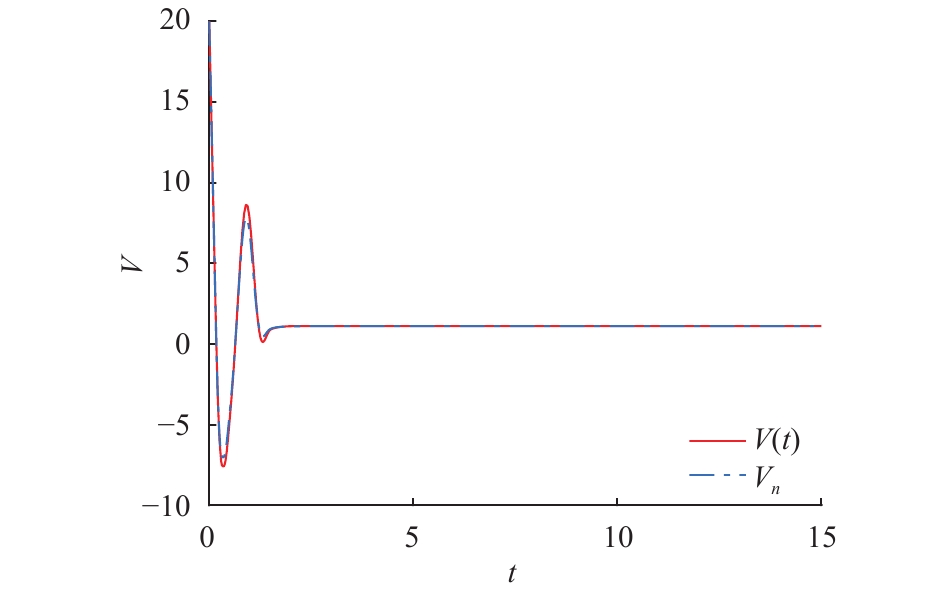
由方程(22)得 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 0.477\;7 > 1/{\rm{e}}$ ，由定理4得方程(22)的解析解关于平衡点 ${V^*} =k{{\rm{e}}^{ - \frac{T}{r}}} \approx$ $ 1.103\;6$ 振动。又 $1 - T\tau = 2/3 > 0$ ，取 $\theta = 0.8 \in [ 1 - 1/$ $({\rm{e}} - 1),1 ]$ ， $m = 10$ ，则 $h = \tau /m \approx 0.016\;7$ ，其中 $(r + T)\tau =$ ${2}/{3} < 1$ ，由定理6可知，对任意的

$h < {h_0} = \frac{{\tau \left( {\ln (r + T)\tau + 1 - T\tau } \right)}}{{1 - T\tau + T\tau \ln (r + T)\tau }} \approx 0.081\;9$

方程(22)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图2)。

考虑方程(23)

$\tag{23}\left\{\begin{array}{l} \dot V(t) = - 4V(t - 0.4)\ln \displaystyle\frac{{V(t - 0.4)}}{7} - \displaystyle\frac{2}{{17}}V(t - 0.4),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 9, - 0.4 \leqslant t \leqslant 0 \\ \end{array} \right. $

(23)

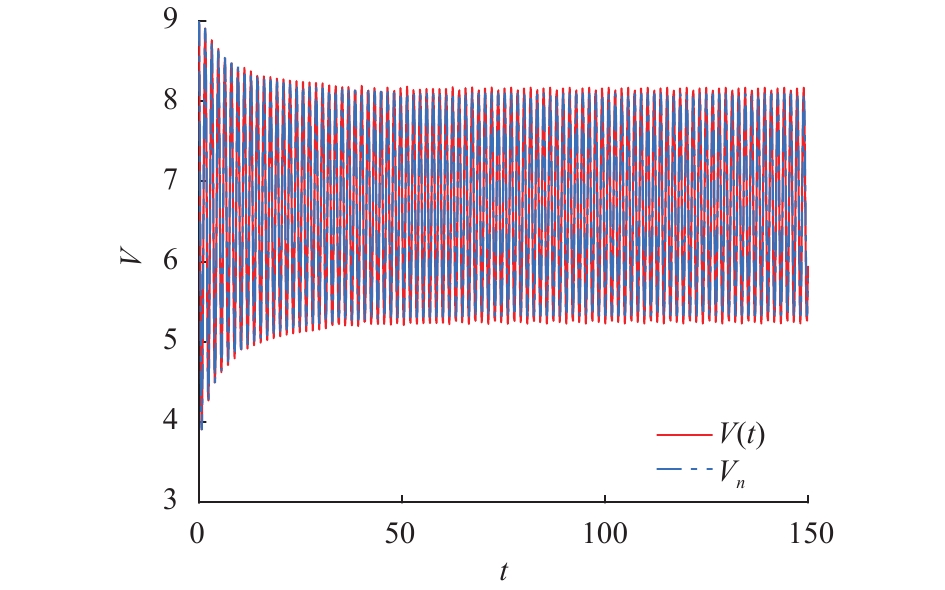
在方程(23)中，易得知 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 1.571\;3 > {1}/{{\rm{e}}}$ ，根据定理4得方程(23)的解析解是关于平衡点 ${V^*} = k{{\rm{e}}^{ - \frac{T}{r}}} \approx 6.797\;1$ 振动的。其中 $1 - T\tau = 0.952\;9 > 1$ ，取 $\theta = 0.5 \in \left[ {0,1 - 1/({\rm{e}} - 1)} \right]$ ， $m = 9$ ， $h = \tau /m \approx 0.044\;4$ ，其中 $(r + T)\tau = 1.647\; 1 > 1$ ，由定理6知，对任意的 $h < \infty $ ，方程(23)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图3)。

下文的例子将验证方程(2)的振动相关理论。首先给出方程(2)中 $\theta \in \left[ {0,1 - 1/{\rm{(e}} - 1)} \right]$ 的数值实验，考虑方程(24)。

$\tag{24}\left\{ \begin{array}{l} \dot V(t) = - 3V(t)\ln \displaystyle\frac{{V(t - 1/6)}}{5} - 2V(t - 1/6),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 10, - 1/6 \leqslant t \leqslant 0 \\ \end{array} \right. $

(24)

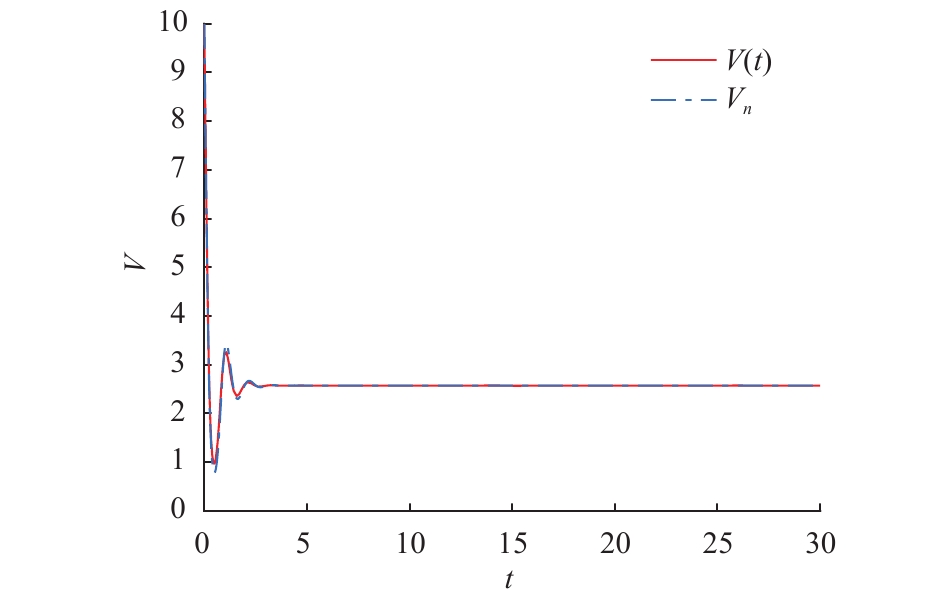
在方程(24)中可知 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 0.597\;1 > {1}/{{\rm{e}}}$ ，由定理5得方程(24)的解析解是关于平衡点 ${V^*} =k{{\rm{e}}^{ - \frac{T}{r}}} \approx$ $ 2.567\;1$ 振动的。取值 $\theta = 0.35 \in \left[ {0,1 - 1/{\rm{(}}{\rm{e}} - 1)} \right]$ ， $m = 5$ ， $h = \tau /m \approx 0.033\;3$ ，由定理6知，对任意的 $h < \infty $ ，方程(24)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图4)。

然后给出方程(2)中 $\theta \in \left[ {1 - 1/{\rm{(e}} - 1),1} \right]$ 的数值实验，考虑方程(25)。

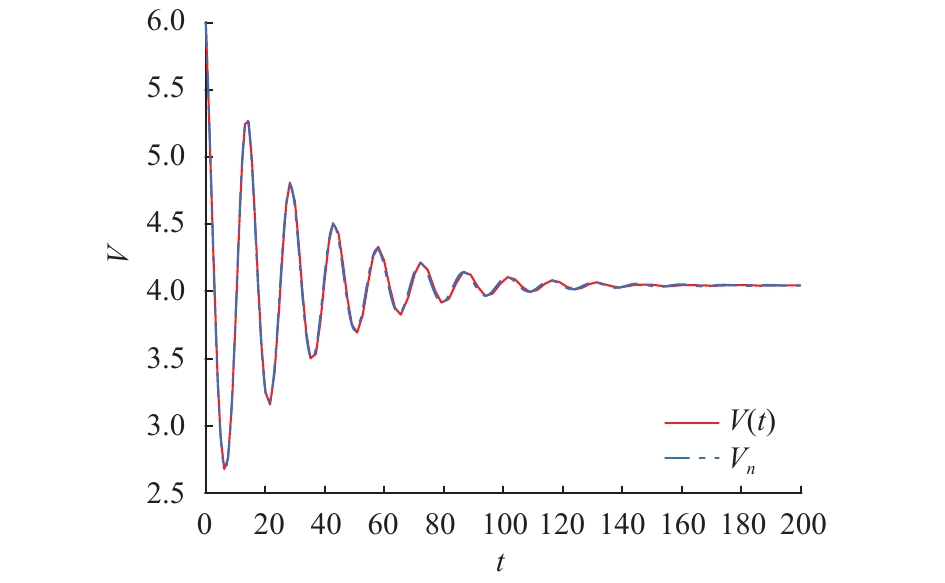
$\tag{25}\left\{ \begin{array}{l} \dot V(t) = - \displaystyle\frac{1}{4}V(t)\ln \displaystyle\frac{{V(t - 2.5)}}{9} - \frac{1}{5}V(t - 2.5),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 6, - 2.5 \leqslant t \leqslant 0 \\ \end{array} \right. $

(25)

在方程(25)中，易知 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 0.606\;5 > {1}/{{\rm{e}}}$ ，由定理5得方程(25)的解析解是关于平衡点 ${V^*} = k{{\rm{e}}^{ - \frac{T}{r}}} \approx $ $ 4.044\;0$ 振动的。又知 $1 - T\tau = 1/2 > 0$ ，取 $\theta = 0.55 \in [ {1 - 1/}$ $({\rm{e}} - 1),1 ]$ ， $m = 10$ ，则 $h = \tau /m \approx 0.25$ ，其中 $(r + T)\tau = 1$ ，由定理6知，对任意的

$h < {h_0} = \frac{{\tau \left( {\ln (r + T)\tau + 1 - T\tau } \right)}}{{1 - T\tau + T\tau \ln (r + T)\tau }} \approx 2.763\;4$

方程(25)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图5)。

考虑方程(26)

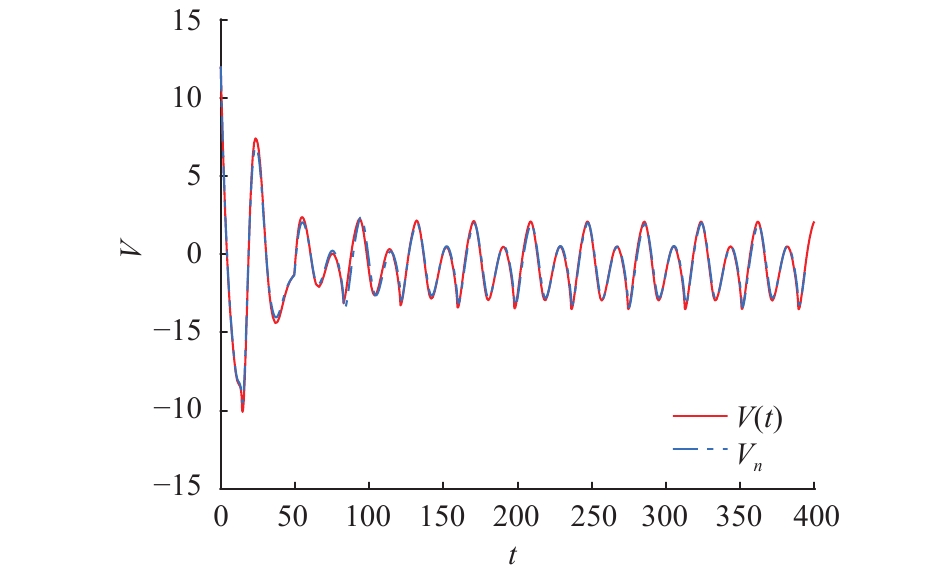
$\tag{26}\left\{ \begin{array}{l} \dot V(t) = - \displaystyle\frac{1}{{11}}V(t)\ln \displaystyle\frac{{V(t - 10)}}{2} - \displaystyle\frac{1}{6}V(t - 10),{\kern 1pt} {\kern 1pt} {\kern 1pt} t \geqslant 0 \\ \phi (t) = 12, - 10 \leqslant t \leqslant 0 \\ \end{array} \right. $

(26)

在方程(26)中，易知 $\tau (r + T){{\rm{e}}^{ - T\tau }} \approx 2.1 > {1}/{{\rm{e}}}$ ，由定理5得方程(26)的解析解关于平衡点 ${V^*} = k{{\rm{e}}^{ - \frac{T}{r}}} \approx $ $0.319\;8$ 振动。又知 $1 - T\tau = 2/5 > 0$ ，取 $\theta = 0.7 \in [ {0,1 - 1/}$ $ ({\rm{e}} - 1)]$ ， $m = 20$ ，则 $h = \tau /m = 0.5$ ，其中有 $(r + T)\tau = $ $2.575\;8 > 1 $ ，由定理6知，对任意的 $h < \infty $ ，方程(26)的数值解也是关于平衡点 ${V^ * }$ 振动的(见图6)。