2. 河南工程学院 电气信息工程学院,河南 郑州 451191
2. School of Electrical Information Engineering, Henan University of Engineering, Zhengzhou 451191, China
如何在配电网发生故障后定位出故障区段以便快速隔离故障和迅速恢复用户供电,一直是提高配电网安全和供电可靠性方面研究的重中之重。随着大量分布式电源(DG)的接入,配网结构变得愈加复杂,由此导致系统的潮流分布及短路电流也发生了变化,使得配电网的短路故障方向判别及故障定位遭受较大影响。虽现阶段的配电网故障定位研究方法种类繁多[1-7],但多是未虑及DG接入配电网进行建模的,在DG并网后这些传统模型将不再适用。
配电网发生故障时,在各断路器与分段开关处装设的馈线终端单元(Feeder Terminal Unit, FTU)可检测到故障过电流,若其值超出预先设定的故障电流定值,那么FTU将会上传故障报警信息至数据采集与监视控制系统(Supervisory Control and Data Acquisition, SCADA)[8]。目前配电网故障定位的方法多是基于FTU上报故障信息进行的[9-13]。文献[14-15]提出基于矩阵分析的故障区段定位方法,通过故障信息和网络拓扑矩阵等进行矩阵运算求解故障馈线区段,但在FTU信息畸变的时候容易误判、漏判。文献[16]所提定位方法虽具备一定的容错性,但只适用于传统的单电源辐射型配电网,DG接入后并不适用。文献[17-18]首次建立了非逻辑关系描述的配电网故障定位新模型,所用故障区段定位方法虽数值性强,稳定性高,但只适用于传统的单电源辐射型配电网,DG接入后并不适用。文献[19-23]虽考虑DG接入配电网引起电流方向变化的影响,但所建立的开关函数都是基于逻辑关系的,所运用的决策方法也均是智能算法,由于智能算法易陷入局部最优,故可靠性不高。
本文提出含DG配电网的故障区段定位方法。首先构建了基于非逻辑运算的适应DG接入的开关函数,引入了DG投切系数来描述DG的投切,并建立含DG的配电网故障区段定位的互补约束模型。仿真算例表明,该方法不仅适用于多个DG的投切情况,还在FTU上传过电流信息发生畸变时,有着较强的容错能力。针对不同DG投切情况,将本文所提方法与智能算法进行比较,仿真结果表明本文所提方法具有更高的准确率和容错性。
1 基于代数关系的DG接入的开关函数 1.1 基于代数关系建模的基本思想本文采用文献[18]的建模思想,此思想的根本目的就是找出对应的故障设备,其最能解释所有 FTU上传的过电流状态值。目标函数就是使所有预设故障过电流状态值与所有FTU实际上传的过电流状态值差异最小,其在残差中加入了平方运算的目的是为避免绝对值运算,用馈线区段的故障状态信息作为变量,并采用0~1离散值进行变量编码,数字0和1分别表示馈线区段运行正常和故障。
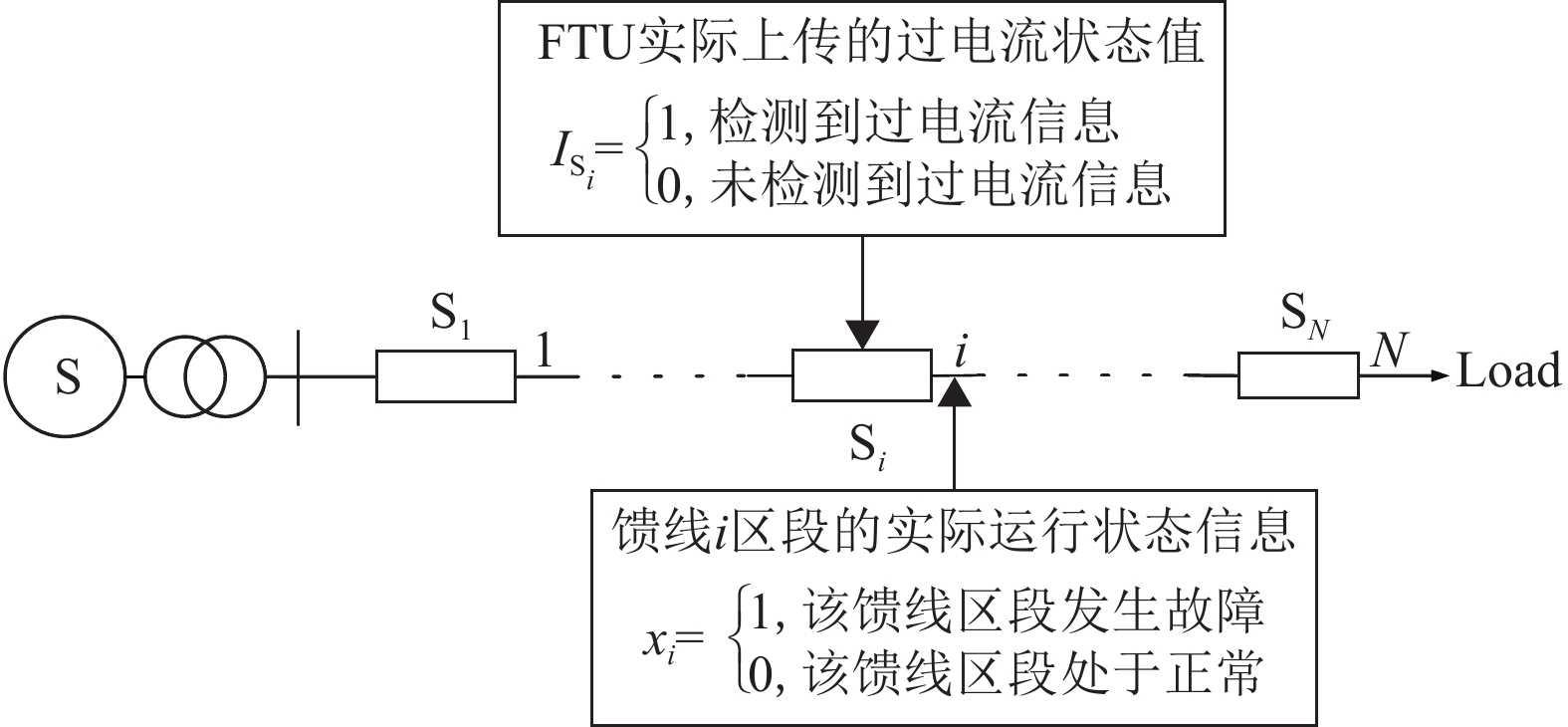
以图1所示单电源辐射型配电网为例,展示以单一故障为前提的基于代数关系的配电网故障定位建模方案(见式(1))。
|
图 1 单电源辐射型配电网 Figure 1 Single-supply radiation distribution network |
| $\left\{ {\begin{array}{*{20}{l}} {\min f\left( x \right) = \sum\limits_{i = 1}^N {{{({I_{{{\rm{S}}_i}}} - I_{{{\rm{S}}_i}}^*(x))}^2}} }\\ {{X} = [x(1),x(2), \cdots x(N)]}\\ {x(i) = 0/1,i = 1,2, \cdots ,N}\\ {{X} \in {{\bf{R}}^N}} \end{array}} \right.$ | (1) |
| ${{{I}}_{\rm{S}}}{\rm{ = }}{\left[ {\begin{array}{*{20}{l}} {{I_{{{\rm{S}}_1}}}}&{{I_{{{\rm{S}}_2}}}}& \cdots &{{I_{{{\rm{S}}_N}}}} \end{array}} \right]^{\rm{T}}}$ | (2) |
| ${I_{{{\rm{S}}_i}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,}&{\text{检测到过电流信息}}\\ {0,}&{\text{未检测到过电流信息}} \end{array}} \right.$ | (3) |
| ${I}_{\rm{S}}^{\bf{*}}\left( {x} \right){\rm{ = }}{\left[ {\begin{array}{*{20}{l}} {I_{{{\rm{S}}_1}}^*(x)}&{I_{{{\rm{S}}_2}}^*(x)}& \cdots &{I_{{{\rm{S}}_N}}^*(x)} \end{array}} \right]^{\rm{T}}}$ | (4) |
| $I_{{{\rm{S}}_i}}^*(x){\rm{ = }}\sum\limits_i^N {x(i)} $ | (5) |
| ${x_i}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,}&{\text{该馈线区段发生故障}}\\ {0,}&{\text{该馈线区段处于正常}} \end{array}} \right.$ | (6) |
式(6)中N为配电网所含开关(含断路器和分段开关)总数;
随着大量DG接入,配网结构变得愈加复杂,导致系统的潮流分布及短路电流方向也发生变化,配电网的故障电流方向不再唯一,因此需要规定正方向来对故障电流方向加以区分。本文的电流方向采用文献[21]的思想,正方向定为以系统电源指向负载的方向,即定义正方向为在单电源情况下发生故障时的潮流方向。
| ${I_{{{\rm{S}}_i}}}{\rm{ = }}\left\{ {\begin{array}{*{20}{l}} \;\;\;{1,}&{\text{检测到正方向的故障电流}}\\ { - 1,}&{\text{检测到反方向的故障电流}}\\ {\;\;\;0,}&{\text{未检测到过电流信息}} \end{array}} \right.$ | (7) |
以开关
| ${K_i} = \prod\limits_{j = 1}^J {K(j)} $ | (8) |
| $K(j){\rm{ = }}\left\{ {\begin{array}{*{20}{l}} {1,}&{{{\rm{S}}_i}{\text{下游第}}j{\text{个}}{\rm{DG}}{\text{接入配电网}}}\\ {0,}&{{{\rm{S}}_i}{\text{下游第}}j{\text{个}}{\rm{DG}}{\text{未接入配电网}}} \end{array}} \right.$ | (9) |
式(9)中
| $I_{{{\rm{S}}_i}}^*(x){\rm{ = }}\sum\limits_{{n_1} = 1}^{{N_1}} {{x_i}({n_1})} - {K_i} \sum\limits_{{n_2}}^{{N_2}} {{x_i}({n_2})} $ | (10) |
式(10)中
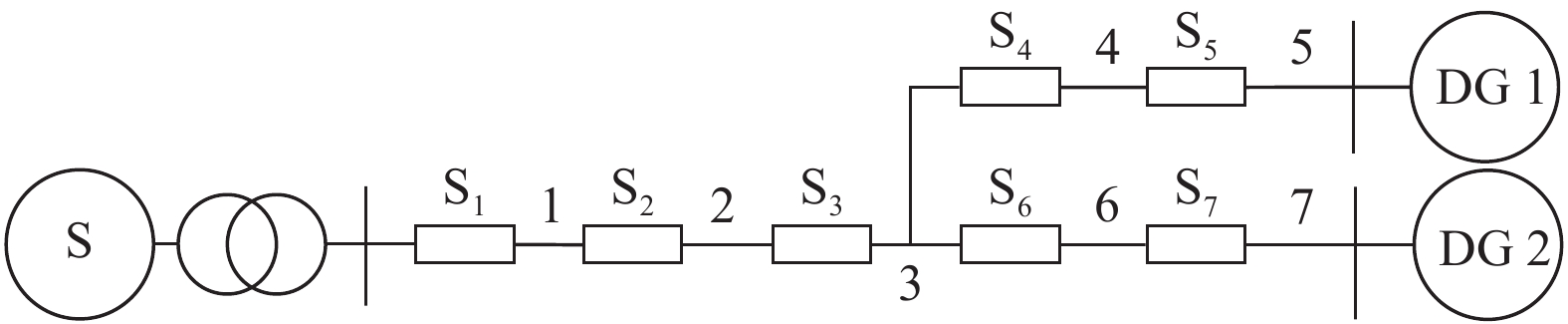
以图2所示含DG的T型耦合节点配电网为例进行分析。假定DG1投入,DG2未投入。
|
图 2 含DG的T型耦合节点的配电网 Figure 2 Distribution network of T-coupled nodes with DG |
根据式(8)~(10),各开关函数的表达式如式(11)所示。预设馈线区段4故障,据式(6)可得
| $\left\{ \begin{array}{l} I_{{{\rm{S}}_1}}^*(x) = x(1) + x(2) + x(3) + x(4) + x(5) + x(6) + x(7)\\ I_{{{\rm{S}}_2}}^*(x) = (x(2) + x(3) + x(4) + x(5) + x(6) + x(7)) - (x(1))\\ I_{{{\rm{S}}_3}}^*(x) = (x(3) + x(4) + x(5) + x(6) + x(7)) - (x(1) + x(2))\\ I_{{{\rm{S}}_4}}^*(x) = (x(4) + x(5)) - (x(1) + x(2) + x(3) + x(6) + x(7))\\ I_{{{\rm{S}}_5}}^*(x) = x(5) - (x(1) + x(2) + x(3) + x(4) + x(6) + x(7))\\ I_{{{\rm{S}}_6}}^*(x) = x(6) + x(7) - 0\\ I_{{{\rm{S}}_7}}^*(x) = x(7) - 0 \end{array} \right.$ | (11) |
由于式(1)存在离散变量,故求解较为复杂,需将离散模型转换成连续模型。依文献[18]的转换思想,若要将式(1)中的离散变量转换成连续变量,则需引入辅助变量
| $\left\{\begin{array}{l} x(i) + \kappa (i) = 1\\ x(i) \kappa (i) = 0 \end{array}\right.$ | (12) |
式(12)中N为馈线区段总数,再将式(12)代入式(1)后即形成了配电网故障定位的互补约束规划模型,如式(13)所示。
| $\left\{ \begin{array}{l} \min f\left( x \right) = \displaystyle\sum\limits_{i = 1}^N {{{({I_{{{\rm{S}}_i}}} - I_{{{\rm{S}}_i}}^*(x))}^2}} \\ {X} + {\kappa } = 1\\ {X} {\kappa } = 0\\ \displaystyle\sum\limits_{n = 1}^N {x(n)} \leqslant 1\\ {X} = [x(1),x(2), \cdots x(N)]\\ {\kappa } = [\kappa (1),\kappa (2), \cdots \kappa (N)]\\ {X},{\kappa } \geqslant 0,{X} \in {{\bf{R}}^N},{\kappa } \in {{\bf{R}}^N} \end{array} \right.$ | (13) |
由于已有的非线性规划不能获得互补约束优化问题在Karush-Kuhn-Tucker (KKT)条件下的局部最优点,故需将互补约束优化模型光滑化,常用方法是Fischer-Burmeiste辅助函数[22],据文献[18],基于扰动因子的Fischer-Burmeister辅助函数
| $\begin{array}{l} {\varPhi _\varepsilon }[x(i),\kappa (i)] = x(i) + \kappa (i) - \sqrt {x{{(i)}^2} + \kappa {{(i)}^2} + 2\varepsilon {{(i)}^2}} \end{array}$ | (14) |
将
| $x(i) \kappa (i) = \varepsilon {(i)^2}$ | (15) |
式(15)中
| $\min F({X},{\kappa }) = f({X}) + \sum\limits_{i = 1}^N {\varepsilon {{(i)}^2}} $ | (16) |
考虑到发生信息畸变时
| $f({X}) \sum\limits_{i = 1}^N {\varepsilon {{(i)}^2}} = 0$ | (17) |
根据式(12),可将式(14)简化为式(18)所示。
| $\begin{array}{l} {\varPhi _\varepsilon }[x(i),{\kappa }(i)] = 1 - \sqrt {x{{(i)}^2} + {\kappa }{{(i)}^2} + 2\varepsilon {{(i)}^2}} \end{array}$ | (18) |
故互补约束故障定位的光滑化模型可表示为式(19),对式(19),可在MATLAB中采用内点法进行优化求解。
| $\left\{ \begin{array}{l} \min F({X},{\kappa }) = f({{X}}) + \displaystyle\sum\limits_{i = 1}^N {\varepsilon {{(i)}^2}} \\ {\varPhi _\varepsilon }[x(i),\kappa (i)] = 0\\ f({{X}}) \displaystyle\sum\limits_{i = 1}^N {\varepsilon {{(i)}^2}} = 0\\ {X} = [x(1),x(2),\cdots,x(N)]\\ {\kappa } = [\kappa (1),\kappa (2),\cdots,\kappa (N)]\\ {\varepsilon } = [\varepsilon (1),\varepsilon (2),\cdots,\varepsilon (N)]\\ {X} + {\kappa } = 1;{X},{\kappa} \geqslant 0\\ {X} \in {{\bf{R}}^N},{\varepsilon } \in {{\bf{R}}^N} \end{array} \right.$ | (19) |
在DG接入配电网后,配电网故障定位互补约束光滑化模型的开关函数将用式(10)代替,另外本模型假设故障情况均为单点故障,故应增加约束,如式(20)所示。
| $\sum\limits_{n = 1}^N {x(n)} \leqslant 1$ | (20) |
故考虑DG接入的配电网故障定位的互补约束光滑化模型如式(21)所示。
| $\left\{ \begin{array}{l} \min F({X},{\kappa },{\varepsilon} ) = \displaystyle\sum\limits_{i = 1}^N {( {I_{S_i}} - (\displaystyle\sum\limits_{{n_1} = 1}^{{N_1}} {{x_i}({n_1})} } - \\ {K_i} \displaystyle\sum\limits_{{n_2}}^{{N_2}} {{x_i}({n_2})} ){) ^2} + \displaystyle\sum\limits_{i = 1}^N {(x(i) {\kappa }(i)} )\\ 1 - \sqrt {{{X}^2} + {{\kappa }^2} + 2{\varepsilon ^2}} = 0\\ \displaystyle\sum\limits_{i = 1}^N {( {I_{{{\rm{S}}_i}}} - (\displaystyle\sum\limits_{{n_1} = 1}^{{N_1}} {{x_i}({n_1})} - } \\ {K_i} \displaystyle\sum\limits_{{n_2}}^{{N_2}} {{x_i}({n_2})} ){) ^2} \displaystyle\sum\limits_{i = 1}^N {(x(i) {\kappa }(i))} = 0\\ \displaystyle\sum\limits_{n = 1}^N {x(n)} \leqslant 1\\ {X} = [x(1),x(2),\cdots,x(N)]\\ {\kappa } = [\kappa (1),\kappa (2),\cdots,\kappa (N)]\\ {X} + {\kappa }{\rm{ = }}1;{X,\kappa } \geqslant 0\\ {X} \in {{\bf{R}}^N},{\varepsilon } \in {{\bf{R}}^N} \end{array} \right.$ | (21) |
针对本文的含DG的配电网故障定位的互补约束光滑化模型,运用内点法优化求解的具体步骤如下:(1) 由所研究配电网中的DG接入情况,确定开关
针对本文的配电网故障定位的互补约束光滑化模型,以图2所示的配电网为例,对所建模型的容错性进行分析。设馈线区段4处故障,DG1投入,DG2未投入,则正常状态下FTU上传的实际过电流信息
| $\begin{array}{l} I_{{{\rm{S}}_4}}^*(x) = (x(4) + x(5)) - (x(1) + x(2) + x(3)) = 1 \;\;\;\; \end{array}$ | (22) |
| $\begin{array}{l} I_{{{\rm{S}}_5}}^*(x) = (x(5)) - (x(1) + x(2) + x(3) + x(4)) = - 1 \end{array}$ | (23) |
由式(22)减式(23)可得x(4)=1,再据式(20)约束可知x(1),x(2),x(3),x(5)均为0,得X=[0 0 0 1 0 0 0]T,畸变时目标函数值虽然不为0,但仍为最小值,此时最小值为1。综上可知本文所提方法在FTU上传的过电流信息发生畸变之时,依旧可以正确定位,故具有一定的容错性能。
3 算例分析 3.1 算例1如上文图2所示,S为系统电源,DG1、DG2为分布式电源。S1为断路器,S2~S7为分段开关。
在FTU上传过电流信息未发生畸变情况下,分别对馈线区段1~7发生单一故障进行仿真实验,使用内点算法进行决策。然后再在FTU上传过电流信息发生畸变情况下,对不同畸变情况进行仿真实验,仿真结果见表1,投切系数K=[k1, k2],表示各DG投切状态。
| 表 1 算例1馈线区段1~7单一故障仿真结果 Table 1 Simulation results of single fault in feeder section 1 ~ 7 |
由表1的仿真结果可知,本文所提出的含DG配电网故障定位的互补约束光滑化模型能对故障馈线区段进行准确定位,当FTU上传的过电流信息发生1~3位畸变时,仍能准确找出故障区段,有着良好的容错性能。通过观察投切系数K,可知本文所提出的含DG配电网故障定位的互补约束光滑化模型可适用于DG全部投切情况。
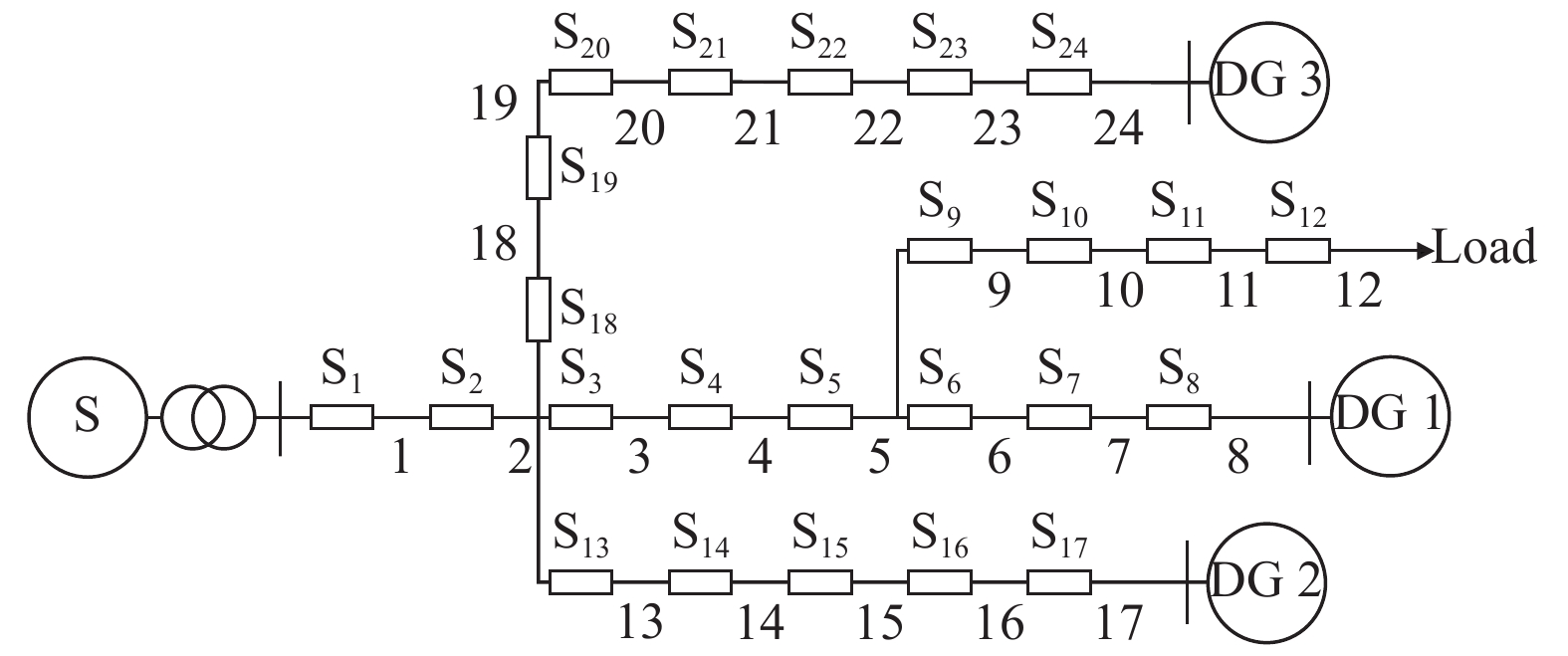
3.2 算例2算例2结构如图3所示,在算例1基础上,在配网线路末端增加负荷和DG接入,对不同畸变情况下分别使用智能算法中的差分进化算法(Differential Evolution Algorithm,DE)和本文所提方法分别进行100次仿真实验。DE的种群规模为50,交叉概率为0.9,变异概率为0.9,最大迭代次数为100次。仿真结果见表2, 表2中准确率是以定位正确次数除以实验总次数计算得出。
|
图 3 24节点配电网 Figure 3 24-node distribution network |
| 表 2 对算例2使用不同算法进行仿真的结果 Table 2 Simulation results of example 2 using different algorithms |
由表2的仿真结果可知,对DG不同投切情况,本文所提方法均可精准定位出故障区段,而差分进化算法的定位结果则不稳定,分析实验结果可知,在FTU上传过电流信息畸变越多时,差分进化算法的准确率就越低。
3.3 与基于逻辑关系的故障定位方法比较除了差分进化算法外,针对基于逻辑关系描述的配电网故障定位方法,根据文献[19-23]所提供的算例和仿真结果,从模型、算例规模、决策方法、故障定位准确性、算法稳定性几方面进行总结对比。
表3中所提及文献,因采用逻辑模型建模,故必须采用智能算法进行故障定位。虽然智能算法对于离散变量的处理较为方便,但其存在不稳定的缺陷,导致定位结果有误。现将本文所提方法与文献[19]及文献[21]中的部分实验进行对比。
| 表 3 基于逻辑关系的故障定位方法结果比较 Table 3 Comparison of results of fault location methods based on logical relationship |
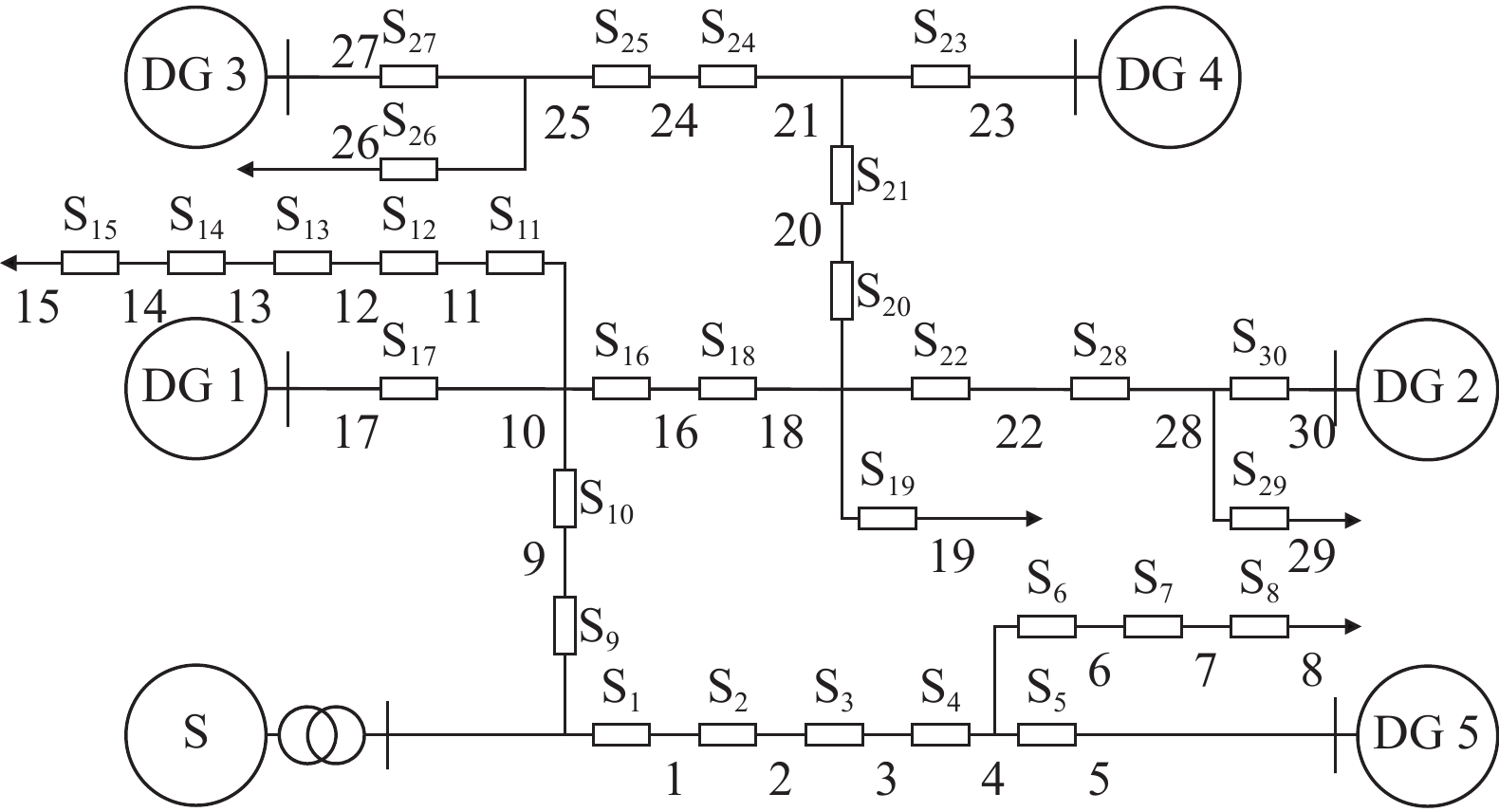
文献[19]采用的和声算法中,和声记忆库大小HMS=5,和声记忆库考虑概率HMCR=0.95,扰动概率PAR=0.8,扰动量bw=5,最大迭代次数J=1 000。改进和声算法中,和声记忆库大小HMS=5,最大迭代次数J=1 000。对30节点算例进行仿真实验,截取部分实验结果如表4所示。30节点算例为如图4所示,其中DG全部投入。
| 表 4 和声算法的部分实验结果 Table 4 Partial experimental results of the harmony algorithm |
|
图 4 30节点配电网 Figure 4 30-node distribution network |
针对30节点配电网,使用本文所提方法在相同故障情况下与和声算法进行对比实验,实验结果如表5所示。
| 表 5 对30节点配电网运用内点法决策的实验结果 Table 5 Experimental results of interior point method decision making for 30-node distribution network |
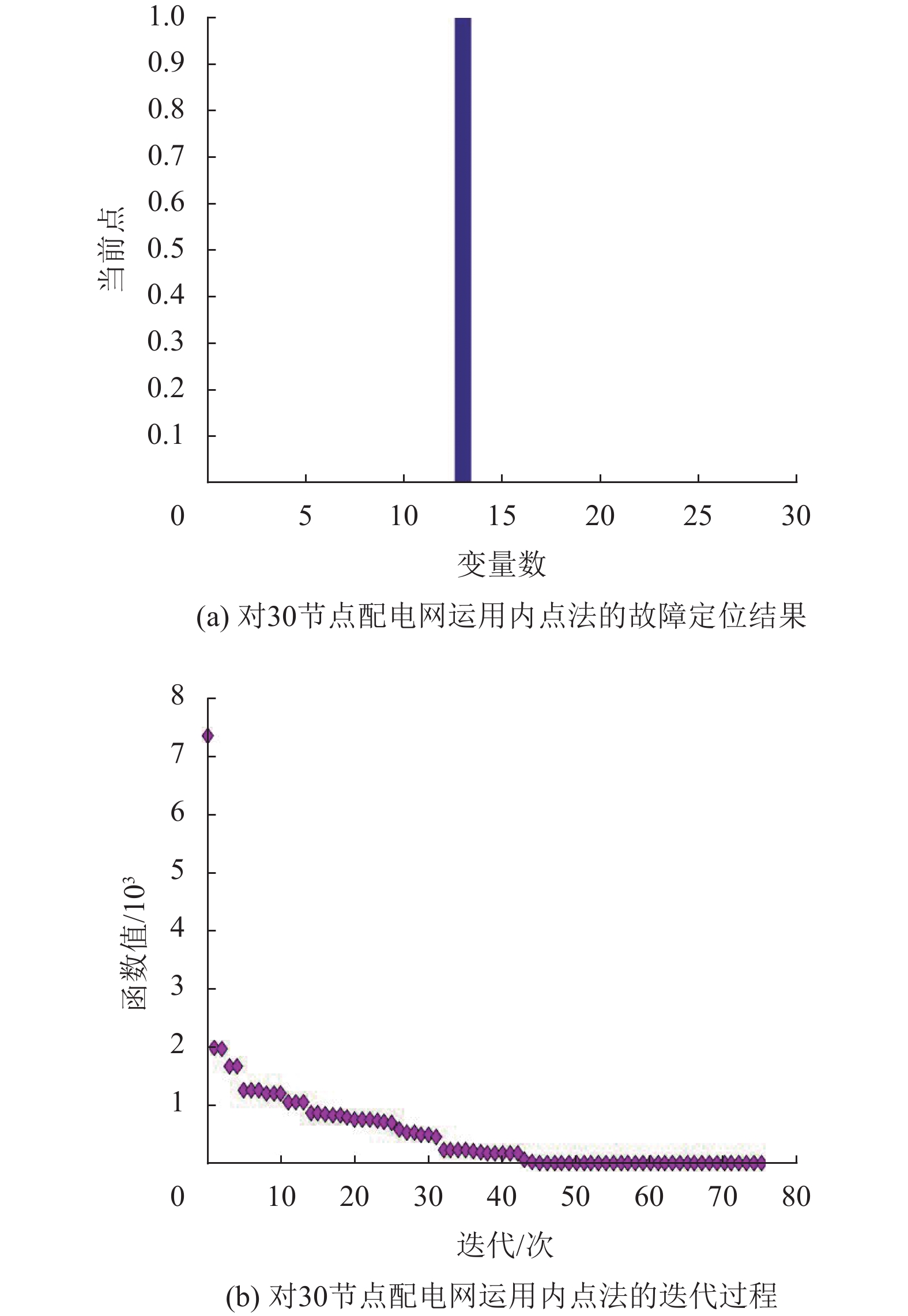
以区段13故障、开关S14畸变为例,本文所提方法仿真结果如图5所示。根据文献[19]数据显示,此情况下和声算法平均迭代439.19次,改进和声算法平均156.91次,由图5(b)可知本文所提方法迭代76次。
|
图 5 对30节点配电网运用内点法的故障定位结果及迭代过程 Figure 5 Fault location results and iterative process using interior point method for 30-node distribution network |
对比可知,本文所提方法在故障定位准确性、算法稳定性上更有优势。
3.3.2 与蝙蝠算法比较文献[21]采用的蝙蝠算法中,蝙蝠种群n=4,蝙蝠脉冲频率上限
|
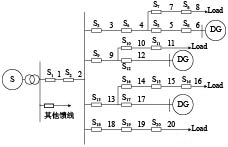
图 6 20节点配电网 Figure 6 20-node distribution network |
针对20节点配电网,使用本文所提方法在相同故障情况下与蝙蝠算法进行对比实验,实验结果如表6所示。
| 表 6 对20节点配电网分别使用内点法与蝙蝠算法的实验结果 Table 6 Experimental results using the interior point method and the bat algorithm for the 20-node distribution network |
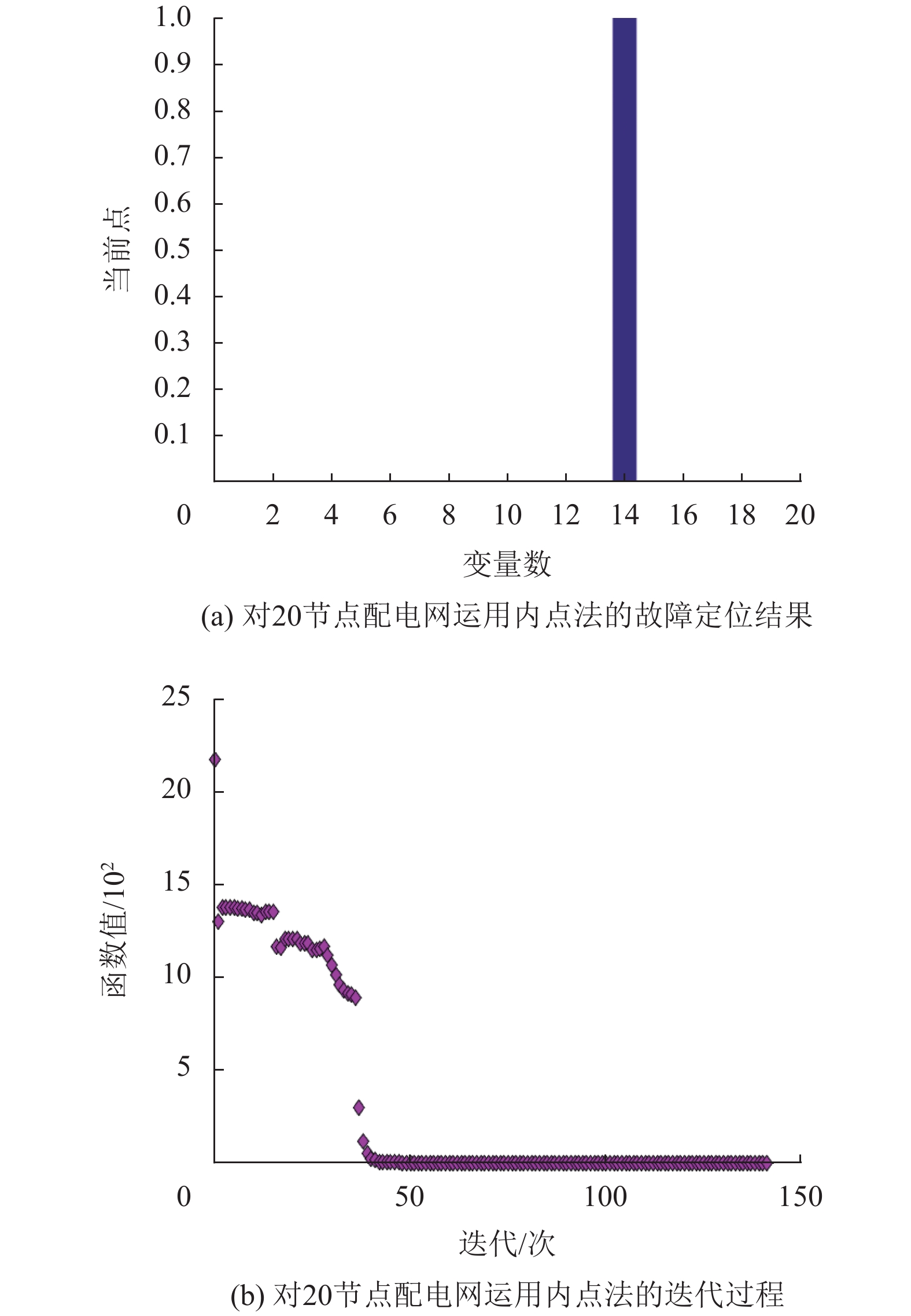
以区段14故障、开关S9畸变为例,根据文献[21]数据显示,此情况下使用蝙蝠算法定位50次,成功定位49次,即成功率平均为98%,而相同情况下使用本文所提方法运行100次,成功定位100次。本文所提方法仿真结果如图7所示。
|
图 7 对20节点配电网运用内点法的故障定位结果及迭代过程 Figure 7 Fault location results and iterative process of 20-node distribution network using interior point |
由表6和图7(a)可知,在FTU上传过电流信息发生畸变的情况下,内点算法的容错性优于蝙蝠算法。由图7(b)可知,使用内点法决策求解时,算法迭代至39次就已经收敛。此外,统计100次内点法优化结果,计得其平均迭代次数为40次。而根据文献[21],相同情况下蝙蝠算法平均迭代为49次。对比可知,本文所提算法更有优势。
4 结论(1) 本文基于约束互补光滑化理论建立了含DG的配电网故障定位模型,该模型可适用于含DG的配电网的故障定位,定位结果准确稳定。
(2) 本文所提方法可适用于DG所有投切情况,对电流正方向的规定较为简便,可适用于各种拓扑结构的配电网。
(3) 因使用代数关系建立模型,求解时可用数值稳定性高的非线性规划进行决策,因此在求解上避免了智能算法易陷入局部最优、收敛性差的问题。对于拓扑结构较为复杂的含DG配电网,故障区段定位成功率高达100%,且在FTU上传的过电流信息发生多位畸变时仍可准确定位,具备一定的容错性能。
(4) 本文研究前提均为单点故障,对于多重故障的模型建立与决策方案仍需继续研究。
| [1] |
杜红卫, 孙雅明, 刘弘靖, 等. 基于遗传算法的配电网故障定位和隔离[J].
电网技术, 2000, 24(5): 52-55.
DU H W, SUN Y M , LIU H J, et al. Fault location and isolation of distribution network based on genetic algorithm[J]. Power System Technology, 2000, 24(5): 52-55. DOI: 10.3321/j.issn:1000-3673.2000.05.013. |
| [2] |
刘俊夫. 基于BP神经网络的配电网故障区段定位优化方法研究[D]. 恩施: 湖北民族学院, 2018.
|
| [3] |
付家才, 陆青松. 基于蝙蝠算法的配电网故障区间定位[J].
电力系统保护与控制, 2015, 43(16): 100-105.
FU J C, LU Q S. Fault sections location of distribution network based on bat algorithm[J]. Power System Protection and Control, 2015, 43(16): 100-105. DOI: 10.7667/j.issn.1674-3415.2015.16.015. |
| [4] |
项晓鸣. 基于蝙蝠算法和元胞自动机的配电网故障定位研究[D]. 武汉: 湖北工业大学, 2017.
|
| [5] |
程璞. 基于粒子群算法的配电网故障定位研究[D]. 淮南: 安徽理工大学, 2017.
|
| [6] |
郑涛, 潘玉美, 郭昆亚, 等. 基于免疫算法的配电网故障定位方法研究[J].
电力系统保护与控制, 2014, 42(1): 77-83.
ZHENG T, PAN Y M, GUO K Y, et al. Fault location of distribution network based on immune algorithm[J]. Power System Protection and Control, 2014, 42(1): 77-83. DOI: 10.7667/j.issn.1674-3415.2014.01.011. |
| [7] |
秦立军, 杨万涛. 蚁群算法在配电网故障定位中的应用及其优化[J].
电气应用, 2015, 34(22): 73-76.
QIN L J, YANG W T.. Application and optimization of ant colony algorithm in fault location of distribution network[J]. Electrical Applications, 2015, 34(22): 73-76. |
| [8] |
ZHANG B, HAO Z, BO Z. New development in relay protection for smart grid[J].
Protection and Control of Modern Power Systems, 2016, 1(1): 14.
DOI: 10.1186/s41601-016-0025-x. |
| [9] |
陈奎, 张云, 王洪寅, 等. 基于免疫算法的含分布式电源配电网的故障定位[J].
电力系统保护与控制, 2017, 45(24): 57-62.
CHEN K, ZHANG Y, WANG H Y, et al. Fault-section location of distribution network containing distributed generation based on immune algorithm[J]. Power System Protection and Control, 2017, 45(24): 57-62. DOI: 10.7667/PSPC161971. |
| [10] |
徐鹏飞, 邢仁周. 粒子群优化算法含分布式电源配电网故障定位[J].
电源技术, 2018, 42(4): 591-592.
XU P F, XING R Z. Fault location of distribution network with distributed generation supply by particle swarm optimization algorithm[J]. Power Technology, 2018, 42(4): 591-592. DOI: 10.3969/j.issn.1002-087X.2018.04.041. |
| [11] |
周湶, 郑柏林, 廖瑞金, 等. 基于粒子群和差分进化算法的含分布式电源配电网故障区段定位[J].
电力系统保护与控制, 2013, 41(4): 33-37.
ZHOU Q, ZHENG B L, LIAO R J, et al. Fault segment location of distributed generation distribution network based on particle swarm optimization and differential evolution algorithm[J]. Power System Protection and Control, 2013, 41(4): 33-37. DOI: 10.7667/j.issn.1674-3415.2013.04.006. |
| [12] |
王一非, 贾燕冰. 含分布式电源配电网故障定位改进矩阵算法[J].
计算机仿真, 2018, 35(4): 58-64.
WANG Y F, JIA Y B. Improved matrix algorithm for fault location in DG distribution network[J]. Computer Simulation, 2018, 35(4): 58-64. DOI: 10.3969/j.issn.1006-9348.2018.04.012. |
| [13] |
刘鹏程, 李新利. 基于多种群遗传算法的含分布式电源的配电网故障区段定位算法[J].
电力系统保护与控制, 2016, 44(2): 36-41.
LIU P C, LI X L. Fault-section location of distribution network containing distributed generation based on the multiple-population genetic algorithm[J]. Power System Protection and Control, 2016, 44(2): 36-41. DOI: 10.7667/j.issn.1674-3415.2016.02.005. |
| [14] |
吴薛红, 郑梅, 唐小波, 等. 配电网故障区间定位的新型矩阵算法[J].
南京师范大学学报(工程技术版), 2003(2): 54-57.
WU X H, ZHENG M, TANG X B, et al. A new matrix algorithm for fault section locating in distribution system[J]. Journal of Nanjing Normal University (Engineering & Technology), 2003(2): 54-57. DOI: 10.3969/j.issn.1672-1292.2003.02.014. |
| [15] |
罗梅, 杨洪耕. 配电网故障定位的一种改进通用矩阵算法[J].
电力系统保护与控制, 2012, 40(5): 64-68.
LUO M, YANG H G. An improved general matrix algorithm for fault locating in distribution system[J]. Power System Protection and Control, 2012, 40(5): 64-68. DOI: 10.3969/j.issn.1674-3415.2012.05.012. |
| [16] |
卫志农, 何桦, 郑玉平. 配电网故障区间定位的高级遗传算法[J].
中国电机工程学报, 2002(4): 128-131.
WEI Z N, HE H, ZHENG Y P. A refined genetic algorithm for the fault sections location[J]. Proceedings of the CSEE, 2002(4): 128-131. |
| [17] |
郭壮志, 徐其兴, 洪俊杰, 等. 配电网快速高容错性故障定位的线性整数规划方法[J].
中国电机工程学报, 2017, 37(3): 786-795.
GUO Z Z, XU Q X, HONG J J, et al. Integer linear programming based fault section diagnosis method with high fault-tolerance and fast performance for distribution network[J]. Proceedings of the CSEE, 2017, 37(3): 786-795. |
| [18] |
郭壮志, 徐其兴, 洪俊杰, 等. 配电网故障区段定位的互补约束新模型与算法[J].
中国电机工程学报, 2016, 36(14): 3342-3751.
GUO Z Z, XU Q X, HONG J J, et al. A novel fault section location model with complementarity constraints and its optimization algorithm for distribution network[J]. Proceedings of the CSEE, 2016, 36(14): 3342-3751. |
| [19] |
陈辉, 周羽生, 刘诗涵, 等. 基于改进和声算法的含DG配电网故障定位[J].
电力科学与技术学报, 2018, 33(2): 123-128.
CHEN H, ZHOU Y S, LIU S H, et al. Fault location of DG-containing distribution network based on improved harmony algorithm[J]. Journal of Electric Power Science and Technology, 2018, 33(2): 123-128. DOI: 10.3969/j.issn.1673-9140.2018.02.017. |
| [20] |
陶维青, 杨刚, 丁明, 等. 改进模因算法在含DG配电网故障定位中的应用[J].
电子测量与仪器学报, 2016, 30(2): 265-273.
TAO W Q, YANG G, DING M, et al. Application of improved memetic algorithm in fault location of DG distribution network[J]. Journal of Electronic Measurement and Instrument, 2016, 30(2): 265-273. |
| [21] |
裴文杰, 谭阳红, 汪沨, 等. 蝙蝠算法在含DG配电网故障定位中的应用[J].
计算机工程与应用, 2016, 52(22): 218-221.
PEI W J, TAN Y H, WANG F, et al. Application of bat algorithm in fault location of DG distribution network[J]. Computer Engineering and Applications, 2016, 52(22): 218-221. DOI: 10.3778/j.issn.1002-8331.1501-0121. |
| [22] |
王迪, 吴鑫强, 王振浩. 基于改进遗传算法的含分布式电源配电网故障定位[J].
东北电力大学学报, 2016, 36(1): 1-7.
WANG D, WU X Q, WANG Z H. Fault location of distributed generation distribution network based on improved genetic algorithm[J]. Journal of Northeast Electric Power University, 2016, 36(1): 1-7. DOI: 10.3969/j.issn.1005-2992.2016.01.001. |
| [23] |
黄知伟. 基于云粒子群算法的含DG配电网故障定位[D]. 武汉: 湖北工业大学, 2016.
|
 2020, Vol. 37
2020, Vol. 37
