示教是工业机器人在喷涂应用中的一个重要环节。机器人的示教方法可以分为两大类:一种是直接面向机器人本体进行示教,称为直接示教;另一种是远离机器人本体通过计算机技术对机器人进行示教,称为离线示教。直接示教方法主要有示教盒示教和手把手示教两种。手把手示教是由操作人员直接拖拽机器人末端工具的方式实现复杂轨迹的示教。与示教盒示教和离线编程相比,手把手示教喷涂效果所见即所得,无需编程,简单易学,效率高,只需简短培训就可使原喷涂工人直接成为机器人的操作工人,解决了中小涂装企业技术升级后机器人应用人才短缺问题,并且避免了大量喷涂工下岗带来的社会问题。
在手把手示教过程中,主要存在两方面的问题。一方面,受到机器人拖拽灵活性和操作人员自身等因素的影响,示教路径和速度难以光顺,喷涂时速度和加速度会有突变,产生振动、冲击,影响喷涂质量。另一方面,由于机器人拖拽灵活性的影响,示教时难以达到或者难以迅速达到机器人期望的工作速度,导致机器人再现喷涂时只能同时提高整体的速度。因为这两方面问题的存在,使手把手示教机器人的现实应用受到一定的诟病。为解决上述问题,本文提出了一种对手把手示教喷涂采样数据进行运动规划的方法。
机器人关节角空间运动规划主要是对关节速度、加速度进行规划,以时间最优和平滑过渡为目标进行优化[1-3]。由于从关节坐标到机器人末端工具轴位姿映射过程存在大量的三角函数等非线性运算,直接对关节坐标优化后会造成机器人末端机构位姿误差难以控制,使再现位姿与采样位姿产生较大误差。本文提出在笛卡尔空间中运用样条曲线对机器人手把手示教轨迹进行光顺处理,对再现运动速度进行重新规划,使得机器人再现运动时能够以较高的速度平稳运行,解决手把手示教存在的上述问题。
1 示教轨迹的位姿拟合在手把手示教过程中,工业机器人控制器对6个关节伺服电机的绝对位置编码器数值进行时间分割采样,得到6关节坐标时间分割采样数据
| ${{{M}}_i} = \left[ {\begin{array}{*{20}{c}} {{{{R}}_i}}&{{{{P}}_i}} \\ 0&1 \end{array}} \right]$ | (1) |
式中,
对手把手示教轨迹进行优化,可以转化为对给定轨迹
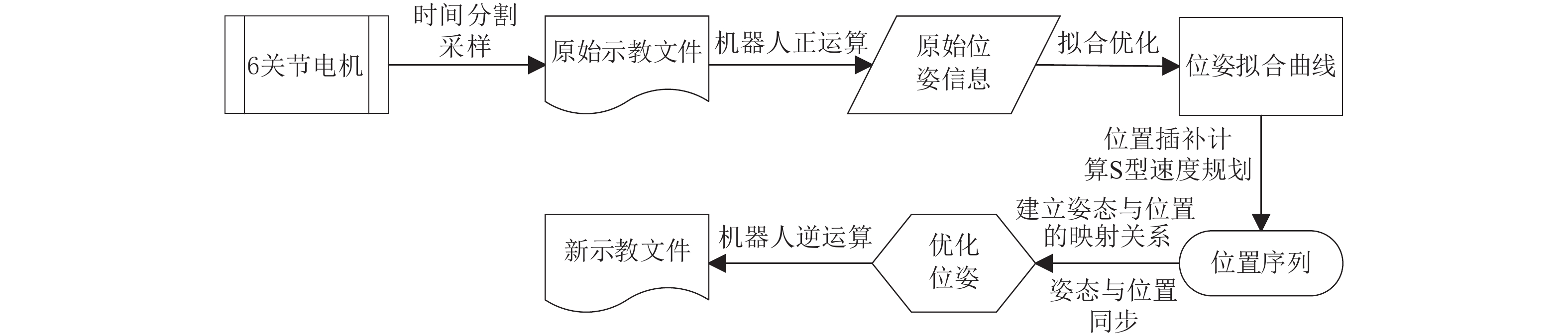
|
图 1 整体优化流程 Figure 1 Optimization process |
轨迹的预处理主要目的是减少后续位姿拟合的计算量,适当去除一些示教点,用较少的示教点来表示轨迹而不丢失轨迹自身的特征。如图2所示,计算空间矢量

|
图 2 特征点的判断示意图 Figure 2 Judgment diagram of feature points |
运用以上方法,对空间位置集合
旋转矩阵R描述轨迹点的姿态较为复杂而且难以量化计算,本文引入单位四元数的方法描述机器人末端执行器的姿态轨迹曲线[4-5]。空间某点在绕轴
| ${{{M}}_i} = (\begin{array}{*{20}{c}} {{{{q}}_i}}&{{{{P}}_{{i}}}} \end{array})$ | (2) |
为获得平滑连续的空间位置曲线和姿态曲线,对示教空间位置序列
对于序列
| ${{C}}(u) = \mathop \sum \limits_{i = 0}^n {{{d}}_i}{N_{i,3}}(u)$ | (3) |
式中,
由单位四元数
| $\left\{\begin{array}{l} {{p}} = {\rm{ln}}({{q}}) = \displaystyle\frac{\theta }{2} {{n}} \\ {{q}} = \exp ({{p}}) = \exp \left(\displaystyle\frac{\theta }{2} {{n}} \right) \end{array}\right.$ | (4) |
令函数
根据式(4),可以将姿态序列
| ${{p}}(t) = \mathop \sum \limits_{i = 0}^n {{{\varphi }}_i}{N_{i,3}}(t)$ | (5) |
根据同样的方法可以计算得到曲线
| ${{q}}(t) = \exp ({{p}}(t))$ | (6) |
为获得新的离散示教路径,需要分别对位置曲线
曲线参数化插补,即由轨迹空间的进给步长∆L映射到参数空间从而求取参数
| ${u_{i + 1}} = {u_i} + {u'}({t_i}){T_c} + o({T_c})$ | (7) |
式中,
对机器人末端位置拟合曲线
| $v(t) = \left\| {\frac{{{\rm{d}}{{C}}(u)}}{{{\rm{d}}t}}} \right\| = \left\| {\frac{{{\rm{d}}{{C}}(u)}}{{{\rm{d}}u}}} \right\|\frac{{{\rm{d}}u}}{{{\rm{d}}t}}$ | (8) |
由式(8),有式(9)
| ${u'}\left( t \right) = \frac{{{\rm{d}}u}}{{{\rm{d}}t}} = \frac{{v(t)}}{{\left\| {{{{C}}'}(u)} \right\|}}$ | (9) |
忽略泰勒余项,式(7)可以写为式(10)所示。
| ${u_{i + 1}} = {u_i} + \frac{{v({t_i})}}{{{\sigma _i}}}{T_c}$ | (10) |
式中,
反向插补计算时,有式(11)。
| ${u_i} = {u_{i + 1}} - \frac{{v\left( {{t_i}} \right)}}{{{\sigma _{i + 1}}}}{T_c}$ | (11) |
工人示教速度不能满足机器人作业速度,不能很好地适用于产品加工,机器人再现速度需要提升。为了使机器人作业时速度更加平稳,插补时使用区域连续S型速度曲线对速度进行规划[12-13]。
位置曲线
| $\left\{ {\begin{array}{*{20}{l}} {\kappa ({u_i}) > \kappa ({u_{i - 1}})}\\ {\kappa ({u_i}) > \kappa ({u_{i + 1}})}\\ {\kappa ({u_i}) > {{{A_{\rm{max}}}} / {v_{f}^2}}} \end{array}} \right.$ | (12) |
式(12)中,
突变点对应的限制速度可以通过系统法向加速度限制和系统弓高误差限制进行确定[14-15]。在找到
对曲线
针对这一问题,采用双向插补离散的方式寻找减速点。如图3所示,点
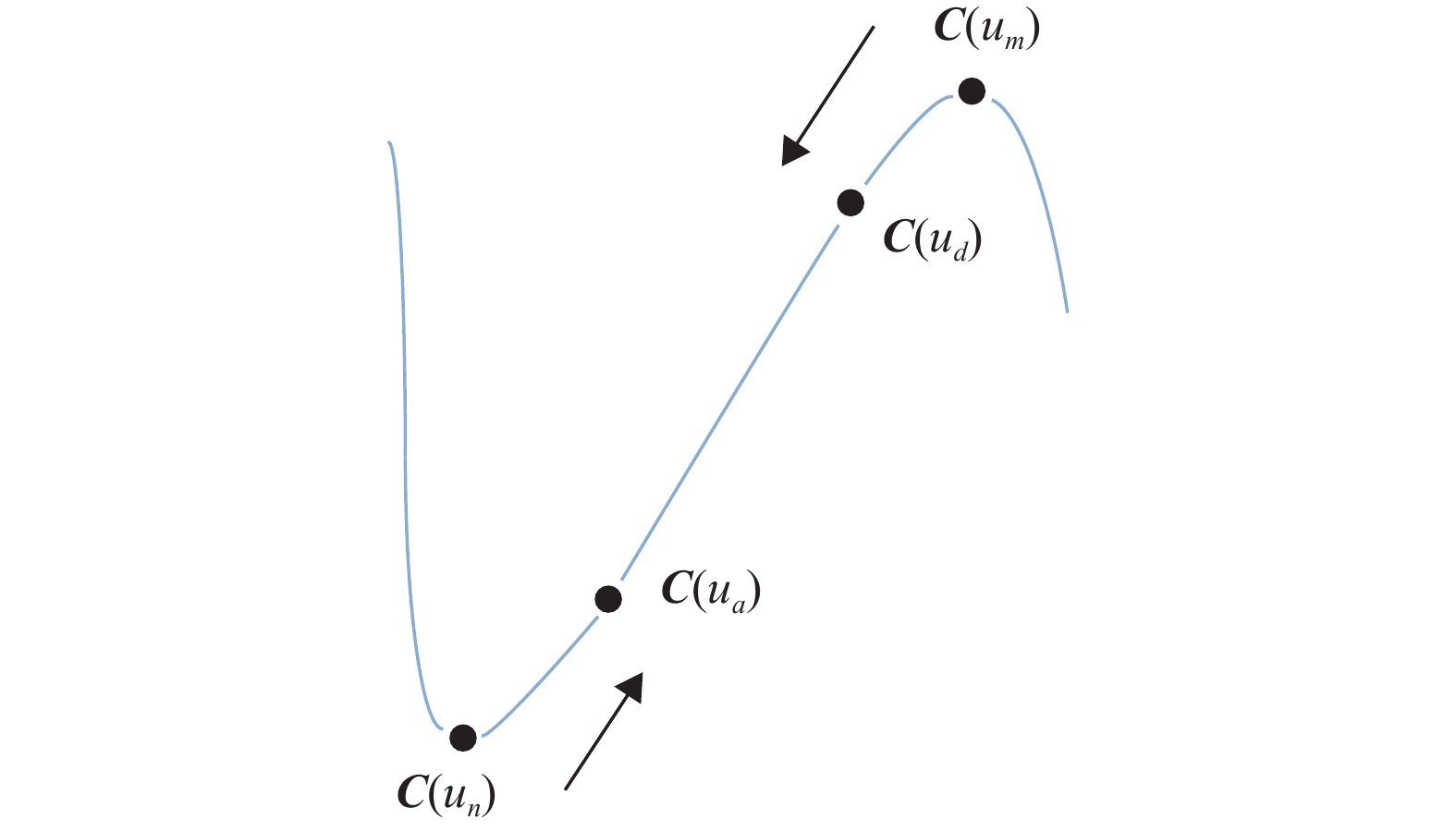
|
图 3 双向插补示意图 Figure 3 Two-way interpolation diagram |
| ${v_a}(t) = - \frac{{4{a_{\rm{max}}}}}{{3T_1^2}}{t^3} + \frac{{2{a_{\rm{max}}}}}{{3{T_1}}}{t^2} + {v_s}$ | (13) |
其中,
寻找减速点
步骤1:假设曲线段
步骤2:初始化正向插参数
步骤3:设置插补次数N,并计算正向插补速度
步骤4:计算正、反向插补参数
步骤5:判断
步骤6:判断插补速度
步骤7:判断
步骤8:令
步骤9:结束查找流程。
上述流程在查找减速点
在对位置曲线
姿态曲线离散化时应该尽可能地保持与原姿态同步,也就是机器人末端机构运行通过新的示教路径上某一空间点时,姿态应当与原来的姿态尽可能保持一致。因此,需要建立位置曲线
| $t = f(u)$ | (14) |
因为位置曲线
首先判断参数u所在的节点矢量区间
| $t = f(u) = {t_j} + \frac{{u - {u_j}}}{{{u_{j + 1}} - {u_j}}}({t_{j + 1}} - {t_j})$ | (15) |
将位置曲线
| ${{M}}_i^* = \left[ {\begin{array}{*{20}{c}} {{{R}}(t)}&{{{P}}(t)}\\ 0&1 \end{array}} \right]$ | (16) |
这样就实现了位置和姿态的同步。对示教路径序列集合
本文以佛山某机器人公司自行研制的手把手示教喷涂机器人为实验平台,对提出的运动轨迹优化算法进行验证。实验截取广州某卫浴公司实际浴缸生产中玻纤−树脂复合材料喷涂的一段手把手示教路径,进行实验分析。该段示教轨迹由870个示教点组成,将这些示教点进行转化得到对应的机器人6个关节角角度,再通过机器人正运算,得到笛卡尔坐标系下的喷枪位姿。经过拟合优化处理,可以得到相应的位姿拟合曲线。给定喷涂速度
|
图 4 优化前后喷枪位姿对比 Figure 4 Comparison of poses before and after optimization |
为了进一步分析其拟合效果,进行位置曲线拟合误差计算,可以得到最大拟合误差为1.095 mm,平均拟合误差为0.073 mm,标准差为0.144 mm,拟合误差能满足机器人的喷涂精度。拟合误差分布如图5所示。
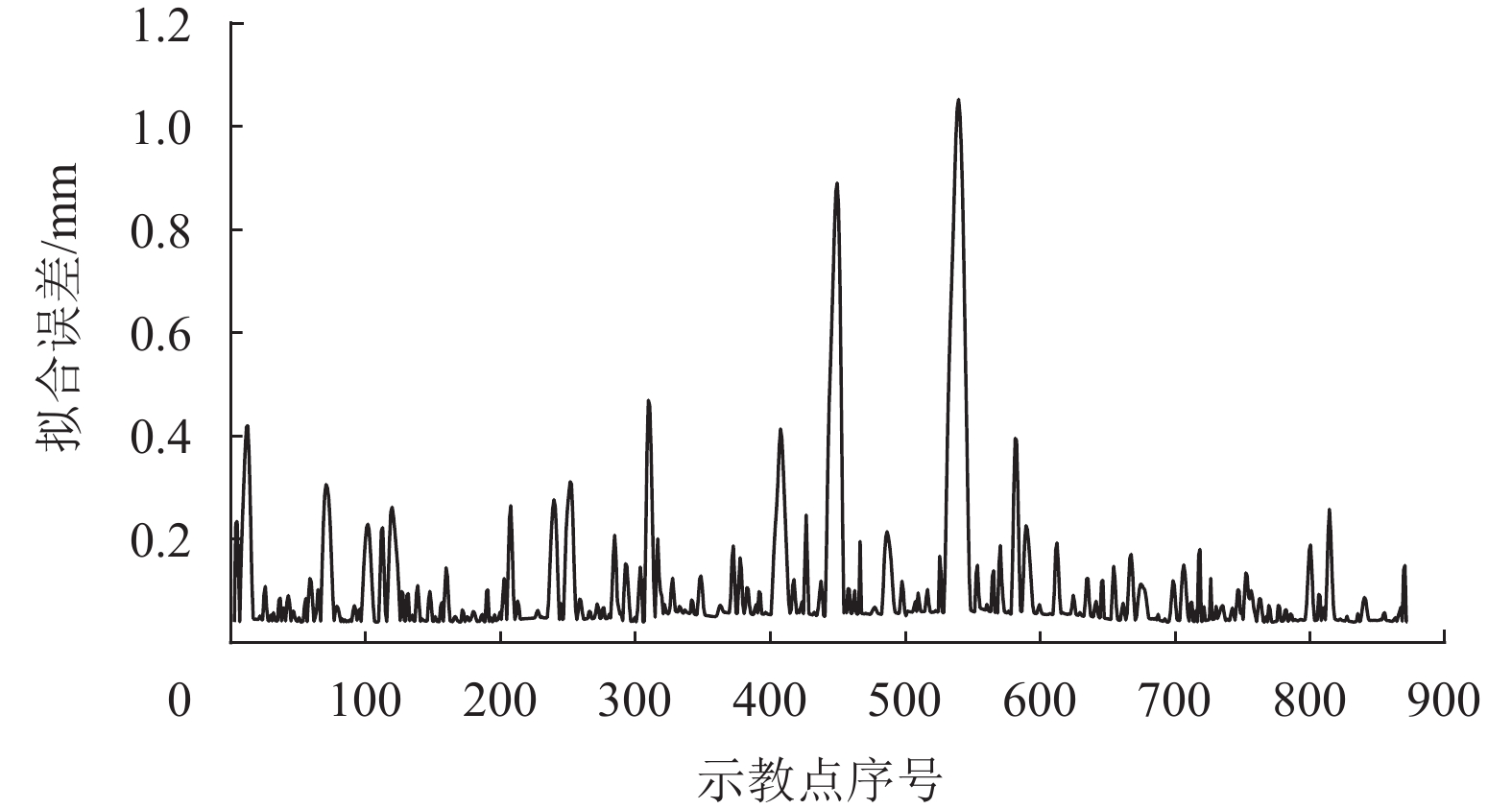
|
图 5 轨迹拟合误差分布 Figure 5 Fitting error distribution of trajectory |
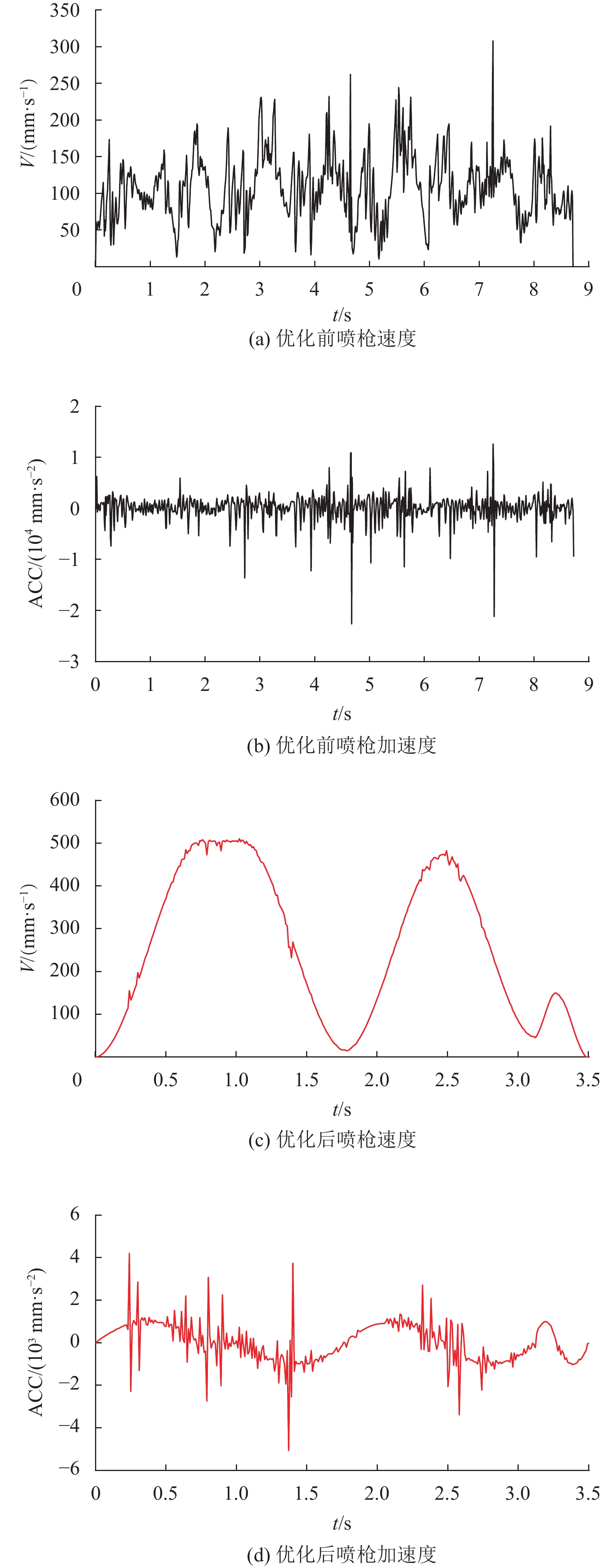
对优化效果进行验证,分别对原始轨迹和优化轨迹的机器人喷枪速度、加速度进行对比分析。图6是优化前、后喷枪速度、加速度对比图。从图6可以明显观察到原始轨迹速度不稳定,波动较大而且整体速度较低。原始轨迹加速度存在不规则波动,而且在一些点处有很大的突变。经过优化处理后的机器人喷枪轨迹运动速度曲线呈现出所规划的S型,整体较为平滑,整体运动速度得到提高,提高了机器人的工作效率。优化轨迹的加速度虽然仍然存在突变,但是比较优化前减小了一个数量级,加速度曲线得到改善。将优化轨迹数据转换成示教再现数据格式,在机器人上进行再现实验,实验结果显示,有效地减小了再现喷涂过程中的振动,喷涂效果明显改善,同时喷涂效率也得到了提高。
|
图 6 优化前后喷枪速度、加速度对比图 Figure 6 Comparison of spray gun speed-acceleration before and after optimization |
本文提出的手把手示教机器人再现运动优化方法得到实验验证,结果表明此优化方法能够在保持原示教喷涂轨迹位姿精度的前提下,提高了机器人再现喷涂的平稳性,喷涂效果明显改善,同时也改善了工人示教速度与预期喷涂速度不匹配的问题,对提高手把手示教机器人在涂装行业上的使用具有一定的应用价值。
| [1] |
董辉, 仲晓帆, 黄胜. 一种六关节机器人关节空间轨迹规划方法[J].
浙江工业大学学报, 2015, 43(3): 336-339, 345.
DONG H, ZHONG X F, HUANG S. Trajectory planning method in joint space for 6-DOF robot[J]. Journal of Zhejiang University of Technology, 2015, 43(3): 336-339, 345. DOI: 10.3969/j.issn.1006-4303.2015.03.021. |
| [2] |
王宁, 张新敏. 基于MATLAB的六自由度机器人轨迹规划与仿真[J].
制造业自动化, 2014, 36(15): 95-97.
WANG N, ZHANG X M. Trajectory planning and simulation of six-DOF robot based on MATLAB[J]. Manufacturing Automation, 2014, 36(15): 95-97. DOI: 10.3969/j.issn.1009-0134.2014.15.025. |
| [3] |
马睿, 胡晓兵, 殷国富, 等. 六关节工业机器人最短时间轨迹优化[J].
机械设计与制造, 2014(4): 30-32, 35.
MA R, HU X B, YIN G F, et al. The shortest time optimal planning of 6-DOF industrial robot’s trajectory[J]. Machinery Design & Manufacture, 2014(4): 30-32, 35. DOI: 10.3969/j.issn.1001-3997.2014.04.010. |
| [4] |
刘宏伟, 王效杰, 梁艳阳, 等. 机器人末端执行器姿态轨迹规划研究[J].
机械设计与制造, 2015(4): 28-30, 34.
LIU H W, WANG X J, LIANG Y Y, et al. Research on the orientation trajectory planning of robot end-effector[J]. Machinery Design & Manufacture, 2015(4): 28-30, 34. DOI: 10.3969/j.issn.1001-3997.2015.04.008. |
| [5] |
成津赛, 张秋菊. 机器人姿态插补的四元数直接逆解方法[J].
机械科学与技术, 2016, 35(9): 1354-1358.
CHENG J S, ZHANG Q J. Orientations interpolation algorithm for robot with quaternion-based direct inverse kinematics[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(9): 1354-1358. |
| [6] |
季晨.工业机器人姿态规划及轨迹优化研究[D].哈尔滨: 哈尔滨工业大学, 2013.
|
| [7] |
施法中.计算机辅助几何设计与非均匀有理B样条[M].北京: 高等教育出版社, 2013: 254-260.
|
| [8] |
邢燕, 樊文, 檀结庆, 等. 一类C~2连续的单位四元数插值样条曲线[J].
计算机辅助设计与图形学学报, 2017, 29(1): 45-51.
XING Y, FAN W, TAN J Q, et al. A C2-Continuous unit quaternion interpolatory spline curve[J]. Journal of Computer-aided Design & Computer Graphics, 2017, 29(1): 45-51. DOI: 10.3969/j.issn.1003-9775.2017.01.006. |
| [9] |
虞铭财, 杨勋年, 汪国昭. 高阶连续的单位四元数插值曲线[J].
计算机辅助设计与图形学学报, 2005, 17(3): 437-441.
YU M C, YANG X N, WANG G Z. Interpolation of unit quaternion curve with high order continuity[J]. Journal of Computer-aided Design & Computer Graphics, 2005, 17(3): 437-441. DOI: 10.3321/j.issn:1003-9775.2005.03.010. |
| [10] |
吴玉香, 王鹏. 基于曲线长度自调整速度方程的非均匀有理B样条插补算法[J].
计算机集成制造系统, 2019, 25(9): 2256-2264.
WU Y X, WANG P. NURBS interpolation algorithm of self-adjusting feed-rate equation based on curve length[J]. Computer Integrated Manufacturing Systems, 2019, 25(9): 2256-2264. |
| [11] |
刘斯亮, 程良伦. 大曲率船体外板水火加工机器人运动轨迹优化研究[J].
广东工业大学学报, 2017, 34(1): 84-89.
LIU S L, CHENG L L. A research of motion trajectory optimization for large curvature of ship hull plate processing line robot[J]. Journal of Guangdong University of Technology, 2017, 34(1): 84-89. DOI: 10.12052/gdutxb.150149. |
| [12] |
凌冠耀. 六关节喷涂机器人的位姿规划算法研究[D].广州: 广东工业大学, 2018.
|
| [13] |
高伟强, 江小成, 刘汝发, 等. 基于多项式的S曲线加减速运动控制算法构建[J].
机床与液压, 2019, 47(4): 124-128.
GAO W Q, JIANG X C, LIU R F, et al. Construction of motion control algorithm for S-shaped curve acceleration and deceleration based on polynomial[J]. Machine Tool & Hydraulics, 2019, 47(4): 124-128. |
| [14] |
秦霞, 李德钊, 邓华. 基于NURBS曲线的工业机器人位置插补算法研究[J].
制造业自动化, 2018, 40(4): 67-72.
QIN X, LI D Z, DENG H. Research on position interpolation algorithm of industrial robot based on NURBS curve[J]. Manufacturing Automation, 2018, 40(4): 67-72. DOI: 10.3969/j.issn.1009-0134.2018.04.017. |
| [15] |
岳晴晴, 林明, 林永才. 基于NURBS算法的工业机器人轨迹规划研究[J].
机床与液压, 2019, 47(9): 28-32, 71.
YUE Q Q, LIN M, LIN Y C. Research on Trajectory Planning of Industrial Robot Based on NURBS Algorithm[J]. Machine Tool & Hydraulics, 2019, 47(9): 28-32, 71. DOI: 10.3969/j.issn.1001-3881.2019.09.006. |
 2020, Vol. 37
2020, Vol. 37

