光子晶体是一种由不同介电常数的材料组成并在空间中呈周期性分布的微型结构,在1987年由E.Yablonovitch[1]提出。同年间,S. John[2]又提出光子能带结构理论。光子晶体存在能带带隙,而频率处于带隙中的光子将无法传播,此特性与半导体特性相似,从而达到控制光传播的作用。因此,光子晶体的应用价值和应用前景非常广阔。如制作太赫兹频段器件[3]、光滤波器件[4],设计全向反射镜[5]、超宽频带天线[6],或是应用在太阳能能源领域[7]。
光子晶体在自然界中的存在极少,通常通过人工制备,其制备方法包括机械制备法[8]、多光束激光全息光刻法[9]、化学刻蚀法[10]、胶体自组装密堆积法[11]等。其中激光全息干涉法是最为有效的方法之一,通过多束干涉激光干涉成有效的光子晶格。其主要原理是光折变效应,当光束入射光子晶体时,光束诱导光子晶体折射率发生变化。光子晶体是一种光敏感材料,采用周期干涉光照射背景光子晶体时,即形成光子晶格。当需要调节光子晶格的参数时,只需要调节干涉激光的参数,例如入射角、方位角、相位等等。其较于其他制备光子晶体的方法,具有参数可调、成本低、制备效率高等优点[9,12-15]。
如果直接进行实验研究,效率往往很低,因此在进行实验之前,理论的计算仿真必不可少。如今针对光学理论计算仿真的软件较多,在光子晶格工作中常使用Matlab进行数值仿真[16-18],但Matlab软件对每次计算都需要重新进行一系列的代码编辑,因此需要将功能集成化。本文使用Matlab GUI(Graphic User Interface)设计了一个基于涡旋光模拟仿真多束光束干涉形成光子晶格的软件,该软件对于仿真螺旋光子晶格类型结构拥有干涉方法新颖、可调参数多、用户交互方式丰富的优势。通过调节输入干涉光束参数,一键生成对应的二维或三维晶格,操作简单,结果直观,不仅保留了仿真优势,降低了使用难度,而且相对于单一的数值模拟而言集成了许多用户功能。
在本文的第一部分,以7束光干涉形成纵向螺旋的光子晶格为例,构建了多光束干涉的理论模型;第二部分,结合GUI功能的说明与展示,实验分析了上述模型中干涉光束的不同参数对光子晶格影响;最后一部分是对分析内容的总结。
1 干涉理论模型满足一定条件的两束光波在空间中相叠加后某些点的振幅加强而某些点的振幅减弱,形成光强分布规则的现象称为光的干涉。自托马斯·杨(Thomas Young)通过杨氏双缝干涉发现光的干涉性质至今,光的干涉在各个行业都有广泛的应用。而全息干涉法则是最为常见的光干涉应用。
全息干涉法中,通过若干光束在空间发生干涉后,形成新的干涉光波,由于光波往往具有周期性的结构,通过干涉光波与介质的相互作用,即可在材料中形成空间周期性的折射率变化的微纳结构。同时,通过对输入光束参数的更改,可以实现对于不同光子晶体结构的设计。多光束干涉理论数学模型基于光的电磁理论,对于一般光束而言,其光场E可由式(1)表示。从式(1)可以看出,光场的分布是关于时间
| $E = {A_0}\cos ({\omega }t - {\vec k} \cdot \vec r + {\phi })\hat e$ | (1) |
涡旋光是一种具有相位结构的特殊光场,其光场E如式(2)所示,式中
| $E(\vec r ,\phi ,z) = {E_0}(\vec r ,\varphi)\exp ( - {\rm{i}}l\varphi )\exp ( - {\rm{i}}kz)$ | (2) |
多光束干涉理论在现在已经非常成熟,早已推导出有相应的干涉理论公式。现假设有若干光束相互干涉,则干涉结构光强分布关系式如式(3)所示。从式(3)可以看出,影响干涉结构光强分布的参数有各光束的入射角度
| $I\left( {\vec r} \right) \!= \!\! \sum\limits_{i = 1}^N {\left( {\frac{1}{2}{E_i}^2(\vec r) +\!\! \sum\limits_{j > 1}^N {{E_i}{E_j}{\hat e_{ij}}} \cos \left( {\left( {{{\vec k}_i} - {{\vec k}_j}} \right) \cdot \vec r +\! ({\phi _i} \!-\! {\phi _j})} \right)} \right)} $ | (3) |
多光束干涉成光子晶格的理论模型如图1所示,干涉模型以涡旋光束
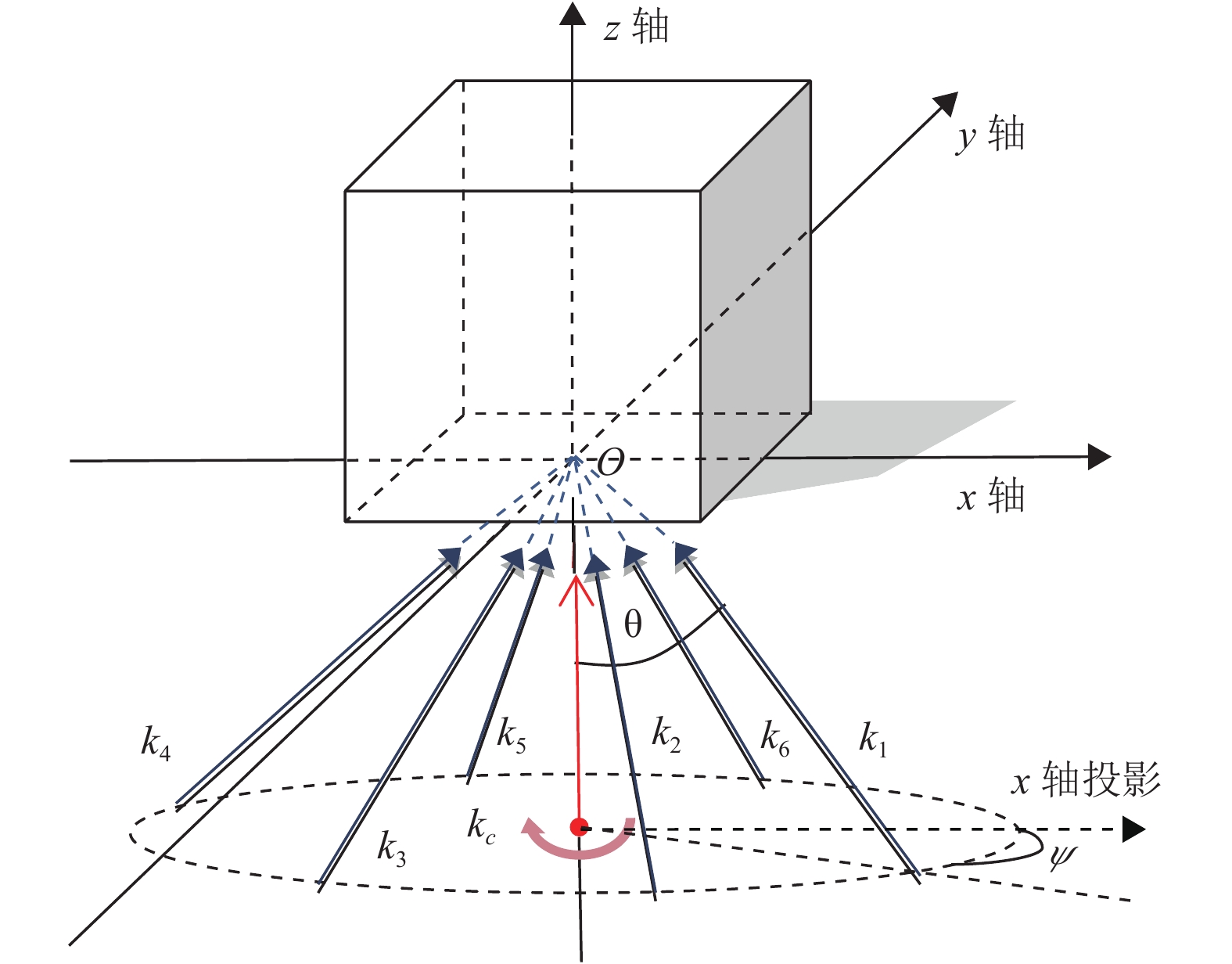
|
图 1 基于涡旋光束的(6+1)束光干涉模型 Figure 1 Interference model of 6+1 beam based on vortex beam |
本文采用Matlab软件进行计算机模拟仿真并进行GUI界面设计。如图2所示,不同的颜色区域表示不同的光场强度。仿真界面包括干涉参数设置、仿真图像显示、用户处理几个部分。使用者对光束数目、偏向角、偏振度(以琼斯矩阵表示)、光束振幅强度、初始相位、入射角度以及波长、曝光阈值等参数进行设置,即可实现不同的光子晶体结构的仿真,并且可对图像以及输入的数据进行保存等操作。
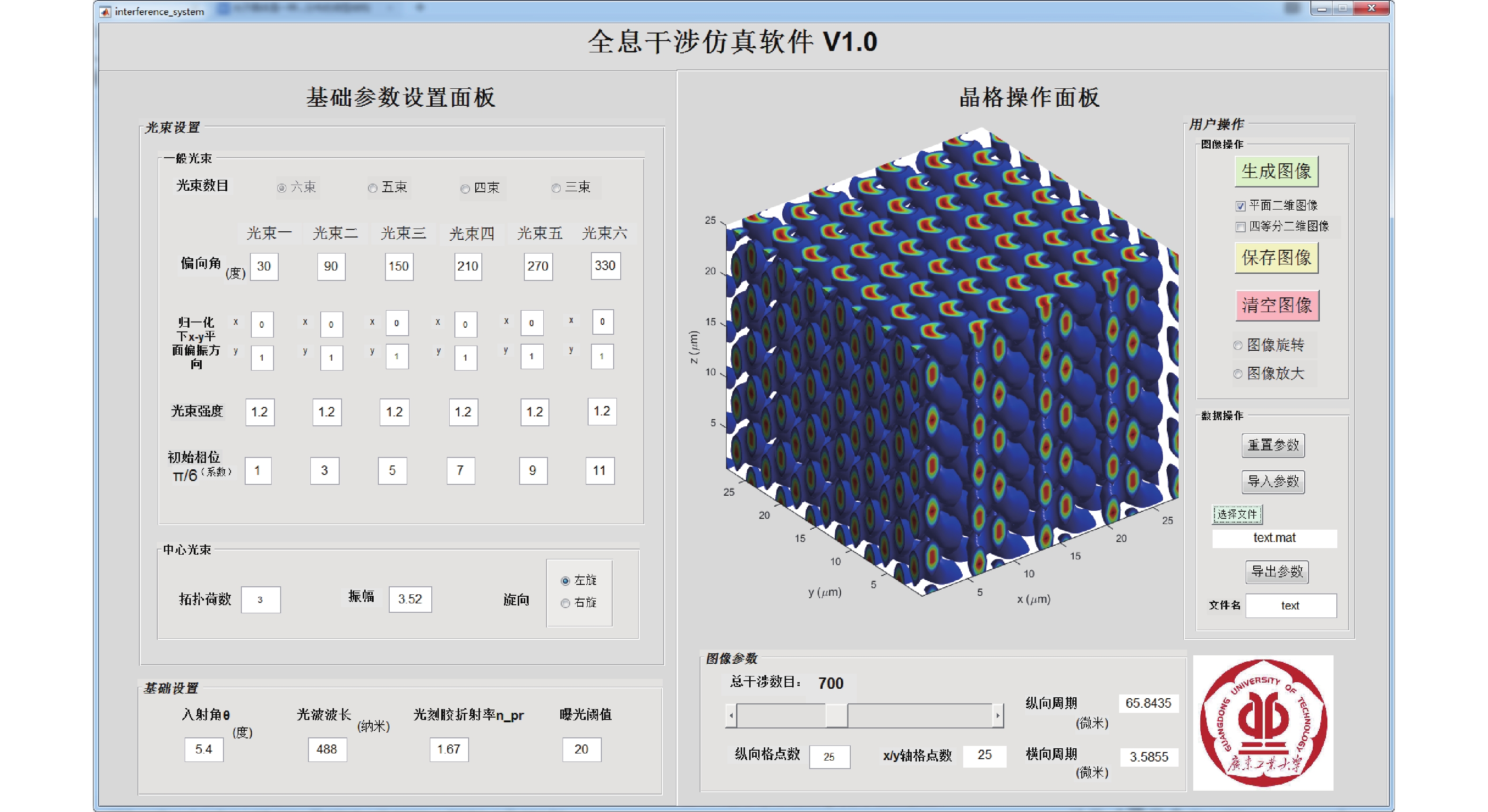
|
图 2 多光束干涉仿真GUI界面截图 Figure 2 GUI interface of Multi-beam interference simulation |
在上述的干涉理论模型中,若无中心光束的伞状分布干涉往往会形成二维平面上单调的阵列型干涉图样;而存在中心光束时,干涉光强分布在纵向上也会存在周期性变化,下面以无中心光束的6束光干涉和添加了中心涡旋光束的6+1束光干涉生成的光子晶格为例进行仿真。
由图3(Ⅰ-Ⅱ)可以看出,无中心光束下的6束光干涉光强在
| 表 1 光束设置参数 Table 1 Beam setting parameters |

|
图 3 中心光束对干涉的影响仿真图,其中(I)为6束光干涉的图像,(II)为6+1束光干涉的图像 Figure 3 The simulation figures of the influence of the central beam on the interference, in which (I) is 6-beam interferometric images, and (II) is 6+1-beam interferometric images |
光束的方位角指各干涉光束在
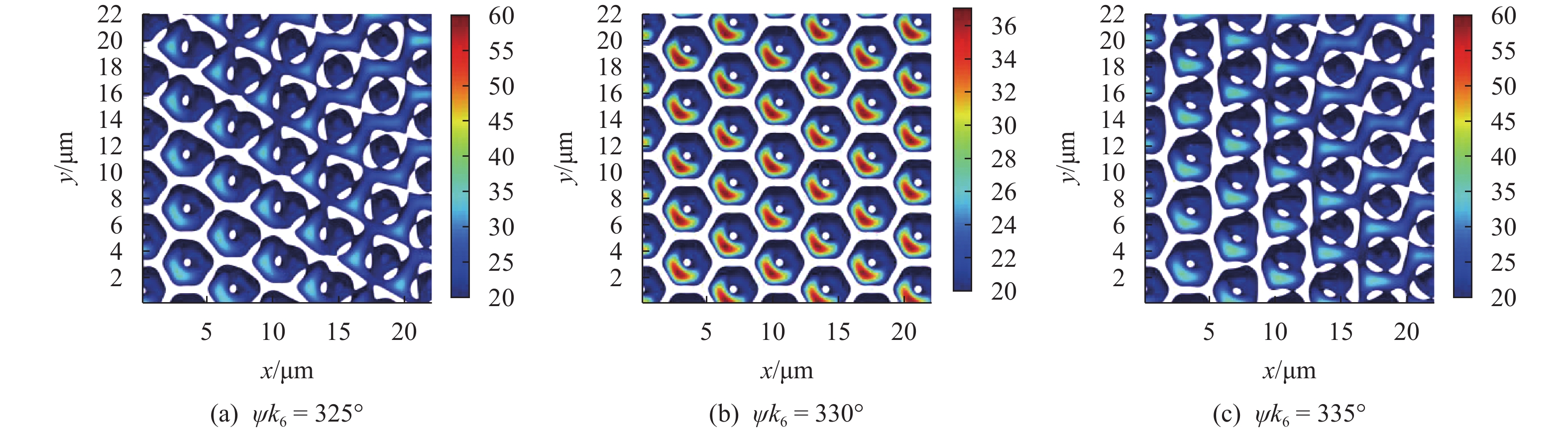
|
图 4 不同方位角下光子晶格仿真图 Figure 4 Optical lattice simulation images at different azimuths |
偏振度对光子晶格的影响主要表现在影响光强极值分布位置的改变,因此会对干涉图像的对比度产生影响。基于表1中参数,保持光束
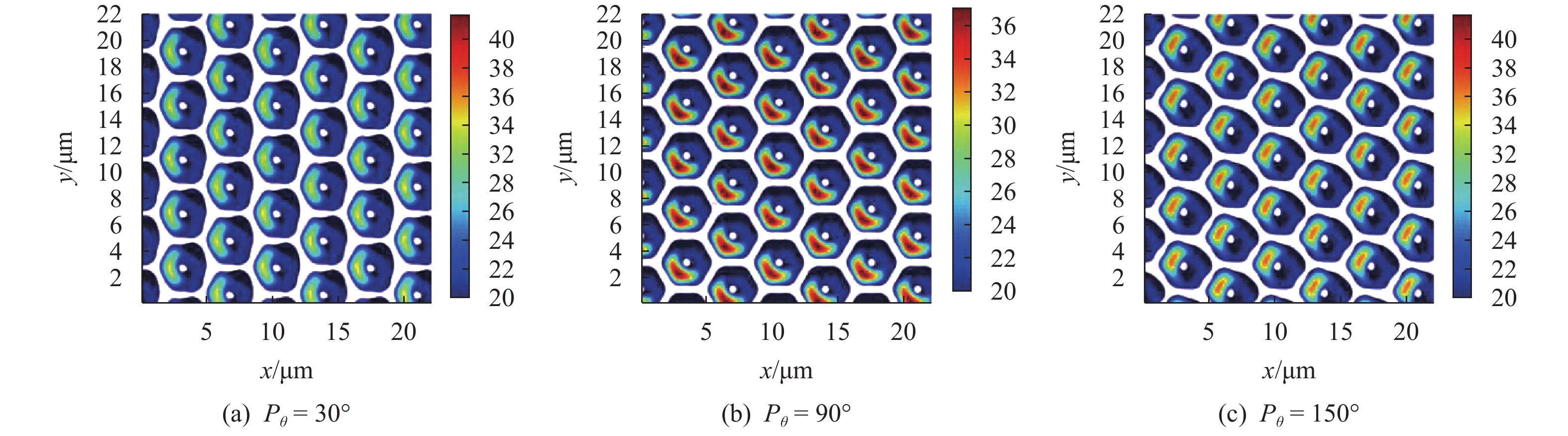
|
图 5 不同偏振度下光子晶格仿真图 Figure 5 The simulations of optical lattices with different degrees of polarization |
入射角
| ${T_{\rm{v}}} = \frac{\lambda }{{2 \times n \times {{\sin }^2}(\theta /2)}}$ | (4) |
| ${T_{\rm{h}}} = \frac{\lambda }{{\sin 60^\circ \sin {\theta } \times n}}$ | (5) |
由式(4-5)可知,当波长λ一定时,入射角的增大会使螺距及螺径变小(即纵向周期和横向周期变小)。基于表1中参数,令拓扑荷数

|
图 6 入射角度变化对光子晶格影响仿真图,(I)、(II)分别是入射角
|
如果螺距过长,往往不能很好地发挥螺旋光子晶格特性,而如果通过入射角、波长来改变螺距又会使螺径的大小同时发生改变。基于涡旋光干涉的光干涉模型可以在调节涡旋光束拓扑荷数参数时仅对螺距进行改变。由式(2)可知,若保持涡旋光电场的相位因子

|
图 7 拓扑荷数对螺旋光子晶体的影响,(I)、(II)分别是拓扑荷数
|
本文提出了一种基于Matlab GUI的三维光子晶格模拟方法,并通过对涡旋光参数、方位角、光束偏振度、入射角等参量对光子晶格产生的影响进行了仿真分析,由结果可知,中间涡旋光束的添加可以生成螺旋光子晶格并为其添加一个纵向周期,改变涡旋光拓扑荷数可以进行晶格螺距的调节;光束的方位角影响了光子晶格的规则性和对称性;光束偏振度影响了干涉光强分布情况进而影响光子晶格形状;增大环绕光束的入射角会使螺旋光子晶格螺距、螺径减小,使结构更紧密。通过该研究不仅证明了基于Matlab GUI的计算机仿真方法的灵活高效,并对入射光束参量对光子晶格的影响有更清晰的认知,对实际研究制备螺旋光子晶格或者一般光子晶格结构具有重要参考意义。
| [1] |
YABLONOVITCH E. Inhibited spontaneous emission in solid-state physics and electronics[J].
Physical Review Letters, 1987, 58(20): 841-844.
|
| [2] |
JOHN S. Strong localization of photons in certain disordered dielectric superlattice[J].
Physical Review Letters, 1987, 58(23): 2486-2489.
DOI: 10.1103/PhysRevLett.58.2486. |
| [3] |
陈麟, 杨冰洋, 雍有, 等. 太赫兹金属光子晶体结构研究[J].
光学仪器, 2018, 40(4): 47-55.
CHEN L, YANG B Y, YONG Y, et al. Study of terahertz metallic photonic crystals[J]. Optical Instruments, 2018, 40(4): 47-55. |
| [4] |
吴立恒, 王明红. 基于微谐振器的光子晶体滤波器工作特性[J].
激光与光电子学进展, 2018, 55(2): 254-262.
WU L H, WANG M H. Operating characteristics of photonic crystal filters based on micro resonators[J]. Laser & Optoelectronics Progress, 2018, 55(2): 254-262. |
| [5] |
ZHENG X Z, YANG Y, CHEN S F, et al. Slow photons for solar fuels[J].
Chinese Journal of Catalysis, 2018, 39(3): 379-389.
DOI: 10.1016/S1872-2067(17)62930-9. |
| [6] |
林斌, 林智鹏. 梯形多缝−六边形阵列复合超宽频带天线[J].
电子产品世界, 2018, 28(25): 35-37.
LIN B, LIN Z P. Trapezoid multi slit-hexagonal array composite ultra wide frequency band antenna[J]. Electronic Engineering & Product World, 2018, 28(25): 35-37. |
| [7] |
ZHANG H F, LIU S B. Enhanced the tunable omnidirectional photonic band gaps in the two-dimensional plasma photonic crystals[J].
Optical and Quantum Electronics, 2016, 48(11): 508-511.
DOI: 10.1007/s11082-016-0782-9. |
| [8] |
YABLONOVITCH E, LEUNG K M. Photonic band structure: non-spherical atoms in the face-centered-cubic case[J].
Physica B, 1991, 175(1-3): 81-86.
DOI: 10.1016/0921-4526(91)90696-C. |
| [9] |
SOSHU K, KOKI N, SHOICHIRO K, et al. Ultraviolet laser lithography of titania photonic crystals for terahertz-wave modulation[J].
Materials, 2018, 11(5): 835-849.
DOI: 10.3390/ma11050835. |
| [10] |
MASUDA H, YAMADA H, SATOH M, et al. Highly ordered nanochannel-array architecture in anodic alumina[J].
Applied Physics Letters, 1997, 71(19): 2770-2772.
DOI: 10.1063/1.120128. |
| [11] |
KRAUSS T F, VOGELE B, STANLEY C R, et al. Wave guide micro-cavity based on photonic micro-structures[J].
IEEE Photonics Technology Letters, 1997, 9(2): 176-178.
DOI: 10.1109/68.553082. |
| [12] |
WANG X, TONG H, PANG Z, et al. Theoretical realization of three-dimensional nanolattice structure fabrication based on high-order waveguide-mode interference and sample rotation[J].
Optical and Quantum Electronics, 2019, 51(2): 38-45.
DOI: 10.1007/s11082-019-1759-2. |
| [13] |
IVANA L, AGATA L, DUSAN P, et al. 2D periodic structures patterned on 3D surfaces by interference lithography for SERS[J].
Applied Surface Science, 2018, 461(1): 171-174.
|
| [14] |
YOSHIKI N, YOSHIDA M, KAZUHITO O, et al. Fabricating a regular hexagonal lattice structure by interference pattern of six femtosecond laser beams[J].
Applied Surface Science, 2017, 417: 69-72.
DOI: 10.1016/j.apsusc.2017.03.236. |
| [15] |
吕浩, 尤凯, 兰燕燕, 等. 非对称光束干涉制备二维维纳光子结构研究[J].
物理学报, 2017, 66(21): 217801.
LYU H, YOU K, LAN Y Y, et al. Fabrication of two-dimensional micro-nano photonic structures by symmetry-lost beams interference[J]. Acta Physica Sinica, 2017, 66(21): 217801. DOI: 10.7498/aps.66.217801. |
| [16] |
梁文耀, 谭希超, 刘基, 等. 基于激光全息法和泰伯效应的光学晶格制作与精确测量实验教学[J].
实验室研究与探索, 2019, 38(6): 144-148.
LIANG W Y, TAN X C, LIU J, et al. Experimental-teaching about fabrication and accurate measurement of optical lattice based on laser holography and Talbot effect[J]. Research and Exploration in Laboratory, 2019, 38(6): 144-148. DOI: 10.3969/j.issn.1006-7167.2019.06.036. |
| [17] |
LOWELL D, GEORGE D, LUTKENHAUS J, et al. Flexible holographic fabrication of 3D photonic crystal templates with polarization control through a 3d printed reflective optical element[J].
Unt Scholarly Works, 2016, 7(7): 128.
|
| [18] |
GEORGE D, LUTKENHAUS J, LOWELL D, et al. Fabrication of 4, 5, or 6-fold symmetric 3D photonic structures u-sing single beam and single reflective optical element based holographic lithography[J].
Proceedings of SPIE-The International Society for Optical Engineering, 2015, 9350: 93501K-93501K-9.
|
| [19] |
LEIBOVICI M C R. Pattern-integrated interference lithography for two-dimensional and three-dimensional periodic-lattice-based microstructures[D]. Georgia, Atlanta: Georgia Institute of Technology, 2015.
|
 2020, Vol. 37
2020, Vol. 37

