近20年来,随着互联网应用的不断深入,网络攻击给用户造成的损失日益严重。为了能更好地保护用户,降低攻击造成的损失,入侵检测系统(Intrusion Detection System, IDS)被提出以识别恶意流量,检测网络攻击。为了更好地监控网络流量,应对未知攻击类型的威胁,许多机器学习算法,如支持向量机(Support Vector Machine, SVM)[1]、随机森林(Random Forest, RF)、神经网络等被应用到IDS研究中以期取得更优的检测效果。
一方面,各类算法自有其优缺点,如一些算法可能对某一攻击类型来说效果不错,但对其他类型攻击的检测效果不佳[2];另一方面,许多研究专注于提高整体的检测精度,而对小样本(攻击样本)的检测效果不佳[3]。但实际上,考虑到攻击样本相对正常样本极端不平衡的情况,更应该关注入侵检测分类器对攻击样本的检测能力[4]。
一些学者提出结合不同算法的混合入侵检测模型,尝试在提高整体检测率的同时,降低误报率,如滕少华等[5]提出模糊C均值聚类算法及决策树(C4.5算法)相结合的入侵检测模型,较好地克服两者缺点,以获得检测效率与精度的提高;Hwang等[6]提出将黑名单、白名单与SSVM (Smooth Support Vector Machine)分类器相结合,以黑名单进行初筛,再依靠白名单来降低误报达到降低误报率(False Positive Rate, FPR)的目的;Li等[7]提出的模型将待测程序与攻击程序集合进行匹配,如果待测程序与攻击程序集合未精确匹配,则再由k-最近邻(k-Nearest Neighbor, kNN)算法进行异常检测;Mairal等[8]提出的混合模型以多个分类器多层级联进行检测,虽然增加了额外的开销,但显著提高了入侵检测系统的检测精度。
本文提出一种基于小样本纠错的多层入侵检测分类模型,该模型尝试在正交投影降维分类算法[9]的研究基础上,结合装袋算法(Bootstrap Aggregating, Bagging)及错分纠错策略,实现入侵检测。本文用NSL-KDD数据集进行实验,验证了该模型的效果,在整体召回率及准确率上提升明显,对于DoS、Probe、R2L类攻击样本的检测能力相对较佳。
1 相关工作针对入侵检测这一课题,许多学者尝试基于近年来出现的各种机器学习算法,如SVM,决策树,极限学习机(Extreme Learning Machine, ELM),无监督学习等做了大量工作,相关研究也成为入侵检测研究的主流方法。
由于攻击样本一般在整个网络流量中占比很小,这就造成了样本不平衡的问题,攻击样本一般远小于正常流量。然而,作为少数类的攻击样本往往携带重要信息,传统分类算法难以从极有限的样本中得到有效训练,如何处理不平衡数据集是当前入侵检测领域的一大难题[10]。对此,部分学者[3]提出欠采样、过采样等抽样方法以平衡数据集,大量文献对欠采样、过采样、合成少数类过采样(Synthetic Minority Oversampling Technique, SMOTE)等[11]方法进行了研究。
传统简单的随机欠采样方法,简单舍弃数据,常丢失多数类样本中的有用信息而效果不佳。Haixiang等[3]基于527篇相关论文对不平衡数据进行分类问题的策略进行了总结,提出一种处理不平衡数据集学习的通用框架。Cao等[12]提出基于时间相关性对样本聚类的过采样方法,其相比非过采样方法具有一定优势。Nekooeimehr等[13]提出一种基于不平衡数据集的自适应半监督加权过采样方法,该过采样方法采用半监督层次聚类对少数类样本进行自适应聚类,实验证明该方法对多数数据集效果明显。Sun等[2]提出基于一种新的集成方法,将不平衡数据集转换为多个均衡的数据集,在此基础上训练基分类器,最后将分类结果整合,但在实际操作中,该欠采样策略可能使得多数类样本的有用数据丢失。Cateni等[11]将过采样与欠采样方法相结合,提出一种重采样方法,在不大量增加合成样本的情况下,获取平衡数据集,以便于分类器学习。
Reunig等[14]提出局部离群点搜索方法,其基于局部离群因子(Local Outlier Factor, LOF)构造了用于入侵检测的LOF模型;Ingre等[15]构造了人工神经网络模型。由于传统机器学习中单分类器自身的局限性,其在IDS的运用中,一定程度上已达到瓶颈,面临难以平衡检测率与误报率的困境。多分类器适时地被提出,如何有效构建混合模型成为该领域研究热点之一。
多数单分类器的检测方法,如SVM、决策树、神经网络等,往往能很好地处理平衡数据集的问题,但面临不平衡数据集时不易优化。实际上,这些分类器设计初衷是优化整体性能,而往往在少数类样本中表现不佳,导致在处理入侵检测问题时,对攻击类别的处理考虑不佳,如决策树的少数类类别样本可能在剪枝操作中被去除。对此,多分类器如集成分类器,混合分类器等被提出。
在入侵检测领域中,集成分类器如Bagging, Boosting等被提出,如胡臻伟等[16]针对单分类器与自适应增强算法(Adaptive Boosting, AdaBoost)进行了比较,相较kNN、ID3 (Iterative Dichotmizer 3)决策树等,Adaboost将多个弱分类器集成为强分类器,以较长的训练时间为代价取得了不错的精确率及召回率。Gaikwad等[17]在常用的Bagging模型的基础上提出一种基于剪枝算法(Reduced Error Pruning Tree, REPTree)的Bagging集成方法,降低了模型的构建时间复杂度并实现了较低的误报率。Salo等[18]提出一种基于SVM、kNN和多层感知机(Multi-Layer Perceptron, MLP)算法的集成分类模型,该模型基于IG-PCA (Information Gain-Principal Component Analysis)算法进行降维,实验证明,该模型相较于单分类器拥有较低的误报率,但难以满足实时的数据流检测需求。
相较于集成分类器,混合分类器期望结合异常检测和误用检测取长补短,提高准确率的同时减少误报,即某一分类器的输出是另一分类器的输入,组成混合分类器,其组合策略对模型检测效果影响较大。Jiang等[19]提出基于C4.5决策树和朴素贝叶斯(Naive Bayes, NB)的混合模型,虽然相比传统C4.5、NB单一算法提高了攻击类别的分类准确率,但并未考虑各自分类器的缺点,即决策树的过拟合问题及NB模型的条件独立性假设(即每个变量的概率分布相互独立)。对此,姚潍等[20]针对上述基于C4.5和NB的混合模型进行改进,提高了攻击类别的检测精度,取得了不错的结果。郭春等[21]提出一种两层入侵检测模型:对降维后的样本先通过基于样本簇中心位置变化的异常检测分类器初筛,然后用kNN进行精筛以降低误报率。Latah等[22]结合kNN及ELM算法,提出用于软件定义网络的多层入侵检测模型,但误报率较高。Horng等[23]提出的攻击检测模型,结合了SVM及层次聚类算法,其对DoS及Probe攻击样本的检测效果较佳,但对U2R及R2L攻击的检测效果不佳。
在入侵检测时间复杂度方面,Pajouh等[24]提出基于NB及CF-kNN的检测模型;Kim等[25]提出基于C4.5及SVM的算法模型,显著减少训练及测试时间,仅为传统模型的50%和60%;滕少华等[9]采用基于正交投影的降维分类方法对纸币真伪等不同数据集进行了分类,该算法性能优势明显,相较于SVM等算法,分类准确率差别较小,且速度优势明显,十分适用于入侵检测等实时性要求高的场景。
最后,由于样本特征维数的选择对于入侵检测系统的检测时间及性能影响很大,在诸如NSL-KDD等入侵检测数据集中,构建表现优异的分类模型并不需要全部的特征维度,删除部分冗余特征反而有利于提高模型的响应时间及准确率[26]。针对这一问题,文献[27]针对不同特征选择方法进行了比较,并指出特征选择的方法主要分为如下3种:Filter过滤器方法、Wrapper包裹式方法及Embedded嵌入式方法。
不同的特征选取方法对模型时间复杂度及检测效率影响很大,一些学者对此进行了较全面的比较[26,28-29]。Darshan等[30]比较了区分特征选择,互信息,类别比例差及Darmstadt标引(Darmstadt Indexing Approach, DIA)4种方法,实验表明区分特征选择及互信息方法在检测准确率上效果更优。Aljawarneh等[31]在预处理的基础上基于训练样本的信息增益(Information Gain, IG)对数据集进行了特征选择,提高了混合模型的准确率并减少了检测时间。
实际上,在高维数据集上进行入侵检测分类模型的构建,特征选择是十分必要的,其常常与入侵检测分类模型相结合,表现优异的特征选择方法能使分类模型的构建效果更佳。
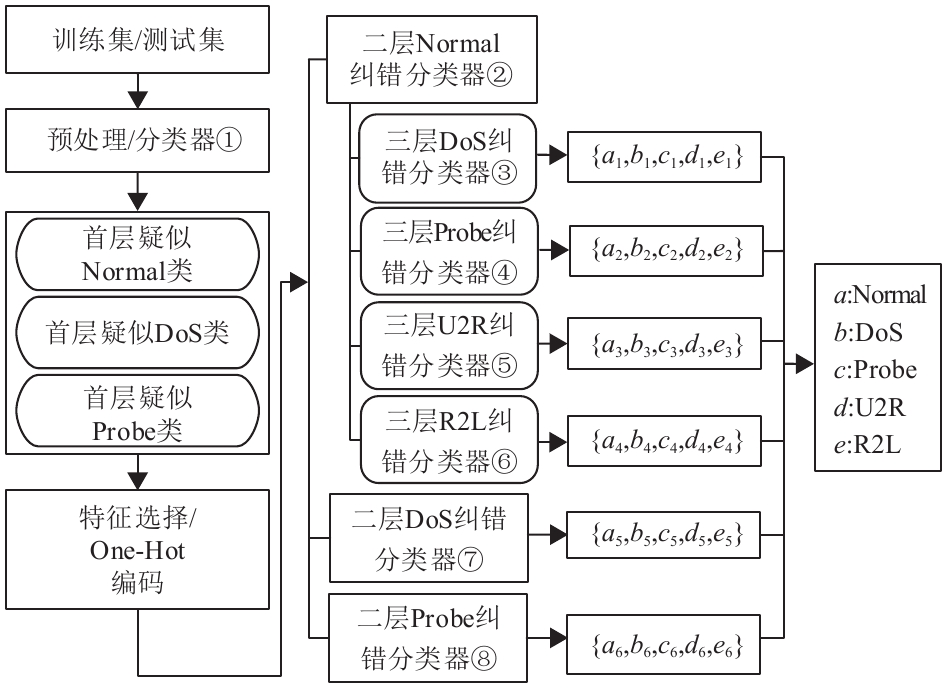
2 小样本纠错多层入侵检测分类模型针对单分类器对攻击样本学习效果不佳的问题,本节对基于小样本纠错的多层入侵检测分类模型进行建模。该模型结合正交投影降维分类算法、RF及基于LibSVM[32]的Bagging算法构建入侵检测混合分类器,如图1所示。
|
图 1 混合分类器示意图 Figure 1 Overall structure of the hybrid classifier |
如图1所示,在初筛部分,使用基于正交投影的降维分类算法构建分类器①进行分类;随后对原训练集的攻击样本进行扩充。第二步,构建第二层的纠错分类器,进行第一次纠错,其中分类器②使用RF算法,分类器⑦⑧使用以SVM算法为基分类器构建的Bagging集成算法。第三步,使用SVM算法构建第三层的纠错分类器③④⑤⑥,进行第二次纠错;最后,输出待测样本的分类结果。
2.1 第一层正交投影降维分类在本模型中,采用NSL-KDD的训练集作为训练样本训练正交投影降维分类器[9],使用NSL-KDD_Train+作为训练集,简记为Train,NSL-KDD_Test+数据集作为测试集,简记为Test,该分类器将待测样本分类为疑似Normal、DoS、Probe 3类,其算法过程如表1所示。
| 表 1 基于正交投影的降维分类算法 Table 1 Classification method based on dimension reduction algorithm |
首先,使用训练集中的Normal、DoS、Probe样本对第一层分类器进行训练,然后以该分类器将训练集Train划分为疑似Normal、疑似DoS及疑似Probe类,记为
其中,仅使用训练集中的Normal、DoS、Probe样本对第一层分类器进行训练。这样,当使用第一层分类器对完全训练集或测试集进行分类时,当中的U2R及R2L样本就会分散到到第一层的疑似Normal、疑似DoS及疑似Probe类中,这是本模型有意的特殊设计,被分散的U2R及R2L样本将在后面层进行处理。本层分类器起到了快速初筛,以及数据划分的作用,为后面各层多个分类器的并行运算打下基础。用于训练的3类数据,数据量级一致而且足够大,一方面能加快训练过程及避免过拟合为降低分类类别数大造成的算法过拟合,另一方面,将特征不够单一的攻击类别分离后,提升了其特征的特异性。
2.2 第二层纠错分类本节将在第一层降维分类的基础上构建第二层纠错分类器,该部分为第一次纠错。在对待测样本的检测中,可将第二层的3个纠错分类器并行执行,互不干扰,并提升模型建立的效率,缩短检测时间。
在第二层纠错分类中,将正交投影分类结果为Normal、DoS及Probe的训练子集和测试子集,分别组成3个子分类器的训练子集及测试子集,先对训练子集及测试子集进行预处理,为错分样本的进一步纠错做准备。预处理过程主要包括:
a) 依IG值进行特征选择:为降低分类器的属性维数,基于IG值将原数据集中的41个属性缩减为9维。本文利用weka中的IG计算方法,对训练集进行特征选择,在Aljawarneh等[31]基于IG理论对NSL-KDD数据集特征选择的基础上,选择其中9维属性(选择IG值大于0.4的属性)分别是:protocol_type,src_bytes,service,dst_bytes,flag,diff_srv_rate,same_srv_rate,dst_host_srv_count,dst_host_same_srv_rate。
b) 归一化:将所有数值型属性数据缩放至[0,1]区间
| $ X' = \frac{{X - {X_{\min}}}}{{{X_{\max}} - {X_{\min}}}} $ | (1) |
c) 非数值型数据进行编码:在NSL-KDD数据集中,存在3种非数值型属性,分别是protocol_type,service及flag。在这一阶段,对训练子集及测试子集中的样本的这3个属性,进行One-Hot编码(如protocol_type中的tcp,udp及icmp被分别编码为[1, 0, 0],[0, 1, 0],[0, 0, 1])。
由于Normal样本在
第二层Normal纠错分类器建模过程如下:
d) 抽取训练集Train中的R2L样本,合并至
e) 将
f) 从
g) 使用
h) 使用网格搜索算法搜索SVM算法的最佳参数(C,γ)(其中C为惩罚因子,γ为核参数)。
上述分类过程中,使用排除Normal样本的训练集
在上述分类过程中,本文利用了RF及SVM算法构建模型,其核函数的引入较好地解决了低维特征空间向高维特征空间映射带来的计算量偏大的问题,使其更具实际意义。
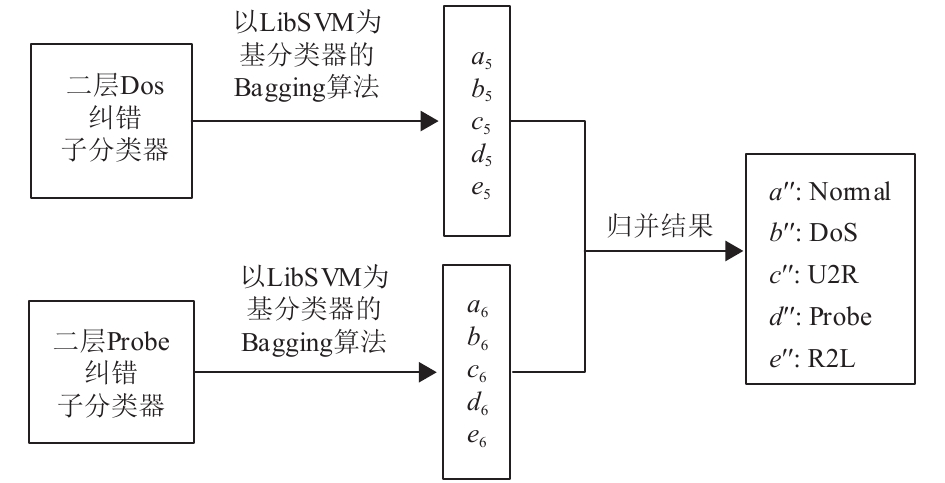
由于构建第二层DoS及Probe纠错分类器部分的训练集
|
图 2 第二层Probe及DoS纠错分类器示意图 Figure 2 The second layer self-correction classifiers’ structure |
由于第二层的DoS纠错分类器⑦及Probe纠错分类器⑧经一次纠错后分类效果较佳,不必另外构建第三层的纠错分类器,故该层只由第二层Normal纠错分类器②的基础上构建分类器,再次进行纠错。其建模过程如下:
a) 依次选取
b) 对于训练子集中样本过少的类别,抽取
c) 对各个分类器的训练子集进行小样本扩充(倍增)。
d) 基于c)训练子集使用SVM算法构建第三层的4个纠错分类器,对各测试子集进行分类。
e) 使用网格搜索算法搜索各算法的最佳参数(C, γ)。
如图2、图3所示,测试子集中的待测样本经过第二层DoS纠错分类器及Probe纠错分类器的检测后,被分类为Normal、DoS、Probe、U2R、R2L这5类,最后将分类结果与第二层Normal纠错分类器中的所有测试样本及分类结果归并得到最终结果,即
| $\begin{array}{*{20}{l}} {\rm{Normal:}}\;a = \left\{ {a' {\bigcup {a''} } } \right\} = \{ {a_i}|i \in \left[ {1,6} \right]\} \end{array}$ | (2) |
| $ \begin{array}{*{20}{l}} {{\rm{DoS}}:b = \left\{ {b'\bigcup {b''} } \right\} = \{ {b_i}|i \in \left[ {1,6} \right]\} \;} \end{array} $ | (3) |
| $\begin{array}{*{20}{l}} {\rm{Probe:}}\;c = \left\{ {c'\mathop {\bigcup {c''} }\nolimits } \right\} = \{ {c_i}|i \in \left[ {1,6} \right]\} \end{array}$ | (4) |
| $\begin{array}{*{20}{l}} {\rm{U2R}}:\;d = \left\{ {d'\mathop {\bigcup {d''} }\nolimits } \right\} = \{ {d_i}|i \in \left[ {1,6} \right]\} \end{array}$ | (5) |
| $\begin{array}{*{20}{l}} {\rm{R2L}}:\;e = \left\{ {e'\mathop {\bigcup {e''} }\nolimits } \right\} = \{ {e_i}|i \in \left[ {1,6} \right]\} \end{array}$ | (6) |
其中式(2)~(6)中,i为整数。
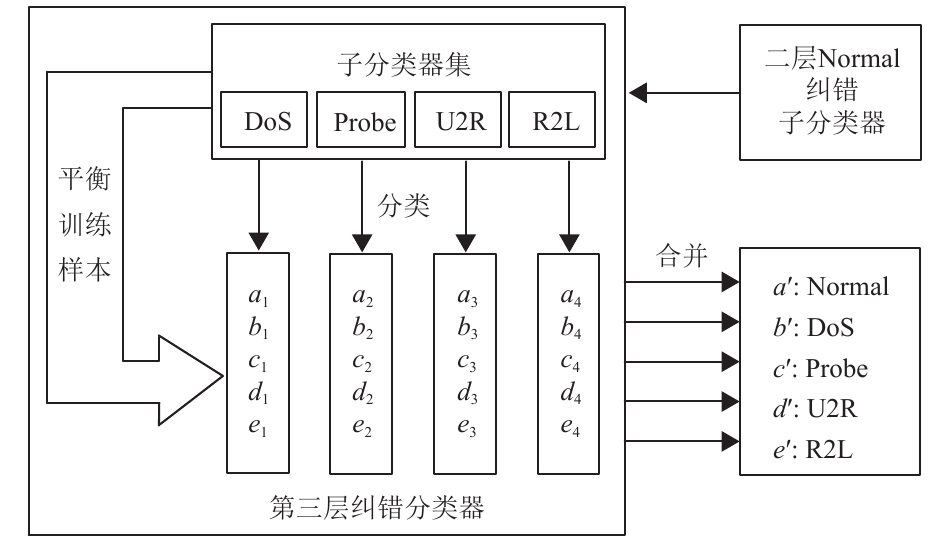
|
图 3 第三层纠错分类器示意图 Figure 3 Structure of the third layer self-correction classifier |
实验环境:Windows7操作系统,weka3.6,JDK1.7,3.2 GHz CPU,16 GB RAM
本文提出的小样本多层纠错模型,针对NSL-KDD数据集进行了实验。作为入侵检测模型应用最广泛的数据集,NSL-KDD数据集较好地解决了KDD99数据集的样本冗余问题,在实验中较具有代表性。NSL-KDD数据集包含125 973个训练样本及22 544个测试样本,其中每一个样本包含41个特征属性及一个类别标签,其特征属性中包括protocol_type,service及flag这3种非数值型属性数据。
为了更好地评估入侵检测分类器的效果,本节选取了准确率(Accuracy,ACC)、误报率(FPR)、精确率(Precision)、召回率(Recall)及F1-Score(F1)作为入侵检测分类器的评价标准。记TP表示正确被分类为攻击的样本数,FP表示正常样本被误分类为攻击的样本数,TN表示正确被分类为正常样本的样本数,FN表示攻击样本被误分类为正常的样本数,各指标计算方法为
| $\text{准确率}:{\rm{ACC = \frac{{TP + TN}}{{TP + TN + FP + FN}}}}$ | (7) |
| $\text{误报率}:{\rm{FPR = \frac{{FP}}{{FP + TN}}}}\qquad\qquad\qquad$ | (8) |
| $\text{精确率}:{\rm{Precision = \frac{{TP}}{{TP + FP}}}}\qquad\qquad$ | (9) |
| $\!\text{召回率}:{\rm{Recall = \frac{{TP}}{{TP + FN}}}}\qquad\qquad\;\;\;\;$ | (10) |
| $F_1-{\rm{Score}}:{F_1} = \frac{{2\left( {{\rm{Precision}}\cdot {\rm{Recall}}} \right)}}{{{\rm{Precision}} + {\rm{Recall}}}}$ | (11) |
本实验在weka3.6环境中进行,其中第三层的子分类器③④⑤⑥采用SVM算法参数设置均为:C1为1.0,γ1为0.2,(a,b,c,d,e)对应权值W1为(1,1,6,6,6)。
第二层DoS纠错分类器⑦和第二层Probe纠错分类器⑧采用以SVM算法为基分类器构建Bagging集成算法。装袋方法Bagging中每次抽样比例为50%,次数为5次;其中,子分类器⑦采用SVM参数设置为:C2为1.0,γ2为0.2,(a5,b5,c5,d5,e5)对应权值W2为(1,1,6,6,6);子分类器⑧采用SVM参数设置为:C3为1.0,γ3为0.2,(a6,b6,c6,d6,e6)对应权值W3为(1,1,3.5,3.5,3.5)。
3.3 实验结果与分析为了更好地评估实验效果,本文选取准确率,误报率,精确率,召回率及F1作为指标进行了对比,各实验结果如下。
表2为训练集Train及测试集Test正交投影分类后的结果,可见Normal样本在第二层的Normal纠错分类器中的占比相当高,在训练集及测试集中分别达到97.26%及67.17%,相对其他类别攻击样本不平衡,这也验证了本文模型中平衡数据集样本的必要性。
| 表 2 正交投影降维分类后的混淆矩阵 Table 2 Confusion matrix of dimension reduction classification method |
表3显示的是本文模型与同类模型的检测结果对比,其中J48是一种基于C4.5实现的决策树算法,RBF-SVM是带径向基核函数的SVM算法。实验结果基于输出样本类别为正常或异常两类对比。可看出,本文模型在ACC及F1上优于其他模型,在Recall上优于ANN、kNN+ELM、RBF-SVM、RF、J48、NB模型,仅次于LOF模型。
| 表 3 五种评判标准实验结果对比 Table 3 Experimental results comparison in five standards |
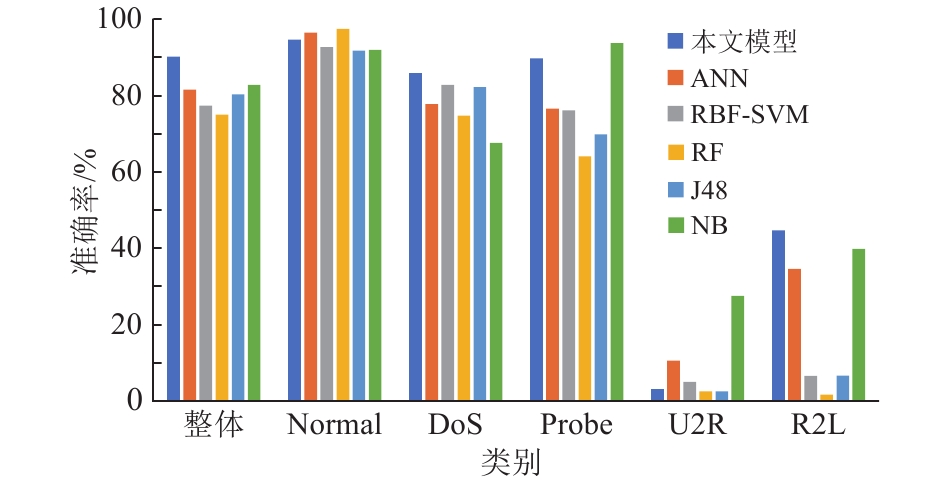
图4显示的是本文多层错分纠错模型与传统机器学习算法在各类别样本的准确率结果对比,其中DoS、Probe、R2L类别的准确率分别达到85.84%、89.76%、44.63%,相较于ANN及RBF-SVM等传统机器学习算法均有一定优势;其中,由于U2R训练样本过稀少等原因,导致分类器训练不足,在对U2R类别的攻击样本的检测上略低于其他算法,但在整体上仍领先于其他对照算法的实验结果。
|
图 4 与传统机器学习算法的准确率对比 Figure 4 Accuracy comparisons with traditional machine learning models |
本文提出了一种基于正交投影的小样本多层纠错分类模型,首先通过正交投影降维分类算法对数据集进行初步划分,然后依据正常样本与攻击样本极端不平衡的特点,对小样本(攻击样本)进行了过采样等处理,尝试解决样本不均衡的问题,再在第二层的3个纠错分类器中实现了对小样本的纠错。该模型在NSL-KDD数据集上的实验结果显示,准确率及
另外,该模型对R2L攻击样本的召回率达到44.67%,这表明,该模型对部分未知攻击类型的样本,也有着不错的泛化能力。在后续研究中,将进一步优化混合分类器算法,优化分类器对U2R攻击样本的训练过程,并进一步降低误报率,以期实现更优的检测效果。
| [1] |
TENG S H, WU N Q, ZHU H B, et al. SVM-DT-based adaptive and collaborative intrusion detection[J].
IEEE/CAA Journal of Automatica Sinica, 2017, 5(1): 108-118.
|
| [2] |
SUN Z B, SONG Q B, ZHU X Y, et al. A novel ensemble method for classifying imbalanced data[J].
Pattern Recognition, 2015, 48(5): 1623-1637.
DOI: 10.1016/j.patcog.2014.11.014. |
| [3] |
GUO H X, LI Y J, JENNIFER S, et al. Learning from class-imbalanced data: review of methods and applications[J].
Expert Systems with Applications, 2017, 73: 220-239.
DOI: 10.1016/j.eswa.2016.12.035. |
| [4] |
TENG S H, ZHANG Z H, TENG L Y, et al. A collaborative intrusion detection model using a novel optimal weight strategy based on genetic algorithm for ensemble classifier[C]//Proceedings of IEEE 22nd International Conference on Computer Supported Cooperative Work in Design (CSCWD). Nanjing, China: IEEE, 2018: 761-766.
|
| [5] |
滕少华, 严远驰, 刘冬宁, 等. 基于 FCM-C4.5 的双过滤入侵检测机制[J].
计算机应用与软件, 2016, 33(1): 307-311.
TENG S H, YAN Y C, LIU D N, et al. A dual filtration intrusion detection mechanism based on FCM and C4.5[J]. Computer Applications and Software, 2016, 33(1): 307-311. DOI: 10.3969/j.issn.1000-386x.2016.01.073. |
| [6] |
HWANG T S, LEE T J, LEE Y J. A three-tier IDS via data mining approach[C]//Proceedings of the 3rd Annual ACM Workshop on Mining Network Data. San Diego, California, USA: ACM, 2007: 1-6.
|
| [7] |
LI Y, LI J L, YUE S J, et al. Research of intrusion detection based on ensemble learning model[J].
Applied Mechanics and Materials, 2013, 336-338(2): 2376-2380.
|
| [8] |
MAIRAL J, BACH F, PONCE J, et al. Online dictionary learning for sparse coding[C]//Proceedings of the 26th Annual International Conference on Machine Learning. Montreal. Quebec, Canada: IMLS, 2009: 689-696.
|
| [9] |
滕少华, 卢东略, 霍颖翔, 等. 基于正交投影的降维分类方法研究[J].
广东工业大学学报, 2017, 34(3): 1-7.
TENG S H, LU D L, HUO Y X, et al. Classification method based on dimension reduction[J]. Journal of Guangdong University of Technology, 2017, 34(3): 1-7. DOI: 10.12052/gdutxb.170008. |
| [10] |
BHOWAN U, JOHNSTON M, ZHANG M J, et al. Evolving diverse ensembles using genetic programming for classification with unbalanced data[J].
IEEE Transactions on Evolutionary Computation, 2012, 17(3): 368-386.
|
| [11] |
CATENI S, COLLA V, VANNUCCI M. A method for resampling imbalanced datasets in binary classification tasks for real-world problems[J].
Neurocomputing, 2014, 135: 32-41.
DOI: 10.1016/j.neucom.2013.05.059. |
| [12] |
CAO H, LI X L, WOON D Y K, et al. Integrated oversampling for imbalanced time series classification[J].
IEEE Transactions on Knowledge and Data Engineering, 2013, 25(12): 2809-2822.
DOI: 10.1109/TKDE.2013.37. |
| [13] |
NEKOOEIMEHR I, LAI Y S K. Adaptive semi-unsupervised weighted oversampling (A-SUWO) for imbalanced datasets[J].
Expert Systems with Applications, 2016, 46: 405-416.
DOI: 10.1016/j.eswa.2015.10.031. |
| [14] |
BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density-based local outliers[C]// Proceedings of 2000 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2000, 29(2): 93-104
|
| [15] |
INGRE B, YADAV A. Performance analysis of NSL-KDD dataset using ANN[C]//International Conference on Signal Processing and Communication Engineering Systems. Andaman and Nicobar Islands, India: IEEE, 2015: 92-96.
|
| [16] |
胡臻伟, 施勇, 薛质. 网络入侵检测的机器学习算法评估与比较[J].
通信技术, 2017, 50(12): 158-163.
HU Z W, SHI Y, XUE Z. Evaluation and comparison of machine-learning algorithm for net work intrusion detection[J]. Communications Technology, 2017, 50(12): 158-163. |
| [17] |
GAIKWAD D, THOOL R C. Intrusion detection system using bagging ensemble method of machine learning[C]//2015 International Conference on Computing Communication Control and Automation. Pune, India: IEEE, 2015: 291-295.
|
| [18] |
SALO F, NASSIF A B, ESSEX A. Dimensionality reduction with IG-PCA and ensemble classifier for network intrusion detection[J].
Computer Networks, 2019, 148: 164-175.
DOI: 10.1016/j.comnet.2018.11.010. |
| [19] |
JIANG L X, LI C Q, WU J, et al. A combined classification algorithm based on C4.5 and NB[C]//ISICA 2008: Proceeding of the Third International Symposium on Computation and Intelligence, LNCV 5370. Berlin: Spring-Verlag, 2008: 350-359.
|
| [20] |
姚滩, 王娟, 张胜利. 基于决策树与朴素贝叶斯分类的入侵检测模型[J].
计算机应用, 2015, 35(10): 2883-2885.
YAO T, WANG J, ZHANG S L. Intrusion detection model based on decision tree and Naive-Bayes classification[J]. Journal of Computer Applications, 2015, 35(10): 2883-2885. |
| [21] |
GUO C, PING Y, LIU N, et al. A two-level hybrid approach for intrusion detection[J].
Neurocomputing, 2016, 214: 391-400.
DOI: 10.1016/j.neucom.2016.06.021. |
| [22] |
LATAH M, TOKER L. An efficient flow-based multi-level hybrid intrusion detection system for software-defined networks[J]. arXiv preprint arXiv: 1806.03875, 2018.
|
| [23] |
HORNG S J, SU M Y, CHEN Y H, et al. A novel intrusion detection system based on hierarchical clustering and support vector machines[J].
Expert Systems with Applications, 2011, 38(1): 306-313.
DOI: 10.1016/j.eswa.2010.06.066. |
| [24] |
PAJOUH H H, JAVIDAN R, KHAYAMI R, et al. A two-layer dimension reduction and two-tier classification model for anomaly-based intrusion detection in IoT backbone networks[J].
IEEE Transactions on Emerging Topics in Computing, 2019, 7(2): 314-323.
DOI: 10.1109/TETC.2016.2633228. |
| [25] |
KIM G, LEE S, KIM S. A novel hybrid intrusion detection method integrating anomaly detection with misuse detection[J].
Expert Systems with Applications, 2014, 41(4): 1690-1700.
DOI: 10.1016/j.eswa.2013.08.066. |
| [26] |
CAI J, LUO J W, WANG S L, et al. Feature selection in machine learning: a new perspective[J].
Neurocomputing, 2018, 300: 70-79.
DOI: 10.1016/j.neucom.2017.11.077. |
| [27] |
JOVIĆ A, BRKIĆ K, BOGUNOVIĆ N. A review of feature selection methods with applications[C]//2015 38th International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO). Opatija, Croatia: IEEE, 2015: 1200-1205.
|
| [28] |
LI J D, CHENG K W, WANG S H, et al. Feature selection[J].
ACM Computing Surveys, 2017, 50(6): 1-45.
|
| [29] |
VENKATESH B, ANURADHA J. A review of feature selection and its methods[J].
Cybernetics and Information Technologies, 2019, 19(1): 3-26.
DOI: 10.2478/cait-2019-0001. |
| [30] |
DARSHAN S S, JAIDHAR C. Performance evaluation of filter-based feature selection techniques in classifying portable executable files[J].
Procedia Computer Science, 2018, 125: 346-356.
DOI: 10.1016/j.procs.2017.12.046. |
| [31] |
ALJAWARNEH S, ALDWAIRI M, YASSEIN M B. Anomaly-based intrusion detection system through feature selection analysis and building hybrid efficient model[J].
Journal of Computational Science, 2018, 25: 152-160.
DOI: 10.1016/j.jocs.2017.03.006. |
| [32] |
CHANG C C, LIN C J. LIBSVM: a library for support vector machines[J].
ACM Transactions on Intelligent Systems and Technology (TIST), 2011, 2(3): 1-27.
|
 2020, Vol. 37
2020, Vol. 37

