物理科学中的许多问题都可以归结为常微分方程的问题。常微分方程对人类生活、学习和工作的各个方面都有着很大的影响。实际上,常微分方程常用于模拟数学物理中的问题。因此,常微分方程的求解一直受到学者们高度关注。
然而,只有少数简单的常微分方程及其逆问题可以解析求解,在科学研究和社会生产中遇到的大多数常微分方程都是非常复杂的,很难得到它们的解析解。因此,考虑常微分方程及其逆问题的数值方法具有十分重要意义。逆问题由于不定性更是极其不易求解,这不仅是在数学理论上,而且在数值计算中都会有许多困难。
传统的求解微分方程的数值方法包括欧拉方法、龙格库塔法、有限差分等,这些方法可以得到满足某一精度的解。然而,它们需要对整个区域进行插值,这会增加计算复杂度,耗费较多的计算时间。
近年来,为了克服传统数值方法的缺陷,研究者们试图寻找更方便的方法来获得近似解析解,从而避免插值过程。利用神经网络求解常微分方程成为一个新的方向[1],此方法虽然可以得到具有解析表达式的近似解,但基于神经网络的常微分方程求解方法依赖于神经网络的函数逼近能力[2],将受限于它们的理论弱点,比如BP神经网络算法可能收敛不到局部最优解。
支持向量机(SVMs)由Vapnik和他的合作者在20世纪90年代提出,是建立在小样本统计学习理论和结构风险最小化原理基础上的通用机器学习算法[3]。这个算法是在有限数据的情况下,寻找由置信区间和经验风险组成的结构风险最小化。另外,这个算法采用核函数可以非常容易地处理高维数问题。其基本思想是将原始问题通过非线性变换映射到高维特征空间,在高维空间中构造决策函数,从而将原问题转化为一个凸二次规划问题,进而得到唯一的全局最优解。因此,该算法能够有效地处理神经网络等经典算法中的维数问题、局部极小问题和过学习问题。支持向量机用于处理函数估计和分类问题,在模式识别等方面已得到广泛的应用[4-10]。
Suykens等[11]提出了最小二乘支持向量机(LS-SVMs),用等式约束替代了支持向量机的不等式约束,避免了求解二次规划问题,运算速度快。文献[12-13]将最小二乘支持向量机用于求解微分方程,通过将解常微分问题转化为函数估计问题进行求解。然而,相比于支持向量机,最小二乘支持向量机虽然求解速度快,但其解不具有稀疏性,对噪声更敏感。
在许多物理现象中,观测数据是在离散的有限个点上获得的。因此对于离散微分方程及其逆问题的解的探究具有十分重要的意义。而上述所提到无论是传统的数值计算方法,还是基于神经网络及最小二乘支持向量机方法,在求解离散微分方程及其逆问题时都将失效。
在文献[14]中,Saitoh等通过利用Tikhonov正则化、迭代以及再生核理论[15-17]给出了一种求解离散线性微分方程及其逆问题近似解的方法。该方法基于再生核理论,选定合适的再生核Hilbert空间,相应的算子就可以进行定义。该方法适用于不同的离散微分方程,且对于原问题以及逆问题都可以得到相同结构的解。然而,该方法需要通过迭代计算
为克服文献[14]的缺陷,在Saitoh等工作的基础上[14],本文考虑结合支持向量机、Tikhonov正则化和再生核理论来求解离散线性微分方程及其逆问题。该方法基于再生核理论和Tikhonov正则化方法,将离散微分方程及其逆问题转化为支持向量机的函数逼近问题,最终转化为求解一个二次规划问题,进而求得具有解析表达式的稀疏解,具有较强的泛化能力,便于后续应用。对比于文献[14]中的方法,该方法具有文献[14]方法的优点,适用于不同的离散微分方程,原问题及其逆问题均具有相同结构的解,而且克服了需要迭代计算
本文将提出一种新的方法来构造离散常微分方程及其相应的逆问题的近似解。所提方法适用于一般的离散微分方程,为便于说明,考虑文献[14]中所求解的微分方程:
| $ LF = g $ | (1) |
其中,
| $LF = F'' + \alpha F' + \beta F$ |
在许多物理现象中,观测数据是在离散的有限个点上获得的。因此,在本文中,笔者将在离散的有限个点上构造微分方程
对于
| $\begin{array}{l} {{L}}\left( F \right)\left( {{x_1},{x_2}, \ldots ,{x_N}} \right): = \\ \left( {\left( {LF} \right)\left( {{x_1}} \right),\left( {LF} \right)\left( {{x_2}} \right), \ldots ,\left( {LF} \right)\left( {{x_N}} \right)} \right) \in {{\mathbb R}^N}\\ \end{array} $ |
则
在本文中将考虑在两个典型的再生核Hilbert空间中求解微分方程及逆问题,这两个空间分别是Sobolev空间和Paley-Wiener空间。
对于实数
| ${K_s}\left( {x,y} \right) = \frac{1}{{2{\rm{\text{π}}} }}\int_{\mathbb R} {{{\left( {1 + {{\left| \zeta \right|}^2}} \right)}^{ - s}}{{\rm{e}}^{{\rm{i}}\left( {x - y} \right) \cdot \zeta }}{\rm{d}}\zeta } $ |
其中
| ${\left\| f \right\|_{{H_{{K_s}}}}} = {\left( {\int_{\mathbb R} {{{\left( {1 + {{\left| \zeta \right|}^2}} \right)}^s}{{\left| {\left( {{\cal F}f} \right)\left( \zeta \right)} \right|}^2}{\rm{d}}\zeta } } \right)^{\tfrac{1}{2}}}$ |
其中
笔者还考虑求解Paley-Wiener空间
| $f\left( z \right): = \frac{1}{{2{\text{π}} }}\int_{\mathbb R} {{\chi _h}\left( t \right)g\left( t \right){{\rm{e}}^{ - {\rm{i}}z \cdot t}}{\rm{d}}t}$ |
其中
当
| $\left| {f\left( z \right)} \right| \leqslant C\;\exp\left( {\frac{{\text{π} \left| z \right|}}{h}} \right)$ |
和
| ${\int_{\mathbb R} {\left| {f\left( x \right)} \right|} ^2}{\rm{d}}x < \infty $ |
其中
| $\begin{array}{l} \displaystyle {K_h}\left( {z,\bar u} \right) = \frac{1}{{2 \text{π} }}\int_{\mathbb R} {{\chi _h}\left( t \right){{\rm{e}}^{ - {\rm{i}}z \cdot t}}\overline {{{\rm{e}}^{ - {\rm{i}}u \cdot t}}} {\rm{d}}t} = \\ \displaystyle \frac{1}{{\text{π} \left( {z - \bar u} \right)}}\sin \frac{\text{π} }{h}\left( {z - \bar u} \right)\\ \end{array} $ |
其中
为了求解离散线性微分方程,在文献[14]中,作者们通过应用再生核理论和Tikhonov正则化,将问题表述如下:
对于任意
| $ \mathop {\inf }\limits_{F \in {H_{{K_h}}}} \left\{ {\lambda \left\| F \right\|_{{H_{{K_h}}}}^2 + \sum\limits_{j = 1}^N {{{\left| {\left( {LF} \right)\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right|}^2}} } \right\} $ | (2) |
其中
为了求解问题
事实上,问题
对于任意常数
| $\mathop {\min}\limits_{F \in {H_{{K_h}}}} \left\{ {\left\| F \right\|_{{H_{{K_h}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {c\left( {\left( {LF} \right)\left( {{x_j}} \right),g\left( {{x_j}} \right)} \right)} } \right\}$ |
其中
在学习理论的指导下,特别地,笔者选取
| $ \begin{array}{l} c\left( {\left( {LF} \right)\left( {{x_j}} \right),g\left( {{x_j}} \right)} \right) = {\left| {\left( {LF} \right)\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right|_\varepsilon } = \\ \max\left\{ {0,\left| {\left( {LF} \right)\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right| - \varepsilon } \right\} \\ \end{array} $ |
其中
接下来,笔者将在支持向量机的框架中,结合再生核理论和Tikhonov正则化方法进行求解。我们将重点讨论在Paley-Wiener空间
对于任意
| $ \mathop {\min}\limits_{F \in {H_{{K_h}}}} \left\{ {\left\| F \right\|_{{H_{{K_h}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {{{\left| {\left( {LF} \right)\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right|}_\varepsilon }} } \right\} $ | (3) |
对于不同点
| $\begin{array}{l} {{L}}:F \in {H_{{K_h}}} \to \\ \left( {\left( {LF} \right)\left( {{x_1}} \right),\left( {LF} \right)\left( {{x_2}} \right), \cdots ,\left( {LF} \right)\left( {{x_N}} \right)} \right) \in {{\mathbb R}^N} \\ \end{array} $ |
在
| $\left( {LF} \right)\left( {{x_j}} \right) = {\left\langle {{{L}}F,{e_j}} \right\rangle _{{{\mathbb R}^N}}} = {\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle _{{H_{{K_h}}}}}$ |
则线性映射
| $ \begin{array}{l} A = {\left\{ {{{\left\langle {{{{L}}^ * }{e_j},{{{L}}^ * }{e_{j'}}} \right\rangle }_{{H_{{K_h}}}}}} \right\}_{j,j' = 1,2, \ldots ,N}} = \\ {\left\{ {{a_{jj'}}} \right\}_{j,j' = 1,2, \ldots ,N}} \end{array} $ | (4) |
其中
| $\begin{array}{l} \left( {{{{L}}^ * }{e_j}} \right)\left( x \right) = {\left\langle {\left( {{{{L}}^ * }{e_j}} \right)\left( \cdot \right),{K_h}\left( { \cdot ,x} \right)} \right\rangle _{{H_{{K_h}}}}} = \\ {\left\langle {{e_j},{{L}}{K_h}\left( { \cdot ,x} \right)} \right\rangle _{{{\mathbb R}^N}}} = \\ \frac{1}{{2 \text{π} }}\int_{ - \text{π} /h}^{\text{π} /h} {\left( { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right)} {{\rm{e}}^{{\rm{i}}\eta \left( {x - {x_j}} \right)}}{\rm{d}}\eta \\ \end{array} $ |
定理1[14] 式(4)中引入的元素
| $ \begin{array}{l} \displaystyle {a_{jj'}} = \frac{{4X\left( { - 6 + {b^2}{X^2}} \right)\cos \left( {bX} \right)}}{{\text{π} {b^4}}} + \\ \displaystyle \frac{{\left( {24 - 12{b^2}{X^2} + {b^4}{X^4}} \right)\sin \left( {bX} \right)}}{{\text{π} {b^5}}} + \\ \displaystyle \frac{{\left( {{\alpha ^2} - 2\beta } \right)\left( {2 - {b^2}{X^2}} \right)\sin \left( {bX} \right)}}{{\text{π} {b^3}}} + \\ \displaystyle \frac{{ - 2\left( {{\alpha ^2} - 2\beta } \right)X\cos \left( {bX} \right)}}{{\text{π} {b^2}}} + \frac{{{\beta ^2}}}{{\text{π} b}}\sin \left( {bX} \right) \\ \end{array} $ |
其中
基于上述结果,求解问题
| $ \mathop {\min}\limits_{F \in {H_{{K_h}}}} \left\{ {\frac{1}{2}\left\| F \right\|_{{H_{{K_h}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {{{\left| {{{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - g\left( {{x_j}} \right)} \right|}_\varepsilon }} } \right\} $ | (5) |
其中,添加因子
为了处理
| $ \mathop {\min}\limits_{F \in {H_{{K_h}}},\xi ,\xi *} \left\{ {\frac{1}{2}\left\| F \right\|_{{H_{{K_h}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {\left( {{\xi _j} + \xi _j^ * } \right)} } \right\} $ | (6) |
其中
| ${\xi _j} = \max\left\{ {0,{{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - g\left( {{x_j}} \right) - \varepsilon } \right\}$ |
和
| $\xi _j^ * = \max\left\{ {0,g\left( {{x_j}} \right) - {{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - \varepsilon } \right\}$ |
可以容易地证明
| $\begin{array}{l} {\xi _j} + \xi _j^ * = \max\left\{ {0,\left| {{{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - g\left( {{x_j}} \right)} \right| - \varepsilon } \right\} = \\ {\left| {\left( {LF} \right)\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right|_\varepsilon } \\ \end{array} $ |
以及
| $\begin{array}{c} {\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle _{{H_{{K_h}}}}} - g\left( {{x_j}} \right) \leqslant \varepsilon + {\xi _j},j = 1, \cdots ,N, \\ g\left( {{x_j}} \right) - {\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle _{{H_{{K_h}}}}} \leqslant \varepsilon + \xi _j^ * ,j = 1, \cdots ,N, \\ \xi _j^{\left( * \right)} \geqslant 0,j = 1, \cdots ,N \\ \end{array} $ |
问题
| $\begin{array}{l} {\cal L}\left( {F,{\xi ^{\left( * \right)}},{\mu ^{\left( * \right)}},{\nu ^{\left( * \right)}}} \right) = \\ \displaystyle \frac{1}{2}{\left\| F \right\|^2} + \frac{C}{N}\sum\limits_{j = 1}^N {\left( {{\xi _j} + \xi _j^ * } \right)} \; - \\ \sum\limits_{j = 1}^N {{\mu _j}} \left[ {\varepsilon + {\xi _j} - {{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} + g\left( {{x_j}} \right)} \right] - \\ \sum\limits_{j = 1}^N {\mu _j^ * } \left[ {\varepsilon + \xi _j^ * + {{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - g\left( {{x_j}} \right)} \right]\; - \\ \sum\limits_{j = 1}^N {\left( {{\nu _j}{\xi _j} + \nu _j^ * \xi _j^ * } \right)} \end{array} $ |
其中
如果原始问题是凸的,则一个解既是原始问题的最优解也是对偶问题的最优解当且仅当这个解满足Karush-Kuhn-Tucker (KKT)条件[19]。显然,原始问题
| $\begin{array}{c} {\mu _j}\left[ {\varepsilon + {\xi _j} - {{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} + g\left( {{x_j}} \right)} \right] = 0 \\ \mu _j^ * \left[ {\varepsilon + \xi _j^ * + {{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - g\left( {{x_j}} \right)} \right] = 0 \\ {\nu _j}{\xi _j} = 0 \\ \nu _j^ * \xi _j^ * = 0 \end{array} $ |
和
| $\begin{array}{c} \displaystyle \frac{{\partial {\cal L}}}{{\partial F}} = F - \sum\limits_{j = 1}^N {\left( {\mu _j^ * - {\mu _j}} \right)\left( {{{{L}}^ * }{e_j}} \right)} = 0 \\ \displaystyle \frac{{\partial {\cal L}}}{{\partial {\xi _j}}} = \frac{C}{N} - {\mu _j} - {\nu _j} = 0 \\ \displaystyle \frac{{\partial {\cal L}}}{{\partial \xi _j^ * }} = \frac{C}{N} - \mu _j^ * - \nu _j^ * = 0 \\ \end{array} $ |
对于
在这些条件下,原始问题
| $\begin{array}{l} \mathop {\max }\limits_{{\mu ^{\left( * \right)}}} - \displaystyle \frac{1}{2}\sum\limits_{j,j' = 1}^N {\left( {\mu _j^ * - {\mu _j}} \right)} \left( {\mu _{j'}^ * - {\mu _{j'}}} \right)\left\langle {{{{L}}^ * }{e_j},{{{L}}^ * }{e_{j'}}} \right\rangle - \\ \displaystyle \varepsilon \sum\limits_{j = 1}^N {\left( {\mu _j^ * + {\mu _j}} \right)} + \sum\limits_{j = 1}^N {g\left( {{x_j}} \right)\left( {\mu _j^ * - {\mu _j}} \right)}\\ \end{array} $ |
对偶问题的约束条件为
| $0 \leqslant \mu _j^{\left( * \right)} \leqslant \frac{C}{N},j = 1, \cdots ,N$ |
从而可得到解
| ${\overset{\frown} F} \left( x \right) = \sum\limits_{j = 1}^N {\left( {\mu _j^ * - {\mu _j}} \right)} \left( {{{{L}}^ * }{e_j}} \right)\left( x \right)$ |
实际上,通过设置适当的
| ${\overset{\frown} F} \left( x \right) = \sum\limits_{j \in J} {\left( {\mu _j^ * - {\mu _j}} \right)} \left( {{{{L}}^ * }{e_j}} \right)\left( x \right)$ |
其中
在光滑
| $\begin{array}{l} \left( {{{{L}}^ * }{e_j}} \right)\left( x \right) = {\left\langle {\left( {{{{L}}^ * }{e_j}} \right)\left( \cdot \right),{K_s}\left( { \cdot ,x} \right)} \right\rangle _{{H_{{K_s}}}}} = \\ {\left\langle {{e_j},{{L}}{K_s}\left( { \cdot ,x} \right)} \right\rangle _{{{\mathbb R}^N}}} = \\ \displaystyle \frac{1}{{2 \text{π} }}\int_{\mathbb R} {\frac{{\left( { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right){{\rm{e}}^{ - {\rm{i}}\eta \left( {x - {x_j}} \right)}}}}{{{{\left( {1 + {\eta ^2}} \right)}^s}}}} {\rm{d}}\eta \\ \end{array} $ |
则线性映射
| ${a_{jj'}} = \frac{1}{{2 \text{π} }}\int_{\mathbb R} {\frac{{{{\left| { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right|}^2}{{\rm{e}}^{{\rm{i}}\eta \left( {{x_j} - {x_{j'}}} \right)}}}}{{{{\left( {1 + {\eta ^2}} \right)}^s}}}} {\rm{d}}\eta$ |
对于任意
| $ \mathop {\min}\limits_{F \in {H_{{K_s}}}} \left\{ {\frac{1}{2}\left\| F \right\|_{{H_{{K_s}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {{{\left| {{{\left\langle {F,{{{L}}^ * }{e_j}} \right\rangle }_{{H_{{K_s}}}}} - g\left( {{x_j}} \right)} \right|}_\varepsilon }} } \right\} $ | (7) |
求解过程类似于Paley-Wiener空间
| $\tilde F\left( x \right) = \sum\limits_{j \in J} {\left( {\upsilon _j^ * - {\upsilon _j}} \right)} \left( {{{{L}}^ * }{e_j}} \right)\left( x \right)$ |
其中
在这一节中,将采用基于支持向量机的方法来考虑微分方程
那就是,对于微分方程
| $LF = g$ |
如果给定函数
首先,考虑在Paley-Wiener空间
| ${{M}}:g \in {H_{{K_h}}} \to \left( {F\left( {{x_1}} \right),F\left( {{x_2}} \right), \ldots ,F\left( {{x_N}} \right)} \right) \in {{\mathbb R}^N}$ |
然后有
| $F\left( {{x_j}} \right) = {\left\langle {{{M}}g,{e_j}} \right\rangle _{{{\mathbb R}^N}}} = {\left\langle {g,{{{M}}^ * }{e_j}} \right\rangle _{{H_{{K_h}}}}}$ |
则线性映射
| $B = {\left\langle {{{{M}}^ * }{e_j},{{{M}}^ * }{e_{j'}}} \right\rangle _{{H_{{K_h}}}}} = {\left\{ {{b_{jj'}}} \right\}_{j,j' = 1,2, \ldots ,N}}$ |
其中
| $ \begin{array}{l} \left( {{{{M}}^ * }{e_j}} \right)\left( x \right) = {\left\langle {\left( {{{{M}}^ * }{e_j}} \right)\left( \cdot \right),{K_h}\left( { \cdot ,x} \right)} \right\rangle _{{H_{{K_h}}}}} = \\ {\left\langle {{e_j},{{M}}{K_h}\left( { \cdot ,x} \right)} \right\rangle _{{{\mathbb R}^N}}} = \\ \displaystyle \frac{1}{{2 \text{π} }}\int_{-\text{π}/h}^{\text{π}/h} {\frac{{\left( { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right){{\rm{e}}^{ - {\rm{i}}\eta \left( {x - {x_j}} \right)}}}}{{\lambda {{\left( {1 + {\eta ^2}} \right)}^2} + {{\left| { - {\eta ^2} + {\rm{i}}\alpha \eta + \beta } \right|}^2}}}} {\rm{d}}\eta \end{array} $ |
元素
| $ {b_{jj'}} = \frac{1}{{2 \text{π} }}\int_{-\text{π}/h}^{\text{π}/h} {\frac{{{{\left| { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right|}^2}{{\rm{e}}^{ - {\rm{i}}\eta \left( {{x_j} - {x_{j'}}} \right)}}}}{{{{\left( {\lambda {{\left( {1 + {\eta ^2}} \right)}^2} + {{\left| { - {\eta ^2} + {\rm{i}}\alpha \eta + \beta } \right|}^2}} \right)}^2}}}} {\rm{d}}\eta $ |
笔者所考虑的逆问题表述为对于任意
| $ \mathop {\min}\limits_{g \in {H_{{K_h}}}} \left\{ {\frac{1}{2}\left\| g \right\|_{{H_{{K_h}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {{{\left| {{{\left\langle {g,{{{M}}^ * }{e_j}} \right\rangle }_{{H_{{K_h}}}}} - F\left( {{x_j}} \right)} \right|}_\varepsilon }} } \right\} $ | (8) |
问题
| ${\overset{\frown} g} \left( x \right) = \sum\limits_{j \in J} {\left( {\theta _j^ * - {\theta _j}} \right)} \left( {{{{M}}^ * }{e_j}} \right)\left( x \right)$ |
其中
在光滑
| $\begin{array}{l} \left( {{{{M}}^ * }{e_j}} \right)\left( x \right) = {\left\langle {\left( {{{{M}}^ * }{e_j}} \right)\left( \cdot \right),{K_s}\left( { \cdot ,x} \right)} \right\rangle _{{H_{{K_s}}}}} = \\ {\left\langle {{e_j},{{M}}{K_s}\left( { \cdot ,x} \right)} \right\rangle _{{{\mathbb R}^N}}} = \\ \displaystyle \frac{1}{{2 \text{π} }}\int_{\mathbb R} {\frac{{\left( { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right){{\rm{e}}^{ - {\rm{i}}\eta \left( {x - {x_j}} \right)}}}}{{{{\left( {1 + {\eta ^2}} \right)}^s}\left( {\lambda {{\left( {1 + {\eta ^2}} \right)}^2} + {{\left| { - {\eta ^2} + {\rm{i}}\alpha \eta + \beta } \right|}^2}} \right)}}} {\rm{d}}\eta \\ \end{array} $ |
则线性映射
| $\begin{array}{l} {b_{jj'}} = \\ \displaystyle \frac{1}{{2 \text{π} }}\int_{\mathbb R} {\frac{{{{\left| { - {\eta ^2} - {\rm{i}}\alpha \eta + \beta } \right|}^2}{{\rm{e}}^{{\rm{i}}\eta \left( {{x_j} - {x_{j'}}} \right)}}}}{{{{\left( {1 + {\eta ^2}} \right)}^s}{{\left( {\lambda {{\left( {1 + {\eta ^2}} \right)}^2} + {{\left| { - {\eta ^2} + {\rm{i}}\alpha \eta + \beta } \right|}^2}} \right)}^2}}}} {\rm{d}}\eta \end{array} $ |
对于任意
| $\mathop {\min}\limits_{g \in {H_{{K_s}}}} \left\{ {\frac{1}{2}\left\| g \right\|_{{H_{{K_s}}}}^2 + \frac{C}{N}\sum\limits_{j = 1}^N {{{\left| {{{\left\langle {g,{{{M}}^ * }{e_j}} \right\rangle }_{{H_{{K_s}}}}} - F\left( {{x_j}} \right)} \right|}_\varepsilon }} } \right\}$ |
类似于3.1节,可以得到上述问题的解。
4 误差分析在这一节中,笔者将给出逼近问题的误差界。为此,首先需要找到解的稳定性和一致性估计,然后得到有界逼近误差。
假设
定理2 根据
| ${\left\| {\tilde F} \right\|_{{H_{{K_\tau }}}\left( \Omega \right)}} \leqslant {\left\| F \right\|_{{H_{{K_\tau }}}\left( \Omega \right)}}$ |
和
| $\mathop {\max }\limits_{1 \leqslant j \leqslant N} \left| {L\tilde F\left( {{x_j}} \right) - g\left( {{x_j}} \right)} \right| \leqslant \frac{N}{{2C}}\left\| F \right\|_{{H_{{K_\tau }}}\left( \Omega \right)}^2 + \varepsilon$ |
定理3 假设
| $\begin{array}{l} {\left\| {F - \tilde F} \right\|_{{L_q}\left( \varOmega \right)}} \leqslant \\ \displaystyle \tilde C\left( {2{h^{\tau - N\left( {\frac{1}{2} - \frac{1}{q}} \right)}} + {{\left\| F \right\|}_{{H_{{K_\tau }}}\left( \varOmega \right)}} + \frac{N}{{2C}}\left\| F \right\|_{{H_{{K_\tau }}}\left( \varOmega \right)}^2 + \varepsilon } \right) \end{array} $ |
对于所有离散集
| $h = {h_{\left\{ {{x_j}} \right\}_{j = 1}^N,\varOmega }} = \mathop {\sup }\limits_{x \in \varOmega } \mathop {\min }\limits_{{x_j} \in \left\{ {{x_j}} \right\}_{j = 1}^N} {\left\| {x - {x_j}} \right\|_2}$ |
为了验证所提出算法的有效性,笔者给出了两个实验。这两个实验都可以在几秒钟内完成。
在实验1中,考虑离散微分方程
| $F''\left( x \right) + F'(x) + F(x) = g(x)$ |
函数
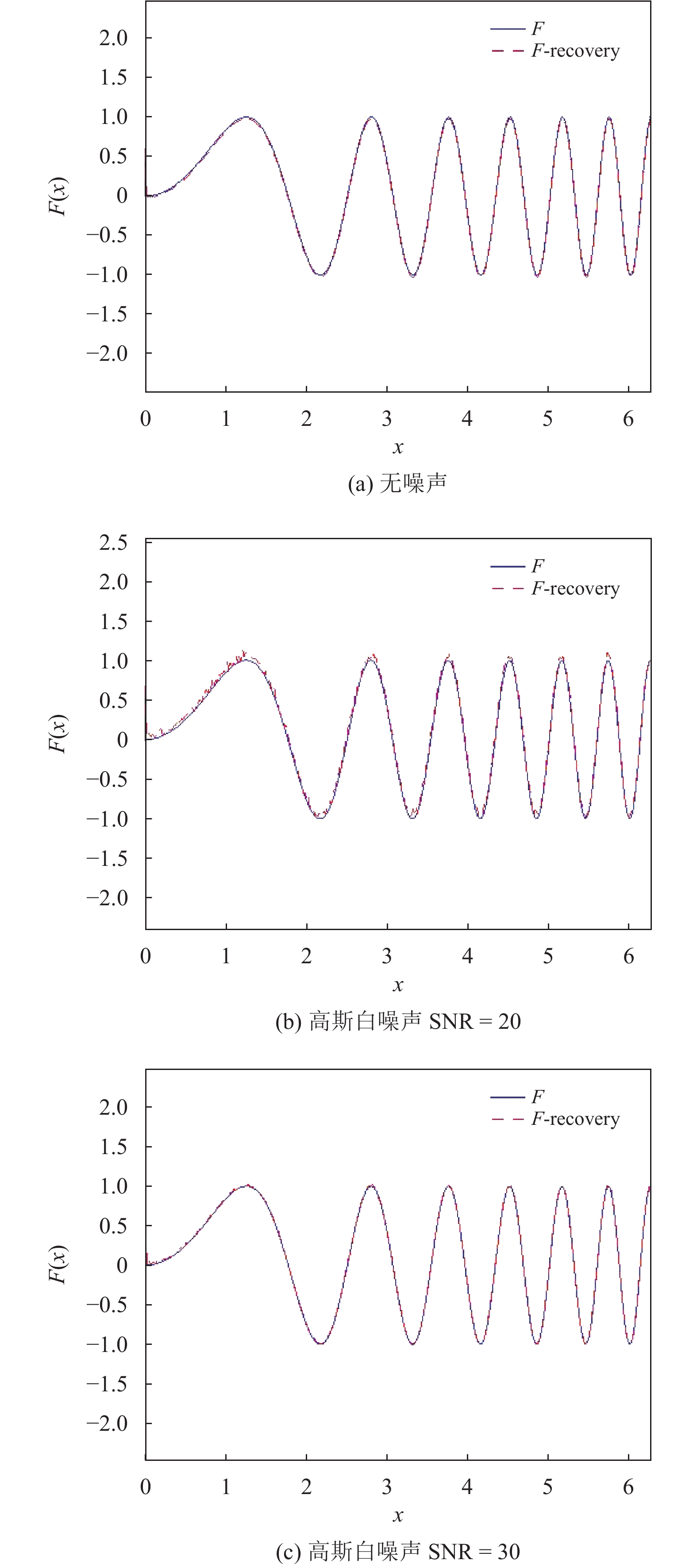
|
图 1 实验1的数值结果 Figure 1 The numerical result of experiment 1 |
在实验2中,笔者考虑逆问题。对于离散微分方程
| $F''(x) + F'(x) + 4F(x) = g(x)$ |
函数
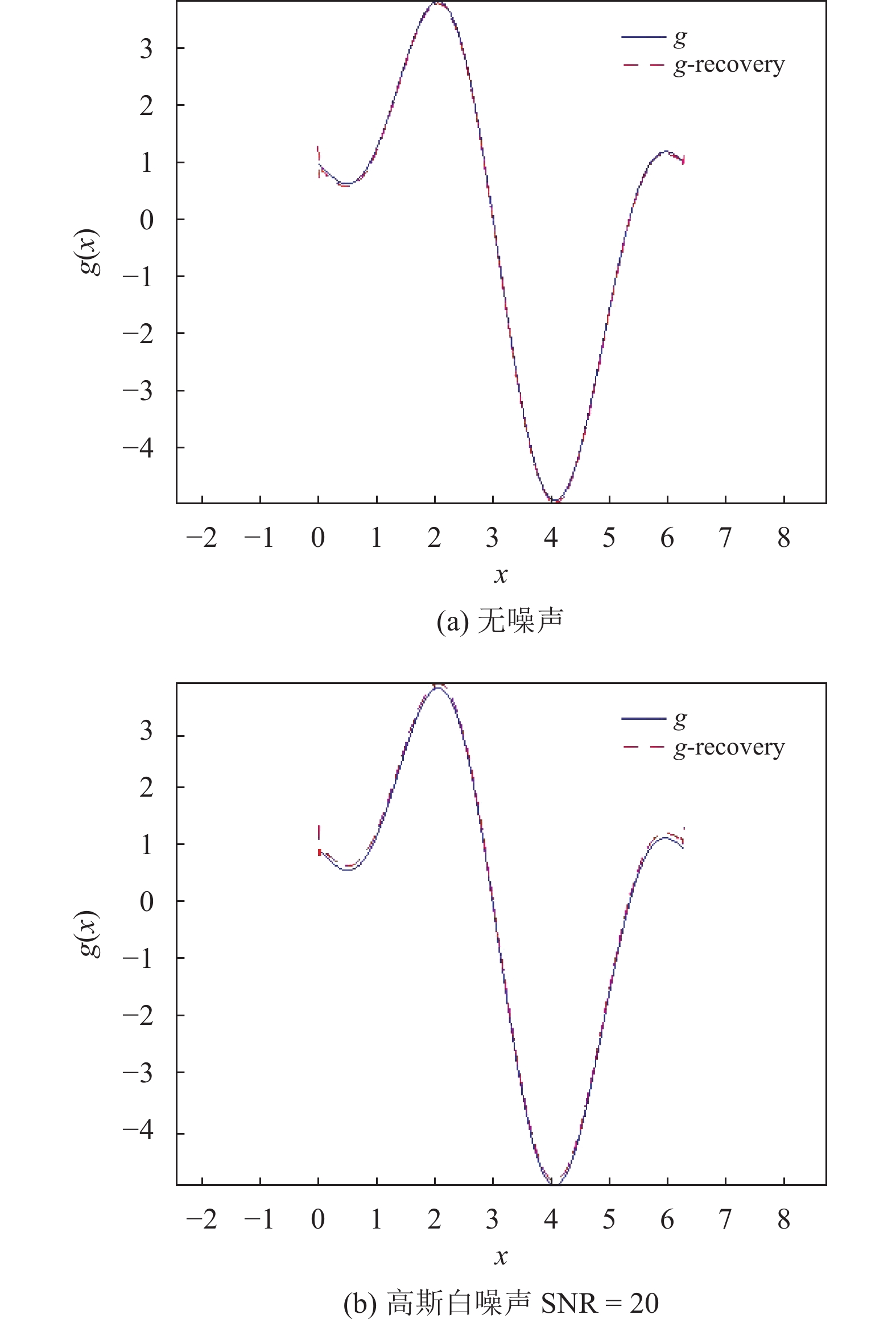
|
图 2 实验2的数值结果 Figure 2 The numerical result of experiment 2 |
本文通过将支持向量机、Tikhonov正则化和再生核理论相结合,提出了一种求解离散线性微分方程及其逆问题的方法。通过将离散微分方程问题及其逆问题转换为对应的目标优化问题,然后在支持向量机的框架下进行求解,得到具有解析表达式的近似解,所得解具有稀疏性,对噪声鲁棒,结构固定的特点,便于后续应用。离散微分方程及其逆问题均有相同结构的解。实验结果证明了该方法的有效性。
| [1] |
LAGARIS I E, LIKAS A, FOTIADIS D I. Artificial neural networks for solving ordinary and partial differential equations[J].
IEEE Transactions on Neural Networks and Learning Systems, 1998, 9(5): 987-1000.
DOI: 10.1109/72.712178. |
| [2] |
MEADE A J J, FERNANDEZ A A. The numerical solution of linear ordinary differential equations by feedforward neural networks[J].
Mathematical & Computer Modelling Math, 1994, 19(12): 1-25.
|
| [3] |
VAPNIK V. The Nature of Statistical Learning Theory [M]. New York: Springer-Verlag, 1995.
|
| [4] |
AHMED S, KHALID M, AKRAM U. A method for short-term wind speed time series forecasting using support vector machine regression model [C]// 2017 6th International Conference on Clean Electrical Power. Santa Margherita Ligure: IEEE, 2017: 190-195.
|
| [5] |
WANG X D. Forecasting short-term wind speed using support vector machine with particle swarm optimization [C]// 2017 International Conference on Sensing, Diagnostics, Prognostics and Control. Shanghai: IEEE, 2017: 241-245.
|
| [6] |
PAN J, YANG B, CAI S B, et al. Finger motion pattern recognition based on sEMG support vector machine [C]// 2017 IEEE International Conference on Cyborg & Bionic Systems. Beijing: IEEE, 2017.
|
| [7] |
WU W, ZHOU H. Data-Driven diagnosis of cervical cancer with support vector machine-based approaches[J].
IEEE Access, 2017, 5: 25189-25195.
DOI: 10.1109/ACCESS.2017.2763984. |
| [8] |
POLAT H, DANAEI M H, CETIN A. Diagnosis of chronic kidney disease based on support vector machine by feature selection methods[J].
Journal of Medical Systems, 2017, 41(4): 55.
DOI: 10.1007/s10916-017-0703-x. |
| [9] |
TAIE S A, GHONAIM W. Title CSO-based algorithm with support vector machine for brain tumor's disease diagnosis [C]// 2017 IEEE International Conference on Pervasive Computing & Communications Workshops. Kona: IEEE, 2017.
|
| [10] |
MO Y, QIAN T. Support vector machine adapted Tikhonov regularization method to solve Dirichlet problem[J].
Applied Mathematics and Computation, 2014, 245: 509-519.
DOI: 10.1016/j.amc.2014.07.089. |
| [11] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J].
Neural Processing Letters, 1999, 9(3): 293-300.
DOI: 10.1023/A:1018628609742. |
| [12] |
MEHRKANOON S, FALCK T, SUYKENS J A K. Approximate solutions to ordinary differential equations using least squares support vector machines[J].
IEEE Transactions on Neural Networks and Learning Systems, 2012, 23(9): 1356-1367.
DOI: 10.1109/TNNLS.2012.2202126. |
| [13] |
ZHOU S S, WANG B J, CHEN L. High precision approximate analytical solutions to ODE using LS-SVM[J].
The Journal of China Universities of Posts and Telecommunications, 2018, 25(4): 94-102.
|
| [14] |
CASTRO L P, SAITOH S, SAWANO Y, et al. Discrete linear differential equations[J].
International Mathematical Journal of Analysis & Its Applications, 2012, 32(3): 181-191.
|
| [15] |
MATSUURA T, SAITOH S, TRONG D D. Numerical solutions of the Poisson equation[J].
Applicable Analysis, 2004, 83(10): 1037-1051.
DOI: 10.1080/00036810410001724616. |
| [16] |
SAITOH S. Integral Transforms, Reproducing Kernels and their applications[J].
Journal of Experimental Medicine, 1997, 188(1): 39-48.
|
| [17] |
SAITOH S. Approximate real inversion formulas of the gaussian convolution[J].
Applicable Analysis, 2004, 83(7): 727-733.
DOI: 10.1080/00036810410001657198. |
| [18] |
邓乃扬, 田英杰. 支持向量机: 理论、算法与拓展[M]. 北京: 科学出版社, 2009.
|
| [19] |
BOYD S, VANDENBERGHE L. Convex Optimization [M]. Cambridge University Press, 2004.
|
| [20] |
RIEGER C, ZWICKNAGL B. Deterministic error analysis of support vector regression and related regularized kernel methods[J].
Journal of Machine Learning Research, 2006, 10(5): 2115-2132.
|
 2020, Vol. 37
2020, Vol. 37

