2. 东源广工大现代产业协同创新研究院,广东 河源 517500
2. Synergy Innovation Institute for Modern Industries of GDUT, Heyuan 517500, China
HEVC (High Efficiency Video Coding)视频编码标准由视频编码联合组(Joint Collaboration on Video Coding, JCT-VC)于2013年正式发布,其相比于上一代视频编码标准H.264最大的特点是在相同的视频编码质量下将压缩比提升了一半[1-2]。为了提升编码器的编码性能和更好地支持高分辨率视频编码,HEVC视频编码标准采用了更加灵活的编码结构,新增了一系列新技术。在这些新技术中,递归四叉树划分、预测模式选择等环节极大提升了编码器的计算复杂度,严重阻碍了HEVC视频编码标准的推广和应用。特别是最佳帧间预测模式选择过程需要经过运动估计和变换单元(Transform Unit, TU)遍历子循环,该过程在运动向量搜索时对每一个搜索点遍历变换单元并计算率失真,从而得到最佳帧间预测各参数的组合,这使帧间预测模式选择成为HEVC视频编码过程中最耗时的模块,大约占视频编码时间的69%[3]。因此,降低最佳帧间预测模式选择过程的时间复杂度十分必要。
在快速视频编码方面,国内外学者做了许多研究。为了降低CTU (Coding Tree Unit)划分为CU过程的循环冗余,文献[4]提出若当前深度CU块的率失真小于子CU块率失真的总和时提前终止向下继续划分。该方法是典型的提前终止算法,已经写入HM的4.0版本中。文献[5]根据当前CU与领近域CU的划分深度相关性和视频内容的运动特性上的一定相关性,提出跳过邻近域CU中不出现的划分深度,和提前终止CU划分的算法,从而达到快速编码的效果。文献[6]根据当前CU块相邻已编码块CU划分深度的相关性,设计一个与相邻CU块相关的阈值来限定当前CU块的划分深度范围。有些学者通过降低CU划分的子循环PU模式的选择情况来降低编码时间。如文献[7]结合CU尺寸决策及其下一层循环的预测模式选择设计了一种基于贝叶斯准则的复杂度因子来跳过除Skip预测模式外的其他模式,以及跳过某些大尺寸CU块遍历和提前终止CU划分。在帧内编码中,文献[8]通过计算PU块的各像素梯度方向,同时对预测角度进行排序,从而降低PU模式的遍历。文献[9]利用参考帧同位置CU的PU模式划分情况来决策当前CU的内容复杂度,通过该复杂度来粗选将要遍历的PU模式,达到降低PU模式选择冗余加速编码的效果。文献[10]对PU块定义一个上层PU模式,同时利用空间PU划分模式相关性,计算划分模式优先级,从而只对优先级高的帧间PU划分模式进行运动估计,优先级低的跳过运动估计,该算法是通过减少运动估计次数来降低编码时间。也有一些研究对PU的子循环TU的划分进行优化,如文献[11]基于TU块非零变换系数的数量修剪编码树来提前决策TU块的大小,从而实现在TU块大小决策层的快速算法。该算法不能有效降低纹理复杂视频序列的编码时间。文献[12]利用视频序列的时空高相关性特征,提出利用当前TU的不同帧同位置TU块和当前TU相邻块TU的划分情况来加权预测当前TU的划分范围。
上述文献算法中在CU尺寸提前决策和PU预测模式,TU尺寸快速决策主要利用的是图像帧在时空域上的相关性,也有一些在帧间预测时选择性跳过运动估计。利用CU的PU子块运动特征来降低PU模式选择复杂度的算法较少。本文利用提前分析PU子块的运动矢量来确定当前CU块的运动特征,提出了一种基于CU块运动特征的帧间预测模式快速选择算法。在保证编码器性能基本不变的情况下,有效降低编码器编码时间。
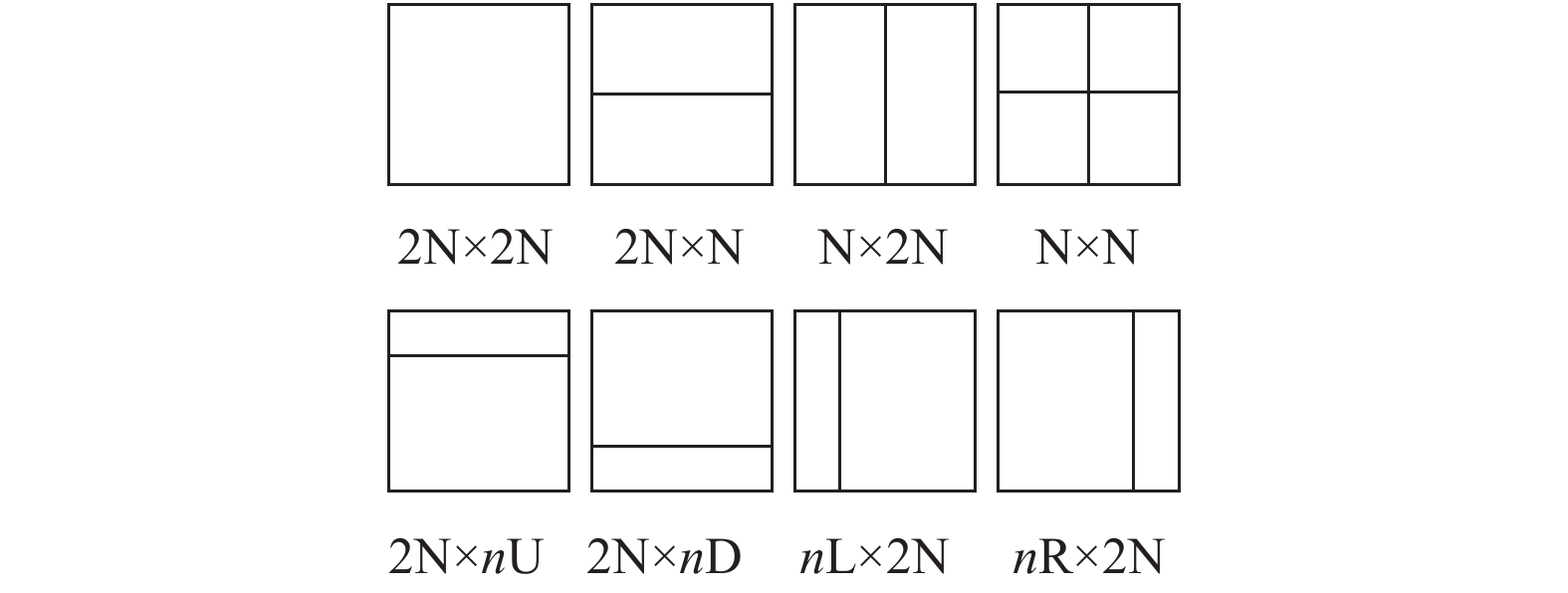
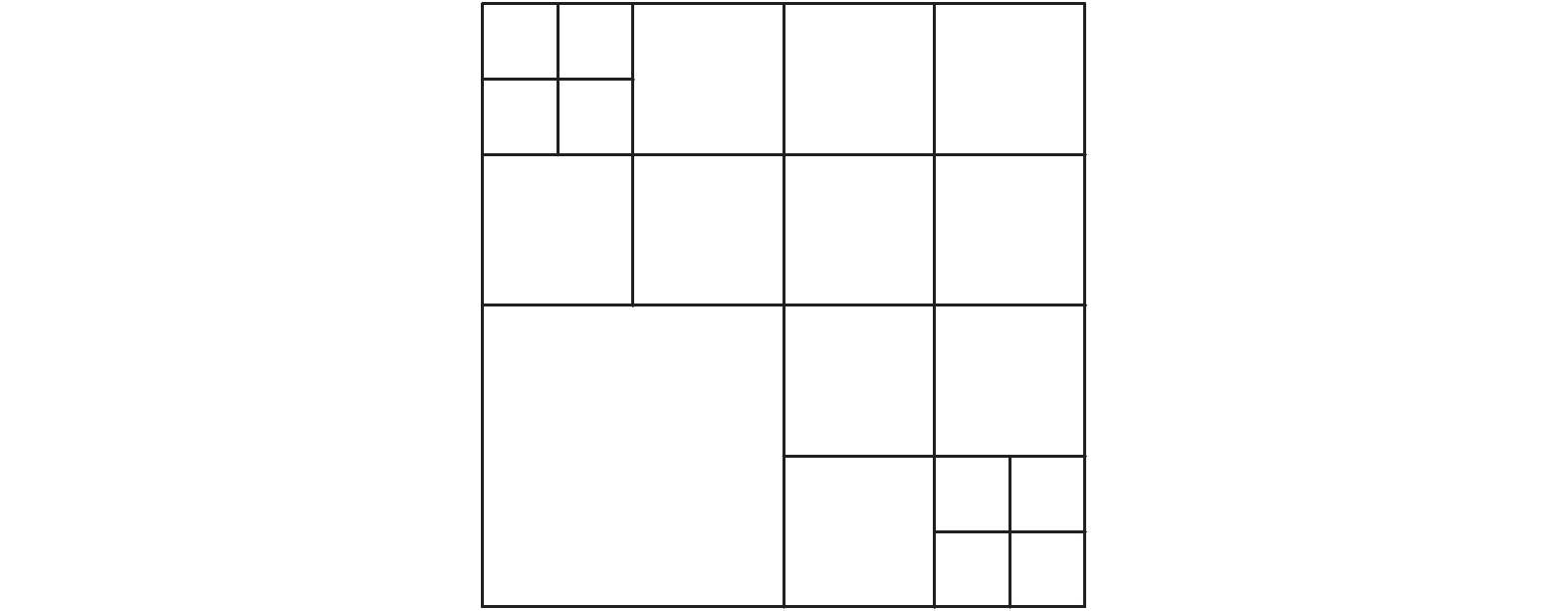
1 HEVC帧间预测模式选择复杂度分析为了适应更高分辨率的视频和实现更高的压缩率,HEVC引入了更加灵活的递归编码树单元划分方式。视频图像帧在编码器中将图像帧分割成一系列CTU块,大小通常为64×64,再以CTU为基本单元,通过四叉树方式划分为4个尺寸为32×32的CU块,每块CU遍历8种帧间预测划分模式,如图1所示,包括4种对称模式2N×2N, 2N×N, N×2N, N×N,和4种非对称模式2N×nU, 2N×nD, nL×2N, nR×2N,同时,对每个划分模式进行RD (Rate Distortion)代价计算,比较获得代价最低的帧间预测模式作为最佳帧间预测模式以及PU划分模式。接着将各个32×32的CU块作为基本单元,以四叉树方式再划分为4块子CU块并预测得到最佳预测模式。如此递归划分,计算各CU块的最佳预测模式,直至CU块的大小为8×8。图2为尺寸64×64的CTU划分为尺寸8×8的过程。
|
图 1 PU帧间预测划分模式 Figure 1 Inter-prediction partition mode |
|
图 2 CTU递归四叉树划分 Figure 2 CTU recursive quadtree partition |
在HEVC官方参考软件HM16.15中,对非对称帧间预测模式的遍历取决于对称预测模式。帧间预测划分模式的遍历顺序为先对称模式后非对称模式,在非对称模式预测之前将得到最佳对称预测模式。若本CU块的最佳对称划分模式BestCuMode为2N×2N或者2N×N,则水平非对称划分标志Test_Hor为真,进行2N×nU, 2N×nD遍历;类似地,若本CU块的最佳对称划分模式BestCuMode为2N×2N或者N×2N,则垂直非对称划分标志Test_Ver为真,遍历nL×2N, nR×2N;其他情况则需全部遍历[13]。因此,对于一个大小为64×64的CTU来说,帧间预测模式的遍历最低次数为1+4+16+256×6=1 662次,最多将遍历1+4+16+256×8=2 216次,由此可见,整个视频编码过程帧间预测模式选择的计算复杂度极高,占用了大部分的编码时间。
2 基于运动特性的帧间预测划分模式快速选择算法 2.1 运动特性与帧间预测划分模式相关性分析在HEVC,运动矢量(Motion Vector, MV)作为帧间预测的重要参数,它描述了当前编码帧PU块与参考帧匹配块内容位移的关系[14],通常PU块与匹配块的内容相似度极高,对于同一个CU块,不管其采用何种PU划分模式,其内容都不会变化,而只是将CU划分为相对较小的PU块或者相对较大的PU块来细化MV,细化MV意味着本CU块的各个子PU的MV并不集中,也就是说子PU块的运动方向不一致。
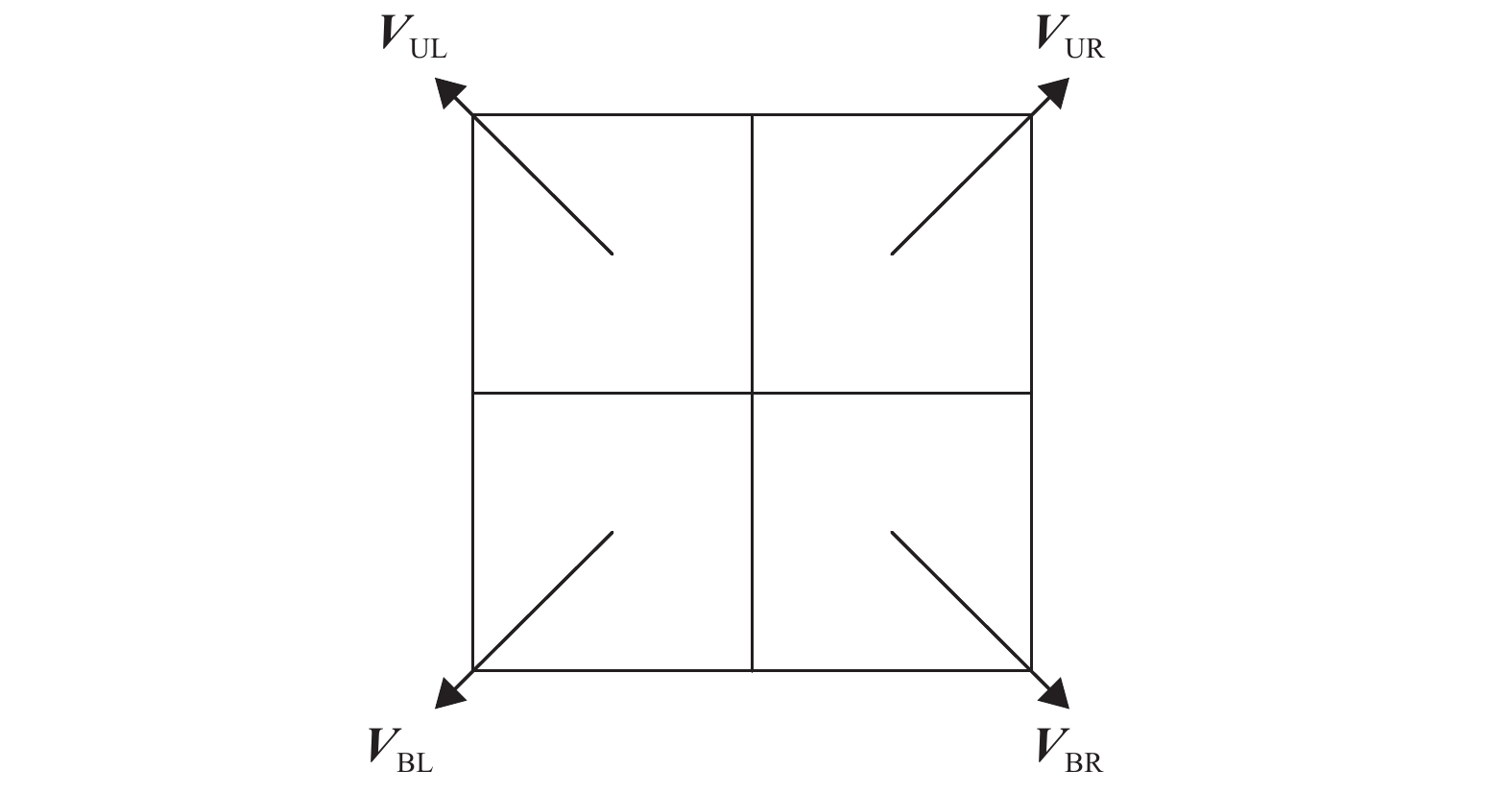
现在,考虑N×N模式的PU单元,如图3所示,将CU块划分为N×N的PU块,并将PU子块标记为PUUL,PUUR,PUBL,PUBR,每个PU子块对应的运动向量分别为VUL,VUR,VBL,VBR。从之前讨论可知Vi描述了PUi的运动特性,因此将当前CU块的运动特性Cmotion描述为
|
图 3 N×N模式的PU子块运动矢量 Figure 3 MVofsub-PU in N×N Mode |
| ${C_{{\rm{motion}}}} = f\left( {{{{V}}_{{\rm{UL}}}},{{{V}}_{{\rm{UR}}}},{{{V}}_{{\rm{BL}}}},{{{V}}_{{\rm{BR}}}}} \right)$ | (1) |
按照运动特性将CU分为统一运动、上下运动、左右运动、分散运动以及未确定性运动,统一运动特性是指4个子PU块都向同一个方向运动,从而导致运动向量具有相似性,包括方向相似和运动长度的相似,因此对于统一运动特性的CU可描述为
| $\{ {\rm{CU}}|{{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{BL}}}} = {{{V}}_{{\rm{BR}}}}\}$ | (2) |
上下运动特性就是指CU块的上方两个子PU块运动情况相似,下方两个子PU块运动情况相似,上下运动特性的CU描述为
| $\{ {\rm{CU}}|{{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{UR}}}} \ne {{{V}}_{{\rm{BL}}}} = {{{V}}_{{\rm{BR}}}}\}$ | (3) |
左右运动特性则是指CU块左方2个子PU块运动情况一致,而右方的2个子PU块运动一致,那么左右运动特性的CU可以描述为
| $\{ {\rm{CU}}|{{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{BL}}}} \ne {{{V}}_{{\rm{UR}}}} = {{{V}}_{{\rm{BR}}}}\}$ | (4) |
未确定性运动定义为在4个子PU块中,有1个子PU块的运动向量MV与其他3个子PU块的运动向量MV都不一致,那么未确定性运动的CU可以描述为
| $\begin{aligned} & \left\{ {{\rm{CU}}|{{{V}}_{{\rm{UL}}}} \ne {{{V}}_{{\rm{UR}}}} = {{{V}}_{{\rm{BL}}}} = {{{V}}_{{\rm{BR}}}}} \right\}\\ & \cup \left\{ {{\rm{CU}}|{{{V}}_{{\rm{BR}}}} \ne {{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{UR}}}} = {{{V}}_{{\rm{BL}}}}} \right\}\\ & \cup \left\{ {{\rm{CU}}|{{{V}}_{{\rm{BL}}}} \ne {{{V}}_{{\rm{BR}}}} = {{{V}}_{{\rm{UL}}}} = {{{V}}_{{\rm{UR}}}}} \right\}\\ & \cup \left\{ {{\rm{CU}}|{{{V}}_{{\rm{UR}}}} \ne {{{V}}_{{\rm{BL}}}} = {{{V}}_{{\rm{BR}}}} = {{{V}}_{{\rm{UL}}}}} \right\} \end{aligned}$ | (5) |
最后,把不符合以上特性描述的CU块均归类为分散运动特性CU。如表1所示是不同视频序列分别在低时延和随机接入配置下不同运动特性的最终PU块划分模式与运动特征描述的相符率。
| 表 1 运动特性与最终划分模式相符率 Table 1 Matching rate of motion characteristics and final partition mode % |
从表1中可以看到在不同编码配置下统一运动特性的CU块与最终PU划分模式相符率分别高达91.4%和92.2%,未确定运动特性的CU块与最终PU划分模式相符率分别达到了98.3%和96.7%,原因是1个运动向量与其他3个运动向量不同的CU均会被归类为未确定性运动。由表1可见从N×N模式划分得到的MV对CU运动特性的分类与当前CU块最终划分模式有着密切关系。
2.2 基于运动特性的帧间预测模式快速划分从之前的分析可知,在H.265/HEVC标准的帧间预测中,由于CU的递归划分特性以及帧间预测划分需要遍历多个参考帧与多种PU划分模式的运动估计,该模块的计算复杂度大。通过分析,CU块的运动特性与该CU块的帧间预测划分模式有很大的相关性,利用这种相关性,可以极大地降低帧间预测的计算复杂度,从而加速帧间预测,达到快速CU划分。
基于2.1的分析,在CU进行帧间PU块划分时,其PU块划分模式与当前CU块的运动特性Cmotion相关,那么CU块划分模式PUMode可表示为
| ${\rm{P}}{{\rm{U}}_{{\rm{Mode}}}} = m\left( {{C_{{\rm{motion}}}}} \right)$ | (6) |
为了使m(Cmotion)具体化为PUMode,将8种划分模式通过运动特性分为5类帧间PU划分模式,分别为统一运动、上下运动、左右运动、分散运动以及未确定性运动,2N×2N分类为统一运动模式PUunion,2N×N, 2N×nU, 2N×nD分类为上下运动模式PUup_down,N×2N, nL×2N, nR×2N定义为左右运动模式PUright_lift,N×N定义为分散运动模式PUscatter。那么根据拉格朗日率失真最优化准则在率失真优化方面的应用可知[15],最优的运动向量V*以及最优的划分模式PU*Mode可以通过式(7)得到
| $\left\{ {{{{V}}^{*}}{\rm{,PU}}_{{\rm{Mode}}}^*} \right\}\!=\! \mathop {{\rm{argmin}}}\limits_{{\rm{M}}{{\rm{V}}_n}} \left( {\mathop {{\rm{argmin}}}\limits_{{\rm{P}}{{\rm{U}}_{{\rm{Mode}}}}} J\left( {{{{V}}_n},{\rm{P}}{{\rm{U}}_{{\rm{Mode}}}}} \right)} \right)$ | (7) |
其中,PUmodeset∈{PUunion,PUup_down,PUright_lift,PUscatter},Vn是指在该PUMode下的运动搜索MV,通过计算即可得出最终最优的划分模式以及对应的运动向量。可见,通过上述算法可极大降低PU划分的遍历计算复杂度。
上述算法具体实现步骤如下:
(1) 对当前CU按照N×N模式进行划分,得到N×N模式下各个子PU块的运动向量VUL, VUL, VBL, VBR,进行步骤(2);
(2) 按照式(1)确定当前CU的运动特征Cmotion,通过Cmotion按照式(6)将本CU可能的PU划分模式归类为PUunion,PUup_down,PUright_lift,PUscatter的其中一种,进行步骤(3);
(3) 归类完成的CU块限定PU划分模式,进行运动搜索,利用式(7)进行拉格朗日率失真最优化处理,获得最优的PU划分模式以及对应的运动向量及其他运动信息,进行步骤(4);
(4) 存储当前CU的最佳帧间预测PU划分模式和其他预测信息,回到步骤(1)进行下一个CU的编码。
上述算法主要是针对帧间预测模式选择过程进行优化。由前文分析可知,帧间预测模式选择过程对于帧间预测模式的遍历最小为1 662次,最大为2 216次。
本文提出的算法,在帧间预测模式过程中将预测模式分为统一运动模式、上下运动模式、左右运动模式以及分散运动模式,它们分别对应1、3、3以及1种PU划分模式。不同CU块具有不同的运动特性,将遍历相应运动模式的PU划分,未确定性运动CU块则遍历统一运动模式、上下运动模式、左右运动模式一共7种PU划分模式。假设所有的CU都遍历非对称模式,那么1个CU最少遍历1次PU划分模式,最多遍历7次PU划分模式。那么对于1个CTU来说,最少的遍历次数为1+4+16+256×1=277次,最多的遍历次数为1+4+16+256×7=1 939次,也就等于原来的12.5%~87.5%。若所有的CU都跳过非对称模式,那么,1个CU块最少遍历1次PU划分模式,最多遍历3次PU划分模式。对于1个CTU来说,最少的遍历次数为1+4+16+256×1=277次,最多的遍历次数为1+4+16+256×3=831次,也就是原来的16.7%~50%。
3 实验与结果分析本小节将通过实验论证本算法的可行性和算法性能,实验采用HEVC官方参考软件HM16.15作为实验平台,操作系统为Linux,CPU为Inter® CoreTMi5-4210M @ 2.64 GHz,内存为8 G。本文测试了不同分辨率的5种级别的视频序列,分别为2 560×1 600的Class A视频序列Traffic、PeopleOnStreet,1 920×1 080的Class B视频序列Cactus、BasketballDrive,832×480的Class C视频序列BQMall、BasketballDrill,416×240的Class D视频序列BQSquare以及1 280×720的Class E视频序列FourPeople。其他具体配置如表2所示。
| 表 2 实验仿真配置参数 Table 2 Experimental configurations |
本算法对比对象为HM16.15,采用的评价标准为平均峰值信噪比BD-PSNR和BD-Bitrate[16],平均编码时间差为ΔET。
| $\Delta {\rm{ET}} = \frac{1}{4}\mathop \sum \limits_{i = 1}^4 \left( {\frac{{{\rm{E}}{{\rm{T}}_o}\left( {{\rm{Q}}{{\rm{P}}_i}} \right) - {\rm{E}}{{\rm{T}}_s}\left( {{\rm{Q}}{{\rm{P}}_i}} \right)}}{{{\rm{E}}{{\rm{T}}_o}\left( {{\rm{Q}}{{\rm{P}}_i}} \right)}}} \right) \times 100{\rm{\% }}$ | (8) |
其中,QPi∈{22, 27, 32, 37},ETo(QPi)表示HM16.15算法在QPi的编码时间,ETs(QPi)表示本文算法在QPi的编码时间。实验结果如表3。从表3中可以看出,在低时延编码结构配置下,5个级别的视频序列在本文算法下相比HM16.15编码时间降低了31.6%,同时BDPSNR下降了–0.06 dB,BDBR增加了1.42%;在随机接入编码结构配置下,编码时间降低了27.4%,同时BDPSNR下降了0.05 dB,BDBR增加了1.43%。说明本文算法在轻微地增加了视频编解码失真度和码率的情况下,显著地降低了编码时间。
| 表 3 实验仿真结果1) Table 3 Experimentalresults |
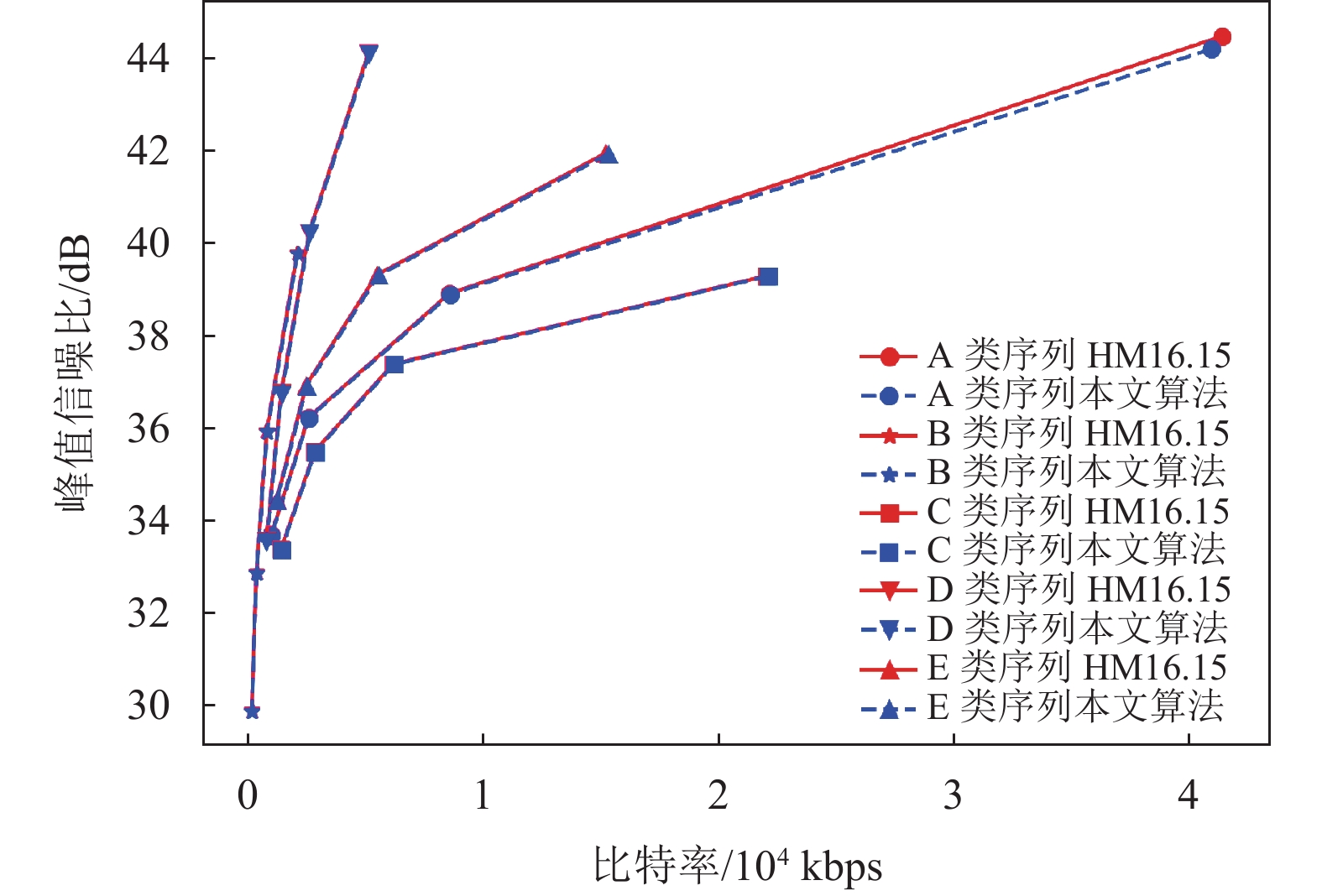
为了展现本算法对编码器编码性能的影响,本文做出HM16.15和本文算法下编码器的RD曲线,如图4和图5所示是不同级别的视频序列的RD曲线。从图4和图5中可以看出,RD曲线都是递增的,这是由于不同的QP对应不同的PSNR,QP越大,量化步长越大,导致失真度增加,此时PSNR则减小,相应地比特率也会减小。在随机接入和低时延2种不同配置下,在不同级别的视频序列中,本算法的RD曲线在HM16.15的RD曲线下方,但是相差极小,这说明本算法对比HM16.15来说,编码器的编码性能基本不变,即对率失真曲线的影响极小,结合表3中的实验结果来看,本算法可以在保证编码性能不受太大影响的条件下对降低编码时间取得较显著的效果。

|
图 4 随机接入配置下的RD曲线 Figure 4 RD performance with random access |
|
图 5 低时延配置下的RD曲线 Figure 5 RD performance with low delay |
本文利用帧间预测的运动矢量来确定一个CU的运动特征,通过分析和实验,表明CU的运动特征与帧间预测划分模式有较强的相关性,从而提出基于编码单元运动特征的帧间预测划分模式快速选择算法。该算法先让CU块进行N×N的划分模式帧间预测,利用子PU块的运动矢量确定当前CU块的运动特征,最后通过CU块的运动特征跳过某些帧间预测划分模式。实验结果表明,本文提出的算法与HM16.15相比,在基本不降低视频编码质量和轻微增加编码比特的情况下,显著降低了编码时间。
| [1] |
SULLIVAN G J, OHM J, HAN W J, et al. Overview of the high efficiency video coding (HEVC) standard[J].
IEEE Transaction on Circuits and System for Video Technology, 2012, 22(12): 1649-1668.
DOI: 10.1109/TCSVT.2012.2221191. |
| [2] |
万帅, 杨付正. 新一代高效视频编码H.265/HEVC: 原理、标准与实现[M]. 北京: 电子工业出版社, 2014: 12-13.
|
| [3] |
HAN W J, MIN J, KIM I K, et al. Improved video compression efficiency through flexible unit representation and corresponding extension of coding tools[J].
IEEE Transaction on Circuits and System for Video Technology, 2010, 20(12): 1709-1720.
DOI: 10.1109/TCSVT.2010.2092612. |
| [4] |
CHOI K, JANG E S. Fast coding unit decision method based on coding tree pruning for high efficiency video coding[J].
OptEng, 2012, 50(3): 030502.
|
| [5] |
JIANG X, SONG T. High efficiency CU depth prediction algorithm for high resolution applications of HEVC[C]//TENCON 2015-2015 IEEE Region 10 Conference. Macao, China: IEEE, 2015: 488-491.
|
| [6] |
KIM D H, KIM Y H, PARK W C. Selective CU depth range decision algorithm for HEVC encoder[C]//The 18th IEEE International Symposium on Consumer Electronics (ISCE 2014). Jeju Island, South Korea: IEEE, 2014: 468-470.
|
| [7] |
LEE J, KIM S, LIM K, et al. A fast CU size decision algorithm for HEVC[J].
IEEE Transactions on Circuits and Systems for Video Technology, 2015, 25(3): 441-421.
|
| [8] |
伍冠健, 宋立峰. HEVC快速帧内模式和深度决策算法[J].
广东工业大学学报, 2015, 32(4): 132-137.
WU G J, SONG L F. Fast intra mode and depth decision algorithm forHEVC[J]. Journal of Guangdong University of technology, 2015, 32(4): 132-137. DOI: 10.3969/j.issn.1007-7162.2015.04.024. |
| [9] |
李强, 覃杨微. 一种基于空时域相关性的HEVC帧间预测模式快速决策算法[J].
重庆邮电大学学报: 自然科学版, 2016, 28(1): 9-16.
LI Q, QIN Y W. A fast inter prediction mode decision algorithm for HEVC based on spatial-temporal correlations[J]. Journalof Chongqing University of Posts and Telecommunications: Natural Science Edition, 2016, 28(1): 9-16. |
| [10] |
LEE A, JUN D S, SEOK J. An efficient inter prediction mode decision method for fast motion estimation in HEVC[C]//2013 International Conference on ICT Convergence. Jeju, South Korea: IEEE, 2013: 504-507.
|
| [11] |
KIHO C, JANG E S. Early TU decision method for fast video encoding in high efficiency video coding [J]. Electronics Letters, 2012, 48(12): 689-691.
|
| [12] |
WANG C C, LIAO Y C, WANG J W, et al. An effective TU size decision method for fast HEVC encoders[C]//2014 International Symposium on Computer, Consumer and Control. Taiwan: IEEE, 2014: 1195-1198.
|
| [13] |
沈晓琳. HEVC低复杂度编码优化算法研究[D]. 杭州: 浙江大学, 2013.
|
| [14] |
MARPE D, WIEGAND T, SULLIVAN G J. The H.264/MPEG4 advanced video coding standard and its applications[J].
IEEE Communications Magazine, 2006, 44(8): 134-143.
DOI: 10.1109/MCOM.2006.1678121. |
| [15] |
SULLIVAN G J, BAKER R L. Rate-distortion optimized motion compensation for video compression using fixed or variable size blocks[C]//IEEE Global TelecommConfGLOBECOM ’91. Phoenix, AZ, USA: IEEE, 1991: 85-90.
|
| [16] |
BJONTEGAARD G. Calculation of average PSNR difference between RD curves[C]//13th VCEG-M33 Meeting. Austin, TX, USA: ITU-T, 2001, 4: 2-4.
|
 2020, Vol. 37
2020, Vol. 37