2. 北京电子工程总体研究所,北京 100854
2. Beijing Institute of Electronic System Engineering, Beijing 100854, China
因为空中目标总是通过一定的战术机动达成其战术意图,判明目标的战术意图是作战的重要任务之一[1]。特别地,由于上下左右4种转弯机动是所有机动运动的基础,所以对4种转弯机动类型进行识别,在军事技术等领域有重要应用。
传统的机动类型识别算法有朴素贝叶斯分类器、决策树等。许多研究者都将贝叶斯分类器[2-3]和决策树[4]等应用于汽车机动类型的识别问题中,并取得了一定的成果。朴素贝叶斯分类器是一种基于贝叶斯定理的分类算法,它假设特征之间相互独立,即给定一个未知的数据样本X,分类器将识别对应数据属于具有最高后验概率的类别。决策树是一种拥有树形结构的分类算法,它由有向边和节点构成,内部节点代表某个属性或特征,叶节点代表类别。但是这些分类算法也存在许多缺点,朴素贝叶斯分类器存在的缺点:需要假设特征之间相互独立,而实际应用中往往不成立,并且无法处理基于特征组合所产生的变化结果;需预先知道先验概率,但是先验概率往往取决于假设;通常情况下,准确率取决于所选取的变量。决策树存在的缺点:当各个类别样本数量不相等时,信息增益会偏向于拥有更多数值的特征,不擅长对数值结果进行预测;忽略数据集中属性之间的相关性,并且决策树不适合识别复杂的机动类型,因为很难找到一个描述它的唯一逻辑[4]。
近年来迅速发展的神经网络方法在诸多领域展示了惊人的效果,出现了基于人工神经网络和专家系统的自动目标识别方法[5]、基于循环神经网络多目标跟踪的方法[6],其中循环神经网络在时序数据处理上展示了优良的效果。为了克服传统算法在机动类型识别上的缺点,本文提出了基于循环神经网络的目标转弯机动类型识别方法。由于采用的转弯机动类型数据是由雷达获取的时序数据,所以适用循环神经网络。首先,由雷达获取一组高度为5 km,距离中心20 km的数据(其中雷达获取数据的精度为5 m,即真实数据与雷达获取的数据在5 m范围内),并由真实数据和创建的机动运动模型进行数据增广;其次利用循环神经网络中Bi-LSTM(Bidirectional Long Short-Term Memory)、LSTM(Long Short-Term Memory)、RNN(Recurrent Neural Networks)和GRU(Gated Recurrent Unit)4种神经网络分别开展样本数据训练,得到转弯类型识别模型;最后,利用模型进行测试,实验结果表明循环神经网络能够有效识别目标转弯机动类型,其中Bi-LSTM网络效果最佳。
1 机动目标运动模型构建匀速转弯(constant velocity, CT)模型[7]是典型的转弯运动模型,它把目标的运动看成是匀速圆周运动,并根据目标运动的速度、加速度和角速度之间的几何关系和运动学关系,从而得出目标状态和角速度之间的转移关系。在一个惯性系统中,设p,v和a分别表示目标的位置、速度和加速度向量。对一个绕着固定中心p0旋转的目标运动模型可以表示为
| $ {{v}} = {{\varOmega}} \times \left( {{{p}} - {{{p}}_0}} \right) $ | (1) |
其中Ω表示角速度向量,
| $ {{a}} = {{\varOmega}} \times {{v}} $ | (2) |
由式(2)进一步可得到
| $ {{\varOmega }} = \frac{{{{v}} \times {{a}}}}{{{{{v}}^2}}} $ | (3) |
即速度、加速度和角速度的方向是两两垂直的,可通过右手定则来确定。
机动目标运动模型的数学表达为
| $ {{{X}}_{k + 1}} = {{{F}}_k}{{{X}}_k} $ | (4) |
其中,近似匀速运动模型(nearly constant velocity,NCV)的状态向量表示为
| ${{{X}}_k} = {[{{{x}}_k}\;{\dot {{x}}_k}\;{{{y}}_k}\;{\dot {{y}}_k}\;{{{z}}_k}\;{\dot {{z}}_k}]^{\rm{T}}}$ | (5) |
近似匀加速运动模型(nearly constant acceleration,NCA)的状态向量表示为
| ${{{X}}_k} = {[{{{x}}_k}\;{\dot {{x}}_k}\;{\ddot {{x}}_k}\;{{{y}}_k}\;{\dot {{y}}_k}\;{\ddot {{y}}_k}\;{{{z}}_k}\;{\dot {{z}}_k}\;{\ddot {{z}}_k}]^{\rm{T}}}$ | (6) |
状态转移矩阵
| ${{{F}}_k} = \left[ {\begin{array}{*{20}{l}} {{{{A}}_k}}&{{{{0}}_{m \times m}}}&{{{{0}}_{m \times m}}} \\ {{{{0}}_{m \times m}}}&{{{{A}}_k}}&{{{{0}}_{m \times m}}} \\ {{{{0}}_{m \times m}}}&{{{{0}}_{m \times m}}}&{{{{A}}_k}} \end{array}} \right]$ | (7) |
近似匀速运动模型可以展示在受控制平面内的机动目标运动的特点。高速运动的目标,在发生机动的时候,它们的速度基本保持不变。对恒速机动目标进行建模的通常方法是假设平面内转弯率保持不变。
| ${{{A}}_k} = \left[ {\begin{array}{*{20}{l}} 1&\displaystyle {\frac{{\sin ({{{\varOmega}}_k}{{{\delta}}_k})}}{{{{{\varOmega}}_k}}}}&\displaystyle {\frac{{1 - \cos ({{{\varOmega}}_k}{{{\delta}}_k})}}{{{{\varOmega}}_k^2}}}\\ 0&{\cos ({{{\varOmega}}_k}{{{\delta}}_k})}&\displaystyle {\frac{{\sin ({{{\varOmega}}_k}{{{\delta}}_k})}}{{{{{\varOmega}}_k}}}}\\ 0&{ - {{{\varOmega}}_k}\sin ({{{\varOmega}}_k}{{{\delta}}_k})}&{\cos ({{{\varOmega}}_k}{{{\delta}}_k})} \end{array}} \right]$ | (8) |
近似匀速运动模型的状态转移矩阵
循环神经网络(Recurrent Neural Networks,RNN)[9-10]是一类流行的神经网络模型,它不仅将当前自身的输入作为网络输入,还将之前感知到的一起作为输入,并且接受其他神经元的信息,所谓的“循环”,指的是隐藏层中每个神经元的循环使用。循环神经网络在自然语言处理,语音识别等任务中展示了良好的效果。但是循环神经网络存在一个长期依赖问题,当输入序列比较长时,会出现梯度消失和梯度爆炸问题。对此人们提出了很多改进型网络,其中最有效的是引入门控机制,由此产生了LSTM、Bi-LSTM和GRU等改进型网络。循环神经网络通过使用带自反馈的神经元,能够处理任意长度的时序数据,给定一个输入序列
| ${h_t} = f({h_{t - 1}},{x_t})$ | (9) |
其中
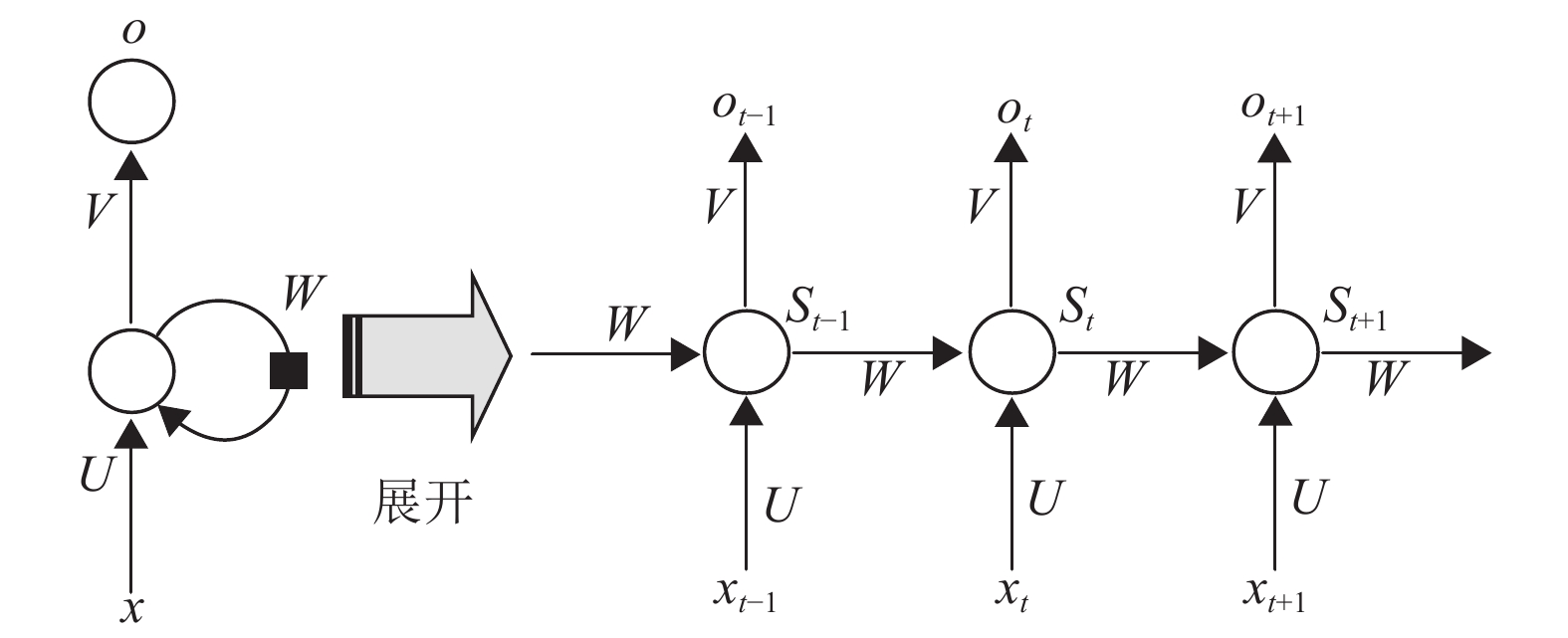
|
图 1 循环神经网络及展开结构图 Figure 1 Recurrent neural networks and expanded structure |
一般的神经网络中每层之间的节点是无连接的,层与层之间是全连接的,而RNN则不同,每层之间的节点是有连接的,隐藏层的输入不但包含输入层的输出,而且包含上一个时刻的输出。具体表现在每次循环中,部分信息会存留在隐藏神经元之中,并与新的信息一起输入至下一个神经元,对最终的输出产生影响。
2.1.2 LSTMLSTM(Long Short-Term Memory,LSTM)为长短期记忆网络,它的出现主要是为了解决训练过程中梯度消失和梯度爆炸问题,与RNN的主要区别在于算法中加入了门控机制,一共有3个门[11-12]:输入门、遗忘门和输出门。信息输入LSTM网络中,会由规则来判断是否有用,算法认可的信息将会留下,否则将被遗忘。
2.1.3 Bi-LSTMBi-LSTM[13]为双向长短期记忆网络,与LSTM的计算流程类似,Bi-LSTM在其基础上添加了反向运算,并且两个方向连接着一个输出层,这种结构很好地提供了上下文信息。
2.1.4 GRUGRU(Gated Recurrent Unit,GRU)是LSTM的一种变体,它保留了LSTM的长期记忆能力,但比LSTM网络更加简单,GRU将LSTM中的输入门、遗忘门和输出门替换为更新门和重置门,并将输出的两个向量合二为一[14]。
2.2 识别算法实现过程针对转弯机动类型数据的特点,图2为转弯机动类型识别模型的系统结构。由雷达获取上下左右4种转弯机动的数据,应用不同类型的循环神经网络模型对其进行识别。首先对获取的数据进行数据预处理,将数据输入至各模型,然后对时序数据提取特征,最后利用Softmax对4种转弯机动类型进行识别。数据集分为两部分:一部分用于训练神经网络,称为训练集,占数据集的80%;另一部分为测试集,占数据集的20%。首先训练出模型,然后利用测试集评估模型的泛化能力,得到各模型对机动类型分类结果的准确率,从而评估模型的优良。
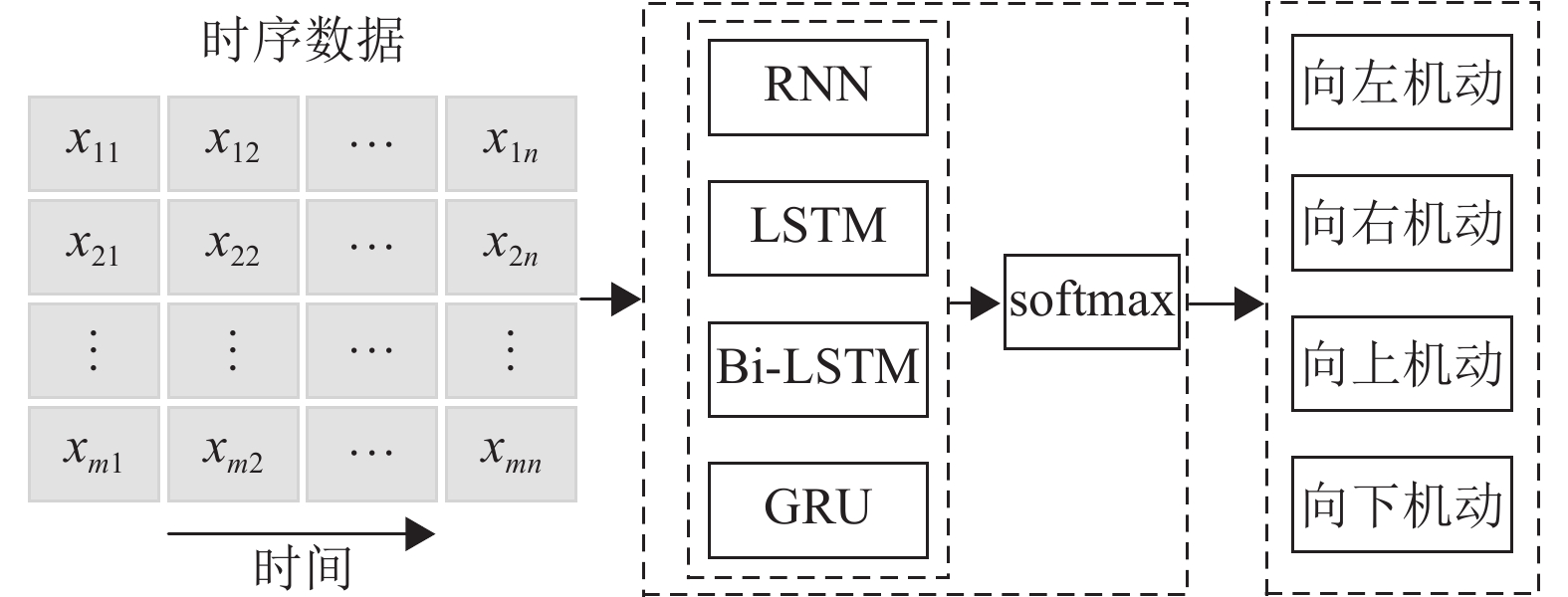
|
图 2 转弯机动识别系统结构 Figure 2 System structure of turning maneuver identification |
实验数据的模型为直线运动加上近似匀速转弯运动,目标(看成质点)先直线匀速运动,然后向左、右、上和下机动转弯运动(如图3所示)。假设目标距离观测中心50 km,高度由5 km至10 km,加速度为5 g,任意方向朝观测中心做机动转弯运动。由于空域中有无数个点,所以实验数据采取距离观测中心每间隔5 km,高度间隔1 km,每间隔45°生成一段包含直线和转弯的采用北天东坐标系[15-16](如图4所示)的数据用于训练循环神经网络。以向左机动运动为例,各角度部分数据如图5所示。
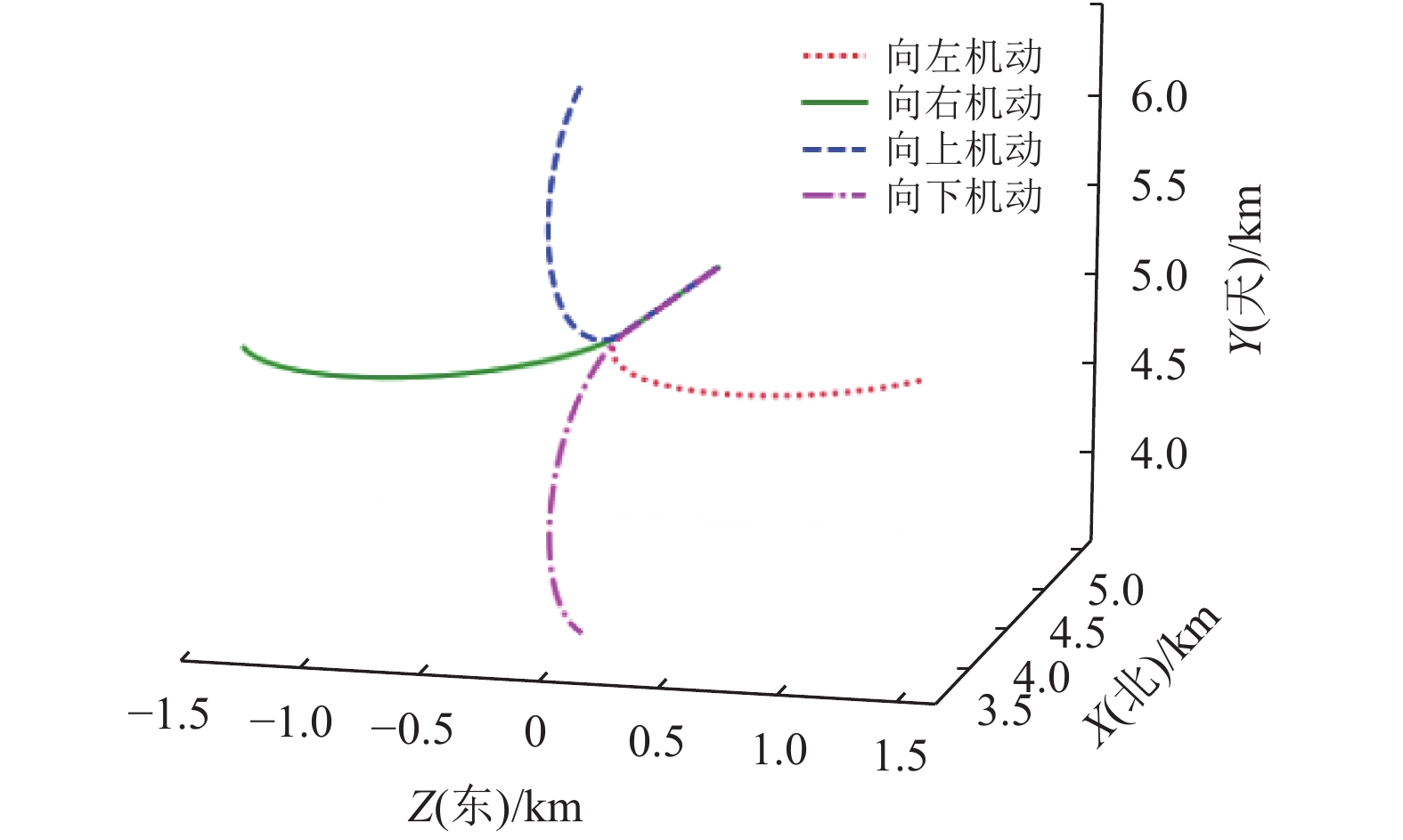
|
图 3 转弯机动类型示意图 Figure 3 Schematic diagram of turning maneuver |
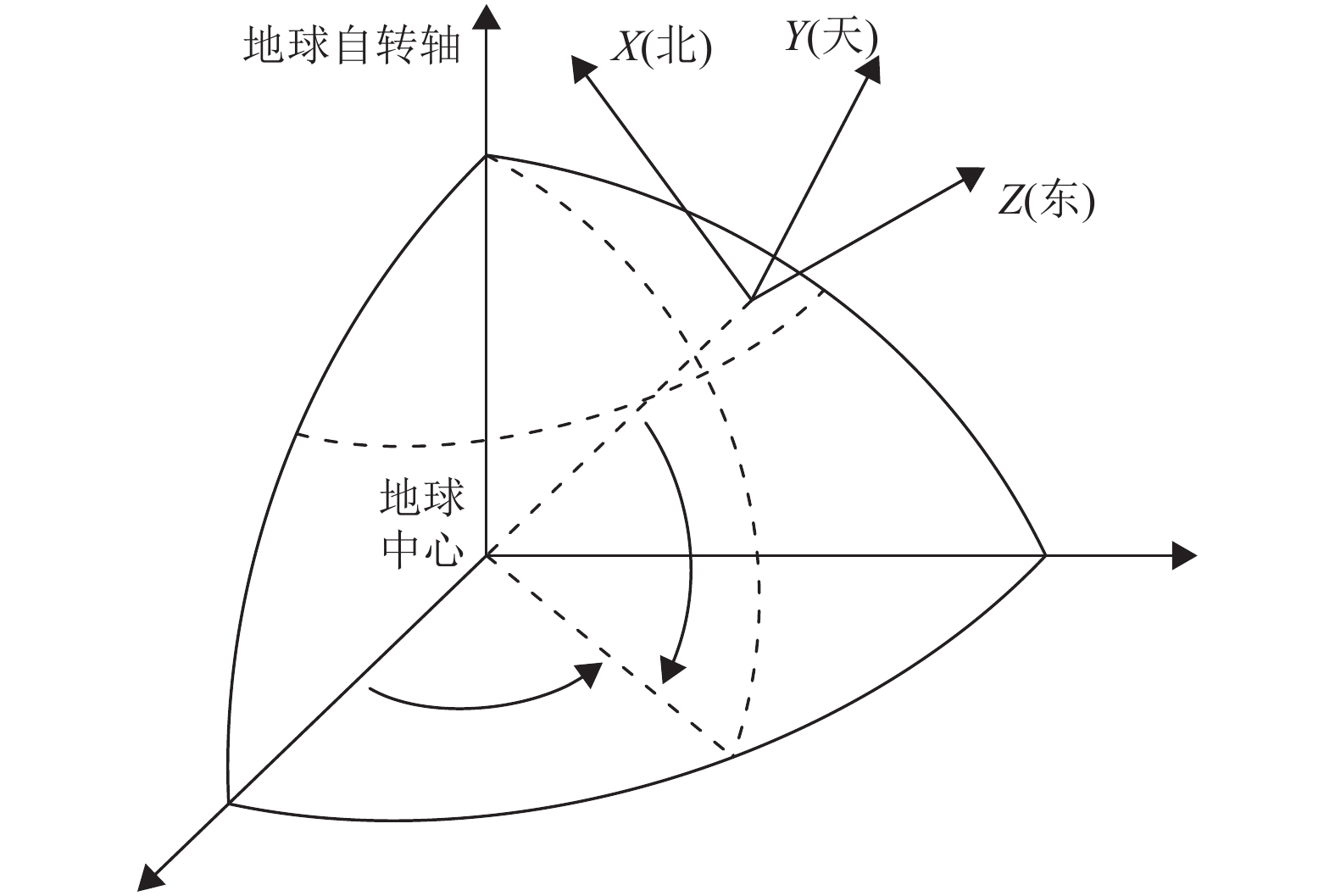
|
图 4 北天东坐标系示意图 Figure 4 Schematic diagram of the local Cartesian coordinates coordinate system |
|
图 5 向左机动各角度部分数据 Figure 5 Maneuvering all angles of data to the left |
本文使用的计算机环境为Ubantu16.04、Python 3.6.4、CUDA9.0、基于TensorFlow后端的Keras深度学习框架,CPU为Intel Xeon(R) E5-1620 v3 @ 3.50 GHz×8,GPU为Quadro M2000,32 GB内存。
在深度学习系统中,调整模型参数是一个手动过程,为了实现最优模型,本文调整了相应的模型参数,如网络层数、神经元个数和学习率等。
(1)网络层数的确定。一般来讲,网络层数越多,所能提取的特征就越全面,精度就越高。但是针对本数据集究竟应该设置几层网络,还需要实验验证。本文取10次实验的平均准确率,结果如表1所示。由表1可知,网络的分类准确率随着网络层数的增加而变化,呈现出先升后降的趋势。这是由于提高网络层数会产生以下影响:训练更多的层数需要更高的培训成本,且更难训练;较高级别的模型由较低级别的隐藏层收缩数据。根据实验结果,RNN、LSTM和GRU增加到4层网络时,准确率并没有提高,为使网络具有较高的准确率,且能保持良好的性能,确定对RNN、LSTM和GRU使用3层网络,而由于多层Bi-LSTM的收敛效果差,并且计算复杂性比较高,1层Bi-LSTM网络准确率就十分高,所以确定对Bi-LSTM使用1层网络。
| 表 1 神经网络不同网络层数准确率对比 Table 1 Comparison of the accuracy of different network layers in four neural networks % |
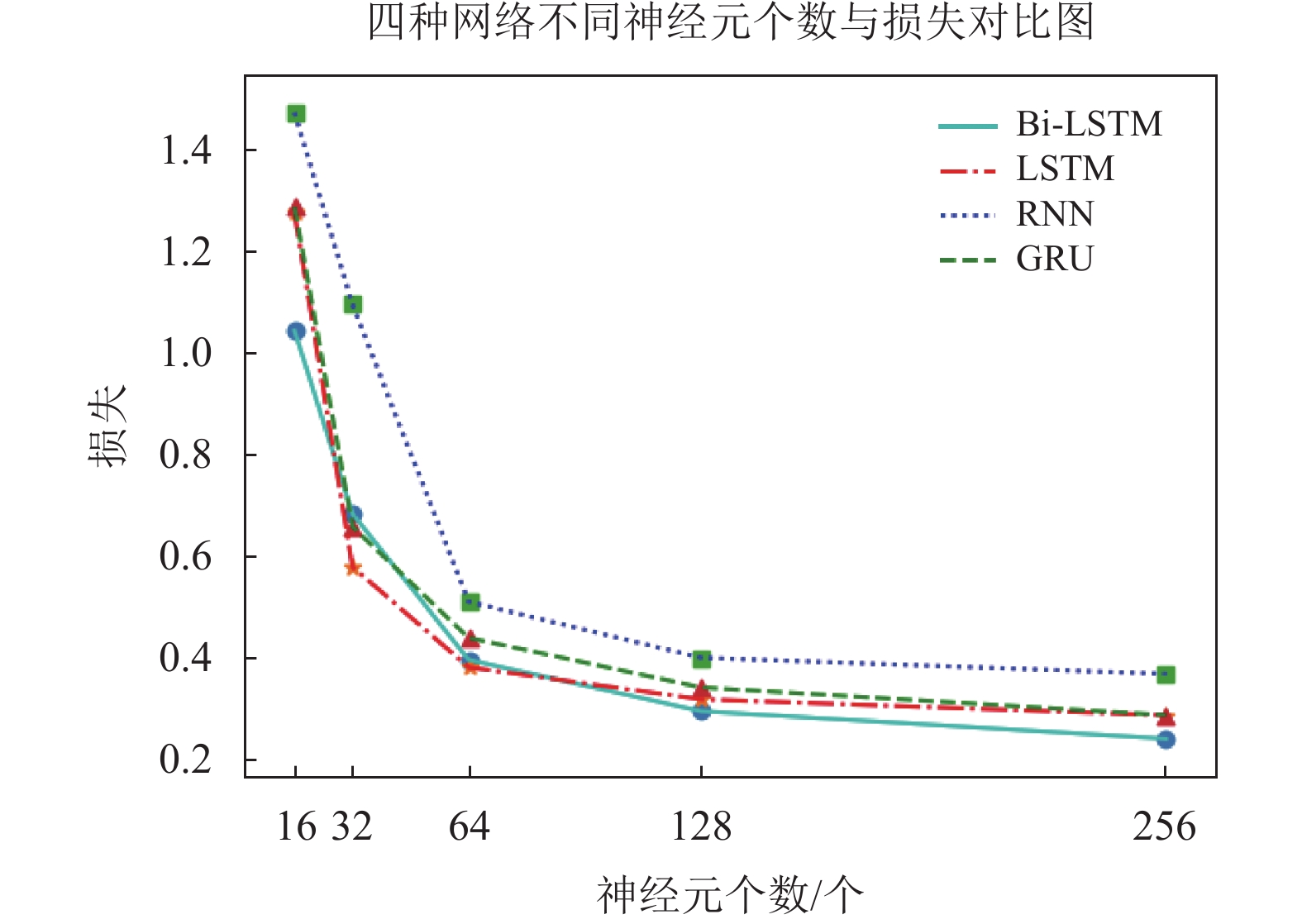
(2)神经元个数的确定。神经元数量即隐藏层的节点数是深层神经网络提取数据特征能力大小的重要参数。隐藏层节点数增多,可使网络的系统误差减小,提高机动类型识别的准确性,但是也会使网络难以训练;隐藏层节点数太少,网络性能可能欠佳。图6为4种神经网络神经元个数与损失的关系对比图,从中可知,随着神经元个数的增加,网络损失逐渐减小,虽然神经元个数为256时的网络损失小于神经元个数为128的网络,但是两者相差很小,并且实验结果表明,神经元个数为256比神经元个数为128时更加难训练,并且训练时间更长。因此,确定4种神经网络各层的神经元个数为128。
|
图 6 不同隐藏层神经元个数的网络损失对比 Figure 6 Comparison of network loss between different hidden layer neurons |
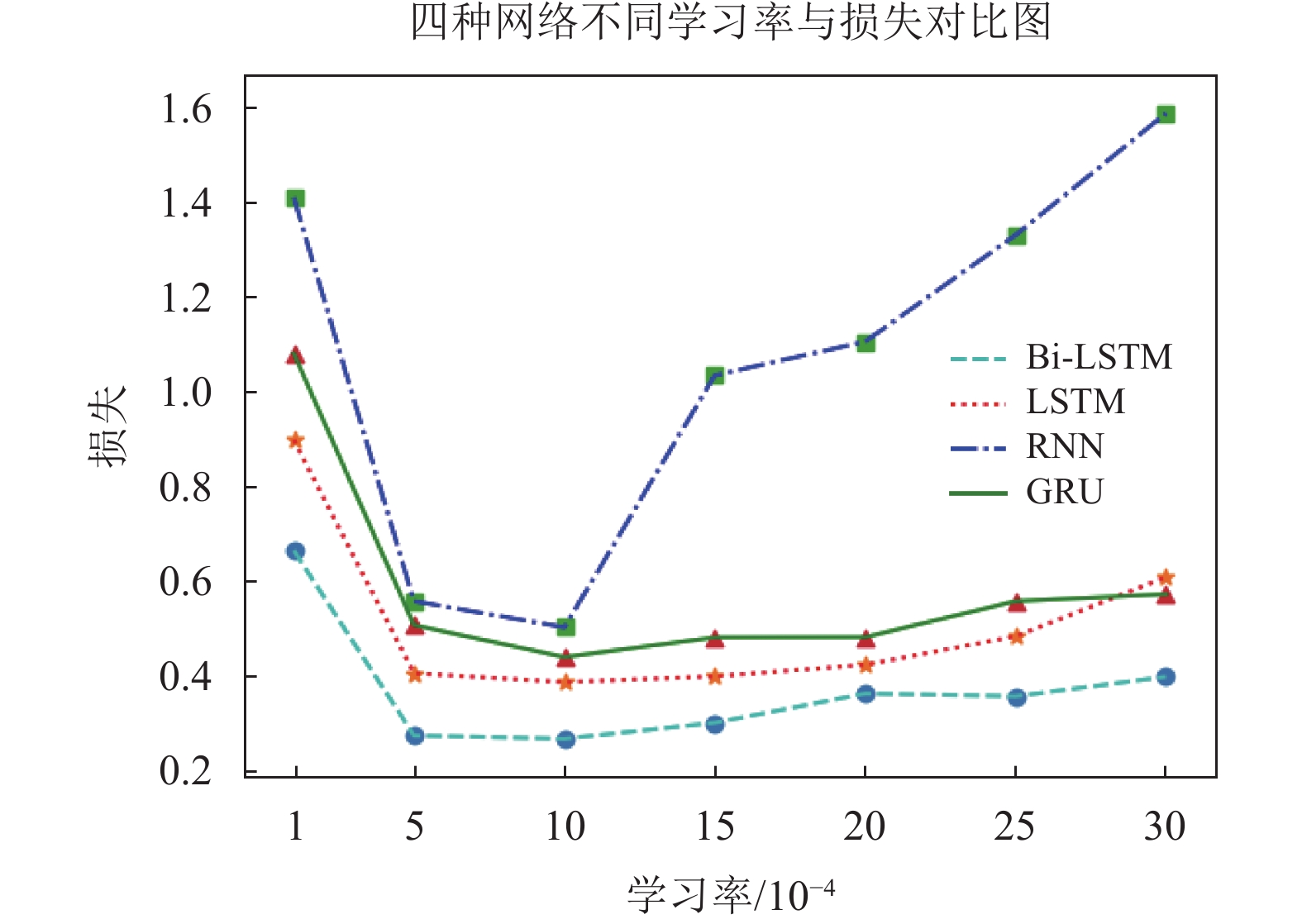
(3)学习率的确定。学习率决定控制参数更新的幅度。学习率太大可能导致参数在最优值的两侧来回取值,学习率太小会大大降低优化速度,导致极长的训练时间,并且不一定效果好。在网络层数和神经元个数确定的情况下,通过多次实验选择不同的学习率,如图7所示,实验了0.000 1~0.003之间的学习率,损失整体呈现先下降后上升的趋势,将损失的最小值对应的学习率设为该网络的学习率。根据实验结果,将Bi-LSTM、RNN和GRU的学习率都设为0.001,将LSTM的学习率设置为0.000 5。
|
图 7 不同学习率的网络损失对比 Figure 7 Comparison of network loss at different learning rates |
模型的其他参数设置为:采用RMSprop优化器,损失函数采用categorical_cross_entropy,激活函数采用softmax,迭代次数为500。
3.3 传统算法和神经网络性能比较本文将4种循环神经网络与朴素贝叶斯(Naive Bayes,NB)及决策树(Decision Tree,DT)算法进行平均识别错误数以及平均识别正确率比较,如表2所示。由表2可知,从整体上来说,循环神经网络的平均识别正确率都比朴素贝叶斯和决策树高,特别是对于朴素贝叶斯算法而言,循环神经网络展示了优良的效果。而循环神经网络,特别是Bi-LSTM的识别正确率远优于朴素贝叶斯和决策树等传统算法。
| 表 2 传统算法和神经网络实验结果对比 Table 2 Comparison of traditional algorithm and neural network experiment results |
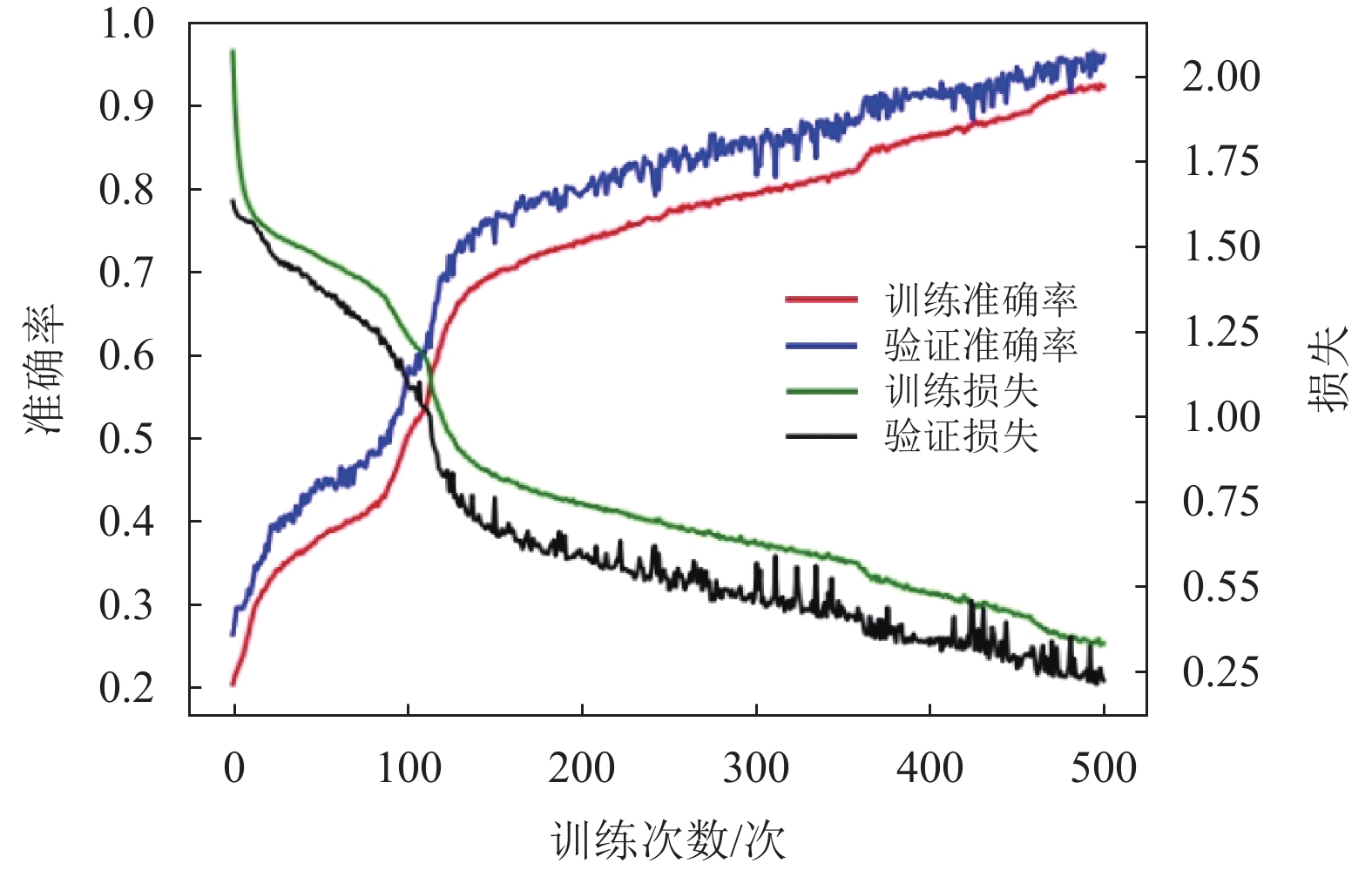
对于4种神经网络,各算法的训练和验证准确率,损失与训练次数的关系如图8至图11所示。由图8可知,RNN训练的损失下降得较慢,并且准确率提高得也较慢,准确率及损失曲线有些异常;由图9可知,LSTM的验证损失波动较大,验证准确率波动也较大;由图10可知,Bi-LSTM的准确率和损失变化比较平稳,随着训练次数的增加,准确率也在慢慢提高;由图11可知,GRU在迭代200次之后训练准确率略有下降,并且损失波动比较大。对比4种网络训练的准确率及损失,从训练的分类准确率来看,RNN、LSTM和Bi-LSTM训练的准确率都比较高,随着迭代次数的增加,三种网络的准确率均呈现上升的趋势。其中,迭代500次后,Bi-LSTM和RNN的准确率比LSTM和GRU要高,并且Bi-LSTM的准确率最高,损失波动最小。为了进一步对比4种网络,由表3可知,Bi-LSTM训练完成时的损失最小,训练集及测试集的准确率均达到98%以上,明显优于其他3种网络。
|
图 8 RNN训练和验证准确率及损失随训练次数的关系图 Figure 8 RNN training and verification accuracy and loss as a function of training times |
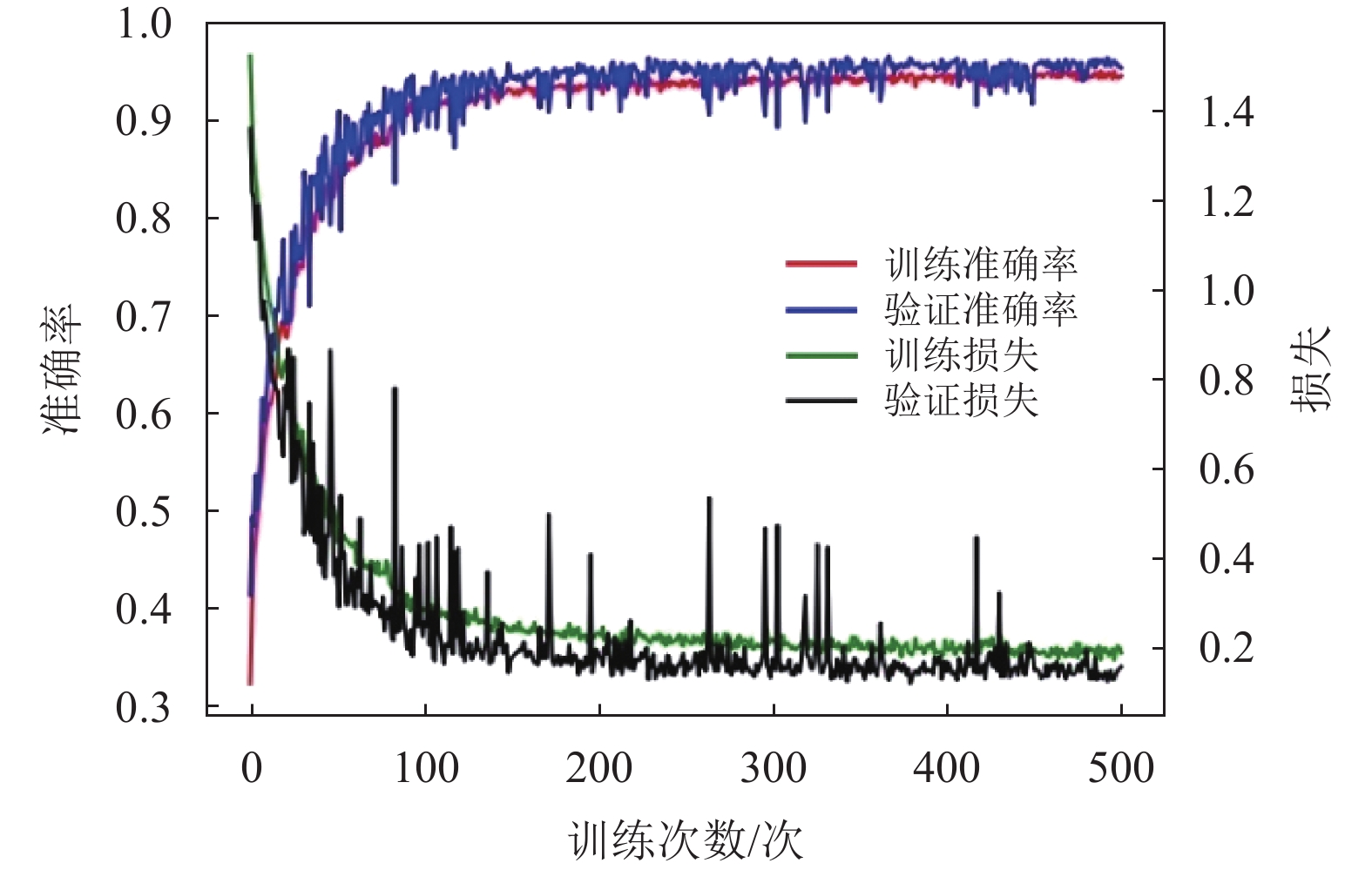
|
图 9 LSTM训练和验证准确率及损失随训练次数的关系图 Figure 9 LSTM training and verification accuracy and loss as a function of training times |
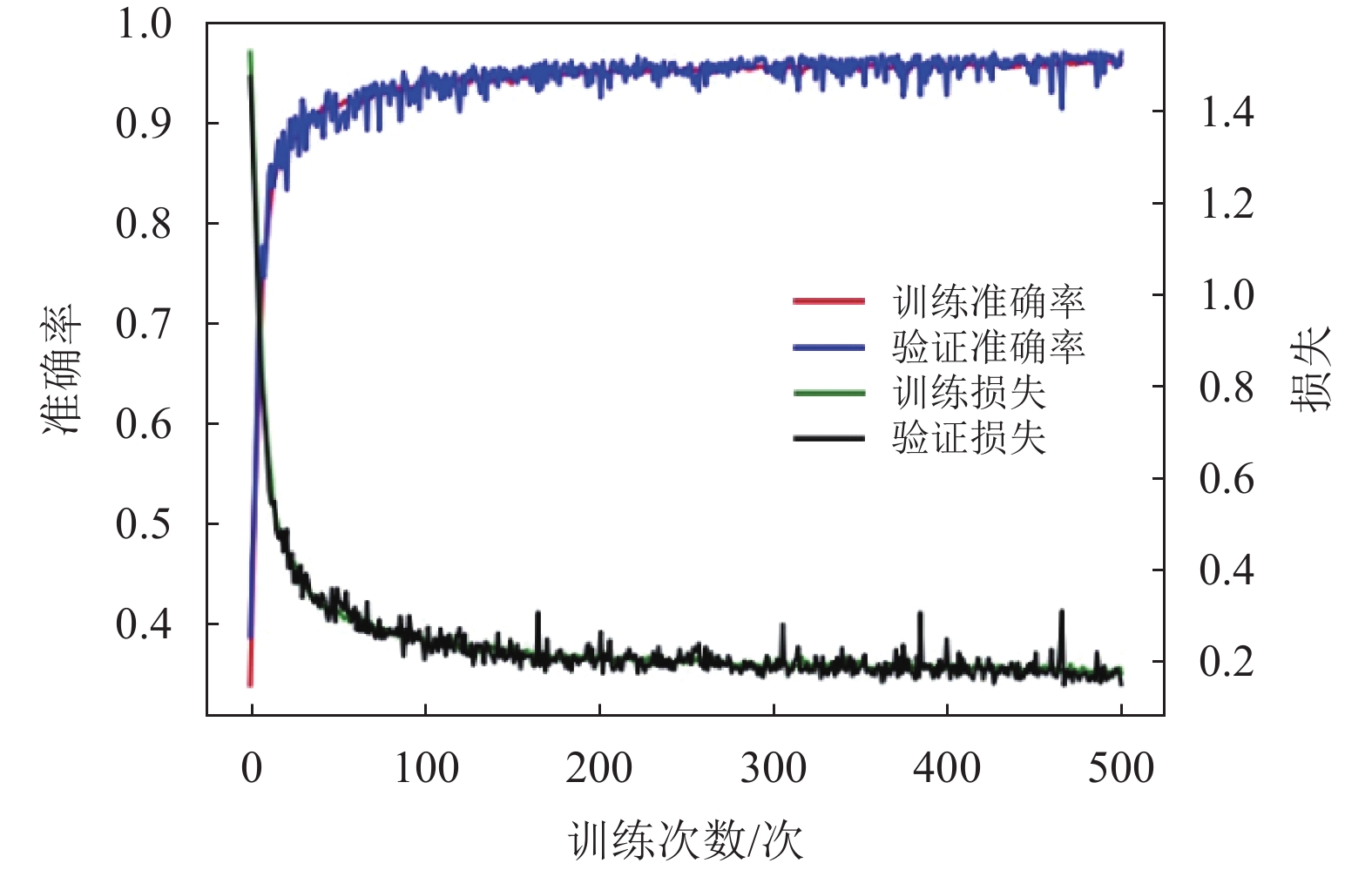
|
图 10 Bi-LSTM训练和验证准确率及损失随训练次数的关系图 Figure 10 Bi-LSTM training and verification accuracy and loss as a function of training times |
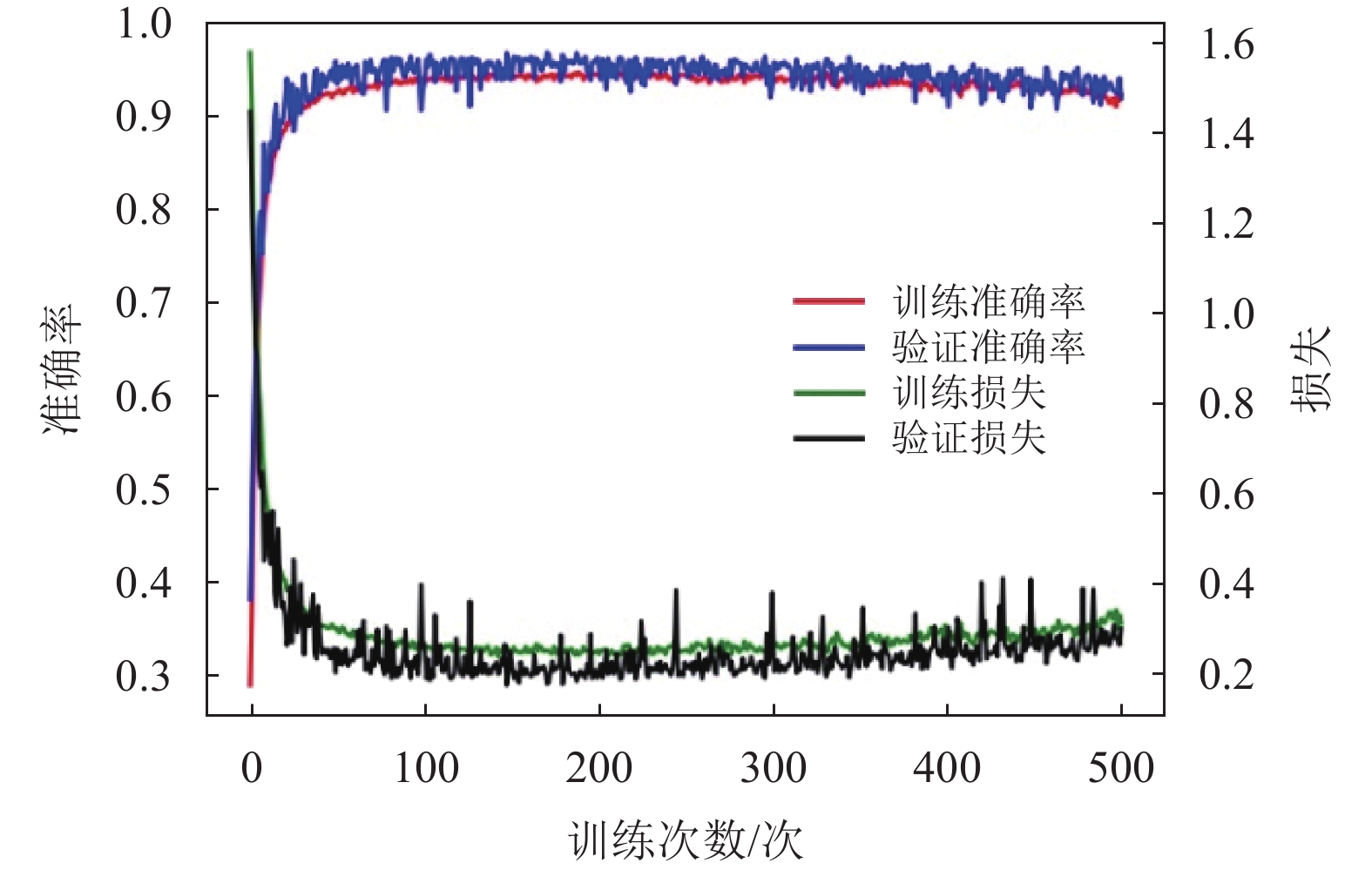
|
图 11 GRU训练和验证准确率及损失随训练次数的关系图 Figure 11 GRU training and verification accuracy and loss as a function of training times |
| 表 3 网络损失及准确率对比 Table 3 Comparison of four network losses and accuracy |
为了进一步验证Bi-LSTM网络的有效性,本文对4种网络分别测试了前4拍(一拍即为一个运动点)的识别准确率,结果见表4。对于机动类型的识别,越早正确识别机动类型,则越有利于开展后续措施。由表4可知,Bi-LSTM在第1拍的识别准确率便略高于其他网络,在第2拍的时候识别准确率便达到了96.64%,第4拍的时候识别准确率更是达到了99.28%,这为机动类型的准确识别提供了有力的保障。另外由于任何传感器均存在误差,所以本文将数据集分别添加了偏差2 m、5 m和9 m的高斯随机噪声对网络性能进行测试,测试结果见表5。由表5可知,对于添加了不同的噪声数据,Bi-LSTM训练完的准确率在不同δ的情况下准确率均高于其他3种网络。因此,对于机动类型的识别,循环神经网络能够对其进行高准确率识别,Bi-LSTM是一种有效的网络。
| 表 4 网络前四拍识别准确率 Table 4 The accuracy of the first four shots of the four networks % |
| 表 5 网络添加噪声数据测试准确率 Table 5 Test accuracy of four types of network added noise data % |
本文通过雷达获取的部分数据加上构建的运动模型生成了有效的数据集,对上下左右4种转弯机动类型进行识别,分别实验了RNN、LSTM、GRU和Bi-LSTM4种循环神经网络,并将实验结果进行了对比分析,结果表明,相对于传统的朴素贝叶斯和决策树算法,本文采用循环神经网络的方法,不需要对数据进行大量计算,直接输入至训练好的模型便能快速识别出目标的转弯机动类型,取得了比较好的识别机动类型的效果,其中,Bi-LSTM的识别准确率最高,达到了98.85%,并且对噪声数据也具有高准确率,是一种有效的转弯机动类型识别网络。未来将在构建更加有效的数据集、更加有效的神经网络、更多的机动类型、复合机动类型、目标高速及变速运动等情况下对目标机动类型识别作进一步研究。
| [1] |
冷画屏, 吴晓锋, 王慕鸿. 空中目标战术机动类型的实时识别[J].
火力与指挥控制, 2011, 36(1): 64-66.
LENG H P, WU X F, WANG M H. Real-time recognition of air target tactical maneuvering type[J]. Fire Control & Command Control, 2011, 36(1): 64-66. DOI: 10.3969/j.issn.1002-0640.2011.01.018. |
| [2] |
GERDES A. Automatic maneuver recognition in the automobile: the fusion of uncertain sensor values using Bayesian models[C]//Proceedings of the 3rdInternational Workshop on Intelligent Transportation. Hamburg, Deutschland: WIT, 2006, 129-133.
|
| [3] |
HUENHAGEN T, DENGLER I, TAMKE A, et al. Maneuver recognition using probabilistic finite-state machines and fuzzy logic[C]//Proceedings of the IEEE Conference on Intelligent Vehicles Symp. (IV), La Jolla, CA: IEEE, 2010, 65-70.
|
| [4] |
TKACHENKO P, ZHOU J, GAGLIARDI D, et al. On-line maneuver identification in highway traffic using elastic template matching[J].
IFAC-Papers on Line, 2018, 51(15): 557-562.
DOI: 10.1016/j.ifacol.2018.09.214. |
| [5] |
杨晓伟, 赵海军. 自动目标识别与机动目标建模及跟踪方法研究[J].
电子科技, 2017, 30(10): 127-130.
YANG X W, ZHAO H J. Research on automatic target recognition and maneuvering target modeling and tracking[J]. Electronic Sci & Tech, 2017, 30(10): 127-130. |
| [6] |
MILAN A, REZATOFIGHI S H, DICK A, et al. Online multi-target tracking using recurrent neural networks[C]//Proceedings of the AAAI conference on Artificial Intelligence. San Francisco, California: AAAI, 2017.
|
| [7] |
LI X R, JILKOV V P. Survey of maneuvering target tracking. Part I. Dynamic models[J].
IEEE Transactions on Aerospace & Electronic Systems, 2004, 39(4): 1333-1364.
|
| [8] |
RICHARDS M A, SCHEER J A, HOLM W A. Principle of Modern Radar: Basic Principles[M]. Rleigh, NC: SciTech, Publishing, 2010.
|
| [9] |
杨丽, 吴雨茜, 王俊丽, 刘义理. 循环神经网络研究综述[J].
计算机应用, 2018, 38(S2): 1-6, 26.
YANG L, WU Y X, WANG J L, et al. Research on recurrent neural network[J]. Journal of Computer Applications, 2018, 38(S2): 1-6, 26. |
| [10] |
LIPTON Z C, BERKOWITZ J, ELKAN C. A critical review of recurrent neural networks for sequence learning[J].
Computer Science, 2015, 10: 1-38.
DOI: 10.1016/j.jocs.2015.04.031. |
| [11] |
张荣, 李伟平, 莫同. 深度学习研究综述[J].
信息与控制, 2018, 47(4): 385-397.
ZAHNG R, LI W P, MO T. Review of deep learning[J]. Information and Control, 2018, 47(4): 385-397. |
| [12] |
GREFF K, SRIVASTAVA R K, KOUTNIK J, et al. LSTM: A search space odyssey[J].
IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(10): 2222-2232.
DOI: 10.1109/TNNLS.2016.2582924. |
| [13] |
GRAVES A, FERNANDEZ S, SCHMI-DHUBER J. Bidirectional LSTM networks for improved phoneme classification and recognition[C]//Proceedings of the International Conference on Artificial Neural Networks (ICANN). Berlin, Heidelberg: Springer, 2005: 799-804.
|
| [14] |
CHUNG J, GALCEHRE C, CHO K H, et al. Empirical evaluation of gated recurrent neural networks on sequence modeling[J].
Eprint Arxiv, 2014, 11: 1-10.
|
| [15] |
何友, 修建娟, 关欣. 雷达数据处理及应用[M]. 北京: 电子工业出版社, 2013: 60-70.
|
| [16] |
周宏仁, 敬忠良, 王培德. 机动目标跟踪[M]. 北京: 国防工业出版, 1991: 78-108.
|
 2020, Vol. 37
2020, Vol. 37

