近年来，无人机由于机动性好、成本低廉、稳定性高等优点，在多个行业得到了广泛应用。然而，无人机在降落过程中仍存在诸多问题，例如GPS定位不准确，近地时存在“地面效应”等。无人机采用位置控制方式降落时，只能降落到以出发点为圆心，半径为1 m左右的圆周内，虽然看似误差不大，但是很多场合下却成为无人机降落的重大隐患^[1]。因此有必要对无人机降落控制系统进行研究，从而实现自主精准降落。

在无人机控制系统方面，利用PID控制^[2-5]实现精准降落是目前研究的主要方向之一。Mou等^[6]使用PID控制算法进行无人机姿态控制，实验表明，PID控制系统能够很好地保持无人机稳定飞行。Yang等^[7]设计了俯仰、偏航和滚转通道的PID控制器，实验表明，PID控制方法能够有效控制无人机飞行。冯培晏^[8]设计了双环PID控制器(内环姿态控制与外环位置控制)，实验表明，外环位置控制采用PID控制方法对四旋翼无人机的控制效果并不理想。张舸等^[9]采用PID控制方法设计了无人机自主降落过程中的位姿控制器和云台控制器，无人机的降落精度在0.5 m以内。通过上述分析可见，PID控制算法能够较好解决无人机精准降落过程的飞行稳定问题，但在外环采用位置PID控制的方式控制效果并不理想。

本文采用外环速度控制的方式进行降落，构建了一个完整的精准降落闭环速度控制系统。结合PID控制和模糊推理机制，设计了外环速度PID控制系统和模糊自适应速度PID控制系统，然后进行2种控制系统的性能测试和对比实验。

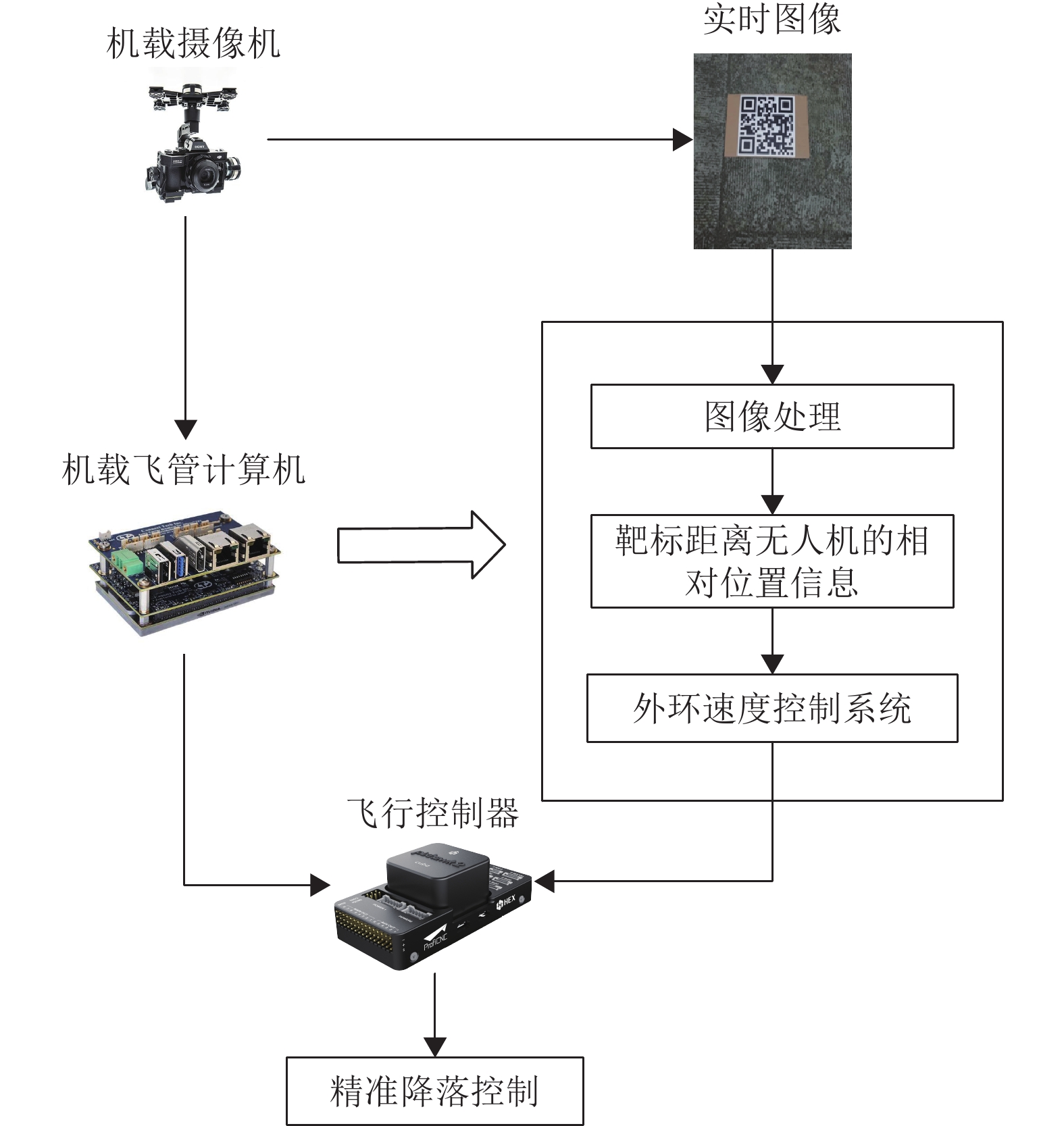
1 系统总体框架

无人机精准降落速度控制系统是由硬件和软件构成的^[10]，其系统整体框架如图1所示。硬件部分是无人机机载设备，包括摄像机、飞管计算机和飞行控制器。软件部分是无人机飞行控制程序，包括图像处理、外环速度控制系统和飞行控制系统。无人机降落时，机载摄像机实时采集靶标图像，并发送到机载飞管计算机，然后通过图像处理技术提取目标距离无人机的位置信息，外环速度控制系统则根据位置信息调整无人机飞行速度，最后由飞管计算机发送控制指令给飞行控制器，引导无人机逐步降落逼近靶标，整个过程构成了一个完整的精准降落闭环速度控制系统。

2 坐标系构建及转换

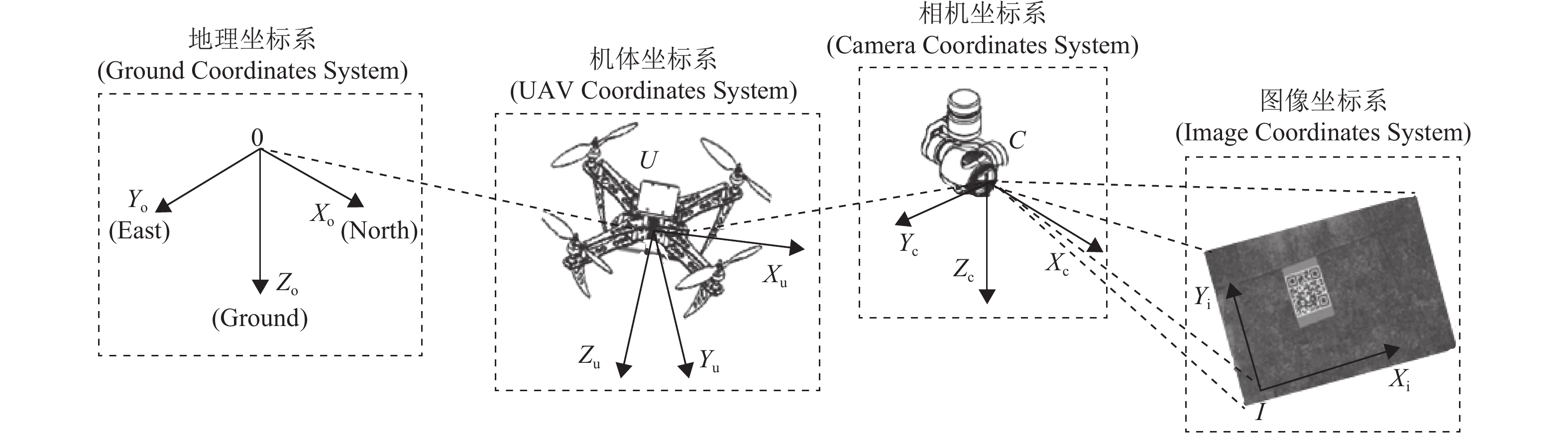
通过识别地面靶标引导无人机降落，这需要构建一套坐标系。如图2所示，分别构建地理坐标系O、机体坐标系U、相机坐标系C以及图像坐标系I。整个降落过程涉及多个坐标系之间的转换，经过坐标转换可获得无人机相对于靶标的准确位置^[11]。

2.1 机体坐标系与地理坐标系之间的转换

设 ${P_1} = {\left[ {\begin{array}{*{20}{c}}{{x_{\rm{u}}},}&{{y_{\rm{u}}},}&{{\textit{z}_{\rm{u}}}}\end{array}} \right]^{\rm{T}}}$ 为机体坐标系下的三维坐标， ${P_2} = {\left[ {\begin{array}{*{20}{c}}{{x_{\rm{o}}},}&{{y_{\rm{o}}},}&{{\textit{z}_{\rm{o}}}}\end{array}} \right]^{\rm{T}}}$ 为地理坐标系下的三维坐标。将三维坐标从P₁点转换到P₂点，可等效为无人机依次绕3个坐标轴旋转复合得到，规定绕Z轴旋转为无人机的航向角(φ)、绕Y轴旋转为无人机的俯仰角(γ)、绕X轴旋转为无人机的翻滚角(θ)，若旋转顺序为Z→Y→X，那么转换公式为

$ \left\{ \begin{array}{l} {\left[ {\begin{array}{*{20}{l}} {{x_{\rm{o}}},}&{{y_{\rm{o}}},}&{{\textit{z}_{\rm{o}}}} \end{array}} \right]^{\rm{T}}} = {{R}} \cdot {\left[ {\begin{array}{*{20}{c}} {{x_{\rm{u}}},}&{{y_{\rm{u}}},}&{{\textit{z}_{\rm{u}}}} \end{array}} \right]^{\rm{T}}}\\ {{R}} = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}\;\gamma \cdot \cos \;\varphi } &{{\rm{cos}}\; \gamma \cdot \sin \;\varphi } &{ - {\rm{sin}}\;\gamma }\\ {{\rm{sin}}\;\theta \cdot \sin \;\gamma \cdot \cos \varphi - {\rm{cos}}\;\theta \cdot \sin \;\varphi }&{{\rm{sin}}\;\theta \cdot {\rm{sin}}\;\gamma \cdot \sin \;\varphi + {\rm{cos}}\;\theta \cdot \cos \;\varphi }&{{\rm{sin}}\;\theta \cdot \cos \gamma }\\ {{\rm{cos}}\;\theta \cdot \sin \;\gamma \cdot \cos \varphi + {\rm{sin}}\;\theta \cdot \sin \;\varphi }&{{\rm{cos}}\;\theta \cdot {\rm{sin}}\;\gamma \cdot \sin \;\varphi - {\rm{sin}}\;\theta \cdot \cos \;\varphi }&{{\rm{cos}}\;\theta \cdot \cos \gamma } \end{array}} \right] \end{array} \right. $

(1)

式(1)中，R表示复合后的转换矩阵。

2.2 相机坐标系与地理坐标系之间的转换 2.2.1 图像坐标系与相机坐标系之间的转换

设 ${P_{{\rm{3}}}} = {\left( {u,\;v,\;1} \right)^{\rm{T}}}$ 为图像坐标系下的齐次坐标， ${P_{\rm{4}}} = {\left( {{x_{\rm{c}}},\;{y_{\rm{c}}},\;{\textit{z}_{\rm{c}}}} \right)^{\rm{T}}}$ 为相机坐标系下的三维坐标。将图像齐次坐标P₃转换到相机三维坐标P₄，先建立相机模型公式：

$ \left\{ {\begin{array}{*{20}{l}} {{\textit{z}_{\rm{c}}}\cdot{P_{{\rm{3}}}} = {{K}}\cdot{P_{\rm{4}}}}\\ {{{K}} = \left[ {\begin{array}{*{20}{c}} \alpha &0&{{u_0}}\\ 0&\beta &{{v_0}}\\ 0&0&1 \end{array}} \right]} \end{array}} \right. $

(2)

式(2)中，K表示摄像头内参，α和β是焦距与像素横纵比的融合，(u₀, v₀) 是像主点坐标。

绝大多数实际情况下，相机内参中的α与β是十分接近的，因此令f = α = β，那么图像坐标系到相机坐标系的转换公式为

$ \left\{ {\begin{array}{*{20}{l}} {{\textit{z}_{\rm{c}}} = f\cdot\sqrt {\dfrac{{{S_{{\rm{Camera}}}}}}{{{S_{{\rm{Image}}}} \cdot \cos\;\theta \cdot \cos\;\varphi }}} }\\ {{x_{\rm{c}}} = {\textit{z}_{\rm{c}}} \cdot \dfrac{{u - {u_0}}}{f}}\\ {{y_{\rm{c}}} = {\textit{z}_{\rm{c}}} \cdot \dfrac{{v - {v_0}}}{f}} \end{array}} \right. $

(3)

式(3)中，z_c表示无人机在相机坐标系下的离地相对高度，S_Camera表示靶标在相机坐标系下的实际面积，S_Image表示靶标在图像坐标系下的面积，θ和φ分别表示无人机的俯仰角和滚转角，x_c和y_c分别表示无人机在相机坐标系下X、Y方向的位置偏差。

2.2.2 相机坐标系与地理坐标系之间的转换

引导无人机降落，需要将三维坐标从相机坐标系转换到地理坐标系。设 ${P_{\rm{o}}} = {\left( {\Delta x,\;\Delta y,\;h} \right)^{\rm{T}}}$ 为地理坐标系下的坐标，将三维坐标从P₄转换到P_o，转换公式为

$ \left\{ {\begin{array}{*{20}{c}} {h = \left( {{\textit{z}_{\rm{c}}} + \tan\;\gamma \cdot \sqrt {{x_{\rm{c}}}^2 + {y_{\rm{c}}}^2} } \right)\cdot\cos\;\gamma }\\ {\Delta x = h \cdot \tan \left( {\varphi - \arctan \dfrac{{\sqrt {{x_{\rm{c}}}^2 + {y_{\rm{c}}}^2} }}{{{\textit{z}_{\rm{c}}}}}} \right)}\\ {\Delta y = h \cdot \tan \left( {\theta + \arctan \dfrac{{\sqrt {{x_{\rm{c}}}^2 + {y_{\rm{c}}}^2} }}{{{\textit{z}_{\rm{c}}}}}} \right)} \end{array}} \right. $

(4)

$ \cos\;\gamma = \cos\;\theta\cdot\cos\;\varphi $

(5)

式 (4) 中， $h$ 表示无人机在地理坐标系下的离地相对高度， $\Delta x$ 和 $\Delta y$ 分别表示无人机在地理坐标系下X、Y方向的位置偏差。式 (5) 中，γ表示俯仰角θ和滚转角φ的合角度。

3 控制系统设计 3.1 图像处理设计 3.1.1 图像预处理

1) 图像灰度化

图像的灰度化是将彩色图像转化成为灰度图像的过程，彩色图像中每个像素的颜色由R、G、B分量决定，而灰度图像是R、G、B分量都相同的一种特殊的彩色图像。本文采用平均值法实现灰度化，首先求出每个像素点的R、G、B分量的平均值，然后再将这个平均值赋予这个像素的3个分量，计算公式为

$ {\rm{Gray}} = \frac{{R + G + B}}{3} $

(6)

式 (6) 中，Gray表示图像灰度值。

2) 直方图变换

将灰度图中总的像素量与每一个灰度值做除法运算，求得灰度直方图，它关乎图像的灰度级和其出现的概率，表达式为

$ P\left( {{r_k}} \right) = \frac{{{n_k}}}{n},0 \leqslant {r_k}\leqslant 1 $

(7)

式(7)中，r_k表示第k个灰度级，且 $k = 0,1, \cdots ,L - 1$ ；n_k，表示图像中第k个灰度级的像素数量；n表示图像中总的像素数量。

然后对灰度直方图均衡化处理，将直方图内比较集中的某个灰度区间变成在全部灰度范围内的均匀分布，从而达到增强图像整体对比度的效果，变换公式为

$ T\left( {{r_k}} \right) = \mathop \sum \limits_{j = 0}^k P\left( {{r_j}} \right) = \mathop \sum \limits_{j = 0}^k \frac{{{n_j}}}{n},0 \leqslant {r_j} \leqslant 1 $

(8)

式 (8) 中， $T\left( {{r_k}} \right)$ 表示输入图像的累积分布函数，且 $k = 0,1, \cdots ,L - 1$ ；r_j表示第j个灰度级； $P\left( {{r_j}} \right)$ 表示图像在第j个灰度级的概率密度函数；n_j表示第j个灰度级的像素数量。

3) 图像平滑减噪

对图像进行减噪处理^[12]，消除噪声对图像质量的影响，使其尽可能达到与原图相近的状态。本文采用高斯滤波法，将一个高斯模板扫描图像中每一个像素，从而确定邻域内像素的加权平均灰度值，然后再将此平均灰度值替代模板中心像素点的值。这种方法在对图像进行平滑的同时，也能更多地保留图像的总体灰度分布特征。高斯模板内的参数是通过高斯函数计算的，计算公式为

$ G\left( {x,y} \right) = \frac{1}{{2 \text{π}{\sigma ^2}}}{{\rm{e}}^{ - \frac{{{x^2} + {y^2}}}{{2{\sigma ^2}}}}} $

(9)

3.1.2 目标分割

将图像进行二值化分割，本文采用大津法(Otsu)，它不受图像亮度和对比度的影响，而且直观、实现简单、计算速度快^[13]。对于一幅图像，按其灰度特性，分成前景(即目标)和背景2个部分，分割阈值记作t，属于前景的像素点数占整幅图像的比例记为ω₀，其平均灰度为 $\bar u_0$ ，背景像素点数占整幅图像的比例为ω₁，其平均灰度为 $\bar u_1 $ ，类间方差记为g，那么类间方差表达式为

$ g = {\omega _0}{\omega _1}{({\bar u_0} - {\bar u_1})^2} $

(10)

当g取得最大值时，t为最佳阈值，此时构成图像的前景和背景2部分之间差别最大，错分概率最小，图像分割效果最好。

分割出目标(地面靶标)后，对其绘制轮廓最小外接矩形，从而求得目标中心点的坐标，再结合图像中心点坐标，经坐标转换后即可求出无人机相对地面靶标X、Y方向的位置偏差值。

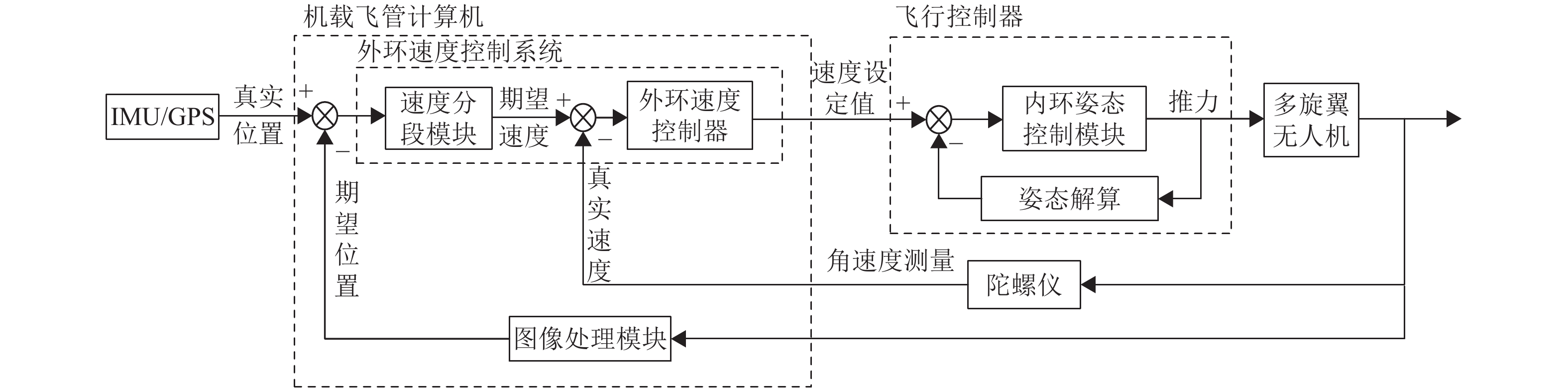
3.2 外环速度控制系统设计

无人机原控制系统采用位置控制方式进行降落，通过设定期望位置(经纬度和海拔)引导无人机飞到指定位置，但存在位置振荡和速度超调的问题。本系统采用速度控制方式，通过控制无人机X、Y方向的飞行速度调整位置。对于位置振荡问题的解决思路是外加一个速度分段模块，对无人机飞行速度进行分段降速控制。对于速度超调问题的解决思路是增加外环速度控制器，结合PID控制原理，根据速度误差改善无人机速度，确保无人机飞行更加快速、稳定、准确^[14]。无人机精准降落控制系统结构框图如图3所示，其中IMU (Inertial Measurement Unit) 是指惯性测量单元，GPS (Global Positioning System) 是指全球定位系统，用于测量无人机的真实位置。

3.2.1 速度分段模块设计

速度分段模块的作用是在无人机降落时，实时根据X、Y方向的位置偏差调整无人机期望飞行速度。由于X、Y方向控制策略相同，因此这里只分析X方向。设X方向位置偏差最大允许误差阈值为T₁、缓冲允许误差阈值为T₂、最小允许误差阈值为T₃，当X方向位置偏差值 $\Delta x$ 大于T₁时，无人机飞行速度设为 ${V_{{{x}_1}}}$ ；当偏差值 $\Delta x$ 介于T₁和T₂之间时，无人机飞行速度设为 ${V_{{x_1}}}$ 的1/2；当偏差值 $\Delta x$ 介于T₂和T₃之间时，无人机飞行速度设为 ${V_{{x_1}}}$ 的1/10；当偏差值 $\Delta x$ 小于T₃时，无人机飞行速度设为0，直接降落。可将上述速度分段过程用式 (11) 表示。

$ {V_{x}} = \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{V_{{x_1}}},}&{\Delta x > {T_1}} \end{array}}\\ {\begin{array}{*{20}{l}} {\dfrac{1}{2}{V_{{x_1}}},}&{{T_2} < \Delta x \leqslant {T_1}} \end{array}}\\ {\begin{array}{*{20}{l}} {\dfrac{1}{{10}}{V_{{x_1}}},}&{{T_3} < \Delta x \leqslant {T_2}} \end{array}}\\ {\begin{array}{*{20}{l}} \;{0,}&{\Delta x \leqslant {T_3}} \end{array}} \end{array}} \right. $

(11)

3.2.2 外环速度控制器设计

1) 速度PID控制器

PID控制是一种线性控制，它将给定值与实际输出值的偏差通过比例(Proportion，P)、积分(Integral, I)、微分(Derivative, D)线性组合后形成控制量，对被控对象进行控制^[15]。本系统采用位置式速度PID控制，将速度分段模块计算得到的期望速度与无人机实际飞行速度之差作为误差e，然后控制器对误差信号进行校正，产生最适宜的速度控制量，从而进行速度控制。相比于位置控制方式，速度控制灵敏度更高，引导时的反应更快。结合速度控制方式，可给出速度的PID控制规律如式(12)所示。

$ {v_k} = {k_{\rm{p}}}{e_k} + {k_{\rm{i}}}\mathop \sum \limits_{j = 0}^k {e_j} + {k_{\rm{d}}}\left( {{e_k} - {e_{k - 1}}} \right) $

(12)

式(12)中，v_k是k时刻的控制量，e_j，e_k和e_k–1分别是j时刻、k时刻、k–1时刻的速度误差， $\displaystyle\sum\limits_{j = 0}^k {{e_j}} $ 表示k时刻内速度误差的累积；k_p是比例项参数，k_i是积分项参数，k_d是微分项参数。

2) 模糊自适应速度PID控制器

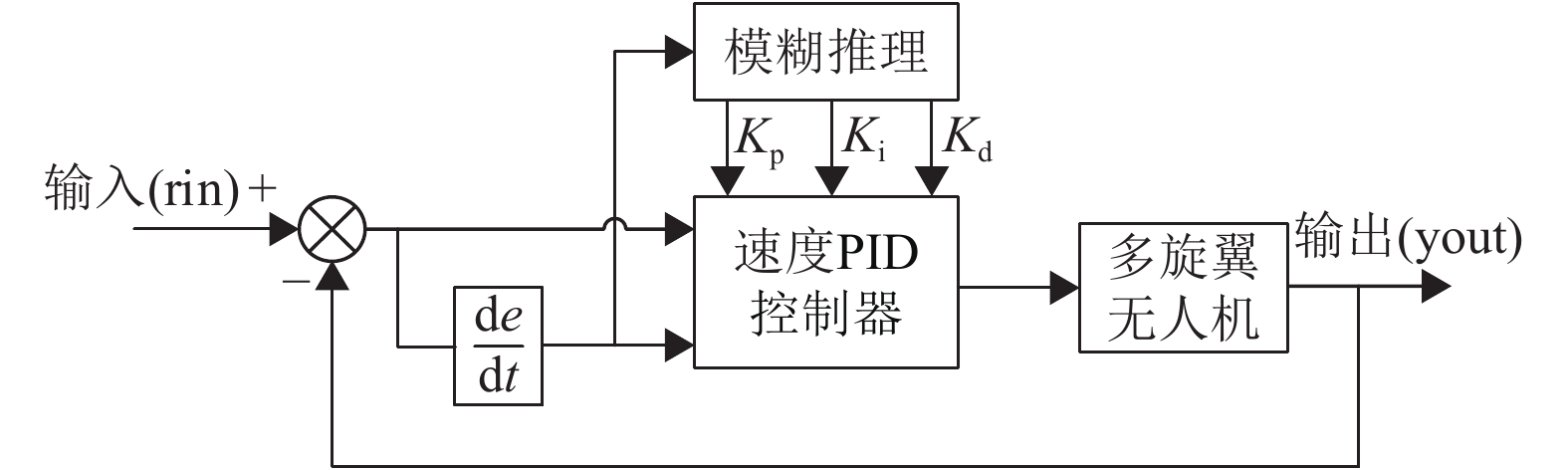
模糊自适应PID属于一种智能PID控制，针对模糊控制和PID控制的各自特点，将两者相结合，根据控制系统的实际响应情况，运用模糊推理，自动调整PID控制器的比例系数K_p、积分系数K_i和微分系数K_d，以达到调节作用的实时最优^[16]，其结构如图4所示。

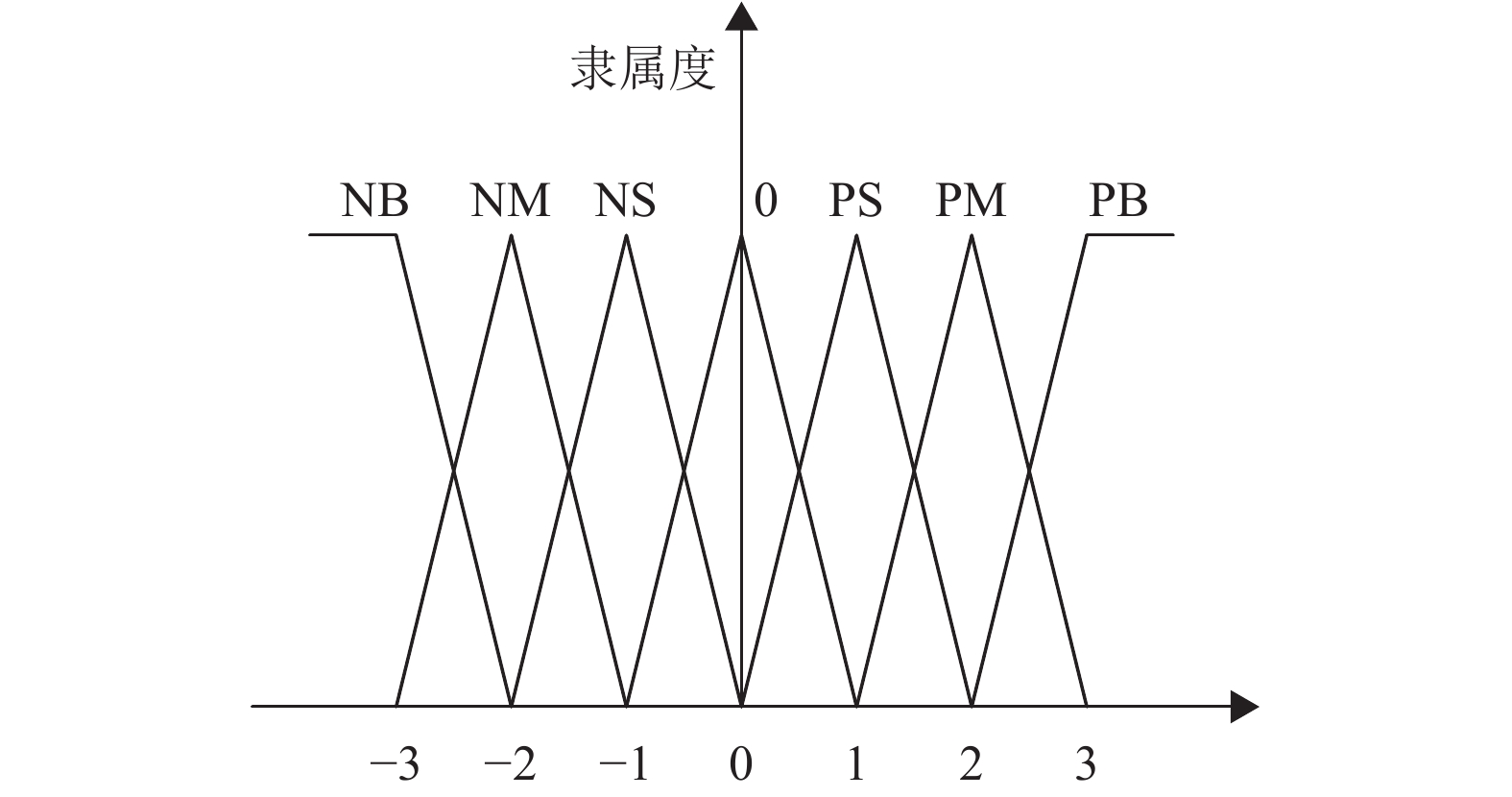
本文采用的模糊自适应速度PID控制系统是在速度PID控制器的基础上，外加模糊推理机制。以速度误差e和速度误差变化率ec作为输入，利用模糊规则在线实时地对PID参数进行调整，来满足不同时刻的e和ec对PID参数自整定的要求。将模糊推理机制的模糊部分按K_p、K_i和K_d分成3部分，分别由相应的子推理器来实现，其输出为PID参数的增量值。误差e和误差变化率ec均取7个模糊子集，分别为NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)，其隶属函数都采用三角形隶属度函数，如图5所示。

飞管计算机中采用离线查表法实现模糊控制，首先模糊化输入到控制器中的e和ec，计算在每个模糊子集中的隶属度，然后找出相应隶属度的模糊子集，最后使用加权平均法计算输出值。解模糊具体公式可由式（13）表示：

$ y = \frac{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{{e_j}}}({\textit{z}_j}) \cdot {\mu _{{\rm{e}}{{\rm{c}}_j}}}({\textit{z}_j}) \cdot {\textit{z}_j}} }}{{\displaystyle\sum\limits_{j = 1}^n {{\mu _{{e_j}}}({\textit{z}_j}) \cdot {\mu _{{\rm{e}}{{\rm{c}}_j}}}({\textit{z}_j})} }} $

(13)

式(13)中， $y$ 表示模糊控制输出值解模糊后的精确值， ${\textit{z}_j}$ 表示隶属度对应的横坐标值， $\;{\mu _{{e_j}}}({\textit{z}_j})$ 和 $\;{\mu _{{\rm{e}}{{\rm{c}}_j}}}({\textit{z}_j})$ 分别表示误差e、误差变化率ec属于模糊子集 ${\textit{z}_j}$ 的隶属度。

4 实验与分析 4.1 实验环境及平台

本次实验以PX4开源飞控系统为平台，在Dronecode SDK实现软件的二次开发。基于Arm架构的机载计算机Jeston TX2，搭载NVIDIA Pascal GPU，ARMCortex-A57 CPU，主存为8 GB，操作系统为Ubuntu 16.04，OpenCV版本为2.4.13。云台相机为大疆Zenmuse X4S相机，视频流分辨率为4 864×3 648像素。无人机飞行仿真模拟器为Gazebo。

4.2 仿真实验过程与结果分析

由于X、Y方向控制策略相同，因此只分析X方向降落控制效果。为了验证外环速度控制系统的有效性，进行以下实验。

实验1：无人机在原控制系统(位置控制)下进行模拟降落实验。

实验2：无人机控制系统改为速度控制方式，在外环增加一个速度分段模块和外环速度PID控制器，构成外环速度PID控制系统。

实验3：在实验2的外环速度PID控制器基础上，外加模糊推理机制，构成模糊自适应PID控制系统。

4.2.1 实验1的结果与分析

多旋翼无人机原控制系统采用位置控制，飞行速度为 1 m/s，模拟器模拟无人机降落的X方向速度曲线如图6所示。

从图6中可以发现：无人机速度从0 m/s提速到1 m/s时，存在较大的速度超调；控制时间达到10 s后，速度曲线趋于稳定；速度从1 m/s降到0 m/s之后，无人机出现了位置振荡现象，无人机位置在位置偏差值为0附近来回调整，经过10 s之后才趋于稳定。

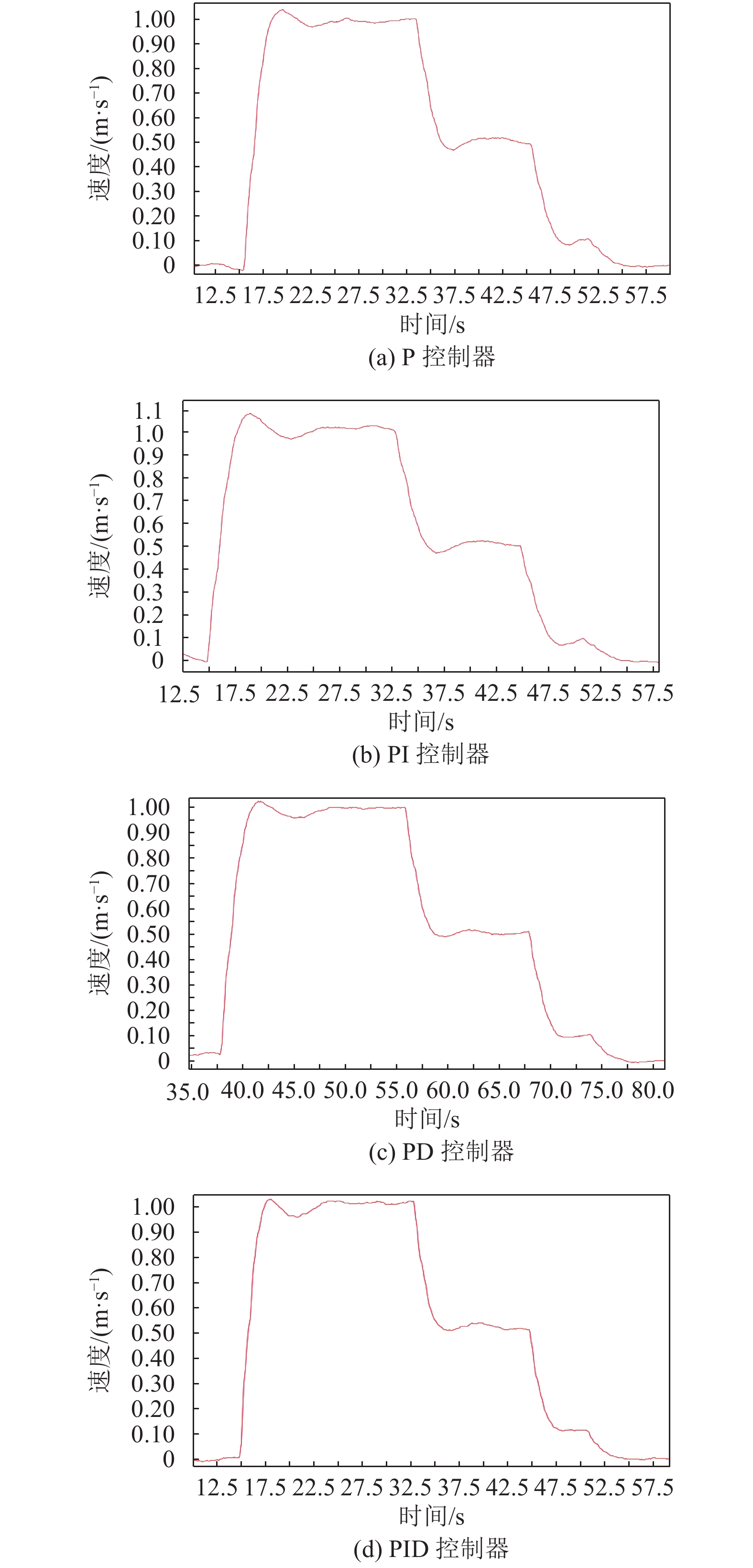
4.2.2 实验2的结果与分析

为了改善无人机降落时的稳定性能，采用了速度控制的方式，通过在外环增加一个速度PID控制系统进行速度调整，实验时考虑了以下4种情况：(1) 速度PID控制系统中控制器采用P控制器。当比例系数K_p取0.36时，相应的X方向速度曲线如图7(a)所示。(2) 速度PID控制系统中控制器采用PI控制器。当比例系数K_p取0.45、积分系数K_i取0.006时，相应的X方向速度曲线如图7(b)所示。(3) 速度PID控制系统中控制器采用PD控制器。当比例系数K_p取0.46、微分系数K_d取0.1时，相应的X方向速度曲线如图7(c)所示。(4) 速度PID控制系统中控制器采用PID控制器。当比例系数K_p取0.45、积分系数K_i取0.005 25、微分系数K_d取0.17时，相应的X方向速度曲线如图7(d)所示。

对比图6与图7(a)~图7(d)可见：(1) 速度PID控制系统相比于原控制系统，速度超调现象得到明显改善。(2) 速度PID控制系统由于采用了分段降速的方法，速度降到0 m/s后就进入稳态，改善了原控制系统的位置振荡现象。(3) 速度PID控制系统的4种控制器中，P控制器和PD控制器均能稳定在1 m/s，而PI控制器和PID控制器稳定时存在稳态误差。(4) 对比P控制器和PD控制器可以发现，PD控制器比P控制器达到1 m/s时的速度超调更小。

由此可见，采用速度控制的方式能够显著改善无人机降落调整时的速度超调现象和位置振荡现象，并且速度PID控制系统采用PD控制器进行控制时效果最佳。

4.2.3 实验3的结果与分析

在实验2的外环速度PID控制器基础上，外加模糊推理机制，根据误差e和误差变化率ec自动调整PD控制器参数。e和ec的基本论域均为[–3, 3]，将其离散成7个等级[–3, –2,–1,0,1,2,3]，PD控制器参数增量∆K_p和∆K_d的模糊论域分别为[–0.15, 0.15]和[–0.08, 0.08]，则∆K_p和∆K_d的比例因子分别为 $K_{\Delta k_{\rm{p}}}=0.043$ 和 $K_{\Delta k_{\rm{d}}}=0.023$ 。模拟器模拟无人机降落的X方向速度曲线如图8所示。

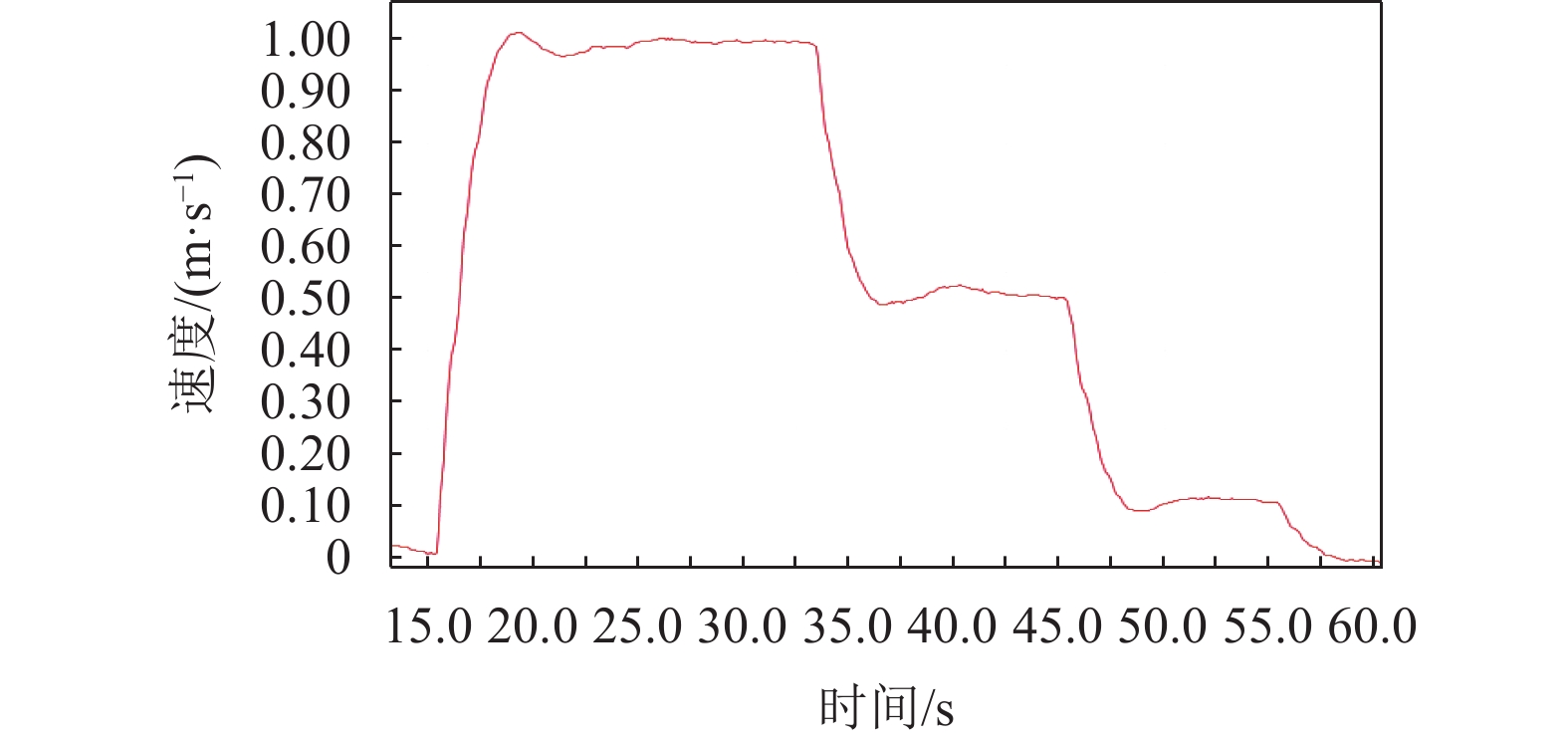
将图8与图7(c)对比可见：(1) 控制时间达到10 s左右，模糊自适应速度PID控制系统和速度PID控制系统均达到1 m/s的稳定速度，稳态误差基本为0。(2) 模糊自适应速度PID控制系统比速度PID控制系统的速度超调更小，且速度曲线相对更加平稳。

由此可见，通过外加模糊推理机制自动调整PD控制器参数，无人机降落时的速度超调较速度PID控制系统得到一定程度的改善。

4.3 自主降落实验验证

为测试速度控制系统在真实环境下的性能特性，搭建了实验环境，并进行多次测试。图9展示了六旋翼无人机在速度PID控制系统和模糊自适应速度PID控制系统下的降落实验。

从图9(a)~9(d)可见：(1) 无人机在2种控制系统下都能成功降落到地面靶标上。(2) 模糊自适应速度PID控制系统比速度PID控制系统降落结果更靠近靶标中心，降落精度更高。

5 结论 5.1 仿真实验结果讨论

将上述所有仿真实验获得的速度曲线结果进行汇总，结果如表1所示。

从表1可见：(1) 实验1的控制系统采用位置控制方式，调整过程中速度超调量达到了11.25%，稳态误差达到了0.02。位置控制方式是通过设定期望位置进行调整的，整个飞行过程不能控制速度，所以存在较大的速度超调和稳态误差。(2) 实验2采用速度控制的方式，对飞行速度进行实时调整。实验结果表明，速度PID控制系统与实验1的原控制系统相比，采用P控制器的速度超调量和稳态误差均减少60%；采用PI控制器的速度超调量减少46.2%，稳态误差保持不变；采用PD控制器下的速度超调量减少80.4%，稳态误差减少92%；采用PID控制器下的速度超调量减少85.8%，稳态误差减少20%。由此可见，速度PID控制系统中4种控制器均能得到比原控制系统更优的结果，且PD控制器的控制效果最好，超调量和稳态误差均得到显著改善。(3) 实验3在实验2的PD控制器基础上，外加模糊推理机制，实现PD控制器参数K_p和K_d的自动调整。实验结果证明，相比于速度PID控制系统(PD控制器)，模糊自适应PID控制系统的速度超调量减少50%，稳态误差保持不变。

5.2 自主降落实验结果讨论

统计所有降落实验的结果，2种控制系统的降落精度如表2所示。

从表2可见：(1) 模糊自适应速度PID控制系统比纯速度PID控制系统降落精度更高，降落结果得到改善。(2) 2种控制系统的降落精度分别为0.2 m和0.13 m，均未达到0.1 m以内。

5.3 总结

本文采用速度控制的方式进行降落，构建一个完整的精准降落闭环速度控制系统。结合图像识别靶标的结果，设计了外环速度PID控制系统和模糊自适应速度PID控制系统，然后进行2种控制系统的性能测试和对比实验。实验结果表明，采用PD控制器设计降落控制系统效果最好，设计的2种控制系统均能使无人机成功降落到地面靶标上，且模糊自适应速度PID控制系统降落精度更高，达到了0.13 m以内。多旋翼无人机采用模糊自适应速度PID控制系统可以实现无人机的自主精准降落。但本文设计时没有考虑风速影响，可能是造成降落精度达不到0.1 m以内的原因，这将是今后研究的主要方向之一。