非正交多址接入(Non-orthogonal Multiple Access, NOMA)是5G的一项关键技术，通过叠加编码和连续干扰消除技术能有效提高频谱效率，近来受到学者的广泛关注^[1-4]。在NOMA系统中采用协同中继技术，把信道质量更好的用户作为中继转发信息能有效提高频谱效率^[5-6]。在多输入多输出(Multiple-input Multiple-output, MIMO)的NOMA系统中，采用协同技术同样可以显著提高系统速率^[7]。

NOMA技术的目标是提高频谱效率，另一个5G的主要目标是最大化能量效率。早在2008年，Varshney提出了无线携能传输(Simultaneous Wireless Information and Power Transfer, SWIPT)技术^[8]，已经吸引了大量学者的关注并做了许多有关能量效率的工作。无线携能传输有2种工作模式：时分(Time Splitting, TS)和功分(Power Splitting, PS)^[9]。由于点到点的SWIPT 通信系统的研究比较完善，近年来关于SWIPT的研究主要针对2种协同中继系统：放大转发(Amplify and Forward, AF)和解码转发(Decode and Forward, DF)。AF协同中继系统提出了基于时分和功分的中继协议^[10]；DF协同中继系统规划了一个新的天线选择SWIPT方案以降低实现复杂度^[11]，且提出了具有大规模天线阵列结构的正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)方案，得到最大化传输信息速率的时间和功率联合分配的最优算法^[12]。

为了提高信道质量较差的弱用户的可靠性，而不耗尽信道质量较好的强用户能量，把SWIPT应用到NOMA系统中，强用户作为能量收集中继帮助弱用户转发信息，可得到中断概率和系统吞吐量的闭式表达式^[13]。此外，把近端用户作为能量收集中继，两用户协同中继系统的中断性能也得到了研究^[14]。然而，在无线携能传输的NOMA 协同中继系统中，关于用户速率的优化研究还是空白。

本文研究了无线携能传输的协同中继NOMA系统，强用户除了接收自己所需的信息，又作为DF中继帮助弱用户转发信息，考虑到发送信息比接收信息需要耗费更多的能量，设定强用户是一个能量受限的用户，采用功分的方式收集一定的能量才能协同转发信息给弱用户。在此系统下，研究了强用户的速率优化问题：在保证强用户能量收集(Energy Harvesting, EH)接收机满足一定的约束下，联合优化强用户功率分配系数和强用户EH接收机的功分系数，最大化该系统的强用户速率。接着研究了传统的无线携能传输协同中继(Time-division Multiple Access, TDMA)系统的强用户速率优化，并通过MATLAB仿真对2个系统的强用户速率性能进行对比。

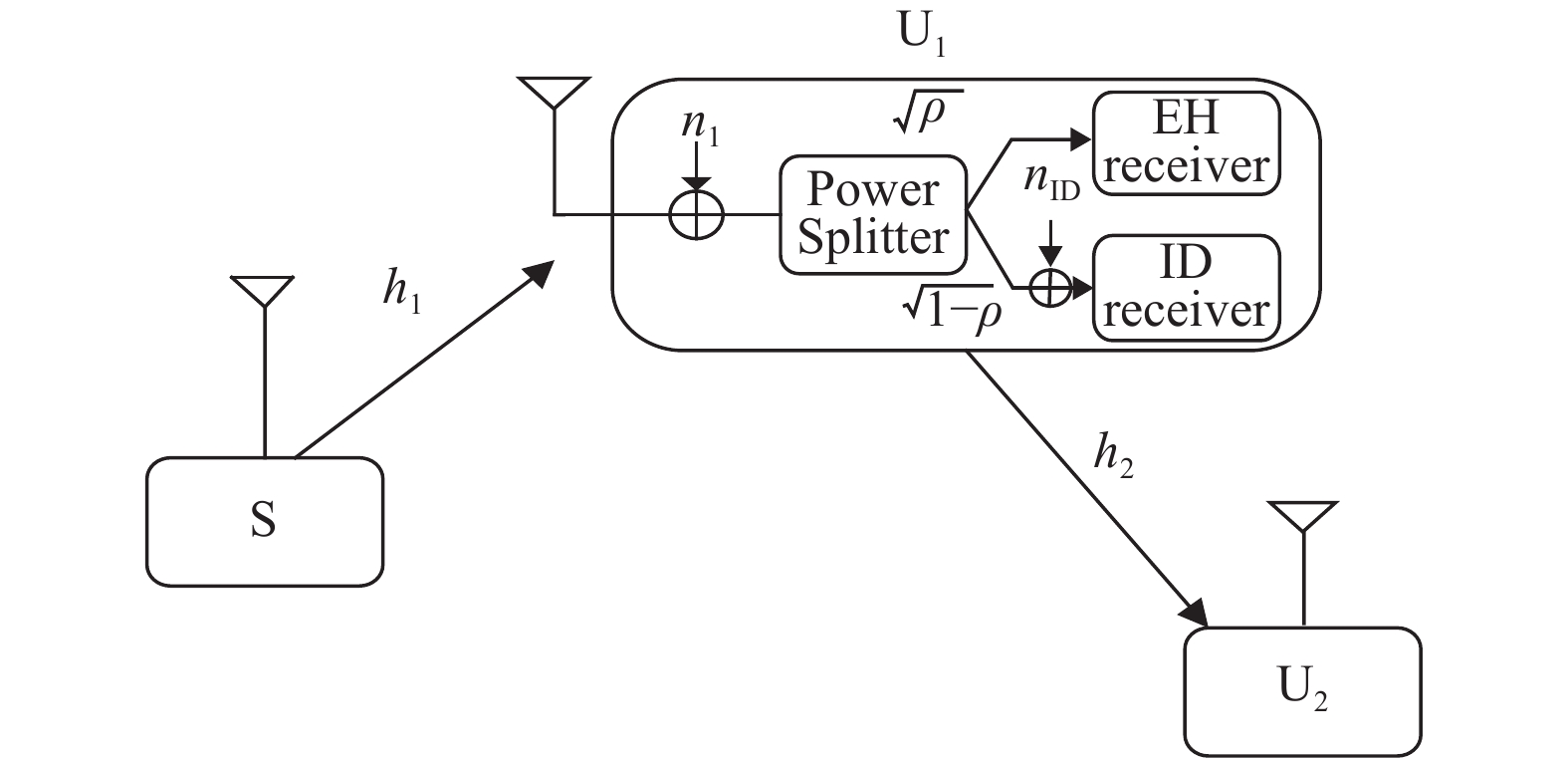
1 无线携能传输协同中继NOMA系统

考虑一个无线携能传输协同中继NOMA系统，如图1所示。系统由一个源节点S、一个强用户U₁和一个弱用户U₂构成，所有节点和用户都配有单根天线。源节点到弱用户的信道由于路损、阴影衰落或者被障碍物挡住而无法正常通信，因此不考虑源节点到弱用户的直接链路。此系统中，考虑强用户作为弱用户的中继协同转发弱用户的信息，同时强用户是一个能量受限的设备，需收集一定的能量才能转发信息。源节点到强用户、强用户到弱用户的信道分别表示为 ${h_1}$ 和 ${h_2}$ ，这些信道都是均值为0、方差分别为 $\delta _1^2$ 和 $\delta _2^2$ 的复高斯随机变量。这里假设 ${h_1}$ 和 ${h_2}$ 的信道状态信息分别对于强用户和弱用户来说都是完美已知的。

1.1 系统模型

在第一时隙，根据NOMA准则^[5]，源节点发送 $s = \sqrt {{a_1}P} {s_1} + \sqrt {{a_2}P} {s_2}$ 给强用户，其中 ${s_1}$ 和 ${s_2}$ 分别是强用户和弱用户需要接收的信息，满足 ${E} \left\{ {{{\left| {{s_i}} \right|}^2}} \right\} = 1, \;$ $i \in \left\{ {1,2} \right\} $ ，E(·) 表示统计期望值， $P$ 是总的发送功率， ${a_i}$ 是功率分配系数，满足 ${a_1} + {a_2} = 1$ 。因此，强用户接收的信息为

${y_1} = {h_1}\left( {\sqrt {{a_1}P} {s_1} + \sqrt {{a_2}P} {s_2}} \right) + {n_1}$

(1)

其中， ${n_1}$ 是强用户端的加性高斯白噪声，它的均值为0，方差为 ${\sigma ^2}$ 。由于强用户是一个能量受限的器件，强用户接收到信息后，采用功分的方式，一部分用于能量接收，记为 ${s_{{\rm{EH}}}}$ ，在单位时间内收集到一定的能量后才能在下一时隙以功率 ${P_{\rm{r}}}$ 转发信息；另一部分用于信息解码，记为 ${s_{{\rm{ID}}}}$ . ${s_{{\rm{EH}}}}$ 和 ${s_{{\rm{ID}}}}$ 的表达式为

${s_{{\rm{EH}}}} = \sqrt \rho \left( {{h_1}\left( {\sqrt {{a_1}P} {s_1} + \sqrt {{a_2}P} {s_2}} \right) + {n_1}} \right)$

(2)

${s_{{\rm{ID}}}} = \sqrt {1 - \rho } \left( {{h_1}\left( {\sqrt {{a_1}P} {s_1} + \sqrt {{a_2}P} {s_2}} \right) + {n_1}} \right) + {n_{{\rm{ID}}}}$

(3)

其中， $\rho $ 是强用户EH接收机的功分系数； ${n_{{\rm{ID}}}}$ 是在解码端的加性高斯白噪声，其均值为0、方差为 ${\sigma ^2}$ 。首先强用户把 ${s_1}$ 作为噪声解码 ${s_2}$ ，然后进行串行干扰消除再解码 ${s_1}$ ，强用户解码 ${s_2}$ 和 ${s_1}$ 的信噪比分别为

$\begin{split} \gamma _1^2 = &\frac{{\left( {1{\rm{ - }}\rho } \right){{\left| {{h_1}} \right|}^2}{a_2}P}}{{\left( {1{\rm{ - }}\rho } \right){{\left| {{h_1}} \right|}^2}{a_1}P + \left( {1 - \rho } \right){\sigma ^2} + {\sigma ^2}}} = \\ & \frac{{{\lambda _1}\left( {1{\rm{ - }}\rho } \right)\left( {1 - {a_1}} \right)}}{{{\lambda _1}\left( {1 - \rho } \right){a_1} + \left( {2 - \rho } \right)\eta }} \\ \end{split} $

(4)

$ \gamma _1^1 = \frac{{\left( {1{\rm{ - }}\rho } \right){{\left| {{h_1}} \right|}^2}{a_1}P}}{{\left( {1 - \rho } \right){\sigma ^2} + {\sigma ^2}}} = \frac{{{\lambda _1}\left( {1{\rm{ - }}\rho } \right){a_1}}}{{\left( {2 - \rho } \right)\eta }}\\ $

(5)

其中， $\eta = \dfrac{{{\sigma ^2}}}{P},{\lambda _1} = {\left| {{h_1}} \right|^2}$ 。

强用户在单位时间内采集到的能量为^[9]

$Q = {E} \left( {{{\left| {{s_{{\rm{EH}}}}} \right|}^2}} \right) = \rho \left( {\delta _1^2P + {\sigma ^2}} \right)$

(6)

第二时隙，强用户以功率 ${P_{\rm{r}}}$ 发送 ${s_2}$ 给弱用户，弱用户接收到的信息为

${y_2} = {h_2}\sqrt {{P_{\rm{r}}}} {s_2} + {n_2}$

(7)

由式(7)可得弱用户解码 ${s_2}$ 的信噪比为

$\gamma _2^2 = \frac{{{{\left| {{h_2}} \right|}^2}{P_{\rm{r}}}}}{{{\sigma ^2}}} = \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}}$

(8)

其中 ${\lambda _2} = {\left| {{h_2}} \right|^2}$ 。

由式(5)可得到解码信息 ${s_1}$ 的可达速率，即强用户的可达速率为

${R_1} = \frac{1}{2}{\log _2}\left( {1 + \gamma _1^1} \right)$

(9)

由于端到端的中继解码转发受限于最弱的链路^[15]， ${s_2}$ 必须经过强用户的正确解码后才能被强用户转发给弱用户，由式(4)和式(8)，解码信息 ${s_2}$ 的可达速率，即弱用户的可达速率为

${R_2} = \frac{1}{2}{\log _2}\left( {1 + \min \left( {\gamma _1^2,\gamma _2^2} \right)} \right)$

(10)

1.2 强用户速率最大化的研究

本节提出最大化强用户速率的优化问题，同时保证弱用户的速率大于阈值 ${r_0}$ ，以及强用户EH接收机的能量在单位时间内大于 ${P_{\rm{r}}}$ ，问题规划如式(11a)~(11c)所示。

$\tag{11a} \begin{gathered} \mathop { {\rm{max}}}\limits_{{\rm{0}} \leqslant {a_{\rm{1}}} \leqslant 1,0 \leqslant \rho \leqslant 1}{R_1} \end{gathered} $

$\tag{11b} {\rm{ s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;{R_2} \geqslant {r_0} $

$\tag{11c} Q \geqslant {P_{\rm{r}}} $

把 ${R_1}$ 、 ${R_2}$ 和 $Q$ 的表达式代入(11)，问题转化为

$\tag{12a} \mathop {\max }\limits_{0 \leqslant {a_1} \leqslant 1,0 \leqslant \rho \leqslant 1} \frac{{{\lambda _1}(1 - \rho ){a_1}}}{{(2 - \rho )\eta }} $

$\tag{12b} {\rm{s}}{\rm{.t}}{\rm{.}}\quad \;\frac{{{\lambda _1}(1 - \rho )(1 - {a_1})}}{{{\lambda _1}(1 - \rho ){a_1} + (2 - \rho )\eta }} \geqslant {\gamma _0} $

$\tag{12c} \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}} \geqslant {\gamma _0} $

$\tag{12d} \rho (\delta _1^2P + {\sigma ^2}) \geqslant {P_{\rm{r}}} $

其中 ${\gamma _0} = {2^{2{r_0}}} - 1$ ，为弱用户端信噪比的阈值。约束(12b)和(12c)是由(11b)推导而来，要使弱用户速率满足 ${R_2} \geqslant {r_0}$ ，由公式(10)可知，必须使得 $\gamma _1^2 $ 和 $\gamma _2^2$ 都大于或等于 ${\gamma _0}$ 。

问题(12)是一个非凸的优化问题，不能直接求解。引入一个松弛变量 $\tau $ ，令 $\dfrac{{{\lambda _1}(1{\rm{ - }}\rho ){a_1}}}{{(2 - \rho )\eta }} \geqslant {\tau ^2}$ ，并进一步化简计算，式(12)可以重写为

$\tag{13a} \mathop {{\rm{max}}}\limits_{{\rm{0}} \leqslant {a_{\rm{1}}} \leqslant 1,0 \leqslant \rho \leqslant 1,\tau } \tau $

$\tag{13b} {\rm{s}}{\rm{.t}}{\rm{.}}\quad \frac{{{\tau ^2}}}{{1 - \rho }} - \frac{{{\lambda _1}}}{\eta }{a_1} + {\tau ^2} \leqslant 0 $

$\tag{13c} \frac{\eta }{{{\lambda _1}(1 - \rho )}} + \left( {1 + \frac{1}{{{\gamma _0}}}} \right){a_1} - \frac{1}{{{\gamma _0}}} + \frac{\eta }{{{\lambda _1}}} \leqslant 0{\kern 1pt} {\kern 1pt} $

$\tag{13d} {\gamma _0} - \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}} \leqslant 0 $

$\tag{13e} {P_{\rm{r}}} - \rho \left( {\delta _1^2P + {\sigma ^2}} \right) \leqslant 0 $

其中(13d)约束虽然不包含优化变量，却是针对信噪比阈值 ${\gamma _0}$ 的约束。当 $1{\rm{ - }}\rho \geqslant 0$ 时，函数 $\dfrac{{{\tau ^2}}}{{1{\rm{ - }}\rho }}$ 和 $\dfrac{1}{{1{\rm{ - }}\rho }}$ 都是凸函数，所以问题(13)是一个凸优化问题，可以用CVX^[16]来解决。

2 无线携能传输协同中继TDMA系统

为了与无线携能传输协同中继NOMA系统的性能做对比，本节讨论无线携能传输协同中继时分多址接入(TDMA)系统的速率性能。TDMA是一种传统的正交多址接入(Orthognal Multiple Access, OMA)方式。该TDMA系统与NOMA系统的系统模型一样，由源节点S、强用户U₁和弱用户U₂组成。强用户是能量收集中继，需收集一定的能量才能协同转发信息给弱用户，同样我们不考虑源节点到弱用户的直接链路。 ${s_1}$ 和 ${s_2}$ 分别是发送给强用户和弱用户的信息。

2.1 系统模型

由于强用户除了接收自己所需信息 ${s_1}$ ，还需协同转发弱用户的信息 ${s_2}$ ，因此源用户要在不同时隙分别发送 ${s_1}$ 和 ${s_2}$ 给强用户. 在第一和第二时隙，源节点分别发送 $\sqrt {{a_1}P} {s_1}$ 和 $\sqrt {{a_2}P} {s_2}$ 给强用户，强用户收到的信息分别表示为

$ y_1^{1{\rm{,T}}} = {h_1}\sqrt {{a_1}P} {s_1} + n_1^{{\rm{1,T}}}$

(14)

$y_1^{2,{\rm{T}}} = {h_1}\sqrt {{a_2}P} {s_2} + n_1^{2,{\rm{T}}}$

(15)

其中，上标 ${\rm{T}}$ 表示TDMA系统中的参数，以便与上一节NOMA系统中的参数区别； $n_1^{i{\rm{,T}}},i \in \left\{ {1, 2} \right\}$ 是强用户端的加性高斯白噪声。

由于强用户是一个能量受限的器件，需要收集一定的能量后才能转发信息。所以，强用户采用功率分配的方法，把接收到的信息一部分用作能量收集，另一部分用作信息解码。 $y_1^{1,{\rm{T}}}$ 用作能量收集和解码的信息分别表示为 $s_{{\rm{EH}}}^{{\rm{1,T}}}$ 和 $s_{{\rm{ID}}}^{{\rm{1,T}}}$ ， $y_{\rm{1}}^{{\rm{2,T}}}$ 用作能量收集和解码的信息分别表示为 $s_{{\rm{EH}}}^{{\rm{2,T}}}$ 和 $s_{{\rm{ID}}}^{{\rm{2,T}}}$ ，分别为

$ s_{{\rm{EH}}}^{{\rm{1,T}}} = \sqrt \rho \left( {{h_1}\sqrt {{a_1}P} {s_1} + n_{\rm{1}}^{{\rm{1,T}}}} \right) $

(16)

$ s_{{\rm{ID}}}^{{\rm{1,T}}} = \sqrt {1 - \rho } \left( {{h_1}\sqrt {{a_1}P} {s_1} + n_1^{1{\rm{,T}}}} \right) + n_{{\rm{ID}}}^{{\rm{1,T}}} $

(17)

$ s_{{\rm{EH}}}^{{\rm{2,T}}} = \sqrt \rho \left( {{h_1}\sqrt {{a_2}P} {s_2} + n_1^{{\rm{2,T}}}} \right) $

(18)

$ s_{{\rm{ID}}}^{{\rm{2,T}}} = \sqrt {1 - \rho } \left( {{h_1}\sqrt {{a_2}P} {s_2} + n_1^{{\rm{2,T}}}} \right) + n_{{\rm{ID}}}^{{\rm{2,T}}} $

(19)

其中， $n_{{\rm{ID}}}^{i,{\rm{T}}},i \in \left\{ {1,\,2} \right\}$ 是在信息解码端的加性高斯白噪声。由式(17)和式(19)得到强用户分别解码 ${s_1}$ 和 ${s_2}$ 的信噪比为

$ \begin{array}{c} \gamma _1^{1,{\rm{T}}} = \dfrac{{\left( {1 - \rho } \right){{\left| {{h_1}} \right|}^2}{a_1}P}}{{\left( {1 - \rho } \right){\sigma ^2} + {\sigma ^2}}} = \dfrac{{{\lambda _1}\left( {1 - \rho } \right)\left( { {a_1}} \right)}}{{\left( {2 - \rho } \right)\eta }} \end{array} $

(20)

$ \begin{array}{c} \gamma _1^{2,{\rm{T}}} = \dfrac{{\left( {1 - \rho } \right){{\left| {{h_1}} \right|}^2}{a_2}P}}{{\left( {1 - \rho } \right){\sigma ^2} + {\sigma ^2}}} = \dfrac{{{\lambda _1}\left( {1 - \rho } \right)\left( {1 - {a_1}} \right)}}{{\left( {2 - \rho } \right)\eta }} \end{array} $

(21)

强用户接收到的能量 $Q$ 为

$\begin{gathered} Q = {E} \left( {{{\left| {s_{{\rm{EH}}}^{{\rm{1,T}}}} \right|}^2}} \right) + {E} \left( {{{\left| {s_{{\rm{EH}}}^{{\rm{2,T}}}} \right|}^2}} \right) = \rho \left( {\delta _1^2P + 2{\sigma ^2}} \right) \end{gathered} $

(22)

第3个时隙，强用户以接收到的能量 ${P_{\rm{r}}}$ 转发 ${s_2}$ 给弱用户，弱用户接收到的信号为

$y_2^{\rm{T}} = {h_2}\sqrt {{P_{\rm{r}}}} {s_2} + n_2^{\rm{T}}$

(23)

弱用户解码 ${s_2}$ 的信噪比为

$\gamma _2^{2,{\rm{T}}} = \frac{{{{\left| {{h_2}} \right|}^2}{P_{\rm{r}}}}}{{{\sigma ^2}}} = \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}}$

(24)

由式(20)可得到解码 ${s_1}$ 的速率，即强用户的速率为

$\begin{gathered} R_1^{\rm{T}} = \frac{1}{3}{\log _2}\left( {1 + \gamma _1^{1,{\rm{T}}}} \right) = \frac{1}{3}{\log _2}\left( {1 + \frac{{{\lambda _1}\left( {1 - \rho } \right){a_1}}}{{\left( {2 - \rho } \right)\eta }}} \right) \end{gathered} $

(25)

由式(21)和(24)，可得解码 ${s_2}$ 的速率，即弱用户的速率为

$R_2^{\rm{T}} = \frac{1}{3}{\rm{min}}\left\{ {{{\log }_2}\left( {1 + \gamma _1^{2,{\rm{T}}}} \right),{{\log }_2}\left( {1 + \gamma _2^{2,{\rm{T}}}} \right)} \right\}$

(26)

2.2 强用户速率最大化的研究

最大化强用户的速率，同时保证弱用户的速率大于 ${r_0}$ ，且满足强用户EH接收机在单位时间的能量大于 ${P_{\rm{r}}}$ . 问题规划如式(27a)~(27c)所示。

$\tag{27a} \mathop {\max }\limits_{0 \leqslant {a_1} \leqslant 1,0 \leqslant \rho \leqslant 1} R_1^{\rm{T}} $

$\tag{27b} {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\;\; R_{\rm{2}}^{\rm{T}} \geqslant {r_0} $

$\tag{27c} {Q^{\rm{T}}} \geqslant {P_{\rm{r}}} $

把 $R_{\rm{1}}^{\rm{T}}$ 、 $R_{\rm{2}}^{\rm{T}}$ 和 ${Q^{\rm{T}}}$ 的表达式代入式(27)，问题可重写为

$\tag{28a} \mathop {\max }\limits_{ 0 \leqslant {a_1} \leqslant 1,0 \leqslant \rho \leqslant 1} \frac{{{\lambda _1}\left( {1 - \rho } \right){a_1}}}{{\left( {2 - \rho } \right)\eta }} $

$\tag{28b} {\rm{s}}{\rm{.t}}{\rm{.}} \;\;\;\;\;\;\;\; \frac{{{\lambda _1}\left( {1 - \rho } \right)\left( {1 - {a_1}} \right)}}{{\left( {2 - \rho } \right)\eta }} \geqslant {\varphi _0} $

$\tag{28c} \quad \quad \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}} \geqslant {\varphi _0} $

$\tag{28d} \quad \quad \;\;\rho \left( {\delta _1^2P + 2{\sigma ^2}} \right) \geqslant {P_{\rm{r}}} $

其中， ${\varphi _0} = {2^{3{r_0}}} - 1$ 为弱用户信噪比阈值。

问题(28)是一个非凸的优化问题，不能直接求解。令 $\dfrac{{{\lambda _1}\left( {1{\rm{ - }}\rho } \right){a_1}}}{{\left( {2 - \rho } \right)\eta }} \geqslant {\alpha ^2}$ ，并进一步化简计算，式(28)可以重写为

$\tag{29a} \mathop {\max }\limits_{0 \leqslant {a_1} \leqslant 1,0 \leqslant \rho \leqslant 1,\alpha }\alpha $

$\tag{29b} {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;\;\;\frac{{{\alpha ^2}}}{{1{\rm{ - }}\rho }} + {\alpha ^2} - \frac{{{\lambda _1}{a_1}}}{\eta } \leqslant 0 $

$\tag{29c} \frac{{{\varphi _0}}}{{1{\rm{ - }}\rho }} + {\varphi _0} + \frac{{{\lambda _1}}}{\eta }\left( {{a_1} - 1} \right) \leqslant 0 $

$\tag{29d} {\varphi _0} - \frac{{{\lambda _2}{P_{\rm{r}}}}}{{{\sigma ^2}}} \leqslant 0 $

$\tag{29e} {P_{\rm{r}}} - \rho \left( {\delta _1^2P + 2{\sigma ^2}} \right) \leqslant 0 $

其中(29d)是对信噪比阈值 ${\varphi _0}$ 取值的约束。可以看出，问题(29) 是一个凸优化问题，可以用CVX 来解决^[16]。

3 仿真结果与分析

在本节中，将无线携能传输协同中继NOMA系统和TDMA系统的强用户速率性能进行对比。

仿真中的基本参数如下：信道系数 ${h_1}$ 、 ${h_2}$ 的方差分别为 $\delta _1^2 = 1$ 、 $\delta _2^2 = 0.5$ ，发射功率 $P = 2$ ， ${P_{\rm{r}}} = 1$ ，信噪比 ${{{P_{\rm{r}}}} / {{\sigma ^2}}}$ 取值范围为0~30 dB。所有的仿真结果都是由1 000次生成的随机复高斯信道进行优化所得结果取平均值而得到。

3.1 不同发射功率P对无线携能传输协同中继NOMA系统的影响

本节在无线携能传输协同中继NOMA系统中最大化强用户速率，讨论不同的发射功率 $P$ 对最大化强用户速率的影响。在仿真中，不同的弱用户速率阈值下，强用户收集能量的单位时间能量阈值 ${P_{\rm{r}}} = 1$ 保持不变，当发射功率 $P$ 分别为 $ 2{P_{\rm{r}}}$ 和 $ 4{P_{\rm{r}}}$ 时，比较最大化强用户的速率。

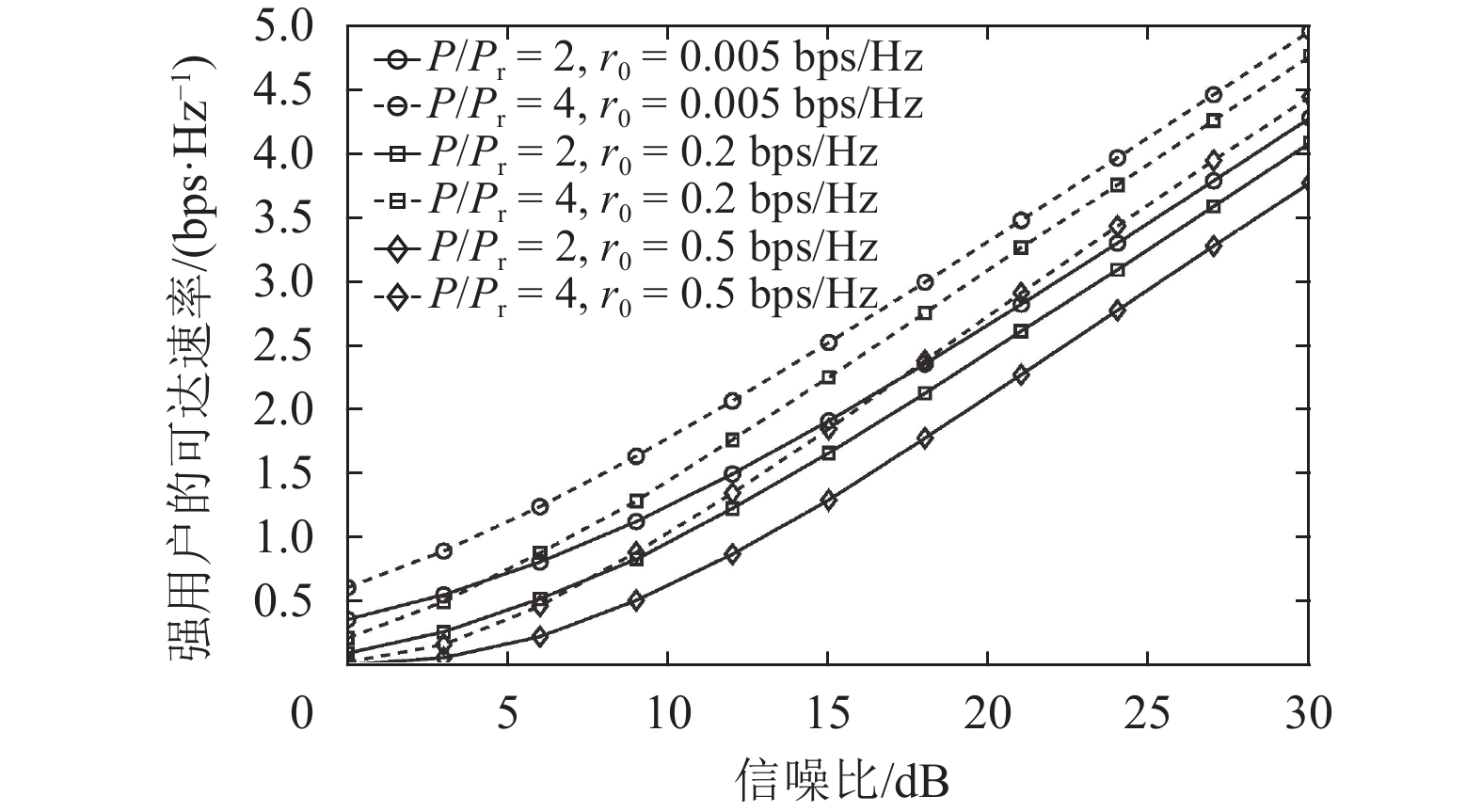
图2是无线携能传输协同中继NOMA系统的强用户速率性能曲线，在不同的弱用户速率阈值 ${r_0}$ 下，不同的发射功率 $P$ 对强用户速率的影响。从图中可以看出：(1) 随着信噪比 ${{{P_{\rm{r}}}} / {{\sigma ^2}}}$ 的增加，强用户的速率不断增大，且强用户的速率随着弱用户的速率阈值增加而下降，这是为了满足更高的弱用户速率要求，此时更多的信号功率分配给了弱用户，造成强用户速率的下降。(2) 当发射功率 $P$ 越大，强用户和弱用户都能得到更多的增益，使强用户的速率得到提高。

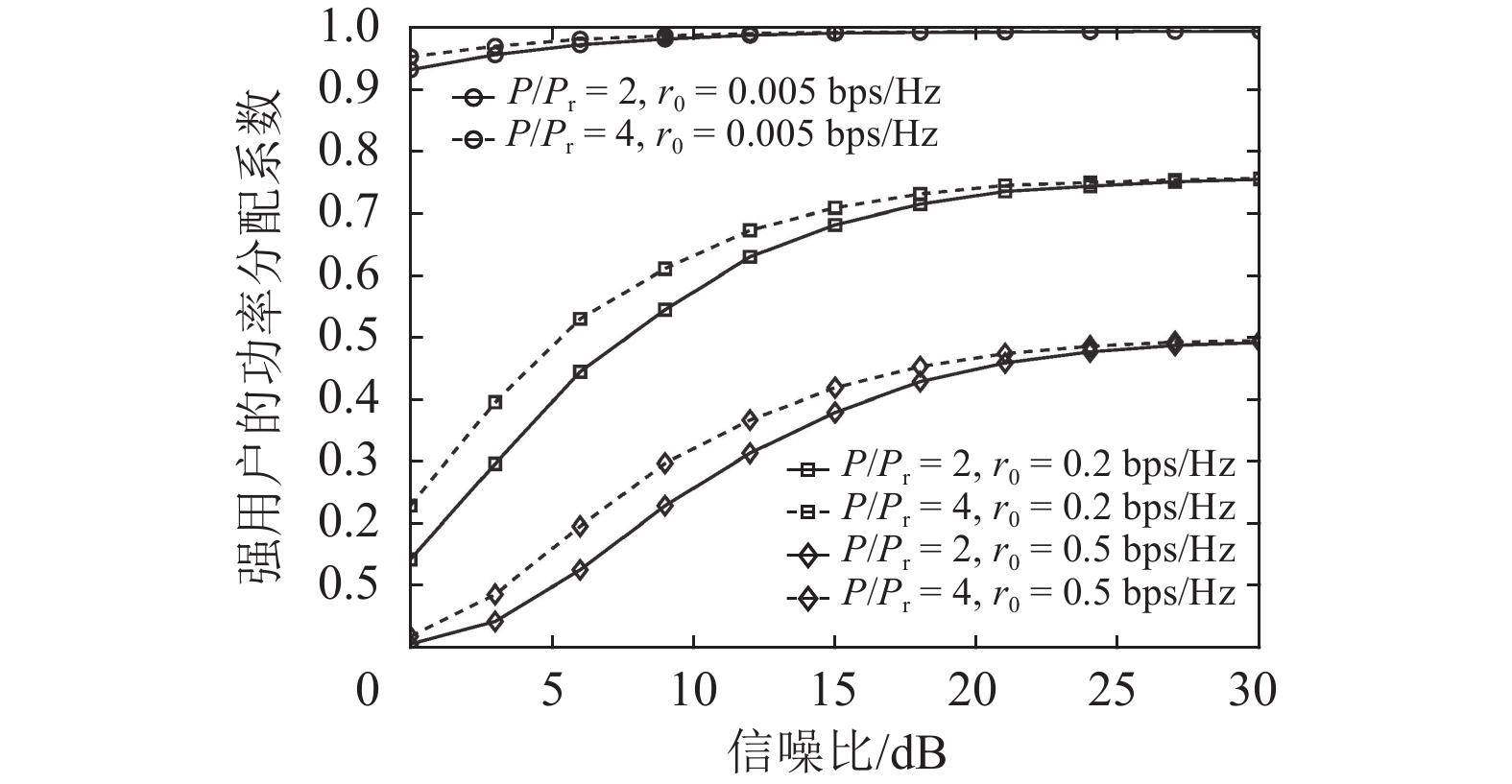
图3是无线携能传输协同中继NOMA系统的强用户速率最大化时，在不同的发射功率下，强用户的功率分配系数 ${a_1}$ 的变化曲线. 从图中可以看出：(1) 在不同的弱用户速率阈值 ${r_0}$ 下， ${a_1}$ 随着 ${r_0}$ 的增加而下降，那是为了满足更大的弱用户速率，更多的信号功率分配给了弱用户，所以给强用户的功率分配系数就会降低。(2) 在不同的信噪比 ${{{P_{\rm{r}}}} / {{\sigma ^2}}}$ 下，随着信噪比的增加，强、弱用户解码信息的信噪比都得到增强，因此，在大信噪比下弱用户更容易满足速率约束，分配给弱用户的信号功率可以更小，为了满足强用户的速率最大化，强用户的信号功率分配系数 ${a_1}$ 更大，所以表现为图中的 ${a_1}$ 随着信噪比的增加而增加。(3) ${a_1}$ 在不同的发射功率 $P$ 时的变化规律相似，且 ${a_1}$ 随着发射功率 $P$ 的增加而增加，其中原因和随着信噪比的增加而增加一样，也是由于发射功率带来的解码信噪比增益增加，使得弱用户用更少的信号分配功率也能保证达到阈值，更多的信号功率分配给了强用户，使得强用户速率最大化。

3.2 无线携能传输协同中继NOMA系统与TDMA系统的对比

本节通过仿真对比了无线携能传输协同中继NOMA系统和TDMA系统的强用户速率最大化性能，也对强用户EH接收机的功分系数性能进行了分析。

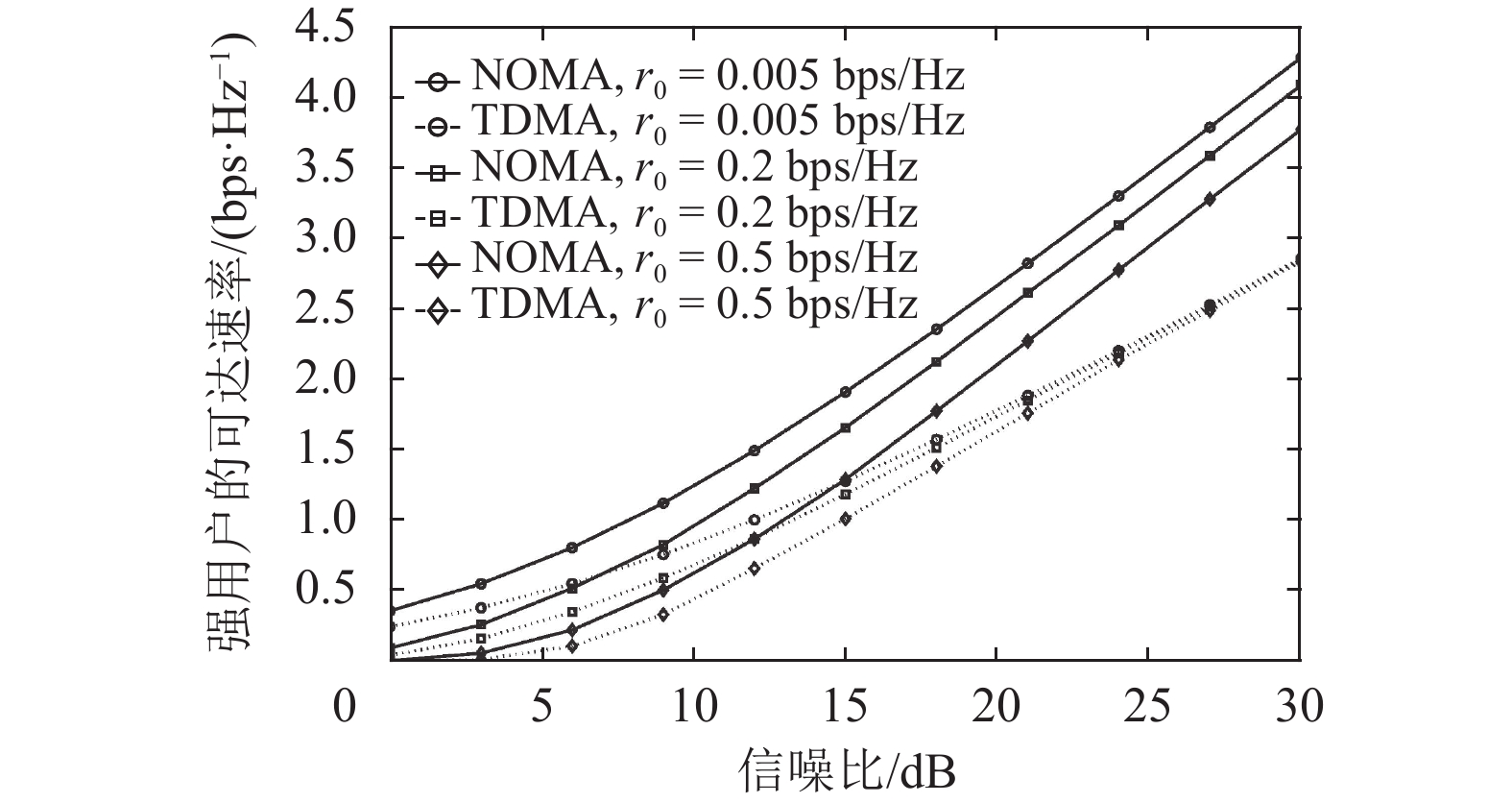
图4显示的是分别在无线携能传输协同中继NOMA系统和TDMA系统中，最大化强用户速率的变化曲线。从图中可以看出：(1) 2个系统的强用户速率都随着信噪比 ${{{P_{\rm{r}}}} / {{\sigma ^2}}}$ 的增加而增加，在不同的弱用户速率阈值 ${r_0}$ 下，2个系统的强用户速率都随着 ${r_0}$ 的增加而降低，这是为了满足更高的弱用户速率而降低对强用户信号功率的分配造成的。(2) 2个系统相比较而言，NOMA系统比TDMA系统的强用户速率性能有了明显的提高，这是因为TDMA系统采用了三时隙来完成中继系统的两用户信息传输，而NOMA系统由于采用叠加编码信号的传输以及串行干扰消除技术，只需2个时隙就可以完成中继系统的两用户信息传输，较大幅度地提高了强用户的解码信噪比，进而有效地提高了强用户的信息速率。这也说明NOMA技术对于传统的OMA来说在频谱利用率上有很大优势。

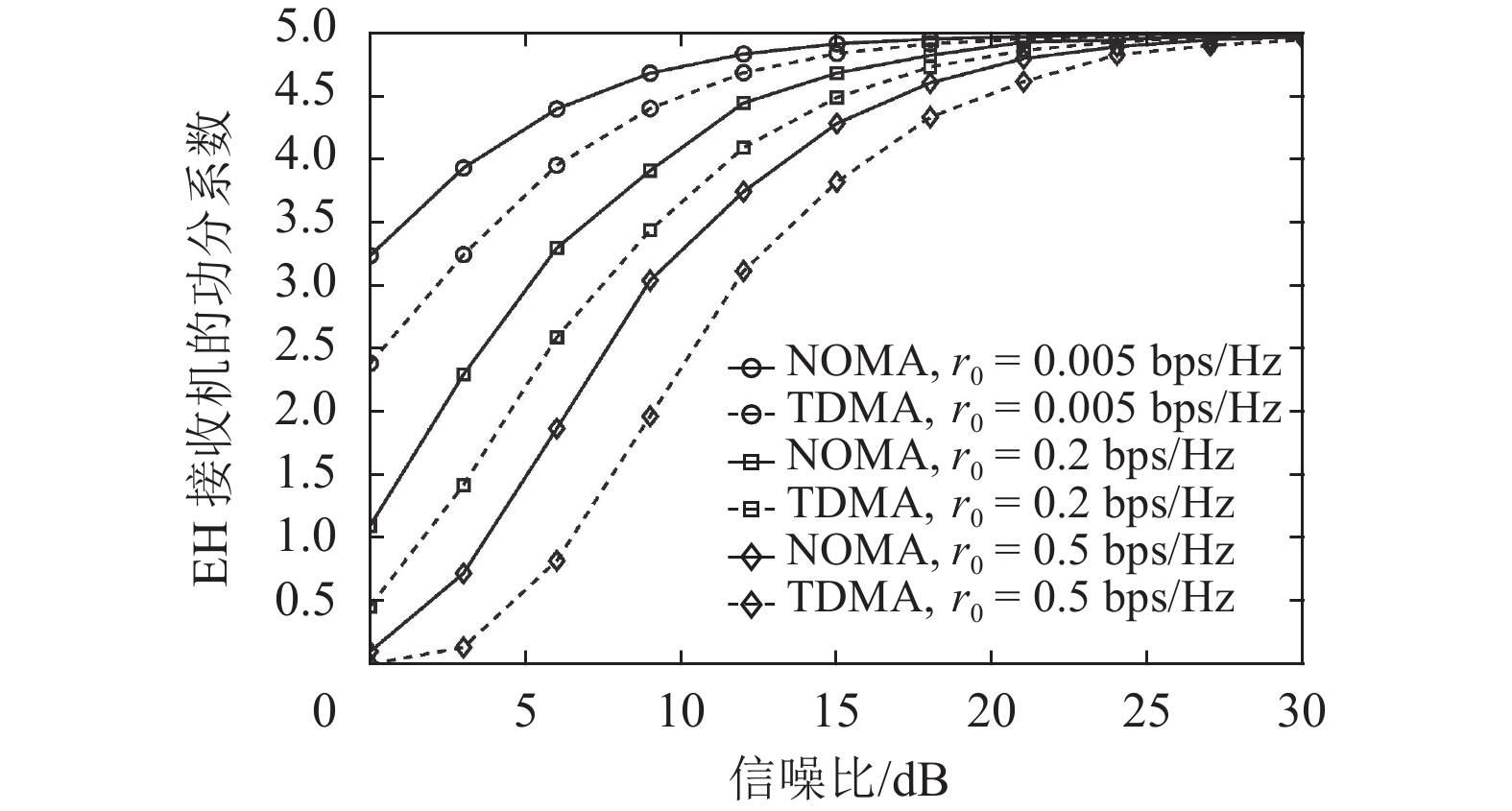
图5给出了在无线携能传输协同中继NOMA系统和TDMA系统中，最大化强用户速率时强用户EH接收机的功分系数的变化曲线。从图中可以看到：(1) 在2个系统中，强用户EH接收机的功分系数 $\rho $ 变化规律相同，都随着信噪比 ${{{P_{\rm{r}}}} / {{\sigma ^2}}}$ 的增加而增加，那是因为无论哪个系统，当信噪比增加时，提供给强、弱用户的信噪比增益更大，弱用户的速率更容易达到阈值，因此对于强用户来说，用于ID接收机的这部分功率可以更低，也能使更多的信息功率分配给EH接收机，所以EH 接收机的功分系数更高。(2) 在不同的弱用户速率阈值 ${r_0}$ 下，2个系统的EH接收机功分系数都随着 ${r_0}$ 的增加而降低，这是因为弱用户要求的速率越高，强用户作为中继端需要更多的信息功率用于ID接收机的信息解码，因此用于EH接收机收集的能量就更少。(3) 2个系统相比较而言，TDMA系统需要的EH 接收机功分系数更低，说明TDMA系统相比NOMA系统需要更多的信息能量用于ID 接收机进行信息的解码，保证弱用户的速率达到阈值。

4 结论

本文研究了无线携能传输协同中继NOMA系统的强用户速率的最大化问题。在该系统中，强用户是一个能量收集中继，除了要接收自己所需信息，还作为中继帮助弱用户转发信息，同时强用户是一个能量受限的器件，需要接收一定的能量后才能转发信息。在此情况下，本文联合优化源节点分配给强用户的信息功率分配系数和强用户EH接收机的功分系数，讨论了强用户的速率最大化的问题，并通过仿真，得到以下结果：(1) 无线携能传输协同中继NOMA系统的强用户速率随着源节点发射功率的增加而增加。(2) 无线携能传输协同中继NOMA系统比传统的TDMA系统的强用户速率更优。