A Simultaneous Optimization of Working Fluid Design and System Parameters in Organic Rankine Cycle
当今世界能源与环境问题日益突出,有效利用太阳能、地热能等可再生能源以及回收余热资源是解决能源环境问题的有效途径,其中有机朗肯循环[1](organic Rankine cycle, ORC)是最具潜力的低品位热−功转换技术之一。工质是ORC能量转换的载体,其与ORC系统之间的匹配将直接影响ORC系统的性能[2]。
近些年来,国内外学者针对纯工质与热源匹配开展了大量的研究。Bao等[3]总结了前人在不同热源条件下的推荐工质,归纳了工质筛选需要考虑的因素。He等[4]将热源分为两类:一类是已知热源进口温度和流量,另一类为已知热源放热量。Yu等[5]按照热源的特性将其分为敏感性热源、联合热源及潜焓热源。这些研究大多以工质物性和ORC循环性能之间的关联匹配实现工质筛选,然而这些研究主要局限于现有工质筛选,而针对ORC设计新工质的研究有限。计算机辅助分子设计(computer-aided molecular design, CAMD)已经被广泛应用,是设计合成新物质的有效方法,在药物设计[6]、生物大分子设计[7]、溶剂[8]等领域得到了广泛应用。CAMD可以针对热源特性实现工质设计和ORC系统的同步优化。Papadopoulos等[9]率先提出将CAMD应用于ORC的工质设计中,针对ORC循环的特点总结了设计ORC工质应该考虑物理、化学、环境等各个方面的性质。作者首先由CAMD设计获得新型工质,从中选出合适的新工质及现有工质通过模拟退火优化方法获得适合的工质。Palma-Flores等[10]基于全局优化思路,将工质物性如潜焓、比热容等作为目标函数,构建了混合整数非线性模型(mixed integer non-line programming, MINLP)并求解获得新型工质。不同于Papadopoulos等[9]的工作,Palma-Flores等[10]所构建的模型中通过构建基团库,在满足化学限制等条件下构成工质,模型中不仅能包含现有工质,同时也包含新工质。但是,符合设计目标的工质拥有最优物性并不一定能保证最优ORC性能。Palma-Flores等[11]提出以ORC循环热效率最大为目标,即将CAMD和ORC循环同步优化设计工质,结果显示以工质物性作为目标函数优化获得的工质并不是在该工况条件下的最优工质。
在CAMD与ORC循环同步优化的过程中,针对ORC循环特点需要对工质设置可行域,以排除不符合的ORC循环的工质。在Palma-Flores等[11]的工作中,仅仅给定热源条件,实际上是确定了蒸发器、冷凝器中的温度,并没有实现真正的工质与热源同步优化。本文基于此,首先通过REFPROP等[12]数据库获得334种工质的物性,确定合理的可行域,同时寻找工质物性之间的关联以给出更合理的可行域。同时,考虑到ORC循环特点,提出新的限制条件剔除湿工质即确保工质从膨胀机出口为过热态。基于优化的CAMD模型,实现不同工况下的全局优化获得新型工质。考虑到原有的工质筛选往往选出几种物性,通过物性与循环性能之间的关系获得工质筛选的准则。而由于CAMD设计所获得工质时缺乏的实验数据,因此本文所构建的模型在计算ORC循环性能时,全部基于工质的物性出发。因此,借助本文所构建的模型进行工质物性与ORC系统的敏感性分析,探究与循环性能有关的物性与循环性能之间的关联,为工质筛选提供准则。
1 问题描述
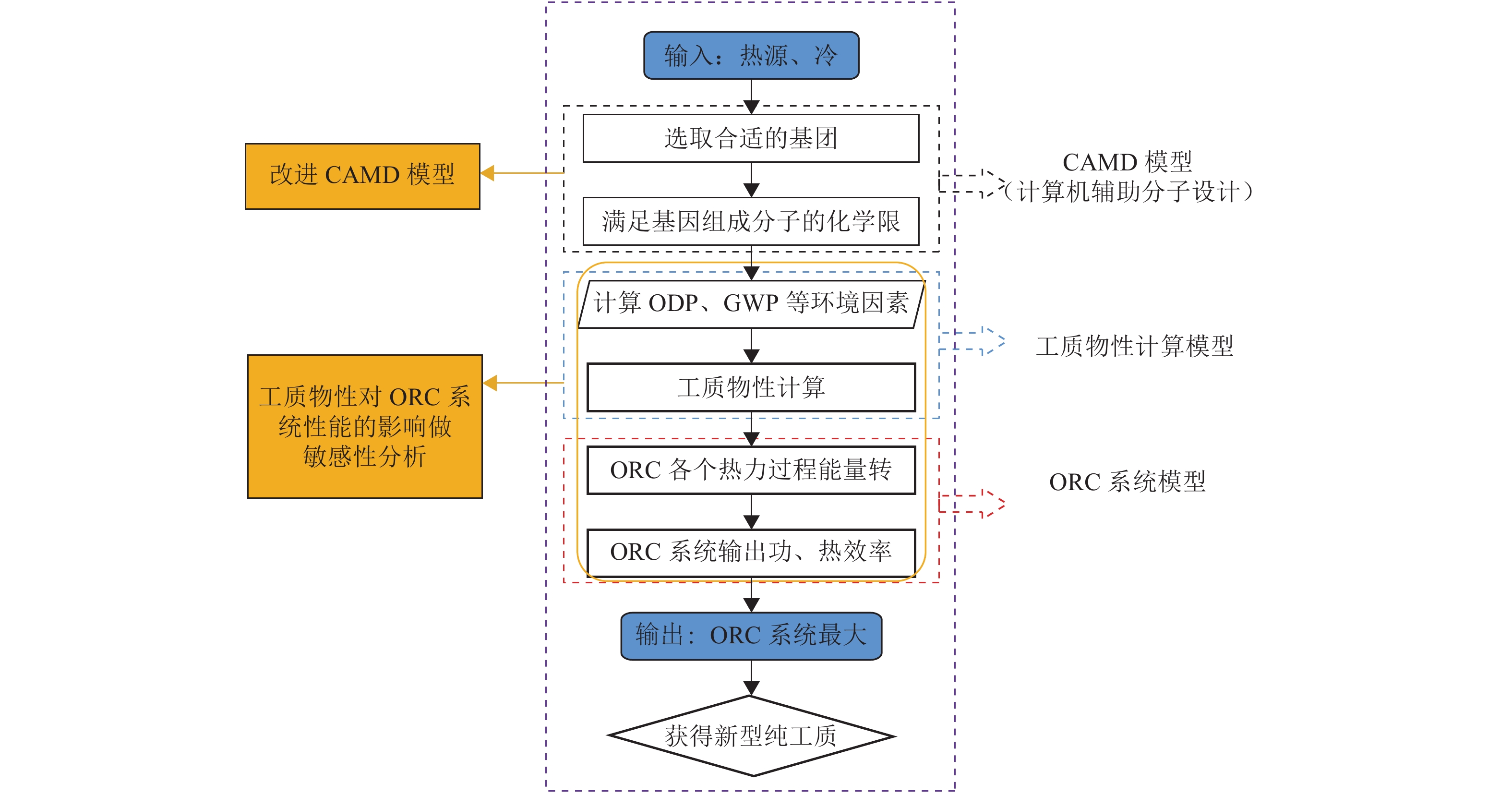
提出了基于CAMD的工质设计与ORC系统同步优化的MINLP模型,分为3个部分:CAMD模型、工质物性计算模型和ORC系统模型,如图1所示。首先提出改进的CAMD模型,针对ORC循环的特点,提出工质物性可行域,并提出新的限制模型以剔除湿工质。基于改进的CAMD模型,在不同工况条件下,实现同步优化获得新工质。同时,基于工质物性计算模型和ORC系统模型对工质物性和ORC循环输出功之间的关系进行敏感性分析。
2 数学模型
基于全局优化的思路,以ORC输出净功最大为目标,设计新型工质。整个模型包含CAMD模型、物性计算模型、ORC系统模型3个部分。模型假设如下:(1) ORC系统处于稳定运行状态;(2) 工质在泵中升压过程温升忽略不计;(3) 换热器压降忽略不计。
2.1 CAMD模型
2.1.1 基团表的构建
CAMD是通过符合化学限制条件的基团之间自由组合获得ORC工质。因此是否能够建立合适的基团表将直接影响CAMD设计的结果。基于ORC的运行条件,考虑到工质的临界物性、毒性、稳定性及ODP、GWP等环境因素,选定C、H、O、N、F、Cl、Br、I、S等9种元素构成基团表的基础元素。CAMD化学限制模型源于Churi和Achenie等[13],主要适用范围为链式结构的分子,因此需要自行组合芳香烃、环烃等作为单个基团。所建立的基团表如表1所示。
表 1(Table 1)
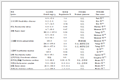
表 1 基团表
Table 1 Group table
含碳
基团
|
含卤族
基团
|
含氧
基团
|
含氮
基团
|
含硫
基团
|
芳香烃
基团
|
环烃
基团
|
| -CH3 |
-F |
-OH |
-NH2 |
-SH |
-C6H5 |
-C3H5 |
| -CH2-
|
-Cl |
-O- |
>NH |
-S- |
-C6H4-
|
-C4H7 |
| >CH- |
-Br |
>C=O |
>N- |
-CO-S- |
>C6H3-
|
-C5H9 |
| >C< |
-I |
-CH=O |
-NO2 |
|
-C6H3-OH
|
-C6H11 |
|
|
-COOH |
-CONH2 |
|
>C6H3-OH
|
-C5H8-
|
|
|
-COO - |
-CONH- |
|
C6H5-NH-
|
-C6H10-
|
|
|
|
-CON- |
|
C6H5-N<
|
|
|
表 1 基团表
Table 1 Group table
|
2.1.2 化学限制约束
基团表中的基团必须符合化学限制约束才能组成分子。为了将基团表与化学限制约束相联系,去除不合理的分子结构,引入了3个整数二元变量用于描述分子与基团之间的联系,分别为yik、zijp和wi。其中yik表示组成分子的第i个基团为基团库中的第k个基团,zijp指相邻两基团之间的共价键的连接位置,wi表示分子中共有几个基团组成。同时定义了4个参量:m是基团表中基团总数,smax是基团中化合价的最大值,nmax是组成分子的基团数的可行域。
式(1)表示组成分子的基团最大数,因为由CAMD设计获得的分子需要化学结构稳定,而过多的基团所组成的分子其吉布斯自由能等数较大,化学结构不稳定,因此nmax上限为10,即最多由10个基团组成分子。
|
$ \sum \nolimits\limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}\leqslant {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(1) |
式(2)为八角规则,即确保在分子内部每个基团的化学键的数量等于其化合价数量,排除基团中的某个化学键无基团与其相连的情况。
|
$ \sum \limits_{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{j=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{ijp}=\sum \limits_{k=1}^{m}{y}_{ik}{v}_{k},\;\;i=1\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(2) |
式(3)是确保基团之间按序排列,首先随机选出一个基团,之后按照顺序将第i个基团和第i−1个基团相连接。
|
$ \sum \limits_{p=1}^{i-1}\sum \limits_{j=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{ijp}\geqslant -{w}_{i},\;\;i=2\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(3) |
按照设定的组成基团的最大个数从基团表中随机选取出10个基团,但这10个基团并不一定全部都用于组成分子,可能只有其中一部分用于分子,式(4)是组成分子的实际基团数与基团最大数之间的关系。
|
$ \sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}+\sum \limits_{I=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{w}_{i}={n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(4) |
式(5)辅助式(3)中限制确保基团之间按顺序连接。
|
$ {w}_{i}\leqslant {w}_{i+1},\;\;\;\;i=1\cdots \left({n}_{{\rm{m}}{\rm{a}}{\rm{x}}}-1\right) $
|
(5) |
式(6)为限制基团与其他基团之间共价键总数小于其化合价,以剔除不合理的连接情况。
|
$\begin{array}{l}\displaystyle \sum \limits_{j={v}_{k}}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{ijp}-\sum \limits_{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{i{v}_{k}p}+{\rm{Minf}}{y}_{ik}\leqslant {\rm{Minf}},\\ i=1\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}},\;k=1\cdots m \end{array}$
|
(6) |
其中,Minf为任意大的正数。
式(7)是确保2个基团之间的连接的共价键数量相同,例如i基团中有两个共价键与i+1基团相连,那么i+1基团也必须有两个共价键与i基团相连。
|
$ \sum\limits _{j=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{ijp}=\sum\limits _{j=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{pji},\;\;\;\;i=1\cdots \left({n}_{{\rm{m}}{\rm{a}}{\rm{x}}}-1\right),\;\\ p=\left(i+1\right)\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(7) |
式(8)为限制两个相连的基团只能在基团中的一个位置相连,即只能形成链式结构。
|
$ \sum \limits_{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{ijp}\leqslant 1,i=1\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}},j=1\cdots {s}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(8) |
式(9)为确保组成分子的基团必须在前一个已经连接的情况下才可以选出下一个用于连接的基团。
|
$ \sum \limits_{k=1}^{m}{y}_{ik}-\sum \limits_{k=1}^{m}{y}_{i-1,k}\leqslant 0,\;i=2\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(9) |
式(10)确保任何基团不能与其自身相连。
|
$ \sum \limits_{j=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{iji}=0,\;i=1\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(10) |
式(11)和(12)将确保基团为从左到右的排列顺序组成分子。这些限制不仅减少了计算异构体的可能性,还帮助确定了独特的结构。
|
$ \sum\limits _{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{i,j-1,p}\geqslant \sum\limits _{p=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{i,j,p},\\ i=1\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}},j=2\cdots {s}_{{\rm{m}}{\rm{a}}{\rm{x}}} $
|
(11) |
|
$ {\textit{z}}_{i,1,p}=\sum\limits _{p=1}^{{s}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{\textit{z}}_{p,j,i},\\ i=2\cdots {n}_{{\rm{m}}{\rm{a}}{\rm{x}}},\;p=1\cdots ({n}_{{\rm{m}}{\rm{a}}{\rm{x}}}-1) $
|
(12) |
式(13)为基于组成分子的基团之间共价键的化学限制设定的约束条件。
|
$ \sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{v}_{k}=2(n-1) $
|
(13) |
考虑到工质物理化学性质的稳定、无毒及环境因素等,式(14)限制了某些特定的基团在分子内出现的次数。
|
$ \sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}{y}_{ik}\leqslant {\delta }_{k}, k=1\cdots m $
|
(14) |
2.2 ORC系统热力学模型
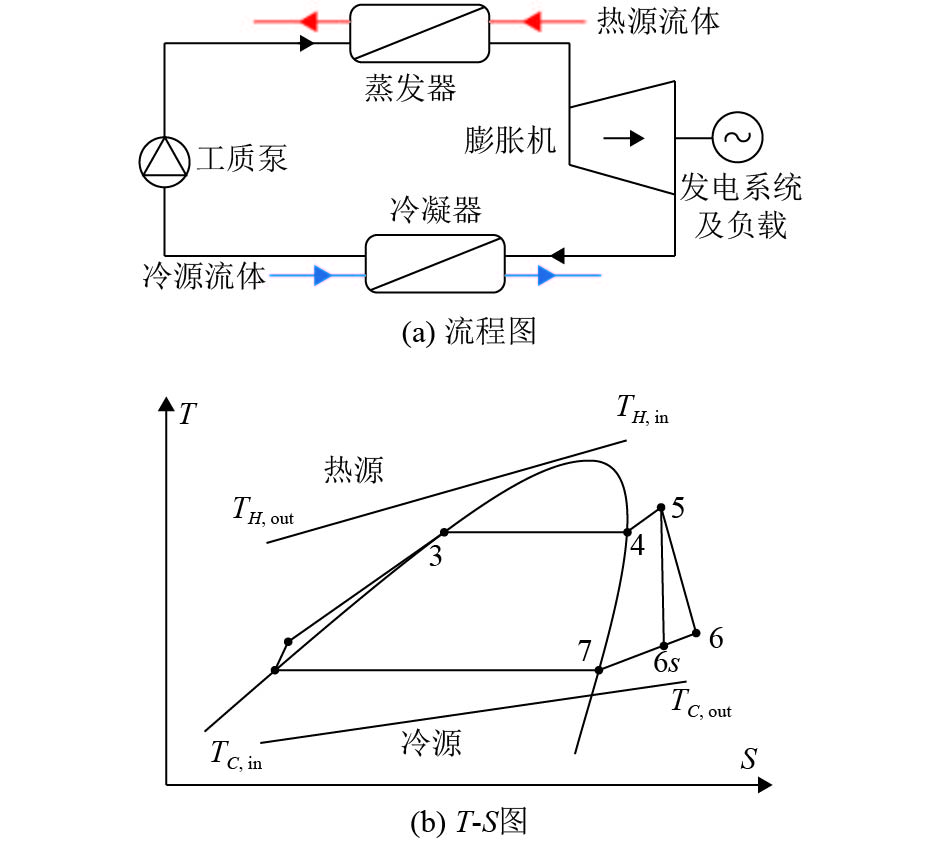
简单ORC包含有4个基本热力过程:加压、蒸发、膨胀和冷凝,如图2(a)所示。图2(b)为ORC的T-S图。对于传统工质,由于有大量的实验数据可以调用,从而直接可以获取各个状态下的焓值获得ORC系统的热效率或输出功等参数。但是通过CAMD获得的工质缺乏实验数据,因此需要借助物性及状态方程等计算ORC循环参数。
2.2.1 加压过程
来自冷凝器出口的工质被输送进入工质泵,工质在工质泵中被绝热压缩至高压过冷液体,工质泵中的耗功可以公式(15)表示:
|
$ {W}_{{\rm{P}}}={m}_{{\rm{w}}{\rm{f}}}\left({h}_{2}-{h}_{1}\right)={m}_{{\rm{w}}{\rm{f}}}\frac{{P}_{2}-{P}_{1}}{\rho {{\eta }_{\rm{P}}}} $
|
(15) |
其中,ρ表示工质在加压过程中的密度,可由公式(16)计算, ηP表示工质泵的等熵效率, P2表示蒸发压力, P1为冷凝压力, mwf表示工质的质量流量。
因为忽略了工质在加压过程中的温升,取工质在T1状态下即饱和液态的密度ρl(g/cm3)作为加压过程中的工质密度[10],选用式(16)计算。
|
$ \rho =\frac{MR{T}_{{\rm{c}}}}{{P}_{{\rm{c}}}}{{Z}_{{\rm{c}}}}^{[1+{(1-{T}_{{\rm{r}}})}^{2/7}]} $
|
(16) |
其中,R为气体常数,为8.314 5 J/(mol·K),M为摩尔质量,g/mol. Tc为临界温度[14]可由公式(17)和(18)计算获得,其中Tb为沸点温度,Pc为临界压力[14]可由公式(19)计获得,Zc为临界压缩因子[14]可由公式(20)和(21)获得,Tr为对比态温度。
|
$ {T}_{{\rm{c}}}=\frac{{T}_{{\rm{b}}}}{0.584+0.965\displaystyle\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{T}_{{{\rm{c}}}_{k}}-{\left(\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{T}_{{{\rm{c}}}_{k}}\right)}^{2}} $
|
(17) |
|
$ {T}_{{\rm{b}}}=198.2+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{T}_{{{\rm{b}}}_{k}} $
|
(18) |
|
$ {P}_{{\rm{c}}}={\left(0.113+0.003\;2\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{N}_{k}-\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{P}_{{{\rm{c}}}_{k}}\right)}^{-2} $
|
(19) |
|
$ {V}_{{\rm{c}}}=17.5+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{V}_{{{\rm{c}}}_{k}} $
|
(20) |
|
$ {Z}_{{\rm{c}}}=\frac{{P}_{{\rm{c}}}{V}_{{\rm{c}}}}{{\rm{R}}{T}_{{\rm{c}}}} $
|
(21) |
其中,Vc为临界比体积[14],
${T}_{{{\rm{c}}}_{k}}$
、
${T}_{{{\rm{b}}}_{k}}$
、
${P}_{{{\rm{c}}}_{k}}$
、
${V}_{{{\rm{c}}}_{k}}$
为基团k的基团贡献值,可在Joback和Reid的文中[14]获得。工质在换热器中的压力[15]可由式(22)获得。
|
$ {\rm{l}}{\rm{n}}{P}_{\rm{vpr}}=A-\frac{B}{{T}_{{\rm{r}}}}+C{\rm{ln}}{T}_{{\rm{r}}}+D{T}_{{\rm{r}}}^{6} $
|
(22) |
方程参数A、B、C和D可通过下列关系式确定,其中K=0.083 8。
|
$ C=42Q+{\alpha }_{{\rm{C}}} $
|
(25) |
|
$ Q=K\left(3.758-{\alpha }_{{\rm{C}}}\right) $
|
(27) |
|
$ {\alpha }_{{\rm{C}}}=\frac{3.758K{\varphi }_{{\rm{b}}}+{\rm{l}}{\rm{n}}({P}_{{\rm{c}}}/101.325)}{K{\varphi }_{{\rm{b}}}-{\rm{ln}}{T}_{{\rm{b}}{\rm{r}}}} $
|
(28) |
|
$ {\varphi }_{{\rm{b}}}=35+\frac{36}{{T}_{{\rm{b}}{\rm{r}}}}+42{\rm{ln}}{T}_{{\rm{b}}{\rm{r}}}-{T}_{{\rm{b}}{\rm{r}}}^{6} $
|
(29) |
|
$ {T}_{{\rm{b}}{\rm{r}}}=\frac{{T}_{{\rm{b}}}}{{T}_{{\rm{c}}}} $
|
(30) |
综上各式可以计算获得工质在加压过程的能量转换,由此可将式(15)表述为工质物性的函数,如式(31)所示。
|
$ {W}_{{\rm{P}}}={m}_{{\rm{wf}}}\left({h}_{2}-{h}_{1}\right)={m}_{{\rm{wf}}}\frac{{P}_{2}-{P}_{1}}{\rho {\eta }_{{\rm{P}}}}=f({P}_{{\rm{c}}},{T}_{{\rm{b}}},{T}_{{\rm{c}}},T,\rho ) $
|
(31) |
2.2.2 蒸发过程
从工质泵出口状态输出的高压过冷态工质,在蒸发器中等压蒸发至过热蒸汽状态,蒸发器中的吸热量可分为过冷段、饱和段及过热段并由式(32)、(33)和(34)分别计算,蒸发器中总的换热量可由式(35)计算:
|
$ {Q}_{23}={m}_{{\rm{wf}}}{\int }_{{T}_{2}}^{{T}_{3}}{C}_{{\rm{p}}}^{l}{\rm{d}}T $
|
(32) |
|
$ {Q}_{34}={m}_{{\rm{wf}}}\Delta {H}_{{\rm{v}}}\left({T}_{3}\right) $
|
(33) |
|
$ {Q}_{45}={\int }_{{T}_{4}}^{{T}_{5}}{C}_{{\rm{p}}}^{g}{\rm{d}}T $
|
(34) |
|
$ {Q}_{\rm{evap}}={Q}_{23}+{Q}_{34}+{Q}_{45}={m}_{{\rm{wf}}}\left({{\rm{h}}}_{5}-{{\rm{h}}}_{2}\right) $
|
(35) |
其中,
${C}_{{\rm{p}}}^{l}$
是工质的定压液态比热容[14],可由式(39)和(40)得出,
${C}^{g}_{{\rm{p}}}$
是定压气态比热容[14]; ΔHv (T3)是工质在T3温度下的蒸发的潜焓[16],可由式(36)、(37)和(38)计算获得。
|
$ \Delta {H}_{{\rm{v}}}=\Delta {H}_{{\rm{vb}}}{\left(\right(1-{T}_{{\rm{r}}})/(1-{T}_{{\rm{br}}}\left)\right)}^{0.38} $
|
(36) |
|
$ \Delta {H}_{{\rm{vb}}}=1.093R{T}_{{\rm{c}}}{T}_{{\rm{br}}}({\rm{ln}}{P}_{{\rm{c}}}-1.013)/(0.93-{T}_{{\rm{br}}}) $
|
(37) |
|
$ {T}_{{\rm{br}}}={T}_{{\rm{b}}}/{T}_{{\rm{c}}} $
|
(38) |
|
$ \begin{split} C_{\rm{p}}^l = & \left[ {1\;045 + 0.145{{\left( {1 - {T_{\rm{r}}}} \right)}^{ - 1}} + } \right.\\ & \left. {0.25\omega \left( {17.11 + 25.2{{\left( {1 - {T_{\rm{r}}}} \right)}^{0.33}}{T_{\rm{r}}}^{ - 1} + 1.742} \right)} \right] + C_{\rm{p}}^0 \end{split} $
|
(39) |
|
$\begin{split} {C}_{{\rm{p}}}^{0}=& \left(\sum\limits _{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum\limits _{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{a}-37.93\right)\!+\!\left(\sum\limits _{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum\limits _{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{b}+0.21\right)T+\\ & \left(\sum\limits _{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum\limits _{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{c}-3.91\times {10}^{-4}\right){T}^{2}+\\ & \left(\sum\limits _{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum\limits _{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{d}+2.06\times {10}^{-7}\right){T}^{3} \\[-20pt]\end{split}$
|
(40) |
定压液态比热容
${C}_{{\rm{p}}}^{l}$
是基于理想气体的定压比热容计算获得,而过热度即式(41)中的
${C}^{g}_{{\rm{p}}}$
为实际气体的定压气态比热容,需要借助P-R状态方程[17]计算获得。
|
$ {C}_{{\rm{p}}}^{g}={C}_{{\rm{p}}}^{0}-{\left(\frac{\partial {h}_{{\rm{r}}}}{\partial T}\right)}_{{\rm{p}}} $
|
(41) |
综上各式可以计算获得工质在蒸发器中的能量转换,由此可将式(35)表述为工质物性的函数,详见式(42)。
|
$\begin{split} {Q}_{\rm{evap}}= & {Q}_{23}+{Q}_{34}+{Q}_{45}={m}_{{\rm{wf}}}\left({h}_{5}-{h}_{2}\right) =\\ & f({P}_{{\rm{c}}},{T}_{{\rm{b}}},{T}_{{\rm{c}}},T,{C}_{{\rm{p}}}^{0}) \end{split}$
|
(42) |
2.2.3 膨胀过程
工质从蒸发器流出,进入膨胀机中做功,可由式(43)计算获得:
|
$ {W}_{{\rm{t}}}={m}_{{\rm{wf}}}\left({h}_{5}-{h}_{6}\right)={m}_{{\rm{wf}}}({h}_{5}-{h}_{6s}){\eta }_{{\rm{t}}} $
|
(43) |
其中,ηt表示工质泵的等熵效率。但是由于缺乏相应的实验数据,无法直接获取膨胀机出口点的温度T6,需要借助膨胀过程5~6s为等熵过程求解出膨胀机出口温度(见图2)。现有的求解方法大都在T6可能取值范围内,即上限为蒸发器出口温度,下限为冷凝器的出口温度,在此范围内通过不断的迭代求解出T6。而本文所面对的情况是工质未定、蒸发器及冷凝器中温度未定,需要大量求解出各种潜在工质的膨胀机出口点温度。那么如果仍然借用迭代的方法求解,难免效率低下,而本文所采用的确定性优化算法可以高效、快速求解此类问题。
借助计算获得的加压过程、蒸发和冷凝过程3段的能量转换可计算膨胀过程的能量转换,可由式(44)表示:
|
$ {W}_{{\rm{t}}}={m}_{{\rm{wf}}}\left({h}_{5}-{h}_{6}\right)={m}_{{\rm{wf}}}\left({h}_{5}-{h}_{6s}\right){\eta }_{{\rm{t}}}={Q}_{\rm{evap}}+{W}_{{\rm{P}}}-{Q}_{\rm{con}} $
|
(44) |
Qcon由式(47)表示。
2.2.4 冷凝过程
工质在膨胀机中做功后,进入冷凝器中放热成为饱和液态。类似于蒸发器中的处理,将冷凝过程分为过热态和饱和态计算,分别由式(45)和(46)计算。冷凝器中的换热量则可表示为式(47)。
|
$ {Q}_{71}={m}_{{\rm{wf}}}\Delta {H}_{{\rm{v}}}\left({T}_{1}\right) $
|
(45) |
|
$ {Q}_{67}={m}_{{\rm{wf}}}{\int }_{{T}_{7}}^{{T}_{6}}{C}_{{\rm{p}}}^{g}{\rm{d}}T $
|
(46) |
|
$ {Q}_{\rm{con}}={Q}_{67}+{Q}_{71}={m}_{{\rm{wf}}}\left({h}_{7}-{h}_{1}\right) $
|
(47) |
其中,ΔHv(T1)是工质在T1温度下冷凝过程的潜焓,而其余物性参数可同蒸发过程的求解方法。综上各式可以计算获得工质在蒸发器中的能量转换,由此可将式(48)表述为工质物性的函数,详见式(48)。
|
$ {Q}_{\rm{con}}={Q}_{67}+{Q}_{71}={m}_{{\rm{wf}}}\left({h}_{7}-{h}_{1}\right) =f({P}_{{\rm{c}}},{T}_{{\rm{b}}},{T}_{{\rm{c}}},T,{C}_{{\rm{p}}}^{0}) $
|
(48) |
2.2.5 ORC系统评价参数
ORC系统的热效率和循环净输出功可由式(49)~(50)表示。
|
$ {\eta }_{\rm{th}}=\frac{{W}_{\rm{net}}}{{Q}_{\rm{evap}}}\times 100\text{%} $
|
(49) |
|
$ {W}_{\rm{net}}={W}_{{\rm{t}}}-{W}_{{\rm{P}}} $
|
(50) |
综上各式可以将计算循环输出净功转换为有关工质物性的函数,其中M为工质的分子量,因为在计算ORC各个流程的能量转换时涉及单位换算,详见式(51)。
|
$ {W}_{\rm{net}}={W}_{{\rm{t}}}-{W}_{{\rm{P}}}=f({P}_{{\rm{c}}},{T}_{{\rm{b}}},{T}_{{\rm{c}}},T,{M,\rho ,C}_{{\rm{p}}}^{0}) $
|
(51) |
2.3 工质的物理和化学性质计算模型
除了上述所提到的临界物性、临界压力、沸点温度、密度和比热容等参数,由CAMD获得的分子作为ORC系统中工质,需要在高压情况下稳定运行,因此需要工质具有稳定的物化性质。本文通过计算吉布斯自由能、生成焓、标准沸点、毒性和可燃性等[10, 14]参数,确保工质符合ORC运行要求,如式(52)~(56)所示。
|
$ \Delta {G}_{298}^{f}=53.88+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}\Delta {G}_{k}^{f} $
|
(52) |
|
$ \Delta {H}_{298}^{f}=68.29+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}\Delta {H}_{k}^{f} $
|
(53) |
|
$ {T}_{f}=122.5+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{T}_{{f}_{k}} $
|
(54) |
|
$ \beta =\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{\alpha }_{k} $
|
(55) |
|
$\begin{split} \varGamma= & {q}_{1}(1+{q}_{2}C+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{\Delta R}_{{A}_{k}})\\ & (1+\sum \limits_{i=1}^{{n}_{{\rm{m}}{\rm{a}}{\rm{x}}}}\sum \limits_{k=1}^{m}{y}_{ik}{\Delta R}_{{B}_{k}}) \end{split}$
|
(56) |
其中,Δ
${G}_{{\rm{k}}}^{f}$
是基团k对工质标准吉布斯生成自由能的贡献值;Δ
${H}_{{\rm{k}}}^{f}$
是基团k对工质生成焓的贡献值;Tfk是基团k对融化温度的贡献值;q1、q2和C是常量;Δ
$R_{A_k} $
和Δ
$R_{B_k} $
为基团k对工质可燃性的贡献值。
3 模型求解策略和完善
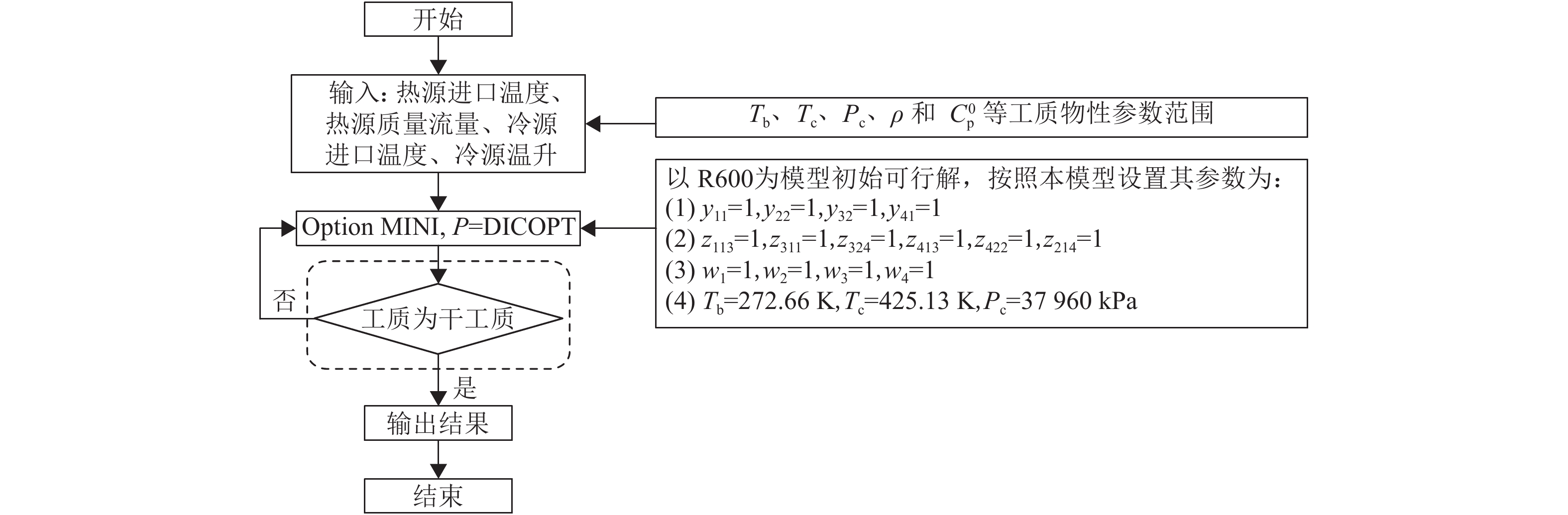
针对建立的模型特点,提出求解策略以降低求解难度及加快求解速度。同时,针对原有模型的不足之处进行改进,图3所示为本文模型求解流程。
3.1 模型的改进
除了求解策略外,针对模型中的不足之处,本文主要进行2个方面的改进。
(1) 对于CAMD设计获得的新型工质,除了ORC循环中的性能,还要考虑环保特性。在基团表中需要重点考虑卤族元素和含硫的基团对环境产生不良影响,因此对含有这两种元素的基团加以限制。同时,由于工质在ORC系统中运行,在蒸发器中的压力较高,要求工质物化性质稳定,所以对于芳香烃和环状烃的基团能够组成分子的最大数进行限制,详见表2。
表 2(Table 2)

表 2 基团组成分子次数限制
Table 2 Group composition molecular number limit
| 基团 |
最大数/次 |
基团 |
最大数/次 |
基团 |
最大数/次 |
| -F |
9 |
-CO-S- |
1 |
-C6H5 |
1 |
| -Cl |
2 |
-C3H5 |
1 |
-C6H4-
|
1 |
| -Br |
2 |
-C4H7 |
1 |
>C6H3-
|
1 |
| -I |
2 |
-C5H9 |
1 |
-C6H3-OH
|
1 |
| -CH=O |
2 |
-C6H11 |
1 |
>C6H3-OH
|
1 |
| -SH |
1 |
-C5H8-
|
1 |
C6H5-NH-
|
1 |
| -S- |
1 |
-C6H10-
|
1 |
C6H5-N<
|
1 |
|
表 2 基团组成分子次数限制
Table 2 Group composition molecular number limit
|
(2) 工质在膨胀过程中,如果进入两相区状态将会对膨胀机造成损害,因此针对ORC循环的特点提出新的限制条件以排除湿工质,确保工质在膨胀过程始终保持过热态。对于干湿工质的判断,本文通过对比工质在饱和气态2个不同的状态下的熵对比判断,即选取4点和7点的状态判断。由于无法直接获取各个状态点的实际熵,本文将两状态点之间的熵差拆分为理想气体的熵差和各状态点余熵两部分求解,如式(57)~(58)所示,理想气体的熵差可由式(59)获得,各个状态点的余熵[17]可由式(60)~(64)计算获得。综上,可获得式(68)所示的关联式,当4点熵大于7点熵时,工质即为干工质。
|
$ {S}_{4}-{S}_{7}={S}_{4}^{0}+\Delta {S}_{4}^{1}-{S}_{7}^{0}+\Delta {S}_{7}^{1} $
|
(57) |
|
$ \Delta s={s}_{4}-{s}_{7}={s}_{4}^{d}+\Delta {s}^{0}-{s}_{7}^{d}>0 $
|
(58) |
|
$ \Delta {s}^{0}={s}_{4}^{0}-{s}_{7}^{0}={\int }_{7}^{4}{\rm{d}}{s}^{0}={\int }_{{T}_{7}}^{{T}_{4}}{C}_{{\rm{p}}}^{0}\frac{{\rm{d}}T}{T}-{\rm{R}}{\rm{ln}}\left(\frac{{P}_{4}}{{P}_{7}}\right) $
|
(59) |
|
$ {s}^{d}=s\left(T,P\right)-{s}^{0}\left(T,P\right) $
|
(60) |
|
$ {s^d} = - {\rm{R}}{\rm{ln}}\left( {Z - \frac{{bP}}{{{\rm{R}}T}}} \right) + \frac{{P\beta }}{{2\sqrt 2 {\rm{R}}T\displaystyle \frac{{bP}}{{{\rm{R}}T}}}}{\rm{ln}}\frac{{Z + \left( {1 - \sqrt 2 } \right)\displaystyle\frac{{bP}}{{{\rm{R}}T}}}}{{Z + \left( {1 + \sqrt 2 } \right)\displaystyle\frac{{bP}}{{{\rm{R}}T}}}} $
|
(61) |
|
$ \beta =\frac{\partial \alpha }{\partial T}=-\frac{0.457\;24{{\rm{R}}}^{2}{T}_{{{\rm{c}}}_{k}}\left[1+k(1-{T}_{{\rm{r}}}^{0.5})\right]}{{P}_{{\rm{c}}}{T}_{{\rm{r}}}^{0.5}} $
|
(62) |
|
$ k=0.374\;64+1.542\;26\omega -0.269\;92 $
|
(63) |
|
$ b=\frac{0.077\;80{\rm{R}}{T}_{{\rm{c}}}}{{P}_{{\rm{c}}}} $
|
(64) |
3.2 求解策略
本文所构建的数学模型包含有CAMD模型,其中有二元整数变量及大量的离散变量,ORC系统模型及工质物性模型中含有大量连续变量,这些模型共同构成了混合整数非线性模型。给定冷、热源作为初始条件,工质的物性参数及ORC的运行工况均为求解模型所获得的优化解。在求解过程一方面存在着无解的情况,另一方面求解时间较长。
针对上述问题,采用确定性算法,在给定的冷、热源条件外,考虑到模型最难求解的问题在于二元整数变量的求解。如二元变量yik表示分子中第i个基团为基团表中的第k个基团,类似这种表示基团的二元整数变量只可能为整数,不存在非整数个基团构成分子的情况。因此将现有工质按照本文的方法表述,即以模型中的整数变量表示工质的组成及内部结构,将其作为模型的初始解,引导程序获得可行解,如图3所示。
模型中涉及大量的工质物性,将这些工质物性设置在合理可行域内不仅可以确保获得工质为合理的ORC工质,同时能加快模型的求解速度。由式(51)可以看到,ORC循环参数主要是基于以下物性求解:Tb、Tc、Pc、ρ、M和
$C_p^0$
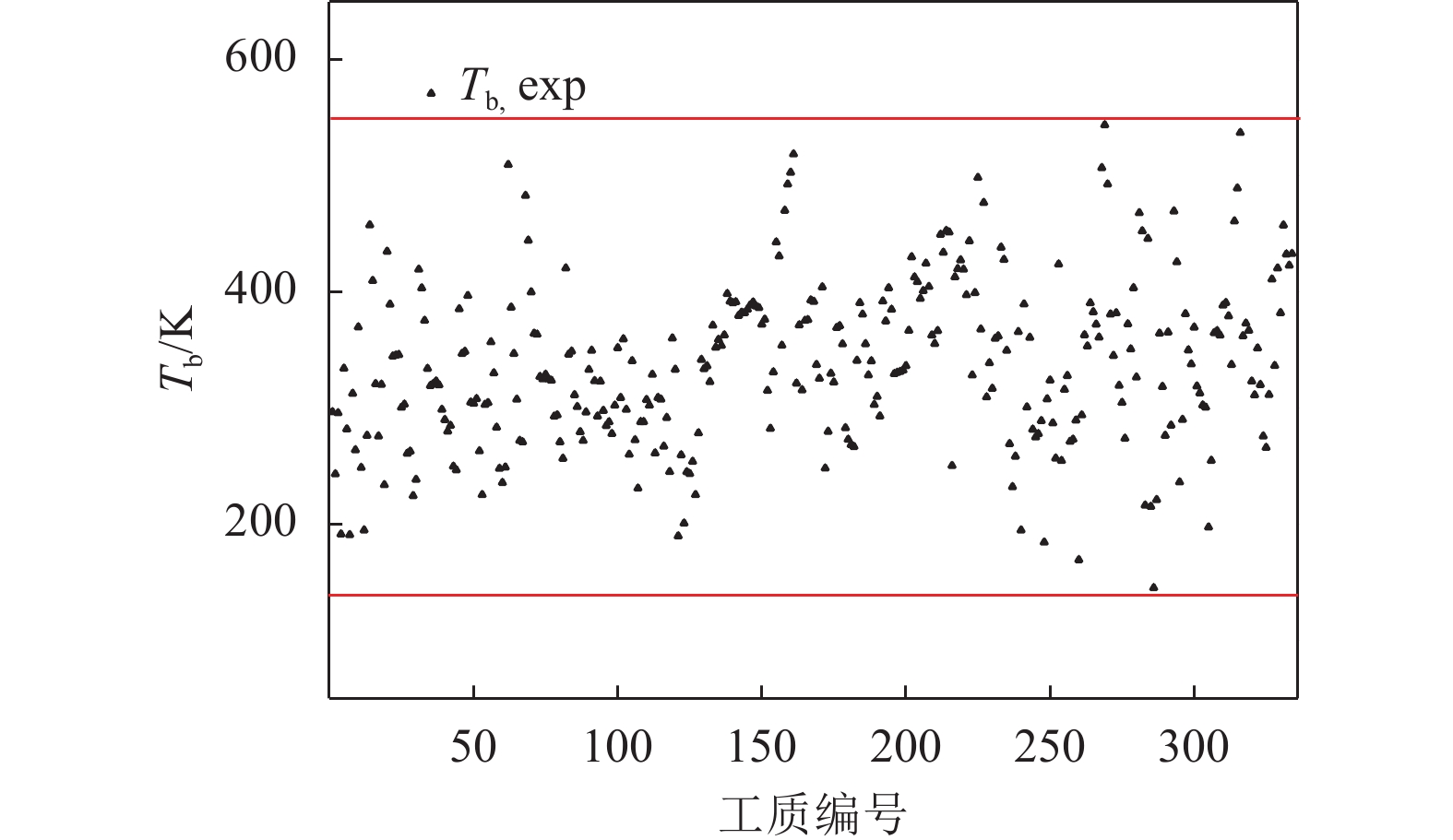
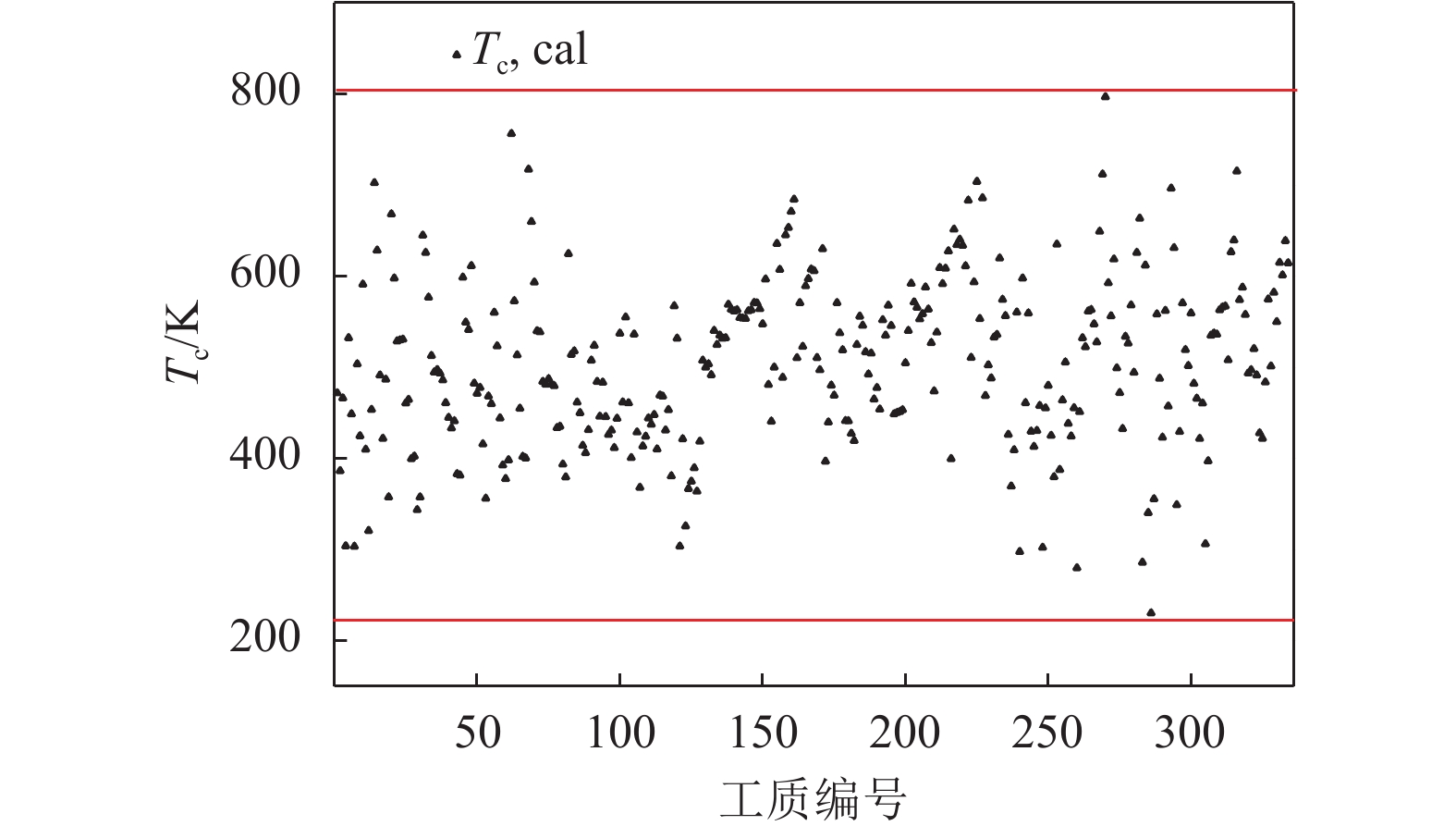
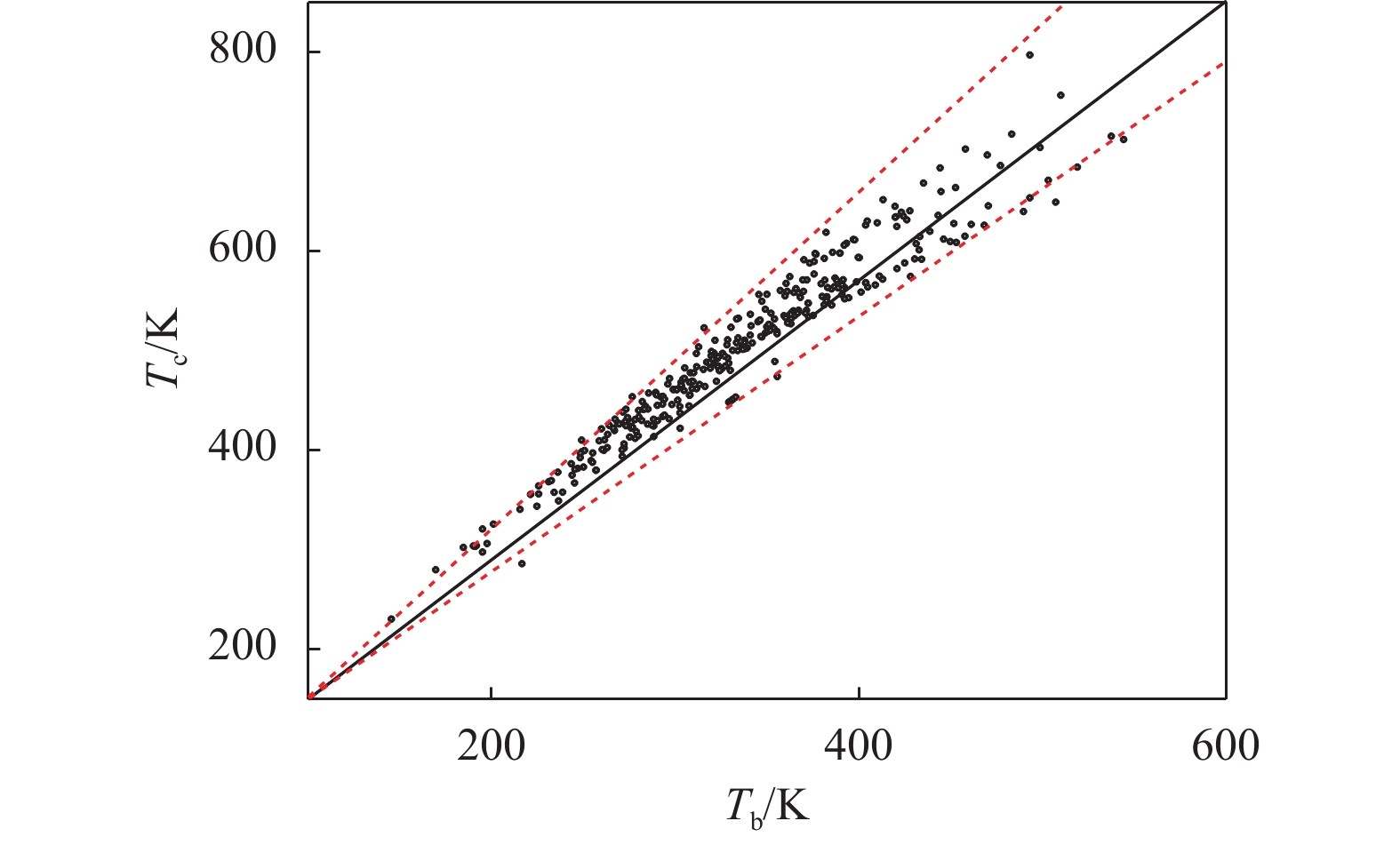
。本文从REFPROP[12]及Ambrose等[18-21]数据库中,选取334种有机工质的Tb参数。图4所示为选定的334种工质Tb的范围。由式(17)可看出Tc的计算是基于Tb计算获得,在Su等[15]方法已验证过式(17)的准确性。本文也通过该方法计算其中51种工质的临界温度并同REFPROP[12]中实验数据对比,获得其平均预测误差小于1%。而这334种的工质的Tc的实验数据无法全部获得,所以通过式(17)计算获得334种工质的Tc。如图4所示334种工质的Tb和Tc存在着一定的线性关系,图5为334种工质的Tc分布,图6为334种工质的Tc/Tb比值分布,Tc/Tb的比值范围在1.28~1.65内取值。Brown等[22]提出蒸发器中的温度应低于0.9Tc,而冷凝器中的温度应高于0.8Tc。ORC系统的热源温度通常在50~200 ℃之间,而冷源通常在常温附近。综上,可以归纳获得Tb和Tc的可行域。
|
$ 180\;{\rm{ K}} < {T_{\rm{b}}} < 500\;{\rm{ K}} $
|
(65) |
|
$ 330\;{\rm{ K}} < {T_{\rm{c}}} < 900\;{\rm{ K}} $
|
(66) |
|
$ {{T}_{{\rm{c}}}} \leqslant a {T_{\rm{b}}},{\text{其中}}\;a \in \left( {1.2,1.8} \right) $
|
(67) |
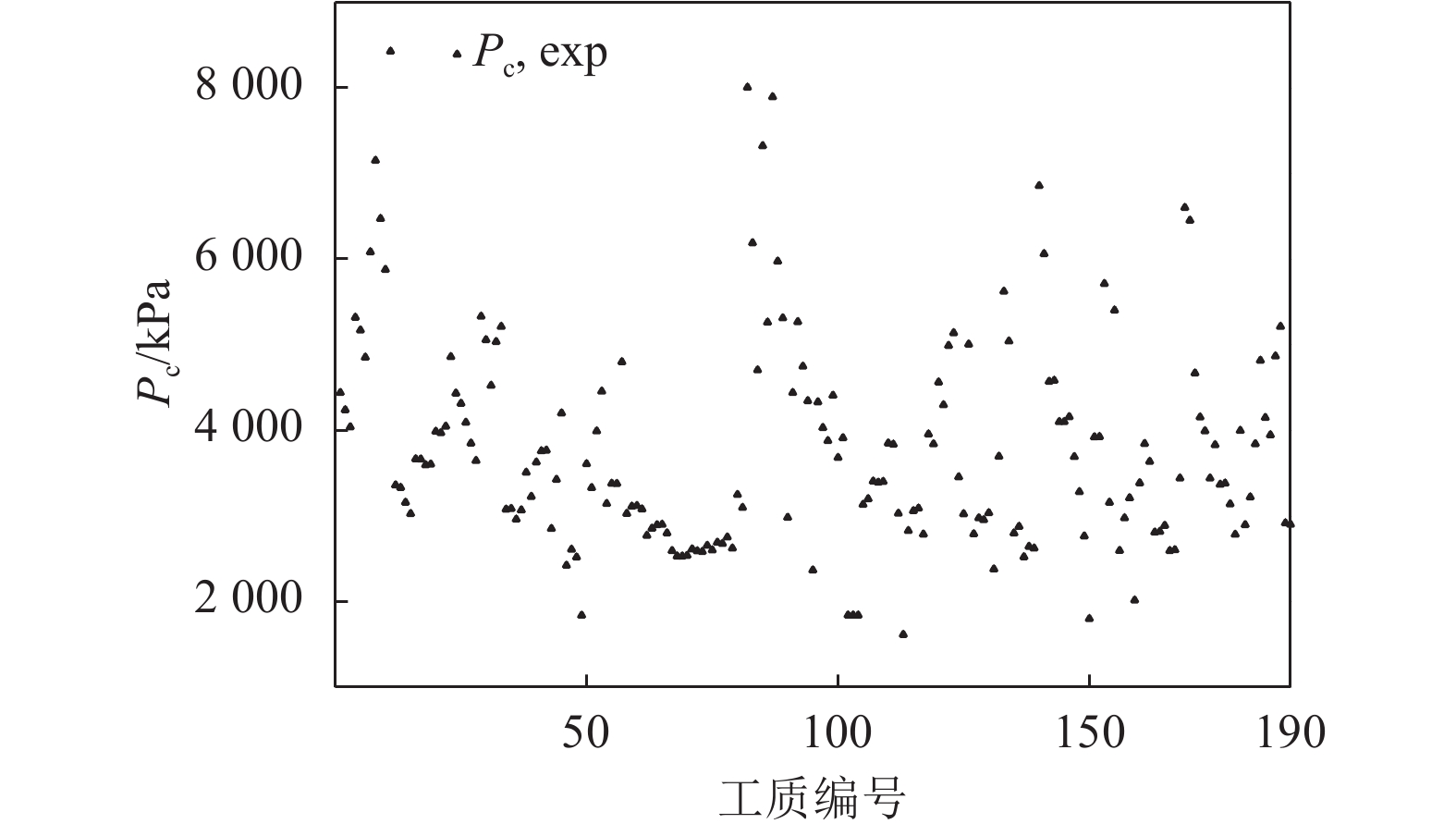
图7所示为本文选取的190种有机工质临界压力的实验数据,归纳得Pc的可行域。临界压力的大小将直接决定工质的运行范围,由于本文所设计的工质均处于亚临界的工况范围,所以综合考虑ORC运行特点得Pc的取值范围,详见式(68)。
|
$ 100\;{\rm{kPa}} < {P_{\rm{c}}} < 9\;000\;{\rm{kPa}} $
|
(68) |
比热容在ORC系统的各个能量转换过程中均出现,所涉及的比热容均基于理想气体定压气态比热容即
$C_{\rm{p}}^0$
.
$C_{\rm{p}}^0$
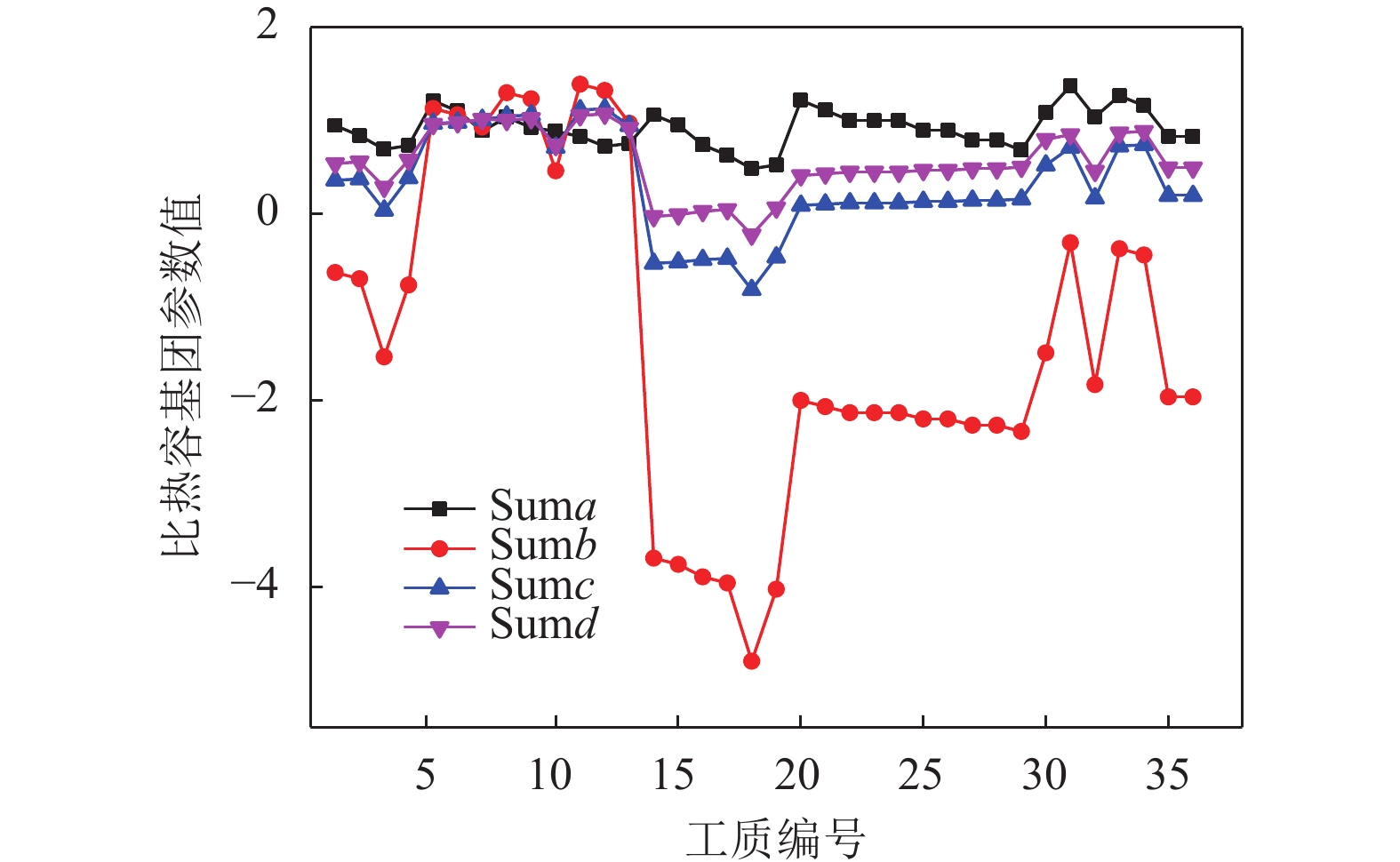
是一个关于温度的多项式,如式(40)所示由4种基团贡献值累加获得。分别设置为4个参数将4种基团贡献值加和,表示为:Suma、Sumb、Sumc和Sumd,详见式(69)~(72). 图8所示为从334种工质中随机选取的36种工质将其Suma、Sumb、Sumc和Sumd等参数与R22的4种基团贡献值加和对比,可以看出4个参数的变化趋势较为相同。但是考虑到4个参数的数量级从10−7到102之间变化,而实际计算中每个参数均对最终结果有影响。因此,通过式(73)对4个参数进行处理。
|
$ {\rm{Sum}}a= \sum \limits_{i=1}^{{n}_{\max}}\sum \limits_{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{a} $
|
(69) |
|
$ {\rm{Sum}}b= \sum \limits_{i=1}^{{n}_{\max}}\sum \limits_{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{b} $
|
(70) |
|
$ {\rm{Sum}}c= \sum \limits_{i=1}^{{n}_{\max}}\sum \limits_{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{c} $
|
(71) |
|
$ {\rm{Sum}}d= \sum \limits_{i=1}^{{n}_{\max}}\sum \limits_{k=1}^{m}{y}_{ik}C{{\rm{p}}}_{k}^{d} $
|
(72) |
|
$\begin{split} {\rm{Sum}}{C_{\rm{p}}} = & {\rm{Sum}}a + {\rm{Sum}}b \times 300 + {\rm{Sum}}c \times 300 \times 300 + \\ & {\rm{Sum}}d \times 300 \times 300 \times 300 \end{split}$
|
(73) |
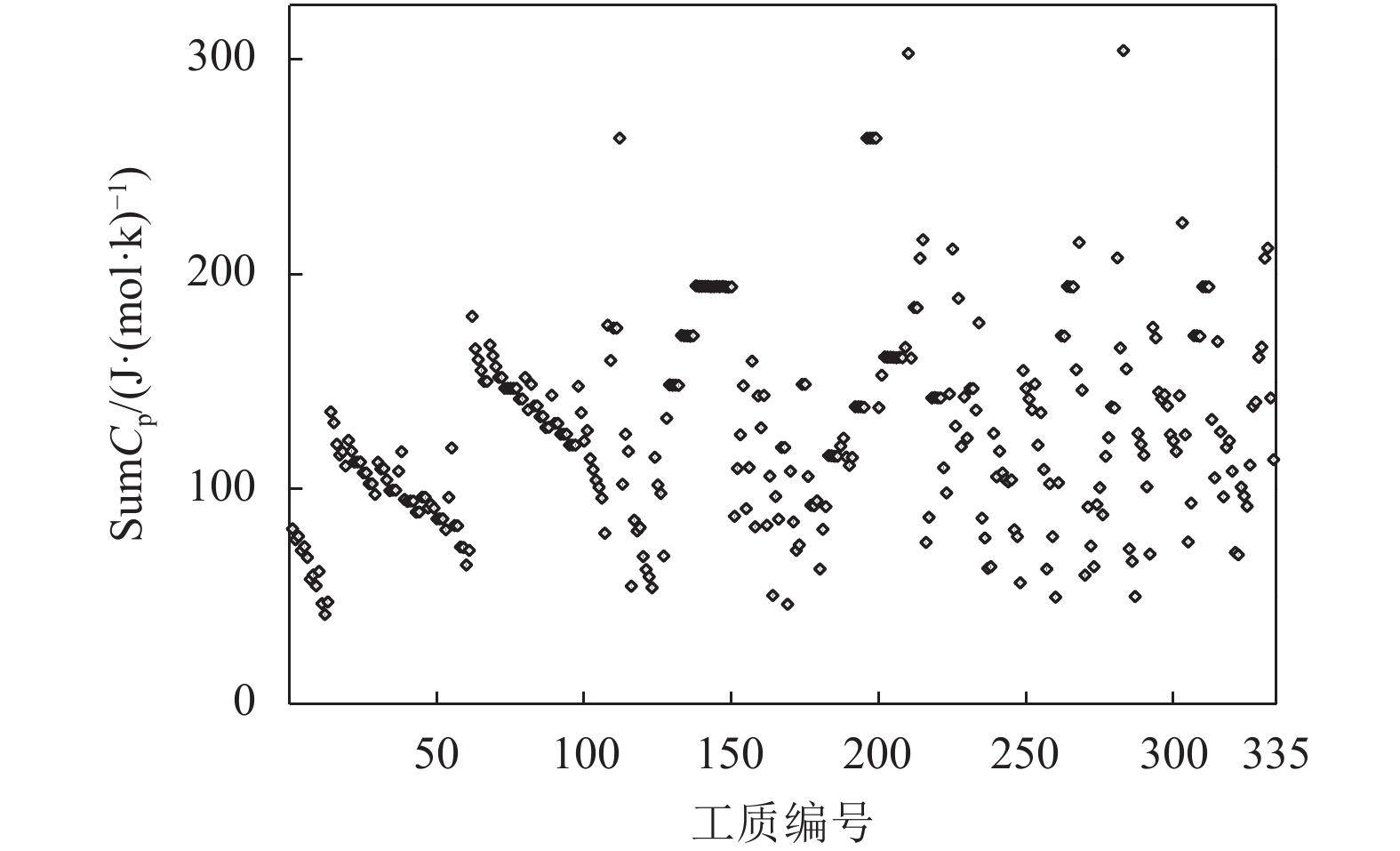
图9所示为通过式(73)处理后获得Cp加和的结果,因此获得Cp的可行域为:
|
$ 20\;{\rm{ J/(mol}} \cdot {\rm{K }}) < {C_{\rm{p}}} < 330\;{\rm{ J/(mol}} \cdot {\rm{K}}) $
|
(74) |
4 结果与讨论
4.1 CAMD和ORC系统同步优化结果
基于GAMS建立的CAMD和ORC系统同步优化的MINLP模型,选用DICOPT作为求解器实现全局优化求解获得优化工质。优化模型有868个变量、781个离散变量和726个限制方程及19 484个非零参数。表3所示为本文设置的模型初始条件,以循环输出净功最大为优化目标。表4所示为在不同的热源、冷源温度下,分别获得不同的优化工质。表4中分别对不同工况条件进行编号,后续表中均以编号代替冷热源条件。表5为优化获得ORC系统运行参数和工质及冷源流量。表6和表7为工质的物性计算结果及循环参数。本文选取了常用的现有工质在373.15 K的热源条件下,对比验证结果的可靠性,从表8的结果可以看出优化获得工质的循环输出功大于现有工质,新型工质的ORC净功比现有工质ORC净功增加12.46%。
表 3(Table 3)

表 3 ORC运行参数
Table 3 ORC operating parameters
热源
温度/K
|
冷源
温度/K
|
热源流量/
(kg·s−1)
|
夹点温度/K |
工质泵的等熵效率/% |
膨胀机的等熵效率/% |
| 353.15 |
298.15 |
50 |
10 |
65 |
85 |
| 373.15 |
298.15 |
50 |
10 |
65 |
85 |
| 393.15 |
298.15 |
50 |
10 |
65 |
85 |
| 423.15 |
293.15 |
50 |
10 |
65 |
85 |
| 443.15 |
293.15 |
50 |
10 |
65 |
85 |
| 463.15 |
293.15 |
50 |
10 |
65 |
85 |
|
表 3 ORC运行参数
Table 3 ORC operating parameters
|
表 4(Table 4)

表 4 不同工况下优化获得的工质
Table 4 Optimized working fluids under different working conditions
| 工况编号 |
热源温度/K |
工质 |
| a |
353.15 |
SH-N(F)-CH(NH2)-F
|
| b |
373.15 |
F-S-CH(F)-N(NH2)-F
|
| c |
393.15 |
CH3-N(NH2)-CH(CH3)-CH(F)2 |
| d |
423.15 |
NH2-CH(C3H5)-F
|
| e |
443.15 |
C4H7-N(CH3)-CH(F)-N(F)2 |
| f |
463.15 |
F-CH2-CH2-C(F)2-CH2-N(F)-C3H5 |
|
表 4 不同工况下优化获得的工质
Table 4 Optimized working fluids under different working conditions
|
表 5(Table 5)

表 5 ORC系统参数
Table 5 ORC system parameters
| 工况编号 |
T3/K
|
T1/K
|
T8/K
|
mwf/(kg·s−1)
|
mc/(kg·s−1)
|
| a |
330.39 |
318.12 |
339.71 |
8.43 |
263.28 |
| b |
340.06 |
318.14 |
347.74 |
16.82 |
483.04 |
| c |
350.08 |
317.74 |
353.75 |
24.50 |
731.49 |
| d |
362.04 |
313.07 |
359.80 |
28.03 |
1 124.87 |
| e |
373.29 |
311.88 |
355.53 |
65.70 |
1 538.21 |
| f |
384.13 |
311.40 |
351.80 |
79.15 |
1 928.80 |
|
表 5 ORC系统参数
Table 5 ORC system parameters
|
表 6(Table 6)

表 6 不同工况条件下优化工质部分物性
Table 6 Optimizing the thermodynamic properties of working fluid under different working conditions
工
况
编
号
|
ΔHlv/
(kJ·
mol–1)
|
Tc/K
|
Pc/kPa
|
Tb/K
|
ω
|
Zc |
G/(kJ·
mol–1)
|
ΔHf/
(kJ·
mol–1)
|
Tf /K
|
$C_{{\rm{pg}}}^0$
/
(J·
mol–1)
|
| a |
40.68 |
559.12 |
7 654 |
367.41 |
0.54 |
0.32 |
–227.9 |
–281.85 |
239.4 |
110.34 |
| b |
41.71 |
553.94 |
6 556 |
372.60 |
0.60 |
0.30 |
–418.98 |
–474.57 |
237.93 |
119.25 |
| c |
39.27 |
541.34 |
4 522 |
372.75 |
0.58 |
0.29 |
–234.47 |
–387.53 |
221.75 |
166.06 |
| d |
37.40 |
559.60 |
5 757 |
368.22 |
0.45 |
0.28 |
–87.25 |
–220.69 |
221.63 |
118.76 |
| e |
35.74 |
529.25 |
3 192 |
370.14 |
0.51 |
0.26 |
–317.02 |
–479.44 |
223.51 |
201.69 |
| f |
35.30 |
524.47 |
2 704 |
372.79 |
0.53 |
0.25 |
–596.81 |
–767.06 |
223.84 |
224.41 |
|
表 6 不同工况条件下优化工质部分物性
Table 6 Optimizing the thermodynamic properties of working fluid under different working conditions
|
表 7(Table 7)

表 7 不同工况条件下优化工质的ORC循环参数
Table 7 ORC cycle parameters of optimized working fluid under different working conditions
| 工况编号 |
Wp/kW
|
Qevap/kW
|
Qcon/kW
|
Wt/kW
|
Wnet/kW
|
ηth/%
|
| a |
0.17 |
2 755.86 |
2 643.34 |
95.78 |
95.62 |
3.470 |
| b |
0.58 |
5 208.70 |
4 849.76 |
305.59 |
305.01 |
5.856 |
| c |
2.31 |
8 077.63 |
7 344.20 |
625.38 |
623.07 |
7.714 |
| d |
6.47 |
12 985.77 |
11 293.70 |
1 443.75 |
1 437.28 |
11.068 |
| e |
17.98 |
17 961.22 |
15 443.62 |
2 115.25 |
2 137.27 |
11.899 |
| f |
32.18 |
22 825.79 |
19 365.18 |
2 968.87 |
2 936.69 |
12.866 |
|
表 7 不同工况条件下优化工质的ORC循环参数
Table 7 ORC cycle parameters of optimized working fluid under different working conditions
|
从表4中可以看到,不同工况条件下的优化工质均为新工质。同时,每个优化的工质均含有F和N元素,归纳现有工质的化学组成也符合这个规律。所有的优化工质仍然基于碳链为主链,通过附加各种基团实现。但是值得注意的是,在d、e和f工况条件下,均出现了环状烃基团。而实际在REFPROP[12]中的有机工质并仍然以链状工质为主,这也指引着将来ORC工质需要关注环状烃的选用。工质在ORC循环中实际上是以物性的变化实现对ORC循环性能的影响,从表6可以看到不同工况条件下的优化工质的沸点温度集中在370 K附近,类似的临界温度也有3种工质出现在555 K附近. 在去除d工况条件下,可以看到临界压力随着热源温度的提高逐渐减小,比热容则随着热源温度的升高而增大。因为在求解过程中,在d工况条件下求解获得为次优解,而最优解为非整数解,因此在4.2节对影响ORC循环性能的各个物性进行敏感性分析,将工质物性作为变量,分析其对ORC系统性能的影响。
表 8(Table 8)

表 8 b工况条件下的优化工质同现有工质对比验证
Table 8 Comparison of optimized working fluids with and existing working fluids under working conditions b
| 工质 |
Wp/kW
|
Qevap/kW
|
Qcon/kW
|
Wt/kW
|
Wnet/kW
|
ηth/%
|
| F-S-CH(F)-N(NH2)-F
|
0.58 |
5 208.70 |
4 849.76 |
305.59 |
305.01 |
5.856 |
| R600 |
13.70 |
5 421.76 |
5 102.36 |
283.14 |
269.45 |
4.996 |
| R600a |
20.96 |
5 505.04 |
5 177.73 |
296.00 |
275.07 |
4.996 |
| R601 |
4.61 |
5 386.55 |
5 067.16 |
275.40 |
270.79 |
5.080 |
| R123 |
6.07 |
5 420.06 |
5 100.39 |
276.89 |
270.82 |
5.053 |
| R1233zd |
5.59 |
5 314.81 |
4 996.18 |
275.57 |
369.98 |
5.053 |
|
表 8 b工况条件下的优化工质同现有工质对比验证
Table 8 Comparison of optimized working fluids with and existing working fluids under working conditions b
|
4.2 工质物性对ORC循环性能影响的敏感性分析
如式(51)所示,ORC系统的输出净功是关于工质临界压力、临界温度、沸点温度、密度、比热容、相对分子量及温度的函数。其中温度为工质在蒸发器、冷凝器等设备中的温度,由冷、热源决定。基于工质物性计算模型和ORC系统模型,以上述7个参数作为自变量,分析不同物性对ORC系统输出净功的影响。以R601作为例,以REFPROP中实验参数作为初始值,在分析某个参数时即将某个参数作为变量。
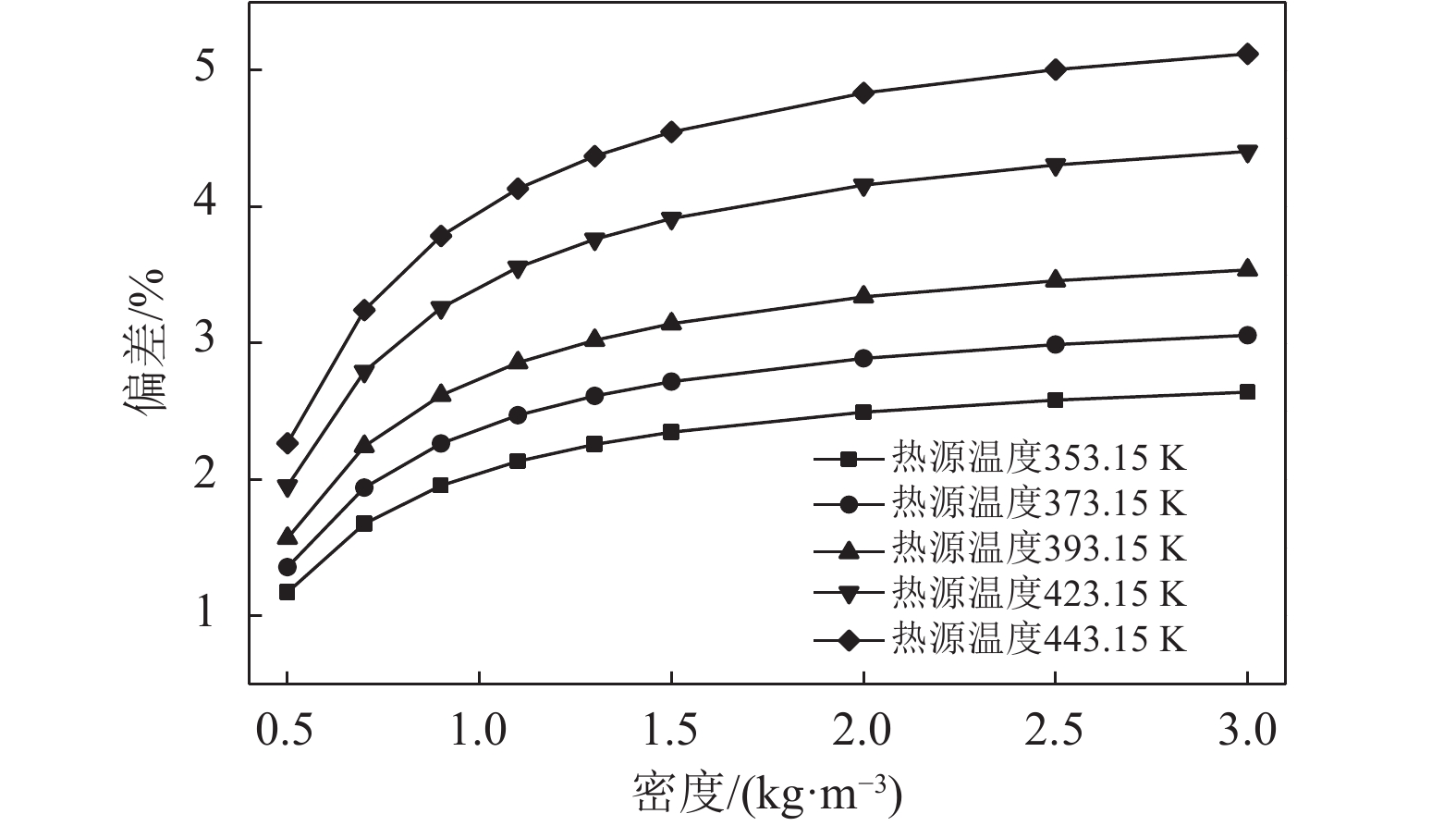
图10所示为密度对ORC循环的影响,取密度为0.3 kg/m3的ORC系统输出净功作为参考值,如图10所示随着热源温度的提高,密度的增大使得ORC系统输出净功的增长量从1.5%提高到3%。而密度在计算ORC系统输出净功时,仅仅影响加压过程能量转换的计算。从式(15)可以看到,在压力不变的情况下,密度减小将导致泵的耗功增加。因此,从图(10)也反映出随着密度的增加,对于ORC系统输出净功影响越来越来大。因此,密度越大的工质将更有利于ORC系统输出净功的提高。
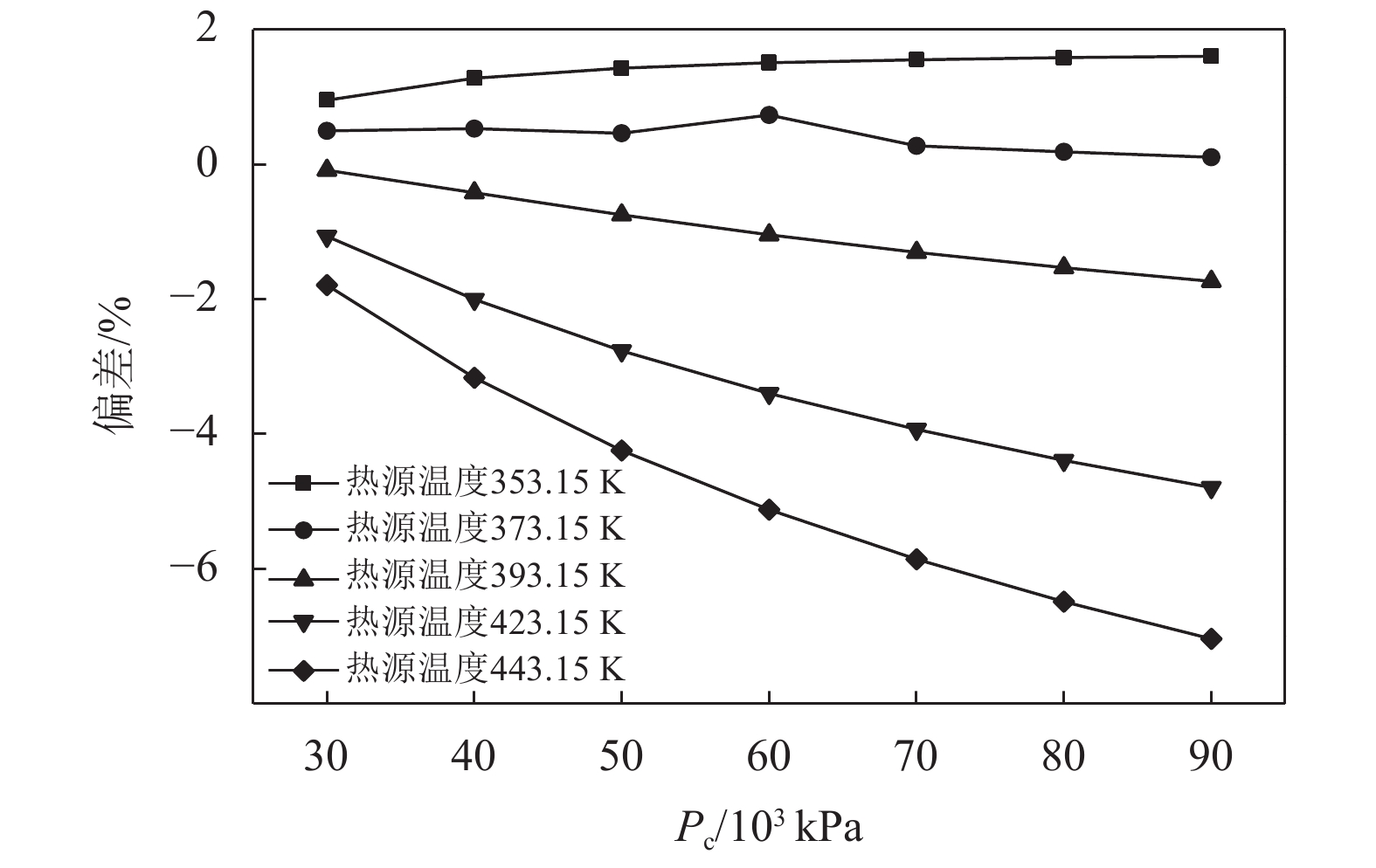
图11为临界压力对ORC系统输出净功的影响,取Pc为2 000 kPa时的ORC系统输出净功作为参考值。在计算ORC系统输出净功时,临界压力贯穿着整个计算过程,对ORC系统的每个流程的能量转换均有影响。从图(11)所示结果可以看出,在热源温度较低时,临界压力对系统输出净功几乎无影响,而当温度升高时,可以看到临界压力越小,系统输出净功将更高。而结合不同工况条件下的优化工质的临界压力的数据对比分析,当进行以ORC循环输出净功为优化目标进行全局优化时,因为当工况温度较低时,临界压力的变化对循环性能几乎没有影响,因此全局优化时优先考虑临界温度等物性的影响。而随着热源温度的升高,临界压力的变化对于ORC循环性能的变化从趋近于0提高到5%。因此可以看到,随着工况温度的提升,所获得的优化工质的临界压力出现下降的趋势。
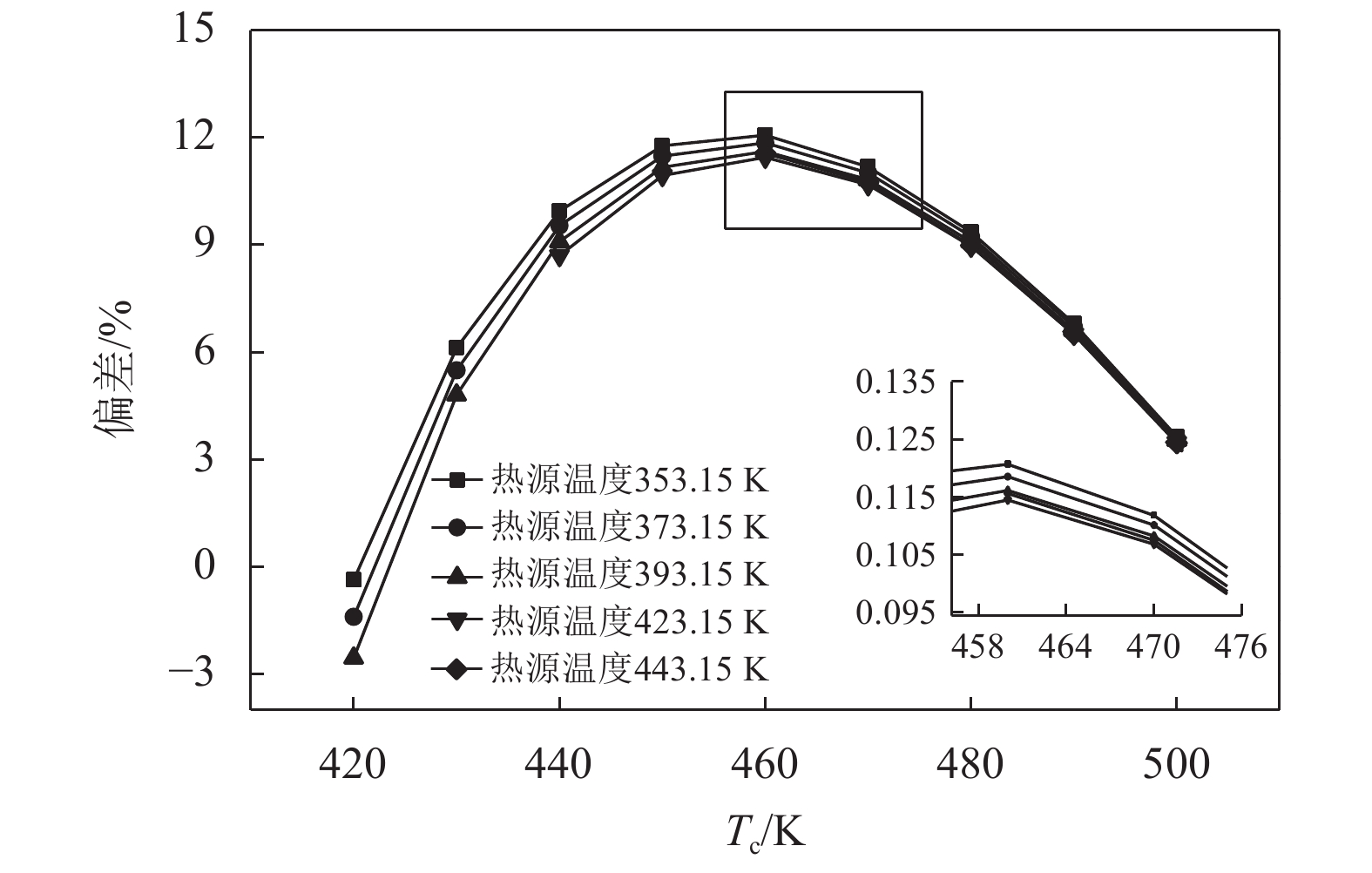
图12所示为临界温度对ORC系统输出净功的影响,取临界温度为510 K时的ORC系统输出净功作为参考值。如图12所示,可以很明显地看到不同工况下对应的最优的临界温度均在458 K附近,因此在对比临界温度的工质筛选时,越靠近最优临界温度其系统输出净功将越多。如图(6)所示,由于Tb和Tc之间的线性关系,计算不同沸点温度对ORC系统输出净功的影响将得到类似Tc的曲线,在此不再赘述。而从不同工况条件下的优化工质的物性可以看到,沸点温度均集中在370 K附近,而临界温度也出现在525~560 K的范围内波动。当以Tc作为变量分析时,无需考虑工质的结构,而在进行全局优化时由于工质的实际结构的限制导致临界温度无法和沸点温度全部趋向于最优的值。而从实际获得不同工况条件下的优化工质物性可以得到沸点温度Tb在优化过程中对结果的影响大于临界温度Tc,因为所有的Tb都基本趋近于最优值。
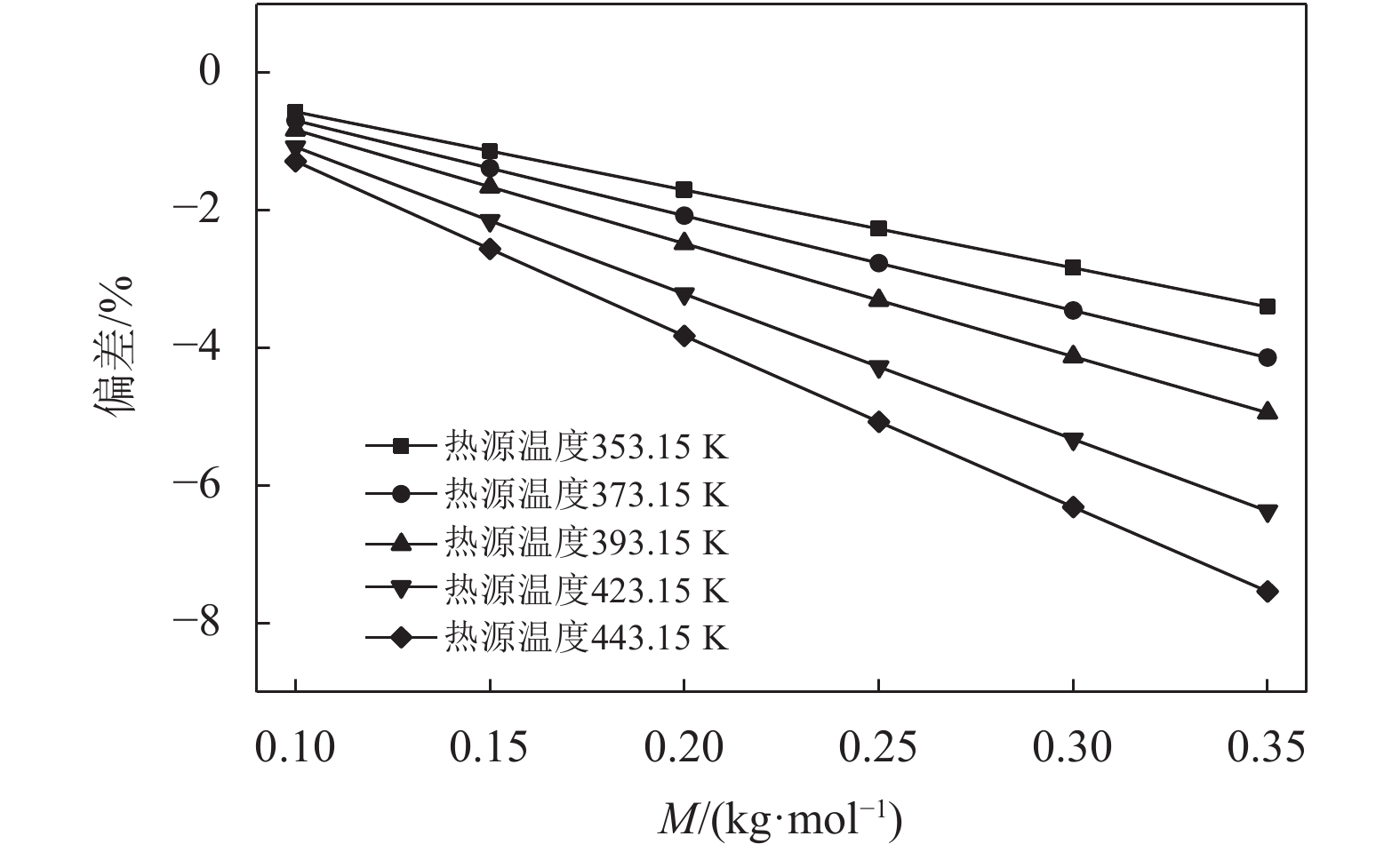
相对分子量作为工质的物性参数之一,常常在分析ORC系统输出净功时被忽略。因为相对分子量出现在ORC各个热力过程的能量的计算中,因此同样对结果产生一定影响。本文将摩尔质量为40×10–3 kg/mol时的ORC系统输出净功作为参考值。如图13所示,摩尔质量的变化和ORC系统输出净功存在着线性关系,同时温度越高摩尔质量变化对系统输出净功影响也越大。因此,在进行工质筛选时,摩尔质量越小,对ORC系统输出净功的提高将越有利。从不同工况条件下获得的工质的分子量可以看到,所有的优化工质的分子量相对于现有常用的工质均较大。
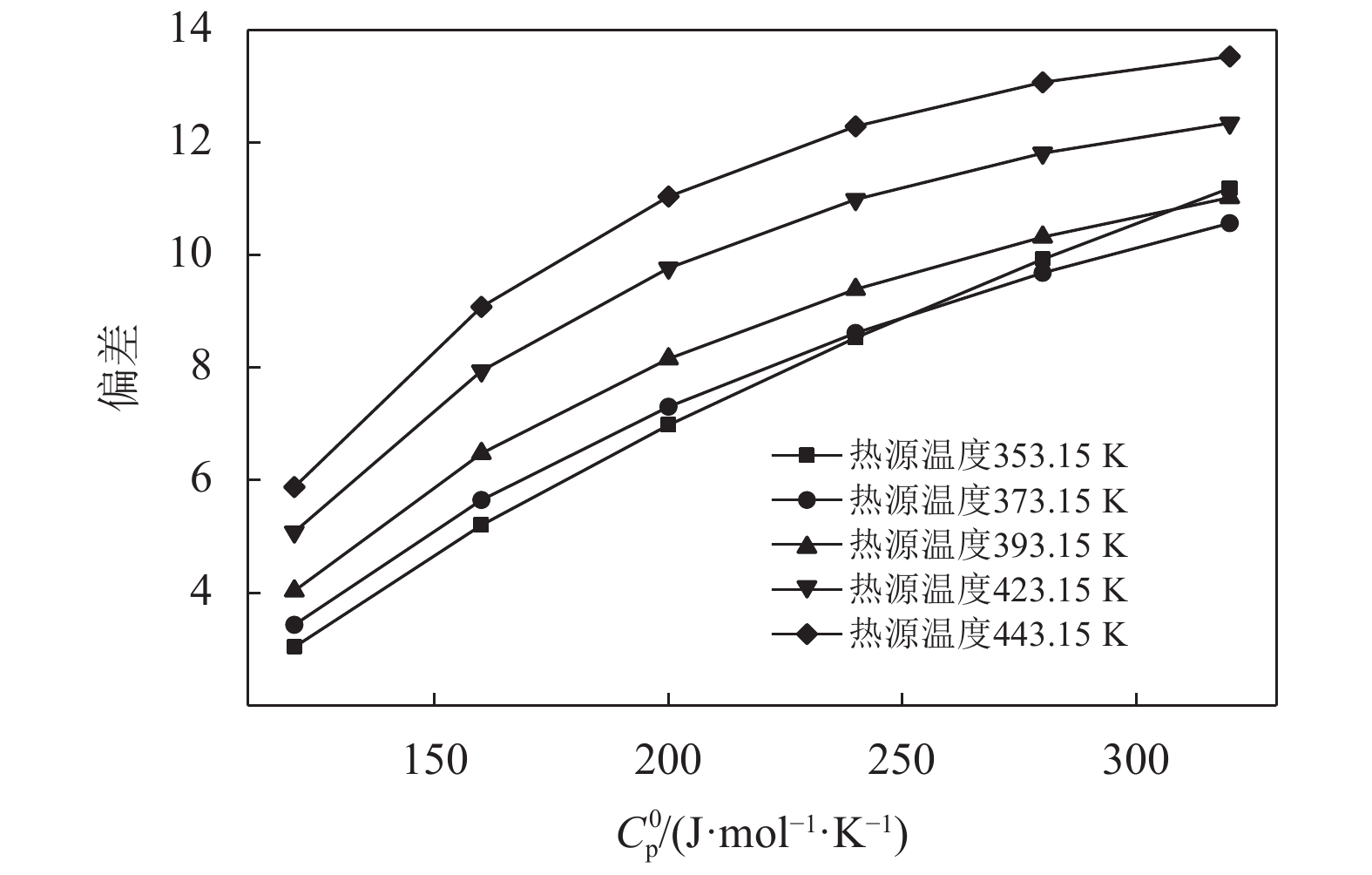
除了上述5种参数外,比热容也是一个重要的物性参数,工质处于换热过程中能量转换的计算均需要用到。而如式(40)所示,比热容是一个关于4种基团贡献值的物性参数,按照在3.1节中的处理4种基团贡献值的方法,将比热容转换为一个参数考虑。取理想气体定压比热容为40 J/mol·K时的ORC系统输出净功作为参考值。如图14所示,可以看到随着比热容的增加,ORC循环的输出净功也越来越大。结合不同工况条件下优化工质的比热容对比,可以看到随着工况的升高,优化工质的比热容也表现出明显的增加趋势。但是由于各种物性可行域的限制,无法达到最优的比热容取值。
5 结论
(1) 本文建立了基于CAMD的分子设计与ORC系统同步优化的MINLP模型,针对模型的特点提出求解策略,给出工质物性的可行域。并针对CAMD模型的不足之处,加入筛选干工质等限制条件改进模型。基于改进的CAMD模型,以ORC循环输出净功最大为优化目标分别获得优化工质SH-N(F)-CH(NH2)-F、F-S-CH(F)-N(NH2)-F、CH3-N(NH2)-CH(CH3)-CH(F)2、NH2-CH(C3H5)-F、C4H7-N(CH3)-CH(F)-N(F)2和F-CH2-CH2-C(F)2-CH2-N(F)-C3H5。
(2) ORC系统性能敏感性分析的结果表明,工质物性对ORC循环性能的影响有较大差异。当以ORC系统输出净功最大作为优化目标时,优先获得Tb为370 K附近的工质,沸点温度大于或小于370 K均会导致ORC循环输出净功减小。由于Tb与Tc之间的线性关系,Tc在458 K左右时可以达到ORC系统输出净功最大。在所有影响ORC循环输出净功的物性中,Tb和Tc对循环性能影响最大。除此之外,临界压力、密度、比热容及相对分子量对ORC循环输出净功均随着热源温度的变化而变化,其中密度、比热容及相对分子量均在可行域内越大越有利于ORC循环输出净功的增加,而临界压力相反则对热源温度较低时的ORC系统输出净功无影响,随着热源温度升高,临界压力越小越有利于系统输出净功的增加。
(3) 建立的分子设计模型是基于设计纯工质出发,而纯工质由于自身在蒸发过程中温度的恒定无法同热源较好的匹配,因此后续将开展基于CAMD和ORC系统的混合工质设计的工作,并基于本文模型中的工质物性和ORC系统模型,探究所有影响ORC循环性能之间的关联,提出合适的工质筛选准则,以实现工质与热源直接快速匹配筛选。
 2020, Vol. 37
2020, Vol. 37

