近年来,化石燃料的加速消耗带来了严重的能源和环境问题,回收和利用低品位热能(工业余热、内燃机余热、太阳能、地热能、生物质能等)被认为是应对能源环境问题的有效途径[1],而有机朗肯循环(Organic Rankine Cycle,ORC)是最具发展潜力的低品位热−功转换的有效途径之一,成为近年的研究热点,国内外学者在ORC系统设计和运行优化方面做了大量工作[2-6].
ORC系统运行参数随着外界条件发生变化,实际性能会偏离理想设计性能,从而造成能源利用率低、运行成本高. 因而,ORC设计工况的确定和偏离工况运行策略研究非常必要. Zhang等[7-8]通过对废热回收系统的建模与多变量控制的研究,提出应用于余热回收电厂的控制策略. Lee等[9-10]通过50 kW级ORC系统,研究系统以及换热设备的瞬态响应特性. Quoilin等[11]通过建立有机朗肯循环废热回收的动态模型,进而提出优化控制策略. 此外,学者在偏离设计工况的ORC系统运行控制策略、预测控制、性能比较以及运行实验[12-15]方面也有研究.
ORC发电系统内部参数与外界环境密切相关,热源参数的变化、冷却温度的变化导致系统运行参数改变,偏离设计工况运行,热效率低. 文献分析显示,目前绝大多数的变工况研究主要是变工况运行控制,而针对变工况的系统设计以及变工况下设计和运行协同优化的研究很有限. 本文提出了考虑环境变工况的ORC设计与运行优化方法,建立了分液冷凝ORC系统设计和运行优化模型,根据环境温度变化特性,选取典型温度作为设计工况,获得ORC最优设计结构和最佳运行方案,通过多个设计工况的对比,获得系统在全年变工况下的性能变化规律,并提出ORC的变工况设计方法.
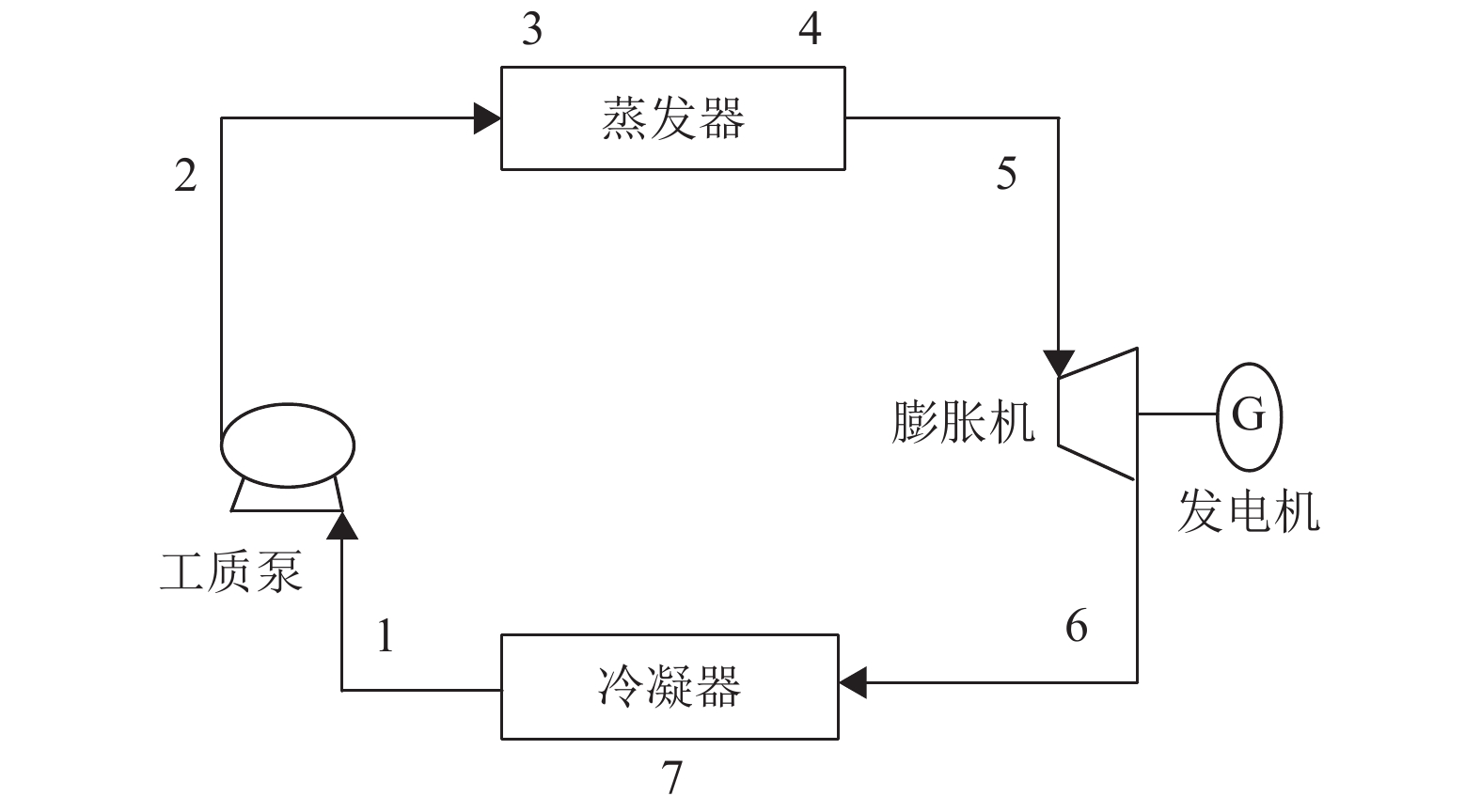
1 系统模型建立 1.1 系统热力学模型基本ORC系统由蒸发器、冷凝器、工质泵、膨胀机4个主要部件组成,流程如图1所示,T-S图如图2所示. 循环工质为R134a,工质泵将工质增压(1-2)后进入蒸发器. 在蒸发器中,工质吸收热源放出的热量成为过热蒸气(2-3-4-5),接着蒸气进入膨胀机对外膨胀(5-6)做功,膨胀机出口乏汽预冷后在冷凝器冷凝为饱和液体(6-7-1),冷凝液进入工质泵完成循环.
|
图 1 基本ORC系统循环图 Figure 1 Schematic of a simple ORC |
|
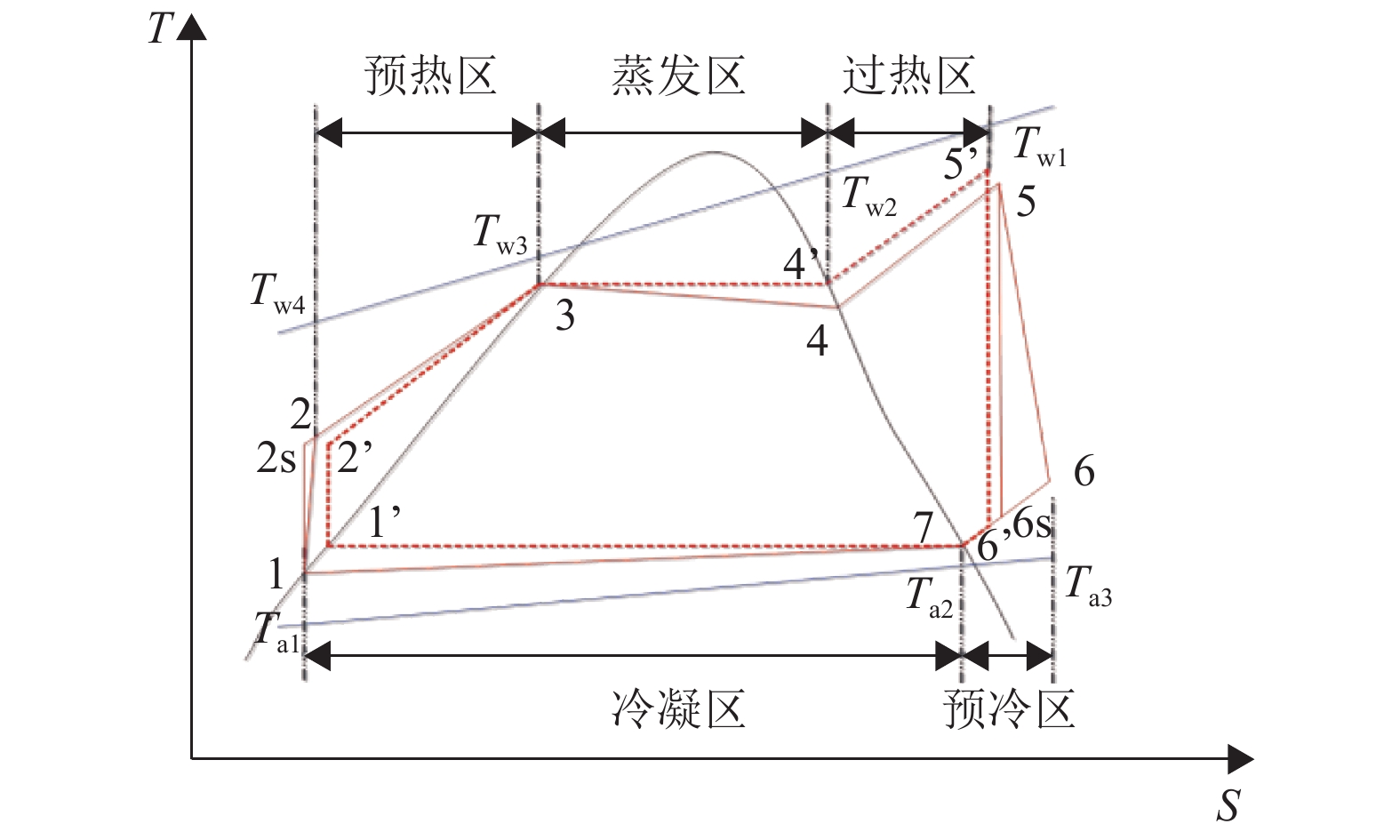
图 2 ORC T-S图 Figure 2 T-S diagram of the ORC |
工质泵内工质转换为高压的液体,耗功如下:
| $ {W_{\rm{p}}} = {M_{{\rm{wf}}}}\left( {{h_2} - {h_1}} \right) = {M_{{\rm{wf}}}}\left( {{h_{2{\rm{s}}}} - {h_1}} \right)/{\eta _{\rm{p}}}. $ | (1) |
式中,Mwf为热源质量流量,kg/s;h1,h2,h2s为工质泵进口、实际出口、理想出口点质量焓值,J/kg;ηp为工质泵绝热效率,本文取0.75.
蒸发器内有机工质吸热后被加热为过热蒸汽,吸收热量如下:
| ${Q_{\rm{e}}} = {M_{{\rm{wf}}}}\left( {{h_5} - {h_2}} \right) = {M_{\rm{w}}}{C_p}_{\rm{w}}\left( {{T_{{\rm{w}}1}} - {T_{{\rm{w}}4}}} \right).$ | (2) |
式中,
过热蒸汽在膨胀机绝热膨胀对外做功,对外做功量为
| ${W_{{\rm{exp}}}} = {M_{{\rm{wf}}}}\left( {{h_5} - {h_6}} \right) = {M_{{\rm{wf}}}}\left( {{h_5} - {h_{6{\rm{s}}}}} \right){\eta _{\rm{e}}}.$ | (3) |
式中,h5,h6,h6s为膨胀机进口、实际出口、理想出口点质量焓值,J/kg;ηe为膨胀机的绝热效率,本文取0.75.
冷凝器内有机工质冷凝为饱和液体,空气作为冷源,冷凝换热计算如下:
| ${Q_{\rm{c}}} = {M_{{\rm{wf}}}}\left( {{h_6} - {h_1}} \right) = {M_{\rm{a}}}{C_p}_{\rm{w}}\left( {{T_{{\rm{a}}3}} - {T_{{\rm{a}}1}}} \right).$ | (4) |
式中,h1为冷凝器出口点焓值,J/kg;Ma为空气质量流量,kg/s;Ta1,Ta3为空气进、出口温度,K.
空气流动压降引起的风机耗电量如下式所示:
| ${W_{\rm{f}}} = \left( {{M_{\rm{a}}}/{\rho _{\rm{a}}}} \right)\Delta {P_{\rm{a}}}/{\eta _{\rm{f}}}.$ | (5) |
式中,ρa为空气平均密度,取空气进出口平均温度为定性温度,kg/m3;ΔPa为空气侧的压降,Pa;ηf为风机的效率,本文取0.7.
系统的净输出功为膨胀机做功减去冷凝器侧风机克服压降消耗的功和泵功:
| ${W_{{\rm{net}}}} = {W_{{\rm{exp}}}} - {W_{\rm{p}}} - {W_{\rm{f}}}.$ | (6) |
系统热效率为
| ${\eta _{{\rm{ORC}}}} = {W_{{\rm{net}}}}/{Q_{\rm{e}}}.$ | (7) |
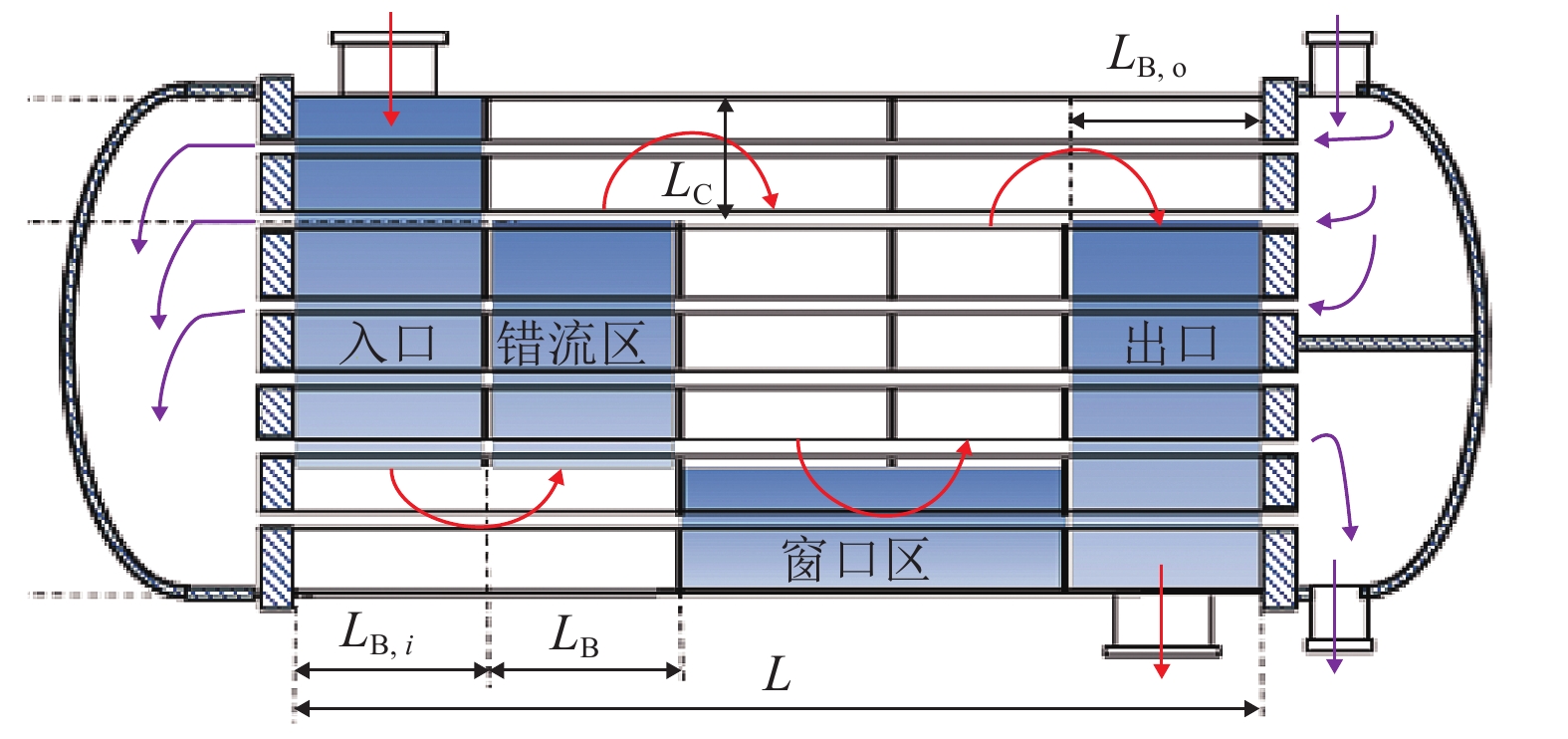
本文系统选用的是管壳式蒸发器,如图3所示,LB为折流板间距,LC为挡板切割长度,L为蒸发器管长,考虑了单相段和两相段流态的差异,故管内的换热以及压降计算也分为单相和两相计算模型. 壳侧以及管侧的预热段和过热段的换热系数采取经典的Dittus-Boelter换热模型,蒸发器管侧两相段的换热系数采用Kandlikar模型[16]. 壳侧压降采用基于范宁摩擦系数的模型[17],管侧压降单相区计算采用文献[18-20]模型,两相段根据均相流模型计算,计算模型跟单相流计算模型相同. 对于蒸发器,蒸发器换热过程热平衡方程式如式(8)~(10),同时,在低温热源和工质换热过程给予换热夹点温度的约束,以保证优化求解的可行性,如式(11)~(12). 同时考虑了湿工质的特性和膨胀机出口状态应为气态的实际要求,过热度取5 K.
|
图 3 管壳式蒸发器示意图 Figure 3 Shell-and-tube evaporator geometrical structures |
| ${Q_{\text{预}}} = {M_{{\rm{wf}}}}\left( {{h_3} - {h_2}} \right) = {M_{\rm{w}}}C{p_{\rm{w}}}\left( {{T_{{\rm{w}}3}} - {T_{{\rm{w}}4}}} \right).$ | (8) |
| ${Q_{\text{两相}}} = {M_{{\rm{wf}}}}\left( {{h_4} - {h_3}} \right) = {M_{\rm{w}}}C{p_{\rm{w}}}\left( {{T_{{\rm{w}}2}} - {T_{{\rm{w}}3}}} \right).$ | (9) |
| ${Q_{\text{过}}} = {M_{{\rm{wf}}}}\left( {{h_5} - {h_4}} \right) = {M_{\rm{w}}}C{p_{\rm{w}}}\left( {{T_{{\rm{w}}1}} - {T_{{\rm{w}}2}}} \right).$ | (10) |
| ${T_{{\rm{w}}3}} - {T_3} \geqslant \Delta {T_{{\rm{min}}}}.$ | (11) |
| ${T_{{\rm{w}}1}} - {T_5} \geqslant \Delta {T_{{\rm{min}}}}.$ | (12) |
式中,h2为蒸发段预热段进口状态点质量焓值,J/kg;h3,h4为蒸发段进、出口饱和状态点质量焓值,J/kg;h5为蒸发段过热段出口状态点质量焓值,J/kg;Tw1为热源在过热段出口处温度,K;Tw3,Tw2为热源在蒸发段进、出口处温度,K;Tw4为热源在预热段进口处温度,K.
1.3 冷凝器模型本文选用多管程布置的风冷式分液冷凝器[21],分液冷凝器呈多管程分布,结合实际换热,各个管程之间的流量以及管程数量的分布需满足一定的要求,约束条件如下:
| ${\chi _{{\rm{in}},k + 1}} = {\chi _{{\rm{out}},k}}{M_k}/{M_{k + 1}}.$ | (13) |
| ${Q_k} = {M_k}{h_{{\rm{LG}}}}\left( {{\chi _{{\rm{in}},k}} - {\chi _{{\rm{out}},k}}} \right).$ | (14) |
| ${\rm{NT}}{{\rm{P}}_{k + 1}} \leqslant {\rm{NT}}{{\rm{P}}_k} \leqslant {\rm{N}}{{\rm{T}}_{{\rm{tot}}}}.$ | (15) |
| ${\rm{N}}{{\rm{T}}_{{\rm{tot}}}} = \mathop \sum \nolimits_k {\rm{NT}}{{\rm{P}}_k}.$ | (16) |
式中:
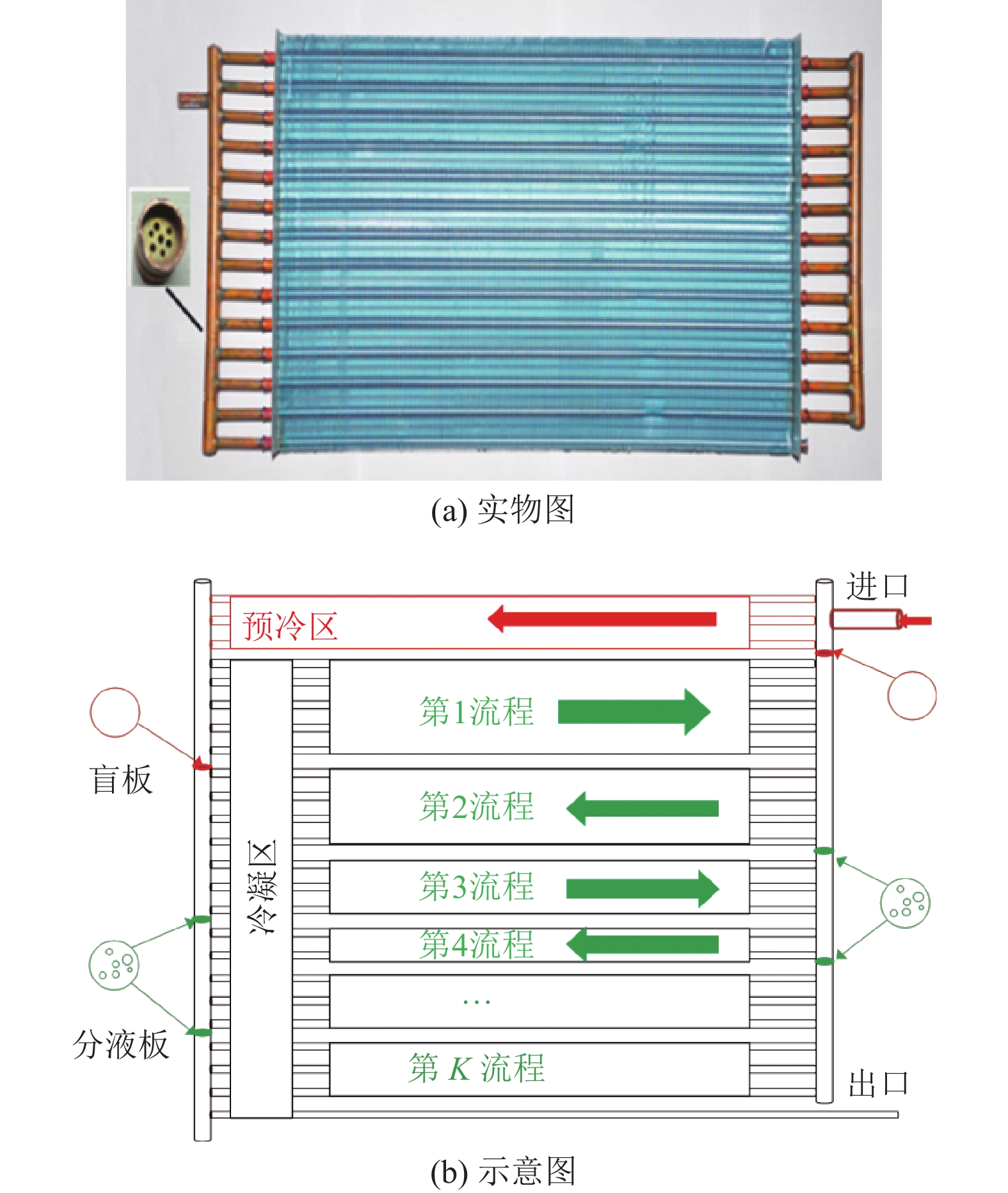
如图4所示,管内换热分为预冷段和两相冷凝段,预冷段换热模型采取单相传热系数和压降计算模型,与蒸发器侧管内单相计算模型相同,两相冷凝段换热系数计算模型为Cavallini模型[22],管内冷凝压降由摩擦压降、局部压降、重力压降和加速压降组成,沿程摩擦压降和加速压降选用Kedzierski模型[23],局部压降选用Collier模型[24],重力压降相较于其他压降较小,忽略不计. 空气侧是开缝百叶窗翅片,采用Wang[25-27]换热系数以及压降模型.
|
图 4 分液冷凝器 Figure 4 Vapor-liquid separation condenser |
本文ORC系统各设备的投资成本采用产品模块成本[28]技术进行估算,年度总成本如式(17)所示,包含设备投资成本和运行费用成本. CRF指资本回收系数,跟年限和通货膨胀率相关,见式(18). Cop指运行费用,ORC系统中,由工质压降引起的耗功已经反馈到净输出功上,本文运行费用指的是在运行阶段产生的维护成本,定为设备总投资成本的1.65%,见式(19). 式(20)代表比投资成本,本文目标函数为度电成本最小,含义是单位发电量的成本,见式(21).
| ${C_{{\rm{annual}}}} = {\rm{CRF}} \cdot {\rm{Cost}} + {C_{{\rm{op}}}}.$ | (17) |
| ${\rm{CRF}} = {\rm{ii}}{\left( {1 + {\rm{ii}}} \right)^y}/\left[ {{{\left( {1 + {\rm{ii}}} \right)}^y} - 1} \right].$ | (18) |
| ${C_{{\rm{op}}}} = {f_k}{\rm{Cost}}.$ | (19) |
| ${\rm{SIC}} = {\rm{Cost}}/{W_{{\rm{net}}}}.$ | (20) |
| $ \min \;{\rm{EPC = }}{C_{{\rm{annual}}}}/\left( {{W_{{\rm{net}}}}{H_{{\rm{year}}}}} \right). $ | (21) |
其中,Cannual为年度总成本,$/a;CRF为资本回收系数;Cost为总投资成本,$;Cop为运行成本,$;y为运行年数;Hyear为每年运行时间,本文为8 000 h/a;ii为通货膨胀率;fk为运行成本占投资成本比例系数;SIC为比投资成本,$/kW;EPC为度电成本,$/(kW·h).
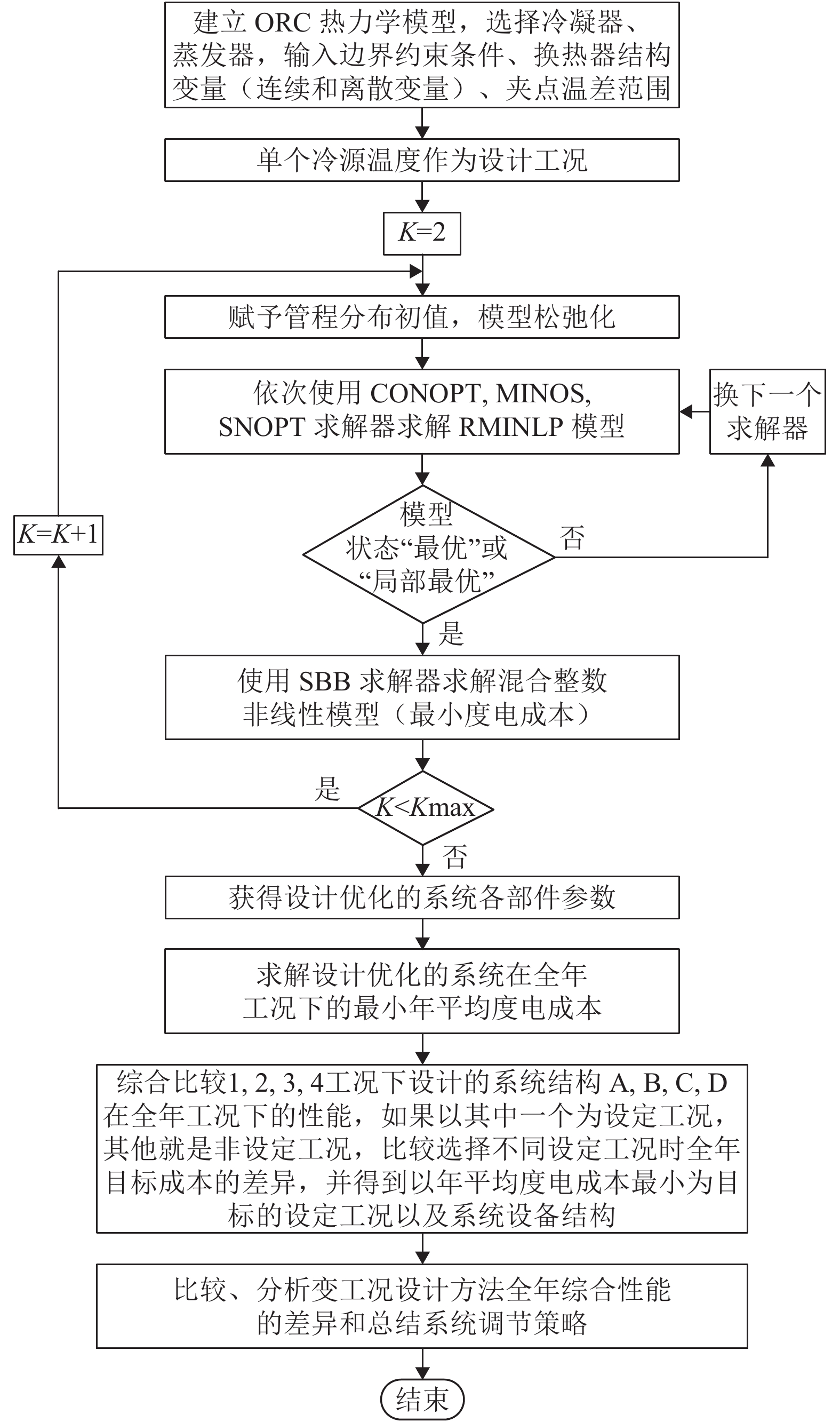
1.5 变工况优化流程图计算给定系统初始条件和约束条件,输入变量的优化范围,基于目标成本系统协同优化,获得不同设计工况的系统参数,比较各设计工况的系统在全年工况下的综合性能,优化流程如图5所示.
|
图 5 变工况优化流程 Figure 5 Process of off-design optimization |
全年环境工况随季节和时间变化,涉及到的系统运行参数和设备实际工况也是持续多变的,多变量优化耦合的系统优化设计中,求解工作繁杂,需对环境工况进行简化. 根据全年的环境温度变化情况,假设环境温度的变化范围为5~35 ℃,为了简化计算量,本文将范围5~35 ℃的环境温度取5,15,25和35 ℃ 4个工况,主要探讨基于设计环境工况的系统优化配置在全年变化工况下的综合性能. 模拟系统进行优化,给定的基本参数如表1所示,系统变量范围如表2所示,蒸发器和冷凝器各个参数如表3和表4所示.
| 表 1 基本参数 Table 1 Basic parameter |
| 表 2 系统优化变量范围 Table 2 The optimization variable range of the system |
| 表 3 蒸发器优化变量范围 Table 3 The optimal variable range of evaporator |
| 表 4 冷凝器优化变量范围 Table 4 The optimal variable range of condenser |
不同的热源和冷源温度,所对应的最佳匹配的冷凝温度和蒸发温度是不同的,其系统四大部件的结构也不同,例如本文设计环境温度为25 ℃,设备结构和系统参数同步优化结果:冷凝器(包括风机)、蒸发器、膨胀机和泵占总投资成本的比例分别为47%,15%,34%和4%,体现了换热设备在系统中的成本比重. 从优化的角度,每一组对应的冷凝温度和蒸发温度都有与之相匹配的最佳的设备结构,离开了设备优化单单优化系统,比如最大输出功,可能其经济性并不好;或者离开了系统参数去优化设备结构,其在该参数下是最好的结构,但是系统参数变化时,其结构并不适合,所以同时优化系统参数及设备结构参数至关重要.
本文设定的环境温度分别为5,15,25和35 ℃,对应得到的设计结构为A、B、C、D. 表5列出了不同设计环境温度下系统的优化结果,结果表明,在环境设计温度为5,15,25和35 ℃时,热效率分别为8.52%,7.93%,6.10%和5.54%,比成本分别为3 046,3 924,4 850和6 348$/kW,度电成本分别为0.042,0.054,0.067和0.088$/(kW·h),随着冷凝温度的上升,热效率、净功率输出呈减小的趋势,而比投资成本和度电成本呈增加的趋势. 相比较之下,设定的环境温度为5 ℃时,所得到的度电成本较其他环境温度的度电成本要小. 值得注意的是,设计工况得到的系统配置方案是否适用于全年工况,需通过计算比较全年综合性能的优劣.
| 表 5 不同设计环境温度下系统的优化结果 Table 5 Optimization results of the system under different design ambient temperatures |
不同设计的系统优化结构在全年不同环境条件的性能如表6所示,A结构4个变工况的度电成本分别为0.042,0.063,0.069和0.221$/(kW·h),B结构4个变工况的度电成本分别为0.043,0.054,0.069和0.093$/(kW·h),C结构4个变工况的度电成本分别为0.048,0.060,0.067和0.090$/(kW·h),D结构4个变工况的度电成本分别为0.066,0.068,0.071和0.088$/(kW·h).
| 表 6 各结构全年性能 Table 6 Year-round performance of each structure |
基于全年不同工况运行时间相同的前提,在环境设计温度为5、15、25和35 ℃对应的优化配置A、B、C、D全年的比投资成本分别为4 665,4 312,4 535和5 242$/kW,度电成本分别为0.065,0.060,0.063和0.073$/(kW·h).
不同结构配置在假设的全年外界条件下的性能变化程度是不一样的,说明性能偏离的程度是不一样的. 结果显示,B结构变工况全年的度电成本最小,其次是C结构和A结构,最大的是D结构.
3 结论本文以度电成本为目标函数建立ORC系统设计和运行优化的数学模型,选取典型的4个环境温度作为设计工况,优化系统的设备结构和系统运行参数,对应得到4个最优设计方案和最佳运行方案,并比较不同运行方案的全年综合性能,得出结论如下:
(1) 本文优化方案中,换热器成本占系统总成本比例为58%~62%,体现了换热设备结构配置在系统中的重要性. 变工况环境设计温度下,对应的最佳匹配冷凝温度和蒸发温度不同,且每组对应的冷凝温度和蒸发温度都有与之相匹配的最佳设备结构,因此同时优化系统参数及设备结构参数至关重要.
(2) 环境设计温度不同,设计的最优结构和运行方案不同,通过对比,15 ℃和25 ℃为环境设计温度的最优结构的全年性能比5 ℃和35 ℃为环境设计温度的最优结构的全年性能要好. 变工况环境温度下,各设计结构运行方案的综合性能不同,其中存在一个最佳的设计工况点,使得优化结构的全年运行性能最优. 结合本文研究,夏季环境温度过高、冬季环境温度过低或是变工况环境温度,系统运行性能产生不同程度的变化,实际性能达不到设计要求,因此可以根据各地区全年多变的环境温度,兼顾考虑多个变工况环境温度对系统进行优化设计,优化全年运行方案.
| [1] |
VÉLEZ F, SEGOVIA J J, MARTÍN M C, et al. A technical, economical and market review of organic Rankine cycles for the conversion of low-grade heat for power generation[J].
Renewable and Sustainable Energy Reviews, 2012, 16(6): 4175-4189.
DOI: 10.1016/j.rser.2012.03.022. |
| [2] |
LEE K M, KUO S F, CHIEN M L, et al. Parameters analysis on organic Rankine cycle energy recovery system[J].
Energy Conversion and Management, 1988, 28(2): 129-136.
DOI: 10.1016/0196-8904(88)90038-6. |
| [3] |
MADHAWA, HETTIARACHCHI H D, GOLUBOVIC M, et al. Optimum design criteria for an Organic Rankine cycle using low-temperature geothermal heat sources[J].
Energy, 2007, 32: 1698-1706.
DOI: 10.1016/j.energy.2007.01.005. |
| [4] |
WEI D, LU X, LU Z, et al. Performance analysis and optimization of organic Rankine cycle (ORC) for waste heat recovery[J].
Energy Conversion and Management, 2007, 48(4): 1113-1119.
DOI: 10.1016/j.enconman.2006.10.020. |
| [5] |
DAI Y, WANG J, LIN G. Parametric optimization and comparative study of organic Rankine cycle (ORC) for low grade waste heat recovery[J].
Energy Conversion and Management, 2009, 50(3): 576-582.
DOI: 10.1016/j.enconman.2008.10.018. |
| [6] |
GU W, WENG Y, WANG Y J, et al. Theoretical and experimental investigation of an organic Rankine cycle for a waste heat recovery system[J].
Proceedings of the Institution of Mechanical Engineers Part A Journal of Power and Energy, 2009, 223(5): 523-533.
DOI: 10.1243/09576509JPE725. |
| [7] |
ZHANG J, ZHOU Y, WANG R, et al. Modeling and constrained multivariable predictive control for ORC (organic Rankine cycle) based waste heat energy conversion systems[J].
Energy, 2014, 66(4): 128-138.
|
| [8] |
ZHANG J, ZHOU Y, LI Y, et al. Generalized predictive control applied in waste heat recovery power plants[J].
Applied Energy, 2013, 102(2): 320-326.
|
| [9] |
LEE Y R, KUO C R, WANG C C. Transient response of a 50 kW organic Rankine cycle system[J].
Energy, 2012, 48(1): 532-538.
DOI: 10.1016/j.energy.2012.10.029. |
| [10] |
LEE Y R, KUO C R, LIU C H, et al. Dynamic response of a 50 kW organic Rankine cycle system in association with evaporators[J].
Energies, 2014, 7(4): 2436-2448.
DOI: 10.3390/en7042436. |
| [11] |
QUOILIN S, AUMANN R, GRILL A, et al. Dynamic modeling and optimal control strategy of waste heat recovery organic rankine cycles[J].
Applied Energy, 2011, 88(6): 2183-2190.
DOI: 10.1016/j.apenergy.2011.01.015. |
| [12] |
CASARTELLI D, BINOTTI M, SILVA P, et al. Power block off-design control strategies for indirect solar ORC cycles[J].
Energy Procedia, 2015, 69: 1220-1230.
DOI: 10.1016/j.egypro.2015.03.166. |
| [13] |
SUN K, TSENG C T, WONG S H, et al. Model predictive control for improving waste heat recovery in coke dry quenching processes[J].
Energy, 2015, 80: 275-283.
DOI: 10.1016/j.energy.2014.11.070. |
| [14] |
HU D, ZHENG Y, WU Y, et al. Off-design performance comparison of an organic Rankine cycle under different control strategies[J].
Applied Energy, 2015, 156: 268-279.
DOI: 10.1016/j.apenergy.2015.07.029. |
| [15] |
KOSMADAKIS G, MANOLAKOS D, PAPADAKIS G. Experimental investigation of a low-temperature organic Rankine cycle (ORC) engine under variable heat input operating at both subcritical and supercritical conditions[J].
Applied Thermal Engineering, 2016, 92: 1-7.
DOI: 10.1016/j.applthermaleng.2015.09.082. |
| [16] |
KANDLIKAR S G. A general correlation for saturated two-phase flow boiling heat transfer inside horizontal and vertical tubes[J].
Journal of Heat Transfer, 1990, 112(1): 219-228.
DOI: 10.1115/1.2910348. |
| [17] |
PATEL V K, RAO R V. Design optimization of shell-and-tube heat exchanger using particle swarm optimization technique[J].
Applied Thermal Engineering, 2010, 30(11–12): 1417-1425.
|
| [18] |
SINNOTT R K. Chemical engineering design: SI Edition [M]. Elsevier, 2009.
|
| [19] |
YANG J, FAN A, LIU W, et al. Optimization of shell-and-tube heat exchangers conforming to TEMA standards with designs motivated by constructal theory[J].
Energy Conversion and Management, 2014, 78: 468-476.
DOI: 10.1016/j.enconman.2013.11.008. |
| [20] |
CHISHOLM D. Two phase flow in pipelines and heat exchangers [M]. 1983.
|
| [21] |
LUO X L, YI Z T, ZHANG B J, et al. Mathematical modelling and optimization of the liquid separation condenser used in organic Rankine cycle[J].
Applied Energy, 2017, 185: 1309-1323.
DOI: 10.1016/j.apenergy.2015.12.073. |
| [22] |
CAVALLINI A, COL D D, MANCIN S, et al. Condensation of pure and near-azeotropic refrigerants in microfin tubes: A new computational procedure[J].
International Journal of Refrigeration, 2009, 32(1): 162-174.
DOI: 10.1016/j.ijrefrig.2008.08.004. |
| [23] |
KEDZIERSKI M A, GONCALVES J M. Horizontal convective condensation of alternative refrigerants within a micro-fin tube[J].
Journal of Enhanced Heat Transfer, 1999, 6(2): 161-178.
|
| [24] |
COLLIER J G, THOME J R. Convective boiling and condensation [M]. Oxford: Oxford University Press, 1994.
|
| [25] |
WANG C C, LEE W S, SHEU W J. A comparative study of compact enhanced fin-and-tube heat exchangers[J].
International Journal of Heat and Mass Transfer, 2001, 44(18): 3565-3573.
DOI: 10.1016/S0017-9310(01)00011-4. |
| [26] |
WANG C C, LEE C J, CHANG C T, et al. Heat transfer and friction correlation for compact louvered fin-and-tube heat exchangers[J].
International Journal of Heat and Mass Transfer, 1998, 42(11): 1945-1956.
|
| [27] |
WANG C C, WEBB R L, CHI K Y. Data reduction for air-side performance of fin-and-tube heat exchangers[J].
Experimental Thermal and Fluid Science, 2000, 21(4): 218-226.
DOI: 10.1016/S0894-1777(00)00005-4. |
| [28] |
BHATTACHARYYA D, SHAEIWITZ J A, BAILIE R C, et al. Analysis, synthesis and design of chemical processes [M]. New Jersey: Prentice Hall, 2012.
|
 2019, Vol. 36
2019, Vol. 36

