因其广泛的应用潜力,人脸聚类近年来受到越来越多的关注,目前主要用于人脸检索与标注[1-2]、人脸识别的预处理[3-4]和人脸数据库的构建[5-6].另外,通过在检索的基础上融合时间、地点等信息,人脸聚类还能用于追踪罪犯和寻找失踪人口等.一般来说,人脸聚类效果的优劣,主要受到所采用的特征提取方法和聚类算法的影响.传统的特征提取方法主要有PCA[7]、LDA[8]、ICA[9]、LBP[10]等.基于PCA的“特征脸”方法把所有样本(包括光照等外来因素)作为一个整体去寻找均方误差最小意义下的最优线性投影,而忽略其类别属性,所以在该投影方向下的人脸不一定具有可分性.基于LDA的“Fisher脸”则引入了类间离散度和类内离散度的概念,它是一种以可分性为目的的算法,但这种方法存在小样本问题,且只利用了人脸的二阶统计特性.ICA进一步考虑了人脸高阶信息,但它需要依靠经验来选取对分类有用的独立元,且计算复杂度较高.上述方法都只是对人脸图像进行简单的线性变换,而实际上人脸的类内和类间变化是复杂、高度非线性的.核PCA[11]和核Fisher判别[12]利用非线性映射把原空间的样本映射到隐特征空间中去,再对样本作分析,考虑了人脸信息的非线性特性,但依然存在可分性不强和小样本问题.考虑到人脸的局部细节信息重要性,LBP提取人脸的局部纹理特征,具有灰度不变性和旋转不变性,但该特征具有较高的维数.
以上传统的特征提取方法都是通过浅层的模型提取特征,特征的好坏很大程度依赖经验,且没有综合考虑人脸变化的复杂性、高度非线性和高阶性.此外,为了使特征对光照、姿势、表情等具有较好的鲁棒性,这些方法还需要进行直方图均衡、光照补偿、姿势矫正等处理,增加了模型的复杂性.
卷积神经网络(Convolutional Neural Networks,CNN)是在近几年发展起来的,并引起广泛重视的一种高效识别方法.由于其深层的结构、强大的学习能力和分层非线性映射,被广泛应用于人脸特征提取[13-15],并成为人脸识别领域的主流方法[6].
在人脸聚类任务中,除了要求提取到有效特征信息外,还需要选取合适的聚类算法.目前文献中有大量聚类算法.其中,K-means算法是最为经典,同时也是应用最为广泛的算法之一.它具有原理简单、收敛速度快、计算时间复杂度是关于样本数的线性量级等优点,但是,其也存在参数k需要事先给定,聚类形状接近球形等缺点.最近,文献[16]提出了一种快速搜索密度极点的聚类算法(Clustering by Fast Search and Find of Density Peaks,CFSFDP),该算法通过构建决策图的可视化方法,达到快速确定聚类中心数目和位置的目的.在聚类中心点确定后,其余各点的类标签分配可以一次完成,且聚类形状不局限于球形.但是,其在计算样本两两之间的相关性度量指标时,时间复杂度为样本数量的平方量级.这就意味着,当样本数量比较大时,该算法运算效率偏低,而这一缺点容易被现有文献忽略.
鉴于CNN在人脸识别任务中的优越性能,本文采用CNN作为人脸特征提取方法,并在此基础上探讨了大规模人脸聚类情境下,K-means和CFSFDP哪一种聚类算法更优的问题.此外,为了更加直观地显示CNN特征提取的有效性,本文在实验中还加入基于全局特征PCA算法作对比.本文采用MSRA-CFW人脸数据库作为实验数据集,选取RI、信息熵和F1-measure三种聚类指标作为评估聚类算法优劣的标准,并对聚类效果进行了可视化处理.实验结果表明,在聚类类别数目足够大且两种聚类算法聚类中心点数目选取准确的情况下,经典的K-means算法的效果显著优于原理相对比较复杂的CFSFDP算法.值得注意的是,K-means算法在计算时间复杂度上同样显著优于CFSFDP算法.因此,CNN特征融合K-means的人脸聚类算法更适用于大样本的情况.这一结论对大规模人脸聚类的实际应用具有重要的指导意义.
1 卷积神经网络 1.1 卷积神经网络的原理和优点20世纪60年代,Hubel和Wiesel发现猫脑皮层用于局部敏感和方向选择的独特网络结构有助于降低反馈神经网络的复杂性[17],继而提出了卷积神经网络.它主要包括卷积层、池化层和全接连层.卷积的目的是使用不同的卷积核提取不同的特征,池化层则对卷积层的特征进行重要特征采样.全连接层的主要作用是把低层特征抽象成维数更高的高层特征.CNN以分类误差作为损失函数,迭代反馈传播误差调整网络参数,直至分类误差最小.具体过程见1.2节.
CNN能够利用大量的样本通过其自身深层的非线性网络结构来学习数据特征表示,具有较强的泛化能力.其独特的结构(局部感受野、权值共享、池化)大大减少了神经网络参数的数量,降低了复杂度,并对位移、缩放和旋转等扭曲具有一定的不变性.和采用全连接结构的传统人工神经网络相比,参数选择不过分依赖经验,且学习深度更深.与传统算法相比,对光照、表情、姿势等具有较好的鲁棒性,另外二维图像可直接作为网络的输入,避免了特征提取和分类过程中数据重建的复杂过程.
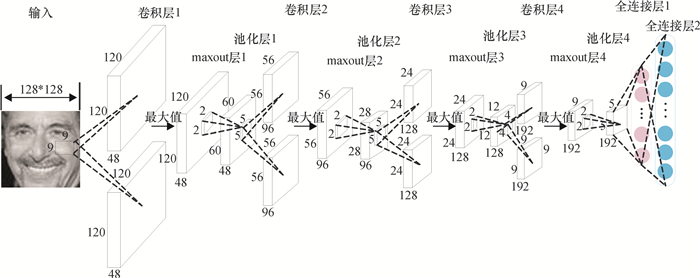
1.2 卷积神经网络模型本文受文献[18]启发,构建一个深度卷积神经网络来学习人脸特征.卷积层和池化层之间采用maxout激活函数.具体的网络结构如图 1所示.
|
图 1 基于人脸特征的卷积神经网络 Figure 1 Convolutional neural networks based on face features |
该深度卷积神经网络主要包括4个卷积层,4个maxout层,4个池化层和2个全连接层.输入图像是128×128的人脸图像,采用96个核大小为9×9的卷积核扫描输入图像,对于每张人脸图像的不同位置,都采用相同的卷积核进行扫描.因此,在卷积层1得到96个特征,即2组120×120×48的特征图.再经过maxout激活函数筛选得到1组120×120×48的特征图,然后采用池化区域大小为2×2的maxpooling来池化这组特征,得到1组60×60×48的池化特征.maxout和maxpooling操作都是为了进一步减少网络参数,防止网络过拟合.
以上步骤重复3次,这样经过一系列的卷积提取特征,池化聚合特征等操作,在池化层4得到了5×5×192全局化的特征图.这192张特征图的每个位置,都是来自不同特征的单元得到的不同类型的特征.最后两层为全连接层,全连接层1是1组256×1的特征,全连接层2是1组10 575×1的特征.本文采用的人脸特征是全连接层1的特征,而全连接层2的特征用来作为softmax分类层的输入.
在该网络搭建的过程中涉及3个重要的数学表达式,它们分别为卷积层输出表达式、maxpool池化函数9表达式和maxout激活函数表达式.具体见公式(1)、(2)、(3).
卷积层输出的表达式为
| $ y_{ij}^{n}=f\left( \sum{x_{ij}^{n-1}\cdot {{W}_{ij}}+{{b}_{j}}} \right)\cdot $ | (1) |
其中,f(·)为Relu激活函数,f(·)=max(0, x),xijn是第n层池化层特征图第i行j列的特征值,特别的,x0表示输入图像,Wij是卷积核,初始值采用xavier filler填充,bj为偏置项,这里设为0.1.
maxpool池化函数的表达式为
| $ x_{ij}^{n}=\underset{a\in \left( N, N \right)}{\mathop{\text{max}}}\, ~\text{ }g_{ij}^{n-1}u\left( a, a \right)\cdot $ | (2) |
其中,gijn是第n层maxout层特征图第i行j列的特征值,u(a, a)是窗口函数,N是窗口的大小,这里N=2.
maxout激活函数的表达式为
| $ g_{ij}^{n}=\underset{1\le k\le m}{\mathop{\text{max }\!\!~\!\!\text{ }}}\, \text{ }\left( y_{ij}^{k}+y_{ij}^{k+m} \right)\cdot $ | (3) |
其中,m是卷积层特征图的数目的
聚类分析是根据数据集之间的相似度将其划分为若干类或簇,使得同一类之间的数据相似度尽可能大,不同类之间的数据相似度尽可能小.与分类最大的区别是,聚类分析是一种无监督的学习方法,学习不依赖标签的数据.
2.2 基于K-means的聚类算法K-means是聚类分析中使用最广泛的算法之一,其算法原理如下:
(1) 随机选取k个样本点作为初始中心点,共有k个类;
(2) 计算其余各点到这k个中心点的距离,样本点归属于距离最小的中心点,距离计算可选择欧氏距离、马氏距离、余弦距离等,其中文献[19]提出一种新的距离在人脸识别中的应用;
(3) 重新计算各类的质心作为中心点;
(4) 迭代步骤(2) 和(3) 直到目标函数达到最优或达到最大的迭代次数.使用不同的距离公式,目标函数不同.目标函数一般误差平方和表示为
| $ \text{SSE}=\text{min}\sum\limits_{i=1}^{k}{\sum\limits_{x\in {{c}_{i}}~}{\text{dist}{{\left( {{c}_{i}}, x \right)}^{2}}\cdot }}\text{ } $ | (4) |
其中k是聚类数目,ci是样本i所归属的类别,dist是指具体的距离度量方式.
对于大规模数据,K-means算法是相对可伸缩和高效的[20].其时间复杂度为O(nkt),其中n为样本数量,k为聚类数目,t为迭代次数.一般来说,k ≪ n, t ≪ n.因此,就时间复杂度而言,K-means算法适用于大数据聚类.另外,由于K-means的聚类形状为球形,也就是说,当样本的特征空间符合欧氏距离,聚类是密集且不同类别之间的区别较为明显时,K-means聚类能取得较好的效果.
2.3 基于密度极点的聚类算法CFSFDP是一种基于密度极点的聚类算法,该算法通过局部密度极点来挖掘潜在聚类中心,再根据就近原则一次完成其余样本点的类标签分配.其基本思想是:聚类中心点被局部密度较小的邻域包围,而与其他局部密度较高的样本点保持相对较大的距离.值得注意的是,虽然该算法只需计算样本点的两个属性值:局部密度值ρi和距离δi,但涉及这两个值计算的dij的时间复杂度为O (n 2),n为样本数量.属性值具体如公式(5) 和(6) 所示.
| $ {{\rho }_{i}}=\sum\limits_{j}{\text{ }\chi \left( {{d}_{ij}}-{{d}_{c}} \right)}\cdot $ | (5) |
当x < 0时,χ(x)=1;当x>0时;χ(x)=0.dc是一个截断距离.
| $ {{\delta }_{i}}=\underset{j:{{\rho }_{j}}>{{\rho }_{i}}}{\mathop{\text{min}~}}\, \left( {{d}_{ij}} \right)~\cdot $ | (6) |
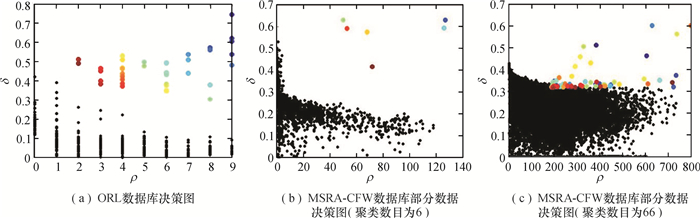
当ρi达到最大值时,δi=maxj(dij).CFSFDP的聚类中心点必须符合:δ值高,ρ值相对较高,即所有数据的密度相对极点,而这两个值只与数据之间的距离dij有关.因此,该算法的准确率依赖于dij.对于结构清晰,即不同类别之间的区别明显,且聚类数目较少的特征空间来说,该算法选择聚类中心点的准确率总是很高.如图 2(a)所示,由于ORL人脸数据库聚类数目较少,变化模式单一,CFSFDP能准确地选取其聚类中心点.然而,在实际生活中,存在着变化模式复杂,且聚类数目和样本规模较大的数据库,该算法在处理这一类数据库时,只能主观地选取中心点.例如,图 2(b)和图 2(c)是同一个数据库不同聚类数目的样本点通过CFSFDP算法得出的决策图.图 2(b)的聚类中心点明显,但随着聚类数目和样本数量的增大,聚类中心点与其余样本点的区别并不明显,如图 2(c)所示.
|
图 2 CFSFDP决策图 Figure 2 Decision graph of CFSFDP |
本文采用CASIA-WebFace人脸数据库作为神经网络的训练数据集.CASIA-WebFace数据集有10 575个人,共494 414张图像,图像需要经过简单的预处理,其步骤具体如下:
(1) 人脸区域检测、人脸关键点检测和人脸对齐,具体方法参考文献[21].
(2) 转化为灰度图像,归一化图像为128×128大小.
在网络训练的过程中,为了防止过拟合,在卷积层、池化层和全连接层1中,权值衰减系数设置为5×10-4,在全连接层2中设置为5×10-3.全连接层采用比率为0.7的dropout操作.整个网络的学习速率从10-3逐渐减小到5×10-5.
整个模型在GPU:GTX Titan X上训练,大约耗时3 d.该模型在LFW人脸数据库上人脸验证准确率的AUC为98.58%,可见该神经网络模型提取的人脸特征较好.
聚类实验数据来源于MSRA-CFW人脸数据库,该数据库有1 583人,每人10~1 000张图像不等,共202 792张图像.由于该数据库规模较大,本文只选用部分数据:66人,每人250~350张图像,共19 109张图像.
为了验证在大规模数据的情况下,基于CNN算法提取的人脸特征的有效性,并进一步对比K-means和CFSFDP算法聚类效果的优劣性,本文设计了两组对比实验,实验在聚类数目和样本规模递增的情况下进行.具体实验如下:
(1) 提取CNN特征,分别采用CFSFDP和K-means算法进行聚类;
(2) 提取PCA特征,分别采用CFSFDP和K-means算法进行聚类.
其中CFSFDP算法和K-means算法均以余弦距离来度量样本之间的相似性.以上实验的聚类效果使用RI、信息熵(Entropy)和F1-measure三种指标进行评价.由于数据规模较大,本文只将聚类数目为66的聚类结果进行可视化.
3.1 RI评价指标及结果分析RI是一种用排列组合原理计算聚类后的数据集与原数据集相似性的评价手段.其定义为
| $ \text{RI}=\frac{\text{TP+TN}}{\text{TP+FP+FN+TN}}\cdot $ | (7) |
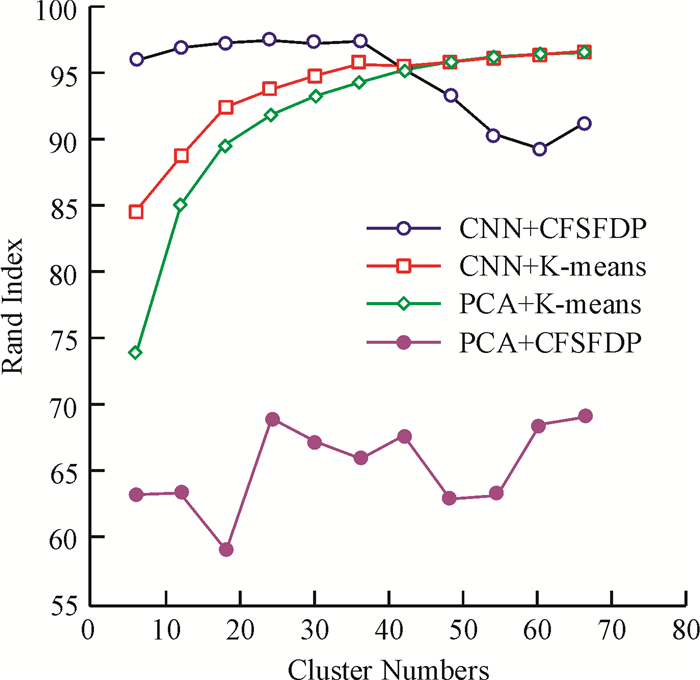
其中,TP(Ture Positive)、TN(Ture Negative)、FP(False Positive)和FN(False Negative)分别表示同一类的数据被分到同一簇,不同类的数据被分到不同簇,不同类的数据被分到同一簇,同一类的数据被分到不同簇的数目.图 3为不同聚类结果的RI指标比较.
|
图 3 不同聚类结果的RI指标 Figure 3 Rand Index of different clustering results |
由图 3可以看出:(1) CNN+CFSFDP的RI指标随着聚类数目的递增而下降,而CNN+K-means的RI指标随着聚类数目的递增而上升,当聚类数目大于42时,后者的指标明显高于前者;(2) PCA+K-means的RI指标远高于PCA+CFSFDP的指标;(3) CNN+K-means的RI指标与PCA+K-means的指标差别不大,当聚类数目大于42时,两者几乎重叠.
RI指标有一个缺陷,就是只适用于聚类数目较少的情况.当聚类数目较大时,由于RI把TP和TN看得同等重要,TN的增大也有可能使RI的值上升,但此时并不代表聚类质量好.因为TN强调不同类的数据分到不同的簇,没有考虑分布的混杂程度.因此,本文用熵和F1-measure来进一步评价聚类质量.
3.2 信息熵评价指标及结果分析信息熵(entropy)是信息论中用来衡量系统有序化程度的度量.在聚类评价中,信息熵表示聚类的混杂程度.信息熵越低,表示聚类后每一簇的类别数目越少,聚类的混杂程度越高,反之聚类的混杂程度越低.其定义为
| $ E=-\sum\limits_{j=1}^{l}{{{P}_{ij}}\text{lo}{{\text{g}}_{2}}{{P}_{ij}}}\cdot $ | (8) |
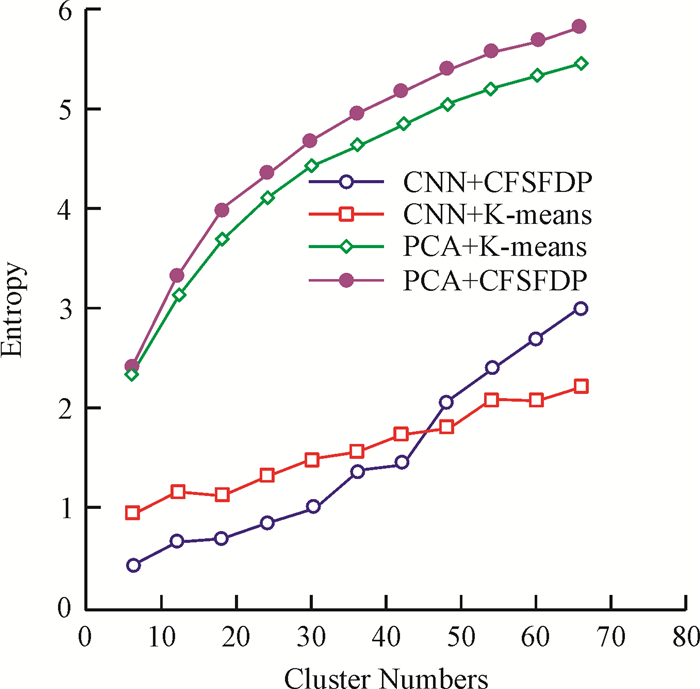
其中Pij=mij/mi,mij是第i个簇中类别j的数目,mi是第i个簇的样本总数.图 4为不同聚类结果的信息熵比较.
|
图 4 不同聚类结果的信息熵指标 Figure 4 Entropy of different clustering results |
由图 4可以看出:(1) 由于数量规模的增大,就整体而言,信息熵随着聚类数目的递增而上升;(2) 由PCA特征得到的信息熵明显高于由CNN特征得到的信息熵,这表明前者聚类的混杂程度较高,后者聚类的混杂程度较低;(3) 当聚类数目大于42时,CNN+K-means的信息熵低于CNN+CFSFDP的信息熵,说明在聚类数目较大的情况下,前者聚类的混杂程度更低.综上所述,当聚类数目较大时,由CNN特征融合K-means算法聚类的混杂程度较低.
3.3 F1-measure评价指标及结果分析精度(Precision)和召回率(Recall)是信息检索和统计分类领域用来评价检索或分类结果质量的度量.在聚类评价中,聚类后每一簇的精度是指某一类别的数目与该簇总样本数目的比率,衡量的是聚类结果的查准率.而每一类的召回率是指在聚类后的指定簇中,某一类别的数目与该类别样本总数的比率,衡量的是聚类结果的查全率.精度和召回率两者越高越好,但实际上随着样本规模的增大,两者是相互制约的,即精度高时,召回率低,召回率高时,精度低.F1-measure是综合精度和召回率的评价指标,反映了整体的聚类质量.当F1-measure值较高时说明相应的聚类方法比较有效.其定义为
| $ {{F}_{1}}-\text{measure}=\text{ }\frac{\sum\limits_{j}{\left( \left| j \right|\text{ }{{F}_{1}}\left( j \right) \right)}}{\sum\limits_{j}{\left| \text{ }j \right|}~}\text{ }\cdot $ | (9) |
其中
|
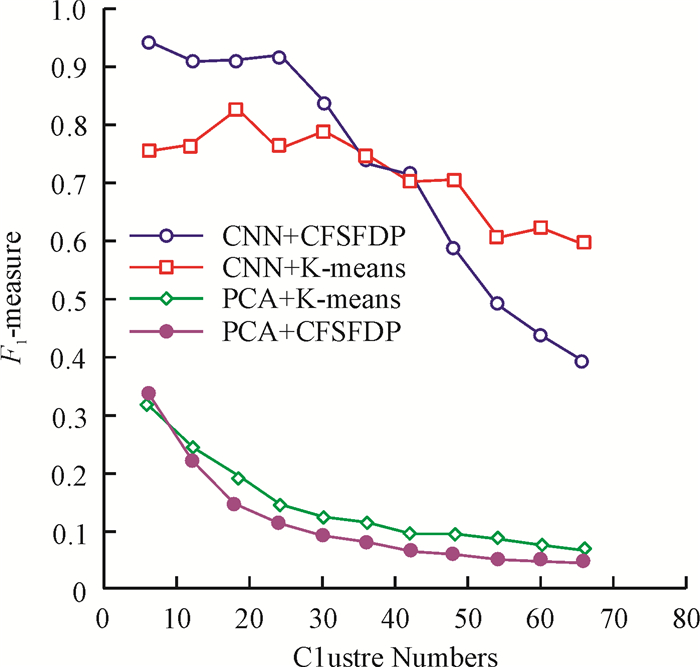
图 5 不同聚类结果的F1-measure指标 Figure 5 F1-measure of different clustering results |
由图 5可以看出:(1) CNN特征得到的F1值明显高于PCA特征得到的F1值,这表明前者的整体综合性能优于后者;(2) 当聚类数目大于42时,CNN+K-means的F1值高于CNN+CFSFDP的F1值,这表明在聚类数目较大的情况下,前者的综合性能优于后者.综上所述,当聚类数目较大时,由CNN特征融合K-means聚类算法综合性能更加优秀.
3.4 聚类结果可视化本文通过混淆矩阵来可视化聚类效果.其中每一行代表聚类前样本的真实归属类别,每一列代表聚类后样本的预测类别.通过混淆矩阵行归一化,可以衡量聚类后每一簇分布的混杂程度;通过列归一化可以衡量原类别分布的混杂程度.图 6、图 7分别是行归一化和列归一化混淆矩阵的可视化结果.图中的正方形越黑则代表对应的比值越大,分布越集中.可视化结果越接近对角线,则说明聚类效果越出色.
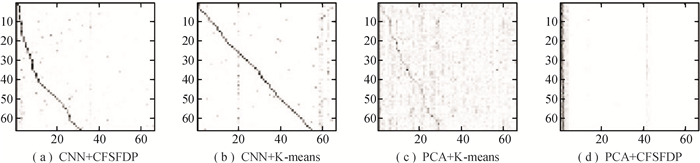
|
图 6 行归一混淆矩阵可视化 Figure 6 Visualization of row-normalized confusion matrix |
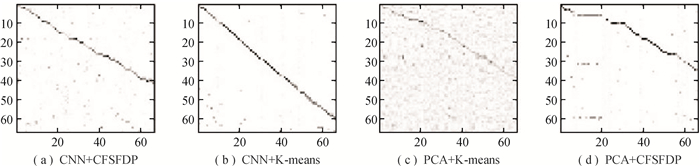
|
图 7 列归一混淆矩阵可视化 Figure 7 Visualization of column-normalized confusion matrix |
由图 6可以看出:(1) PCA+K-means的效果比较差,聚类后的每一簇混杂程度最高;(2) PCA+CFSFDP的样本主要聚集在几个簇中,且每个簇的混杂程度较高,多数的簇只有少量样本;(3) CNN+CFSFDP的聚类效果一般,虽然每一簇的混杂程度较低,但接近一半的簇只聚集到少量样本;(4) CNN+K-means的聚类效果最好,绝大多数的簇混杂程度低,且同一类别的样本基本聚集到同一簇中,只有少部分的簇聚集了多类别样本.
同理,由图 7可以看出:(1) PCA+K-means的聚类效果比较差,原类别分布混杂;(2) PCA+CFSFDP的聚类效果一般,多数原类别分布的混杂程度较低;(3) CNN+CFSFDP的效果在整体上比PCA+CFSFDP的好;(4) CNN+K-means的聚类效果最出色,绝大多数原类别分布的混杂程度低,且同一类别的样本基本聚集到同一簇中,只有少部分的原类别分散到不同的簇中.
4 结语本文通过CNN提取人脸特征,然后融合CFSFDP和K-means算法分别进行人脸聚类.为了对比聚类数目和样本规模对实验的影响,实验都在其递增的情况下进行.另外,实验所选取的人脸数据库来源于因特网,变化模式复杂,更接近于实际情况.本文采用RI、信息熵和F1-measure三种聚类评价指标去评估聚类的质量,结果表明在聚类数目较少情况下,CNN特征融合CFSFDP算法略优于CNN特征融合K-means算法,但在聚类数目较多的情况下,后者明显优于前者.另外,考虑到CFSFDP计算的时间复杂度为样本数量的平方量级,而K-means计算的时间复杂度接近线性,因此,在大规模人脸聚类的情境下,CNN特征融合K-means聚类算法更为有效.
本文的不足之处在于实验的人脸数据库分布较均匀,即每人的图像数量都在一定范围内.下一步重点研究非均匀分布下的大规模人脸聚类.
| [1] |
杨之光, 艾海舟. 基于聚类的人脸图像检索及相关反馈[J].
自动化学报, 2008, 34(9): 1033-1039.
YANG Z G, AI H Z. Cluster-based face image retrieval and its relevance feedback[J]. Acta Automatica Sinica, 2008, 34(9): 1033-1039. |
| [2] |
刘胜宇, 刘家锋, 黄庆成, 等. 基于改进AP聚类算法的人脸标注技术研究[J].
智能计算机与应用, 2011, 01(3): 35-38.
LIU S Y, LIU J F, HUANG Q C, et al. Research on annotation technology of face based on improved AP clustering algorithm[J]. Intelligent Computer and Application, 2011, 01(3): 35-38. |
| [3] |
刘帅, 林克正, 孙旭东, 等. 基于聚类的SIFT人脸检测算法[J].
哈尔滨理工大学学报, 2014, 19(1): 31-35.
LIU S, LIN K Z, SUN X D, et al. Scale-invariant feature transform based on clustering in face recognition[J]. Journal of Harbin University of Science and Technology, 2014, 19(1): 31-35. |
| [4] |
高璐, 李文辉, 王莹. 基于模糊聚类分析和多特征融合的人脸识别方法[J].
吉林大学学报(理学版), 2012, 50(2): 293-298.
GAO L, LI W H, WANG Y. A face recognition method based on Fuzzy clustering analysis and multi-feature fusion[J]. Journal of Jilin University (Science Edition), 2012, 50(2): 293-298. |
| [5] | ZHU C, WEN F, SUN J. A rank-order distance based clustering algorithm for face tagging[C]//2013 IEEE Conference on Computer Vision and Pattern Recognition. Providence, RI: IEEE, 2011: 481-488. |
| [6] | YI D, LEI Z, LIAO S, et al. Learning face representation from scratch[J]. arXiv preprint arXiv:14117923, 2014, |
| [7] | TURK M, PENTLAND A. Eigenfaces for recognition[J]. Journal of Cognitive Neuroscience, 1991, 3(1): 71-86. DOI: 10.1162/jocn.1991.3.1.71. |
| [8] | BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection[M]. Berlin: Springer, 1996. |
| [9] | BARTLETT MS, MOVELLAN JR, SEJNOWSKI T J. Face recognition by independent component[J]. Neural Networks IEEE Transactions on, 2002, 13(6): 1450-1464. DOI: 10.1109/TNN.2002.804287. |
| [10] | TIMO A, ABDENOUR H, MATTI P I. Face description with local binary patterns: application to face recognition[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2006, 28(12): 2037-2041. |
| [11] | 高绪伟. 核PCA特征提取方法及其应用研究[D]. 南京: 南京航空航天大学民航学院, 2009. |
| [12] | 刘晓亮, 王福龙, 黄诚, 等. 一种加权的核Fisher鉴别分析在人脸识别中的应用[J]. 广东工业大学学报, 2009, 26(4): 65-69. |
| [13] | CHEUNG B. Convolutional neural networks applied to human face classification[C]//Machine Learning and Applications (ICMLA), 2012 11th International Conference on. Boca Raton, FL: IEEE, 2012: 580-583. |
| [14] | SUN Y, WANG X, TANG X. Deep learning face representation from predicting 10, 000 classes[C]// Proceedings of the Computer Vision and Pattern Recognition (CVPR), 2014 IEEE Conference on, Columbus, OH:IEEE, 2014. |
| [15] | SUN Y, WANG X, TANG X. Hybrid deep learning for face verification[C]//Proceedings of the 2013 IEEE International Conference on Computer Vision. Sydney, NSW: IEEE, 2013: 1489-1496. |
| [16] | RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI: 10.1126/science.1242072. |
| [17] | HUBEL D H, WIESEL T N. Receptive fields, binocular interaction and functional architecture in the cat′s visual cortex[J]. Journal of Physiology, 1962, 160(1): 106-154. DOI: 10.1113/jphysiol.1962.sp006837. |
| [18] | WU X. Learning Robust Deep Face Representation[J]. arXiv preprint arXiv:150704844, 2015. |
| [19] |
蔡正, 王福龙, 徐爱辉. 一种新的图像距离在人脸识别中的应用[J].
广东工业大学学报, 2010, 27(3): 64-67.
CAI Z, WANG F L, XU A H. A new distance applied in face recognition[J]. Journal of Guangdong University of Technology, 2010, 27(3): 64-67. |
| [20] | 李应安. 基于MapReduce的聚类算法的并行化研究[D]. 广州: 中山大学信息科学与技术学院, 2010. |
| [21] | KAZEMI V, SULLIVAN J. One millisecond face alignment with an ensemble of regression trees[C]// Computer Vision and Pattern Recognition, 2014 IEEE Conference on Columbus, OH: IEEE, 2014: 1867-1874. |
 2016, Vol. 33
2016, Vol. 33

