2. 建峰索具有限公司,广东 广州 511356
2. Jianfeng Sling Co., Ltd., Guangzhou 511356, China
索具作为起重机械伸缩臂的关键部件,牵引着伸缩臂的平稳升降,是保证起重机械正常工作重要的一环.相比单根钢丝绳索具而言,在承受同等载荷下,单根钢丝绳索具需要配备直径较大的钢丝绳,占据较大的机构空间,难以满足工程起重机械伸缩臂灵活运行的要求.采用绳排索具的工程起重机械无论是在伸缩臂空间占有比,还是在灵活度、承载能力、使用寿命等方面均较有优势.但是,由于起重机械在使用过程往往需要承受交变载荷及恶劣使用环境等因素的影响,绳排索具力学性能的好坏及疲劳寿命的长短成为影响起重机械正常作业的重要因素[1-2].
国外发达国家的索具工业有两百多年的历史,已经具备了完善的设计、生产制造和检验标准,并且在索具钢丝绳相关方面进行了深入的研究.Drucker和Tachau[3]通过对实验数据的分析,得出了钢丝绳设计准则;Beretta[3]提出了预测钢丝绳疲劳寿命的方法.而国内索具工业正处于行业导入期,相关研究方面极其有限.谷海涛等对起重用钢丝绳进行了受力分析及疲劳寿命估算;李超等[4-5]对索具用浇铸接头整体锻造工艺进行了深入分析.
目前在索具研究方面,针对钢丝绳的研究较多,而对索具整体建模与性能的研究却颇少.本文拟在研究绳排索具整体实体建模的基础上,运用有限元法分析绳排索具应力分布及其疲劳寿命变化规律,希望能为绳排索具的可靠设计、优化改进、寿命预测等方面提供一定的参考.
1 索具钢丝绳建模与力学特性分析本文研究的绳排索具由钢丝绳组、索节、销轴以及浇注合金4部分组成,其中,钢丝绳与索节是影响整个绳排索具正常使用的关键部件.该索具拟选用6×7+IWS型钢丝绳,故首先单独对钢丝绳相关方面进行研究,为绳排索具钢丝绳的选用提供参考.
1.1 钢丝绳的结构特点与几何建模6×7+IWS型钢丝绳属于金属捻线制品,具有受力均匀、制造简单、使用寿命长的特点,在工程起重机械领域应用广泛.其中,6×7代表围绕绳芯共6股,每股含7根钢丝,IWS代表是独立钢芯结构.
钢丝绳的捻制方式有同向捻及交互捻两种方式,故本文将首先研究两种情况下钢丝绳应力相关情况,从而为钢丝绳的选用提供依据.根据钢丝绳独有的空间螺旋结构,基于Solidworks三维建模平台,对6×7+IWS型两种捻制方式的钢丝绳进行三维实体建模,材料类型为carbon steel,其他参数见表 1.
| 表 1 钢丝绳相关参数 Table 1 Parameters of wire rope |
为建立钢丝绳有限元分析模型,首先对钢丝绳进行网格划分.考虑到钢丝绳空间结构的特殊性,基于Ansys-workbench平台对钢丝绳采用扫掠法进行网格划分,建立钢丝绳有限元分析模型(见图 1).接着对该有限元模型一端施加100 MPa轴向集中力作为工作载荷,另一端约束3个方向自由度作为约束条件,求解可得到其应力分布情况如图 2所示.

|
图 1 不同捻制方式钢丝绳实体模型 Figure 1 The entity model of steel wire ropes with different lay direction |

|
图 2 右同向捻钢丝绳网格划分及应力场分布图 Figure 2 The result of meshing and section stress field distribution of the steel wire rope with right hand lang's lay way |
同样,可对交互捻钢丝绳进行应力分布情况进行分析.通过应力分析结果发现:在轴向载荷的作用下,同向捻钢丝绳的最大接触应力为250.2 MPa,而交互捻钢丝绳最大接触应力则为220.5 MPa,比同向捻要低12%,且最大应力均分布于侧丝与芯丝接触处.因此,本设计选用右交互捻6×7+IWS型钢丝绳作为绳排索具用钢丝绳的选用对象.
2 绳排索具整体建模及力学特性分析 2.1 索节结构设计与索具整体有限元建模索节是绳排索具设计的主要部件,结构参数设计的合理程度将直接影响索具的正常使用.根据前文选用的钢丝绳,设计的索节主要结构参数如下:销轴孔直径为46.5 mm,壁厚为14 mm,销轴孔中心离最底端距离为190 mm,且根据工程应用要求,关键结构参数内锥角取10°~22°范围内,现初步拟取为14°,外锥角为确定值6°,结构示意图如图 3所示.

|
图 3 索节基本尺寸示意图 Figure 3 The basic size of the funiculus |
在通用场合下,伸缩臂式起重机采用配备6根钢丝绳的绳排索具,故论文对索具整体建模时作如下处理:将钢丝绳简化为同等直径大小的6根圆柱体,直径大小均为13.5 mm,钢丝绳组与内部的浇注合金视为一个整体与采用放样切除法建立的索节进行装配,上端孔处装配直径大小为46.5 mm的销轴,从而得到绳排索具的简化分析模型.
通过三维参数化建模软件Solidworks与有限元分析软件Ansys的无缝对接,将建立的绳排索具分析模型导入到Ansys-workbench分析平台.基于该平台的mesh模块,将Element Size设置为0.2 mm,划分网格后得到绳排索具有限元分析模型.具体过程如图 4所示.

|
图 4 绳排索具有限元分析模型建立过程 Figure 4 The process of building the finite element model of the funiculus |
为得到索节在受载状态下的力学特性及变形分布情况,首先对该实体模型整体进行应力及变形分析.根据实际工况下受载情况,对绳排索具销轴处3方向自由度进行约束,另一端施加100 MPa竖直向下的集中力作为模型的边界条件,且材料类型统一为carbon steel,设置浇注体与索节之间的接触类型为No separation.取中间剖面观察其应力分布及总体受载变形情况,具体分析结果如图 5所示.
|
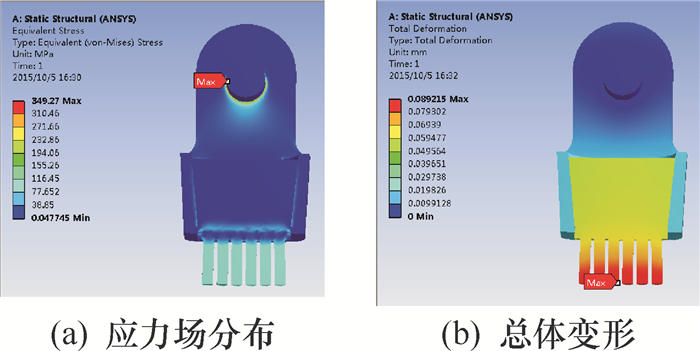
图 5 索节装配体应力场分布及总体变形 Figure 5 Stress distribution and total deformation of the funiculus |
通过有限元仿真结果可以看出,索节的最大应力为349.27 MPa,分布于上部销轴与销轴孔接触处;索节总体变形分布在索节下端锥体部分,为0.03 mm左右.其中,内锥角作为索节内腔的主要结构设计参数,影响着整个索具的承载能力,需重点进行研究.为探讨出符合工程应用的最佳索节内锥角,在外锥角及壁厚一定的情况下,分别对比分析索节内锥角为10°、12°、14°、16°、18°、20°、22°时应力分布及总体变形情况.根据有限元仿真分析结果,绘制出索节的最大接触应力与索节内锥角关系曲线以及最大变形量与内锥角关系曲线图(见图 6).

|
图 6 不同内锥角下索节最大接触应力及变形量分布图 Figure 6 The maximum contact stress and deformation of different internal cone angle of the funiculus |
通过曲线分布情况可知,当索节内锥角为12°时,索节的最大接触应力为325.2 MPa;当内锥角为16°时,其最大接触应力仅为303.4 MPa;而当索节的内锥角大于16°以后,索节的最大接触应力基本都大于355 MPa.在索节外锥角及壁厚一定的情况下,内锥角为16°时索节承受的最大接触应力最小;随着索节内锥角的变化,其最大变形量保持在0.025~0.03 mm范围内变化,变动量仅为0.005 mm,未见明显波动.故绳排索具索节的变形总体比较稳定,索节内锥角在一定的范围内变动将不会对其最大变形量有较大的影响.
综合考虑绳排索具索节的最大接触应力及变形量可知,索节的最佳内锥角为16°时可明显改善索节的应力特性,有利于提升索具的承载能力.
3 绳排索具疲劳寿命分析研究根据工程应用实际,绳排索具在工作过程中不仅要保证足够的承载能力,疲劳寿命也是影响索具正常工作的重要因素.根据图 2、图 5分析结果可知,钢丝绳丝与丝之间的接触部分为整个索具的应力强度最薄弱部分,故钢丝绳是整个索具易于发生疲劳破坏的部位,需重点对钢丝绳疲劳寿命特性进行研究.
疲劳分析的基本方法包括基于S-N曲线的疲劳损伤法、寿命估算法以及断裂力学法3种.其中,S-N曲线疲劳损伤法是钢丝绳疲劳分析中应用最为广泛的方法[6-10].
S-N曲线表示结构的应力幅值与其能承受的应力循环次数之间的关系.在一定的应力波动范围内,结构存在一个理论循环次数,当达到甚至超过理论循环次数时,结构便会发生疲劳失效[11-13].通常把许用循环次数N和应力范围S之间的关系用S-N曲线来表达,且S-N曲线的一般表达式为
| $ {N_r} = AS_r^{ - m}, $ | (1) |
式中, Sr表示应力的波动范围,Nr表示应力的循环次数,A和m均为疲劳试验常数.
特殊情况下,对于双斜率S-N曲线,当S≤SQ时,为公式(1) 所示;当S≥SQ时,表达式为
| $ {N_r} = CS_r^{ - r}, $ | (2) |
此处,SQ表示应力幅值极限;C和r均由疲劳试验确定其值大小[14-15].
本研究将基于S-N曲线基本理论,对选用的右交互捻6×7+IWS型钢丝绳疲劳寿命特性进行研究.首先,在前面右交互捻钢丝绳应力分析基础上,在Ansys-workbench平台插入疲劳分析模块,并设置载荷比例为3,比例因子设为1,交变循环次数为106次.通过仿真平台分析可得出钢丝绳疲劳寿命分布云图如图 7所示.

|
图 7 右交互捻钢丝绳疲劳寿命云图 Figure 7 Fatigue life distribution of the steel wire rope with right hand ordinary lay way |
根据疲劳寿命分布云图可以看出,在捻距、承受应力一定的情况下右交互捻钢丝绳疲劳寿命最小值为11 709次(即可承受应力循环次数),且最小值发生于钢丝绳芯股与侧股丝与丝接触处.而根据钢丝绳S-N曲线理论可知该钢丝绳的理论循环次数为15 502次,远远大于钢丝绳疲劳寿命最小值,不会发生疲劳失效.因此,在应力一定的情况下,由于最易发生疲劳破坏的钢丝绳疲劳寿命次数远小于其理论值,故绳排索具的疲劳寿命可满足伸缩臂式起重机的使用要求,论文设计的绳排索具具有一定的实用价值.
4 结论(1) 通过三维参数化设计软件平台Solidworks采用放样切除法设计出一种具有良好力学性能的新型楔腔形索节结构.
(2) 楔腔形索节的应力最大部位发生在上端销轴与销轴孔接触处,且最大接触应力与索节内锥角有很大的关联,在外锥角及壁厚一定的情况下,内锥角为16°时,索节承受的接触应力最小.
(3) 在楔腔形索节的外锥角及壁厚一定的情况下,索节的总体变形主要发生在下端锥体部分,且内锥角在一定范围内变动不会对索节总体变形造成大的影响.
(4) 在捻距一定的情况下,6×7+IWS型钢丝绳交互捻比同向捻钢丝绳能承受最大应力要大,可作为绳排索具优先选用的对象;一定应力条件下,交互捻钢丝绳承受应力循环次数远远小于钢丝绳理论值,能满足伸缩臂式起重机用绳排索具的疲劳寿命要求.
| [1] | 张玖.多级伸缩臂油缸钢丝绳同步伸缩结构动静态特性研究[D].哈尔滨:哈尔滨工业大学机电工程学院, 2009. |
| [2] |
石鹏飞, 刘志斌, 徐国荣. 登高平台消防车臂架伸缩机构设计研究[J].
制造业自动化, 2011, 33(10): 123-127.
SHI P F, LIU Z B, XU G R. Design and research for the arm flexible body of hydraulic platform fire[J]. Manufacturing Automation, 2011, 33(10): 123-127. DOI: 10.3969/j.issn.1009-0134.2011.5(B).37. |
| [3] | 浦汉军.起重机用不旋转钢丝绳理论研究及其寿命估算[D]. 广州:华南理工大学机械与汽车工程学院, 2012. |
| [4] | 谷海涛.起重机用钢丝绳受力分析及疲劳寿命估算研究[D]. 太原:太原科技大学机械工程学院, 2013. |
| [5] | 李超.索具用浇铸接头(BJ40)整体锻造工艺研究[D]. 石家庄:河北科技大学材料科学与工程学院, 2013. |
| [6] | 许津豪.自升式平台桩腿动力响应与疲劳分析研究[D].广州:华南理工大学土木与交通学院, 2014. |
| [7] |
何柏林, 王斌. 疲劳失效预测的研究现状和发展趋势[J].
机械设计与制造, 2012(4): 279-281.
HE B L, WANG B. Research status and development trend of fatigue failure prediction[J]. Machinery Design & Manufacture, 2012(4): 279-281. |
| [8] | DA G W, DE K Z, SONG Q W. Finite elements analysis of hoisting rope and fretting wear evolution and fatigue life estimation of steel wires[J]. Engineering Failure Analysis, 2013(27): 173-193. |
| [9] | FONTANARI V, BULF U, BENEDETTI M. Numerical analysis of the rolling process of shaped wires for locked steel ropes[J]. Journal of Materials Processing Technology, 2005, 170: 97-107. DOI: 10.1016/j.jmatprotec.2005.04.088. |
| [10] |
刘燕龙, 原玲. 基于Calculix的船舶疲劳强度并行计算方法研究与应用[J].
广东工业大学学报, 2015, 32(4): 77-82.
LIU Y L, YUAN L. Parallel mechanism research and application research and application of calculix in ship fatigue analysis environments[J]. Journal of Guangdong University of Technology, 2015, 32(4): 77-82. |
| [11] |
吕文阁, 骆少明. 基于疲劳短裂纹扩展条件的疲劳极限估算方法[J].
广东工业大学学报, 2005, 22(4): 31-34.
LYU W G, LUO S M. A method for determining fatigue limit based on the analysis of propagation condition of short fatigue crack[J]. Journal of Guangdong University of Technology, 2005, 22(4): 31-34. |
| [12] | RAOOF M, HOBBS R E. Analysis of axial fatigue data for wire ropes[J]. International Journal of Fatigue, 1994, 16(7): 493-501. DOI: 10.1016/0142-1123(94)90200-3. |
| [13] | GIGLIO M, MANES A. Bending fatigue tests on a metallic wire rope for aircraft rescue hoists[J]. Eng Fail Anal, 2003, 10(2): 223-235. DOI: 10.1016/S1350-6307(02)00043-2. |
| [14] | 张惠波.提升钢丝绳几何特性及有限元分析研究[D].沈阳:辽宁工程技术大学机械工程学院, 2011. |
| [15] | SCHREMS K K, DOGAN C P, HAWK J A. Wear mechanisms in a nonrotating wire rope[J]. Journal of Materials Engineering and Performance, 1995, 4(2): 136-144. DOI: 10.1007/BF02664106. |
 2016, Vol. 33
2016, Vol. 33