2. 中山大学 信息科学与技术学院,广东 广州,510006
2. School of Information Science and Technology, Sun Yat-sen University, Guangzhou 510006, China
复杂网络是互联网、基础物理设施网、社交网络等的抽象,级联故障研究是其中一项重要课题.以电力系统为例:电力系统是社会生产和人民生活的物质基础设施,关系着整个国民经济命脉.电力系统由大量超高压设备和电子元件通过大规模的线路连接,电子元件在运行中因各种因素的相互制约,导致电力系统的运行过程异常复杂.现实的数次大规模停电事故,大多是由少数初始节点发生故障,然后通过节点的连接关系迅速地引起其他节点发生故障,连锁效应导致整个电力系统的崩溃,我们称之为级联故障[1-3].
复杂网络的级联故障机制和演化特性造成的复杂性使得级联故障研究面临着巨大挑战.文献[2]首次引入容量和负载的概念,提出经典的负载容量ML模型,指出一个或若干节点失效即可导致网络的整体故障,网络对级联故障的抵制能力相当弱.文献[3]率先对无标度网络的故障进行研究,发现无标度网络对随机故障鲁棒、对恶意攻击脆弱,并指出根源在于无标度网络中度分布的非均匀性.文献[4]在研究欧洲电力网络和路由器自治网络故障基础上,通过随机交换节点边的策略有效地提高网络的鲁棒性.文献[5]研究加权无标度网络的级联故障,其将节点的初始负载表示为节点度的函数形式.文献在构建故障模型的初始负载时考虑节点本身以及邻居节点.文献从宏观上研究了社团对网络整体抗毁性的影响.
目前的级联故障研究,大多关注节点本身或节点的简单邻居关系,已有的社群角度研究也较宏观不够细致.本文认为故障节点引发的级联故障是节点所处社群的内外因共同作用的结果.随着网络性质的深入研究,发现许多实际网络具备社群性质,即整个网络由若干群构成,群内部的节点连接相对紧密,而群之间的连接相对稀疏[10-11].目前,社群分析已经在生物学、物理学、计算机图形学和社会学中广泛应用.同时,经典的ML模型依据容忍系数对全部节点同等程度地提高容量,从而提高抵制故障的能力.基于此,本文所提的级联故障CML模型(Commuinity with ML)考虑社群结构对电网级联故障的影响,CML模型中节点的社群内外邻居对节点施加不同权重的影响.
1 级联故障抵制模型 1.1 社群结构社群划分一般采用分级聚类的方法,依据是否移除边的思想大体分为凝聚法和分裂法两大类[12-13].本中采用凝聚法中经典的louvain社群划分算法[14],其划分结果可靠且效率较高,满足大数据集的要求.louvain算法采用式(1) 模块度指标Q,通过不断压缩探测社群的规模,以达到社群的快速划分目的.
| $ Q=\frac{1}{2m}\sum\limits_{u, w}{\left[{{A}_{uw}}-\frac{{{k}_{u}}{{k}_{w}}}{2m} \right]\delta \left( {{c}_{u}}, {{c}_{w}} \right)}\cdot $ | (1) |
其中,m为网络总边数,A为网络的邻接矩阵,Auw=1表示节点u和w有边,否则无边;ku为节点u度,cu为节点u所在社群,当u和w位于同一社群,则δ(cu, cw)=1,否则为0.
本文对网络的社群划分过程分为两个阶段:
第一阶段:初始化网络的所有节点为N个社团;计算节点u加入邻居节点w所在社团后的模块度增量ΔQ,并将u加入ΔQ最大的社团中,若ΔQ非正值,则节点u不移动;遍历所有节点判断是否存在需移动节点,若无则遍历结束且开始第二阶段,否则重复上一步.
第二阶段:依据第一阶段结果,将社团内的全部节点视作一个新节点,新节点之间的权值为原节点间的权值之和;迭代第一阶段的模块度增量的计算方法,直至网络稳定.
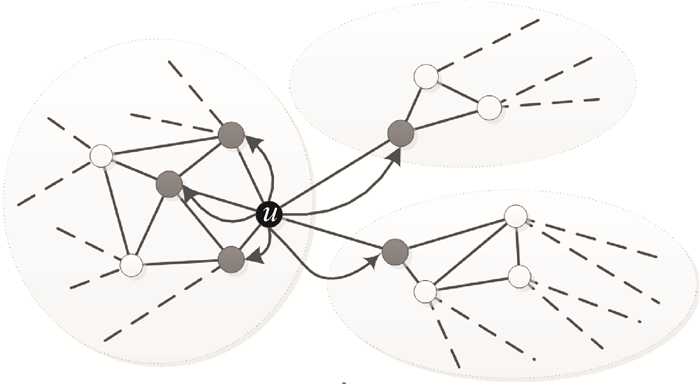
1.2 建立级联故障抵制模型首先,本文定义社群边界节点为连接2个或2个以上社群的节点,即社群边界节点的邻居节点至少分布在2个以上社群中(具体计算依据社群划分后的节点社群属性).文中所提级联故障抵制模型中,节点的级联故障的影响力来源节点社群内外属性共同作用的结果,依据节点的社群特性,赋予节点容量不同的社群容量附加值.考虑社群的特性,可以形象地将社群间的边界节点视作“门”,则进出不同的社群均需通过该“门”.基于此,在社群内节点的容量保持不变的情况下,可以仅仅通过对社群边界节点的容量附加二次容忍值,以提高抵制社群外(内)故障的能力,达到保护社群内(外)部的节点,同时降低抵制成本.图 1是级联故障发生时的负载重分配示意图,图中存在3个社群,节点u的5个邻居节点中有2个位于其他社群中,直观上我们发现节点u作为“防火墙”节点可以有效地阻隔社群外的故障干扰(u为社群边界节点);换一个角度,若u作为“引爆点”却可以引发社群内外的大规模的级联故障.在此,前文暂时主要考虑前一种情况,后一种情况在后文补充说明.
|
图 1 考虑社群结构的级联故障的负载重分配 Figure 1 Load redistribution of cascading failures considering community structure |
在现实不同网络中,节点负载一般与经过该节点的最短路径数目有关,因此可以定义节点u的初始负载为节点介数的函数式:
| $ {{L}_{u}}=~b_{u}^{\alpha }\cdot $ | (2) |
其中bu为节点u的介数,α>1为可调参数,控制着节点初始负载的强度.
节点u的容量Cu在经典的ML模型中与初始负载Lu存在线性关系[15-17],即Cu=(1+T)Lu.本文在ML模型基础上依据节点的社群属性对节点容量附加不同的二次容忍值,定义为
| $ {C_u}=\left( {1 + T} \right){L_u} + S\sum\nolimits_{_{m \in {\mathit{\Gamma }_u}}} {{L_m}} \cdot $ | (3) |
其中,Γu为节点u的社群外邻居节点的集合;常量1≥T≥0为网络的容忍系数(相应成本在本文也称一次容忍值),0≥S≥1为CML模型中新增的二次容忍系数,用以调节社群边界节点的容量附加值幅度.显然,T和S越大,网络抵制故障能力越强,但抵制成本也越高.当S=0,CML模型退化成经典的ML模型.
一旦某节点发生故障,该节点的负载将重分配,定义故障节点u的β%的负载依照式(4) 分配到邻居节点上.
| $ {\mathit{\Pi }_w}=\frac{{{C_w}}}{{\sum\nolimits_{_{m \in {\mathit{\Gamma }_u}}} {{C_m}} }} \cdot $ | (4) |
其中,Γu为故障节点u的邻居节点集合.因此,节点u故障后分配给节点w的负载为ΔLuw=βΠwLu,其中β用以调节故障节点传递给邻居节点的负载大小.
故障节点的邻居节点接收额外负载,若Lw+ΔLuw>Cw,则节点u的邻居节点w因总负载大于所能承受的容量,节点w级联失效,相应的负载进一步迭代分配给w的邻居节点.
本文需要一个量化指标用以评估级联故障的崩溃规模.假设级联故障的初始节点为u,级联故障结束时的故障节点总数为CFu,则归一化衡量网络故障崩溃规模的指标[18]为:
| $ {\rm{C}}{{\rm{F}}_N}=\sum\nolimits_{m \in h} {\frac{{{\rm{C}}{{\rm{F}}_m}}}{{{N_h}\left( {N - 1} \right)}}}, $ | (5) |
其中h为初始故障节点的集合.
最后,抵制故障所耗成本也是评估模型优劣的指标之一,故本文新定义成本为网络总容量与总负载的差值占总负载比例,即
考虑到不同类型的网络具备不同的拓扑结构,从而对模型的仿真结果产生影响,本文选择了2类不同的电力网络(IEEE标准电网、广东某电网),以求仿真结果的普适性.表 1是网络的拓扑性质.显然,网络直径普遍较小,说明网络满足“小世界”效应[14-19].大部分网络的模块度值较高,说明网络的社群结构明显[14].同时,本文计算了各个网络的社群边界节点数目占全部节点的比例, IEEE标准电网为30.5%,广东某电网为19.6%,这说明社群边界节点只占总节点的小部分,表明较ML模型等对全部节点扩容以提高抵制故障能力而言,CML模型选取部分社群边界节点扩容可以有效地降低选取目标节点数目.
| 表 1 不同网络的拓扑性质 Table 1 Topological properties of different networks |
运行状态的网络在遭受干扰(或攻击)的几秒或几分钟内,系统中某些节点的负载会产生较大幅度的变化,进而连锁破坏网络系统的完整性.一般情况下,节点的重要性与自身的度值成正比,故本文攻击网络的度大节点模拟大干扰,攻击度小节点模拟小干扰.其中,文中的干扰策略获取的故障结果为通过100次不同仿真结果取均值,仿真平台采用Python与Networkx(不失一般性,令α=1,β=100).
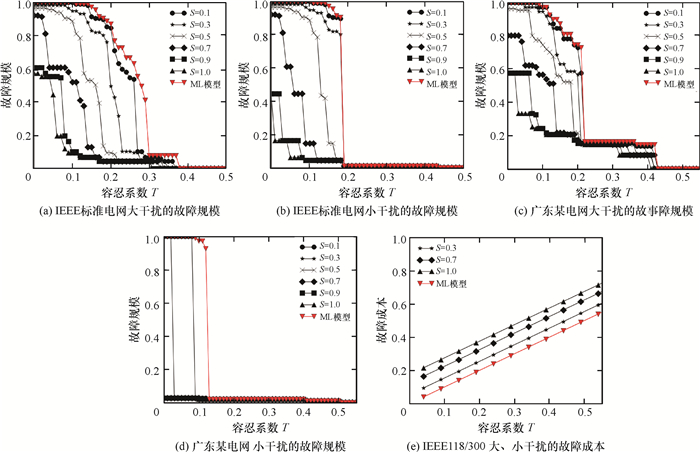
图 2所示为IEEE标准电网的级联故障仿真结果.首先,如果曲线越倾斜于左下方,说明网络抵制故障的能力越强,且成本越低.显然,IEEE标准电网在T和S均较小时,由于电网中全局节点的容量均很小,任意节点均没有足够的容量抵制额外的负载,故微小的扰动也可以导致电网全部瘫痪.在T大于等于某一临界值Tc时(下文统一称之“关键阈值”),即T≥Tc,即便不考虑S,网络中每个节点的容量已然足够大,任意节点的故障均不会导致级联故障,电网基本保持完整;而T < Tc时, CFN突然增大,级联故障发生.从图 2可知,对大干扰而言,关键阈值Tc≈0.4,对小干扰而言Tc≈0.2(或0.25).
|
图 2 IEEE标准电网的级联故障仿真结果 Figure 2 Cascading failures simulation results of IEEE standard grid |
分析T < Tc的情形:图 2(a)对应的IEEE标准电网的大干扰中,假设T∈(0,0.3),随着S的增大,故障规模逐渐下降;再令T=0.1,通过对30.5%的社群边界节点容量附加二次容忍值,在S≈0.7左右时,故障规模约为50%;分析成本图形2(e),其抵制成本为20%左右.对比经典的ML模型,同样将故障规模降到50%,成本需提高至35%左右,且扩容的对象是全部节点.图 2(b)说明IEEE标准电网抵制小干扰效果更好.值得注意,IEEE标准电网中,当S大于一定值时,即便T为0,电网络仍具备较强的故障抵制能力(此时,所有节点均不考虑一次容忍值,仅社群边界节点附加二次容忍值).广东某电网具备相同的性质.
总的来说,在可调的T和S参数下,小干扰对应的安全阈值Tc较小,触发的级联故障规模能更快地收敛到稳态.安全阈值通常小于0.4,不区分网络类型和干扰类型,级联故障抵制的成本最大不会超过50%.
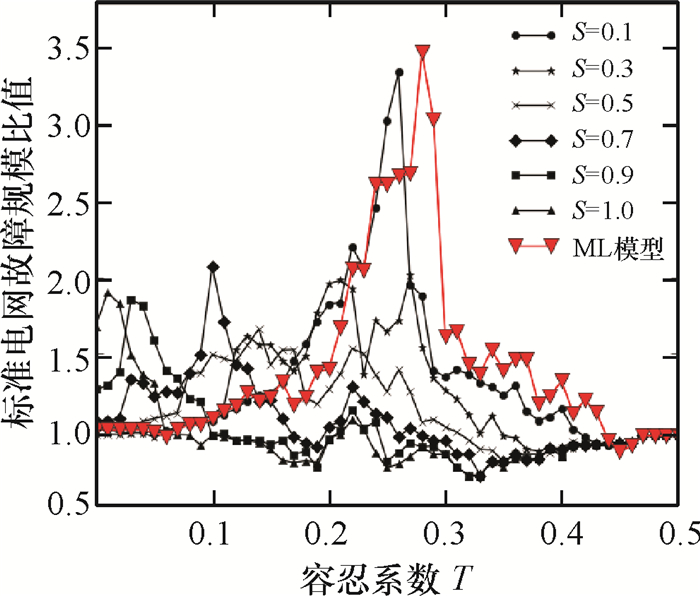
2.3 社群边界节点与内部节点触发级联故障规模的比较在前文中,本文仅对特定节点(最大度节点或最小度节点)进行级联故障仿真并分析.为了更好地评估整体网络的抵制级联故障能力,本文同样选择IEEE标准电网对全部节点迭代仿真级联故障,并将节点分成社群边界节点和内部节点两大类,对同一类中的节点导致的故障规模取均值,并定义CFdiff=CFbou/CFint为社群边界节点平均故障规模与社群内部节点平均故障规模的比值,结果如图 3所示.显然,在同等参数条件下,CFdiff越大,相对社群内部节点而言,社群边界节点引发故障的能力越大.
|
图 3 社群边界节点与内部节点的平均故障规模比 Figure 3 Difference of average failures between community boundary nodes and internal nodes |
从图 3中观察到,平均故障规模比值在参数T下具有“峰值现象”.首先,经典的ML模型中,单纯地提高节点的容量,虽然可以提高节点抵制故障的能力[2],同时也会造成某些社群边界节点成为“引爆点”,一旦故障发生在此类节点,破坏程度比一般节点严重.其次,“引爆点”存在阈值,T过高或过低均不会触发,ML模型中T≈0.3.CML模型虽同样存在该问题,但是通过调节S,一定程度可以减弱“峰值现象”,从而降低社群边界节点成为“引爆点”的可能性.分析大小干扰策略、成本和社群边界与内部节点的平均故障差,笔者认为当T∈(0,0.2),S∈(0.5,0.8),可以在成本可控的前提下,降低不同干扰造成的故障规模,同时降低社群边界节点“引爆”的可能性(具体的T和S依据不同的网络而定).最后,留意该处“峰值”与前文中网络的安全阈值存在关系,即安全阈值对应参数下,社群边界节点的引发故障能力同样也是最强的.
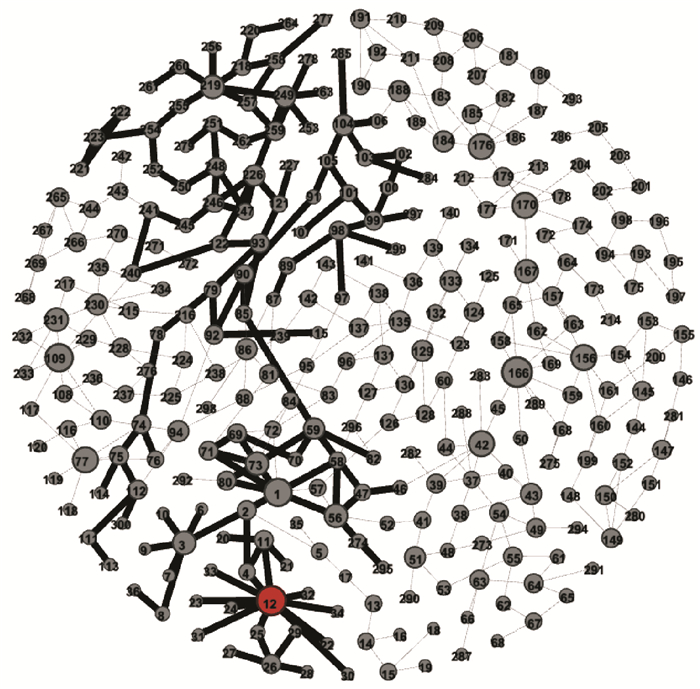
2.4 级联故障的网络可视化通过图形化的方式,可以更好地帮助我们理解级联故障的内在连锁机制.令T=0.1、S=0.85,图 4为攻击IEEE标准电网的最大度节点(编号12,度为11,用红色标记)导致的级联故障效果图,黑色粗边相连的节点表示已失效.从图中可知,一旦某一节点失效,则会演化为“引爆点”,大规模地引发全局雪崩.
|
图 4 IEEE标准电网的级联故障可视化过程 Figure 4 Visualization of cascading failures of IEEE grid |
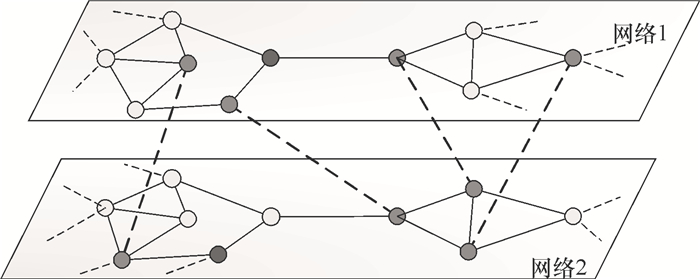
为了验证本文所提CML模型的普适性,笔者将研究对象由单一网络推广到多层耦合网络,即相依网络.目前不同系统之间的交互性大大增强,系统或网络构成的相依网络对干扰的抵制相当脆弱.文献[20-21]提出一种相依网络构建方案,即对两个具有相同节点数目的网络进行网络间的节点一对一随机连接,最后构建的相依网络的节点总数为原先两个网络节点数之和,如图 5所示.依据该思想,本文选择广东某电网进行耦合,将单个网络耦合成两层网络,构建相依网络.表 2为耦合网络的拓扑性质.由于耦合网络的构建采用节点一对一随机连接,在一定程度上这种构建方式不利于社群结构的形成,故构建的耦合网络的社群结构不明显,模块度较低,社群边界节点数目较多.
|
图 5 多层耦合网络构建示例图 Figure 5 Construction of multilayer coupled network |
| 表 2 耦合网络的拓扑性质 Table 2 Topological properties of coupled networks |
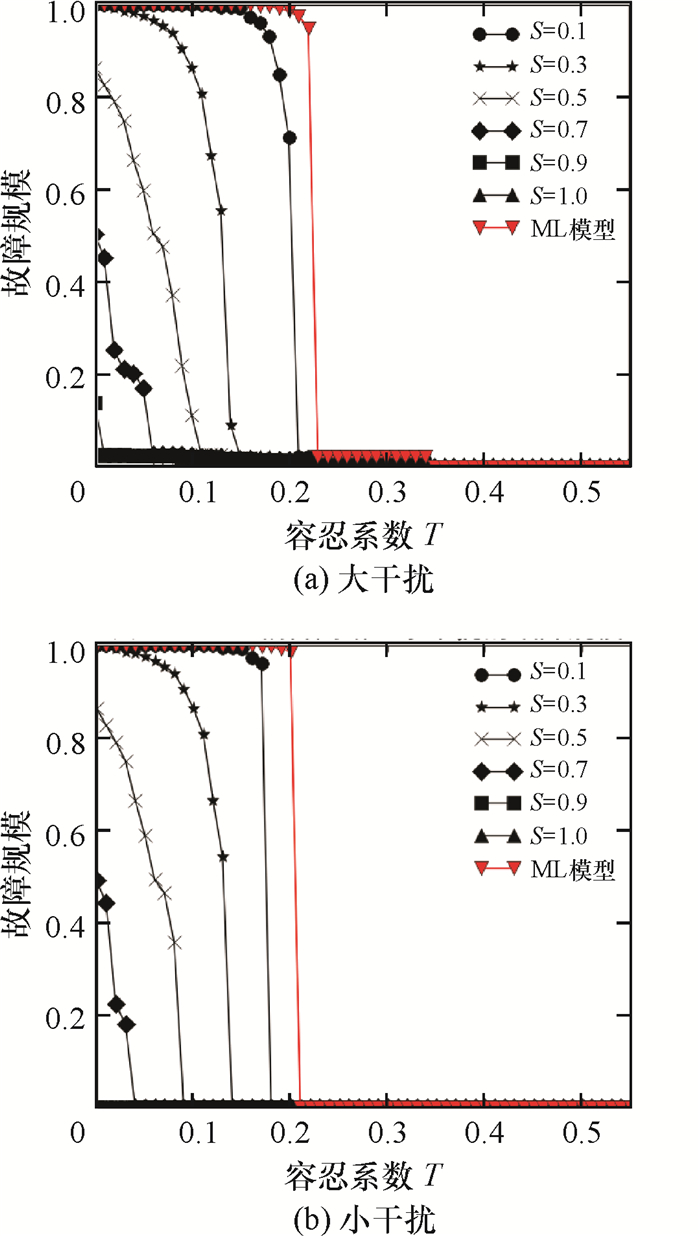
图 6为广东耦合网络的大干扰和小干扰仿真结果.从图中可知干扰策略对耦合网络的故障结果与单一网络显著不同.一方面,在可调参数范围内,耦合网络的抵制故障性能更早地收敛到极大.ML模型下,耦合网络更加脆弱,关键阈值Tc≈0.2成为“绝对”临界点,网络或崩溃或完整.另一方面,CML模型中,在可调参数下,随着S的增大,故障规模逐渐减小.值得注意的一点,CML模型中,耦合网络的关键阈值Tc不是近似的固定常量,即不同网络的关键阈值均随S的不同而不同,说明CML模型对于耦合网络同样具备较好的抵制故障能力.耦合网络的成本图形同样和前文中的单层网络类似.
|
图 6 耦合网络的级联故障仿真结果 Figure 6 Cascading failures simulation results of coupled network |
复杂系统中结构复杂、节点众多,某一节点的失效会“雪崩式”干扰整个网络系统,故障发生的快速性和全局性导致相关研究较难准确把握.本文通过在IEEE标准电网和真实的电网引入介于宏观和微观的中观特性—社群结构,对于了解网络的级联故障具有积极作用.
实验仿真表明,CML级联故障抵制模型对单一网络和耦合网络均有较好的抵制故障能力,且可以降低经典ML模型中社群边界节点成为“引爆点”的可能性.社群边界节点的特殊性决定其“抵制”又“级联”的双重特性,即抵制故障却又能触发级联故障,一定程度取决于初始故障节点所处社群位置和合适的模型参数.
| [1] | HOLME P, KIM B J, YOON C N, et al. Attack vulnerability of complex networks[J]. Physical Review E, 2002, 65(5): 056109. DOI: 10.1103/PhysRevE.65.056109. |
| [2] | MOTTER A E, LAI Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102. DOI: 10.1103/PhysRevE.66.065102. |
| [3] | CRUCITTI P, LATORA V, MARCHIORI M, et al. Error and attack tolerance of complex networks[J]. Physica A:Statistical Mechanics and its Applications, 2004, 340(1): 388-394. |
| [4] | SCHNEIDER C M, MOREIRA A A, ANDRADE J S, et al. Mitigation of malicious attacks on networks[J]. Proceedings of the National Academy of Sciences, 2011, 108(10): 3838-3841. DOI: 10.1073/pnas.1009440108. |
| [5] | WU Z X, PENG G, WANG W X, et al. Cascading failure spreading on weighted heterogeneous networks[J]. Journal of Statistical Mechanics:Theory and Experiment, 2008, 2008(05): P05013. |
| [6] | WANG J W, RONG L L. A model for cascading failures in scale-free networks with a breakdown probability[J]. Physica A:Statistical Mechanics and its Applications, 2009, 388(7): 1289-1298. DOI: 10.1016/j.physa.2008.12.067. |
| [7] | YU K, RONG L L, WANG J W. A new attack on scale-free networks based on cascading failures[J]. Modern Physics Letters B, 2009, 23(20): 2497-2505. |
| [8] |
丁超, 姚宏, 杜军, 等. 基于社团划分的复杂网络级联抗毁攻击策略[J].
计算机应用, 2014, 34(6): 1666-1670.
DING C, YAO H, DU J, et al. Cascading invulnerability attack strategy of complex network via community detection[J]. Journal of Computer Applications, 2014, 34(6): 1666-1670. |
| [9] |
李浩敏, 杜军, 彭兴钊, 等. 蓄意攻击下一类多社团网络级联抗毁性研究[J].
计算机应用, 2014, 34(4): 935-938.
LI M H, DU J, PENG X Z, et al. Research on cascading invulnerability of community structure networks under intentional-attack[J]. Journal of Computer Applications, 2014, 34(4): 935-938. |
| [10] | FLAKE G W, LAWRENCE S, GILES C L, et al. Self-organization and identification of web communities[J]. Computer, 2002, 35(3): 66-70. DOI: 10.1109/2.989932. |
| [11] | ADAMIC L A, ADAR E. Friends and neighbors on the web[J]. Social Networks, 2003, 25(3): 211-230. DOI: 10.1016/S0378-8733(03)00009-1. |
| [12] | NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E, 2004, 69(6): 066133. DOI: 10.1103/PhysRevE.69.066133. |
| [13] | GIRVAN M, NEWMAN M E J. Community structure in social and biological networks[J]. Proceedings of the National Academy of Sciences, 2002, 99(12): 7821-7826. DOI: 10.1073/pnas.122653799. |
| [14] | BLONDEL V D, GUILLAUME J L, LAMBIOTTE R, et al. Fast unfolding of communities in large networks[J]. Journal of Statistical Mechanics:Theory and Experiment, 2008, 2008(10): P10008. DOI: 10.1088/1742-5468/2008/10/P10008. |
| [15] | ZHENG J F, YANG L X, GAO Z Y, et al. Cascading failures in congested scale-free networks[J]. International Journal of Modern Physics C, 2010, 21(08): 991-999. DOI: 10.1142/S0129183110015646. |
| [16] | WANG J W. Modeling cascading failures in complex networks based on radiate circle[J]. Physica A:Statistical Mechanics and its Applications, 2012, 391(15): 4004-4011. DOI: 10.1016/j.physa.2012.02.006. |
| [17] | MOTTER A E. Cascade control and defense in complex networks[J]. Physical Review Letters, 2004, 93(9): 098701. DOI: 10.1103/PhysRevLett.93.098701. |
| [18] |
王建伟, 荣莉莉. 基于袭击的复杂网络上的全局相继故障[J].
管理科学, 2009, 22(3): 113-120.
WANG J W, RONG L L. Universal cascading failures on complex networks based on attacks[J]. Journal of Managerment Science, 2009, 22(3): 113-120. |
| [19] | OPSAHL T, AGNEESSENS F, SKVORETZ J. Node centrality in weighted networks:Generalizing degree and shortest paths[J]. Social Networks, 2010, 32(3): 245-251. DOI: 10.1016/j.socnet.2010.03.006. |
| [20] | BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J]. Nature, 2010, 464(7291): 1025-1028. DOI: 10.1038/nature08932. |
| [21] | HUANG X, GAO J, BULDYREV S V, et al. Robustness of interdependent networks under targeted attack[J]. Physical Review E, 2011, 83(6): 065101. DOI: 10.1103/PhysRevE.83.065101. |
 2016, Vol. 33
2016, Vol. 33
