为了能够让移动机器人在室内环境中安全地航行,机器人除了能够实现自身的定位和导航[1-4]、制图[5-8]、障碍回避,墙壁跟踪、目标识别[9-10]和目标达成[11]的行为外,还需要能够识别走廊,以明确走廊状况,为机器人的下一步行为提供预判依据[12].在走廊识别相关问题上已有学者做了部分研究和探索[11-15],识别方式主要有基于图像特征识别[12-13]和基于深度信息特征识别[14-15]两种.前者主要依据场景图像的特征进行识别.Park和Suh[12]利用Canny边缘侦测算子对从传感器获得的图像进行走廊边缘的提取,再采用隐马尔可夫模型对提取的特征进行归类运算,从而实现走廊类型识别,但该方法在一些走廊类型相近的识别上误判率较高,同时该模型在使用前需要进行前期训练,增加了额外的人工辅助;张晓辉等[13]采用基于模型的目标匹配和遗传算法实现了对走廊踢脚线的搜索和跟踪,同时通过对识别模型匹配值的变化率分析实现了对走廊拐角的识别,但其计算量较大,且模型依赖于走廊踢脚线,不适合无明显走廊踢脚线或昏暗的室内场景情况.由于图像识别的方式受环境因素影响较大,近年来研究者转向了抗扰能力更强的深度信息识别,该方式较前者能更适应环境变化.Wang和Hou等[14]采用pSNM神经网络模型处理从声呐传感器获得的数据,再经神经网络聚类区分七种走廊类型,该算法相比于传统的PCA(主元分析法),BP(反向传播)分类器以及IAF尖峰神经元模型等算法具备更高的鲁棒性,但由于机器人在采集数据时,需要位于走廊拐角的中心处才能较好得到表征走廊周围环境的数据信息,同时该模型算法的实时性难以保证,这就导致其算法预判性较差,不能够给予机器人及时的反馈.
Cheng等[15]则利用Kinect传感器获得深度图像并从中提取深度曲线,再根据深度曲线构造描述环境的二维几何平面并对其进行x轴和z轴两个方向上的投影,接着对这两个投影曲线斜率进行符号区间的划分,再用贝叶斯分类器完成对走廊类型的识别,该方法相对以上提及的方法而言,对环境的约束较少,实时性较高,但该方法主要依赖于深度曲线的识别,由于实际环境的复杂性,很容易导致Kinect传感器产生不规则的深度曲线,增加了对深度曲线识别的复杂性.
为解决上述问题,本文提出一种新的走廊识别算法,该算法采用Kinect传感器提供的深度图信息,利用连续点间的深度差值和最小二乘法拟合直线,最后结合贝叶斯分类器实现对走廊类型的判定.该算法不仅避免了对不规则深度曲线识别的复杂性,提高了识别效率,而且实验结果表明具有更好的识别率和鲁棒性.
1 问题描述 1.1 走廊类型特征编码室内环境的走廊拐角类型通常由8种基本的简单类型组成,如图 1所示,分别为:(a)短“I”型;(b)右“L”型;(c)长“I”型;(d)右“T”型;(e)左“L”型;(f)正“T”型;(g)左“T”型和(h)“十”字型.因此总共可以将走廊类型编码为8种,使用3位数的二进制编码表示,用符号表示为:Yi=[f1,f2,f3],(fi∈{0,1}),其中Yi代表第i种走廊类型,fi是表征相应出口方位存在性的特征位,(“f1”:左出口位;“f2”:前出口位;“f3”:右出口位).当机器人在向前探测走廊类型时,其前方左、中和右3个方向上要么存在出口,要么无出口,因此可以使用1表示该方位上出现了出口,使用0表示该方向上没有出口;由于机器人传感器探测的不确定性,机器人有时可能会无法判断其中一个方位上是否存在出口,此时将不确定的出口方位表示为-1,综上所述,特征编码的取值范围为{-1,0,1}(其中,“-1”:不确定;“0”:不存在;“1”:存在).特征编码与走廊类型之间的对应关系可以参见表 1.
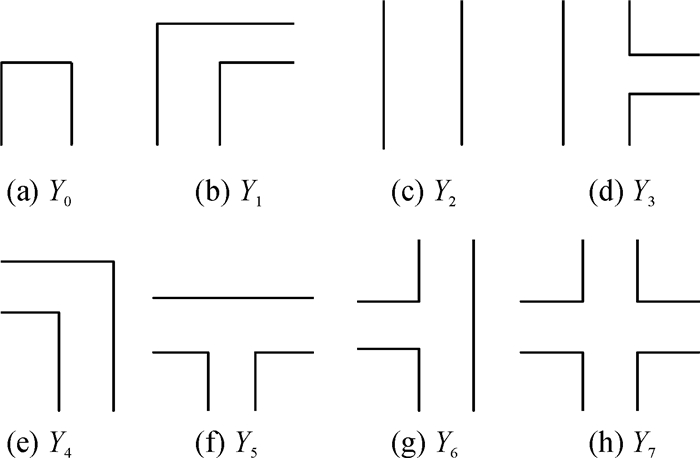
|
图 1 走廊类型 Figure 1 Types of corridors |
| 表 1 特征编码与走廊类型的关系 Table 1 Relationship between the feature coding and corridor types |
对观察得到的特征组需要进行聚类运算,采用贝叶斯分类公式[15]
| $ P\left( {{Y}_{i}}|{{X}_{1}}, \ldots {{X}_{K}} \right)=\frac{P\left( {{Y}_{i}} \right)\prod\limits_{l=1}^{k}{P\left( {{X}_{l}}|{{Y}_{i}} \right)}}{\sum\limits_{j=1}^{N}{\left[P\left( {{Y}_{j}} \right)\prod\limits_{l=1}^{k}{P\left( {{X}_{l}}|{{Y}_{j}} \right)} \right]}}, $ | (1) |
其中Xi表示第i个观察量,Yi表示第i个走廊类型.由日常经验可知,遇到走廊类型为死路的情形通常低于其他类型的出现情况.据此假设Y0类型的出现情况.据此假设的出现概率为q,其他类型为2q,但如果机器人在观测过程中始终不能得到完全观测量时,会出现无法确定走廊类型的情况.为此本文通过提升高概率与低概率类型间的倍数比进行纠正,凭试验选取倍数为4,因此有P(Y0)=q,P(Y1~Y7)=4q.其中,q=1/29.同时基于这样一种事实:观测到全部特征或者无特征的概率会低于其他情况,因此假设这两种情况的概率为p,其他情形为2p[15],其中,
| $ p=\frac{1}{{{2}^{M+1}}-2}, $ | (2) |
M为特征编码数,其条件概率P(Xl|Yj)取值如下:
| $ P\left( {{X}_{l}}|{{Y}_{j}} \right)=\left\{ \begin{align} & \frac{1}{{{2}^{M+1}}-2}\left( \text{完全置信} \right); \\ & \frac{1}{{{2}^{M}}-1}\left( \text{部分置信} \right); \\ & \frac{1}{{{2}^{M+1}}-2}\left( \text{完全不置信} \right); \\ & \text{ }\ \ \ \ \ 0\left( {{X}_{l}}, {{Y}_{j}}\text{冲突} \right)\cdot \\ \end{align} \right.\text{ } $ | (3) |
值得注意的是,算法借助机器人在移动过程中产生的一系列观察量来度衡最终运算结果,但由于环境对传感器造成的干扰使得观察序列并不稳定,导致观察量序列的出现模式不恒定,影响计算结果稳定性,为提高观察量X的计算可信度,本文为其添加可信度估算:
| $ C\left( {{X}_{i}} \right)=\left\{ \begin{align} & 1, {{n}_{{{x}_{i}}}}\ge {{N}_{\text{Threshold}}}; \\ & 0, {{n}_{{{x}_{i}}}}<{{N}_{\text{Threshold}}}\cdot \\ \end{align} \right. $ | (4) |
C(Xi)表示观察量Xi的可信度,nxi表示观察量Xi出现的次数,NThreshold为满足可信度的最小次数阈值.当C(Xi)=1,表明Xi可信,可以纳入后期的分类运算,否则该观察量Xi应被遗弃.如此一来可保证观察量较高的可信度,提高了观察序列的稳定性.
2 改进的走廊识别算法为提高走廊识别的正确率,降低深度曲线识别的复杂度,同时提升移动机器人的方位自由性,本文提出一种改进的走廊识别算法.算法识别思路是利用深度曲线相邻点间的深度差值和最小二乘法拟合直线判断出口的存在性,再利用贝叶斯分类器对获得的特征进行聚类运算,最后实现走廊类型的识别.
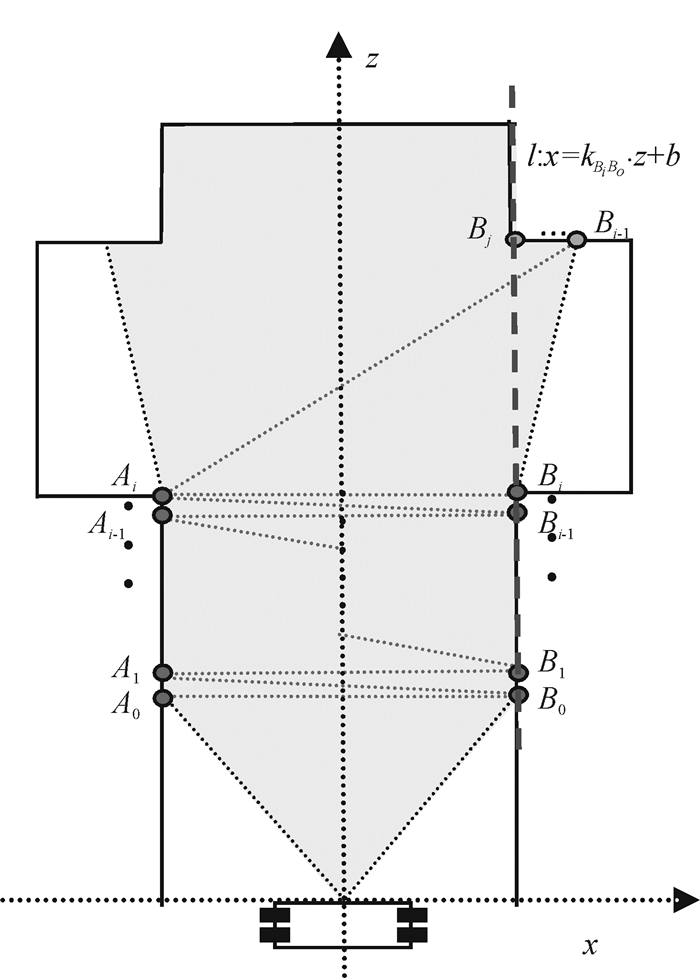
2.1 原理阐述判断走廊类型的关键在于检测出构成走廊出口的所在位置.由实际经验可知,如果走廊一侧存在出口,则出口处宽度相邻两点间差值相比于非出口处的相邻点差值会突然增大,因此可将这一特点作为检验走廊出口存在性判断,原理如图 2所示.
|
图 2 走廊检测原理示意图 Figure 2 Schematic diagram of corridor detection |
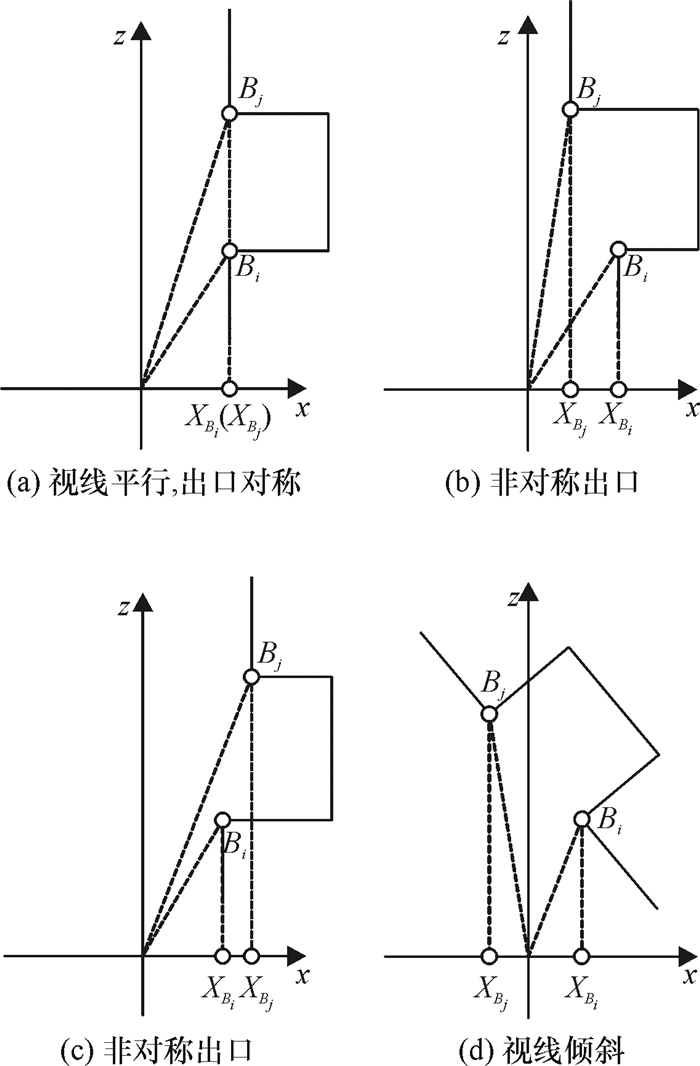
图 2中,A0,A1,…Ai和B0,B1,…Bi为走廊两侧数据点,Bi+1,…Bj是出口处的数据点序列,直线方程l:x=kBiBo·z+b是由B0至Bi段的离散数据点经最小二乘法拟合而成.图 2中阴影部分是机器人所能探知的区域,由Kinect传感器获得的深度图像包含场景到机器人之间的距离信息,各个点相对于摄像头平面中心的三维坐标可由点云坐标转换公式[16]计算得到.从深度曲线的两个初始端点A0、B0开始检测,计算每后续两点距离值|AiBi-1|(或|AiBi|),并与当前两点的距离|Ai-1Bi-1|(或|AiBi-1|)作差值比较.由于在同一侧的两个连续点间间隔极小,因此它们分别与另一侧点所构成的连线长度将非常相近,因而所形成的差值d极小(通常d趋近于0).当检测到可能的出口点处(假设在图 2中为Bi+1)时,出口点处的连线值|AiBi+1|与先前的连线长度|AiBi|间形成的差值d(d=|AiBi+1|-|AiBi|)将会突然增大.因此可将之视为可能的出口点作进一步检测,对从Bi+1以后开始的每一点与Bi点形成的连线距离|BiBk|(k∈[i+1,j])进行长度检验,以判断整个通道是否足够容纳移动机器人,其中Bj是长度检验的终止点.通常情况下,机器人在探索环境的移动过程中,其位置会经常发生改变,因而机器人(摄像头)视线也并非总是平行于走廊过道中轴线,且由于出口两侧墙壁也并非绝对对称,以及墙壁平面凹凸不平等原因都造成了移动机器人无法直接获知检测的终止点Bj,进而造成了识别出口点的难度.机器人视线相对于走廊出口的各种情形如图 3所示.
|
图 3 移动机器人视线相对于走廊出口的各种情形 Figure 3 Various scenarios of mobile robot vision with respect to the corridor export |
在图 3(a)中,可通过Bi在X轴上的垂直投影点XBi反向检测具有相同投影的另一点Bj(投影点为XBj,XBj=XBi);而(b)、(c)和(d)的情况,则会造成Bj点的识别困难(XBj≠XBi),因此需要对Bj点的直线归属进行判断,可通过对B0至Bi间离散数据点拟合直线l得到,此时Bj是B0、Bi所属直线方程l:x=kBiBo·z+b上一点,直线方程可使用最小二乘法拟合得到,最后还需计算间距|Bi+1Bj|是否大于指定可以被视为出口的深度阈值D0,当以上条件都满足时,则可判定该处是一个出口,将观察量X的相应特征值位赋值为1(即Xi=[f1,f2,f3]=[f1,f2,1],X表示第i个观察量),当所有特征位都赋值后,得到一个观察量Xi,通过不断积累观察量,最终将得到一组可用于贝叶斯分类运算的观察序列X1,X2,…,Xk.
2.2 算法步骤走廊识别算法按以下步骤进行.
步骤1 深度曲线初步修复.
深度曲线取自深度图的中间行数据,而由Kinect从场景中获得的深度图容易存在白点噪音(由透明物体、光滑的物体表面等因素造成),也因此导致了所提取深度曲线的信息缺失.为修复空洞信息,可采取纵(横)向最近相邻数据点修补空洞信息:当某一点处缺失数据时,首先在该点处不超过图像2/3高度的纵向范围内寻找最近邻有效数据点作为替代;如果未能找到,则在该点横向上不超过10个数据点(左右各5个数据点)的范围内寻找最近邻有效值点,否则忽略该点,进行下一处数据空洞点的检测与修复.
步骤2 走廊出口边缘检测.
从深度曲线的两个初始端点A0、B0开始检测,计算每两个点间的欧氏距离|AiBi-1|(或|AiBi|),并将之与先前的两点距离|Ai-1Bi-1|(或|AiBi-1|)作差值比较,当差值|d|≥W0(其中|d|=||AiBi-1|-|Ai-1Bi-1||,W0为指定的走廊最小宽度)时,则表明找到一点Bi+1(或Ai+1),将该点视作可能的出口点进入步骤3作进一步检验.
步骤3 出口深度探测与离散数据点拟合.
若检测到了可能的出口点(假设为Bi+1),则从该点Bi+1开始,若检验的每一个点Bk(k∈[i+1,j])至Bi点处的欧氏距离|BiBk|始终满足:|BiBk|≥W0,且直到检测到有这样一点Bj,在该点处同时满足以下3个条件:
(1)|BjBi|≥W0;
(2)|kBiBj-kBiBo|<dk;
(3)|BjBi+1|≥D0.
其中,W0为宽度阈值,D0为走廊的深度阈值,kBiBj为Bi、Bj两点的连线斜率,dk为可以确定点Bj在直线l上的最小阈值,kBiBo为从点B0至点Bi范围内的离散数据点拟合而成的直线斜率,其拟合的公式为:x=kBiBo·z+b,其中
| $ {{k}_{{{B}_{i}}{{B}_{o}}}}=\frac{\sum\limits_{i=1}^{n}{{{z}_{i}}{{x}_{i}}}-\frac{1}{n}\sum\limits_{i=1}^{n}{{{z}_{i}}}\sum\limits_{i=1}^{n}{{{x}_{i}}}}{\sum\limits_{i=1}^{n}{z_{i}^{2}}-\frac{1}{n}\sum\limits_{i=1}^{n}{{{z}_{i}}}\sum\limits_{i=1}^{n}{{{x}_{i}}}}, $ | (5) |
| $ b=\frac{1}{n}\left( \sum\limits_{i=1}^{n}{{{x}_{i}}}-a\sum\limits_{i=1}^{n}{{{z}_{i}}} \right)\cdot $ | (6) |
若符合以上条件,则表明Bj是出口点,且Bi和Bj一道构成了一处出口,将该处对应特征位赋值1.在完成其中一侧Bj出口点的检测后,在该检测点保持不动,从另一侧Ai开始检测出口点Aj的存在性,当检测到点Ai+1,重复步骤2和步骤3,否则,进入步骤4.
步骤4 贝叶斯聚类运算.
将得到的观察序列X1,X2,…Xk代入式(1)进行运算,直到P(Yi|X1,X2,…Xk)=1时,得到走廊类型的判定结果Yi.
3 实验结果与分析本次实验采用HCR家用机器人平台搭载微软开发的Kinect传感器(如图 4所示),传感器输出的RGB-D深度图分辨率为640*480,实验环境为一般室内场景,实验测试次数为300次,测试角度(摄像头视线与走廊过道中轴线形成的夹角)范围从0°至90°.

|
图 4 HCR家用机器人搭载Kinect摄像头 Figure 4 HCR household robots equipped with kinect camera |
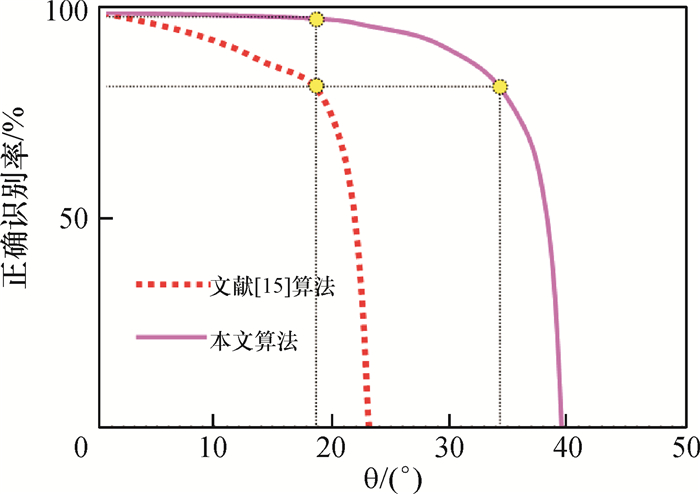
首先对比了文献[15]算法(深度曲线识别法)与本文新算法的走廊识别率对比图,实验结果如图 5所示.其中纵轴表示走廊正确识别率,横轴表示移动机器人摄像头视线相对于走廊过道中轴线的夹角θ.
|
图 5 原算法和新算法走廊识别率对比图 Figure 5 Comparison between the original algorithm and the new algorithm in corridor recognition rate |
由图 5可以看出,两个算法的走廊识别率都随着角度θ的增大而减小.在摄像头视线与中轴线形成的角度θ接近0°时两种算法都有98%以上的成功率,而当角度θ增大至某个阈值时(θ≈19°),文献[15]算法(深度曲线识别法)的识别率降至约83%,本文算法则仍保持在97%~98%,而对比两者在相同方位角度的走廊识别率上,则本文算法比文献[15]算法高出近16°的识别范围.
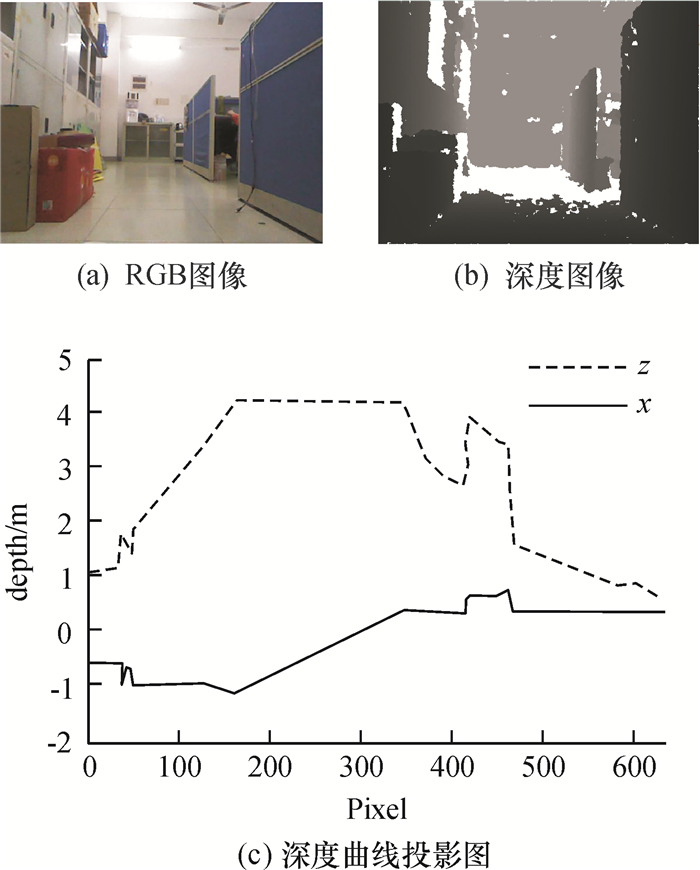
识别结果上的差异是由两者识别方式不同造成的,这可由一个实验场景(如图 6所示)得到很好的解释.在机器人探索环境的过程中,当摄像头视线平行于过道中轴线时,原算法(深度曲线识别法)提取出了良好表征走廊出口的特征曲线,如图 6(c)所示.
|
图 6 机器人视线平行于过道 Figure 6 Robot vision parallel to the aisle |
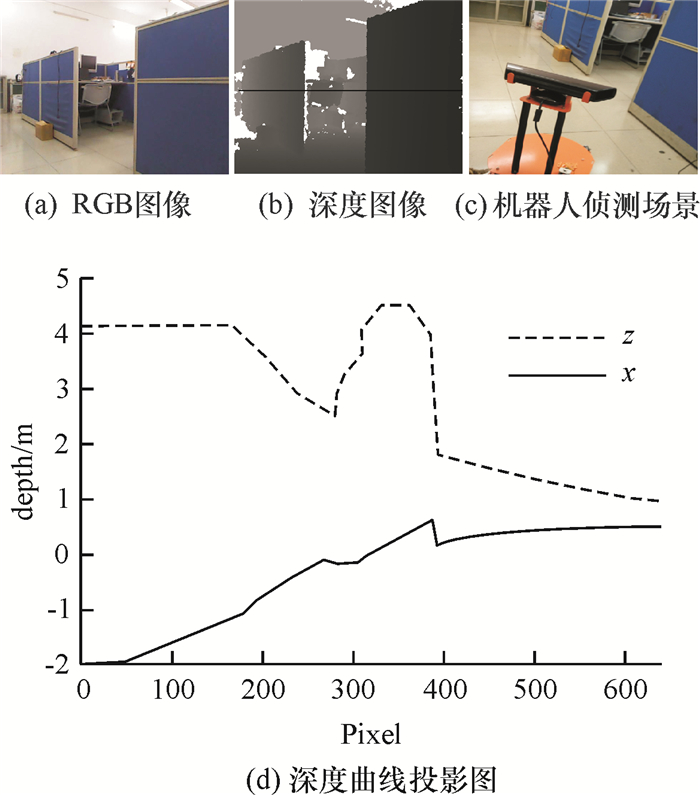
图 6(c)中,虚线和实线分别表示深度曲线在z轴和x轴上的投影.深度曲线投影能够清楚地描绘出走廊出口类型特征,该曲线特征对应了一种走廊类型,可以正确区分走廊类型为右“T”型.然而当移动机器人摄像头与走廊过道中轴线形成较大的夹角较大(约23.1°)时(如图 7所示),该识别方法将出现错误的判读.
|
图 7 机器人视线与过道间夹角为23.1° Figure 7 The angle between robot vision and aisle is 23.1° |
当机器人处于场景图 7所示的位姿时,深度曲线提取的特征投影线段已严重失真,不再属于8种类型中的任何一种特征线段,但由于部分线段映射了一些(比如类Y6)类型的特征,所以此时文献[15]算法[9]将走廊类型错误地识别为左“T”型,结果有误.而采用本文算法在此情况下依然能够将走廊类型正确地区分为右“T”型.
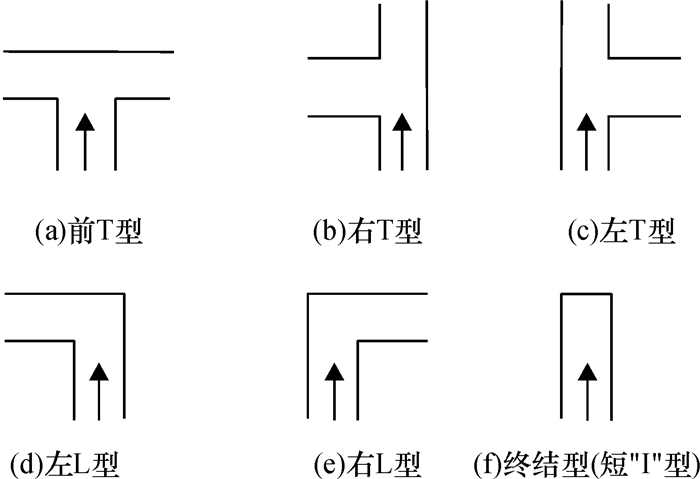
实验还对比了采用隐马尔科夫法[12]对于6种非“I”类型(NIC)(如图 8所示)的走廊识别率(见表 2).
|
图 8 6种非“I”型(NIC) Figure 8 Six kinds of Non-I-Corridor type (NIC) |
| 表 2 NIC类型识别率对比 Table 2 Comparison of NIC type recognition rate |
从表 2可以看出在相同类型的走廊识别上,本文算法的走廊类型识别正确率为98.96%,高于隐马尔科夫算法的86.21%,失误率则小于隐马尔科夫法,这表明本文算法在走廊识别的效果上好于隐马尔科夫法.
注意,文献[12]将走廊类型为死路的情况表示成“终结型”(图 8(f))并将之归入为非“I”型,而在本文中将其表示为短“I”型(图 1(a)),这里仅是表示方式不同,但实际上两者所代表的类型一致,为避免混淆,这里仍然将短“I”型当做非“I”型进行处理,以便于结果比对,已在图 8(f)中注明.
新算法对全部走廊类型(包含长“I”型和“十”字型)的识别率为97.69%,相比于在识别六种非“I”型走廊类型时的正确率98.96%下降了约1%,这是由于新添加的两种走廊类型——长“I”型和“十”字型所导致.这两种类型分别介于“L”型和“T”型之间,它们之间的相似性增加了算法对走廊特征的提取和聚类运算复杂度,同时由前述可知,当机器人相对于走廊过道的位姿发生变化(角度变大)时,算法对走廊类型的误判率也随之增加,所以整体正确识别率稍有下降,但算法仍然保持了很高的走廊类型的正确识别率.
4 结论与展望实验结果表明,新算法能够实现走廊类型的正确识别和区分,相比以往的识别方法具有更高的识别率,同时在方位角识别范围上更大,具备较高的鲁棒性,增加了机器人移动方位的灵活性.
虽然,本文算法在走廊分类识别中取得了较高的识别率,但是还需要对其进行进一步更加深入地探索和研究,下面给出若干可以改进和需要进一步探究问题的建议:
(1) 文中采用的观测条件概率P(X|Y)是一种基于经验值的假设,还可以通过神经网络等算法进行训练以得到改进.
(2) 算法从深度图中只提取了一条深度曲线进行判断,并没有充分利用深度图中丰富的三维信息,高维特征是未来研究的一个方向.
(3) 基于本文算法的检测原理,原则上可以检测不限于上述所定义的8种基本走廊类型,即能够实现多类型走廊侦测,因而可以去除8种编码的限制,将其扩展至n维特征,增强机器人对走廊的多种类型识别能力.
| [1] | CORCORAN P, BERTOLOTTO M, LEONARD J. Cognitively adequate topological robot localization and mapping[C]//Proceedings of the Sixth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness. New York:ACM, 2014:17-24. |
| [2] | MUR-ARTAL R, TARDóS J D. ORB-SLAM:tracking and mapping recognizable features[C]//MVIGRO Workshop at Robotics Science and Systems (RSS). USA, Berkeley:[s.n.], 2014. |
| [3] | WANG B, ZHOU S, LIU W, et al. Indoor localization based on curve fitting and location search using received signal strength[J]. Industrial Electronics, IEEE Transactions on, 2015, 62(1): 572-582. DOI: 10.1109/TIE.2014.2327595. |
| [4] | LEE S M, JUNG J, KIM S, et al. DV-SLAM (Dual-Sensor-Based Vector-Field SLAM) and Observability Analysis[J]. Industrial Electronics, IEEE Transactions on, 2015, 62(2): 1101-1112. DOI: 10.1109/TIE.2014.2341595. |
| [5] | WANG K, ZHAO L, LI R. Mobile robot map building in eigenspace—A pea-based approach[C]// 2013 25th Chinese. Control and Decision Conference (CCDC) Guiyang:IEEE, 2013:3199-3203. |
| [6] | VARADARAJAN K M. Topological mapping for robot navigation using affordance features[C]//Automation, Robotics and Applications (ICARA), 2015 6th International Conference on. Queenstown:IEEE, 2015:42-49. |
| [7] | CHIN W H, LOO C K, KUBOTA N. Multi-channel Bayesian adaptive resonance associative memory for environment learning and topological map building[C]//Informatics, Electronics & Vision (ICIEV), 2015 International Conference on. Fukuoka:IEEE, 2015:1-5. |
| [8] | ITO A, TAKAHASHI K, KANEKO M. Robust mapping for mobile robot based on immobile area grid map considering potential moving objects[J]. Electrical Engineering in Japan, 2015, 192(4): 30-43. DOI: 10.1002/eej.2015.192.issue-4. |
| [9] |
蒋玉玲, 杨宜民. 基于SOM算法的机器视觉颜色识别[J].
广东工业大学学报, 2011, 28(2): 40-42.
JIANG Y L, YANG Y M. Color recognition of machine vision based on SOM algorithm[J]. Journal of Guangdong University of Technology, 2011, 28(2): 40-42. |
| [10] |
夏琴晔, 杨宜民. 基于biSCAN和SVM的机器人目标识别新算法研究[J].
广东工业大学学报, 2014(04): 65-69.
XIA Q Y, YANG Y M. Research on a new algorithm for robots' recognition of objects based on biSCAN and SVM[J]. Journal of Guangdong University of Technology, 2014(04): 65-69. DOI: 10.3969/j.issn.1007-7162.2014.04.012. |
| [11] | FAROOQ U, ABBAS G, SALEH S O, et al. Corridor navigation with fuzzy logic control for sonar based mobile robots[C]// Industrial Electronics and Applications (ICIEA), 2012 7th IEEE Conference on.Singapore:IEEE, 2012:2087-2093. |
| [12] | PARK Y B, SUH I H. Predictive visual recognition of types of structural corridor landmarks for mobile robot navigation[C]// 19th International symposium in Robot and Human Interactive Communication. Viareggio:IEEE, 2010:391 -396. |
| [13] |
张晓晖, 刘丁. 自主移动机器人走廊视觉识别与跟踪方法研究[J].
西安理工大学学报, 2006, 22(2): 158-162.
ZHANG X H, LIU D. Research on vision recognition and tracking for corridor of autonomous driving robot[J]. Journal of Xi'an University of Technology, 2006, 22(2): 158-162. |
| [14] | WANG X, HOU Z G, TAN M, et al. Improved mobile robot's Corridor-Scene Classifier based on probabilistic Spiking Neuron Model[C]// Cognitive Informatics & Cognitive Computing (ICCI*CC), 2011 10th IEEE International Conference on Banff, AB:IEEE, 2011:348-355. |
| [15] | CHENG H, CHEN H, LIU Y. Topological indoor localization and navigation for autonomous mobile robot[J]. IEEE Transactions on Automation Science & Engineering, 2015, 12(2): 729-738. |
| [16] | KAMARUDIN K, MAMDUH S M, SHAKAFF A Y M, et al. Method to convert Kinect's 3D depth data to a 2D map for indoor SLAM[C]// Signal Processing and its Applications (CSPA), 2013 IEEE 9th International Colloquium on Kuala Lumpur:IEEE, 2013:247-251. |
 2016, Vol. 33
2016, Vol. 33