受到环保意识增强和技术发展迅速等因素的影响,分布式能源的应用变得越来越广泛,光伏逆变并网技术也愈来愈被重视[1].在并网逆变器中,并网处常用的滤波器一般为L型滤波器或LCL滤波器.L型滤波器结构简单,但体积较大并且对高频谐波的抑制能力有限;LCL滤波器具有三阶低通滤波特性,不仅成本低而且对高频谐波有很好的衰减效果[2-3],在逆变并网中被广泛使用.但LCL滤波器的频率响应存在明显的谐振,文献[4-5]分析了LCL滤波器各种谐振阻尼方案的运行机理,其中基于滤波电容电流反馈的有源阻尼方案不仅控制系统结构简单,而且阻尼效果较好.
除了高频谐波,公共并网点(PCC)附近的非线性负载会使PCC处的电网电压存在背景谐波,不仅影响锁相环性能还会给并网电流带来低阶谐波.
为消除电网电压背景谐波的影响,一般会采用基于静止坐标系的比例积分(PI)控制及电网电压前馈的控制策略[6].这种方法结构简单,且对于抑制电网干扰有不错的效果,但PI控制在静止坐标系中不能有效处理稳态误差,而且对于以低开关频率运行的大功率设备来说,电网前馈对抑制低阶谐波的作用十分有限.另一种方法是基于旋转坐标系的PI+HC控制[7],这种方法克服了前一种方法的缺点,但信号解耦、两次dq坐标变换和谐波补偿大大增加了系统的计算量.
在旋转坐标系中,PI控制可转换为静止坐标系中的PR控制[8-9],若PR控制与HC控制相结合,则能够对指定频率处提供足够大的增益,达到无稳态误差控制,并有效抑制低阶谐波[10].该控制策略结构相对简单,容易实现,文献[11-14]已分析了PR+HC的控制策略在逆变并网系统的运用.
本文在建立单相并网逆变器模型基础上,通过滤波器电容电流的反馈来抑制LCL滤波器的谐振,采用PR+HC的控制策略来提高系统的性能,通过对HC给系统带来的影响和系统稳定性的分析来设计控制器的参数.
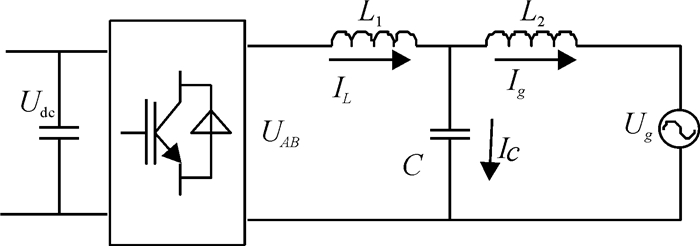
1 系统模型图 1为并网逆变器结构图,为简化分析,设直流母线电压Udc为常数,UAB为逆变桥的输出电压,Ug为电网电压.忽略器件的寄生电阻,L1,L2和C组成LCL滤波器.LCL滤波器的谐振频率为
| $ {f_r} = \sqrt {\left( {{L_1} + {L_2}} \right)/\left( {{L_1}{L_2}C} \right)} /\left( {2{\rm{\pi }}} \right). $ |
|
图 1 LCL并网逆变器 Figure 1 LCL-type grid-connected inverter |
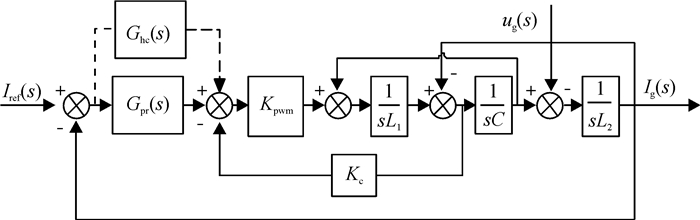
图 2为系统的控制框图,其中Kpwm为逆变比例系数;Gpr(s)为PR控制器,Ghc(s)为谐波补偿控制器;Kc为电容电流Ic的反馈系数.
|
图 2 系统控制框图 Figure 2 System block diagram |
由图 2,可得出系统的开环传递函数
| $ T\left( s \right) = \frac{{{K_{{\rm{pwm}}}}{G_c}\left( s \right)}}{{{s^3}{L_1}{L_2}C + {s^2}{L_2}C{K_c}{K_{{\rm{pwm}}}} + s\left( {{L_1} + {L_2}} \right)}}. $ | (1) |
其中Gc(s)=Gpr(s)+ Ghc(s).
并网电流Ig(s)可表示为
| $ {I_g}\left( s \right) = \frac{{T\left( s \right)}}{{1 + T\left( s \right)}}{I_{{\rm{ref}}}}\left( s \right) + \frac{{{G_x}\left( s \right)}}{{1 + T\left( s \right)}}{U_g}\left( s \right). $ | (2) |
其中,
| $ {G_x}\left( s \right) = \frac{{{s^2}C{L_1} + sC{K_{{\rm{pwm}}}}{K_c} + 1}}{{{s^3}{L_1}{L_2}C + {s^2}{L_2}C{K_{{\rm{pwm}}}}{K_c} + s\left( {{L_1} + {L_2}} \right)}}. $ | (3) |
| $ {G_{{\rm{pr}}}}\left( s \right) = {K_p} + \frac{{2{K_r}\xi {\omega _{\rm{o}}}s}}{{{s^2} + 2\xi {\omega _{\rm{o}}}s + \omega _{\rm{o}}^2}}, $ | (4) |
| $ {G_{{\rm{hc}}}}\left( s \right) = \sum\limits_{n = 3, 5, \cdot \cdot \cdot }^h {\frac{{2{K_n}\xi {\omega _{\rm{o}}}s}}{{{s^2} + 2\xi {\omega _{\rm{o}}}s + {{\left( {n{\omega _{\rm{o}}}} \right)}^2}}}} . $ | (5) |
式(4) 为PR控制器的传递函数,其中Kp为比例系数;Kr为基波谐振项的积分增益;ωo=2πfo,ωo为基波角频率,fo为基波频率;式(5) 为HC控制器的传递函数,它是由若干个谐振项组成的,其中ξ为阻尼系数,决定着谐振项的带宽;Kn为谐波补偿谐振项的积分增益,n为谐波补偿次数;h为最高谐波补偿次数.
2.1.1 比例系数Kp在LCL滤波器中,电容C主要滤除高阶谐波,则在系统的低频段(小于fr/2), LCL滤波器可简化为L型滤波器[15-16],式(1) 可改写为
| $ T\left( s \right) \approx \frac{{{K_{{\rm{pwm}}}}{G_c}\left( s \right)}}{{s\left( {{L_1} + {L_2}} \right)}}. $ | (6) |
T(s)在截止频率fc的幅频为
| $ \left| {\;T\left( {{\rm{j}}2{\rm{\pi }}{{f}_c}} \right)\;} \right| \approx \left| {\;\frac{{{K_{{\rm{pwm}}}}{G_c}\left( {{\rm{j}}2{\rm{\pi }}{{f}_c}} \right)}}{{{\rm{j}}2{\rm{\pi }}{f}\left( {{L_1} + {L_2}} \right)}}\;} \right|. $ | (7) |
若截止频率fc足够大,Gc(s)可简化为一个比例环节[17],则|Gc(j2πfc)|≈Kp,令| T(j2πfc)|=1,得
| $ {K_p} \approx \frac{{2{\rm{\pi }}{{f}_c}\left( {{L_1} + {L_2}} \right)}}{{{K_{{\rm{pwm}}}}}}. $ | (8) |
在计算稳态误差时,式(6) 依然有效.将式(6) 代入式(2),得
| $ \begin{array}{l} \;\;\;\;\;{I_g}\left( s \right) = \frac{{T\left( s \right)}}{{1 + T\left( s \right)}}{I_{{\rm{ref}}}}\left( s \right) + \\ \frac{1}{{1 + T\left( s \right)}} \cdot \frac{1}{{s\left( {{L_1} + {L_2}} \right)}}U\left( s \right). \end{array} $ | (9) |
PR控制器在fo处提供了足够大的增益,并网电流Ig(s)与参考电流Iref(s)的相位误差被消除,但仍存在一定的幅值误差.由于|T(j2πfo)|≫1,根据式(6) 和式(9),系统的幅值误差为
| $ \begin{array}{l} \;\;\;\;\;\;\eta = \frac{{\left| {{I_g}\left( {2{\rm{\pi }}{{f}_{\rm{o}}}} \right) - {I_{{\rm{ref}}}}} \right|}}{{{I_{{\rm{ref}}}}}} \approx \\ \left| {\frac{1}{{{G_c}\left( {2{\rm{\pi }}{{f}_{\rm{o}}}} \right)}}} \right| \cdot \frac{{{U_g}}}{{{K_{{\rm{pwm}}}}{I_{{\rm{ref}}}}}}, \end{array} $ | (10) |
其中并网电流Ig,参考电流Iref和电网电压Ug为有效值.
HC控制器中各谐振项对带宽范围外的频段的影响很小,则忽略HC控制器对fo处的影响,|Gc(s)|在fo处可化简为|Gc(j2πfo)|≈Kp+Kr.若希望系统的幅值误差η≤ηst,将ηst和|Gc(j2πfo)|≈Kp+Kr代入式(10),得
| $ {K_r} \ge {K_{r\_}}\eta = \frac{{{U_g}}}{{{K_{{\rm{pwm}}}}{\eta _{{\rm{st}}}}{I_{{\rm{ref}}}}}} - {K_p}. $ | (11) |
文献[18]指出,若系统的截止频率大于PR控制器的转折频率,则PR控制器可化简成一个拥有相同积分系数的PI控制器.同理,若系统的截止频率fc大于Gc(s)的转折频率fz,则Gc(s)可化简为
| $ {G_{c2}}\left( s \right) = {K_p} + \frac{{\left( {{K_r} + \sum\limits_{n = 3, 5, \cdot \cdot \cdot }^h {{K_n}} } \right)2\xi {\omega _{\rm{o}}}}}{s}, $ | (12) |
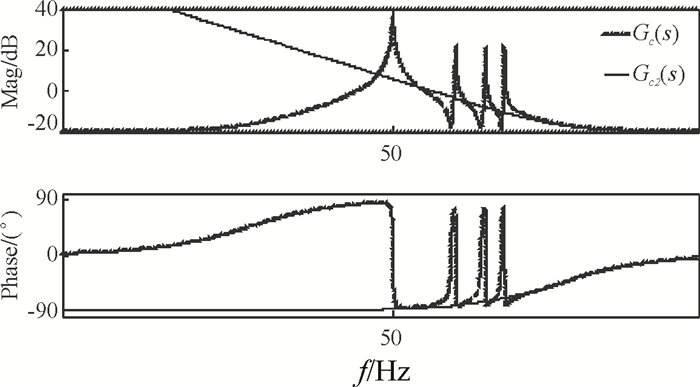
其中,Gc2(s)积分项的积分系数等于Gc(s)所有谐振项的系数之和.Gc(s)中各谐振项对其带宽以外频段的幅频增益影响不大,因此在截止频率fc或更高频段处Gc(s)弱化成一PI控制器.Gc(s)和Gc2(s)的波特图如图 3所示,可以看出在Gc(s)的转折频率fz前后,Gc(s)和Gc2(s)幅频曲线的斜率都为-20 dB/dec和0 dB/dec,相频曲线都从-90°上升到0°,当fc>fz时,Gc(s)≈Gc2(s).
|
图 3 Gc(s)与Gc2(s)的波特图(h=7) Figure 3 Bode diagram of Ghc(s) and Ghc2(s)(h=7) |
根据式(1) 和式(12),系统的相位裕度为
| $ {\rm{PM = arctan}}\frac{{2{\rm{\pi }}{{L}_1}\left( {f_r^2 - f_c^2} \right)}}{{{K_c}{K_{{\rm{pwm}}}}{f_c}}} - {\rm{arctan}}\frac{{{K_x}\xi {\omega _{\rm{o}}}}}{{{\rm{\pi }}{{f}_c}{K_p}}}, $ | (13) |
其中
若希望系统的相位裕度PM≥PMst,将PMst代入式(13) 可得
| $ \begin{array}{l} \;\;\;\;\;\;\;{K_x} \le {K_{x\_{\rm{PM}}}} = \\ \frac{{{\rm{\pi }}{f_c}{K_p}}}{{\xi {\omega _{\rm{o}}}}} \times \frac{{2{\rm{\pi }}{{L}_1}\left( {f_r^2 - f_c^2} \right) - {K_c}{K_{{\rm{pwm}}}}{f_c}\tan {\rm{P}}{{\rm{M}}_{{\rm{st}}}}}}{{{K_c}{K_{{\rm{pwm}}}}{f_c} + 2{\rm{\pi }}{{L}_1}\left( {f_r^2 - f_c^2} \right)\tan {\rm{P}}{{\rm{M}}_{{\rm{st}}}}}}. \end{array} $ | (14) |
由式(11) 和式(14) 可得Kr和Kn的约束关系:
| $ {K_{r\_\eta }} \le {K_r} \le {K_{x\_{\rm{PM}}}}. $ | (15) |
| $ 0 \le \sum\limits_{n = 3, 5, \cdot \cdot \cdot }^h {{K_n} \le } \;{K_{x\_{\rm{PM}}}} - {K_r}. $ | (16) |
系统开环传递函数的相频曲线在fr处穿越-180°,系统在fr处的幅值裕度可表达为
| $ {\rm{GM = }} - {\rm{20lg}}\left| {\;T\;\left( {{\rm{j}}2{\rm{\pi }}{{f}_r}} \right)} \right|. $ | (17) |
由于fr比hfo要大很多,Gc(s)简化为Gc(s)≈Kp.假设Kx=Kr, 若希望系统的幅值裕度GM≥GMst,把式(1) 和式(8) 代入式(17),把式(8) 和式(11) 代入式(13),分别得到Kc关于fc的边界值函数:
| $ {K_c} \ge {K_{c\_{\rm{GM}}}}\left( {{f_c}} \right) = \frac{{2{\rm{\pi }}{{f}_c}{L_1}}}{{{K_{{\rm{pwm}}}}}} \cdot {10^{\frac{{{\rm{G}}{{\rm{M}}_{{\rm{ST}}}}}}{{20}}}}. $ | (18) |
| $ \begin{array}{*{20}{l}} {\;\;\;\;\;\;{K_c} \le {K_{c\_P{\rm{M}}}}\left( {{f_c}} \right) = \frac{{2\pi {L_1}\left( {f_r^2 - f_c^2} \right)}}{{{K_{{\rm{pwm}}}}{f_c}}}/}\\ {{\rm{tan}}\left\{ {{\rm{P}}{{\rm{M}}_{{\rm{ST}}}} + \arctan \left[ {\frac{{\xi {\omega _o}{U_g} - \xi {\omega _o}2\pi {I_{{\rm{ref}}}}{\eta _{{\rm{st}}}}{f_c}\left( {{L_1} + {L_2}} \right)}}{{2{\pi ^2}{I_{{\rm{ref}}}}{\eta _{{\rm{st}}}}f_c^2\left( {{L_1} + {L_2}} \right)}}} \right]} \right\}.} \end{array} $ | (19) |
根据图 3可知,Gc(s)的输出与电容电流反馈量的误差为PWM调制的调制波,为了避免调制波与载波多次交截,调制波的最大变化率应低于载波的变化率,因此要求[17]
| $ {K_c} \le {K_{c\_\max }} = \frac{{4{f_{{\rm{sw}}}}{L_1}}}{{{K_{{\rm{pwm}}}}}}. $ | (20) |
为验证分析的正确性,在Matlab\Simulink中搭建一个1kW的模型,具体参数如表 1所示.为保证系统稳定,这里取PMst=45°,GMst=3dB, ηst=0.8%.
| 表 1 系统参数 Table 1 System parameters |
根据式(13) 式建立PM关于ξ的函数PM(ξ),则PM′(ξ) < 0,PM关于ξ单调递减.文献[19]中取ξ=0.001,Ghc(s)拥有极小的带宽从而提升了谐波补偿的精确度,Ghc(s)对系统的负面影响可以忽略不计,补偿效果也更好.这里为了提高控制器对电网频率的适应性,以文献[20]为标准,电网频率允许偏差±0.5Hz,取ξ=0.01.
若Kn满足式(16) 的约束条件,h对PM的影响可以忽略.在低阶谐波中,一般3次、5次和7次谐波为主流谐波,在这里取h=7.
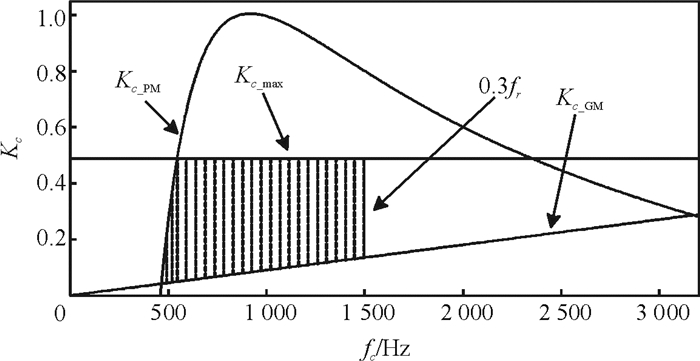
3.2.2 截止频率fc与比例系数Kp根据由式(18)、(19) 和(20) 可得到Kc关于fc的取值范围,如图 4的阴影部分.关于系统fc的限制,有如下两点:
|
图 4 Kc和fc的取值范围 Figure 4 The possible region of Kc and fc |
(1) fc>fz:这样可以保证Gc(s)化简的准确性,也不会因Gc(s)谐振项的相频在其谐振频率(nωo)有-180°的相移导致系统的PM过小.
(2) fc≤0.3 fr:为避免对fr的谐振阻尼产生干扰,系统带宽不能超过fr.另外,受到采样和调制的延时影响,fc应限制在0.3fr之内[21].
较大的Kp让系统形成较大的带宽,让系统的瞬态响应更快.由式(8) 可知Kp与fc近似成正比,fc尽量取大,取fc=0.3fr=1496Hz,得Kp=0.109.fc确定后,由图 4可得到Kc的取值范围[Kc_GM, Kc_max].
3.2.3 电容电流反馈系数Kc根据式(13) 建立PM关于Kc的函数PM(Kc),可知PM′(Kc) < 0,PM关于Kc单调递减.为了不让系统的PM过小,Kc不宜取大.取Kc=0.15.
3.2.4 基波谐振项积分系数KrKr越大,fo处的幅频越大,基波的追踪效果越好,但系统的PM也越小(证明方法与前文类似).另外,由前面分析可知加入HC后,系统的PM会减小.根据式(11)、(13) 和(15) 可得Kr的取值范围为[Kr_GM, Kx_PM),取这个范围的中值,Kr=64.304.
3.2.5 谐波补偿谐振项积分系数Kn根据式(2),代表电网电压对并网电流的干扰或系统输出导纳的传递函数可表示为
| $ {G_{{\rm{adm}}}}\left( s \right) = \frac{{{I_g}\left( s \right)}}{{{U_g}\left( s \right)}} = \frac{{{G_x}\left( s \right)}}{{1 + T\left( s \right)}}. $ | (22) |
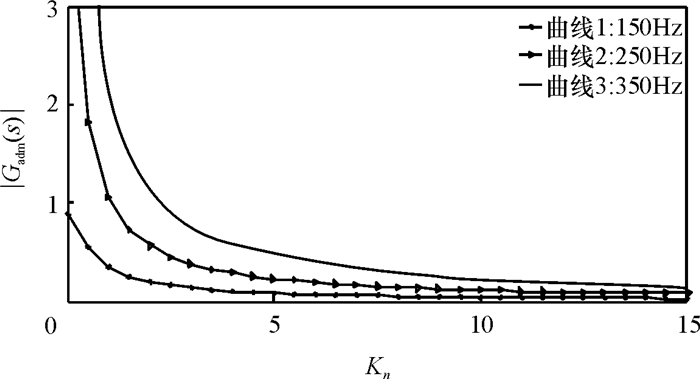
根据式(16) 可得出Kn的取值范围,由式(22) 作出输出导纳的幅值|Gadm(s)|在补偿频率150Hz、250Hz和350Hz处关于Kn的曲线图,如图 5所示.
|
图 5 |Gadm(s)|在150、250和350 Hz处关于Kn的曲线图 Figure 5 Curves of |Gadm(s)| as the function of Knat 150, 250 and 350 Hz |
结合图 5,关于Kn的取值有如下分析.
(1) 当Kn < 6时,随着Kn的值越大,各曲线中|Gadm(s)|值越小,而|Gadm(s)|的值越小代表系统输出导纳越小,系统对低阶谐波的抑制效果越好;当12≥Kn≥6时,除了曲线3的|Gadm(s)|值还在递减外,曲线1和曲线2的|Gadm(s)|值基本稳定.
(2) 当Kn≥12时,曲线3的|Gadm(s)|值也稳定下来.随着Kn的值增大,三条曲线|Gadm(s)|的值基本不变, 即Kn的值继续增大对相关频率处低阶谐波的抑制已经十分有限.
(3) 根据(13) 式建立PM关于Kn的函数PM(Kn),PM′(Kn) < 0,PM关于Kn单调递减.为保证系统的PM值,Kn的值不宜取太大.
综合上述3点,取K1=K2=6,K3=12.
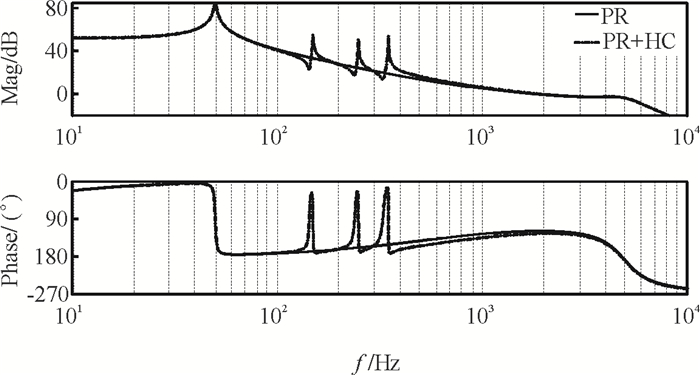
4 仿真结果图 6是根据上述参数得出的系统开环波特图.可以看出,在添加HC控制后,在谐振项的带宽内谐波补偿频率的幅频都拥有足够大的增益[22],使系统产生极小的输出导纳去抑制低阶谐波.当控制器是单一PR控制时,系统GM=3.4 dB,PM=60.8°;当控制器是PR+HC控制时,系统GM=3.2 dB,PM=54.8°.系统的幅值裕度和相位裕度稍有下降,但对系统稳定性的影响不大.
|
图 6 T(s)的波特图 Figure 6 Bode diagram of T(s) |
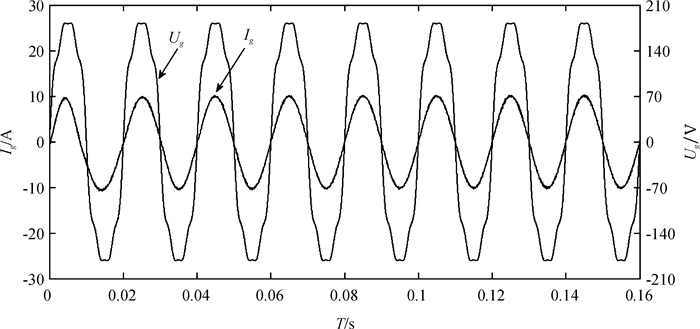
在有背景谐波环境下对系统进行仿真,其中背景谐波环境为在基频(50Hz)电网电压中叠加15V(有效值)的3次谐波电压分量、10V(有效值)的5次谐波电压分量和7V(有效值)的7次谐波电压分量,叠加谐波分量后,电网电压THD为13.82%.图 7是系统采用PR+HC控制策略的仿真结果图,并网电流关于采用PR+HC与单一PR控制策略的谐波率见表 2.可以看出在电网电压背景谐波的干扰下,PR+HC的控制策略使并网电流的3次、5次和7次的谐波率与总谐波率明显下降.
|
图 7 电网电压Ug,电流ig仿真图(Gc(s)=Gpr(s)+Ghc(s)) Figure 7 Simulation result of grid vlotage Ug and grid current Ig(Gc(s)=Gpr(s)+Ghc(s)) |
| 表 2 并网电流的谐波含量 Table 2 The harmonics content of the grid current |
本文建立了单相LCL型并网逆变器在静止坐标系下数学模型,分析了PR+HC控制器中各参数对系统性能的影响,并基于系统的幅值裕度、相位裕度和稳态误差,给出了PR和HC控制器的参数设计方法.与单一的PR控制相比,仿真证明了控制器Gc(s)在添加了HC的情况下能有效地消除主流低阶谐波而不影响系统的稳定性.
| [1] | KOURO S, LEON J I, VINNIKOV D, et al. Grid-connected photovoltaic systems:an overview of recent research and emerging PV converer technology[J]. IEEE Industrial Electronics Magazine, 2015, 9(1): 47-61. DOI: 10.1109/MIE.2014.2376976. |
| [2] | LISERRE M, BLAABJERG F, HANSEN S. Design and control of an LCL-filtered-based three-phase active rectifier[J]. IEEE Industrial Electronics Magazine, 2005, 41(7): 1281-1291. |
| [3] | SOSA J, ESCOBAR G, VAZQUEZ G, et al. Comparative evaluation of L and LCL filters in transformerless grid tied converters for active power injection[C]//2014 IEEE International Autumn Meeting on Power Electronics and Computing.Mexico: IEEE, 2014:1-6. |
| [4] | 张兴, 曹仁贤, 等. 太阳能光伏逆变并网及其逆变控制[M]. 北京: 机械工业出版社, 2010: 160-176. |
| [5] |
许津铭, 谢少军, 肖华锋. LCL滤波器有源阻尼控制机制研究[J].
中国电机工程学报, 2012, 32(12): 27-33.
XU J M, XIE S J, XIAO H F. Research on control mechanism of active damping for LCL filters[J]. Proceedings of the CSEE, 2012, 32(12): 27-33. |
| [6] | WANG X H, RUAN X B, LIU S W, et al. Full feedforward of grid voltage for grid-connected inverter with LCL filter to suppress current distortion due to grid voltage harmonics[J]. IEEE Transactions on Power Electronics, 2010, 25(2): 3119-3127. |
| [7] | GOLESTAN S, MONFARED M, GUERRERO J M.A novel control technique for single-phase grid-connected inverters[C] //2011 International Conference on Electrical Engineering and Informatics.Bandung: IEEE, 2011:1-6. |
| [8] | TWINING E, HOLMES D G. Grid current regulation of a three-phase voltage source inverter with an LCL input filter[J]. IEEE Transactions on Power Electronics, 2003, 18(7): 888-895. |
| [9] | ZMOOD D N, HOLMES D G. Stationary frame Current regulation of PWM inverters with zero steady-state error[J]. IEEE Transactions on Power Electronics, 2003, 18(7): 814-822. |
| [10] | TEODORESCU R, BLAABJERG F, BORUP U, et al.A new control structure for grid-connected LCL PV inverter with zero steady-state error and selective harmonic compensation[C]//2004 Nineteenth Annual IEEE Applied Power Electronics Conference and Exposition.[S.l.]: IEEE, 2004, 1:580-586. |
| [11] | CASTILLA M, MIRET J, MATAS J, et al. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators[J]. IEEE Transactions on Industrial Electronics, 2009, 56(14): 4492-4501. |
| [12] | XU J M, XIE S J, TANG T. Evaluations of current control of in weak grid case for grid-connected LCL-filtered inverter[J]. IET Power Electronics, 2013, 6(6): 227-234. |
| [13] | XU J M, TANG T, XIE S J. Research on low-order current harmonics rejections for grid-connected LCL-filtered inverters[J]. IET Power Electronics, 2014, 7(9): 1227-1234. |
| [14] | LI B, ZHANG M, HUANG L, et al.A robust multi-resonant pr regulator using direct pole placement design strategy[C]//2013 Twenty-Eighth Annual IEEE Applied Power Electronics Conference and Exposition.Long Beach, CA, USA: IEEE, 2013:960-966. |
| [15] | DANNEHL J, WESSELS C, FUCHS F W. Limitations of voltage-oriented PI current control of grid-connected PWM rectifiers with LCL Filters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(6): 380-388. |
| [16] | TEODORESCU R, LISERRE M, RODRíGUEZ P. Grid converter for photovoltaic and wind power systems[M]. United Kingdom: Wiley-IEEE Press, 2011: 313-315. |
| [17] | BAO C L, RUAN X B, WANG X H, et al. Step-by-step controller design for LCL-type grid-connected inverter capacitor-with-current-feedback active-damping[J]. IEEE Transactions on Power Electronics, 2014, 29(7): 1239-1253. |
| [18] | CHEN X R, RUAN X B, YANG D S, et al.Step-by-step controller design of voltage closed-loop control for virtual synchronous generator[C]//2015 IEEE Energy Conversion Congress and Exposition.Montreal, QC, 2015:3760-3765. |
| [19] | CASTILLA M, MIRET J, MATAS J, et al. Control design guidelines for single-phase grid-connected photovoltaic inverters with damped resonant harmonic compensators[J]. IEEE Transactions on Industrial Electronics, 2009, 56(14): 4492-4501. |
| [20] | 中国国网电力科学研究院, 中国电力科学研究院. Q/GDW 617-2011光伏电站接入电网技术规定[S]. 北京: 国家电网公司, 2011. |
| [21] | TANG Y, LOH P C, WANG P, et al. Generalized design of high performance shunt active power filter with output LCL filter[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7): 1443-1452. |
| [22] |
宋修奎, 唐雄民, 章云, 等. 一种适合于单相电压型逆变电源的并联控制方案研究[J].
广东工业大学学报, 2015, 32(2): 79-82.
SONG X K, TANG X M, ZHANG Y, et al. A methord of parallel control for single-phase voltage source inverters[J]. Journal of Guangdong University of Technology, 2015, 32(2): 79-82. |
 2016, Vol. 33
2016, Vol. 33
