由于目前市面上大部分的清洁机器人产品仅依靠碰撞开关进行避障清扫,由此造成的主要问题有:(1) 在家庭里有老人小孩的情况下,随机碰撞避障存在一定安全隐患;(2) 对于较轻的障碍物无法发现,会造成推动障碍物一起移动的状况;(3) 清扫覆盖区域存在大量卫生死角,效率较低.而使用人工势场法能够提高清洁机器人的避障能力,但由于其算法自身存在的不足会导致路径结果不能满足清扫要求.相反,牛耕模式的全覆盖路径规划算法能够使清洁机器人遍历室内环境,但在动态环境中存在多个障碍物的情况下,会使得覆盖路径变得重复且杂乱.因此,为清洁机器人增加合适的传感器及智能控制算法,是清洁机器人又一发展趋势[1-5].
近年来,对于机器人的全覆盖路径规划问题,郝宗波等[6]提出了基于栅格的ISC算法,而Grant G P等[7]提出了BC-Sweep覆盖算法,增加了对电量等因素的考虑.也有学者[8]提出将牛耕算法与遗传算法结合的覆盖算法.但此类算法在已知环境中存在多个无记录的障碍物时,其覆盖效果仍存在重复率高和死角位的问题,不能满足清洁机器人的实际应用需求.针对以上问题本文结合360°激光雷达传感器,提出了结合人工势场法与牛耕式全覆盖算法优点的改进势场栅格算法,既能够解决两者自身的缺点,实现优势互补,也能够满足清洁机器人的应用需求.并将其与现有的覆盖算法作比较,体现出改进后的势场栅格法所具备的优越性.
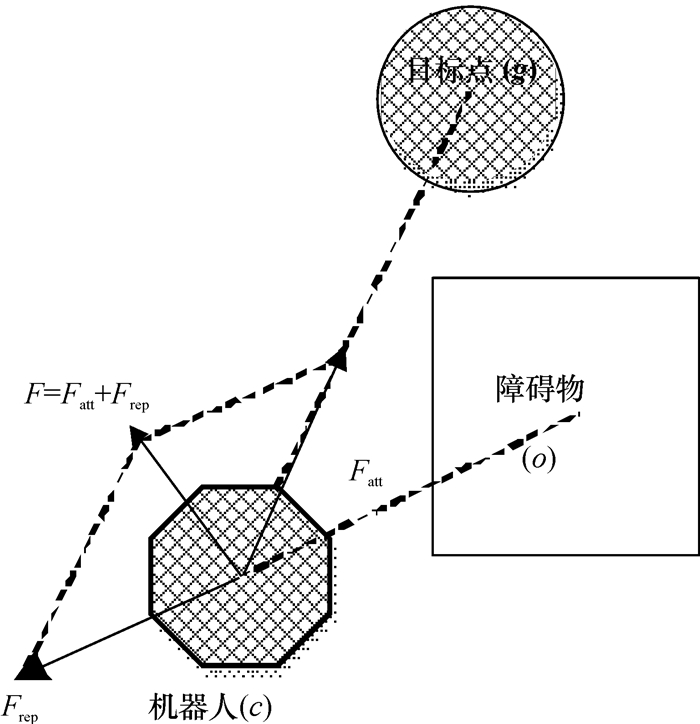
1 相关算法 1.1 人工势场法人工势场法的基本思想[9-11]是将机器人路径规划问题看作是在虚拟力场中的一种受力运动.如图 1所示,目标点g对机器人c产生吸引力Fatt; 相反,障碍物o对其产生排斥力Frep,最终机器人在斥力Frep与吸引力Fatt的合力F作用下,向着目标点逐步靠近,多次迭代后最终绕过障碍物到达目标点,实现无碰撞的路径规划.
|
图 1 机器人受力分析 Figure 1 Robot force analysis |
虽然人工势场法具备实时性高、运算量少的优点,但是它自身也有较多缺陷需要改进.
(1) 机器人在障碍物附近震荡而无法到达目标点;
(2) 存在局部极小点导致的陷阱区域;
(3) 在临近的障碍物之间不能发现路径.
由于使用势场法进行路径规划能够提高清洁机器人的安全性,但是规划的路径只能保证是无碰撞的.对于清洁机器人在墙边、窄缝与全面清扫等方面的实际清扫要求,仍需结合其他算法来取长补短,以满足应用需求[12-13].
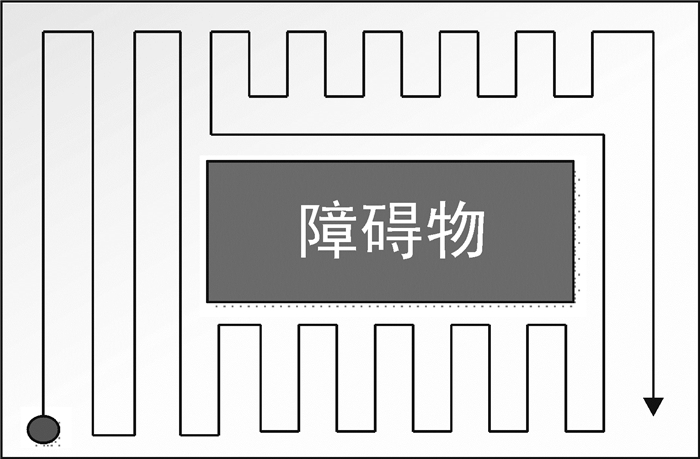
1.2 牛耕式全覆盖路径规划算法目前最常用的全覆盖算法是牛耕式的全覆盖路径规划算法,其基本思想[14]是:按照“左、下、上、右”4个固定的顺序,使机器人在室内进行全覆盖的移动,具体结果如图 2所示.
|
图 2 牛耕式全覆盖路径规划结果 Figure 2 Cattle farming full-coverage path planning algorithm result |
对于牛耕式的全覆盖路径规划算法,其优点是能够静态规划出全覆盖的清扫路径, 并且算法运算量少.而在较多障碍物的动态环境中使用牛耕模式全覆盖路径规划法会造成的问题是:单纯依靠“左、下、上、右”顺序进行避障会使最终的全覆盖路径结果存在更多的死节点与清扫盲点.为实现全覆盖,当进入死节点后需反复寻找未遍历区域进行回扫,而逃离过程会造成大量的路径重复,从而使得遍历路径更长,在障碍物数量较多情况下,该问题尤为严重.
牛耕全覆盖法规划路径结果较符合清洁的需求,但对于清洁机器人来说在保证覆盖效果的同时,仍需提高工作效率和动态避障能力.
2 改进的势场栅格法为充分发挥牛耕模式全覆盖路径规划算法的静态规划能力,以及人工势场法的动态避障优势,针对清洁机器人的实际应用需求,本文提出一种改进的势场栅格算法.该方法可让清洁机器人在已知环境中静态构建出全覆盖路径后再进行清扫,即使遇到无记录在地图文件中的障碍物时,仍能顺利无碰避障,有效减少了路径死节点与清扫盲点.
2.1 算法分析及流程介绍本节结合流程图分步解释提出的改进势场栅格法的具体实现方法:
(1) 将室内环境地图通过栅格法表示,本文划分栅格的大小根据市面上清洁机器人尺寸而定,每单元格约35 cm2,障碍物超过单元格1/3则判定该栅格机器人不可达.
(2) 确定机器人在栅格地图中的起始位置C,通过牛耕式全覆盖算法静态规划出遍历环境地图的全局总路径L.
(3) 在栅格地图上,将全局总路径L拆分为连续的栅格点集合:
| $ {\mathit{L}_\mathit{c}}{\rm{ = }}\left\{ {{\mathit{O}_{\rm{1}}}{\rm{, }}{\mathit{O}_{\rm{2}}}{\rm{, }}{\mathit{O}_{\rm{3}}}{\rm{ \ldots }}, {\mathit{O}_\mathit{n}}} \right\}{\rm{.}} $ | (1) |
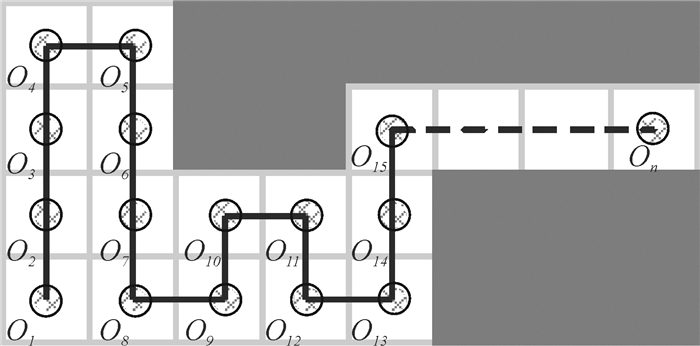
其中n的值与路径长短有关,但保证最后一个点On与总路径终点O重合,当机器人到达点On时表示算法结束.
其对应的路径拆解如图 3所示.
|
图 3 路径拆解图 Figure 3 Path decomposition |
(4) 在路径集合Lc中,将集合第一个点作为机器人的起始位置Xc=(x y)T,则集合L中下一个目标子点Oi会对机器人产生引力,机器人当前位置的引力势场函数为
| $ {U_{{\rm{att}}}}\left( {{X_c}} \right){\rm{ = }}\frac{1}{2}{k_{{\rm{att}}}}{\left( {{X_c}{\rm{ - }}{O_i}} \right)^2}. $ | (2) |
当机器人上下左右4个方向栅格中存在障碍物Xb时,会对机器人产生斥力,则机器人当前位置的斥力势场函数为
| $ \begin{array}{l} \;\;\;{\mathit{U}_{{\rm{rep}}}}\left( {{\mathit{X}_\mathit{c}}} \right){\rm{ = }}\\ \left\{ \begin{array}{l} \frac{1}{2}\mathit{\eta }{\left[{\frac{1}{{\mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right)}}-\frac{1}{{{\mathit{\rho }_{\rm{0}}}}}} \right]^2}\;, \mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right) \le {\mathit{\rho }_{\rm{0}}};\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right) > {\mathit{\rho }_{\rm{0}}}. \end{array} \right. \end{array} $ | (3) |
式(2)、(3) 中,katt为引力势场正比例增益系数;η为斥力势场正比例增益系数;ρ0为障碍物影响距离,可根据实际情况而定,本文设置为两个栅格长度;ρ(Xc, Xb)为机器人在当前空间位置Xc与障碍物Xb的最短距离,约一个栅格长度;
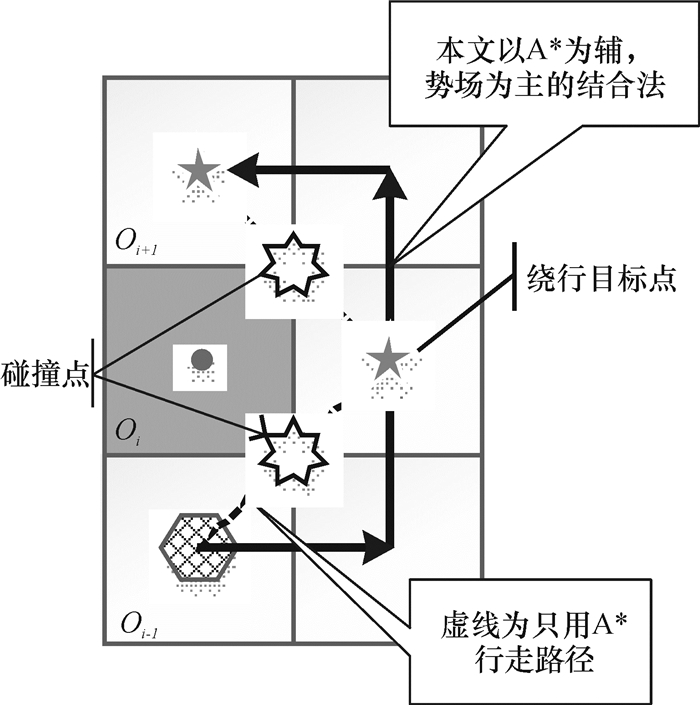
(5) 机器人在Oi-1处,判断下一个目标子点Oi是否被新增加的障碍物占据,如图 4所示,若被占据则再取下一个目标子点Oi+1作为目标点.实际上由于机器人与障碍物有一定尺寸,并且在机器人可八方位移动的条件下,如果此时只依靠A*算法绕行,当下一目标点在机器人的45°方向时,机器人会径直向目标点移动,则会出现如图 4所示的碰撞点,此时A*算法需重新迭代规划路径,使其目标点保证在机器人的上下左右4个连续的方向上.而本文采用以A*为辅寻找绕行目标点、势场法为主的移动方法优势在于只需通过一次A*算法求解最短路径后,每次向目标点移动时根据受力分析运算实现无碰避障的目的,而合力运算的时间复杂度远低于A*算法的代价函数时间复杂度.因此相比反复规划路径绕行障碍物时所消耗的运算代价更少.
|
图 4 障碍物绕行方法 Figure 4 Detour to avoid obstacles |
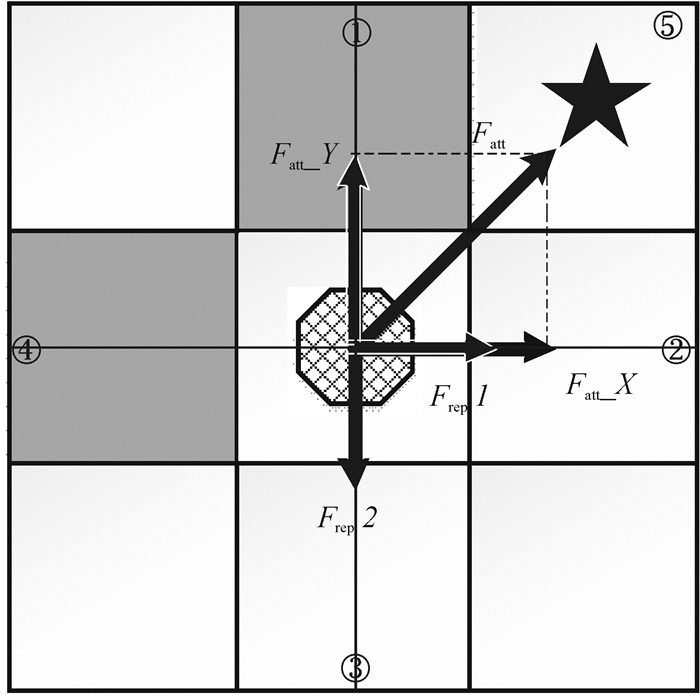
(6) 机器人每次移动时,根据当前位置Xc与目标子点Oi之间使用人工势场法进行受力分析及移动,其受力分析方法如图 5所示.
|
图 5 势场栅格法受力分析 Figure 5 Potential field grid method of stress analysis |
图 5中,中心处为机器人当前位置,而⑤ 处为目标子点Oi.⑤ 处目标子点会对机器人产生引力,吸引力Fatt(Xc)为引力势场函数的负梯度:
| $ {\mathit{F}_{{\rm{att}}}}\left( {{\mathit{X}_\mathit{c}}} \right){\rm{ = - grad}}\left[{{\mathit{U}_{{\rm{att}}}}\left( {{\mathit{X}_\mathit{c}}} \right)} \right]{\rm{ = }}{\mathit{k}_{{\rm{att}}}}\left( {{\mathit{O}_\mathit{i}}{\rm{ - }}{\mathit{X}_\mathit{c}}} \right){\rm{.}} $ | (4) |
将引力Fatt分解到X与Y轴上的两个分量Fatt_X与Fatt_Y,当Oi与Xc的Y轴相同、X轴不同时:
| $ {\mathit{F}_{{\rm{att\_}}\mathit{Y}}}{\rm{ = }}{\mathit{F}_{{\rm{att}}}}{\rm{|}}{\mathit{F}_{{\rm{att\_}}\mathit{X}}}{\rm{ = 0}}{\rm{.}} $ | (5) |
当Oi与Xc的X轴相同、Y轴不同时:
| $ {\mathit{F}_{{\rm{att\_}}\mathit{x}}}{\rm{ = }}{\mathit{F}_{{\rm{att}}}}{\rm{|}}{\mathit{F}_{{\rm{att\_}}\mathit{y}}}{\rm{ = 0}}{\rm{.}} $ | (6) |
其他情况:
| $ {\mathit{F}_{{\rm{att\_}}\mathit{X}}}{\rm{ = }}{\mathit{F}_{{\rm{att\_}}\mathit{Y}}}{\rm{ = }}{\mathit{F}_{{\rm{att}}}}{\rm{cos45^\circ }}{\rm{.}} $ | (7) |
而如图 5中的① 与④ 位置上的障碍物与机器人距离小于ρ。,则其会对机器人产生斥力Frep:
| $ \begin{array}{l} \;\;\;\;\;{\mathit{F}_{{\rm{rep}}}}{\rm{ = - grad}}\left( {{\mathit{U}_{{\rm{rep}}}}\left( {{\mathit{X}_\mathit{c}}} \right)} \right){\rm{ = }}\\ \left\{ \begin{array}{l} \mathit{\eta }\left[{\frac{1}{{\mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right)}}-\frac{1}{{{\mathit{\rho }_{\rm{°}}}}}} \right]\frac{1}{{{\mathit{\rho }^{\rm{2}}}\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right)}}\frac{{\partial \mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right)}}{{\partial {\mathit{X}_\mathit{c}}}}, \\ \;\;\;\;\;\;\;\mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right) \le {\mathit{\rho }_{\rm{0}}};\\ 0, \;\;\;\;\;\mathit{\rho }\left( {{\mathit{X}_\mathit{c}}{\rm{, }}{\mathit{X}_\mathit{b}}} \right) \le {\mathit{\rho }_{\rm{0}}}. \end{array} \right. \end{array} $ | (8) |
式(8) 中,
由于障碍物的作用范围仅且只有在机器人4个方向时才会对机器人产生斥力作用,并距离相同,所以
| $ \left| {{\mathit{F}_{{\rm{rep1}}}}} \right|{\rm{ = }}\left| {{\mathit{F}_{{\rm{rep2}}}}} \right|{\rm{.}} $ | (9) |
但两者的作用方向不同,按照斥力只对引力起削弱作用而不起增强作用规则,最终受力分析则如图 5所示,可得知② 方向的引力最大,其次为① 方向被斥力Frep2削弱的引力Fatt_2,代表机器人接下来的移动规则是,先右转移动一步,再向上移动一步,到达目标子点.为避免斥力完全抵消引力的情况出现,可通过调节katt引力增益系数与η斥力增益系数来对引力Fatt与斥力Frep大小作出相应的调节,调整结果需保证:
| $ \left| {{\mathit{F}_{{\rm{rep}}}}} \right| < \left| {{\mathit{F}_{{\rm{att}}}}{\rm{cos45^\circ }}} \right|{\rm{.}} $ | (10) |
由欧阳鑫玉等提出的势场栅格法只是把栅格作为辅助控制力逃离陷阱区域[15].而雷艳敏等改进的势场栅格法[16],需要每次求解8个方向势场极小点,而且如图 5情况时机器人会直接向目标点移动,而实际情况中会与障碍物① 发生碰撞.对比这些方法,本文提出的改进势场栅格法具有较好优势,只需求解一次合力运算,并且考虑了机器人与障碍物尺寸问题避免碰撞.关于障碍物其他分布情况下的受力分析亦如图 5例子所示.
(7) 每当机器人到达下一个目标子点后,将当前位置Xc=(x y)T设置为到达的目标子点Oi的坐标值,并且将i值自加一,取下一目标子点.
(8) 判断机器人当前位置是否已经到达最终目标点O,若否则跳转到步骤(4),继续迭代逐步移动.若是则算法结束,代表清洁机器人已经完成了全覆盖的清扫任务.
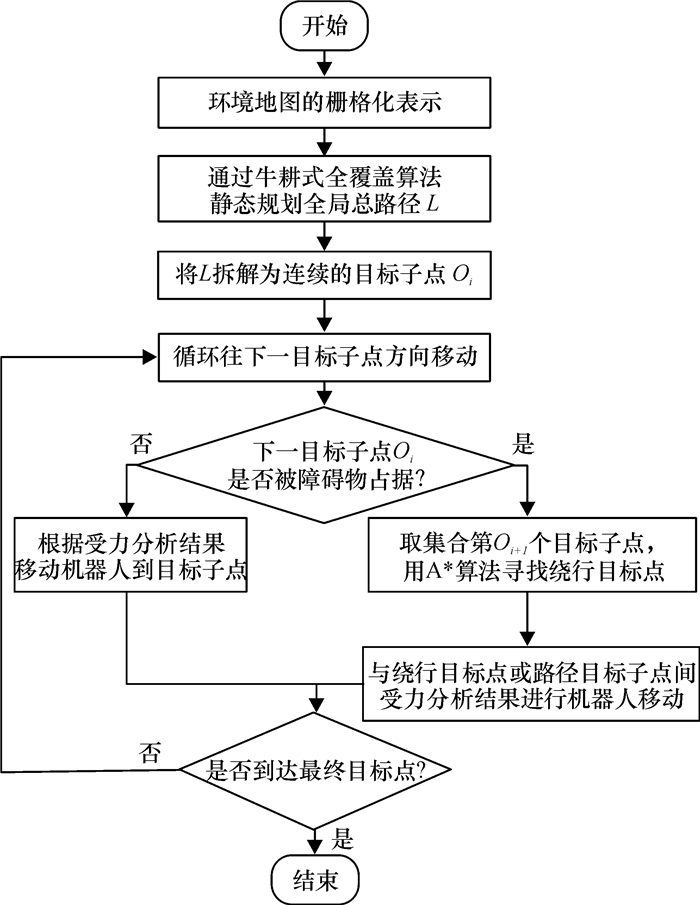
其对应的算法流程图如图 6所示.
|
图 6 改进的势场栅格法流程图 Figure 6 Flow chart of improved potential field grid method |
针对人工势场法中与目标点进行路径规划时存在的问题,本节主要介绍用本文提出的改进势场栅格法,是如何可以对存在的问题进行逐一解决.
2.2.1 机器人在障碍物附近震荡而无法到达目标点的问题解决由于机器人作用范围内有随机分布的障碍物以及目标点靠近障碍物时导致所受合力方向经常变化,使得机器人在移动过程中会出现震荡、摆动及无法到达目标点现象.
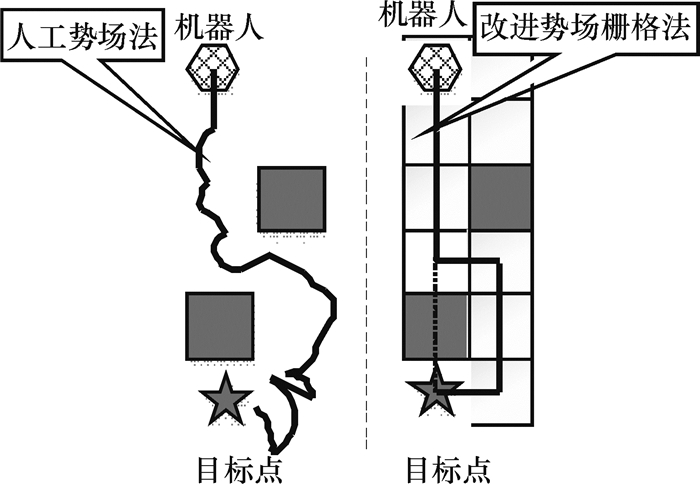
而本文提出的方法主要考虑机器人下一步可能会移动的4个方向中存在的障碍物,并且将合力分解到相邻的栅格中,这样机器人根据合力移动时会逐个栅格移动,从而解决了没有栅格引导情况下出现的震荡、摆动以及无法到达目标点问题.具体如图 7所示.
|
图 7 平稳到达障碍物附近目标点 Figure 7 Safe arrival of the target near the barrier |
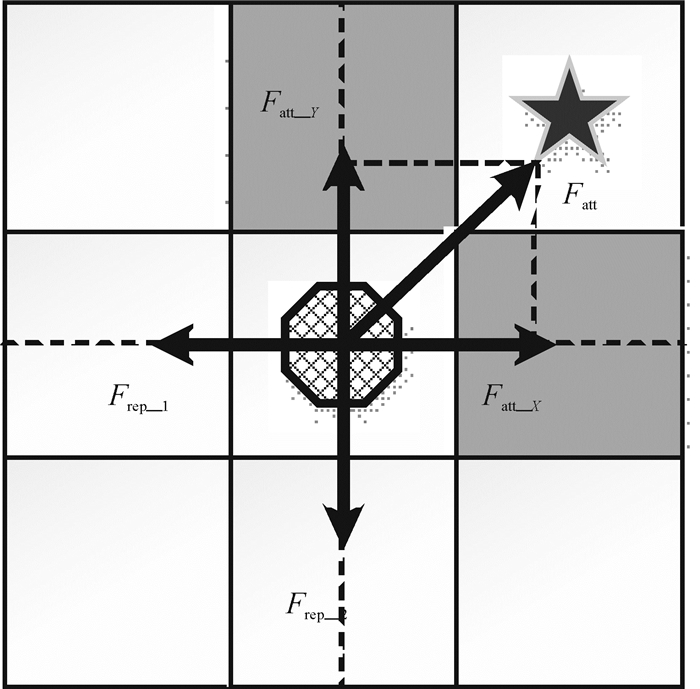
局部极小点的出现是由于机器人所受斥力与吸引力的合力为零的时候,无法判断下一步移动方向而导致的,即如图 8所示代表机器人进入了陷阱区域,但根据式(10) 可知斥力无法完全抵消引力,假设出现:
| $ {\rm{|}}{\mathit{F}_{{\rm{ATT\_X}}}}\left| {\rm{ = }} \right|{\mathit{F}_{{\rm{ATT\_Y}}}}\left| {\rm{ = }} \right|{\mathit{F}_{{\rm{ATT}}}}{\rm{cos45^\circ }}\left| {\rm{ - }} \right|{\mathit{F}_{{\rm{rep}}}}{\rm{|, }} $ | (11) |
|
图 8 机器人进入陷阱区域 Figure 8 Robots into trap area |
则认为机器人进入陷阱区域,无法判断下一步移动方向.
这种情况下,由于静态规划全局总路径的时候,每次选取的目标子点是保证上下左右4个方向连续的,即可得知图 8中两个障碍物或之一是规划出路径之后出现的移动障碍物,本文采取的方法是先等待时间t s后再查看障碍物是否仍然存在(t为固定时间值,不宜过长,本文设置为1 s),若否就继续移动,否则把该目标子点作为逃离目标点,然后如步骤(5) 中通过A*算法寻找绕行目标子点作为临时目标点,使机器人顺利逃离陷阱区域.
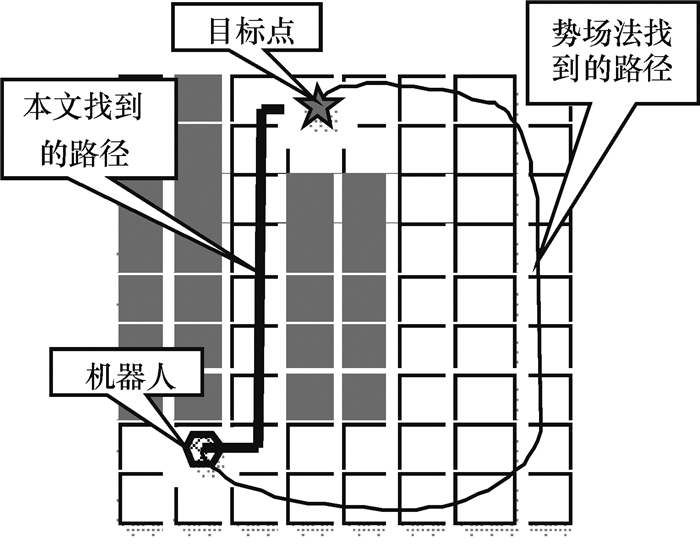
2.2.3 邻近障碍物之间不能发现路径的问题解决在虚拟的势场中,邻近的障碍物与目标点对机器人的合力方向,通常是不会指向两个障碍物间的路径,而是绕过障碍物到达目标点,这使得清洁机器人无法清扫窄缝区域.而本文提出的方法能够遍历出障碍物间的清扫路径,对如图 9所示的情形, 只要栅格大小是根据机器人尺寸而定,则可保证找出的路径结果能够使机器人顺利通过,从而使清洁机器人实现清扫窄缝区域的目的.
|
图 9 邻近障碍物间发现路径 Figure 9 The path between adjacent obstacles |
本文提出的方法已在实际开发的清洁机器人系统中得以验证,该系统在市面清洁机器人的基础上进行二次开发,安装了360°激光雷达传感器,并配备自主研发的智能软件系统,如图 10所示.本系统处理器采用的是常用的ARM-32位芯片,型号为STM32F103VBT6,主频72 MHz,其中智能路径规划和避障部分就是采用本文的改进势场栅格法.

|
图 10 带激光雷达的清洁机器人 Figure 10 Cleaning robot with laser radar |
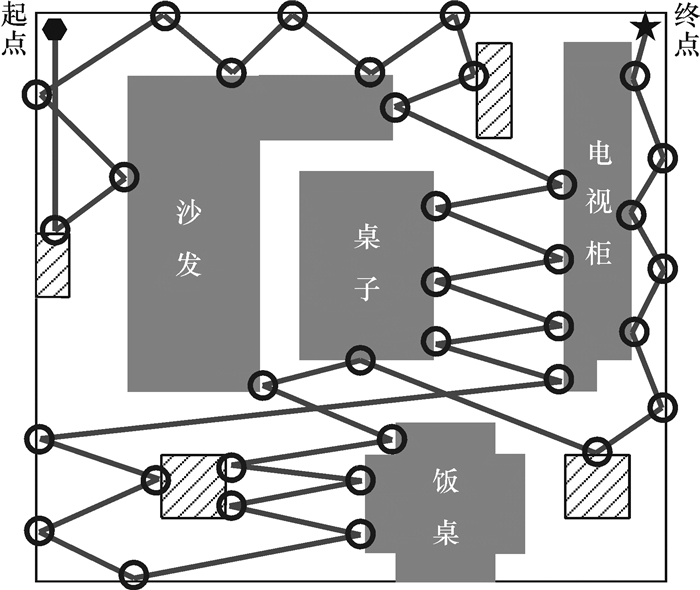
实验环境如图 11所示,是一个尺寸约6 m×7 m大小的家庭客厅环境空间,其中包含沙发、桌子、饭桌与电视柜等家具,通过SLAM算法[17]可以构建室内的环境地图.除了在环境地图中保存的家具障碍物外,环境空间内还可能存在若干个没有记录在地图文件中的新增障碍物(图中斜线方格表示).实验期望结果是,清洁机器人能够有序完成家庭环境内的全面清扫,包括墙边、窄缝等卫生死角,当遇到无记录的新增障碍物时能够实现无碰撞避障后,仍能继续全覆盖清扫.
|
图 11 清洁机器人清扫时经过路径结果 Figure 11 Cleaning robot path result |
将普通清洁机器人不作任何改进,放在左上角开始清扫工作,其将会在室内进行碰撞随机全覆盖清扫,即碰撞到障碍物后随机转一定角度后继续前行,如此反复,清洁机器人所走的这些路径随机性和不确定性较大[14].持续一段时间后,将清洁机器人本次的移动轨迹记录如图 11所示,图中圆圈位置代表机器人与障碍物发生碰撞处.
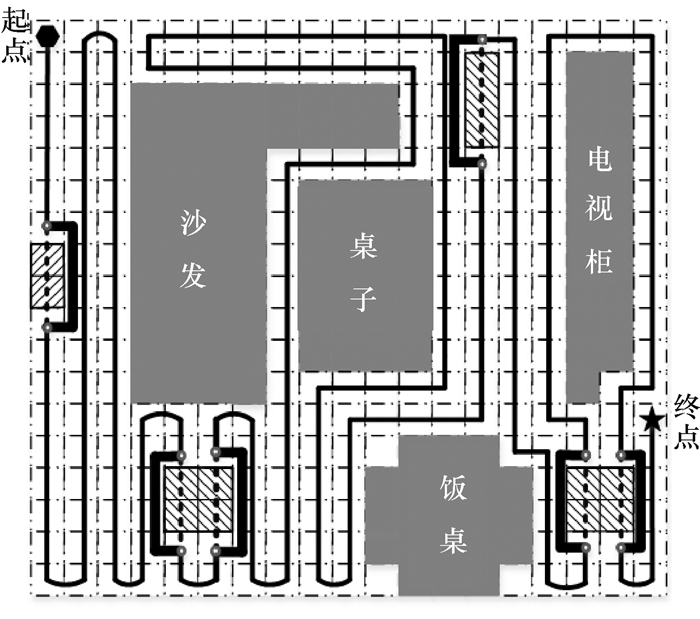
而在普通清洁机器人上添加激光雷达传感器或其他红外传感器,结合本文提出的改进势场栅格法,在得到的环境地图上静态规划出全覆盖的清扫总路径后,再通过势场栅格法实现动态的无碰撞避障,在相同的实验环境做对比实验,结果如图 12所示.考虑到机器人在实际移动过程中存在的累积误差,本文通过陀螺仪传感器实现误差的修正[18].
|
图 12 本文算法的清扫路径结果 Figure 12 Cleaning path result of this algorithm |
通过两次对比实验结果可知,当清扫过程中出现未记录在环境地图中的障碍物时,仍能使清洁机器人无碰撞的动态避障(图 12中斜线方格旁边的粗线为避障路径),并且避障后仍能保持全覆盖路径继续清扫,实现了低路径重复率的高效清扫路径规划,能够有效解决目前市面上清洁机器人存在的不足之处.保证了其安全性的同时,对于窄缝、墙边等卫生盲点也能自动清扫,很好地提高工作效率,达到了预期的实验目标.两者对比结果如表 1所示.
| 表 1 对比结果 Table 1 Results of comparison |
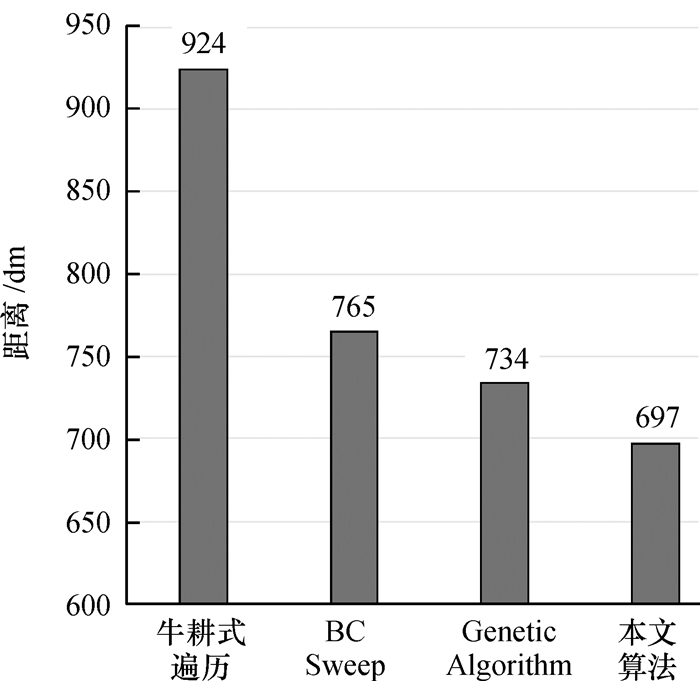
如果在动态的室内环境中仅依靠牛耕式全覆盖算法进行空间环境的遍历,会出现如本文第1.2节所述的问题,使得路径结果过长.而使用文献[7]中提出的BC-Sweep覆盖算法,每次进行路径选择时会根据路径的能量消耗量f(x)与目前剩余量来决定下一步的决策.对于文献[8]提出的遗传算法与牛耕算法结合的覆盖算法,先以牛耕法设置环境中区域点后,再通过选择、交叉与变异等操作后,得到遍历所有目标点的最短路径,是一个类似TSP问题的解决方法.由于路径重复率较大会造成过度清洁的问题,而且使得清洁机器人的耗电更大.经过对比实验,在遍历约40 m2的空间环境、包含5个无记录障碍物时,本文方法与其他全覆盖算法遍历路径长度结果如图 13所示.
|
图 13 遍历距离长度对比 Figure 13 Comparison of traversing distance length |
在较大环境空间及更多障碍物的情况下,各个算法结果差距会更大.虽然加入人工智能算法或其他控制条件后提高了路径规划的效果,但是在硬件资源受限的嵌入式系统中设计算法时,对于算法运行时的系统消耗也是一项重要指标.在本嵌入式系统的硬件条件下,分别按照上述的4种算法运算后得出下一步移动目标,每种算法取10次计算时间做对比实验,结果如图 14所示.
|
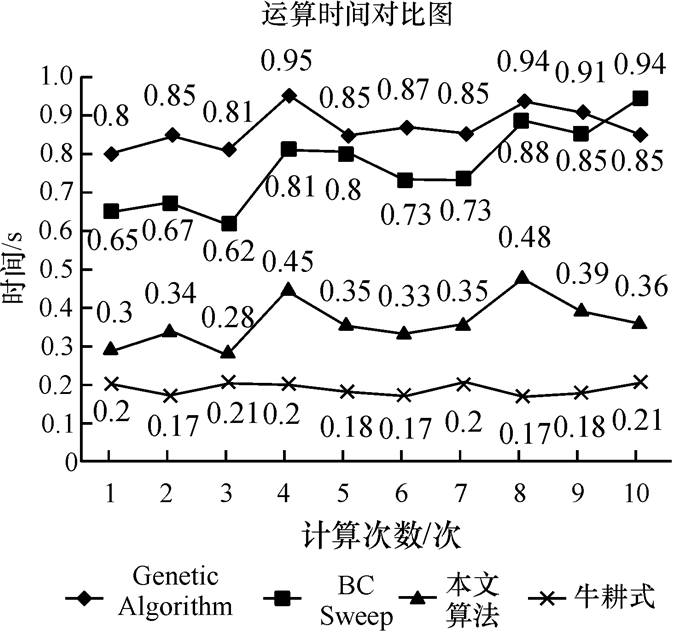
图 14 计算时间对比 Figure 14 Comparison of Computing time |
从图 14可知,只根据4个方向障碍物情况的牛耕算法运算量少,计算下一运动方向的耗时最短,但其路径过长.而遗传算法与牛耕法结合的覆盖算法由于增加了大量的选择、交叉与变异等运算,系统耗时最大,每次平均运算时间约0.87 s,使得机器人每步移动间隔有明显的停顿感.而BC-Sweep算法在电量充足情况下能较快计算出下一步移动方向,但随着电量的减少,更多的路径限制条件使得计算时间略有上升,平均计算时间约0.76 s.相比可知本文提出的势场栅格法具有算法运算量少、实时性高的优势,平均计算时间0.36 s,使得机器人每步移动时的间隔短,覆盖清扫过程更加流畅.其中各个算法的第4和第8次运算时间有一定的波动是由于机器人遇到无记录的障碍物,进行避障时造成的一些额外开销导致的.
4 结论本文针对目前市面上清洁机器人上存在的实际问题,提出了一种结合牛耕式全覆盖算法与人工势场法优点的改进势场栅格法,使清洁机器人在已知室内环境的栅格地图中,静态规划出全局路径进行全覆盖清扫,发现障碍物时具备避障能力.由实际的实验结果可知,综合路径长度与运算耗时等因素,在保证全覆盖清扫的最终目的下,本文提出的算法能提高清洁机器人安全性的同时,对于窄缝、墙边等卫生死角也能清洁到位,并且能在资源受限的嵌入式实时系统中以更短的时间、更少功耗遍历家庭空间环境,有效提高工作效率.该方法已应用于实际智能清洁机器人产品,结合激光雷达装置使得系统整个运行过程实现无碰撞、低路径重复率的高效清扫,在实际中获得了满意的实验效果.
| [1] |
简毅, 张月. 移动机器人全局覆盖路径规划算法研究进展与展望[J].
计算机应用, 2014, 34(10): 2844-2849.
JIAN Y, ZHANG Y. Complete coverage path planning algorithm for mobile robot: progress and prospect[J]. Journal of Computer Applications, 2014, 34(10): 2844-2849. DOI: 10.11772/j.issn.1001-9081.2014.10.2844. |
| [2] |
徐李超, 张祺. 一种仿人机器人步态优化的新方法研究[J].
广东工业大学学报, 2012, 29(1): 50-54.
XU L C, ZHANG Q. Gait Optimizing of humanoid robots using a new method[J]. Journal of Guangdong University of Technology, 2012, 29(1): 50-54. |
| [3] | GUAN H K, CHI Y C, CHEN J W.Design and implementation of a remote monitoring cleaning robot[C]//Automatic Control Conference, 2014 CACS International.Kaohsiung:IEEE, 2014:281-286. |
| [4] |
刘杰, 闫清东, 唐正华. 基于激光雷达的移动机器人避障控制研究[J].
计算机测量与控制, 2015, 23(3): 787-790.
LIU J, YAN Q D, TANG Z H. Research on indoor obstacle avoidance of mobile robot base on laser radar[J]. Computer Measurement and Control, 2015, 23(3): 787-790. |
| [5] |
夏琴晔, 杨宜民. 基于biSCAN和SVM的机器人目标识别新算法研究[J].
广东工业大学学报, 2013, 30(4): 65-69.
XIA Q Y, YANG Y M. Research on a new algorithm for robots' recognition of objects based on biSCAN and SVM[J]. Journal of Guangdong University of Technology, 2013, 30(4): 65-69. |
| [6] |
郝宗波, 洪炳镕, 黄庆成. 基于栅格地图的机器人覆盖路径规划研究[J].
计算机应用研究, 2007, 24(10): 56-58.
HAO Z B, HONG B R, HUANG Q C. Study of coverage path planning based on grid-map[J]. Application Research of Computers, 2007, 24(10): 56-58. DOI: 10.3969/j.issn.1001-3695.2007.10.016. |
| [7] | STRIMEL G P, VELOSO M M. Coverage planning with finite resources[C]//2014 IEEE/RSJ International Conference on Intelligent Robots and Systems. Chicago, Illinois:IEEE, 2014:2950-2956. |
| [8] | WANG Z M, BO Z.Coverage path planning for mobile robot based on genetic algorithm[C]//2014 IEEE Workshop on Electronics, Computer and Applications.Ottawa, Ontario:IEEE, 2014:732-735. |
| [9] |
殷路, 尹怡欣. 基于动态人工势场法的路径规划仿真研究[J].
系统仿真学报, 2009, 21(11): 3325-3329.
YIN L, YIN Y X. Simulation research on path planning based on dynamic artificial potential field[J]. Journal of System Simulation, 2009, 21(11): 3325-3329. |
| [10] |
于振中, 闫继宏, 赵杰. 改进人工势场法的移动机器人路径规划[J].
哈尔滨工业大学学报, 2011, 43(1): 50-55.
YU Z Z, YAN J H, ZHAO J. Mobile robot path planning based on improved artificial potential field method[J]. JOURNAL OF HARBIN INSTITUTE OF TECHNOLOGY, 2011, 43(1): 50-55. DOI: 10.11918/j.issn.0367-6234.2011.01.011. |
| [11] |
王芳, 李昆鹏, 袁明新. 一种人工势场导向的蚁群路径规划算法[J].
计算机科学, 2014, 41(11): 47-50.
WANG F, LI K P, YUAN M X. Ant colony algorithm based on optimization of potential field method for path planning[J]. Computer Science, 2014, 41(11): 47-50. |
| [12] |
张殿富, 刘福. 基于人工势场法的路径规划方法研究及展望[J].
计算机工程与科学, 2013, 35(6): 88-95.
ZHANG D F, LIU F. Research and development trend of path planning based on artificial potential field method[J]. Computer Engineering and Science, 2013, 35(6): 88-95. |
| [13] | HASSANZADEH I, MADANI K, BADAMCHIZADEH M A.Mobile robot path planning based on shuffled frog leaping optimization algorithm[C]//2010 IEEE Conference on Automation Science and Engineering. Toronto, Ontario:IEEE, 2010:680-685. |
| [14] | HASAN K M, REZA K J.Path planning algorithm development for autonomous vacuum cleaner robots[C]//2014 International Conference on Informatics, Electronics&Vision.Dhaka:IEEE, 2014:1-6. |
| [15] |
欧阳鑫玉, 杨曙光. 基于势场栅格法的移动机器人避障路径规划[J].
控制工程, 2014, 21(1): 134-137.
OUYANG X Y, YANG S G. Obstacle avoidance path planning of mobile robots based on potential grid method[J]. Control Engineering of China, 2014, 21(1): 134-137. |
| [16] |
雷艳敏, 冯志彬. 改进的势场栅格法在机器人路径规划中的应用[J].
长春大学学报, 2009, 19(1): 38-42.
LEI Y M, FENG Z B. The application of the improved potential grid method in robot path planning[J]. Journal of Changghun University, 2009, 19(1): 38-42. |
| [17] | Thrun S. Probabilistic Robotics[M]. USA: MIT Press, 2005: 281-308. |
| [18] |
季秀才, 郑志强, 张辉. SLAM问题中机器人定位误差分析与控制[J].
自动化学报, 2008, 34(3): 323-333.
JI X C, ZHENG Z Q, ZHANG H. Analysis and control of robot position error in SLAM[J]. Acta Automatica Sinica, 2008, 34(3): 323-333. |
 2016, Vol. 33
2016, Vol. 33