2. 广东怡创科技股份有限公司,广东 广州 510006
2. Guangdong Iscreate Polytron Technologies Inc, Guangzhou 510006, China
随着移动互联网的迅速发展,通信网络的结构越来越复杂, 导致各个电信运营商的成本和维护工作量迅速增加,因此,控制网络运维成本成为提高企业竞争力的重要方面.对网络运维成本的控制不但要保证网络运行的安全与可靠,还要注意适度的原则,平衡好网络运行质量和企业成本及效益间的关系[1].而网络运维中现场作业的调度成本是网络运维成本的重要组成部分,网络运维中现场作业调度是根据作业任务的目标和服务质量保证约束条件,为每个现场作业任务分配合适的资源(维护人员、工具、车辆)来完成作业任务.网络运维中的现场作业任务调度与传统的任务调度问题不同,所需要进行分配资源的状态、位置是不断动态变化的,因此,这也是一类NP-hard问题.
近年来,遗传算法经常被引入到大规模的资源调度中,并取得了不错的效果.遗传算法(Genetic Algorithm)是模拟自然界生物进化过程的经典寻优算法,常被用来解决各种工程问题.本文主要讨论的是如何有效降低网络运维现场作业的调度成本,以提高资源的利用率和服务质量.同时随着运营商网络的讯速发展,需要完成作业任务的数量也越来越多,如何在完成大量作业任务的同时,又能保证服务质量是通信代维企业需要考虑的问题.
1 问题描述本文主要讨论当作业任务数量远多于资源数量时的调度策略,对于如何获取资源信息、获取作业任务的详细信息等问题不在此讨论范围.网络运维现场作业调度问题描述如下:这里的资源分为3类,即维护人员、车辆、工具.资源的总数为M,其中维修人员P的数量为f,对应集合P={P1,P2,…,Pf };车辆A的数量为c,对应的集合A={A1,A2,…,Ac };工具S的数量为t,对应的集合S={S1,S2,…,St };需要完成的作业任务O的数量是n,对应的集合O={O1,O2,…,On },一个f×n的矩阵E[f,n]表示维护人员Pi完成作业任务Oj预计需要的时间,一个m×m的矩阵D[m,m]表示维护人员完成从一个任务地点到达另一个任务地点的时间.网络运维中的资源调度就是根据作业任务对不同种类资源的需求为其分配合适的资源,并且能够保证每个作业任务在任务的截止日期之前完成.网络运维中的一次有效的调度是每个作业任务获取到所需资源之后,总任务执行时间最短,以期望能够获得较好的服务质量,降低网络运维的成本.
2 遗传算法求解遗传算法(Genetic Algorithm)是一种全局优化的搜索算法,借鉴于生物界的进化思想和自然界的“优胜劣汰”的自然选择机制,具有全局性和并行性特点[2-3],经常被用来求解大规模的资源调度问题,网络运维中现场作业的资源调度问题也是一类任务分配与调度问题,这里同样采用遗传算法来解决网络运维现场作业调度问题,并对遗传算法当中易陷入局部最优、过早收敛等缺点进行了一些改进.
2.1 染色体的编码与解码目前染色体的编码方式有很多种,而对于任务调有度问题,编码方式可以分为两种:直接编码和间接编码.直接编码比较简单,直接针对问题空间进行编码;而间接编码的针对性更强,更能反映问题的实际情况[4-7].结合遗传算法的特点和网络运维中现场作业调度的实际情况,这里采用基于作业任务-资源的间接编码方式,每一个作业任务和资源都有一个编号,而每一条染色体是由一系列的资源编号组成.设CHk代表种群中的第k条染色体,Pki、Aki、Ski代表k条染色体的基因,其中Pki表示第i个作业任务使用编号Pki的维护人员,Aki表示第i个作业任务使用编号Aki的车辆,Ski表示第i个作业任务使用编号Ski的工具,因此一条染色体可以表示为
| $ \text{C}{\text{H}_\mathit{k}}{\rm{=\{ }}{\mathit{P}_{\mathit{k}{\rm{1}}}}, {\mathit{A}_{\mathit{k}{\rm{1}}}}, {\mathit{S}_{\mathit{k}{\rm{1}}}}, {\mathit{P}_{\mathit{k}{\rm{2}}}}, {\mathit{A}_{\mathit{k}{\rm{2}}}}, {\mathit{S}_{\mathit{k}{\rm{2}}}}{\rm{ \ldots }}, {\mathit{P}_{\mathit{kn}}}{\rm{, }}{\mathit{A}_{\mathit{kn}}}{\mathit{S}_{\mathit{kn}}}{\rm{\} }}{\rm{.}} $ |
现在假设维护人员的数量f为2,对应集合为P={P1,P2},车辆数量c为2,对应的集合为A={A1,A2},工具的数量t为2,对应的集合为S={S1,S2},现有的作业任务数量n为5,对应的集合O={O1,O2,O3,O4,O5 },这里的染色体的长度为l, 则l=2f+1,因为每个维护人员都需要一个工具来执行任务,同时需要一辆车来运送他们到达目的任务地点.染色体上的每一位的基因值代表了对应资源的编号,采用随机的方式可以确定多种不同的分配方案,例如:
(1)P1:1→3→4,P2:2→5,A1:1→2→3,A2:4→5,S1:1→3→4,S2:2→5.
(2)P1:1→4,P2:2→3→5,A1:1→2→5,A2:3→4,S1:1→4,S2:2→3→5.
(3)P1:3→4,P2:1→2→5,A1:1→3,A2:2→4→5,S1:3→4,S2:1→2→5.
其中每个作业任务需要的维护人员的数量和对应的工具的数量一致,因为维护人员需要相应的工具去执行任务.由于在网络运维现场作业调度中各个作业任务并无任何依赖关系,因此各个作业任务的执行顺序可以任意排列,对于上述分配方案对应的染色体编码如下:
(1) 111212111121222,P1:1→3→4,P2:2→5,A1:1→2→3,A2:4→5,S1:1→3→4,S2:2→5.
(2) 111212222121212,P1:1→4,P2:2→3→5,A1:1→2→5,A2:3→4,S1:1→4,S2:2→3→5.
(3) 212222111121222,P1:3→4,P2:1→2→5,A1:1→3,A2:2→4→5,S1:3→4,S2:1→2→5.
其中{111212111121222}表示第1,3,4个作业任务由维护人员P1完成,第2、5个作业任务由维护人员P2完成,同理可以得到其他染色体对应的含义.
此外,如果作业任务的数量或者资源的数量超过10,则在编码的过程中每一位资源需要用2位或者更多位来表示.例如维护人员的数量为15,车辆的数量为10,工具的数量为15,则其中一个染色体编码为06050902041013……表示第一个作业任务使用编号为6、5和9的维护人员,编号为2的车辆以及编号为4、10和13的工具来完成作业任务,以此类推.
2.2 初始种群的生成结合网络运维中现场作业调度的实际情况,本文采用基于作业任务地理位置的随机方式生成初始种群,这样有利于降低调度成本,缩短任务的完成时间.由于这里主要的调度对象是人,而不是机器,因此需要考虑人的主观感受、能力差异、心理因素、公平原则等,所以在生成初始种群的过程中,将某个作业任务O分配维护人员P的时候,首先需要获取该作业任务周边可用的维护人员,然后从中选出负担的作业任务数量低于事先设置的任务数量临界值h并且拥有的任务数量较少的维护人员分配给该作业任务,使得每个维护人员负担的任务数量尽量平均,有利于提高任务的完成质量和资源的利用率.
2.3 适应度函数适应度函数是决定遗传算法的进化方向,因此适应度函数的选取对于遗传算法的搜索效率尤为重要.在网络运维现场作业调度中,作业任务调度需要同时满足企业对调度成本的控制和用户对服务质量的需求这两个目标,而传统的遗传算法多以单一目标作为适应度函数,并不适合网络运维中的现场作业调度,这里结合网络运维中现场作业调度的实际情况选取调度成本、任务的总完成时间作为目标来衡量用户对服务质量的需求.这里使用一个权重向量α来衡量用户对这两个目标的不同偏好程度:
| $ \mathit{\alpha }{\rm{=\{ }}{\mathit{\alpha }_{\rm{1}}}{\rm{, }}{\mathit{\alpha }_{\rm{2}}}{\rm{\}, (}}{\mathit{\alpha }_{\rm{1}}}{\rm{+}}{\mathit{\alpha }_{\rm{2}}}{\rm{=1)}}{\rm{.}} $ | (1) |
设任务Oi实际的资源消耗量为Mi,预期的资源消耗量为Yi,则对任务Oi的用户满意度函数为
| $ {\mathit{D}_\mathit{i}}{\rm{=}}\mathit{\theta }{\rm{ln(}}{\mathit{M}_\mathit{i}}{\rm{/}}{\mathit{Y}_\mathit{i}}{\rm{), }}\left( {{\rm{0 < }}\mathit{\theta } \le {\rm{1}}} \right). $ | (2) |
其中θ代表企业对于资源消耗的满意系数,当作业任务实际资源消耗量Mi与预期资源消耗量Yi越接近时,用户的满意度就越高,函数值越接近于0.如果Di>0,说明实际的资源消耗量大于预期的资源消耗量;反之,如果Di<0,说明实际的资源消耗量小于预期的资源消耗量.
2.3.1 调度成本调度成本是通信维护企业对于成本控制的一部分,网络运维中现场作业的调度成本主要包括维护人员的费用、车辆运送维护人员的费用以及其他的费用.
设现有M×N维的矩阵S[M,N],其中S[i,j]表示第j个维护人员完成第i个作业任务所期望的成本,P×Q维的矩阵V[P,Q],则V[i,j]表示从任务地点i到任务地点j的期望成本,则执行第Pi个作业任务所需的成本表示为
| $ \mathit{c}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)=}}\sum\nolimits_{\mathit{i}{\rm{=1}}}^\mathit{k} {\mathit{\boldsymbol{S}}\left[{\mathit{i}{\rm{, }}\mathit{j}} \right]} {\rm{+}}\sum\nolimits_{\mathit{i}{\rm{=1}}}^\mathit{k} {\mathit{\boldsymbol{V}}\left[{\mathit{i}{\rm{, }}\mathit{j}} \right]} . $ | (3) |
对于
| $ \mathit{E}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)=}}\mathit{\theta }{\rm{ln}}\left[{\mathit{c}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)}}/{\mathit{c}_\mathit{e}}} \right]. $ | (4) |
每个作业任务的总完成时间包括任务的完成时间、开始时间最迟完成时间等,这里选取作业任务执行的总完成时间作为企业对时间需求的判断标准.
设有M×N维的矩阵T[M,N],T[i,j]表示维护人员i完成作业任务j的期望完成时间,另有P×Q的矩阵C[P,Q],C[i,j]表示车辆从任务地点i到任务地点j的期望时间,因此作业Pi的执行时间可以表示为
| $ \mathit{t}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)=}}\sum\nolimits_{\mathit{i}{\rm{=1}}}^\mathit{k} {\mathit{\boldsymbol{T}}\left[{\mathit{i}{\rm{, }}\mathit{j}} \right]} +\sum\nolimits_{\mathit{i}{\rm{=1}}}^\mathit{k} {\mathit{\boldsymbol{C}}\left[{\mathit{i}{\rm{, }}\mathit{j}} \right].} $ | (5) |
对于
| $ \mathit{I}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)=}}\mathit{\theta }{\rm{ln}}\left[{\mathit{t}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)}}/{\mathit{c}_\mathit{t}}} \right]. $ | (6) |
对于网络运维中现场作业调度来说,需要同时考虑调度总成本和任务总完成时间这两个目标.但是如果这两个目标分别达到最优有可能无法达到整体最优,因此必须要在这两者之间寻找一种平衡.因此现场作业调度的适应度函数为
| $ \mathit{F}{\rm{=}}{\mathit{\alpha }_{\rm{1}}}\sum\limits_{\mathit{i}{\rm{=1}}}^\mathit{n} {\mathit{E}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)}}} {\rm{+}}{\mathit{\alpha }_{\rm{2}}}\sum\limits_{\mathit{i}{\rm{=1}}}^\mathit{n} {\mathit{I}{\rm{(}}{\mathit{P}_\mathit{i}}{\rm{)}}} {\rm{, (0}} \le {\mathit{\alpha }_\mathit{i}} \le {\rm{1)}}. $ | (7) |
其中αi是前面设定的权重系数,最终的目标就是求min(F)的解.
2.4 遗传操作算子 2.4.1 选择选择建立在种群的个体适应度基础上,是遗传算法对个体的评价方式[8].结合网络运维中现场作业调度的实际情况,选择算子根据每个个体的适应值占整个种群总适应值比例来确定.设种群的规模为Z,对适应度函数值为Fi的染色体个体,选择概率为
| $ {\mathit{Q}_\mathit{i}}{\rm{=}}{\mathit{F}_\mathit{i}}{\rm{/}}\sum\nolimits_{\mathit{j}{\rm{=1}}}^\mathit{z} {{\mathit{F}_\mathit{j}}} {\rm{.}} $ | (8) |
交叉是将两个染色体的部分结构互相替换而生成新染色体的操作[9-16],本文的交叉操作采用单点交叉.首先,产生一个随机数k,k即为杂交点,然后通过将两个染色体杂交点前后的部分交换来生成两个新的染色体.例如,111212111121222和21222111121222是两条染色体,设随机产生的交叉位置随机数为5,则进行交叉操作后新生成的两条染色体为111212111121222和212222111121222.
本文对于交叉概率的选取采用自适应的方式,避免交叉概率选择过大对于高适应度的个体结构造成破坏或者交叉概率选取过小降低算法的搜索效率.交叉概率pc的自适应调整公式为
| $ {\mathit{p}_\mathit{c}}{\rm{= }}\left\{ \begin{array}{l} \frac{{{\mathit{k}_{\rm{1}}}{\rm{(}}{\mathit{F}_{{\rm{max}}}}{\rm{ - }}\mathit{F'}{\rm{)}}}}{{{\mathit{F}_{{\rm{max}}}}{\rm{ - }}\mathit{F'}}}{\rm{, }}\mathit{F'} \ge {\mathit{F}_{{\rm{avg}}}}{\rm{;}}\\ {\mathit{k}_{\rm{2}}}, \mathit{F' < }{\mathit{F}_{{\rm{avg}}}}. \end{array} \right. $ | (9) |
其中,Favg表示当前种群的平均适应度函数值,Fmax是种群的最大适应值,F′是进行交叉操作两个染色体中较大的适应值,0<k1,k2≤1.根据计算交叉概率的表达式可以看出交叉概率与适应值的大小有关,适应度值越大,交叉的概率就越小,这样可以将优良的基因遗传给后代.
2.4.3 变异变异一方面可以增强算法的随机搜素能力,另一方面也可以加快算法向最优解收敛的速度[4-7].对于算法的变异操作采用随机的方式,这里的随机有两个方面,一是随机产生一个变异位置,二是对于要替换的资源随机选择一个同类型的资源进行替换.不同类型资源的替换规则不同.对于维护人员,需要替换拥有任务较少的维护人员,而对于其他类型的资源,则采用随机的方式选取.例如,对于染色体111212222121212,产生一个随机数4,则变异后的染色体变为111112222121212.
采用自适应的方式表示变异概率pm,具体公式为
| $ {\mathit{p}_\mathit{m}}{\rm{= }}\left\{ \begin{array}{l} \frac{{\mathit{\theta }{\rm{(}}{\mathit{F}_{{\rm{max}}}}{\rm{ - }}{\mathit{F}_{\rm{m}}}{\rm{)}}}}{{{\mathit{F}_{{\rm{max}}}}{\rm{ - }}{\mathit{F}_{{\rm{avg}}}}}}{\rm{, }}{\mathit{F}_{{\rm{m}}}} \ge {\mathit{F}_{{\rm{avg}}}}{\rm{;}}\\ \mathit{\eta }, {\mathit{F}_{\rm{m}}}\mathit{ < }{\mathit{F}_{{\rm{avg}}}}. \end{array} \right. $ | (10) |
其中,Fm为当前选中个体的适应度值,0<θ,η≤1,根据变异概率的计算公式可知,变异概率和交叉概率都与个体的适应值有关.
3 算法求解根据遗传算法的基本流程,网络运维中现场作业调度遗传算法的求解过程如下:
(1) 根据2.2节中方法生成初始种群I(0),计算每条染色体的适应值,设定种群的进化迭代计数器i=0,I(i)是第i代种群.
(2) 设置种群迭代终止的条件.当进化代数达到预定的最大进化代数或者发现种群中个体的状态维持在标价稳定的状态时终止迭代,输出最终结果,否则继续执行.
(3) 选择操作.根据2.4.1节中选择算子选择当前种群中的个体直接复制到下一代或者继续进行交叉操作产生新的个体.
(4) 交叉操作.根据2.4.2节中交叉算子进行交叉操作产生新的个体放入下一代种群中.
(5) 变异操作.根据2.4.3节中个体进行变异操作,并将符合要求的个体放入新的种群I(i+1) 中.
(6) 更新种群进化的迭代计数器i=i+1,转到步骤(2).
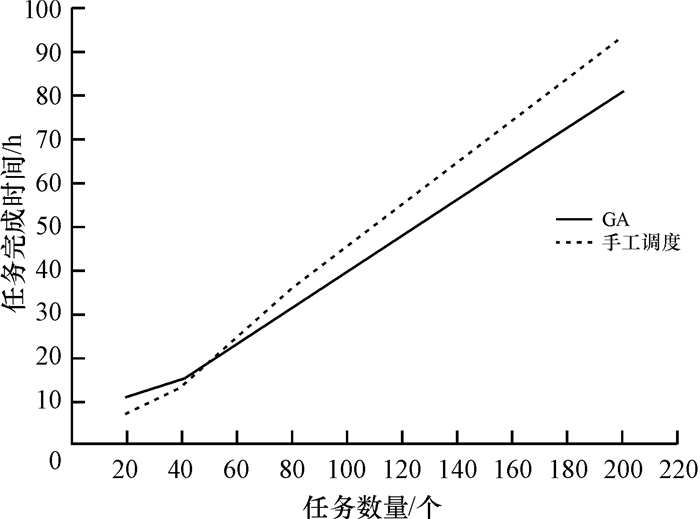
4 算法的仿真结果及分析为了验证本文中提出算法的有效性,将算法应用到实际的网络运维现场作业调度中,并与传统的手工调度进行比较,算法中的主要参数设置为:种群规模为100,算法的最大进化代数为300,交叉概率和变异概率分别设置为0.6和0.1,此外在网络运维现场作业调度中对于企业来说通常调度成本更为重要,因此将调度成本的权重系数设置得更大些,设置α1=0.6,α2=0.4.算法的终止条件:(1) 算法达到最大进化代数MaxAge,这里设置MaxAge为300;(2) 如果连续75代的任务总完成时间与任务的平均完成时间变化不大以及任务的总调度成本与任务的平均调度成本变化不大时,则任务算法已经基本收敛,算法终止.在本次仿真实验的过程中,关于任务所需资源的数量设置为:维护人员10个,车辆5个,工具数量10个.任务完成时间和调度成本对比见图 1、图 2.
|
图 1 任务完成时间对比图 Figure 1 Job completion time comparison chart |
|
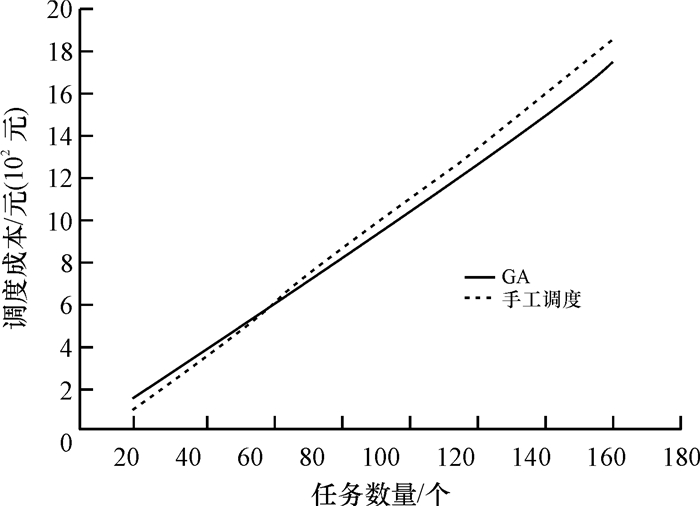
图 2 调度成本的对比 Figure 2 Comparison of scheduling cost |
从图 1和图 2可以看出,在任务数量较少时, 传统的手工调度无论是在调度成本方面还是在任务完成时间方面都是优于遗传算法.但是随着任务数量的增多,使用遗传算法来解决网络运维中现场作业资源调度问题具有明显的优势,无论在调度成本还是任务完成时间均低于使用传统手工调度.
5 总结本文提出了一种基于遗传算法的网络运维中现场作业资源调度算法,从实验结果可以看出随着作业任务数量的增多,遗传算法相对于传统的人工调度任务完成时间和调度成本都有所下降,这充分说明了使用遗传算法解决网络运维中现场作业调度是一种有效的解决方案.由于在网络运维中作业调度中所调度的资源主要是维护人员,下一步要考虑不同维护人员之间技能的差异,如何进一步降低调度成本以及缩短任务的总完成时间.
| [1] | 石红胜. 中国通信运营行业网络运维成本与内部控制问题的研究[D]. 北京: 首都经济贸易大学会计学院, 2012: 1-2. |
| [2] |
涂井先, 刘伟. 基于最速方向搜索的混合遗传算法[J].
广东工业大学学报, 2011, 28(4): 34-37.
TU J X, LIU W. A hybrid genetic algorithm based on the search algorithm of the steepest direction[J]. Journal of Guangdong University of Technology, 2011, 28(4): 34-37. |
| [3] |
汤雅连, 蔡延光, 郭帅, 等. 单车场关联物流运输调度问题的混沌遗传算法[J].
广东工业大学学报, 2013, 30(3): 53-57.
TANG Y L, CAI Y G, GUO S, et al.Single-depot incident vehicle routing problem based on chaos genetic algorithm[J]. Journal of Guangdong University of Technology, 2013, 30(3): 53-57. |
| [4] |
林剑柠, 吴慧中. 基于遗传算法的网格资源调度算法[J].
计算机研究与发展, 2004, 41(12): 2195-2199.
LIN J N, WU H Z. Scheduling in grid computing environment based on genetic algorithm[J]. Journal Computer Research and Development, 2004, 41(12): 2195-2199. |
| [5] |
杨秋辉, 游志胜, 冯子亮, 等. 一种改进的基于遗传算法的多跑道到达飞机调度[J].
四川大学学报(工程科学版), 2006, 38(2): 141-145.
YANG Q H, YOU Z S, FENG Z L, et al.Scheduling arrival aircrafts on multiple runways based on an improved generic algorithm[J]. Journal of Sichuan University(Engineering Science Edition), 2006, 38(2): 141-145. |
| [6] |
钟求喜, 谢涛, 陈火旺. 基于遗传算法的任务分配与调度[J].
计算机研究与发展, 2000, 37(10): 1197-1203.
ZHONG Q X, XIE T, CHEN H W. Task matching and scheduling by using genetic algorithms[J]. Journal Computer Research and Development, 2000, 37(10): 1197-1203. |
| [7] |
路平, 葛小伟, 郭向阳. 基于遗传算法的分组调度[J].
计算机工程与设计, 2006, 27(24): 4784-4788.
LU P, GE X W, GUO X Y. Apply GA in inputqueued switch[J]. Computer Engineering and Design, 2006, 27(24): 4784-4788. DOI: 10.3969/j.issn.1000-7024.2006.24.051. |
| [8] |
李建锋, 彭舰. 云计算环境下基于改进遗传算法的任务调度算法[J].
计算机应用, 2011, 31(1): 184-186.
LI J F, PENG J. Task scheduling algori-thm based on imporved genetic algorithm in cloud computing environment[J]. Journal of Computer Applications, 2011, 31(1): 184-186. |
| [9] | HOU E S H, ANSARI N, REN L. A genetic algorithm for multiprocessor scheduling[J]//IEEE Trans on Parallel and distributed Systems, 1994, 5(2):113-120. |
| [10] | FOO S Y, ARRADONDO M.Mobile agents for computer intrusion detection[C]//IEEE Proceedings of the 36th Southeastern Sym-posium on System Theory. Atlanta: IEEE, 2004:517-521. |
| [11] | HOLLAND J H. Adaptation in Natural and Artificial System[M]. Michigan:Annarbor:: Unversity of Michigan Press, 1975. |
| [12] | WANG L, SIEGEL H J, ROYCHOWDHURY V P, et al.Task matching and scheduling in heterogeneous computing environments using a genetic-algorithm-based approach[J]. Journal of Parallel and Distributed Computer, 1997, 47(1): 8-22. DOI: 10.1006/jpdc.1997.1392. |
| [13] | DIMARTINO V. Sub optimal scheduling in a grid using genetic alogrithms[J]. Parallel Computing, 2004, 30(5/6): 553-565. |
| [14] | HOLLAND J H. Adaptation in Natural and Arti-ficial Systems[M]. Ann Arbor: The MIT Press, 1992. |
| [15] | TU Z G, LU Y. A Robust stochastic gen-etic algorithm for global numerical optimizat-ion[J]. Evolutionary Computation, IEEE Transac-tions on, 2004, 8(5): 456-470. DOI: 10.1109/TEVC.2004.831258. |
| [16] | ZHAO C X, JI Y M. Particle swarm opti-mization for 0/1 knaps problem[J]. Microcomputer Develepment, 2005, 30(10): 23-25. |
 2016, Vol. 33
2016, Vol. 33